用动态规划模型求解最短路问题的研究
动态规划求最短路径的两种方法
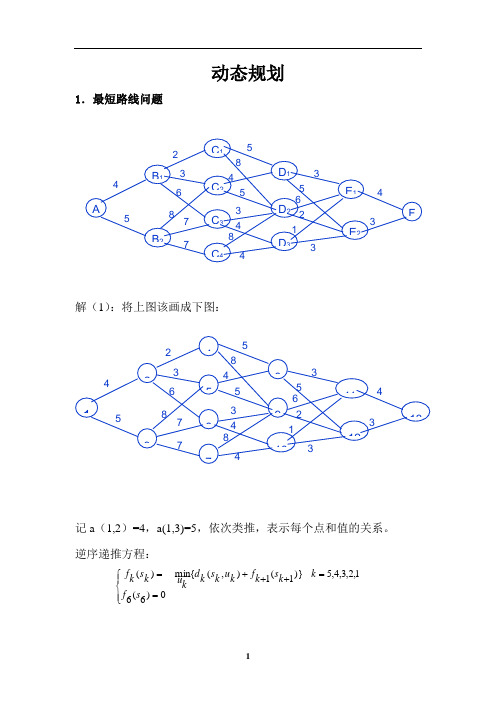
动态规划1.最短路线问题解(1):将上图该画成下图:记a (1,2)=4,a(1,3)=5,依次类推,表示每个点和值的关系。
逆序递推方程:⎪⎩⎪⎨⎧==+++=0)6(61,2,3,4,5)}1(1),({min )(s f k k s k f k u k s k d k uk s k fAB 1B 2C 1 C 2C 3 C 4D 1D 2 D 3E 1 E 2F4523 6 8 7 75845348435 6 2 314 31234 5 6 789 101112134523 6 8 7 7584534 8435 6 2 314 3如图各状态:逆序递推,找出上一个状态到下一阶段的最小路径值。
例如,当K=4时,状态 它们到F 点需经过中途 点E ,需一一分析从E 到 F 的最短路:先说从D1到F 的最短路 有两种选择:经过 E1, E2, 比较最短。
这说明由 D1 到F 的最短距离为7,其路径为AB 1B 2C 1 C 2C 3 C 4D 1 D 2 D 3E 1 E 2F4523 6 87 75845348435 62 31 4 3第1阶段 第2阶段 第3阶段 第4阶段 第5阶段状态 1状态 2状态3状态 4状态 5状态 6)}(),(),(),(m in{)(252141511414E f E D d E f E D d D f ++=.7}35,43min{=++=.11F E D →→},,{3214D D D S =a=[0,4,5,inf,inf,inf,inf,inf,inf,inf,inf,inf,inf 4,0,inf,2,3,6,inf,inf,inf,inf,inf,inf,inf 5,inf,0,inf,8,7,7,inf,inf,inf,inf,inf,inf inf,2,inf,0,inf,inf,inf,5,8,inf,inf,inf,inf inf,3,8,inf,0,inf,inf,4,5,inf,inf,inf,inf inf,6,7,inf,inf,0,inf,inf,3,4,inf,inf,inf inf,inf,7,inf,inf,inf,0,inf,8,4,inf,inf,inf inf,inf,5,4,inf,inf,inf,0,inf,inf,3,5,inf inf,inf,inf,8,5,3,8,inf,0,inf,6,2,inf inf,inf,inf,inf,inf,4,4,inf,inf,0,1,3,inf inf,inf,inf,inf,inf,inf,inf,3,6,1,0,inf,4 inf,inf,inf,inf,inf,inf,inf,5,2,3,inf,0,3 inf,inf,inf,inf,inf,inf,inf,inf,inf,inf,4,3,0]; s8=min(a(8,11)+a(11,13),a(8,12)+a(12,13)); s9=min(a(9,11)+a(11,13),a(9,12)+a(12,13)); s10=min(a(10,11)+a(11,13),a(10,12)+a(12,13)); s4=min(a(4,8)+s8,a(4,9)+s9); s5=min(a(5,8)+s8,a(5,9)+s9); s6=min(a(6,9)+s9,a(6,10)+s10); s7=min(a(7,9)+s9,a(7,10)+s10); s2=[a(2,4)+s4,a(2,5)+s5,a(2,6)+s6]; s2=min(s2);s3=[a(3,5)+s5,a(3,6)+s6,a(3,7)+s7]; s3=min(s3);s1=min(a(1,2)+s2,a(1,3)+s3)运行结果为:s8 = 7 s9 = 5 s10 = 5 s4 = 12 s5 = 10 s6 = 8 s7 = 9 s2 =13s3 = 15 s1 = 17结果分析:s 表示每个点到终点的最短距离,那么最短路程为17。
智慧树答案管理运筹学(山东联盟)知到课后答案章节测试2022年

第一章1.运筹学的主要分支包括()答案:非线性规划;整数规划;图论;线性规划;目标规划2.运筹学是应用系统的、科学的、数学分析的方法,通过建模、检验和求解数学模型而获得最优决策的科学。
答案:对3.运筹学是用数学方法研究各种系统中最优化问题的科学,它主要用数学模型来求得合理运用现有条件的最优方案,为决策者提供科学决策的依据。
答案:对4.运筹学着重以管理、经济活动方面的问题及解决这些问题的原理和方法作为研究对象。
答案:对5.制定决策是运筹学应用的核心,而()则是运筹学方法的精髓。
答案:建立模型6.运筹学可用()来进行概括。
答案:寻优科学7.运筹学的简称是()。
答案:OR8.下列哪一项不是运筹学的特点()。
答案:主观的9.下列哪一项不是运筹学的研究步骤()。
答案:实施模型10.运筹学模型是以()模型为其主要形式。
答案:数学第二章1.线性规划问题的一般模型中不能出现等式约束。
答案:错2.用图解法求最优解时,只需求出可行域顶点对应的目标值,通过比较大小,就能找出最优解。
答案:对3.线性规划模型中增加一个约束条件,可行域的范围一般将缩小,减少一个约束条件,可行域的范围一般将扩大。
答案:对4.单纯形法计算中,如不按最小比值原则选取换出变量,则在下一个解中至少有一个基变量的值为负。
答案:对5.单纯形法的迭代运算过程是从一个可行解转换到目标函数值更大的另一个可行解。
答案:错6.检验数λj表示非基变量xj增加一个单位时目标函数值的改变量。
答案:对7.利用单纯形法求解线性规划问题的过程中,所有基变量的检验数必为零。
答案:对8.若某个bk≤0, 化为标准形式时原不等式( )。
答案:两边同乘负19.将线性规划问题转化为标准形式时,下列说法不正确的是:答案:若约束条件为=,则要增加一个人工变量10.标准形式的线性规划问题,其可行解()是基本可行解,最优解一定是可行解。
答案:不一定11.关于线性规划问题的图解法,下面()的叙述正确。
运用动态规划模型解决最短路径问题

运用动态规划模型解决物流配送中的最短路径问题王嘉俊(盐城师范学院数学科学学院09(1)班)摘要:随着现代社会的高速发展,物流配送成为了连接各个生产基地的枢纽,运输的成本问题也成为了企业发展的关键。
运费不但与运量有关,而且与运输行走的线路相关。
传统的运输问题没有考虑交通网络,在已知运价的条件下仅求出最优调运方案,没有求出最优行走路径。
文中提出“网络上的物流配送问题“,在未知运价,运量确定的情况下,将运输过程在每阶段中选取最优策略,最后找到整个过程的总体最优目标,节省企业开支。
关键词:动态规划,数学模型,物流配送,最优路径1 引言物流配送是现代化物流系统的一个重要环节。
它是指按用户的订货要求, 在配送中心进行分货、配货, 并将配好的货物及时送交收货人的活动。
在物流配送业务中, 合理选择配送径路, 对加快配送速度、提高服务质量、降低配送成本及增加经济效益都有较大影响。
物流配送最短径路是指物品由供给地向需求地的移动过程中, 所经过的距离最短(或运输的时间最少, 或运输费用最低) , 因此, 选定最短径路是提高物品时空价值的重要环节。
[1]经典的Dijkstra 算法和Floyd 算法思路清楚,方法简便,但随着配送点数的增加,计算的复杂性以配送点数的平方增加,并具有一定的主观性。
我国学者用模糊偏好解试图改善经典方法[]5,取得了较好的效果。
遗憾的是,模糊偏好解本身就不完全是客观的。
文献[]6详细分析了经典方法的利弊之后,提出将邻接矩阵上三角和下三角复制从而使每条边成为双通路径,既适用于有向图也适用于无向图, 但复杂性增加了。
为了避免上述方法存在的不足,本文以动态规划为理论,选择合理的最优值函数,用于解决物流配送最短路径问题。
动态规划是解决多阶段决策过程最优化问题的一种数学方法。
1951年美国数学家Bellman(贝尔曼)等人根据一类多阶段决策问题的特性,提出了解决这类问题的“最优性原理”,并研究了许多实际问题,从而创建了最优化问题的一种新方法——动态规划。
用动态规划模型求解最短路问题的研究

当‘
,
,
“ 发 点 只有一 个
‘
,
点
则‘
,
。
,
,
。
距离为
一 至此 , 可 得最优决 策 函数序列 气 , 其 中
人
飞 万 。‘
丙
算法 , 矩 阵算法 , 动态规划方法等
枷 算法可用 于计算 网络 图中某一点到各 点的最短距
离 , 但实 际问题 中有时需要求 网络 中所 有各点 之间 的最短 距离 , 如果 仍采用
加 算法分别计 算 ,
效率很低 矩 阵算法可用于 计算所 有节点之 间的最短路 径 , 但计算 量较大 , 适 于用计算机计算 动态规
二
,
,
…,
,
式 中 为 阶段变量 为阶段数 , 。分别 为第 阶段 的状态 变量和决 策变量
动态规划可 分为正 向思维法和逆 向思 维法 , 逆 向思 维法是 指从问题 目标状 态 出发倒 推 回初始状
态或边界状 态 的思维方法 , 而 正 向思维法则正 好与之相反 在运 用求解最短路问题时 , 则有两种解法
划方法主要是研究与解决多阶段决策过程 的最优化问题 , 是求最短路 问题的好算法 , 动态规划方法是
将求解分成多 阶段进行 , 求 出的不 但是全过程 的解 , 而 且包括后部子过程 的一族解 , 在某些情况下 , 实
际问题需要族解时 , 更显其优越性
动态规划所处理的问题 是一个 多阶段 决策间题 , 一 般由初始状态开始 , 通过对中间阶段决策 的选
收稿 日期 二双刃名一 一
— 作者简介 王 百级 盯
, 女 , 白城 师范 学院毅学 系讲 师 , 研 究方 向 橄分 方 权理 论 。
用动态规划模型求解最短路问题 的研究
动态规划实现最短路径问题

动态规划实现最短路径问题⼀、设计最短路径的动态规划算法 <算法导论>中⼀般将设计动态规划算法归纳为下⾯⼏个步骤: 1)分析最优解的结构 2)递归定义最优解的值 3)⾃底向上计算最优解的值 4)从计算的最优解的值上⾯构建出最优解⼆、最短路径的结构 从最优解的结构开始分析(我们假设没有权值为负的路径),对于图G<V,E>的所有结点对最短路径的问题,我们能知道⼀条最短路径的⼦路径都是最短路径。
假设⽤邻接矩阵W=w(ij)来表⽰输⼊带权图,考虑从结点i到结点j的⼀条最短路径p,如果p最多有m(m为有限值)条边。
若i=j,则p的权值为0⽽且不包含其他边。
若i ≠ j,可以将i到j的路径转换为i -> k、k->j。
三、⼀个给定的图 1)给定⼀个有向图 2)我们可以给出这个有向图的邻接矩阵四、C++实现1 #include <iostream>2 #include<fstream>3 #include<sstream>4 #include<vector>5 #include<string>6using namespace std;7const int Max_Num = 100;89 typedef struct Point {10int n; //点的个数11double p[Max_Num];12double q[Max_Num];13int root[Max_Num][Max_Num];14double w[Max_Num][Max_Num];15double e[Max_Num][Max_Num];16 }Point;1718 vector<Point> points;19 vector<string> res;20 vector<int> num;2122void file_read();23void createPoint();24void optimalBST();25void printRoot(Point P);26void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite);27 template <class Type>28 Type stringToNum(const string& str) {29 istringstream iss(str);30 Type num;31 iss >> num;32 iss.str("");33return num;34 }3536void file_read() {37string str2, str1 = "", result;38 ifstream fileRead("in.dat");39if (fileRead.is_open()) {40while (getline(fileRead, str2, '\n')) {41if (str2.find("") != -1) {42 str1.append(str2 + "");43 }44else {45 num.push_back(stringToNum<int>(str2));46if (str1 != "") {47 res.push_back(str1);48 }49 str1 = "";50 }51 }52 res.push_back(str1);53 fileRead.close();54 }55 }5657void createPoint() {58string temp;59 Point P;60for (int i = 0; i < res.size(); i++) {61 vector<string> temp_str; //存放按照空格分开后的数字62int n = num[i];63 stringstream input(res[i]);64while (input >> temp) {65 temp_str.push_back(temp);66 }67 P.n = n;68for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);69for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]);70 points.push_back(P);71 }72 }7374//根据书上的伪代码:接收概率列表p1....pn和q0.....qn以及规模n作为输⼊计算出e和root75void optimalBST(){76 Point P;77for(int i = 0; i<res.size(); i++) {78 vector<string> temp_str; //存放按照空格分开后的数字79int n = num[i];80string temp;81 stringstream input(res[i]);82while (input >> temp) {83 temp_str.push_back(temp);84 }85 P.n = n;8687for(int k = 0; k<=n; k++) P.p[k] = stringToNum<double>(temp_str[k]);88for(int k = n + 1; k<temp_str.size(); k++) P.q[k-(n+1)] = stringToNum<double>(temp_str[k]); 8990//初始化只包括虚拟键的⼦树91for (int i = 1;i <= P.n + 1;++i){92 P.w[i][i-1] = P.q[i-1];93 P.e[i][i-1] = P.q[i-1];94 }95//由下到上,由左到右逐步计算96for (int len = 1;len <= P.n;++len){97for (int i = 1;i <= P.n - len + 1;++i){98int j = i + len - 1;99 P.e[i][j] = Max_Num;100 P.w[i][j] = P.w[i][j-1] + P.p[j] + P.q[j];101//求取最⼩代价的⼦树的根102for (int r = i;r <= j;++r)103 {104double temp = P.e[i][r-1] + P.e[r+1][j] + P.w[i][j];105if (temp < P.e[i][j])106 {107 P.e[i][j] = temp;108 P.root[i][j] = r;109 }110 }111 }112 }113 points.push_back(P);114 }115 }116117void printOptimalBST(int i, int j, int r, Point P, ofstream &fileWrite){118int root_node = P.root[i][j];//⼦树根节点119if (root_node == P.root[1][P.n]){120//输出整棵树的根121 fileWrite << "k" << root_node << "是根" << endl;122 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);123 printOptimalBST(root_node +1 , j, root_node, P, fileWrite);124return;125 }126127if (j < i - 1){128return;129 }else if (j == i - 1){//遇到虚拟键130if (j < r)131 fileWrite << "d" << j << "是" << "k" << r << "的左孩⼦" << endl;132else133 fileWrite << "d" << j << "是" << "k" << r << "的右孩⼦" << endl;134return;135 }136else{//遇到内部结点137if (root_node < r)138 fileWrite << "k" << root_node << "是" << "k" << r << "的左孩⼦" << endl; 139else140 fileWrite << "k" << root_node << "是" << "k" << r << "的右孩⼦" << endl; 141 }142 printOptimalBST(i, root_node - 1, root_node, P, fileWrite);143 printOptimalBST(root_node + 1, j, root_node, P, fileWrite);144 }145146//输出最优⼆叉查找树所有⼦树的根147void printRoot(Point P){148 cout << "各⼦树的根:" << endl;149for (int i = 1;i <= P.n;++i){150for (int j = 1;j <= P.n;++j){151 cout << P.root[i][j] << "";152 }153 cout << endl;154 }155 cout << endl;156 }157158int main(){159 file_read();160 optimalBST();161 ofstream fileWrite("out.dat");162 Point P ;163for(int i = 0; i<points.size(); i++) {164 P = points[i];165 printRoot(P);166 printOptimalBST(1,P.n,-1, P, fileWrite);167 }168 fileWrite.clear();169return0;170 } 上述代码是将给定的邻接矩阵从⽂件中读取 然后根据输⼊的邻接矩阵求出最短路径。
matlab floyd最短路算法例题

matlab floyd最短路算法例题摘要:一、Floyd 算法介绍二、MATLAB 实现Floyd 最短路算法的例题三、Floyd 算法的应用案例四、总结正文:一、Floyd 算法介绍Floyd 算法是一种经典的动态规划算法,用于求解加权连通图(有向图、无向图)中所有顶点之间最短路的长度。
该算法可以处理带有负权边的图,并且时间复杂度为O(n3)。
Floyd 算法的基本思想是:从任意节点i 到任意节点j 的最短路径不外乎2 种可能,1 是直接从i 到j,2 是从i 经过若干个节点k 到j。
所以,我们假设Dis(i,j) 为节点u 到节点v 的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) Dis(k,j) < Dis(i,j) 是否成立,如果成立,证明从i 到k 再到j 的路径比i 直接到j 的路径短,我们便设置Dis(i,j) Dis(i,k) Dis(k,j)。
二、MATLAB 实现Floyd 最短路算法的例题以下是一个使用MATLAB 实现Floyd 算法的例题:```MATLABfunction [T,pred] = floyd(adj_matrix)% 输入:邻接矩阵% 输出:最短路径矩阵,预测矩阵= size(adj_matrix, 1);T = zeros(n, n);pred = zeros(n, n);for i = 1:nfor j = 1:nfor k = 1:nif i ~= k && i ~= j && k ~= jT(i, j) = min(T(i, j), T(i, k) + T(k, j));pred(i, j) = T(i, k) + T(k, j);endendendendend```三、Floyd 算法的应用案例Floyd 算法在网络分析、社交网络、生物信息学等领域具有广泛的应用。
例如,在网络分析中,Floyd 算法可以用于寻找网络中的最短路径,以便快速传递信息或货物。
基于LINGO软件的最短路线问题研究
2020·4(下)145信息科技探索作者简介:丁正阳,深圳市福田区红岭中学。
基于LINGO软件的最短路线问题研究丁正阳摘 要 文章介绍了解决LINGO 软件最短路线问题的数学模型和两种方法:动态规划法和0-1整数规划法。
接着利用一个实际问题,用两种方法和LINGO 软件解决问题,论证了模型和方法的实用性和有效性。
关键词 LINGO ;动态规划法;0-1整数规划法;最短路径中图分类号 TP3 文献标识码 A 文章编号 1674-6708(2020)257-0145-03目前,科技的发展越来越快,计算机和信息技术得到越来越广泛的发展。
既然要发展,我们就要选择最优的方案,换句话说,也就是消耗资源最小的方案。
这也是为了实现资源优化配置的一个主要途径。
因此最短路线问题就显得尤为重要,它在交通运输、网络通讯、资源配置等方面有着极为广泛的应用。
前人也对这个问题做了大量的研究。
参考文献[1]对任意城市间的最短路径问题进行了研究,简单介绍了Dijkstra 算法和Floyd 算法,并且用用MATLAB 软件编写了一段简单的程序Floyd 算法进行了进一步的验证,证明了方法的正确性。
参考文献[2]对动态规划的基本原理进行了介绍,并将动态规划成功运用到了运输问题的最短路径当中,结合实例对该方法进行了说明,并且阐述了动态规划整体最优思想和其在求解最短路径问题中的独特优越性。
参考文献[3]对大城市的公共交通网络进行了分析,利用图论方法对观光旅游的乘车路径问题进行了设计规划,最后得到的结果能够进行进一步推广应用。
LINGO 软件具有十分强大的功能,可以通过内部已有的函数对0-1整数规划问题进行求解,软件求解精度高,速度快,并且小巧方便。
1 建模1.1 数学模型最短路径问题旨在寻找图中节点与节点之间的最短路径,可以广泛应用到人工智能,神经网络,通信和计算机等学科当中,实际生活中的道路建设,电网铺设,路线规划等等问题也可以用最短路径问题进行描述。
动态规划在最短路径问题中的应用
动态规划在最短路径问题中的应用动态规划是一种解决复杂问题的方法,它将问题分解成更小的子问题,并通过保存子问题的解来避免重复计算,从而提高解决问题的效率。
最短路径问题是在图或者网络中找到从起点到终点的最短路径的问题,可以使用动态规划算法来解决。
本文将介绍动态规划在最短路径问题中的应用及其算法实现。
一、最短路径问题在最短路径问题中,我们需要在图或网络中找到从一个节点到另一个节点的最短路径。
最短路径可以通过边的权重来衡量,权重可以表示距离、时间、代价等。
最短路径问题有多种变体,其中最常见的是单源最短路径和全源最短路径。
单源最短路径问题是在给定一个起点的情况下,找到该起点到其他所有节点的最短路径。
最常用的算法是Dijkstra算法和Bellman-Ford算法。
二、动态规划原理动态规划通过保存子问题的解来避免重复计算,从而提高算法的效率。
它将问题分解成更小的子问题,并使用递推关系来计算子问题的解。
在最短路径问题中,我们可以使用动态规划来计算从起点到每个节点的最短路径。
首先,我们定义一个一维数组dist[]来保存从起点到每个节点的最短路径长度。
初始化时,dist[]的值为无穷大,表示路径长度未知。
然后,我们从起点开始逐步计算每个节点的最短路径长度。
具体的动态规划算法如下:1. 初始化dist[]为无穷大,起点的dist[]为0。
2. 对于每个节点v,按照拓扑顺序进行如下操作:2.1. 对于节点v的所有邻接节点u,如果dist[v] + weight(v, u) < dist[u],则更新dist[u]。
2.2. 拓扑顺序可以根据节点的拓扑顺序进行计算或者使用深度优先搜索(DFS)算法。
三、算法实现下面是使用动态规划算法解决最短路径问题的示例代码:```// 定义图的邻接矩阵和节点个数int graph[MAX][MAX];int numNodes;// 定义dist[]数组来保存最短路径长度int dist[MAX];// 定义拓扑排序和DFS算法需要的变量bool visited[MAX];stack<int> s;// 动态规划算法求解最短路径void shortestPath(int startNode) {// 初始化dist[]数组为无穷大for (int i = 0; i < numNodes; i++) {dist[i] = INT_MAX;}dist[startNode] = 0;// 拓扑排序或DFS计算每个节点的最短路径长度 for (int i = 0; i < numNodes; i++) {if (!visited[i]) {DFS(i);}}// 输出最短路径长度for (int i = 0; i < numNodes; i++) {cout << "Node " << i << ": " << dist[i] << endl; }}// 深度优先搜索void DFS(int node) {visited[node] = true;for (int i = 0; i < numNodes; i++) {if (graph[node][i] != 0 && !visited[i]) {DFS(i);}}s.push(node);}```以上示例代码演示了使用动态规划算法求解最短路径问题的基本原理和步骤。
最短路径问题的动态规划算法
最短路径问题的动态规划算法动态规划是一种解决复杂问题的有效算法。
最短路径问题是指在给定的图中找到从起点到终点路径中距离最短的路径。
本文将介绍动态规划算法在解决最短路径问题中的应用。
1. 最短路径问题简介最短路径问题是图论中的经典问题之一,旨在找到从图中一点到另一点的最短路径。
通常使用距离或权重来衡量路径的长度。
最短路径问题有多种算法可以解决,其中动态规划算法是一种常用且高效的方法。
2. 动态规划算法原理动态规划算法的核心思想是将原问题分解为更小的子问题,并存储已解决子问题的结果,以供后续使用。
通过逐步解决子问题,最终得到原问题的解。
在最短路径问题中,动态规划算法将路径分解为多个子路径,并计算每个子路径的最短距离。
3. 动态规划算法步骤(1)定义状态:将问题转化为一个状态集合,每个状态表示一个子问题。
(2)确定状态转移方程:通过递推或计算得到子问题之间的关系,得到状态转移方程。
(3)确定初始状态:设置与最小子问题相关的初始状态。
(4)递推求解:根据状态转移方程,逐步计算中间状态,直到得到最终解。
(5)回溯路径:根据存储的中间状态,找到最短路径。
4. 动态规划算法示例以经典的Dijkstra算法为例,演示动态规划算法在解决最短路径问题中的应用。
假设有带权重的有向图G,其中节点数为n,边数为m。
算法步骤如下:(1)定义状态:对于图G中的每个节点v,定义状态d[v]代表从起点到节点v的最短距离。
(2)确定状态转移方程:d[v] = min(d[u]+w[u,v]),其中u为节点v 的直接前驱节点,w[u,v]为边(u,v)的权重。
(3)确定初始状态:设置起点s的最短距离d[s]为0,其他节点的最短距离d[v]为无穷大。
(4)递推求解:根据状态转移方程逐步计算中间状态d[v],更新最短距离。
(5)回溯路径:根据存储的前驱节点,从终点t开始回溯,得到最短路径。
5. 动态规划算法的优缺点优点:(1)求解速度快,适用于大规模问题。
运筹学
23
动态规划 Dynamic Programming(DP)
5、状态转移方程(equation of state transition) 在确定型多阶段决策过程中,一旦某阶段的状态和决策为 已知,下一阶段的状态便完全确定,用状态转移方程反映这种 状态间的演变规律,写作: sk+1 = Tk(sk,uk) k =1,2,…,n 6、阶段指标值(objective value in a stage) 衡量在一个阶段某个状态下各决策所对应的某种数量指标 或效果,即每阶段选定决策xk后所产生的效益,记vk(sk, uk)。
此时加圈 0 元素的个数 m = 5, 而 n = 5,独立零元素(加圈零元素)等于 n 个,此时已得到最优解,其解矩
阵为
21
动态规划 Dynamic Programming(DP)
基本概念: 1、阶段(stage) 对整个决策过程的自然划分,通常根据时间顺序或空间特 征来划分阶段,以便按阶段的次序逐段解决整个过程的优化问 题。阶段变量通常用k表示(k = 1,2,3,…,n)。 2、状态(state) 每个阶段开始时过程所处的自然状况或客观条件。它应能 描述过程的特征并具有“无后效性”,即当前阶段状态给定时, 这个阶段以后过程的演变与该阶段以前各阶段的状态无关。 状态变量 —— sk(state variable) 状态集合 —— Sk(set of admissible states)
9
整数规划 Integer Programming(IP)
建立模型 引入 0-1 变量 xi = 1 当 Ai 点被选用 0 当 Ai 没点被选用 (i=1,2,…,7)
max z = ∑cixi ∑bixi ≤ B x1 + x2 + x3 x4 + x5 xi = 0,或1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,
,
,
,
关幼 词 动态 规划 最短 路 径 中圈分类 号
、
口刊宕口 程 序
文 献 标识 码
,
文 章绷 号
一
加
,
肠切
供
,
丙
,
在交通运输 道路铺设 等实 际工作 中 最短 路问题应 用得非 常广泛 求最短 路 的算 法有多 种 如 算法 可 用 于 计算 网络 图中某 一 点到各 点的最短距 算法 矩 阵算法 动态规划方法 等
第
卷第 期 乞刃吕年 月
白城 师 范
例回 间 试
越 卜
学 院 学报
司
公 刀 】 即
,
,
,
场
伽旧
伪也 ,
用 动 态 规 划 模 型 求解 最 短 路 问题 的研 究
王 丽颖
白城师范学院 数学系 吉林 白城
,
砚】 】
摘 要 动态 规划 法是求解具有多阶段 的最 短路径 的算 法 本 文 以 动态规划理 论为指 导 研 究 了铺 设 管道 最短路 问题 实 例 采用 顺 序递推 法和逆 序递推 法 两 种解决方 法 并 用
点 峨
,
,
从‘ 到 且
,
点可 以 通过
汽
点“ 几 ,
人 人 凡 关
二
。 ‘
‘
,
峨 凡 几 人
,
,
几
几
,
同理 到 几 点必须 通 过 两点 且 到
汽
凡关 几
‘
几
‘
人 凡 几
,
人 凡
,
立卜
,
,
几 凡 只过 点 点关 时 从 人
,
人 凡 到 ‘ 点
,
,
且
叭
当
才
澎复 粼
内
,
}
‘
卜
, ’巧 ‘ ”
,
二 ’
从
到
,
同理 若从 凡 出发 则 其最短 路线为 凡
线为 凡 当
一
二
凡
, ,
一
二
‘
,
,
且
二
、
凡
,
二
。
一
,
凡
一
。
‘
,
凡 从 凡 出发 则 其最短 路
无
时 同理可 推
‘
,
,
当‘
。
,
“ 发 点 只 有一 个
,
点 则‘
人 人 凡
,
飞
凡
,
。 ‘
万
‘
,
’
二
,
至此
求得 图的最短路 线为
,
距离为
、
二
,
一
,
一
凡
再按计算的顺 序反推之 可 得最优 决策 函数序列 几
, ,
个 选 择 一是 到
,
, ,
,
,
一是 到
,
,
同时又 是 第
、
阶段的始 点 依此类推
,
二 模型建 立与求解 方法 一 顺序递 推法 根 据动态规划 的正向思维法 从 当 时 考虑 第一个 阶段 从
, ,
点 开始 计算逐 步 移至 时 最 短 路径 到
, ,
‘点
人
二
,
,
当
且
、
时 从
,
到
只有通过 点和
收稿 日期
二
,
地点铺设一条管道到 ‘ 点 中间经过如下五个 中间站 两地 之间距离用数字表出 要 点 到 ‘ 点 的铺设路线 使总距离最 短
,
,
,
,
,
双刃名一
一
作 者简介 王 百 级
盯
—
女 白 城 师范 学院 毅学 系 师 研 究方 向 橄分 方 权理 论 讲
,
,
。
用动态规划模型 求解最短路问题 的研究
, ,
一
一
凡
一
一
相应 的最短 距离为
点
,
依据动态规划 的基 本
方程 当
凡
二
二
心 凡 时 若从
,
,
再 出发 则有
, ,
二
,
人 凡
,
二
,
个选择 一是 至 ‘
一 是至 凡 则
,
,
“ ’
,
。 ‘
凡 凡
凡 凡
儿 凡 几 凡
,
卜
这说明 由 凡
,
至终 点 ‘ 的最距 离 为
,
其最 短 路 线 是
一
且 凡
一
‘
,
而 相应 的决策 变 量
图 一 问厄 的分 析 图 点为 第
、
具有标准模型特点的管道 网络
,
可视为一 定 阶段最短 路 问题的标 准模 型 图 阶段 这 时有
,
可 划分为
,
个 阶段 即
, ,
,
二
从
,
点 出发到
,
,
就 是第 阶段决 策 的结果 若选 择 到 则 它 既是这一 阶段路线 的终点 又是下一个 阶段 路线 的始点 在 第 阶段 再从 出发 对 于 点 有一 个 可 供选择 的终点 集合 若选择 由 至 为第 阶段的 决策 则 就是第 阶段 的终点
点关
,
内
二
二
几
从
到
点关
叫之 爱 段
。 ‘
卜 罗
‘, 一 ‘”】 ’
,
几
二
白坡师范学院学报
第欢 卷 第 期
当
二
,
二
,
时 同理 可推 点到
, ,
,
当 盖二
时 从
二
点
,
““,
。 ‘
凡
凡
二
‘
内 凡 求得图 的最短 路线为
,
人
心 黔 ,
一 一
,
“ ,
二
凡
‘
,
方法二 逆序递推法 按照动态规划的方法 将 图 从最后一段开 始计 算 由后 向前逐 步推移至 至 ‘ 的最 短距 离 距 离 氏 凡 当 几 二 时关 表示 在第 段
, ,
离 但实 际问题 中有时需要求 网络 中所 有 各点 之间 的最短 距离 如果 仍采用 加 算法分别 计 算 效率很低 矩 阵算法可用 于 计算所 有节点之 间的最 短路 径 但计算 量较大 适 于用 计算机 计算 动态规
, ,
枷
,
,
划方法主要是研究与解 决多阶段决策过程 的最优化问题 是 求最短路 问题的好算法 动态规划 方法是 将求解分成多 阶段进行 求 出的不 但是全过程 的解 而 且包括后 部子过程 的一族解 在某些 情况下 实
, , , ,
,
,
际问题需要 族解时 更显 其优越性
,
动态规划所处理的问题 是一个 多阶段 决策间题 一 般由初始状态开始 通过对中间阶段 决策 的选 择 达到结束状态 这 些决 策形成 了一个决 策序列 同时确 定 了完 成整个 过程的一条 活动 路线 通常 是 求最优 的活动 路线 如 图所示 动态规划 的设 计都有着一定 的模式 一般 要 经历 以下 几不步骤
, , , , , ,
,
,
初 始状态
一
,
用 于 衡 量 所选决 策优 劣的 数量指标 称为指标 函数 人 为最优 指标 函数 最 短 路线 问题 中的 最优指标 函数是最短距离 叭 为 无 阶段的距离 在每一 阶段 的决策中有一个赖 以决策 的 策略或 目标
, ,
画
,
一
画
,
一
,
一画
‘
一
结束
,
、
这种策略或 目标是 由问题 的性 质和 特 点所 确定 通 常以 函数 的形式表 示 并具有递 推关系 称 为动态规 划 函数 动态 规划 的基本方程 为
,
,
娇
式中
凡
二
, ,
,
。
乓
人
气 乓
,
二
,
,
…
,
,
。
为 阶段变 量 为阶段 数 分别 为第 阶段 的状态 变 量 和决 策变 量 动态规划可 分为正 向思维法和逆 向思维法 逆 向思 维法是 指 从问 题 目标状 态 出发倒 推 回初始状
, , , , ,
。
态或边界状 态 的思维方法 而正 向思维法则 正 好与 之相反 在运 用求解最 短 路问题时 则有两种解法 从前 向后 求解 的顺 序递 推法 和从后 向前求解的逆序递推法 由于 最短 路相同 所 以 两种解法 的结果是 唯 一 确定的 下 面我 们研究一个具 体实例 如下 图 从 求选择一条 由
