2009江苏高考数学科考试说明及典型题示例(完美word版).doc
江苏高考数学科考试申明及典型题示例word版

第 1 页 共 21 页
部分作答;选修测试物理的考生需对试题中必做题和附加题这两部分作答.必
做题பைடு நூலகம்分考
查的内容是高中必修内容和选修系列 1 的内容;附加题部分考查的内容是选修
系列 2(不
含选修系列 1)中的内容以及选修系列 4 中专题 4-1《几何证明选讲》、4-
2《矩阵与变换》、
4-4《坐标系与参数方程》、4-5《不等式选讲》这 4 个专题的内容(考生只需
选考其中两
个专题).对知识的考查要求依次分为了解、理解、掌握三个层次(在下表中
分别用 A、B、
C 表示).
了解:要求对所列知识的含义有最基本的认识,并能解决相关的简单问题.
理解:要求对所列知识有较深刻的认识,并能解决有一定综合性的问题.
平面向量的数量积
平面向量的平行与垂直
平面向量的应用
数列的概念
等差数列
等比数列
基本不等式
一元二次不等式
线性规划
复数的概念
复数的四则运算
复数的几何意义
导数的概念
导数的几何意义
导数的运算
利用导数研究函数的单调性与极值 √
导数在实际问题中的应用
算法的含义
第 3 页 共 21 页
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2009年江苏省高考数学试卷及详解

2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据12,,n x x x L 的方差()2211n i i s x x n ==-∑,其中11n i i x x n ==∑. 一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1.若复数i z i z 96,29421+=+=其中i 是虚数单位,则复数i z z )(21-的实部为 .2.已知向量a 和向量b 的夹角为30o,3||,2||==b a ,则向量a 和向量b 的数量积b a ⋅= .3.函数63315)(23+--=x x x x f 的单调减区间为 .4.函数)sin(ϕω+=x A y (ϕω,,A 为常数,0,0>>ωA )在闭区间[]0,π-上的图象如图所示,则ω= .5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 .6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:学生1号 2号 3号 4号 5号 甲班6 7 7 8 7 乙班 6 76 7 9 则以上两组数据的方差中较小的一个为2s = .7.右图是一个算法的流程图,最后输出的=W .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 .9.在平面直角坐标系xoy 中,点P 在曲线310:3+-=x x y C 上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为 .10.已知215-=a ,函数x a x f =)(,若实数m 、n 满足)()(n f m f <,则m 、n 的大小关系为 .11.已知集合{}),(,2log |2a B x x A -∞=≤=,若B A ⊆则实数a 的取值范围是),(+∞c ,其中c =12.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直;(4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直.上面命题中,真命题的序号 (写出所有真命题的序号)13.如图,在平面直角坐标系xoy 中,2121,,,B B A A 为椭圆)0(12222>>=+b a by a x 的四个顶点,F 为其右焦点,直线21B A 与直线F B 1相交于点T ,线段OT 与椭圆的交点M 恰为线段OT 的中点,则该椭圆的离心率为 ▲ .14.设{}n a 是公比为q 的等比数列,1>q ,令),2,(1⋅⋅⋅=+=n a b n n ,若数列{}n b 有连续四项在集合{}82,37,19,23,53--中,则q 6= .二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15.(本小题满分14分)设向量)sin 4,(cos ),cos 4,(sin ),sin ,cos 4(β-β=ββ=αα=c b a (1)若a 与c b 2-垂直,求)tan(β+α的值;(2)求c b +的最大值;(3)若16tan tan =βα,求证:a ∥b16.(本小题满分14分)如图,在直三棱柱111C B A ABC -中,E 、F 分别是B A 1、C A 1的中点,点D 在11C B 上,C B D A 11⊥.求证:(1)EF ∥平面ABC ;(2)平面FD A 1⊥平面C C BB 11..17.(本小题满分14分)设{}n a 是公差不为零的等差数列,n S 为其前n 项和,满足7,725242322=+=+S a a a a .(1)求数列{}n a 的通项公式及前n 项和n S ;(2)试求所有的正整数m ,使得21++m m m a a a 为数列{}n a 中的项.18.(本小题满分16分)在平面直角坐标系xoy 中,已知圆4)1()3(:221=-++y x C 和圆4)5()4(:222=-+-y x C .(1)若直线l 过点)0,4(A ,且被圆1C 截得的弦长为32,求直线l 的方程; (2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂直的直线1l 和2l ,它们分别与圆1C 和圆2C 相交,且直线1l 被圆1C 截得的弦长与直线2l 被圆2C 截得的弦长相等,试求所有满足条件的点P 的坐标.19.(本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a 元,如果他卖出该产品的单价为m 元,则他的满意度为am m +;如果他买进该产品的单价为n 元,则他的满意度为a n n +.如果一个人对两种交易(卖出或买进)的满意度分别为1h 和2h ,则他对这两种交易的综合满意度为21h h .现假设甲生产A 、B 两种产品的单件成本分别为12元和5元,乙生产A 、B 两种产品的单件成本分别为3元和20元,设产品A 、B 的单价分别为A m 元和B m 元,甲买进A 与卖出B 的综合满意度为甲h ,乙卖出A 与买进B 的综合满意度为乙h(1)求甲h 和乙h 关于A m 、B m 的表达式;当B A m m 53=时,求证:甲h =乙h ; (2)设B A m m 53=,当A m 、B m 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为0h ,试问能否适当选取A m 、B m 的值,使得0h h ≥甲和0h h ≥乙同时成立,但等号不同时成立?试说明理由.20.(本小题满分16分)设a 为实数,函数a x a x x x f --+=)(2)(2.(1)若1)0(≥f ,求a 的取值范围;(2)求)(x f 的最小值;(3)设函数),(),()(+∞∈=a x x f x h ,直接写出(不需给出演算步骤)不等式1)(≥x h 的解集.数学Ⅱ 参考公式:2222(1)(21)123.6n n n n ++++++=L 21.[选做题]在A 、B 、C 、D 四小题中只能选做两题......,每小题10分,共计20分.请在答.题卡指定区域......内作答,解答时应写出文字说明、证明过程或演算步骤. A .选修4 - 1:几何证明选讲如图,在四边形ABCD 中,△ABC ≌△BAD .求证:AB ∥CD .B . 选修4 - 2:矩阵与变换,求矩阵3221A ⎡⎤=⎢⎥⎣⎦的逆矩阵. C . 选修4 - 4:坐标系与参数方程 已知曲线C 的参数方程为,13()x t t y t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数,0t >).求曲线C 的普通方程. D . 选修4 - 5:不等式选讲 :设a ≥b >0,求证:3332a b +≥2232a b ab +.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本题满分10分)在平面直角坐标系xoy 中,抛物线C 的顶点在原点,经过点A (2,2),其焦点F 在x 轴上.(1)求抛物线C 的标准方程;(2)求过点F ,且与直线OA 垂直的直线的方程;(3)设过点(,0)(0)M m m >的直线交抛物线C 于D 、E 两点,ME=2DM ,记D 和E 两点间的距离为()f m ,求()f m 关于m 的表达式.23.(本题满分10分)对于正整数n ≥2,用n T 表示关于x 的一元二次方程220x ax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈L (a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈L (a 和b 可以相等),记n P 为关于x 的一元二次方程022=++b ax x有实数根的概率.(1)求2n T 和2n P ;(2)求证:对任意正整数n ≥2,有n P n 11->.2009年普通高等学校招生全国统一考试(江苏卷)答案及解读数学Ⅰ一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1. -20【解析】 本题考查了复数的基本运算,属基础概念题.由i z i z 96,29421+=+=, 可得i i i i z z 220)202()(21--=+-=-, 则复数i z z )(21-的实部为-20.2. 3【解析】 本题考查了复数的数量积公式及其简单应用.由向量a 和向量b 的夹角为ο30, 3||,2||==b a ,可得330cos 32=⨯⨯=⋅οb a .3.)11,1(-【解析】 本题考查了导数法求函数的单调区间问题. 由63315)(23+--=x x x x f ,可得)1110(333303)(22--=--='x x x x x f , 令0)(<'x f 可解得111<<-x ,∴函数63315)(23+--=x x x x f 的单调减区间为)11,1(-.4. 3【解析】 本题考查了由三角函数图象求三角函数解析式问题.由图象可得该函数的周期为ωπ=π=232T , ∴3=ω. 5.51【解析】 本题考查了古典概型问题,从2.5,2.6,2.7,2.8,2.9,这五个数据中任意抽取2个有2.5 , 2.6; 2.5 , 2.7; 2.5 , 2.8; 2.5 , 2.9; 2.6 , 2.7; 2.6 , 2.8;2.6 , 2.9; 2.7 , 2.8; 2.7 , 2.9; 2.8 , 2.9,共10种抽取方法, 其中长度恰好相差0.3m 仅2.5 , 2.8; 2.6 , 2.9两组, 即得2,10==m n , ∴它们的长度恰好相差0.3m 的概率为51102===n m P . 6.52【解析】 本题考查了统计初步中样本数据的方差的求解问题,属简单的公式应用问题.同时也考查了学生的估算能力.由图表可得7)78776(51=++++=甲x , 7)97676(51=++++=乙x , ∴52)01001(512=++++=甲S , 56)40101(512=++++=乙S ,22乙甲S S < , ∴两组数据的方差中较小的一个为522=S .本题也可由表格估算出22乙甲S S <,因此,不必计算2乙S 7. 22【解析】 本题考查了算法的流程图,以循环结构为主要考查对象,是近几年高考中常见的命题方式.由流程图可得, 第一次循环时得到的S 与T 的值分别为1-0=1,1; 第二次循环时得到的S 与T 的值分别为9-1=8,3; 第三次循环时得到的S 与T 的值分别为25-8=17,5, 此时退出循环结构得22517=+=W .8. 1:8【解析】 本题考查了推理与证明中合情推理之中类比推理的应用.由于相似的几何图形中面积比是边长的平方比, 类比的相似的几何体的体积比是棱长的立方比, 即若两个正四面体的棱长的比为1:2,则它们的体积比为1:8.9. (-2, 15)【解析】 本题考查了导数的几何意义, 曲线方程对应的函数的导数的几何意义是曲线上某点的切线的斜率.由21032=-='x y 可解得2±=x , ∵切点P 在第二象限内,∴2-=x , 由此可得点P 的坐标为(-2, 15).10. n m <【解析】 本题考查了指数函数及指数函数的单调性的应用.∵)1,0(215∈-=a , ∴函数x a x f =)(为R 上的减函数,又∵)()(n f m f >, ∴n m <.11. 4【解析】 本题考查了对数不等式及集合的子集运算,此题中要注意对数函数的定义域及集合边界值的验证.由已知条件可得{}(]4,02log |2=≤=x x A ,),(a B -∞=,若B A ⊆则4>a ,即得4=c .12. (1)(2)【解析】 本题考查了平面与平面、直线与平面的平行与垂直的位置关系,是高考中常见的开放题型之一. 若α内的两条相交直线分别平行于β内的两条直线,则α平行于β,这是两个平面平行的判定定理,即(1)正确;若α外一条直线l 与α内的一条直线平行,则l 和α平行,这是直线与平面平行的判定定理,即(2)正确;设α和β相交于直线l ,α内有一条直线垂直于l ,但该直线不一定能够垂直β内两条相交直线,即直线l 不一定垂直于平面β,所以平面α和β不一定垂直,即(3)不正确; 直线l 与α垂直的充分必要条件是l 与α内的两条相交直线垂直,即(4)不正确, 综上可得真命题的序号为(1)(2).13.572-【解析】 本题考查了直线方程,两直线的交点及椭圆的几何意义,离心率 的考查是高考客观题考查的热点.由已知条件可得直线21B A 的方程为1=-+-bx a x ①, 直线F B 1的方程为1=-+b y c x ②,联立①②可得两直线交点T 的坐标为(c a ac -2,c a c a b -+)(),则线段OT 的中点M 的坐标为(ca ac -,)(2)(c a c ab -+),代入椭圆12222=+b y a x 可得222)(4)(4c a c a c -=++,即得03102=-+e e ,解之得725±-=e ,∵)1,0(∈e , ∴572-=e .【别解】设)sin ,cos (θθb a M ,则)sin 2,cos 2(θθb a T ,由T B A 21共线得a b a a b =+θθcos 2sin 2化简得1cos 2sin 2+θ=θ ① 由FT B 1共线得cb a b b =θ+θcos 2sin 2化简得θ=+θcos 2)1sin 2(e ② 由①②解得⎪⎪⎩⎪⎪⎨⎧-+=θ-=θ)1(21sin 1cos e ee e 代入1sin cos 22=θ+θ得03102=-+e e ,解得725+-=e .14. -9【解析】 本题考查了等比数列的通项与基本量的求解问题,此题利用等比数列构造另一个数列,利用所构造数列的性质去研究等比数列是高考的热点问题.由已知数列{}n b 有连续四项在集合{}82,37,19,23,53--中,则数列{}n a 必有连续四项在集合{}81,36,18,24,54--中, 若公比q 为正则该数列的四项必均为正或均为负值, 显然不合题意, 所以公比q 必为负值,又由1>q 知1-<q ,按此要求在集合{}81,36,18,24,54--中取四个数排成数列可得数列81,54,36,24--或54,36,24,18-- (此数列不成等比数列,故舍去), ∵数列81,54,36,24--的公比23-=q , ∴96-=q . 二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.[15题解析] 本小题主要考查向量的基本概念、数乘、数量积,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明等基本能力.满分14分.(Ⅰ)由a 与c b 2-垂直,02)2(=⋅-⋅=-⋅c a b a c b a ,即0)cos(8)sin(4=β+α-β+α,2)tan(=β+α.(Ⅱ))sin 4cos 4,cos (sin β-ββ+β=+c b ,β+ββ-β+β+ββ+β=+22222sin 16sin cos 32cos 16cos cos sin 2sin c b β-=ββ-=2sin 1517cos sin 3017,最大值为32, 所以c b +的最大值为24.由16tan tan =βα得βα=βαcos cos 16sin sin ,即0sin sin cos 4cos 4=βα-β⋅α,所以a ∥b . [16题解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力、推理论证能力.满分14分.(Ⅰ)因为E ,F 分别是C A B A 11,的中点,所以EF ∥BC ,又ABC EF 面⊄,ABC BC 面⊂,所以EF ∥平面ABC .(Ⅱ)因为直三棱柱111C B A ABC -,所以1111C B A BB 面⊥,D A BB 11⊥,又C B D A 11⊥,所以C C BB D A 111面⊥,又FD A D A 11面⊂,所以平面⊥FD A 1平面C C BB 11.[17题解析] 本小题主要考查等差数列的通项、求和的有关知识,考查运算和求解的能力.满分14分.(1)设公差为d ,则23242522a a a a -=-,由性质得)()(33434a a d a a d +=+-,因为0≠d ,所以034=+a a ,即0521=+d a ,又由77=S 得726771=⨯+d a ,解得51-=a ,2=d ,所以{}n a 的通项公式为72-=n a n ,前n 项和n n S n 62-=.(2)(方法一)32)52)(72(21---=++m m m a a a m m m ,设t m =-32, 则68)2)(4(21-+=--=++tt t t t a a a m m m , 所以t 为8的约数 因为t 是奇数,所以t 可取的值为1±当2,1-==m t 时,3752,368=-⨯=-+t t ,是数列{}n a 中的项; 当1,1=-=m t 时,,1568-=-+tt 数列{}n a 中的最小项是5-,不符合. 所以满足条件的正整数2=m (方法二)因为222222186)2)(4(++++++++-=--=m m m m m m m m a a a a a a a a 为数列{}n a 中的项, 故28+m a 为整数,又由(1)知:2+m a 为奇数,所以1322±=-=+m a m ,即2,1=m经检验,符合题意的正整数只有2=m这两种解法看似相同,但却有本质的区别,解法二是紧扣数列通项公式解题,而解法一是紧扣等差数列的概念解题,学生掌握的基本思路是解法二,本题是中极题.[18题解析] 本小题主要考查直线与圆的方程、点到直线的距离公式,考查数学运算求解能力、综合分析问题的能力.满分16分.(1)设直线l 的方程为:)4(-=x k y ,即04=--k y kx 由垂径定理,得:圆心1C 到直线l 的距离,1)232(422=-=d 结合点到直线距离公式,得:114132=+---k kk化简得:247,,0.07242-===+k or k k k 求直线l 的方程为:0=y 或)4(247--=x y ,即0=y 或028247=-+y x (2) 设点P 坐标为),(n m ,直线1l 、2l 的方程分别为:)(1),(m x k n y m x k n y --=--=-,即:011,0=++--=-+-m kn y x k km n y kx因为直线1l 被圆1C 截得的弦长与直线2l 被圆2C 截得的弦长相等,两圆半径相等.由垂径定理,得::圆心1C 到直线1l 与2C 直线2l 的距离相等.故有:1115411322+++--=+-+--km kn k k kmn k ,化简得:5)8(,3)2(-+=+---=--n m k n m n m k n m 或 关于k 的方程有无穷多解,有:⎩⎨⎧=-+=+-⎩⎨⎧=--=--0508,0302n m n m n m m m 或 解之得:点P 坐标为)213,23(-或)21,25(-. [19题解析] 本小题主要考查函数的概念、基本不等式等基础知识,考查数学建模能力、抽象概括能力以及数学阅读能力.满分16分. (1) [][])20,5,12,3(,203,512∈∈+⋅+=+⋅+=B A B B A A B B A A m m m m m m h m m m m h 乙甲当B A m m 53=时,)5)(20(51253532++=+⋅+=B B B B B B B m m m m m m m h 甲,)20)(5(20353532++=+⋅+=B B BB B B B m m m m m m m h 乙,h 甲=h 乙(2)当B A m m 53=时,h ==甲由[]⎥⎦⎤⎢⎣⎡∈∈51,201120,5B B m m 得,故当2011=B m 即12,20==A B m m 时, 甲乙两人同时取到最大的综合满意度为510. (3)(方法一)由(2)知:5100=h 由5105120=≥+⋅+=h m m m m h B B A A 甲得:25512≤+⋅+B B A A m m m m ,令y m x m B A ==5,3则⎥⎦⎤⎢⎣⎡∈1,41,y x ,即:25)1)(41(≤++y x . 同理,由5100=≥h h 乙得:25)41)(1(≤++y x 另一方面,[]5,241,41,1,41,∈++⎥⎦⎤⎢⎣⎡∈y x y x ,⎥⎦⎤⎢⎣⎡∈++2,251,1y x25)41)(1(,25)1)(41(≥++≥++y x y x 当且仅当41==y x ,即B A m m =时,取等号.所以不能否适当选取A m 、B m 的值,使得00h h h h ≥≥乙甲和同时成立,但等号不同时成立. 方法二:由⑵知320=h ,因为 9425100201536122020351212≤++⋅++=+⋅+⋅+⋅+=yy x x y x x y y x h h 乙甲所以,当32,32≥≥乙甲h h 时,有32==乙甲h h ,因此,不能取到B A m m ,的值,使得0h h ≥甲和0h h ≥乙同时成立,但等号不同时成立.[20题解析] 本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力.满分16分(1)若1)0(≥f ,则1112-≤⇒⎩⎨⎧≥<⇒≥-a a a a a(2)当a x ≥时,⎪⎩⎪⎨⎧<≥=⎪⎩⎪⎨⎧<≥=+-=0,320,20),3(0),()(,23)(22min22a a a a a a f a a f x f a ax x x f 当a x ≤时,⎪⎩⎪⎨⎧<≥-=⎩⎨⎧<≥-=-+=0,20,20),(0),()(,2)(22min22a a a a a a f a a f x f a ax x x f 综上⎪⎩⎪⎨⎧<≥-=0,320,2)(22mina a a a x f (3)),(+∞∈a x 时,1)(≥x h 得012322≥-+-a ax x ,222812)1(124a a a -=--=∆当2626≥-≤a a 或时,),(,0+∞∈≤∆a x ; 当2626<<-a 时,△>0,得:⎪⎩⎪⎨⎧>≥-+----ax a a x a a x 0)323)(323(22 讨论得:当)26,22(∈a 时,解集为),(+∞a ; 当)22,26(--∈a 时,解集为⎪⎪⎭⎫⎢⎢⎣⎡+∞-+⋃--,323]323,(22a a a a a ; 当⎥⎦⎤⎢⎣⎡-∈22,22a 时,解集为⎪⎪⎭⎫⎢⎢⎣⎡+∞-+,3232a a . 数学Ⅱ[A .选修4 - 1几何证明选讲答案] :本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力.满分10分.证明:由△ABC ≌△BAD 得∠ACB=∠BDA ,故A 、B 、C 、D 四点共圆,从而∠CBA=∠CDB .再由△ABC ≌△BAD 得∠CAB=∠DBA .因此∠DBA=∠CDB ,所以AB ∥CD .[B .选修4 - 2:矩阵与变换答案] :本小题主要考查逆矩阵的求法,考查运算求解能力.满分10分.解:设矩阵A 的逆矩阵为⎥⎦⎤⎢⎣⎡w y z x ,则⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡10011223 = w y z x 即⎥⎦⎤⎢⎣⎡=⎥⎦⎤++⎢⎣⎡+100122322z 3 +w y w y z x x ,故⎩⎨⎧=+=+⎩⎨⎧=+=+,12,023,,02,123w y w y z x z x解得:3,2,2,1-===-=w y z x ,从而A 的逆矩阵为⎥⎦⎤-⎢⎣⎡-=-32211 A . [C . 选修4 - 4:坐标系与参数方程答案] :本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力.满分10分.解:因为212-+=t t x ,所以3122y t t x =+=+,故曲线C 的普通方程为:2360x y -+= [ D . 选修4 - 5:不等式选讲答案] :本小题主要考查比较法证明不等式的常见方法,考查代数式的变形能力.满分10分.证明:3322222232(32)3()2()(32)().a b a b ab a a b b b a a b a b +-+=-+-=-- 因为a ≥b >0,所以a b -≥0,2232a b ->0,从而22(32)()a b a b --≥0, 即3332a b +≥2232a b ab +.[必做题第22题答案] :本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力.满分10分.解:(1)由题意,可设抛物线C 的标准方程为px y 22=,因为点)2,2(A 在抛物线C 上,所以1=p ,因此,抛物线C 的标准方程为x y 22=.(2)由(1)可得焦点F 的坐标是)0,21(,又直线OA 的斜率为122=,故与直线OA 垂直的直线的斜率为1-,因此,所求直线的方程是021=-+y x .(3)解法一:设点D 和E 的坐标分别为),(11y x 和),(22y x ,直线DE 的方程是)(m x k y -=,0≠k 将m kyx +=代入x y 22=,有0222=--km y ky ,解得kmk y 22,1211+±=.由DE ME 2=知)121(221122-+=++mk mk ,化简得m k 42=. 因此22122212212))(11()()(y y ky y x x DE -+=-+-=)4(49)21(4)11(2222m m k mk k +=++=.所以)0(423)(2>+=m m m m f . 解法二:设),2(),,2(22t t E s s D ,由点)0,(m M 及DMME 2=得)0(20),2(22122s t s m m t -=--=-.因此2,2s m s t =-= 所以)0(423)2()22()(222222>+=--+-==m m m s s s s DE m f .[必做题第23题答案] :本小题主要考查概率的基本知识和记数原理,考查探究能力.满分10分.(1)解:因为方程022=++b ax x 有实数根,所以0442≥-=∆b a ,即2a b ≤(i )当2n a n ≤≤时,有22a n ≤,又2,,2,1n b ⋅⋅⋅∈,故总有b ,有12+-n n 种取法,b有2n 种取法,所以共有22)1(n n n +-组有序数组),(b a 满足条件;(ii )当11-≤≤n a 时,满足21ab ≤≤的b有2a个,故共有6)12)(1()1(3212222--=-+⋅⋅⋅+++n n n n 组有序数组),(b a 满足条件.由(i )(ii )可得6)1346(6)12)(1()1(23222++-=--=+-=n n n n n n n n n n T n ,从而32346134622n n n n n T P n n ++-==.⑵证明:我们只需证明:对于随机选取的n b a ,,2,1,⋅⋅⋅∈,方程022=++b ax x 无实数根的概率nP n 11<-.若方程022=++b ax x 无实数根,则0442<-=∆b a ,即b a <2的有序数组),(b a 的组数小于n n ,从而,方程022=++b ax x 无实数根的概率nn n n P n 112=<-,所以n P n 11->.试卷综合解读与评析2009年高考江苏卷保持了2008年高考江苏卷的特点,以稳为主,稳中有变,更加体现新课程理念,所有试题的建构,不偏不怪,难易得当,紧扣考纲,贴近课本.注重考查基础知识,基本技能,基本数学思想和方法,对当前高中数学教学和高三数学复习备考有着鲜明的导向作用.下面从数学I、II试题的答案,别解、知识点、苏教版教材的出处,考纲要求,课本要求,用到的数学思想方法,容易导致失误的地方等方面进行综合解读.(要说明的是:江苏高考试题分文、理科,除选修的科目不同外,语、数、外三门必修科目的设置也有同有异:英语科目文理科试题相同,分值为120分;数学、语文两门必修科目,文理试题的设置分I、II两部分,对于文科和理科的考生数学和语文的I卷试题相同、分值均为160分,对理科生要加考数学II试题,文科考生要加考语文II试题分值均为40分.这样语数外三门必修科目文、理试题的总分值一样——200分+160分+120分=480分.)1.数学I试题(文理同卷)填空题部分填空题没有难度,从1至12题都平铺直叙,送分送到位,13、14题属于中档题,也容易拿分,没有难题.对照考纲和教材将14条填空题进行分析和解读如下:(附:表中的“等级”是指:江苏《考试说明》将考点要求分成A、B、C三个等级,其中C级要求最高,B 级次之、A级要求最低;表中的“层次”是指:江苏教材上的习题分为三个层次即:感受·理解、思考·运用和探究·拓展)2 数学I试题(文理同卷)解答题部分对于15题,此题主要考查平面向量数量积的坐标运算,两角和与差的三角函数,二倍角的正弦,考纲要求分别为C、C、B,坚持了重点知识重点考查的原则,数学思想方法主要考查了转化思想题型常规,思路清晰可循,三基好的考生容易得满分.对于16题,此题是立体几何题,仍然是考察平行与垂直的证明,题目简单明了,但要注重过程,判定定理的条件必须写全,线面平行是三个条件,面面垂直是两个条件,但之前需证明线面垂直,那是五个条件.对于17、18题第一小问,比较简单,但第二小问难度加大.17题数列题的第一小问是基本量的运算,大多考生不会有问题,第二小问有一丝数论的味道,题目简洁而又精彩!18题是解析几何题,考查直线与圆的位置关系,第二小问思路其实比较清晰,因为圆1C 与圆2C 的半径相等,及直线1l 被圆1C 截得的弦长与直线 2l 被圆2C 截得的弦长相等,所以圆1C 的圆心到直线1l 的距离和圆2C 的圆心到直线2l 的距离相等,列出等式,题目中要求“存在无数对直线”转化为“等式有无数解”即可,但是字母运算较复杂,考察考生的耐心与细心. 对于19题,此题主要考查函数与基本不等式等基础知识,比较好地考查了考生对信息的接收、加工和输出等数据处理能力,数学建模能力、抽象概括能力以及数学阅读能力达到有效考查综合素质的目的.考查与以往不同的是,大题的顺序有了明显的颠倒,数列难度下降了很多,放在了大题第三题的位置,而以往应用题是不会放在这个位置的,虽然难度适中,以生活中的满意度为背景,但题干中的字比较多,问题的表述较长,变量均以字母形式出现,提高了应用题的难度,这就要求考生多读几遍题目,多读几遍还是可以理解的,第⑴、⑵小题能够做出,第⑶小题有点难度;有些考生就承受不了了,所以对最后一题也有心理干扰,这也是广大考生不太适应的又一方面,从中可以看到今年的高考试卷在知识与能力考查的同时,体现了对课改新理念的创新与发展.对于20题,此题主要考查函数的概念、性质、图像及解一元二次不等式等基础知识,考查灵活运用数型结合、分类讨论的思想方法.这样的的分类讨论其实高中训练得很多了,但在考场上想得满分也并不容易.第(3)小问不要考生写过程,只要结果,需要一定的数学直觉思维,如果结合图形问题可以得到很好地解决,命题很有新意,不落浴套,具有较强的选拔功能.3. 数学Ⅱ附加题(理科做)今年是执行必做、选做分卷考试新模式的第二年,附加题部分难度控制的比较适中,在全省考生慢慢接受并熟悉了这种模式后,相比去年,今年的选作题方面考点上没有任何的变动,但圆锥曲线、函数中不等关系的证明出现在该部分作为压轴考题,难度明显比去年有了很大的提升. 4 全卷综合点评 4.1 全卷综合解读2009年高考数学试题,对考试说明中的8个C 级要求的知识点和B 级要求中传统的问题都进行了有效的考查,在保持题型稳定的基础上,进行适度的改革和创新,试卷贴近教学实际,坚持能力立意,全面检测考生的数学素养,充分体现新课程的基本理念.试卷主要有以下几个方面的特点:4.1.1 多题把关,有效发挥选拔功能第17,18题第二小问,第19题、第20题的第三问有一定的难度,改变了过去一题或两题把关的习惯,在凸显文理公平基础上,命题者这样处理对不同层次考生群体更有区分度,有利于高校选拔人才.基于同样的原因,数学Ⅱ附加题(理科做)部分,两道必做题对数学语言的转化以及数学思想方法有一定的要求,相对较难,其他试题很简单.4.1.2 能力立意,旨在考察数学素养全卷在考查知识的同时,注重考查学生的数学思维能力和应用意识.许多试题实际上并不难,对于知识点考生很熟悉,但需要考生自主综合所学知识,才能解决问题,如第17题第二问,其实是恒成立问题.许多试题若能先想清楚问题的关键或本质,确定了合适的解题思路和方向后再动手,解答会容易的多,否则会陷入繁琐的运算之中,比如第13题,第14题.部分题目在考查基础知识点上有所创新,题目设计灵活.如数学卷第17题第(2)问,第18题第(2)问,都是对一个问题进行纵向探究,考查学生创新意识,同时要求学生掌握通性通法,淡化特殊技巧,例如第18题第(2)问,如果用几何方法解决在考场上几乎不能成功,试题的设问已将几何法排除在外,命题者的意思很明确,考察解析几何的本质——用代数方法研究图形的几何性质,体现数形结合和等价转化的重要数学思想4.1.3 引领课改,全面体现课程标准试卷以朴素的数学知识为载体,综合考查最基本的数学思想和方法,体现了高考命题重实质、重内涵的指导思想,注重通性通法、淡化特殊技巧,对中学数学教学有较好的导向作用.不少试题注意在具体的情景中、在解决问题的过程中突出考查学生数学思想和数学方法.如第20题以二次函数为载体,重点考查分类谈论、数形结合思想,其中的第三问,只要直接写出解,不需要过程,打破了长期以来人们所固有的解答题不能以图代证的模式,给平时积极主动、勇于探索的考生有发挥的空间.这也是新课改的明确要求,新课程标准明确指出:“高中数学课程应注重提高学生的数学思维能力,这是数学教育的基本目标之一,人们在学习数学和运用数学解决问题时,不断地经历直观感知、观察发现、归纳推理、空间想象、抽象概括……等思维过程”.另外,试题加强了对应用意识和创新意识的考查,力求对现实世界中蕴涵的一些数学模式进行思考和做出判断,例如第19题以生活中的满意度为背景,问题的表述较长,需要考生耐心读懂题目,但模式识别方便,同时还考查了学生将文字语言转化为数学语言的能力.4.1.4 保持稳定,凸显公平公正原则(1)整卷试题呈现:低起点、入手宽、由易到难,逐步深入、多题把关的格局,全卷结构、题型包括难度都基本稳定,依据考试说明,突出对教材基本内容的考查.填空题比较平和,不需太繁的计算,考生普遍感觉顺手.许多试题源于课本,略高于课本,如第1、2、3、4、5、7、11、15题等,都由课本例题、习题进行恰当变更、迁移、综合、创新整合而成,给人以似曾相识的感觉.最后6个解答题由易到难,涉及的知识内容基础、常规,入手容易,但深入有一定困难.附加题部分,选做题对知识点的考查单一,结论要求明确,学生入手较易.(2)通览全卷试题和答案:不见偏题怪题、人为陷阱,处处体现人文关怀、呈现关爱.如填空题14题,求6q ,正常应该求q ,有谬常理.细细想来,为命题者的良苦用心所折服,这是因为如果所编题目答案q 是整数,学生很易猜到,失去考察知识的意义,现在所编题目的23-=q ,凭借以前阅卷的经验,学生的答案很易将“—”和分数线“——”连在一起成为“23”,从而引起失分,试题中“求6q ”可以有效避免这种非智力因素的失分;再如,填空题11题按常理该设问为“求实数a 的范围”,而试题中设问为“实数a 的取值范围是),(+∞c ,其中c = ____”,从中大家不难发现命题者的用心,还有应用题的表述命题者不惜大量篇幅,也是为了学生只要认真读题就不会因为审题困难而失分.(3)试卷注重对重点知识的考察,但编制题目时目的很明确——只针对性地考察要考知识、方法,不人为设置其他难点,避免因为其他知识的不熟悉而解答错误.例如新增内容“导数”,试题中填空题部分两次用到,但难度都很低,这是因为新课标只要求“能利用导数研究函数单调性、会用导数求简单函数的极值和最值”, “导数”其实在中学教材中只是一种“工具”的地位,要重点考察但不会考很复杂的函数,以免考生因为求导数出错而失误.再如立体几何的考察,载体是直三棱柱,只考察了基本的平行与垂直的证明,这是因为理科学过空间向量,如果考角与距离或比较难的证明,那样对于文科生就极不公平.其他的题目基本都是如此.以上三点是试卷所呈现的实际情况,如果我们进一步地思考可以发现命题者这样做的真正原因——保持稳定、体现公平.江苏高考的现行模式才第二年,数学I 试题文科和理科同卷,而他们所用的教材必修部分相同,选修部分不同,文科教材要简单些,另外他们的数学基础也不同,而高校录取时是同等录取,这就要求数学命题时文理要公平,做到真正公平很困难,唯一的办法就“简单”——载体简单、知识点单一,只有这样才能相对公平.还有应用题的编拟也体现了另一公平——城乡考生之间的公平,试题中的应用题背景对所有学生是公平的.4.2 备考备战的几点启示4.2.1 平时教学要灵活、有变化,模式教学已不适应平时的教学活动要灵活、要开展一题多变、多题一解、一题多解的数学解题教学模式,要注重情境教学,揭示知识的生成、发展和应用的过程,不能因为教学时间的有限而给学生不同知识点以不同的模式化,学生的数学活动不应只限于接受、记忆、模仿和练习,应积极倡导自主探索、动手实践、合作交流、阅读自学等学习数学的方式,发挥学生学习的主动性. 平时教学要严格按课程标准和考试说明进行,对教材内容不要人为地加深和无限地拓展,或是反复训练自认为重要的个别问题,这样浪费学生很多宝贵时间,在高考中将会处于劣势. 4.2.2 高考试题没有绝对,吃透课程标准是关键。
2009年高考数学(江苏卷)(word版含答案)
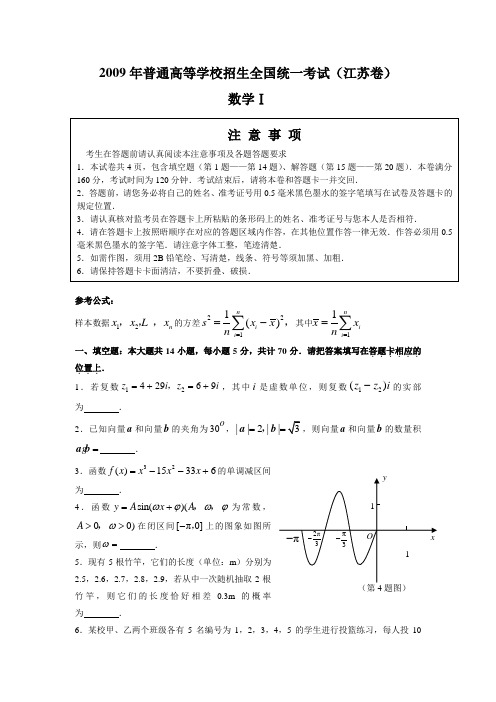
π
2π 3
π 3
O 1
x
5.现有 5 根竹竿,它们的长度(单位:m)分别为 2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取 2 根 竹 竿 , 则 它 们 的 长 度 恰 好 相 差 0.3m 的 概 率 为 .
(第 4 题图)
6.某校甲、乙两个班级各有 5 名编号为 1,2,3,4,5 的学生进行投篮练习,每人投 10
2 .已知向量 a 和向量 b 的夹角为 30 , | a | 2 , | b |
3 ,则向量 a 和向量 b 的数量积
a b
.
3 2
3.函数 f ( x ) x 15 x 33 x 6 的单调减区间 为 . 1
y
( x ) ( , A , 为 常 数 , 4 . 函 数 y As i n A 0, 0 )在闭区间 [ π, 0] 上的图象如图所
次,投中的次数如下表: 学生 甲班 乙班 1号 6 6 2号 7 7
2
3号 7 6
4号 8 7
5号 7 9
则以上两组数据的方差中较小的一个为 s
. . 开始
7.右图是一个算法的流程图,最后输出的 W
8.在平面上,空间中,若两个正四面体的棱 长的比为 1∶2,则它们的体积比为 9.在平面直角坐标系
3
S 0
T 1
. 中,点 P 在曲线
xoy
C : y x 10x 3 上,且在第二象限内,已知曲线 C 在点
P 处的切线的斜率为 2,则点 P 的坐标为 10 .已知 a .
S T 2 S
S ≥10
Y
T T 2
N
5 1 2
20092009年高考数学(江苏卷)

解(1)设l: y=k(x-4), 1 2 1 k 7 解出 k 0或- 24 , l : y 0或7 x 24 y 28 0 (2)设P(a,b),l1: y b k ( x a), 1 | 5 (4 a) b | |1 k (3 a) b | k 1 1 k 2 1 2 ky B2 NhomakorabeaT
M
A1
O
B1
x
F
14.设 {an }是公比为q的等比数列,|q|>1,
{b n } 有连 令 bn an 1(n 1, 2,...) ,若数列
续四项在集合{-53,-23,19,37,81}中,
则6q=
-9
.
2.解答题中容易题(三角,立几)考查教材最基
础的内容和最基本的数学方法和技能;难题
A1 , A2 , B1 , B2为椭圆 13.如图,在平面直角坐标系 xoy 中,
x2 y 2 2 1(a b 0) 的四个顶点,F为其右焦点,直线 2 a b A1 B2与直线 B1 F 相交于点T,线段OT与椭圆的交点M恰
2 7 5 为线段OT的中点,则该椭圆的离心率为_________.
15.设向量 a (4cos ,sin ), b (sin , 4sin ), c (cos , 4cos )
(1) 若 a 与b 2c 垂直,求 tan( ) 的值;
(2) 求 | b c | 的最大值;
(3)若 tan tan 16, 求证 a // b .
解析几何.江苏高考解几多考中档题,这是有别
于其他省的又一特色,在江苏<考试说明>中,双曲线,
2009江苏高考数学试卷 排版精编 答案详解

2009江苏高考数学试卷注意事项:考生在答题前请认真阅读本注意事项及各题答题要求1、本试卷共4页,均为非选择题(第1题-第20题,共20题)。
本卷满分为160分。
考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回。
2、答题前请务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡的规定位置。
3、请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与您本人是否相符。
4、作答试题,必须用0.5毫米黑色墨水签字笔在答题卡上的指定位置作答,在其他位置作答一律无效。
5、如需作图,须用2B 铅笔绘,写清楚,线条,符号等须加黑加粗。
参考公式:样本数据12,,,n x x x 的方差221111(),n n i ii i s x x x x n n ===-=∑∑其中一、填空题:本大题共14小题,每小题5分,共70分。
1.若复数12429,69z i z i =+=+,其中i 是虚数单位,则复数12()z z i -的实部为______ 2.已知向量a 和向量b 的夹角为30,||2,||3==a b ,则向量a 和向量b 的数量积=a b __________ .3.函数32()15336f x x x x =--+的单调减区间为_____4.函数s i n ()(y A x A ωϕωϕ=+为常数,0,0)A ω>>在闭区间[,0]π-上的图象如图所示,则ω=_______ .5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为________ .6.6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表: 学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班6767911 π-23π-3π-O xy则以上两组数据的方差中较小的一个为2s=________ .7.右图是一个算法的流程图,最后输出的W=________ .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间,若两个正四面体的棱长的比为1:2,则它们的体积比为________ .9.在平面直角坐标系xoy 中,点P 在曲线3:103C y x x =-+上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为________.10.已知512a -=,函数()xf x a =,若实数,m n满足()()f m f n >,则,m n 的大小关系为 ________. 11.已知集合{}2|log 2A x x =≤,(,)B a =-∞,若A B ⊆则实数a 的取值范围是(,)c +∞,其中c =________ .12.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直; (4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直. 上面命题中,真命题的序号________(写出所有真命题的序号). 13.如图,在平面直角坐标系xoy 中,1212,,,A A B B 为椭圆22221(0)x ya b a b +=>>的四个顶点,F 为其右焦点,直线12A B 与直线1B F 相交于点T ,线段OT 与椭圆的交点M恰为线段OT的中点,则该椭圆的离心率为________.xyA1 B2A2 OTM开始0S ← 1T ←2S T S ←-10S ≥2T T ←+W S T ←+输出W 结束YN14.设{}n a 是公比为q 的等比数列,||1q >,令1(1,2,)n n b a n =+=若数列{}n b 有连续四项在集合{}53,23,19,37,82--中,则6q = ________二、解答题:本大题共6小题,共计90分。
完整word版2009年江苏省高考数学试卷答案与解析

2009年江苏省高考数学试卷参考答案与试题解析一、填空题(共14小题,每小题5分,满分70分)1.(5分)(2009?江苏)若复数z=4+29i,z=6+9i,其中i是虚数单位,则复数(z﹣z)i2112的实部为﹣20.【考点】复数代数形式的乘除运算.【专题】数系的扩充和复数.【分析】把复数z=4+29i,z=6+9i,代入复数(z﹣z)i,化简,按多项式乘法法则,展2112开,化简为a+bi(a,b∈R)的形式,即可得到实部.【解答】解:∵z=4+29i,z=6+9i,21∴(z﹣z)i=(﹣2+20i)i=﹣20﹣2i,21∴复数(z﹣z)i 的实部为﹣20.21故答案为:﹣20【点评】本题考查复数代数形式的乘除运算,考查计算能力,是基础题.0,则向量,江苏)已知向量和和向量的夹角为2.(5分)(2009?30.3向量的数量积=【考点】平面向量数量积的运算.【专题】平面向量及应用.【分析】向量数量积公式的应用,条件中给出两个向量的模和向量的夹角,代入公式进行计算即可.×=3,【解答】解:由题意知:=2故答案为:3.【点评】本题是向量数量积的运算,条件中给出两个向量的模和两向量的夹角,代入数量积的公式运算即可,两个向量的数量积是一个数量,它的值是两个向量的模与两向量夹角余弦的乘积.32).的单调减区间为(﹣1,11=x(5分)2009?江苏)函数f(x)﹣15x﹣33x+6.3(【考点】利用导数研究函数的单调性.【专题】函数的性质及应用.的不等式求出解,并令其小于零得到关于x′(x)f【分析】要求函数的单调减区间可先求出集即可.22﹣11)(30x﹣33=3x﹣10x﹣(【解答】解:f′x)=3x ,)<x﹣110(=3(x+1)).,<1<x11,故减区间为(﹣111解得﹣,111)(﹣故答案为:此题考查学生利用导数研究函数的单调性的能力.【点评】14.(5分)(2009?江苏)函数y=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)在闭区间[﹣π,0]的图象如图所示,则ω=3.【考点】由y=Asin(ωx+φ)的部分图象确定其解析式.【专题】三角函数的图像与性质.【分析】根据函数图象求出函数的周期T,然后求出ω.【解答】解:由图中可以看出:=,T=πT=π,∴∴ω=3.故答案为:3【点评】本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查逻辑思维能力,是基础题.5.(5分)(2009?江苏)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为0.2.【考点】古典概型及其概率计算公式.【专题】概率与统计.【分析】由题目中共有5根竹竿,我们先计算从中一次随机抽取2根竹竿的基本事件总数,及满足条件的基本事件个数,然后代入古典概型计算公式,即可求出满足条件的概率.【解答】解:从5根竹竿中一次随机抽取2根的可能的事件总数为10,它们的长度恰好相差0.3m的事件数有2.5和2.8,2.6和2.9,共2个∴所求概率为0.2.故答案为:0.2.【点评】本题考查的知识点是古典概型及其概率计算公式,计算出满足条件的基本事件总数及其满足条件的基本事件个数是解答此类题型的关键.6.(5分)(2009?江苏)某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如表:学7 7 8 7 6甲班7 6 7 9 6乙班2.0.4则以上两组数据的方差中较小的一个为S=【考点】极差、方差与标准差.【专题】概率与统计.先写出两组数据的平均数,再求出两组数据的方差,把根据表中所给的两组数据,【分析】方差进行比较,方差小的一个是甲班,得到结果.,8,7,,,解:由题意知甲班的投中次数是【解答】677 ,这组数据的平均数是72,甲班投中次数的方差是,6,7,9乙班的投中次数是6,7,,这组数据的平均数是7这组数据的方差是,∴两组数据的方差中较小的一个为0.40.4故答案为:这种问题一旦出现是比较两组数据的方差的大小,是一个基础题,【点评】本题考查方差,一个必得分题目,注意运算过程中不要出错..江苏)如图是一个算法的流程图,最后输出的W=227.(5分)(2009?【考点】循环结构.【专题】算法和程序框图.,不满足则循环,直到满足就跳10,判定是否满足S≥S【分析】根据流程图可知,计算出值即可.出循环,最后求出W10≥S=1;不满足S【解答】解:由流程图知,第一次循环:T=1,210≥;不满足ST=3,S=3﹣1=8第二次循环:210 S≥S=5﹣8=17,满足T=5第三次循环:,W=5+17=22.此时跳出循环,∴22故答案为当型循环结构和直到型循循环结构有两种形式:本题主要考查了直到型循环结构,【点评】环结构,当型循环是先判断后循环,直到型循环是先循环后判断,属于基础题.,则它们的面积比为:21分)(2009?江苏)在平面上,若两个正三角形的边长的比为.8(5 则它们的体积比8,:若两个正四面体的棱长的比为类似地,41:,在空间内,12【考点】类比推理.立体几何.【专题】3【分析】根据平面与空间之间的类比推理,由点类比点或直线,由直线类比直线或平面,由平面图形面积类比立体图形的体积,结合三角形的面积比的方法类比求四面体的体积比即可.【解答】解:平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,由平面图形面积类比立体图形的体积,得出:在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为1:8故答案为:1:8.【点评】本题主要考查类比推理.类比推理是指依据两类数学对象的相似性,将已知的一类数学对象的性质类比迁移到另一类数学对象上去.一般步骤:①找出两类事物之间的相似性或者一致性.②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(或猜想).3上,且在10x+3y=x﹣P在曲线C:(5分)(2009?江苏)在平面直角坐标系xOy中,点9..2,15)P处的切线斜率为2,则点P的坐标为(﹣C第二象限内,已知曲线在点【考点】导数的几何意义.【专题】导数的概念及应用.处的)在x=xf(x)y(x<0),根据导数的几何意义求出函数【分析】先设切点P(x,0000导数,从而求出切线的斜率,建立方程,解之即可.2,=3x﹣10=20),由题意知:y′|x=x<【解答】解:设P(x,y)(x000002.∴x=40,=﹣2∴x0.∴y=150.15)∴P点的坐标为(﹣2,),15故答案为:(﹣2本题考查了导数的几何意义,以及导数的运算法则和已知切线斜率求出切点坐标,【点评】本题属于基础题.x)(m,n满足f,函数f(x)=log,若正实数200910.(5分)(?m江苏)已知a>f(n),则m,n的大小关系为m<n.【考点】对数函数的单调性与特殊点.【专题】函数的性质及应用.x在=logx)<1,故函数f(【分析】,即因为已知条件中对数函数的底数0<a a(0,+∞)上为减函数,根据函数的单调性,结合足f(m)>f(n),不难判断出m,n的大小关系.解:∵【解答】∴0<a<1x∴f(x)=log在(0,+∞)上为减函数a若f(m)>f(n)则m<n故答案为:m<n4x时,指数函数和对数函数在其定义域上均1,在底数a>【点评】函数y=a和函数y=logx a)x 时,指数函数和对数函数在其定义域上均为减函数,而f(﹣0<a<1为增函数,当底数x﹣,在底x)轴对称,其单调性相反,故函数y=a和函数y=log(﹣与f(x)的图象关于Y a时,指数函数1时,指数函数和对数函数在其定义域上均为减函数,当底数0<a<a数>1 和对数函数在其定义域上均为增函数.的取aA?B则实数,≤2},B=(﹣∞a),若(11.5分)(2009?江苏)已知集合A={x|logx2.c= 4值范围是(c,+∞),其中集合的包含关系判断及应用.【考点】集合.【专题】A 先化简集合,然后根据子集的定义求出集合B的取值范围,总而求出所求.【分析】【解答】解:A={x|logx≤2}={x|0<x≤4} 2而B=(﹣∞,a),∵A?B∴a>4即实数a的取值范围是(4,+∞),故答案为:4【点评】本题属于以对数不等式为依托,考查集合子集的基础题,也是高考常会考的题型.12.(5分)(2009?江苏)设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β;(2)若α外一条直线l与α内的一条直线平行,则l和α平行;(3)设α和β相交于直线l,若α内有一条直线垂直于l,则α和β垂直;(4)直线l与α垂直的充分必要条件是l与α内的两条直线垂直.上面命题,真命题的序号是(1)(2)(写出所有真命题的序号)【考点】空间中直线与平面之间的位置关系;命题的真假判断与应用.【专题】空间位置关系与距离.【分析】从线面平行、垂直的判定定理,判断选项即可.【解答】解:由面面平行的判定定理可知,(1)正确.由线面平行的判定定理可知,(2)正确.对于(3)来说,α内直线只垂直于α和β的交线l,得不到其是β的垂线,故也得不出α⊥β.对于(4)来说,l只有和α内的两条相交直线垂直,才能得到l⊥α.也就是说当l垂直于α内的两条平行直线的话,l不一定垂直于α.【点评】本题考查空间中直线与平面之间的位置关系,理解定理是判断的前提,是中档题.13.(5分)(2009?江苏)如图,在平面直角坐标系xoy中,A,A,B,B为椭圆2112的四个顶点,F为其右焦点,直线AB与直线BF相交于点T,112.OTMOT线段与椭圆的交点恰为线段的中点,则该椭圆的离心率为 5【考点】椭圆的简单性质.【专题】圆锥曲线的定义、性质与方程.,联立的方程为,直线B【分析】解法一:可先直线ABF的方程为112的坐标,代入椭圆的方程即可解出离的坐标,进而表示出中点M两直线的方程,解出点T 心率的值;'2'2根),F'.(解法二:,对椭圆进行压缩变换,0,,椭圆变为单位圆:x+y=1 轴交点的横坐标就是该椭圆的离心率.T与x据题设条件求出直线BT方程,直线直线B11的方程为,的方程为直线BF【解答】解法一:由题意,可得直线AB112(M)T(,则),由于此点在椭圆两直线联立则点上,故有22=0﹣c10ac,整理得3a﹣2 +10e﹣,解得3=0即e故答案为解法二:对椭圆进行压缩变换,,,'2'2.,0+y=1,F')(椭圆变为单位圆:x ,TM=MO=ON=1,AB斜率为1,交圆延长TOO于N,易知直线21′+1,′),则,y′=x,T设(x′y,×TN由割线定理:TB×TA ,=TM12,(负值舍去)方程:T1(B0,﹣),直线B易知:11=0令y′F,即横坐标6e=.即原椭圆的离心率故答案:.【点评】本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答.14.(5分)(2009?江苏)设{a}是公比为q的等比数列,|q|>1,令b=a+1(n=1,2,…),nnn若数列{b}有连续四项在集合{﹣53,﹣23,19,37,82}中,则6q=﹣9.n【考点】等比数列的性质;数列的应用.【专题】等差数列与等比数列.【分析】根据B=A+1可知A=B﹣1,依据{Bn}有连续四项在{﹣53,﹣23,19,37,82}nnnn中,则可推知则{A}有连续四项在{﹣54,﹣24,18,36,81}中,按绝对值的顺序排列上述n数值,相邻相邻两项相除发现﹣24,36,﹣54,81是{A}中连续的四项,求得q,进而求n得6q.【解答】解:{Bn}有连续四项在{﹣53,﹣23,19,37,82}中B=A+1 A=B﹣1nnnn则{A}有连续四项在{﹣54,﹣24,18,36,81}中n{A}是等比数列,等比数列中有负数项则q<0,且负数项为相隔两项n等比数列各项的绝对值递增或递减,按绝对值的顺序排列上述数值18,﹣24,36,﹣54,81相邻两项相除﹣=﹣=﹣=﹣=很明显,﹣24,36,﹣54,81是{A}中连续的四项n﹣(|q|>1,∴此种情况应舍)q= ﹣或q=﹣q= ∴∴6q=﹣9故答案为:﹣9【点评】本题主要考查了等比数列的性质.属基础题.二、解答题(共6小题,满分90分)15.(14分)(2009?江苏)设向量与垂直,求tan(α+β)的值;1()若的最大值;2()求7∥.,求证:)若tanαtanβ=16(3【考点】平面向量数量积坐标表示的应用;平行向量与共线向量;两向量的和或差的模的最值.【专题】平面向量及应用.与与先根据向量的线性运算求出,的再由【分析】(1)垂直等价于数量积等于0可求出α+β的正余弦之间的关系,最后可求正切值.||,然后根据向量的求模运算得到的关系,最后根据正(2)先根据线性运算求出弦函数的性质可确定答案.∥β,正是α)?(4cosβ)=sinαsin(3)将tanαtanβ=16化成弦的关系整理即可得到(4cos 的充要条件,从而得证.垂直,β,4cosβ+8sinβ)与(【解答】解:1,)∵=(sinβ﹣2cos∴4cosα(sinβ﹣2cosβ)+sinα(4cosβ+8sinβ)=0,即sinαcosβ+cosαsinβ=2(cosαcosβ﹣sinαsinβ),∴sin(α+β)=2cos(α+β),cos(α+β)=0,显然等式不成立∴tan(α+β)=2.)∵=(sinβ+cosβ,4cosβ﹣(24sinβ),||=∴,=.||1β=﹣时,取最大值,且最大值为sin2∴当,即sinαsin β=16,∴β=16cosαcosβ,α(3)∵tantan 4cosα∴(4cos)?(β)=sin,sinβα)共线,,sinsin,α=)与(β4cosβα(即=4cos∥.∴求模运算、向量垂直和数量积之间的关系.向量和【点评】本题主要考查向量的线性运算、三角函数的综合题是高考的热点,要强化复习.的分别是ABA,CFE中,CB﹣江苏)如图,在直三棱柱2009分)(16.14(?ABCA,11111在中点,点DB⊥.求证:BCDA上,C1111(∥平面EF1);ABC 2()平面CBB⊥平面FD.AC1118直线与平面平行的判定;平面与平面垂直的判定.【考点】立体几何.【专题】即可;∥BCEF ∥平面ABC,证明EF【分析】(1)要证明即可,利用平面与平面CBBC,通过证明AD⊥面)要证明平面(2AFD⊥平面BBCC111111垂直的判定定理证明即可.C的中点,A分别是B,A 【解答】证明:(1)因为E,F11 ABC;ABC,所以EF∥平面EF?面ABC,BC?面所以EF∥BC,又D,BB⊥A,所以BB⊥面ABC,ABC(2)因为直三棱柱﹣ABC111111111⊥FD所以平面A,D?面AFD⊥面BC=B,所以ADBBCC,又AB又AD⊥C,BB∩11111111111.CC平面BB11本题考查直线与平面平行和垂直的判断,考查学生空间想象能力,逻辑思维能力,【点评】是中档题.项和,满足为其前nS?江苏)设a是公差不为零的等差数列,17.(14分)(2009nn2222=7,Sa+a=a+a72435 S;的通项公式及前n项和(1)求数列a nn中的项.,使得为数列(2)试求所有的正整数ma n数列的求和;等差数列的性质.【考点】等差数列与等比数列.【专题】代入等差数列的通项da,)先把已知条件用a及d表示,然后联立方程求出【分析】(111 n项和公式可求.公式及前ma2的通项公式可寻求)先把已知化简可得,然后结合数列(n满足的条件.)由题意可得【解答】解:(1d=2 ﹣5,=联立可得a1,×)2=2n﹣71n5+=a∴﹣(﹣n(2中的项a=1)由()知若使其为数列n9为正整数必需为整数,且m则;,m=1m=2 是最小值)故舍去.﹣5时不满足题意,(a=m=11.所以m=2解题的重点是要熟练掌握项和的公式,本题主要考查了等差数列的通项公式及前n【点评】基本公式,并能运用公式,还要具备一定的运算能力.22和﹣1)=4C:(x+3)+(y18.(16分)(2009?江苏)在平面直角坐标系xoy中,已知圆122=4 ﹣5)x﹣4)+(yC圆:(2,求直线l0),且被圆C的方程;截得的弦长为I()若直线l过点A(4,1的斜,l)为平面上的点,满足:存在过点P的两条互相垂的直线l与l(II)设P(a,b112截得C被圆C截得的弦长与直线l被圆相交,率为2,它们分别与圆C和圆C且直线l212121的关系式.的弦长相等,试求满足条件的a,b直线的一般式方程;直线和圆的方程的应用.【考点】直线与圆.【专题】的点斜式方程,又由直线被圆,故可以设出直线l4,0)I 【分析】()因为直线l过点A(,根据半弦长、半径、弦心距满足勾股定理,我们可以求出弦心距,截得的弦长为C1lk值,代入即得直线即圆心到直线的距离,得到一个关于直线斜率k的方程,解方程求出的方程.的圆心到直C与ll的点斜式方程,分析可得圆(II)根据题意,可以设出过P点的直线112的方程,整理ba、的距离相等,即可以得到一个关于l的距离和圆C的圆心到直线l线212变形可得答案.不相交,与圆C (Ⅰ)若直线l的斜率不存在,则直线x=4【解答】解:1),x﹣4l故直线l的斜率存在,不妨设为k,则直线的方程为y=k()到直线的距离,C圆心(﹣3,1圆﹣即kxy﹣4k=01=1,则,l直线被圆C截得的弦长为1k=0联立以上两式可得,或故所求直线.y=0方程为l或10:,l x﹣a),(Ⅱ)依题意直线的方程可设为l:y﹣b=2(21因为两圆半径相等,且分别被两直线截得的弦长相等,l的距离相等,l的距离和圆C的圆心到直线的圆心到直线故圆C2112即,解得:a﹣3b+21=0或3a+b﹣7=0.【点评】在解决与圆相关的弦长问题时,我们有三种方法:一是直接求出直线与圆的交点坐标,再利用两点间的距离公式得出;二是不求交点坐标,用一元二次方程根与系数的关系得出,即设直线的斜率为k,直线与圆联立消去y后得到一个关于x的一元二次方程再利用弦长公式求解,三是利用圆中半弦长、弦心距及半径构成的直角三角形来求.对于圆中的弦长问题,一般利用第三种方法比较简捷.本题所用方法就是第三种方法.19.(16分)(2009?江苏)照某学者的理论,假设一个人生产某产品单件成本为a元,如果元,则他的满意度为;如果他买进该产品的单价为n他卖出该产品的单价为m元,则.如果一个人对两种交易(卖出或买进)的满意度分别为h和他的满意度为h,则他21.对这两种交易的综合满意度为现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为m元和m元,甲买进A与卖出B BA的综合满意度为h,乙卖出A与买进B的综合满意度为h.乙甲=m时,求证:h的表达式;当m=h;(1)求h和h关于m、m BAAB乙甲甲乙=m,当mm、m分别为多少时,甲、乙两人的综合满意度均最大?最大的综(2)设BBAA合满意度为多少?(3)记(2)中最大的综合满意度为h,试问能否适当选取m、m的值,使得h≥h和00AB甲h≥h 同时成立,但等号不同时成立?试说明理由.0乙【考点】函数模型的选择与应用.【专题】函数的性质及应用.=mm时,表示出要证【分析】(1)表示出甲和乙的满意度,整理出最简形式,在条件BA明的相等的两个式子,得到两个式子相等.(2)在上一问表示出的结果中,整理出关于变量的符合基本不等式的形式,利用基本不等式求出两个人满意度最大时的结果,并且写出等号成立的条件.≤,不能取到m,m=h)知hh=.因为h的值,使)先写出结论:不能由((32B0A0乙甲同时成立,但等号不同时成立.h 和≥hh≥h得00乙甲=;hB=的满意度为)甲:买进(【解答】解:1Ah,卖出的满意度为B1A111=;h= 所以,甲买进A与卖出B的综合满意度为甲=;=,买进B的满意度为:乙:卖出A的满意度为:hh B2A2=;= A与买进B的综合满意度h所以,乙卖出乙=,所以hh,=h当m=m时,BA甲甲乙=h乙=m时,0),当mm(2)设=x(其中x>BAB≤;= =h=h乙甲=×10=6m时,=10时,上式“=”成立,即m当且仅当,x=,即x=10AB甲、乙两人的综合满意度均最大,最大综合满意度为;≤h =.因为(3)不能由(2)知hh0乙甲同时成立,但等号不同时成立.h≥hm的值,使得h≥h和因此,不能取到m,0BA0乙甲【点评】本题考查函数模型的选择和应用,本题解题的关键是理解题意,这是最主要的一点,题目中所用的知识点不复杂,只要注意运算就可以.2.﹣a|x﹣a)|x江苏)设a为实数,函数f(x)=2x+(1620.(分)(2009? a的取值范围;10)≥,求(1)若f(x)的最小值;2)求f((的解集.)≥1)+∞,求不等式h(x,h3)设函数(x)=f(x)x∈(a,(二次函数的性质;一元二次不等式的解法.【考点】函数的性质及应用;不等式的解法及应用.【专题】a再去绝对值求的取值范围,﹣a|a|≥1≥【分析】(1)f(0)1?借助二次函数的a两种情况来讨论去绝对值,再对每一段分别求最小值,和x<≥(2)分xa 对称轴及单调性.最后综合即可.22,因为不等式的解集由对应方程的根决定,所以再0﹣﹣2ax+a1≥转化为x3()h()≥13x 对其对应的判别式分三种情况讨论求得对应解集即可. 1 ≤?≥,则﹣≥0f1解:【解答】()若()1a|a|1?a﹣1222,∴,﹣2ax+a xx≥a时,f()=3x2()当如图所示:22﹣af(x)=x,+2ax≤当xa时,∴.综上所述:.1,h(x)≥a(3)x∈(,+∞)时,22222﹣8a(a﹣1)=12△得3x﹣2ax+a1﹣≥0,=4a12﹣);∞(0≤,x∈a,+△a≤当a﹣或≥时,>时,<当﹣a<△0,得:13即2类讨论:进而分<时,a,当﹣<a<﹣;+,∞,]∪)[a此时不等式组的解集为(a;≤<时,<x当﹣≤).此时不等式组的解集为,[+∞综上可得,);,+∞+,∞当a∈(﹣∞,﹣)∪()时,不等式组的解集为(a);[,+∈当a∞(﹣,﹣)时,不等式组的解集为(a,]∪.+,∞)时,不等式组的解集为[a当∈﹣,][分段函数的最值的求法是先对每一段分别求最值,【点评】本题考查了分段函数的最值问题.最后综合最大的为整个函数的最大值,最小的为整个函数的最小值.14。
2009年全国高考数学试题及答案-江苏卷
题号年级知识点是否有答案是否有解析1高二复数的计算是无
2高一平面向量的数量积是有
3高一函数的单调性是有
4高一三角函数的图像和性质是有
5高二随机事件的概率是无
6高二离散型随机变量的期望与方差是无
7高一算法的含义与程序框图是无
8高一空间几何体的体积是无
9高二曲线的切线是无
10高一指数函数的基本性质是无
11高一集合的基本运算是有
12高一命题及其关系
直线与平面的位置关系
是无
13高二椭圆的离心率是是14高一等比数列是是
15高一1.平面向量的数量积
2.二倍角公式
3.向量共线的充要条件
是是
16高一1.直线与平面平行的判定
2.平面与平面垂直的判定
是是
17高一1.等差数列的通项公式和求和公式
2.数列的中项
是是
18高一1.直线方程
2。
直线与圆的方程的应用
是是
19高一1.函数模型的选择和应用
2.函数的性质和应用
是是
20高一1.二次函数的性质
2.一元二次不等式的解法
3.二次函数求最值
是是
2009年全国高考数学试题及答案-江苏卷。
2009年江苏省高考数学真题(解析版)
绝密★启用前2009年普通高等学校招生全国统一考试(江苏卷)数学参考公式:样本数据1x,2x,,nx的标准差(ns x x=++-其中x为样本平均数柱体体积公式V Sh=其中S为底面积,h为高一、填空题:本大题共1小题,每小题5分,共70分.1.若复数z1=4+29i,z2=6+9i,其中i是虚数单位,则复数(z1−z2)i的实部为▲.【答案】−20.【解析】z1−z2=−2+20i,故(z1−z2)i=−20−2i.【说明】考查复数的四则运算.2.已知向量a和向量b的夹角为30︒,|a|=2,|b|=3,则向量a和向量b的数量积a·b= ▲.【答案】3.【解析】cos23θ===a b a b.【说明】考查向量的数量积(代数)运算.锥体体积公式13V Sh=其中S S为底面积,h为高球的表面积、体积公式24S Rπ=,343V Rπ=3. 函数f (x )=x 3−15x 2−33x +6的单调减区间为 ▲ . 【答案】(1,11)-.【解析】2()330333(11)(1)f x x x x x =--=-+',由(11)(1)0x x -+<得单调减区间为(1,11)-.【说明】考查函数的单调性,考查导数在研究函数性质中的应用.4. 函数y =A sin(ωx +φ)(A ,ω,φ为常数,A >0,ω>0)2π3-在闭区间[−π,0]上的图象如图所示,则ω= ▲ . 【答案】3.【解析】如图,2π3T =,所以3ω=.【说明】考查三角函数的图象和性质,考查周期性的概念.5. 现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 ▲ . 【答案】0.2 【解析】随机抽取2根竹竿的取法有10种,而长度恰好相差0.3m 的取法有2种,所以概率为0.2. 【说明】考查古典概型.6. 某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表:则以上两组数据的方差中较小的一个2s 为 ▲ .【答案】25.【解析】第一组数据7x =甲,212(10010)55S =++++=甲;第二组数据7x =乙,245S =乙.【说明】考查总体特征数的估计.实际上,根据数据的分布,知甲班的数据较为集中(甲班极差为2,众数为7,乙班极差为3,众数为6,7). 7. 右图是一个算法的流程图,最后输出的W = ▲ . 【答案】22. 【解析】追踪表:故出循环时,S =17,T =5,故W=22.【说明】本题考查算法初步,考查流程图(循环结构).值得注意的是,本题的循环结构并非是教材中所熟悉的当型或直到型,因此该流程图是一个非结构化的流程图,对学生的识图能力要求较高.8. 在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4.类似地,在空间中,若两个正四面体的棱长的比为1:2,则它们的体积比为 ▲ . 【答案】1:8【解析】由题意知,面积比是边长比的平方,由类比推理知:体积比是棱长比的立方. 【说明】本题考查合情推理之类比推理.9. 在平面直角坐标系xOy 中,点P 在曲线C :y =x 3−10x +3上,且在第二象限内,已知曲线C在点P 处的切线的斜率为2,则点P 的坐标为 ▲ . 【答案】(2,15)-.【解析】设点P 的横坐标为x 0,由2310y x '=-知203102x -=,又点P 在第二象限,02x =-,所以(2,15)P -.【说明】本题考查导数的几何意义——曲线切线的斜率.10. 已知a =f (x )=a x ,若实数m ,n 满足f (m )>f (n ),则m ,n 的大小关系为 ▲.【答案】m n <【解析】由01<<知01a <<,函数()x f x a =是减函数,由()()f m f n >知m n <.【说明】本题考查函数的单调性,指数函数的性质等概念.11. 已知集合A ={x |log 2x ≤2},B =(−∞,a ),若A ⊆B ,则实数a 的取值范围是(c ,+∞),其中c =▲ . 【答案】4【解析】由log 2x ≤2得0<x ≤4,(0,4]A =;由A B ⊆知4a >,所以c =4.【说明】本题考查对数函数的性质,集合间的基本关系(子集)等概念. 12. 设α 和β为不重合的两个平面,给出下列命题:(1)若α 内的两条相交直线分别平行于β内的两条直线,则α 平行于β; (2)若α 外一条直线l 与α 内的一条直线平行,则l 和α 平行;(3)设α 和β相交于直线l ,若α 内有一条直线垂直于l ,则α 和β垂直; (4)直线l 与α 垂直的充分必要条件是l 与α 内的两条直线垂直. 上面命题中,真命题的序号 ▲ .(写出所有真命题的序号). 【答案】(1)(2)【解析】由线面平行的判定定理知,(2)正确;相应地(1)可转化为一个平面内有两相交直线分别平行于另一个平面,所以这两个平面平行.【说明】本题考查空间点、线、面的位置关系.具体考查线面、面面平行、垂直间的关系与转化. 13. 如图,在平面直角坐标系xOy 中,A 1,A 2,B 1,B 2为椭圆22221(0)y x a b a b +=>>的四个顶点,F 为其右焦点,直线A 1B 2与直线B 1F 相交于点T ,线段OT 与椭圆的交点M 恰为线段O T 的中点,则该椭圆的离心率为 ▲ .【答案】5【解析】直线12A B 的方程为1y x a b +=-,直线1B F 的方程为1yx c b+=-,两方程联立方程组得T 2(,)ac ab bc a c a c+--,则点M (,)2()ac ab bc a c a c +--,由点M 在椭圆上,代入整理得:223100a ac c --=,23100e e --=,又 0e >,所以离心率为5.【说明】本题考查椭圆的概念、标准方程与几何性质.14. 设{a n }是公比为q 的等比数列,|q |>1,令b n =a n +1(n =1,2,…)若数列{b n }有连续四项在集合{−53,−23,19,37,82}中,则6q = ▲ . 【答案】9-【解析】由条件知数列{a n }中连续四项在集合{}54,24,18,36,81--中,由||1q >,所以{a n }中连续四项可能为(1)24-,36,54-,81,32q =-,69q =-;(2)18,24-,36,54-,不合;其它情形都不符合.【说明】本题考查等比数列的概念与通项公式.在本题中,如果将集合中的各数均除以3,得到集合{}232323,2,23,32,3-⨯-⨯⨯,再从其中选出四个数进行适当地排列,这样的解法更利于看清问题本质.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15. (本小题满分14分)设向量a =(4cos α ,sin α ),b =(sin β,4cos β),c =(cos β,−sin β), (1)若a 与b −2c 垂直,求tan(α +β)的值; (2)求+b c 的最大值;(3)若tan α tan β=16,求证:a ∥b . 【解析】(1)∵a ⊥b −2c ,∴(2)20⋅-=⋅-⋅=a b c a b a c .即4sin()8cos()0αβαβ+-+=,∴tan()2αβ+=. (2)(sin cos ,4cos 4sin )ββββ+=+-b c ,()()222sin cos 16cos sin ββββ+=++-b c 1730sin cos ββ=-1715sin 2β=-,∴当sin2β=−1时,2+b c 最大值为32,所以+b c的最大值为(3)∵tan tan 16αβ=,∴sin sin 16cos cos αβαβ=,即4cos 4cos sin sin 0αβαβ⋅-=, 所以a ∥b .16. (本小题满分14分)如图,在直三棱柱ABC −A 1B 1C 1中,E ,F 分别是A 1B ,A 1C 的中点,点D 在B 1C 1上,A 1D ⊥B 1C . 求证:(1)EF ∥平面ABC ; (2)平面A 1FD ⊥平面BB 1C 1C .【解析】(1)因为E ,F 分别是A 1B ,A 1C 的中点,所以EF ∥BC ,又EF ⊄平面ABC ,BC ⊂平面ABC ,∴EF ∥平面ABC ; (2)在直三棱柱ABC −A 1B 1C 1中,1111BB A BC ⊥面,AB CA 1B 1C 1 EF D第16题图∵A 1D ⊂平面A 1B 1C 1,∴11BB AD ⊥. 又11AD BC ⊥,BB 1 B 1C =B 1,∴111AD BC C ⊥面B . 又11AD AFD ⊂面,所以平面A 1FD ⊥平面BB 1C 1C .17. (本小题满分14分)设{a n }是公差不为零的等差数列,S n 为其前n 项和,满足22225234a a a a +=+,S 7=7. (1)求数列{a n }的通项公式及前n 项和S n ; (2)试求所有的正整数m ,使得12m m m a a a ++为数列{S n }中的项. 【解析】(1)设公差为d ,则22225243a a a a -=-,由性质得43433()()d a a d a a -+=+,因为0d ≠,所以430a a +=,即1250a d +=,又由77S =得176772a d ⨯+=,解得15a =-,2d =所以{}n a 的通项公式为27n a n =-,前n 项和26n S n n =-. (2)12(27)(25)(23)m m m m m a a a m ++--=-,令23m t -=,12(4)(2)m m m t t a a a t++--=86t t =+-,因为t 是奇数,所以t 可取的值为1±,当1t =,2m =时,863t t +-=,2573⨯-=,是数列{}n a 中的项;1t =-,1m =时,8615t t +-=-,数列{}n a 中的最小项是5-,不符合.所以满足条件的正整数2m =. 18. (本小题满分16分)在平面直角坐标系xOy 中,已知圆C 1∶(x +3)2+(y −1)2=4和圆C 2∶(x −4)2+(y −5)2=4.(1)若直线l 过点A (4,0),且被圆C 1截得的弦长为l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂的直线l 1和l 2,它们分别与圆C 1和圆C 2相交,且直线l 1被圆C 1截得的弦长与直线l 2被圆C 2截得的弦长相等,试求所有满足条件的点P 的坐标.【解析】(1) 0y =或7(4)24y x =--,(2)法一)设点P (,)a b ,1l :()y b k x a -=-,则2l :1()y b x a k -=--由截得的弦长相等可得1C 到1l 与2C 到2l 的距离相等,即第18题图11|4()5()|a bk k----+=,即|31||45|k ka b k a kb---+=--++,整理得:222222(3)2(3)(1)(1)(5)2(4)(5)(4)a k ab k b b k a b k a+++-+-=-+--+-因为有无数组解,所以对应项系数相等,解得:32a=-,132b=;或52a=,12b=-.所以满足条件的点P坐标为313(,)22-或51(,)22-.法二)依题意点P在线段1C2C的中垂线上,且与1C、2C构成等腰直角三角形,设点P(,)a b,则713()42b a-=--,又120PC PC⋅=,即22670a b a b+---=,解得:32a=-,132b=;或52a=,12b=-.满足条件的点P坐标为313(,)22-或51(,)22-.19.(本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a元,如果他卖出该产品的单价为m元,则他的满意度为mm a+;如果他买进该产品的单价为n元,则他的满意度为nn a+.如果一个人对两种交易(卖出或买进)的满意度分别为h1和h2,现假设甲生产A,B两种产品的单件成本分别为12元和5元,乙生产A,B两种产品的单件成本分别为3元和20元,设产品A,B的单价分别为m A元和m B元,甲买进A与卖出B的综合满意度为h甲,乙卖出A与买进B的综合满意度为h乙.(1)求h甲和h乙关于m A,m B的表达式;当35A Bm m=时,求证:h甲=h乙;(2)设35A Bm m=,当m A,m B分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?(3)记(2)中最大的综合满意度为h0,试问能否适当选取m A,m B的值,使得0h h甲≥和h h乙≥同时成立,但等号不同时成立?试说明理由.【解析】h=甲h=乙当35A Bm m=时,h=甲h=乙h甲=h乙.当35A Bm m=时,h==甲,而520Bm≤≤,所以当20Bm=时,甲、乙两人的综合满意度均最大,此时12Am=.(3≥即31024120A B A B m m m m ≥++ ①且3406120A B A B m m m m ≥++ ②, 由①及520B m ≤≤得:24120310B A B m m m +≥-,又241202008[12,48]310310B B B m m m +=+∈--, 只有当12A m =,20B m =时,不等式①成立. 由②及312A m ≤≤得:4012036A B A m m m +≥-,又4012040200[20,80]36336A A A m m m +=+∈--, 只有当20B m =,12A m =时,不等式②成立.综上,不存在满足条件的A m 、B m 的值.20. (本小题满分16分)设a 为实数,函数f (x )=2x 2+(x −a )|x −a |. (1)若f (0)≥1,求a 的取值范围; (2)求f (x )的最小值;(3)设函数h (x )=f (x ),x ∈(a ,+∞),直接写出(不需给出演算步骤)不等式h (x )≥1的解集. 【解析】(1)若(0)1f ≥,即||1a a -≥,则{21a a <≥,所以1a ≤-. (2)当x a ≥时,22()32,f x x ax a =-+22min(),02,0()2(),0,033f a a a a f x a a f a a ≥≥⎧⎧⎪⎪==⎨⎨<<⎪⎪⎩⎩当x a ≤时,22()2,f x x ax a =+-{{2min2(),02,0()(),02,0f a a a a f x f a a a a -≥-≥==<<综上22min2,0()2,03a a f x a a -≥⎧⎪=⎨<⎪⎩. (3)x a ≥时,()1h x ≥得223210x ax a -+-≥,222412(1)128a a a ∆=--=-,①当a a ≤≥时,0∆≤,不等式的解集为(,)a +∞;②当a <<0,∆>得(0x x x a⎧⎪≥⎨>⎪⎩, ia <<时,不等式的解集为(,)a +∞; ii)a ≤≤)+∞;iii)a <<时,不等式的解集为3([)3a a +-+∞.数学Ⅱ(附加题)参考公式:2222(1)(21)123.6n n n n ++++++=21. [选做题]在A 、B 、C 、D 四小题中只能选做两题........ A.选修4 - 1:几何证明选讲如图,在四边形ABCD 中,△ABC ≌△BAD .求证:AB ∥CD .证明:由△ABC ≌△BAD 得∠ACB =∠BDA ,故A 、B 、C 、D 四点共圆,从而∠CBA =∠CDB .再由△ABC ≌△B AD 得∠CAB =∠DBA .因此∠DBA =∠CDB ,所以AB ∥CD . B. 选修4 - 2:矩阵与变换,求矩阵3221A ⎡⎤=⎢⎥⎣⎦的逆矩阵. 解:设矩阵A 的逆矩阵为,x y z w ⎡⎤⎢⎥⎣⎦则3210,2101x y z w ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦即323210,2201x z y w x z y w ++⎡⎤⎡⎤=⎢⎥⎢⎥++⎣⎦⎣⎦故321,320,20,21,x z y w x z y w +=+=⎧⎧⎨⎨+=+=⎩⎩ 解得1,2,2,3x z y w =-===-, 从而A 的逆矩阵为11223A --⎡⎤=⎢⎥-⎣⎦.C. 选修4 - 4:坐标系与参数方程已知曲线C 的参数方程为1,13()x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数,0t >).求曲线C 的普通方程.解:因为212,x t t=+-所以212,3y x t t +=+= 故曲线C 的普通方程为:2360x y -+=. D. 选修4 - 5:不等式选讲设a ≥b >0,求证:3332a b +≥2232a b ab +.证明:3322222232(32)3()2()(32)().a b a b ab a a b b b a a b a b +-+=-+-=--因为a ≥b >0,所以a b -≥0,2232a b ->0,从而22(32)()a b a b --≥0,即3332a b +≥2232a b ab +.22. 在平面直角坐标系xOy 中,抛物线C 的顶点在原点,经过点A (2,2),其焦点F 在x轴上(如图).(1)求抛物线C 的标准方程;(2)求过点F ,且与直线OA 垂直的直线的方程;(3)设过点(,0)(0)M m m >的直线交抛物线C 于D 、E 两点,ME =2DM ,记D 和E 两点间的距离为()f m ,求()f m 关于m 的表达式.23. 对于正整数n ≥2,用n T 表示关于x 的一元二次方程220x ax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈(a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈(a 和b 可以相等),记n P 为关于x 的一元二次方程220x ax b ++=有实数根的概率。
2009年江苏高考数学试卷及答案
13.【答案】
【分析】用 表示交点T,得出M坐标,代入椭圆方程即可转化解得离心率.
14.【答案】
【分析】将各数按照绝对值从小到大排列,各数减1,观察即可得解.
15.【分析】由 和 垂直, ,
即 , ;
,最大值为32,所以 的最大值为 。
由 得 ,即 ,
所以 ∥ .
16.【分析】证明:(1)因为 分别是 的中点,所以 ,又 , ,所以 ∥ ;
综上
(3) 时, 得 ,
当 时, ;
当 时, 得
1) 时,
2) ;
设 ,当 、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
记(2)中最大的综合满意度为 ,试问能否适当选取 、 的值,使得 和 同时成立,但等号不同时成立?试说明理由。
求 和 关于 、 的表达式;当 时,求证: = ;
设 ,当 、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少?
按照某学者的理论,假设一个人生产某产品单件成本为 元,如果他卖出该产品的单价为 元,则他的满意度为 ;如果他买进该产品的单价为 元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为 和 ,则他对这两种交易的综合满意度为 .
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为 元和 元,甲买进A和卖出B的综合满意度为 ,乙卖出A和买进B的综合满意度为
上面命题中,真命题的序号________(写出所有真命题的序号).
13.如图,在平面直角坐标系 中, 为椭圆 的四个顶点, 为其右焦点,直线 和直线 相交于点T,线段 和椭圆的交点 恰为线段 的中点,则该椭圆的离心率为________.
mjt-2009年普通高等学校招生全国统一考试(江苏卷)试题及点评
2009年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ参考公式:样本数据12,,n x x x L 的方差()2211n i i s x x n ==-∑,其中11n i i x x n ==∑.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1.若复数i z i z 96,29421+=+=其中i 是虚数单位,则复数i z z )(21-的实部为 .2.已知向量a 和向量b 的夹角为30o,3||,2||==b a ,则向量a 和向量b 的数量积b a ⋅= .3.函数63315)(23+--=x x x x f 的单调减区间为 .4.函数)sin(ϕω+=x A y (ϕω,,A 为常数,0,0>>ωA )在闭区间[]0,π-上的图象如图所示,则ω= .5.现有5根竹竿,它们的长度(单位:m )分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m 的概率为 . 6.某校甲、乙两个班级各有5名编号为1,2,3,4,5的学生进行投篮练习,每人投10次,投中的次数如下表: 学生 1号 2号 3号 4号 5号 甲班 6 7 7 8 7 乙班67679则以上两组数据的方差中较小的一个为2s = . 7.右图是一个算法的流程图,最后输出的=W .8.在平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,在空间内,若两个正四面体的棱长的比为1:2,则它们的体积比为 .9.在平面直角坐标系xoy 中,点P 在曲线310:3+-=x x y C 上,且在第二象限内,已知曲线C 在点P 处的切线的斜率为2,则点P 的坐标为 . 10.已知215-=a ,函数xa x f =)(,若实数m 、n 满足)()(n f m f <,则m 、n 的大小关系为 .11.已知集合{}),(,2log |2a B x x A -∞=≤=,若B A ⊆则实数a 的取值范围是),(+∞c ,其中c =12.设α和β为不重合的两个平面,给出下列命题:(1)若α内的两条相交直线分别平行于β内的两条直线,则α平行于β; (2)若α外一条直线l 与α内的一条直线平行,则l 和α平行;(3)设α和β相交于直线l ,若α内有一条直线垂直于l ,则α和β垂直;(4)直线l 与α垂直的充分必要条件是l 与α内的两条直线垂直.上面命题中,真命题的序号 (写出所有真命题的序号)13.如图,在平面直角坐标系xoy 中,2121,,,B B A A 为椭圆)0(12222>>=+b a by a x 的四个顶点,F 为其右焦点,直线21B A 与直线F B 1相交于点T ,线段OT 与椭圆的交点M 恰为线段OT 的中点,则该椭圆的离心率为 ▲ .14.设{}n a 是公比为q 的等比数列,1>q ,令),2,(1⋅⋅⋅=+=n a b n n ,若数列{}n b 有连续四项在集合{}82,37,19,23,53--中,则q 6= .二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.15.(本小题满分14分)设向量)sin 4,(cos ),cos 4,(sin ),sin ,cos 4(β-β=ββ=αα=c b a (1)若a 与c b 2-垂直,求)tan(β+α的值;(2)求c b +的最大值; (3)若16tan tan =βα,求证:a ∥b16.(本小题满分14分)如图,在直三棱柱111C B A ABC -中,E 、F 分别是B A 1、C A 1的中点,点D 在11C B 上,C B D A 11⊥.求证:(1)EF ∥平面ABC ; (2)平面FD A 1⊥平面C C BB 11..17.(本小题满分14分)设{}n a 是公差不为零的等差数列,n S 为其前n 项和,满足7,725242322=+=+S a a a a .(1)求数列{}n a 的通项公式及前n 项和n S ;(2)试求所有的正整数m ,使得21++m m m a a a 为数列{}n a 中的项.18.(本小题满分16分)在平面直角坐标系xoy 中,已知圆4)1()3(:221=-++y x C 和圆4)5()4(:222=-+-y x C .(1)若直线l 过点)0,4(A ,且被圆1C 截得的弦长为32,求直线l 的方程;(2)设P 为平面上的点,满足:存在过点P 的无穷多对互相垂直的直线1l 和2l ,它们分别与圆1C 和圆2C 相交,且直线1l 被圆1C 截得的弦长与直线2l 被圆2C 截得的弦长相等,试求所有满足条件的点P 的坐标.19.(本小题满分16分)按照某学者的理论,假设一个人生产某产品单件成本为a 元,如果他卖出该产品的单价为m 元,则他的满意度为am m+;如果他买进该产品的单价为n 元,则他的满意度为a n n +.如果一个人对两种交易(卖出或买进)的满意度分别为1h 和2h ,则他对这两种交易的综合满意度为21h h .现假设甲生产A 、B 两种产品的单件成本分别为12元和5元,乙生产A 、B 两种产品的单件成本分别为3元和20元,设产品A 、B 的单价分别为A m 元和B m 元,甲买进A 与卖出B 的综合满意度为甲h ,乙卖出A 与买进B 的综合满意度为乙h(1)求甲h 和乙h 关于A m 、B m 的表达式;当B A m m 53=时,求证:甲h =乙h ; (2)设B A m m 53=,当A m 、B m 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为0h ,试问能否适当选取A m 、B m 的值,使得0h h ≥甲和0h h ≥乙同时成立,但等号不同时成立?试说明理由.20.(本小题满分16分)设a 为实数,函数a x a x x x f --+=)(2)(2. (1)若1)0(≥f ,求a 的取值范围;(2)求)(x f 的最小值;(3)设函数),(),()(+∞∈=a x x f x h ,直接写出(不需给出演算步骤)不等式1)(≥x h 的解集.数学Ⅱ参考公式:2222(1)(21)123.6n n n n ++++++=L21.[选做题]在A 、B 、C 、D 四小题中只能选做两题......,每小题10分,共计20分.请在答.题卡指定区域......内作答,解答时应写出文字说明、证明过程或演算步骤. A .选修4 - 1:几何证明选讲如图,在四边形ABCD 中,△ABC ≌△BAD .求证:AB ∥CD .B . 选修4 - 2:矩阵与变换,求矩阵3221A ⎡⎤=⎢⎥⎣⎦的逆矩阵. C . 选修4 - 4:坐标系与参数方程已知曲线C 的参数方程为,13()x t ty t t ⎧=-⎪⎪⎨⎪=+⎪⎩(t 为参数,0t >).求曲线C 的普通方程. D . 选修4 - 5:不等式选讲 :设a ≥b >0,求证:3332a b +≥2232a b ab +.[必做题]第22题、第23题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.22.(本题满分10分)在平面直角坐标系xoy 中,抛物线C 的顶点在原点,经过点A (2,2),其焦点F 在x 轴上.(1)求抛物线C 的标准方程; (2)求过点F ,且与直线OA 垂直的直线的方程;(3)设过点(,0)(0)M m m >的直线交抛物线C 于D 、E 两点,ME=2DM ,记D 和E 两点间的距离为()f m ,求()f m 关于m 的表达式.23.(本题满分10分)对于正整数n ≥2,用n T 表示关于x 的一元二次方程220x ax b ++=有实数根的有序数组(,)a b 的组数,其中{},1,2,,a b n ∈L (a 和b 可以相等);对于随机选取的{},1,2,,a b n ∈L (a 和b 可以相等),记n P 为关于x 的一元二次方程022=++b ax x有实数根的概率.(1)求2n T 和2n P ;(2)求证:对任意正整数n ≥2,有nP n 11->. 2009年普通高等学校招生全国统一考试(江苏卷)答案及解读 数学Ⅰ一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题卡相应的位置上.1. -20【解析】 本题考查了复数的基本运算,属基础概念题.由i z i z 96,29421+=+=, 可得i i i i z z 220)202()(21--=+-=-, 则复数i z z )(21-的实部为-20.2. 3【解析】 本题考查了复数的数量积公式及其简单应用.由向量a 和向量b 的夹角为ο30,3||,2||==b a ,可得330cos 32=⨯⨯=⋅οb a .3.)11,1(-【解析】 本题考查了导数法求函数的单调区间问题. 由63315)(23+--=x x x x f ,可得)1110(333303)(22--=--='x x x x x f , 令0)(<'x f 可解得111<<-x , ∴函数63315)(23+--=x x x x f 的单调减区间为)11,1(-.4. 3【解析】 本题考查了由三角函数图象求三角函数解析式问题.由图象可得该函数的周期为ωπ=π=232T , ∴3=ω. 5.51【解析】 本题考查了古典概型问题,从2.5,2.6,2.7,2.8,2.9,这五个数据中任意抽取2个有2.5 , 2.6; 2.5 , 2.7; 2.5 , 2.8; 2.5 , 2.9; 2.6 , 2.7; 2.6 , 2.8; 2.6 , 2.9; 2.7 , 2.8; 2.7 , 2.9; 2.8 , 2.9,共10种抽取方法, 其中长度恰好相差0.3m 仅2.5 , 2.8; 2.6 , 2.9两组, 即得2,10==m n , ∴它们的长度恰好相差0.3m 的概率为51102===n m P . 6.52【解析】 本题考查了统计初步中样本数据的方差的求解问题,属简单的公式应用问题.同时也考查了学生的估算能力. 由图表可得7)78776(51=++++=甲x , 7)97676(51=++++=乙x , ∴52)01001(512=++++=甲S , 56)40101(512=++++=乙S ,22乙甲S S < ,∴两组数据的方差中较小的一个为522=S .本题也可由表格估算出22乙甲S S <,因此,不必计算2乙S7. 22【解析】 本题考查了算法的流程图,以循环结构为主要考查对象,是近几年高考中常见的命题方式.由流程图可得, 第一次循环时得到的S 与T 的值分别为1-0=1,1; 第二次循环时得到的S 与T 的值分别为9-1=8,3; 第三次循环时得到的S 与T 的值分别为25-8=17,5, 此时退出循环结构得22517=+=W .8. 1:8【解析】 本题考查了推理与证明中合情推理之中类比推理的应用.由于相似的几何图形中面积比是边长的平方比, 类比的相似的几何体的体积比是棱长的立方比, 即若两个正四面体的棱长的比为1:2,则它们的体积比为1:8.9. (-2, 15)【解析】 本题考查了导数的几何意义, 曲线方程对应的函数的导数的几何意义是曲线上某点的切线的斜率.由21032=-='x y 可解得2±=x , ∵切点P 在第二象限内,∴2-=x , 由此可得点P 的坐标为(-2, 15).10. n m <【解析】 本题考查了指数函数及指数函数的单调性的应用.∵)1,0(215∈-=a , ∴函数xa x f =)(为R 上的减函数,又∵)()(n f m f >, ∴n m <.11. 4【解析】 本题考查了对数不等式及集合的子集运算,此题中要注意对数函数的定义域及集合边界值的验证.由已知条件可得{}(]4,02log |2=≤=x x A ,),(a B -∞=,若B A ⊆则4>a ,即得4=c .12. (1)(2)【解析】 本题考查了平面与平面、直线与平面的平行与垂直的位置关系,是高考中常见的开放题型之一. 若α内的两条相交直线分别平行于β内的两条直线,则α平行于β,这是两个平面平行的判定定理,即(1)正确;若α外一条直线l 与α内的一条直线平行,则l 和α平行,这是直线与平面平行的判定定理,即(2)正确;设α和β相交于直线l ,α内有一条直线垂直于l ,但该直线不一定能够垂直β内两条相交直线,即直线l 不一定垂直于平面β,所以平面α和β不一定垂直,即(3)不正确; 直线l 与α垂直的充分必要条件是l 与α内的两条相交直线垂直,即(4)不正确, 综上可得真命题的序号为(1)(2).13.572-【解析】 本题考查了直线方程,两直线的交点及椭圆的几何意义,离心率 的考查是高考客观题考查的热点.由已知条件可得直线21B A 的方程为1=-+-b x a x ①, 直线F B 1的方程为1=-+byc x ②,联立①②可得两直线交点T 的坐标为(c a ac -2,ca c ab -+)(),则线段OT 的中点M的坐标为(c a ac -,)(2)(c a c a b -+),代入椭圆12222=+b y a x 可得222)(4)(4c a c a c -=++,即得03102=-+e e ,解之得725±-=e ,∵)1,0(∈e , ∴572-=e .【别解】设)sin ,cos (θθb a M ,则)sin 2,cos 2(θθb a T , 由T B A 21共线得aba ab =+θθcos 2sin 2化简得1cos 2sin 2+θ=θ ①由FT B 1共线得cba b b =θ+θcos 2sin 2化简得θ=+θcos 2)1sin 2(e ②由①②解得⎪⎪⎩⎪⎪⎨⎧-+=θ-=θ)1(21sin 1cos e e e e 代入1sin cos 22=θ+θ得03102=-+e e ,解得725+-=e .14. -9【解析】 本题考查了等比数列的通项与基本量的求解问题,此题利用等比数列构造另一个数列,利用所构造数列的性质去研究等比数列是高考的热点问题.由已知数列{}n b 有连续四项在集合{}82,37,19,23,53--中,则数列{}n a 必有连续四项在集合{}81,36,18,24,54--中, 若公比q 为正则该数列的四项必均为正或均为负值, 显然不合题意,所以公比q 必为负值,又由1>q 知1-<q ,按此要求在集合{}81,36,18,24,54--中取四个数排成数列可得数列81,54,36,24--或54,36,24,18-- (此数列不成等比数列,故舍去), ∵数列81,54,36,24--的公比23-=q , ∴96-=q . 二、解答题:本大题共6小题,共计90分,请在答题卡指定区域内作答,解答时应写出文字说明、证明或演算步骤.[15题解析] 本小题主要考查向量的基本概念、数乘、数量积,同时考查同角三角函数的基本关系式、二倍角的正弦、两角和的正弦与余弦公式,考查运算和证明等基本能力.满分14分.(Ⅰ)由a 与c b 2-垂直,02)2(=⋅-⋅=-⋅c a b a c b a ,即0)cos(8)sin(4=β+α-β+α,2)tan(=β+α.(Ⅱ))sin 4cos 4,cos (sin β-ββ+β=+c b ,β+ββ-β+β+ββ+β=+22222sin 16sin cos 32cos 16cos cos sin 2sin c b β-=ββ-=2sin 1517cos sin 3017,最大值为32,所以c b +的最大值为24. 由16tan tan =βα得βα=βαcos cos 16sin sin ,即0sin sin cos 4cos 4=βα-β⋅α, 所以a ∥b .[16题解析] 本小题主要考查直线与平面、平面与平面的位置关系,考查空间想象能力、推理论证能力.满分14分.(Ⅰ)因为E ,F 分别是C A B A 11,的中点, 所以EF ∥BC ,又ABC EF 面⊄,ABC BC 面⊂, 所以EF ∥平面ABC .(Ⅱ)因为直三棱柱111C B A ABC -,所以1111C B A BB 面⊥,D A BB 11⊥,又C B D A 11⊥,所以C C BB D A 111面⊥,又FD A D A 11面⊂,所以平面⊥FD A 1平面C C BB 11. [17题解析] 本小题主要考查等差数列的通项、求和的有关知识,考查运算和求解的能力.满分14分.(1)设公差为d ,则23242522a a a a -=-,由性质得)()(33434a a d a a d +=+-,因为0≠d ,所以034=+a a ,即0521=+d a ,又由77=S 得726771=⨯+d a ,解得51-=a ,2=d ,所以{}n a 的通项公式为72-=n a n ,前n 项和n n S n 62-=.(2)(方法一)32)52)(72(21---=++m m m a a a m m m ,设t m =-32, 则68)2)(4(21-+=--=++tt t t t a a a m m m , 所以t 为8的约数 因为t 是奇数,所以t 可取的值为1± 当2,1-==m t 时,3752,368=-⨯=-+tt ,是数列{}n a 中的项; 当1,1=-=m t 时,,1568-=-+tt 数列{}n a 中的最小项是5-,不符合. 所以满足条件的正整数2=m (方法二)因为222222186)2)(4(++++++++-=--=m m m m m m m m a a a a a a a a 为数列{}n a 中的项, 故28+m a 为整数,又由(1)知:2+m a 为奇数,所以1322±=-=+m a m ,即2,1=m经检验,符合题意的正整数只有2=m这两种解法看似相同,但却有本质的区别,解法二是紧扣数列通项公式解题,而解法一是紧扣等差数列的概念解题,学生掌握的基本思路是解法二,本题是中极题.[18题解析] 本小题主要考查直线与圆的方程、点到直线的距离公式,考查数学运算求解能力、综合分析问题的能力.满分16分.(1)设直线l 的方程为:)4(-=x k y ,即04=--k y kx 由垂径定理,得:圆心1C 到直线l 的距离,1)232(422=-=d 结合点到直线距离公式,得:114132=+---k kk化简得:247,,0.07242-===+k or k k k 求直线l 的方程为:0=y 或)4(247--=x y ,即0=y 或028247=-+y x (2) 设点P 坐标为),(n m ,直线1l 、2l 的方程分别为:)(1),(m x k n y m x k n y --=--=-,即:011,0=++--=-+-m kn y x k km n y kx因为直线1l 被圆1C 截得的弦长与直线2l 被圆2C 截得的弦长相等,两圆半径相等.由垂径定理,得::圆心1C 到直线1l 与2C 直线2l 的距离相等.故有:1115411322+++--=+-+--k m kn k k kmn k ,化简得:5)8(,3)2(-+=+---=--n m k n m n m k n m 或关于k 的方程有无穷多解,有:⎩⎨⎧=-+=+-⎩⎨⎧=--=--0508,0302n m n m n m m m 或 解之得:点P 坐标为)213,23(-或)21,25(-. [19题解析] 本小题主要考查函数的概念、基本不等式等基础知识,考查数学建模能力、抽象概括能力以及数学阅读能力.满分16分. (1) [][])20,5,12,3(,203,512∈∈+⋅+=+⋅+=B A B B A A B B A A m m m m m m h m m m m h 乙甲当B A m m 53=时,)5)(20(51253532++=+⋅+=B B B B B B B m m m m m m m h 甲,)20)(5(20353532++=+⋅+=B B BB B B B m m m m m m m h 乙,h 甲=h 乙(2)当B A m m 53=时,h ==甲由[]⎥⎦⎤⎢⎣⎡∈∈51,201120,5B B m m 得,故当2011=B m 即12,20==A B m m 时, 甲乙两人同时取到最大的综合满意度为510. (3)(方法一)由(2)知:5100=h 由5105120=≥+⋅+=h m m m m h B B A A 甲得:25512≤+⋅+B B A A m m m m ,令y m x m B A ==5,3则⎥⎦⎤⎢⎣⎡∈1,41,y x ,即:25)1)(41(≤++y x . 同理,由5100=≥h h 乙得:25)41)(1(≤++y x 另一方面,[]5,241,41,1,41,∈++⎥⎦⎤⎢⎣⎡∈y x y x ,⎥⎦⎤⎢⎣⎡∈++2,251,1y x25)41)(1(,25)1)(41(≥++≥++y x y x 当且仅当41==y x ,即B A m m =时,取等号.所以不能否适当选取A m 、B m 的值,使得00h h h h ≥≥乙甲和同时成立,但等号不同时成立. 方法二:由⑵知320=h ,因为 9425100201536122020351212≤++⋅++=+⋅+⋅+⋅+=yy x x y x x y y x h h 乙甲所以,当32,32≥≥乙甲h h 时,有32==乙甲h h ,因此,不能取到B A m m ,的值,使得0h h ≥甲和0h h ≥乙同时成立,但等号不同时成立.[20题解析] 本小题主要考查函数的概念、性质、图象及解一元二次不等式等基础知识,考查灵活运用数形结合、分类讨论的思想方法进行探索、分析与解决问题的综合能力.满分16分(1)若1)0(≥f ,则1112-≤⇒⎩⎨⎧≥<⇒≥-a a a a a(2)当a x ≥时,⎪⎩⎪⎨⎧<≥=⎪⎩⎪⎨⎧<≥=+-=0,320,20),3(0),()(,23)(22min22a a a a a a f a a f x f a ax x x f 当a x ≤时,⎪⎩⎪⎨⎧<≥-=⎩⎨⎧<≥-=-+=0,20,20),(0),()(,2)(22min22a a a a a a f a a f x f a ax x x f 综上⎪⎩⎪⎨⎧<≥-=0,320,2)(22mina a a a x f (3)),(+∞∈a x 时,1)(≥x h 得012322≥-+-a ax x ,222812)1(124a a a -=--=∆当2626≥-≤a a 或时,),(,0+∞∈≤∆a x ; 当2626<<-a 时,△>0,得:⎪⎩⎪⎨⎧>≥-+----ax a a x a a x 0)323)(323(22 讨论得:当)26,22(∈a 时,解集为),(+∞a ; 当)22,26(--∈a 时,解集为⎪⎪⎭⎫⎢⎢⎣⎡+∞-+⋃--,323]323,(22a a a a a ; 当⎥⎦⎤⎢⎣⎡-∈22,22a 时,解集为⎪⎪⎭⎫⎢⎢⎣⎡+∞-+,3232a a . 数学Ⅱ[A .选修4 - 1几何证明选讲答案] :本小题主要考查四边形、全等三角形的有关知识,考查推理论证能力.满分10分.证明:由△ABC ≌△BAD 得∠ACB=∠BDA ,故A 、B 、C 、D 四点共圆,从而∠CBA=∠CDB .再由△ABC ≌△BAD 得∠CAB=∠DBA .因此∠DBA=∠CDB ,所以AB ∥CD .[B .选修4 - 2:矩阵与变换答案] :本小题主要考查逆矩阵的求法,考查运算求解能力.满分10分.解:设矩阵A 的逆矩阵为⎥⎦⎤⎢⎣⎡w y z x ,则⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡10011223 = w y zx即⎥⎦⎤⎢⎣⎡=⎥⎦⎤++⎢⎣⎡+100122322z 3 +w y w y z x x ,故⎩⎨⎧=+=+⎩⎨⎧=+=+,12,023,,02,123w y w y z x z x 解得:3,2,2,1-===-=w y z x ,从而A 的逆矩阵为⎥⎦⎤-⎢⎣⎡-=-32211 A . [C . 选修4 - 4:坐标系与参数方程答案] :本小题主要考查参数方程和普通方程的基本知识,考查转化问题的能力.满分10分.解:因为212-+=t t x ,所以3122y t t x =+=+,故曲线C 的普通方程为:2360x y -+= [ D . 选修4 - 5:不等式选讲答案] :本小题主要考查比较法证明不等式的常见方法,考查代数式的变形能力.满分10分.证明:3322222232(32)3()2()(32)().a b a b ab a a b b b a a b a b +-+=-+-=-- 因为a ≥b >0,所以a b -≥0,2232a b ->0,从而22(32)()a b a b --≥0, 即3332a b +≥2232a b ab +.[必做题第22题答案] :本小题主要考查直线、抛物线及两点间的距离公式等基本知识,考查运算求解能力.满分10分.解:(1)由题意,可设抛物线C 的标准方程为px y 22=,因为点)2,2(A 在抛物线C 上,所以1=p ,因此,抛物线C 的标准方程为x y 22=.(2)由(1)可得焦点F 的坐标是)0,21(,又直线OA 的斜率为122=,故与直线OA 垂直的直线的斜率为1-,因此,所求直线的方程是021=-+y x .(3)解法一:设点D 和E 的坐标分别为),(11y x 和),(22y x ,直线DE 的方程是)(m x k y -=,0≠k 将m kyx +=代入x y 22=,有0222=--km y ky ,解得kmk y 22,1211+±=.由DE ME 2=知)121(221122-+=++mk mk ,化简得m k 42=. 因此22122212212))(11()()(y y ky y x x DE -+=-+-= )4(49)21(4)11(2222m m k mk k +=++=.所以)0(423)(2>+=m m m m f . 解法二:设),2(),,2(22t t E s s D ,由点)0,(m M 及DMME 2=得)0(20),2(22122s t s m m t -=--=-.因此2,2s m s t =-= 所以)0(423)2()22()(222222>+=--+-==m m m s s s s DE m f .[必做题第23题答案] :本小题主要考查概率的基本知识和记数原理,考查探究能力.满分10分.(1)解:因为方程022=++b ax x 有实数根,所以0442≥-=∆b a ,即2a b ≤(i )当2n a n ≤≤时,有22a n ≤,又2,,2,1n b ⋅⋅⋅∈,故总有b ,有12+-n n 种取法,b有2n 种取法,所以共有22)1(n n n +-组有序数组),(b a 满足条件;(ii )当11-≤≤n a 时,满足21ab ≤≤的b有2a个,故共有6)12)(1()1(3212222--=-+⋅⋅⋅+++n n n n 组有序数组),(b a 满足条件.由(i )(ii )可得6)1346(6)12)(1()1(23222++-=--=+-=n n n n n n n n n n T n ,从而32346134622nn n n n T P n n ++-==. ⑵证明:我们只需证明:对于随机选取的n b a ,,2,1,⋅⋅⋅∈,方程022=++b ax x 无实数根的概率nP n 11<-.若方程022=++b ax x 无实数根,则0442<-=∆b a ,即b a <2的有序数组),(b a 的组数小于n n ,从而,方程022=++b ax x 无实数根的概率nn n n P n 112=<-,所以n P n 11->.试卷综合解读与评析2009年高考江苏卷保持了2008年高考江苏卷的特点,以稳为主,稳中有变,更加体现新课程理念,所有试题的建构,不偏不怪,难易得当,紧扣考纲,贴近课本.注重考查基础知识,基本技能,基本数学思想和方法,对当前高中数学教学和高三数学复习备考有着鲜明的导向作用.下面从数学I、II试题的答案,别解、知识点、苏教版教材的出处,考纲要求,课本要求,用到的数学思想方法,容易导致失误的地方等方面进行综合解读.(要说明的是:江苏高考试题分文、理科,除选修的科目不同外,语、数、外三门必修科目的设置也有同有异:英语科目文理科试题相同,分值为120分;数学、语文两门必修科目,文理试题的设置分I、II两部分,对于文科和理科的考生数学和语文的I卷试题相同、分值均为160分,对理科生要加考数学II试题,文科考生要加考语文II试题分值均为40分.这样语数外三门必修科目文、理试题的总分值一样——200分+160分+120分=480分.)1.数学I试题(文理同卷)填空题部分填空题没有难度,从1至12题都平铺直叙,送分送到位,13、14题属于中档题,也容易拿分,没有难题.对照考纲和教材将14条填空题进行分析和解读如下:(附:表中的“等级”是指:江苏《考试说明》将考点要求分成A、B、C三个等级,其中C级要求最高,B 级次之、A级要求最低;表中的“层次”是指:江苏教材上的习题分为三个层次即:感受·理解、思考·运用和探究·拓展)2 数学I试题(文理同卷)解答题部分对于15题,此题主要考查平面向量数量积的坐标运算,两角和与差的三角函数,二倍角的正弦,考纲要求分别为C、C、B,坚持了重点知识重点考查的原则,数学思想方法主要考查了转化思想题型常规,思路清晰可循,三基好的考生容易得满分.对于16题,此题是立体几何题,仍然是考察平行与垂直的证明,题目简单明了,但要注重过程,判定定理的条件必须写全,线面平行是三个条件,面面垂直是两个条件,但之前需证明线面垂直,那是五个条件.对于17、18题第一小问,比较简单,但第二小问难度加大.17题数列题的第一小问是基本量的运算,大多考生不会有问题,第二小问有一丝数论的味道,题目简洁而又精彩!18题是解析几何题,考查直线与圆的位置关系,第二小问思路其实比较清晰,因为圆1C 与圆2C 的半径相等,及直线1l 被圆1C 截得的弦长与直线 2l 被圆2C 截得的弦长相等,所以圆1C 的圆心到直线1l 的距离和圆2C 的圆心到直线2l 的距离相等,列出等式,题目中要求“存在无数对直线”转化为“等式有无数解”即可,但是字母运算较复杂,考察考生的耐心与细心. 对于19题,此题主要考查函数与基本不等式等基础知识,比较好地考查了考生对信息的接收、加工和输出等数据处理能力,数学建模能力、抽象概括能力以及数学阅读能力达到有效考查综合素质的目的.考查与以往不同的是,大题的顺序有了明显的颠倒,数列难度下降了很多,放在了大题第三题的位置,而以往应用题是不会放在这个位置的,虽然难度适中,以生活中的满意度为背景,但题干中的字比较多,问题的表述较长,变量均以字母形式出现,提高了应用题的难度,这就要求考生多读几遍题目,多读几遍还是可以理解的,第⑴、⑵小题能够做出,第⑶小题有点难度;有些考生就承受不了了,所以对最后一题也有心理干扰,这也是广大考生不太适应的又一方面,从中可以看到今年的高考试卷在知识与能力考查的同时,体现了对课改新理念的创新与发展.对于20题,此题主要考查函数的概念、性质、图像及解一元二次不等式等基础知识,考查灵活运用数型结合、分类讨论的思想方法.这样的的分类讨论其实高中训练得很多了,但在考场上想得满分也并不容易.第(3)小问不要考生写过程,只要结果,需要一定的数学直觉思维,如果结合图形问题可以得到很好地解决,命题很有新意,不落浴套,具有较强的选拔功能.3. 数学Ⅱ附加题(理科做)今年是执行必做、选做分卷考试新模式的第二年,附加题部分难度控制的比较适中,在全省考生慢慢接受并熟悉了这种模式后,相比去年,今年的选作题方面考点上没有任何的变动,但圆锥曲线、函数中不等关系的证明出现在该部分作为压轴考题,难度明显比去年有了很大的提升. 4 全卷综合点评 4.1 全卷综合解读2009年高考数学试题,对考试说明中的8个C 级要求的知识点和B 级要求中传统的问题都进行了有效的考查,在保持题型稳定的基础上,进行适度的改革和创新,试卷贴近教学实际,坚持能力立意,全面检测考生的数学素养,充分体现新课程的基本理念.试卷主要有以下几个方面的特点:4.1.1 多题把关,有效发挥选拔功能第17,18题第二小问,第19题、第20题的第三问有一定的难度,改变了过去一题或两题把关的习惯,在凸显文理公平基础上,命题者这样处理对不同层次考生群体更有区分度,有利于高校选拔人才.基于同样的原因,数学Ⅱ附加题(理科做)部分,两道必做题对数学语言的转化以及数学思想方法有一定的要求,相对较难,其他试题很简单.4.1.2 能力立意,旨在考察数学素养全卷在考查知识的同时,注重考查学生的数学思维能力和应用意识.许多试题实际上并不难,对于知识点考生很熟悉,但需要考生自主综合所学知识,才能解决问题,如第17题第二问,其实是恒成立问题.许多试题若能先想清楚问题的关键或本质,确定了合适的解题思路和方向后再动手,解答会容易的多,否则会陷入繁琐的运算之中,比如第13题,第14题.部分题目在考查基础知识点上有所创新,题目设计灵活.如数学卷第17题第(2)问,第18题第(2)问,都是对一个问题进行纵向探究,考查学生创新意识,同时要求学生掌握通性通法,淡化特殊技巧,例如第18题第(2)问,如果用几何方法解决在考场上几乎不能成功,试题的设问已将几何法排除在外,命题者的意思很明确,考察解析几何的本质——用代数方法研究图形的几何性质,体现数形结合和等价转化的重要数学思想4.1.3 引领课改,全面体现课程标准试卷以朴素的数学知识为载体,综合考查最基本的数学思想和方法,体现了高考命题重实质、重内涵的指导思想,注重通性通法、淡化特殊技巧,对中学数学教学有较好的导向作用.不少试题注意在具体的情景中、在解决问题的过程中突出考查学生数学思想和数学方法.如第20题以二次函数为载体,重点考查分类谈论、数形结合思想,其中的第三问,只要直接写出解,不需要过程,打破了长期以来人们所固有的解答题不能以图代证的模式,给平时积极主动、勇于探索的考生有发挥的空间.这也是新课改的明确要求,新课程标准明确指出:“高中数学课程应注重提高学生的数学思维能力,这是数学教育的基本目标之一,人们在学习数学和运用数学解决问题时,不断地经历直观感知、观察发现、归纳推理、空间想象、抽象概括……等思维过程”.另外,试题加强了对应用意识和创新意识的考查,力求对现实世界中蕴涵的一些数学模式进行思考和做出判断,例如第19题以生活中的满意度为背景,问题的表述较长,需要考生耐心读懂题目,但模式识别方便,同时还考查了学生将文字语言转化为数学语言的能力.4.1.4 保持稳定,凸显公平公正原则(1)整卷试题呈现:低起点、入手宽、由易到难,逐步深入、多题把关的格局,全卷结构、题型包括难度都基本稳定,依据考试说明,突出对教材基本内容的考查.填空题比较平和,不需太繁的计算,考生普遍感觉顺手.许多试题源于课本,略高于课本,如第1、2、3、4、5、7、11、15题等,都由课本例题、习题进行恰当变更、迁移、综合、创新整合而成,给人以似曾相识的感觉.最后6个解答题由易到难,涉及的知识内容基础、常规,入手容易,但深入有一定困难.附加题部分,选做题对知识点的考查单一,结论要求明确,学生入手较易.(2)通览全卷试题和答案:不见偏题怪题、人为陷阱,处处体现人文关怀、呈现关爱.如填空题14题,求6q,正常应该求q,有谬常理.细细想来,为命题者的良苦用心所折服,这是因为如果所编题目答案q是整数,学生很易猜到,失去考察知识的意义,现在所编题目。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009江苏高考数学科考试说明一、命题指导思想2009年普通高等学校招生全国统一考试数学科(江苏卷)命题将遵循教育部考试中心颁发的《普通高等学校招生全国统一考试(数学科)大纲》精神,依据教育部《普通高中数学课程标准(实验)》和江苏省《普通高中课程标准教学要求》,既考查中学数学的基础知识和方法,又考查考生进入高等学校继续学习所必须的基本能力.1.突出数学基础知识、基本技能、基本思想方法的考查对数学基础知识和基本技能的考查,贴近教学实际,既注意全面,又突出重点,注重知识内在联系的考查,注重对中学数学中所蕴涵的数学思想方法的考查.2.重视数学基本能力和综合能力的考查数学基本能力主要包括空间想象、抽象概括、推理论证、运算求解、数据处理这几方面的能力.(1)空间想象能力的考查要求是:能够根据题设条件想象并作出正确的平面直观图形,能够根据平面直观图形想象出空间图形;能够正确地分析出图形中基本元素及其相互关系,并能够对空间图形进行分解和组合.(2)抽象概括能力的考查要求是:能够通过对实例的探究,发现研究对象的本质;能够从给定的信息材料中概括出一些结论,并用于解决问题或作出新的判断.(3)推理论证能力的考查要求是:能够根据已知的事实和已经获得的正确的数学命题,运用归纳、类比和演绎进行推理,论证某一数学命题的真假性.(4)运算求解能力的考查要求是:能够根据法则、公式进行运算及变形;能够根据问题的条件寻找与设计合理、简捷的运算途径;能够根据要求对数据进行估计或近似计算.(5)数据处理能力的考查要求是:能够运用基本的统计方法对数据进行整理、分析,以解决给定的实际问题.数学综合能力的考查,主要体现为分析问题与解决问题能力的考查,要求能够综合地运用有关的知识与方法,解决较为困难的或综合性的问题.3.注重数学的应用意识和创新意识的考查数学的应用意识的考查,要求能够运用所学的数学知识、思想和方法,构造数学模型,将一些简单的实际问题转化为数学问题,并加以解决.创新意识的考查要求是:能够综合,灵活运用所学的数学知识和思想方法,创造性地解决问题.二、考试内容及要求数学试卷由必做题与附加题两部分组成.选修测试历史的考生仅需对试题中的必做题部分作答;选修测试物理的考生需对试题中必做题和附加题这两部分作答.必做题部分考查的内容是高中必修内容和选修系列1的内容;附加题部分考查的内容是选修系列2(不含选修系列1)中的内容以及选修系列4中专题4-1《几何证明选讲》、4-2《矩阵与变换》、4-4《坐标系与参数方程》、4-5《不等式选讲》这4个专题的内容(考生只需选考其中两个专题).对知识的考查要求依次分为了解、理解、掌握三个层次(在下表中分别用A、B、C表示).了解:要求对所列知识的含义有最基本的认识,并能解决相关的简单问题.理解:要求对所列知识有较深刻的认识,并能解决有一定综合性的问题.掌握:要求系统地掌握知识的内在联系,并能解决综合性较强的或较为困难的问题.具体考查要求如下:1.必做题部分2.附加题部分三、考试形式及试卷结构(一)考试形式闭卷、笔试,试题分必做题和附加题两部分.必做题部分满分为160分,考试时间120分钟;附加题部分满分为40分,考试时间30分钟.(二)考试题型1.必做题 必做题部分由填空题和解答题两种题型组成.其中填空题14小题,约占70分;解答题6小题,约占90分.2.附加题 附加题部分由解答题组成,共4小题.其中,必做题2小题,考查选修系列2(不含选修系列1)中的内容;选做题共4小题,依次考查选修系列4中4-1、4-2、4-4、4-5这4个专题的内容,考生只须从中选2个小题作答.填空题只要求直接写出结果,不必写出计算和推理过程;解答题应写出文字说明、证明过程或演算步骤.(三)试题难易比例必做题部分由容易题、中等题和难题组成.容易题、中等题和难题在试卷中的比例大致为4:4:2.附加题部分由容易题、中等题和难题组成.容易题、中等题和难题在试卷中的比例大致为5:4:1.四、典型题示例 A.必做题部分(一)填空题1.已知函数)sin(2ϕω+=x y 0>ω在区间]2,0[π上的图象如图,则=ω 【解析】本题主要考查三角函数的图象与周期.本题属容易题. 【答案】2.2.已知)2,(),6,0(-a B A 两点间距离是10,则实数=a 【解析】本题主要考查两点间距离公式.本题属容易题. 【答案】 6或6- 3.若将复数ii-+11表示为i R b a bi a ,,(∈+是虚数单位)的形式,则=+b a【解析】本题主要考查复数的运算.本题属容易题. 【答案】l .4.设集合},,73)1(|{2R x x x x A ∈+<-=则集合Z A 中有 个元素. 【解析】本题主要考查一元二次不等式的解法、集合的运算等基础知识.本题属容易题. 【答案】 6.5.在平面直角坐标系xOy 中,设D 是横坐标与纵坐标的绝对值均不大于2的点构成的区域,E 是到原点的距离不大于l 的点构成的区域.向D 中随机投一点,则所投的点在E 中的概率是 .【解析】本题主要考查几何概型的意义及概率计算公式.本题属容易题. 【答案】16π. 6.经过圆0222=++y x x 的圆心,且与直线0=+y x 垂直的直线方程是 【解析】本题主要考查直线的方程与圆的方程,以及两直线的垂直关系等基础知识.本题属容易题.【答案】.01=+-y x7.已知数列}{n a 的前n 项和,92n n S n -=第k 项满足,85<<k a 则=k a 【解析】本题主要考查数列的前n 项的和与其通项的关系,以及解简单的不等式等基础知识.本题属中等题. 【答案】6.8.已知向量),,1(),,1(n n -==若-2与垂直,则||等于 【解析】本题主要考查以坐标表示的平面向量的加、减、数乘及数量积的运算等基础知识.本题属中等题. 【答案】2.9.某地区为了解80~70岁老人的日平均睡眠时间(单位:h),随机选择了50位老人进行调查.下表是这50位老人睡眠时间的频率分布表.在上述统计数据的分析中,一部分计算见算法流程图,则输出的S 的值为【解析】本题考查了频率分布表、样本数据的平均数, 以及流程图等基础知识.本题属中等题. 【答案】6.42.10.在平面直角坐标系xOy 中,已知ABC ∆的顶点)0,4(-A 和)0,4(C ,顶点B 在椭圆192522=+y x 上, 则=+BCA sin sin sin 【解析】本题主要考查椭圆的定义、正弦定理等基础知识. 本题属中等题. 【答案】45. 11.设z y x ,,为正实数,满足,032=+-z y x 则xz y 2的最小值是【解析】本题主要考查代数式的恒等变形及基本不等式等基础知识.本题属中等题. 【答案】3.12.满足条件BC AC AB 2,2==的三角形ABC 的面积的最大值是【解析】本题主要考查灵活运用有关的基础知识解决问题的能力.本题属难题. 【答案】22. (二)解答题13.如图,在平面直角坐标系xOy 中,以Ox 轴为始边作两个锐角,,βα它们的终边分别与单位圆交于B A 、两点.已知B A 、两点的横坐标分别是⋅552102、(1)求)tan(βα+的值; (2)求βα2+的值.【解析】本题主要考查三角函数的基本概念,以及两角和(差)的三角函数公式的简单运用等基础知识,考查运算求解能力.本题属容易题. 【参考答案】(1)由已知条件及三角函数的定义可知,⋅==552cos ,102cos βα 因α为锐角,故,0sin >α从而1027cos 1sin 2=-=αα. 同理可得55cos 1sin 2=-=ββ.因此⋅==21tan ,7tan βα 所以.32171217tan tan 1tan tan )tan(-=⨯-+=-+=+βαβαβα .121)3(1213])tan[()2tan()2(-=⨯--+-=++=+ββαβα 又,20,20πβπα<<<<故,2320πβα<+< 从而由1)2tan(-=+βα得432πα-+r . 14.如图,在四面体ABCD 中,BD AD CD CB ⊥=,,点F E 、分别是BD AB 、 的中点.求证:(1)直线//EF 平面ACD ;(2)平面⊥EFC 平面BCD . 【解析】本题主要考查直线与平面、 平面与平面的位置关系等基础知识,考查空间想象能力、推理论证能力.本题属容易题. 【参考答案】(1)在ABD ∆中,因为F E 、分别是BD AB 、的中点,所以AD EF //. 又⊂AD 平面⊂/EF ACD ,平面ACD , 所以直线//EF 平面ACD(2)在ABD ∆中,因为,//,AD EF BD AD ⊥所以.BD EF ⊥在BCD ∆中,因为F CD CB ,=是BD 的中点,所以BD CF ⊥. 因为⊂EF 平面⊂CF EFC ,平面EFC ,EF 与CF 交于点F ,所以⊥BD 平面EFC .又因为⊂BD 平面,BCD 所以平面⊥EFC 平面.BCD15.设函数,)(xb ax x f -=曲线)(x f y =在点))2(,2(f 处的切线方程为.01247=--y x (1)求)(x f 的解析式;(2)证明:曲线)(x f y =上任一点处的切线与直线0=x 及直线x y =所围成的三角形的面积是一个(与b a ,无关的)定值,并求此定值.【解析】本题主要考查导数的几何意义、导数的运算以及直线方程等基础知识,考查运算求解能力、推理论证能力.本题属中等题.【参考答案】(1)方程01247=--y x 可化为.347-=x y 当2=x 时,⋅=21y 又,)(2x b a x f +='于是⎪⎪⎩⎪⎪⎨⎧=+=-,474,2122b a b a 解得⎩⎨⎧==.3,1b a 故⋅-=xx x f 3)( (2)设),(00y x P 为曲线上任一点.由231x y +='知曲线在点),(00y x P 处的切线方程为 ),)(31(0200x x x y y -+=-即).)(31()3(02000x x x x x y -+=-- 令,0=x 得,60x y -=从而切线与直线0=x 的交点坐标为)6,0(0x - 令,x y =得,20x x y ==从而切线与直线x y =的交点坐标为)2,2(00x x .所以点),(00y x P 处的切线与直线x y x ==,0所围成的三角形的面积为.6|2||6|.2100=⋅-x x 故曲线)(x f y =上任一点处的切线与直线x y x ==,0所围成的三角形的面积为定值,此定值为6.16.(1)设n a a a ,,,21 是各项均不为零的)4(≥n n 项等差数列,且公差,0=/d若将此数列删去某一项后得到的数列(按原来的顺序)是等比数列,(i)当4=n 时,求 da 1的数值;(ii)求n 的所有可能值. (2)求证:存在一个各项及公差均不为零的)4(≥n n 项等差数列,任意删去其中的k 项 ),31(-≤≤n k 都不能使剩下的项(按原来的顺序)构成等比数列.【解析】本题以等差数列、等比数列为平台,主要考查学生的探索与推理能力. 本题属难题.【参考答案】首先证明一个“基本事实”一个等差数列中,若有连续三项成等比数列,则这个数列的公差00=d .事实上,设这个数列中的连续三项00,,d a a d a +-成等比数列,则),)((002d a d a a +-=由此得2022d a a -=,故.00=d (1)(i)当4=n 时,由于数列的公差,0=/d 故由“基本事实"推知,删去的项只可能为2a 或3a .①若删去2a ,则由431,,a a a 成等比数列,得)3()2(1121d a a d a +⋅=+.因,0=/d 故由上式得,41d a -=即.41-=da 此时数列为,3,4d d --,,2d d --满足题设. ②若删去3a ,则421,,a a a 由成等比数列,得).3()(1121d a a d a +⋅=+因,0=/d 故由上式得,1d a =即.11=d a 此时数列为d d d d 4,3,2,满足题设. 综上可知da 1的值为4-或1. (ii)当6≥n 时,则从满足题设的数列n a a a a ,,,,321 中删去任意一项后得到的数列,必有原数列中的连续三项,从而这三项既成等差数列又成等比数列,故由“基本事实”知,数列n a a a a ,,,,321 的公差必为0,这与题设矛盾.所以满足题设的数列的项数.5≤n又因题设,4≥n 故4=n 或5=n .当4=n 时,由(i)中的讨论知存在满足题设的数列.当5=n 时,若存在满足题设的数列54321,,,,a a a a a 则由“基本事实”知,删去的项只能是3a ,从5421,,,a a a a 而成等比数列,故),3()(1121d a a d a +⋅=+及).4)(()3(1121d a d a d a ++=+分别化简上述两个等式,得21d d a =及,521d d a -= 故.0=d 矛盾.因此,不存在满足题设的项数为5的等差数列. 综上可知,n 只能为4.)2(我们证明:若一个等差数列)4(,,,21≥n b b b n 的首项1b 与公差d '的比值为无理数,则此等差数列满足题设要求.证明如下:假设删去等差数列)4(,,,21≥n b b b n 中的)31(-≤≤n k k 项后,得到的新数列(按原来的顺序)构成等比数列,设此新数列中的连续三项为+1b ),10(,,32131211-≤<<≤'+'+'n m m m d m b d m b d m 于是有),)(()(3111221d m b d m b d m b '+'+='+化简得d b m m m d m m m '-+='-123123122)2()(………………(*)由01=/'d b 知,3122m m m -与2312m m m -+同时为零或同时不为零.若,02231=-+m m m 且,03122=-m m m 则有,0)2(31231=-+m m m m 即,0)(231=-m m 得,31m m =从而,321m m m ==矛盾.因此,2312m m m -+与3122m m m -都不为零,故由(*)式得⋅-+-='231312212m m m m m m d b …………………(**) 因为321,,m m m 均为非负整数,所以(**)式右边是有理数, 而d b '1是一个无理数,所以(**)式不成立.这就证明了上述结果. 因12+是一个无理数.因此,取首项,121+=b 公差.1='d 则相应的等差数列)4(2,,32,22,12≥++++n n 是一个满足题设要求的数列.B .附加题部分1.随机抽取某厂的某种产品200件,经质检,其中有一等品l26件、二等品50件、三等品20件、次品4件.已知生产l 件一、二、三等品获得的利润分别为6万元、2万元、1万元,而生产l 件次品亏损2万元.设l 件产品的利润为ξ(单位:万元).(1)求ξ的分布列;(2)求1件产品的平均利润(即ξ的数学期望);(3)经技术革新后,仍有四个等级的产品,但次品率降为%,1一等品率提高为%.70 如果此时要求l 件产品的平均利润不小于4.73万元,则三等品率最多是多少?【解析】本题主要考查概率的基础知识,如概率分布、数学期望等.本题属中等题.【参考答案】(1)由题设知,ξ的可能取值为,2,1,2,6-且,25.020050)2(,63.0200126)6(======ξξP P .02.02004)2(,1.020020)1(==-====ξξP P由此得ξ的分布列为ξ)2(的数学期望为:,34.463.062521.0102.0)2(=⨯+⨯+⨯+⨯-=αξE即1件产品的平均利润是4.34万元.(3)设技术革新后的三等品率为x ,二等品率为y .由题设可知,ξ的可能取值为,2,1,2,6-且ξ的分布列为:又,17.001.0=+++y x得.29.0=+y x 特别地,.29.00≤≤x 于是技术革新后l 件产品的平均利润为:).29.00(76.47.062101.0)2(≤≤-=⨯+⨯+⨯+⨯-=x x y x E ξ故要求l 件产品的平均利润不小于4.73万元,等价于,73.4≥ξE即,73.476.4≥-x 解得.03.0≤x因此,要使1件产品的平均利润不小于4.73万元,则三等品率最多为%.32.如图,设动点P 在棱长为l 的正方体1111D C B A ABCD -的对角线1BD 上, 记λ=BD P D 11.当APC ∠为钝角时,求λ的取值范围. 【解析】本题主要考查向量的坐标表示、向量运算及其几何意义等基础知识. 本题属中等题.【参考答案】 由题设可知,以1,,DD 为单位正交基底,建立如图所示的空间直角坐标系,xyz D -则有)1,0,0(),0,1,0(),0,1,1(),0,0,1(1D C B A .由),,,(),1,1,1(111λλλλ-==-=B D P D B D 所以D PD 11+=)1,0,1(),,(-+--=λλλ),1,,1(---=λλλ)1,1,0(),,(11-+--=+=λλλD PD).1,1,(---=λλλ显然APC ∠不是平角,所以APC ∠为钝角等价于>=<=∠PC PA APC ,cos cos 0||||<⋅PC PA 这等价于,0<⋅ 即0)1()1()())(1(2<-+-⋅-+--λλλλλ, 0)13)(1(<--λλ,解得131<<λ因此,λ的取值范围是⋅)1,31(3.选修14-几何证明选讲如图,设ABC ∆的外接圆的切线AE 与BC 的延长线交于点E ,BAC ∠的平分线与BC 交于点D .求证:EB EC ED ⋅=2.【解析】本题主要考查三角形与圆的一些基础知识,如三角形的外接圆、角平分线,圆的切线性质、圆幂定理等.本题属容易题.【参考答案】如图,因为AE 是圆的切线,所以.CAE ABC ∠=∠又因为AD 是BAC ∠的平分线,所以,CAD BAD ∠=∠从而.CAD CAE BAD ABC ∠+∠=∠+∠因为,,CAE CAD DAE BAD ABC ADE ∠+∠=∠∠+∠=∠所以,DAE ADE ∠=∠故.ED EA =因为AE 是圆的切线,所以由切割线定理知.2EB EC EA ⋅=而.ED EA =所以.2EB EC ED ⋅= 4.选修24-矩阵与变换在直角坐标系中,已知ABC ∆的顶点坐标为)2,0(),1,1(),0,0(C B A ,求ABC ∆在矩阵MN作用下变换所得到的图形的面积,这里矩阵=M ⋅⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡0110,0110N 【解析】本题主要考查矩阵的运算、矩阵与变换之间的关系等基础知识.本题属容易题.【参考答案】方法一:由题设得⋅⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=100101100110MN 由,20201001,11111001,00001001⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡- 可知C B A 、、三点在矩阵MN 作用下变换所得到的点分别是)2,0(),1,1(),0,0(-'-''C B A计算得C B A '''∆的面积为l .所以△ABC 在矩阵MN 作用下变换所得到的图形C B A '''∆ 的面积为1.方法二:在矩阵⎥⎦⎤⎢⎣⎡-=0110N 作用下,一个图形变换为其绕原点逆时针旋转︒90得到的图形;在矩阵⎥⎦⎤⎢⎣⎡=0110M 作用下,一个图形变换为与之关于直线x y =对称的图形. 因此,ABC ∆在矩阵MN 作用下变换所得到的图形,与ABC ∆全等.从而其面积等于△ABC 的面积,即为l .5.选修44-坐标系与参数方程在平面直角坐标系xOy 中,点),(y x P 是椭圆1322=+y x 上的一个动点, 求y x S +=的最大值.【解析】本题主要考查曲线的直角坐标方程与参数方程的互化,以及求三角函数的最大(小)值等基础知识.本题属容易题.【参考答案】 因椭圆1322=+y x 的参数方程为θθθ(,sin ,cos 3⎩⎨⎧==y x 为参数),故可设动点P 的坐标为),sin ,cos 3(θθ其中.20πθ<≤因此y x S +=θθsin cos 3+= )sin 21cos 23(2θθ+⨯=)3sin(2πθ+=,所以,当6πθ=时,S 取最大值2. 6.选修54-不等式选讲设实数*,,1N n x ∈->证明:.1)1(nx x n +≥+【解析】本题主要考查不等式的证明以及数学归纳法等基础知识.本题属容易题.【参考答案】(1)当1=n 时,题中不等式显然成立.(2)假设当k n =时,有.1)1(kx x k +≥+,因为,1->x 所以01>+x因此,有)1()1()1(1x x x k k +⋅+=++)1()1(x kx +⋅+≥2)1(1kx x k +++=x k )1(1++≥,即当1+=k n 时题中不等式成立.综合(1)、(2)及数学归纳法可知,当1->x 时,不等式nx x n +≥+1)1(对任何*N n 成立.。
