第六章+材料的变形
材料科学基础习题与参考答案(doc14页)完美版

材料科学基础习题与参考答案(doc14页)完美版第⼀章材料的结构⼀、解释以下基本概念空间点阵、晶格、晶胞、配位数、致密度、共价键、离⼦键、⾦属键、组元、合⾦、相、固溶体、中间相、间隙固溶体、置换固溶体、固溶强化、第⼆相强化。
⼆、填空题1、材料的键合⽅式有四类,分别是(),(),(),()。
2、⾦属原⼦的特点是最外层电⼦数(),且与原⼦核引⼒(),因此这些电⼦极容易脱离原⼦核的束缚⽽变成()。
3、我们把原⼦在物质内部呈()排列的固体物质称为晶体,晶体物质具有以下三个特点,分别是(),(),()。
4、三种常见的⾦属晶格分别为(),()和()。
5、体⼼⽴⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),晶胞中⼋⾯体间隙个数为(),四⾯体间隙个数为(),具有体⼼⽴⽅晶格的常见⾦属有()。
6、⾯⼼⽴⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),晶胞中⼋⾯体间隙个数为(),四⾯体间隙个数为(),具有⾯⼼⽴⽅晶格的常见⾦属有()。
7、密排六⽅晶格中,晶胞原⼦数为(),原⼦半径与晶格常数的关系为(),配位数是(),致密度是(),密排晶向为(),密排晶⾯为(),具有密排六⽅晶格的常见⾦属有()。
8、合⾦的相结构分为两⼤类,分别是()和()。
9、固溶体按照溶质原⼦在晶格中所占的位置分为()和(),按照固溶度分为()和(),按照溶质原⼦与溶剂原⼦相对分布分为()和()。
10、影响固溶体结构形式和溶解度的因素主要有()、()、()、()。
11、⾦属化合物(中间相)分为以下四类,分别是(),(),(),()。
12、⾦属化合物(中间相)的性能特点是:熔点()、硬度()、脆性(),因此在合⾦中不作为()相,⽽是少量存在起到第⼆相()作⽤。
13、CuZn、Cu5Zn8、Cu3Sn的电⼦浓度分别为(),(),()。
材料力学第六章 弯曲变形

4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 (rad)
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w (3)校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知:EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
材料力学第6章弯曲变形

M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下,弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时,梁截面上有弯矩也有剪力,对于跨 度远大于截面高度的梁,剪力对弯曲变形的影响可以 省略,(a)式便可以作为横力弯曲变形的基本方程。其 中,M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合, 造成磨损不匀,产生噪音, 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大,会 使梁上小车行走困难, 出现爬坡现象,还会引 起较严重的振动。
变形超过允许数值,即 使在弹性范围内,也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为: 3 1 Fb 2 2 wmax l b 9 3 EIl
材料力学基础-6-1

6.1.2 滞弹性
对于完全弹性体,加上和除去应力,应变都是瞬时 达到平衡值,没有考虑时间的关系。若在弹性范围内 加载和卸载,发现应变不是瞬时达到其平衡值,而是 通过时间的延长,逐步趋于平衡值。
图中的0a为瞬时产生的弹性 应变;a`b是在应力作用下逐 渐产生的弹性应变叫滞弹性 应变。bc=0a,是应力去除时 瞬时消失的弹性应变; c`d= a`b是除去应力后,随时间的 延长逐步消失的滞弹性应变。
滑 移 带 与 滑 移 面 的 关 系
滑移是靠位错的运动实现的。位错沿滑移面滑移,
当移动到晶体表面时,便产生了大小等于柏氏矢量的
滑移台阶,该台阶称为滑移线,就是滑移面和表面的
交线。每个台阶的高度越为100nm。在金相显微镜下
看到的滑移痕迹往往是许多相距10nm左右的滑移线
形成的滑移带。
2. 滑移系
结论:单晶体没有确定的屈服极限,其屈服极限由 取向因子决定。
同一晶体可有几组晶体学上完全等价的滑移 系,但实际先滑移的是处在软位向的滑移系。密 排六方金属滑移时,只有一组滑移面,故晶体位 向的影响就十分显著。如图。面心立方金属有多 组滑移面,晶体位向的影响就不显著,不同取向 的晶体拉伸屈服强度仅相差两倍。
晶体发生弹性变形时,应力与应变成线性关系, 去掉外力后能够完全恢复原状。弹性变形阶段应力 与应变服从虎克定律(Hooke's law) :
E 或 G
其中σ为正应力,τ为切应力,ε为正应变,γ为切应 变,E为杨氏模量(Modulus of elasticity) ,G为切变 模量。
E与G的关系满足:
映象方法”或“映象规则” —— 一种快速确定具 有最大取向因子的滑移系统的方法。
第六章金属的塑性变形和断裂分析
1、单相固溶体的塑性变形:
塑变方式基本上与纯金属多晶体的变形相同, 但:
1.1产生固溶强化:由于溶质原子存在使强度、 硬度增高,塑性、韧性下降的现象;
原因:
①发生晶格畸变;
②形成柯氏气团:溶质原子在位错线附近的偏聚, 如图6-26所示;柯氏气团对位错有钉扎作用, 使位错运动的阻力增大;
a)溶质原子大于溶剂原子的置换固溶体; b)溶质原子小于溶剂原子的置换固溶体; c)间隙固溶体;
④fcc晶体孪生变形的示意过程,如图6-21所示; ⑤孪生时可听到声音; ⑥孪生对总变形量贡献不大;
⑦孪生的特点: 使一部分晶体发生了均匀的切变; 引起了晶体取向的变化; 不会改变晶体的点阵类型; 所需的切应力比滑移大许多倍; 在光学显微镜下观察到的是条带状;
第三节 多晶体的塑性变形
孪晶:以孪晶面为对称面而处于镜面对称位置的 一对晶体叫做孪晶(双晶),如图6-20所示;
说明: ①孪生是晶体塑变的另一种方式;
②孪生经常发生在:不易产生滑移的金属中、 某些金属滑移困难时、变形速度大时;
③孪生面和孪生方向: 例如:fcc:孪生面{111},孪生方向为
〈112〉; bcc: 孪生面{112},孪生方向为〈111〉
σ S—e
S — e:真应力真应变曲线
σ—ε
颈
σ—ε:工程应力应变曲线
缩
ε
工程应力—应变曲线中“颈缩”现 象掩盖了 “加工硬化”
3、弹性变形: 定义:金属受力发生变形,当外力去除,立即 恢复原状的变形,叫做弹性变形; 实质:利用双原子作用力模型解释: 仅原子间距发生微小的弹性变化,无显微组织 的变化; 特点:①变形是可逆的;
2.1滑移带:
高锰钢中的滑移带,500X
材料科学基础第六章

编辑课件
24
• 6.2.1.4 滑移时晶体的转动:晶体被拉伸而 产生滑移时,由于拉力共线的影响,晶面 位向会发生改变, 结果使滑移面和滑移方向 逐渐趋于平行于拉力轴线;而压缩时,晶 面改变的
• 结果使滑
• 移面逐渐
• 趋于与压
• 力轴线垂
• 直。
编辑课件
25
• 滑移面和滑移方向的改变必然导致斯密特 因子m的改变。
编辑课件
27
编辑课件
28
• 面心立方金属的滑移系为{111}<110>,4个{111} 面构成一个八面体。当拉力轴为[001]时,
• (1) 对所有{111}面, cosφ=02+02+12/(12+12+12·02+02+12)=1/3 φ=54.7º,
• (2) λ角对[101],[101] • [011],[011]也都为45º, • (3) 锥体底面上的两个 • <110>方向与[001]垂 • 直。
编辑课件
29
• 因此,八面体上有8个滑移系具有相同的取 向因子,当τ=τk时可以同时开动。但由于这 些滑移系有不同位向的滑移面和滑移方向 构成,滑移时有交互作用,产生交割和反 应,使滑移变得困难,产生较强的加工硬 化。
• 当两个以上的滑移
• 面沿同一方向滑移
• 便形成交滑移。
编辑课件
30
• 发生交滑移时, • 晶体表面会出现 • 曲折或波纹状的 • 滑移带。 • 最容易发生交滑 • 移的是体心立方 • 金属,滑移面为 • {110},{112}和{123},滑移方向总是<111>。 • 因滑移面不受限制,所以交滑移必是纯螺形位错,
第六章 金属和合金的塑性变形
第六章 金属和合金的塑性变形和再结晶金属材料(包括纯金属和合金)在外力的作用下引起的形状和尺寸的改变称为变形。
去除外力,能够消失的变形,称弹性变形;永远残留的变形,称塑性变形。
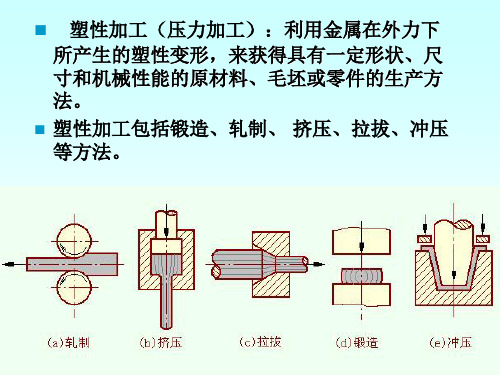
工业生产上正是利用塑性变形对金属材料进行加工成型的,如锻造、轧制、拉拔、挤压、冲压等。
塑性变形不仅能改变工件的形状和尺寸,还会引起材料内部组织和结构的变化,从而使其性能发生变化。
以再结晶温度为界,金属材料的塑性变形大致可分为两类:冷塑性变形和热塑性变形,在生产上,通常称为冷加工和热加工。
经冷塑性变形的金属材料有储存能,自由能高,组织不稳定。
若升高温度,使原子获得足够的扩散能力,则变形组织会恢复到变形前的状态,这个恢复过程包括:回复、再结晶和晶粒长大三个阶段。
从金属材料的生产流程来看,一般是先进行热加工,然后才进行冷加工和再结晶退火。
但为了学习的方便,本章先讨论冷加工,再讨论再结晶和热加工。
§6.1 金属材料的变形特性一、 应力—应变曲线金属在外力作用下,一般可分为弹性变形、塑性变形、断裂三个阶段。
图6.1是低碳钢拉伸时的应力—应变曲线,这里的应力和应变可表示为:000,L L L L L A F ∆=-==εσ 公式中F 是拉力,00,L A 分别是试样的原始横截面积和原始长度。
从图中可以得到三个强度指标:弹性极限e σ,屈服强度s σ,抗拉强度b σ。
当拉应力小于弹性极限e σ时,金属只发生弹性变形,当拉应力大于弹性极限e σ,而小于屈服强度s σ时,金属除发生弹性变形外,还发生塑性变形,当拉应力大于抗拉强度b σ时,金属断裂。
理论上,弹性变形的终结就是塑性变形的开始,弹性极限和屈服强度应重合为一点,但由于它们不容易精确测定,所以在工程上规定:将残余应变量为0.005%时的应力值作为弹性极限,记为005.0σ,而将残余应变量为0.2%时的应力值作为条件屈服极限,记为2.0σ。
s σ和2.0σ都表示金属产生明显塑性变形时的应力。
材料力学 第6章 梁的弯曲变形
(c)
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
在本章所取的坐标系中,
上凸的曲线w″为正值,下凸的为负值。
如图6-5所示。 按弯矩正负号的规定,正弯矩对应着负的w″, 负弯矩对应着正的w″,故(c)式
w
M (x)
(1
w2 )3 2
EI z
在小变形情况下, w dw 是一个很小的量, dx
则 w'2为高阶微量,可略去不计,故
挠曲线的近似微分方程
M x
w EI z
EIw''= −M (x)
(6-1b)
图6-5
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
6.4 积分法计算梁的变形
对于等直梁,可以直接积分,计算梁的挠度和转角。 将式(6-1b)积分一次,得到
EIw′ = EIθ = −∫ M (x) dx + C
maxFl 2 2EI来自A xyF
θmax B
x
wmax
l
图6-7 例题 6-1 图
wm a x
Fl 3 3EI
θ max为正值,表明梁变形后,截面B顺时针转动;
wmax为正值,表明点B位移向下。
材料力学
第2章第剪6章切与梁连的接弯件曲的变实形用计算
例题6-2 一简支梁受均布荷载q作用,如图6-8所示。试求梁的转角方程和 挠度方程, 并确定最大挠度和A、B截面的转角。设梁的弯曲刚度为EI。
A x
y
F
θmax B
x
wmax
l
进行两次积分,得到
EIw EI Flx Flx2 C
(a)
2
EIw Flx2 Fx3 Cx D
材料力学课件第六章1 弯曲变形
2 F 1 3 (0) Fl (0) 2 C (0) D 0 6 2 D0
解得: C 0, 6、确定挠曲线方程和转角方程: F EIw ' x 2 Flx 2 F Fl 2 EIw x 3 x 6 2 7、求截面位移
由方程所确定的曲率:
1 3 2 2 ( x) dw 1 dx
d w dx2 dw 1 dx
2 2
d 2w dx2
y
w x
x
3
F
因此有:
2
2
M ( x) EI
dw d 2 w M ( x) 又 1 得: 2 dx EI dx
二、画AB、DE受力图
三、变形协调条件 三、建立补充方程
v AB中 vDE中
( P RC ) L RC L2 48EI1 48EI 2
3 1 3
D
E
3 I 2 L1 P 解得:RC 3 3 I 2 L1 I1 L2 I1 L3 P 2 AB梁负担:P RC 3 3 I 2 L1 I1 L2
ห้องสมุดไป่ตู้
水平位移 2、弯曲变形的度量: (1)截面位移及特点: •横截面形心的竖向线位移 •横截面绕中性轴的角位移。 •横截面形心的水平线位移, 较竖向线位移小许多。
(2)度量变形的基本量: •挠度w: 横截面形心的竖向线位移,向上为正。 •截面转角θ :横截面绕中性轴的角位移,逆时针为正。
3、弯曲变形简化计算 (1)简化: 认为截面只有竖向位移。 y (2)简化后问题的特点: •挠曲线方程为挠度方程:
《材料力学》第六章-弯曲变形
当载荷P处于梁中点,即b=l/2时,xl=0.5l;
当载荷P移至支座B,即b→0时
x1
l2 0.577l 3
即使在这种极端的情况下,最大挠度的位置距中 点只有0.077l,也就是说点的位置影响甚小,最大挠 度总是发生在梁跨中点的附近。可以认为在工程中 当有一集中力作用在简支梁上时,梁的最大挠度发 生在梁的中点,其结果误差不超过3%。
§6.1 工程中的弯曲变形问题
工程中有些受弯构件在载荷作用下虽能满足强度 要求,但由于弯曲变形过大,刚度不足,仍不能保证 构件的正常工作,成为弯曲变形问题。
出现“爬坡”现象
使齿轮啮合力沿齿宽分布极 不均匀,加速齿轮的磨损。
一、挠度和转角
构件的弯曲变形通常用截面的挠度和转角度量。
梁在横向力作用下发生弯曲变形, y
§6.3 用积分法求弯曲变形
一、积分法求弯曲变形 w Mx
EI
积分
挠曲线近似微分方程
w E 1IM xd x C
积分
转角方程
w E 1IM xd x CD x 挠曲线方程
式中C和D是待定的积分常数,可根据梁的具体条件来确定。
积分法计算梁的变形的步骤: 1.建立梁截面的弯矩方程式M(x); 2.代人挠曲线近似微分方程式,并积分; 3.确定积分常数,得到具体的挠度和转角方程式; 4.求梁任一截面的转角和挠度。
令
w1 10 F 2lx b12-F 6lb l2-b2 0
当a>b时,x1<a,wmax发生在AC段内。
得: x1
l2 -b2 3
wm若求最大转角,求θA、θB,比较大小,取其大者。
当
x1
l2 -b2 3
wmax-
Fb 9
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
l li l0 l0 l0
li l0
z x
x
d d i d 0 d0 d0
22
F
Example 2
F d0 di
Solution: 样品在F力作用下,在z方向拉长,同时 在x方向上直径变小,d = 2.5 x 10-3 mm, 因此,在x方向上的应变:
37
当外力在某一滑移系中的分切应力达到 临界分切应力c 一定临界值时,该滑移系方向首先发生 滑移,该分切应力称为临界分切应力 critical resolved shear stress。 外力F 作用在面积为A 的园柱体上, 在滑移面上产生的分切应力
位错的运动
slip
climb
第五章 材料的变形
deformation of materials
1
材料承受载荷时发生的变形称为形变。
载荷类型:拉伸载荷Tension,压缩Compression、剪 切Shear和扭转Torsion。
拉伸 Tension
压缩 Compression
剪切 Shear
扭转 Torsion
450MPa MPa 345MPa
150
250MPa
0.0016
0.06
4.2.1 单晶体金属的塑性变形
正应力
外力
切应力
外 力 在 晶 面 上 的 分 解
切 应 力 作 用 下 的 变 形 锌 单 晶 的 拉 伸 照 片
弹性变形 解理断裂 塑性变形
滑移 slip dominant 孪生 twinning 扭折 kink
加载Load
= E• = G•
E-杨氏弹性模量; G —切变弹性模量;
应变 线性弹性变形
Linear elastic deformation
— 切应变; —泊松比;
E G 10 2(1 )
非线性弹性变形:应力和应变之间不保持线性关系,即不 满足虎克定律,但卸载后,变形依然消失并恢复原状的弹 性变形。
位错的滑移?
32
滑移带slip bands和滑移线slip lines
滑移的结果在晶体表面形成台阶,称滑
移线,若干条滑移线组成一个滑移带。
通常,滑移带是很狭窄的,往往观察 到的是呈线状的滑移带。
铜拉伸试样表面滑移带 33
滑移发生在晶体的密排面上,并沿密排方向进行。 ?
密排晶向原子间距最小, 单位滑移量小; 相互作用力最大,滑移 原子间距保持不变。
20
Polystyrene (PS)
聚苯乙烯
Nylon
尼龙
Polyesters
聚脂
Rubbers
橡胶
Example 1
A piece of copper originally 305 mm long is pulled in tension with a stress of 276 MPa. If the deformation is entirely elastic, what will be the resultant elongation? (已知铜的弹性模量E为110 GPa) Solution:
非线性弹性变形
Nonlinear elastic behavior
11
弹性变形的主要特征
1. 可逆变形:加载时变形,卸载后变形消失并恢复 原状;
2. 线性区域: 应力-应变保持单值线性函数,满足 虎克定律; 3. 弹性模量E:
12
弹性变形的本质
attractive repulsive
原子之间的作用力!
由于形变为完全弹性,因此,应力-应变满足虎克定律,即 = E• =E •(l/l0) 所以, l = ( l0)/E 将已知数据代入得:
l = ( l0)/E = (276 MPa x 305 mm)/110 x 103 MPa = 0.77 mm
21
Example 2
A tensile stress is to be applied along the long axis of a cylindrical brass rod that has a diameter of 10 mm. Determine the magnitude of the load(F) required to produce a 2.5 x 10-3 mm change in diameter if the deformation is entirely elastic. (已知黄铜的泊松比为 F 0.34,弹性模量为97 GPa)
4
正应力Stress 与 正应变Strain (拉伸、压缩情况)
材料受外力 F 作用后产生的
F 应力: A0 l l0 l 应变: l0 l0
F-载荷 A0-试样的原始截面面积 l0-试样的原始长度 l-试样变形后的长度
拉伸 Tensile 压缩 Compressive
5
切应力 与 切应变 (剪切、扭转情况)
31
a. 滑移 slip
• 滑移是指晶体的一部分沿一定的晶面和晶向相对于另一 部分发生滑动位移的现象。
滑移带slip bands的形成
弹性变形-外力克服单晶原子间的键合力, 使原子偏离其平衡位置,试样开始伸长。 晶面滑移-当外力大于屈服极限后,沿单 晶的某一特定晶面原子产生相对滑移。随应 力的增加,发生滑移的晶面增加,塑性变形 量加大。
F
作用于z方向上的应力为
z z E (7.35 104 )(97 103 MPa) 71.3MPa
最终,作用于z方向上的外力F为:
3 d0 2 6 2 10 10 m 2 Fz z A0 z ( ) (71.3 10 N / m )( ) 5600 N 2 2
29
工程应力-应变曲线
Example 3
From the tensile stress-strain behavior for the brass specimen shown in below figure, determine the following: (a)E;(b)0.2;(c)Fmax on a 12.8 mm cylindrical specimen (d)The change in length of a specimen original 250 mm long that is subjected to a tensile stress of 345 MPa。
Tensile strength
塑性变形 — 材料横截面变化的考虑
F F
初横截面积 A0
缩颈
变横截面积 AC
F 工程应力 A0
<
F Ac
真实应力
28
工程应力—— 真实应力
Engineering stress — True stress
在加载过程中
真实应力-应变曲线
真实应力始终 是增加的。评 价材料时通常 采弹性模量与温度、原子结合键类型的关系
陶瓷 (离子键)
弹性模量 大
金属 (金属键)
小
聚合物 (共价键)
15
应 力 的 几 何 考 虑
—不同应力种类相互联系
应力实际上是应力所作用平面的方向 取向的函数。
如:正应力可分解为对于PP’面的正应力’ 和切应力’。
' cos ' sin cos
7
测试仪器
拉伸实验 Tensile Test
标准样品
8
拉伸实验 Tensile Test
Standard stress-strain curve of low-C steel
9
5.1 弹性变形 Elastic deformation
卸载Unload
应力
斜率Slope = 弹性模量E
在弹性变形阶段,应力与应变有线性关系, 服从虎克定律 Hooke’s law,即:
当拉伸试样屈服以后,欲继续变形,必须不断增加载荷。当 载荷达到最大值Pb后,试样的某一部位截面开始急剧缩小, 出现了"缩颈necking",致使载荷下降,直到最后断裂。 试样能承受的最 大载荷除以试样 原始截面积所得 的应力,称为抗 拉强度,记为σb, 即:σb = Pb / F0
27
Fracture point
在剪切变形的情况下,则有 切应力:τ = F / Ao
A0
F
T T
切应变: = tan ( 100 %)
— 应变角;
扭转变形情况与剪切相似 静载:转矩T; 应变:转角
F
剪切 Shear
扭转 Torsion
6
材料受力后: elastic deformation plastic deformation fracture
2
16
E 泊松比 Poisson Ratio G 2(1 ) 杨氏模量(E)与切变弹性模量(G)的关联
各向同性材料 z 则有 x y l x l0 x l z l0 z
y x 泊松比 z z E 2G (1 )
大部分金属G 0.4 E
Solution: (a)弹性模量E为弹性变形区内应 力-应变曲线的斜率,计算得E=93.8 GPa; (b)根据 0.002偏移法,屈服强度 为250MPa; (c)抗拉强度为=450MPa,因此, 最大载荷F= A0= (d0/2)2,计算 得,F=57900 N; (d)应力345MPa对应的应变 =0.06,因此,长度变化l= l,计 30 算得, l= 15mm。
密排面的d最大,点阵阻 力最小,最容易滑移
滑移系 slip systems
滑移系 = 滑移面 * 滑移方向
34
FCC结构
