2018北京市昌平区高三二模数学试题及答案
2018北京昌平区高三数 学 (文)第二次统一练习

2018北京昌平区高三数 学 (文)第二次统一练习2018.5本试卷共5页,共150分. 考试时长120分钟. 考生务必将答案答在答题卡上,在试卷上作答无效.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1. 已知全集U =R ,集合A ={x ∣x> 1或x <1- },则U A =ðA. (,1)(1,)-∞-+∞B. (,1][1,)-∞-+∞C. (1,1)-D. [1,1]-2.下列函数中,在定义域上既是奇函数又是增函数的是 A. 1y x= B. 3y x = C. sin y x = D. lg y x =3. 在平面直角坐标系中,不等式组0,10,0x y x y y -≥⎧⎪+-≤⎨⎪≥⎩表示的平面区域的面积是A. 1B. 12C. 14D. 184. 设0.21()2a =,2log 3b =,0.32c -=,则A. b c a >>B. a b c >>C. b a c >>D. a c b >>5. 执行如图所示的程序框图,若输入 x 值满足24x -<≤,则输出y 值的取值范围是A. [3,2]-B. [1,2]C. [4,0)-D. [4,0)-U [1,2]6. 设,x y ∈R ,则||1||1x y ≤≤“且”是22+2x y ≤“”的A.充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件7. 某四棱锥的三视图如图所示,则该四棱锥的所有面中最大面的面积是 A .42log y x=2x <23y x =-y输出 结束否x输入开始是B .5C . 2D .28. 2011年7月执行的《中华人民共和国个人所得税法》规定:公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累进计算:全月应纳税所得额(含税级距)税率(%) 不超过1500元3 超过1500元至4500元的部分 10 超过4500元至9000元的部分20 ……某调研机构数据显示,希望将个税免征额从3500元上调至7000元.若个税免征额上调至7000元(其它不变),某人当月工资、薪金所得8500元,则此人当月少缴纳此项税款A. 45元B. 350元C. 400元D. 445元第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9. 在复平面内,复数1+ii对应的点的坐标为 . 10. 若抛物线212x y =,则焦点F 的坐标是 .11. 在∆ABC 中,2a =,263b =, π=3A ,则C = . 12. 能够说明命题“设,,a b c 是任意实数,若>>a b c ,则2a b c +>”是假命题的一组整数,,a b c 的值依次为 .13. 向量a ,b 在边长为1的正方形网格中的位置如图所示,则向量a ,b 所成角的余弦值是_________;向量a ,b 所张成的平行四边形的面积是__________.ab14.已知函数()22,1ln 1.x ax x f x a x x x ⎧-+<⎪=⎨≥⎪⎩‚‚①当1a =时,函数()f x 极大值是 ;②当1x <时,若函数()f x 有且只有一个极值点,则实数a 的取值范围是 ____ . 三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15. (本小题13分)已知函数()2sin()cos()3sin 244f x x x x =--+ππ. (I )求函数()f x 的最小正周期;(II )求函数()f x 在区间[0,]2π上的最值及相应的x 值.16. (本小题13分) 已知数列{}n a 满足1211,2a a ==,数列{}n b 是公差为2的等差数列,且11n n n n b a a na +++=. (I )求数列{}n b 的通项公式; (II )求数列{}n a 前n 项的和n S . 17.(本小题13分)为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A ,B 两地区分别随机抽取了20天的观测数据,得到A ,B 两地区的空气质量指数(AQI ),绘制如下频率分布直方图:根据空气质量指数,将空气质量状况分为以下三个等级:空气质量指数AQI (0,100)[100,200)[200,300)空气质量状况优良轻中度污染 重度污染(I )试根据样本数据估计A 地区当年(365天)的空气质量状况“优良”的天数;0.007AQI0.0030.0012502001500.008100频率/组距50O图1 A 地空气质量指数(AQI )0.005AQI0.0030.0022502001500.008100频率/组距50O图2 B 地空气质量指数(AQI )(II) 若分别在A 、B 两地区上述20天中,且空气质量指数均不小于150的日子里随机各抽取一天,求抽到的日子里空气质量等级均为“重度污染”的概率.18.(本小题14分)如图,四边形ABCD 是正方形,平面ABCD ⊥平面ABEF ,//,AF BE ,2,1AB BE AB BE AF ⊥===.(Ⅰ)求证:AC ⊥平面BDE ; (Ⅱ)求证: //AC 平面DEF ; (III )求三棱锥D -FEB 的体积.19. (本小题14分)已知椭圆()2222:10x y E a b a b+=>>的经过点(0,1),且离心率为22.(I )求椭圆E 的标准方程;(II )过右焦点F 的直线l (与x 轴不重合)与椭圆交于,A B 两点,线段AB 的垂直平分线交y 轴于点(0)M m ,,求实数m 的取值范围.20. (本小题13分)设函数3()f x x c =+,2()820g x x x =-,方程()()f x g x =有三个不同实根123123,,()x x x x x x <<. (I )求曲线()y f x =在点(1,(1))f 处的切线方程; (II )求c 的取值范围; (III )求证:124x x +>.FEBOADC数学试题答案一、选择题(共8小题,每小题5分,共40分) 题号 1 2 3 4 5 6 7 8 答案 DBCCAABC二、填空题(共6小题,每小题5分,共30分)9. (1,1)- 10. (0,3) 11. 5π(75)12︒或12. 1,2,3--- 13. 45; 3 14. 1e ;1a <三、解答题(共6小题,共80分) 15.(共13分)解:(I )π()sin(2)3sin 22f x x x =-+cos23sin 2x x=+π2sin(2)6x =+所以()f x 的最小正周期是π. -------------------8分 (II )因为 π02x ≤≤, 所以 02πx ≤≤,所以 ππ7π2666x ≤≤+,当π6x =时,max ()2f x =. 当π2x =时,m ()1in -f x =. --------------------13分16.(共13分)解:(Ⅰ)因为 11n n n nb a a na +++=,所以 1221b a a a += . 又因为1212a a =1,= , 所以11b =.所以数列{}n b 的通项公式是2-1n b n =. --------------------7分 (Ⅱ) 由(Ⅰ)知2-1n b n =,且11n n n n b a a na +++=.所以11(21)n n nn a a na ++-+=,得到112n n a a += .所以数列{}n a 是以1为首项,12为公比的等比数列. 那么数列{}n a 前n 项和111()222112nn n S --==--. --------------------13分17.(共13分)解:(Ⅰ)从A 地区选出的20天中随机选出一天,这一天空气质量状况“优良”的频率为(0.0080.007)500.75+⨯=,估计A 地区当年(365天)的空气质量状况“优良”的频率为0.75,A 地区当年(365天)的空气质量状况“优良”的天数约为3650.75274⨯≈天 .--------------------4分(Ⅱ)A 地20天中空气质量指数在[150,200)内,为200.003503⨯⨯=个,设为123,,a a a ,空气质量指数在[200,250)内,为200.001501⨯⨯=个,设为4a , B 地20天中空气质量指数在[150,200)内,为200.002502⨯⨯=个,设为12,b b , 空气质量指数在[200,250)内,为200.003503⨯⨯=个,设为345,,b b b , 设“A ,B 两地区的空气质量等级均为“重度污染””为C , 则基本事件空间1112131415212223242531323334354142434445{,,,,,,,,,,,,,,,,,,,}a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b Ω=,基本事件个数为20n =,434445{,,}C a b a b a b =,包含基本事件个数为3m =,所以A ,B 两地区的空气质量等级均为“重度污染”的概率为3()20P C =. --------------------13分18.(共14分)证明:(I )因为正方形ABCD ,所以AC BD ⊥.又因为平面ABEF ⊥平面ABCD , 平面ABEF I 平面ABCD=AB ,,AB BE ⊥ BE ⊂平面ABEF ,所以BE ⊥平面ABCD. 又因为AC ⊂平面ABCD.故BE ⊥AC. 又因为BE BD B =I ,所以 AC ⊥平面BDE . --------------------5分(II )取DE 的中点G ,连结OG ,FG ,因为四边形ABCD 为正方形,所以O 为BD 的中点. 则OG //BE ,且12OG BE =. 由已知AF //BE ,且12AF BE =,则//AF OG 且AF OG =,所以四边形AOGF 为平行四边形,所以AO //FG , 即AC //FG .因为AC ⊄平面DEF ,FG ⊂平面DEF ,所以AC //平面DEF . --------------------10分(III )因为平面ABCD ⊥平面ABEF ,四边形ABCD 是正方形,平面ABEF I 平面ABCD=AB , 所以//,AD BC AD AB ⊥.由(I )知,BE ⊥平面ABCD ,AD ⊂平面ABCD 所以BE AD ⊥ 所以 AD ⊥平面BEF .所以11143323D BEF BEF V S AD BE AB AD -∆=⨯⨯=⨯⨯⨯⨯=. --------------------14分19.(共14分)解:(Ⅰ)由题意,得222122b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩, 解得 21a b ⎧=⎪⎨=⎪⎩.所以椭圆E 的标准方程是2212x y +=. -------------------5分(II )(1)当直线x AB ⊥轴时,m = 0符合题意.(2)当直线AB 与x 轴不垂直时,设直线AB 的方程为()1y k x =-,由22(1)220y k x x y =-⎧⎨+-=⎩,得()()2222124210k x k x k +-+-=, GFEBOADC由2222(4)8(12)(1)0k k k ∆=--+->,得k ∈R .设()11,x y A ,()22,x y B ,则2212122242(1)1212k k x x x x k k-+=⋅=++,. 所以121222(2)12ky y k x x k -+=+-=+,所以线段AB 中点C 的坐标为2222,1212k k k k ⎛⎫- ⎪++⎝⎭.由题意可知,0k ≠,故直线C M 的方程为222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭, 令x = 0,212k y k =+,即212k m k =+当k > 0时,,得2120=11242k m k kk<=≤++,当且仅当22k =时“=”成立. 同理,当 k < 0时,2120=11242k m k kk>=≥-++,当且仅当22k =-时“=”成立. 综上所述,实数m 的取值范围为22,44⎡⎤-⎢⎥⎣⎦.--------------------14分20. (共13分)解:(Ⅰ)2'()3x f x =,'(1)3f =,又(1)1f c =+,则曲线()y f x =在点(1,(1))f 处的切线方程为:32y x c =+-. --------------------3分(Ⅱ)设32()820h x x x x c =-++,2'()31620h x x x =-+, 令'()0f x =,则2,x =或103x =当x 变化时,'()h x 与()h x 的变化情况如下表:x(,2)-∞210(2,)310310(,)3+∞ '()h x + 0- 0+ ()h x16c +40027c +所以,当160,c +>且400027c +<时,因为(0)0,(4)160h c h c =<=+>,故存在1(0,2),x ∈210(2,),3x ∈310(,4),3x ∈使得123()()()0h x h x h x === 由()h x 的单调性知,当且仅当400(16,)27c ∈--时,函数()h x 有三个不同的零点, 即当且仅当400(16,)27c ∈--时,方程()()f x g x =有三个不同实根. -------------------9分 (III )由(Ⅱ)知1(0,2),x ∈210(2,),3x ∈224(,2)(0,2),3x -∈⊆()h x 在(0,2)上单调递增,则122144x x x x +>⇔-< 212(4)()()0h x h x h x ⇔-<==222()()(4)0u x h x h x ⇔=-->,210(2,),3x ∈ 由32322222222(4)(4)8(4)20(4)4416h x x x x c x x x c -=---+-+=-+-++,3232222222222()()(4)(820)(4416)u x h x h x x x x c x x x c =--=-++--+-++322222(6128)x x x =-+-设32()2122416u x x x x =-+-,则2'()6(2)u x x =-所以当10(2,)3x ∈时,'()0u x >,即()u x 在10(2,)3上单调递增,而(2)0u = 所以当10(2,)3x ∈时,()(2)0u x u >=,所以2()0u x >,210(2,)3x ∈所以124x x +>. --------------------13分。
2018年北京各区高三二模文科数学分类汇编--概率统计
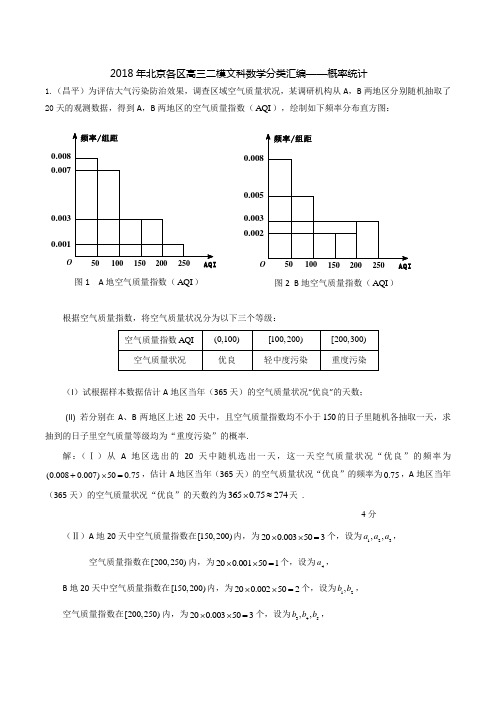
2018年北京各区高三二模文科数学分类汇编——概率统计1.(昌平)为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A ,B 两地区分别随机抽取了20天的观测数据,得到A ,B 两地区的空气质量指数(AQI ),绘制如下频率分布直方图:根据空气质量指数,将空气质量状况分为以下三个等级:(I )试根据样本数据估计A 地区当年(365天)的空气质量状况“优良”的天数;(II) 若分别在A 、B 两地区上述20天中,且空气质量指数均不小于的日子里随机各抽取一天,求抽到的日子里空气质量等级均为“重度污染”的概率.解:(Ⅰ)从A 地区选出的20天中随机选出一天,这一天空气质量状况“优良”的频率为(0.0080.007)500.75+⨯=,估计A 地区当年(365天)的空气质量状况“优良”的频率为0.75,A 地区当年(365天)的空气质量状况“优良”的天数约为3650.75274⨯≈天 .--------------------4分(Ⅱ)A 地20天中空气质量指数在[150,200)内,为200.003503⨯⨯=个,设为123,,a a a ,空气质量指数在[200,250)内,为200.001501⨯⨯=个,设为4a , B 地20天中空气质量指数在[150,200)内,为200.002502⨯⨯=个,设为12,b b , 空气质量指数在[200,250)内,为200.003503⨯⨯=个,设为345,,b b b ,150图1 A 地空气质量指数(AQI ) 0.0050.0030.0020.008图2 B 地空气质量指数(AQI )设“A ,B 两地区的空气质量等级均为“重度污染””为C , 则基本事件空间1112131415212223242531323334354142434445{,,,,,,,,,,,,,,,,,,,}a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b Ω=,基本事件个数为20n =,434445{,,}C a b a b a b =,包含基本事件个数为3m =,所以A ,B 两地区的空气质量等级均为“重度污染”的概率为()P C =分(Ⅰ)根据表中数据写出这10年内栽种银杏数量的中位数,并计算这10年栽种银杏数量的平均数;(Ⅱ)从统计的数据中,在栽种侧柏与银杏数量之差的绝对值不小于300株的年份中,任意抽取2年,恰有1年栽种侧柏的数量比银杏数量多的概率.解:(Ⅰ)这10年中栽种银杏数量的中位数为3700株.设平均数为x ,则34003300360036003700420044003700+4200+4200=383010x +++++++=株.……… 4分(Ⅱ)根据表中数据,满足条件的年份有2009,2010,2011,2013,2014共5年.从这5年中抽取2年,有2009,2010;2009,2011;2009,2013;2009,2014;2010,2011;2010,2013;2010,2014;2011,2013;2011,2014;2013,2014共10种情况.设事件A 表示“任取2年,恰有1年栽种侧柏的数量比银杏的数量多”.则事件A 包括2009,2010;2009,2013;2009,2014;2010,2011;2011,2013;2011,2014共6种情况. 所以63()==105P A . 答:任取2年,恰有1年栽种侧柏的数量比银杏的数量多的概率为35………………13分 3. (东城)某校高一年级有400名学生,高二年级有360名学生,现用分层抽样的方法在这760名学生中抽取一个样本.已知在高一年级中抽取了60名学生,则在高二年级中应抽取的学生人数为 B (A )66 (B )54 (C )40 (D )364.(东城)2017年北京市百项疏堵工程基本完成.有关部门为了解疏堵工程完成前后早高峰时段公交车运行情况,调取某路公交车早高峰时段全程所用时间(单位:分钟)的数据,从疏堵工程完成前的数据中随机抽取5个数据,记为A组,从疏堵工程完成后的数据中随机抽取5个数据,记为B组.A组:128,100,151,125,120.B组:100,102,96,101,a.已知B组数据的中位数为100,且从中随机抽取一个数不小于100的概率是45.(Ⅰ)求a的值;(Ⅱ)该路公交车全程所用时间不超过100分钟,称为“正点运行”.从A,B两组数据中各随机抽取一个数据,求这两个数据对应的两次运行中至少有一次“正点运行”的概率;(Ⅲ)试比较A,B两组数据方差的大小(不要求计算),并说明其实际意义.解:(Ⅰ)因为B组数据的中位数为100,所以100a≤.因为从B组中随机抽取一个数不小于100的概率是45,所以100a≥.所以100a=. …………5分(Ⅱ)从A组中取到128,151,125,120时,B组中符合题意的取法为100,96,100,共4312⨯=种;从A组中取到100时,B组中符合题意的取法为100,102,96,101,100,共155⨯=种;因此符合题意的取法共有12517+=种,而所有不同的取法共有5525⨯=种,所以该路公交车至少有一次“正点运行”的概率1725P=. …………10分(Ⅲ)B组的方差小于A组的方差,说明疏堵工程完成后,该路公交车全程所用时间更加稳定,而且“正点运行”率高,运行更加有保障.…………13分5.(房山) 1995年联合国教科文组织宣布每年的4月23日为世界读书日,主旨宣言为“希望散居在全球各地的人们,都能享受阅读带来的乐趣,都能尊重和感谢为人类文明作出巨大贡献的文学、文化、科学思想的大师们,都能保护知识产权。
昌平区第二中学2018-2019学年高三上学期11月月考数学试卷含答案

昌平区第二中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. 已知命题p :“∀x ∈R ,e x >0”,命题q :“∃x 0∈R ,x 0﹣2>x 02”,则( )A .命题p ∨q 是假命题B .命题p ∧q 是真命题C .命题p ∧(¬q )是真命题D .命题p ∨(¬q )是假命题2. (m+1)x 2﹣(m ﹣1)x+3(m ﹣1)<0对一切实数x 恒成立,则实数m 的取值范围是( ) A .(1,+∞) B .(﹣∞,﹣1) C.D.3. 若关于x 的不等式07|2||1|>-+-++m x x 的解集为R ,则参数m 的取值范围为( ) A .),4(+∞ B .),4[+∞ C .)4,(-∞ D .]4,(-∞【命题意图】本题考查含绝对值的不等式含参性问题,强化了函数思想、化归思想、数形结合思想在本题中的应用,属于中等难度.4. 已知f (x )=x 3﹣3x+m ,在区间[0,2]上任取三个数a ,b ,c ,均存在以f (a ),f (b ),f (c )为边长的三角形,则m 的取值范围是( )A .m >2B .m >4C .m >6D .m >85. 若复数满足71i i z+=(为虚数单位),则复数的虚部为( ) A .1 B .1- C . D .i -6. 下列四个命题中的真命题是( )A .经过定点()000,P x y 的直线都可以用方程()00y y k x x -=-表示B .经过任意两个不同点()111,P x y 、()222,P x y 的直线都可以用方程()()()()121121y y x x x x y y --=-- 表示C .不经过原点的直线都可以用方程1x ya b+=表示 D .经过定点()0,A b 的直线都可以用方程y kx b =+表示7. 函数f (x )=﹣lnx 的零点个数为( ) A .0B .1C .2D .38. 已知()(2)(0)x b g x ax a e a x =-->,若存在0(1,)x ∈+∞,使得00()'()0g x g x +=,则b a的 取值范围是( )A .(1,)-+∞B .(1,0)- C. (2,)-+∞ D .(2,0)- 9. 直线在平面外是指( ) A .直线与平面没有公共点 B .直线与平面相交C .直线与平面平行班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________D .直线与平面最多只有一个公共点10.()0﹣(1﹣0.5﹣2)÷的值为( )A .﹣B .C .D .11.设F 1,F 2分别是椭圆+=1(a >b >0)的左、右焦点,过F 2的直线交椭圆于P ,Q 两点,若∠F 1PQ=60°,|PF 1|=|PQ|,则椭圆的离心率为( )A .B .C .D .12.如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB=60°,E 为AB 的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则P ﹣DCE 三棱锥的外接球的体积为( )A .B .C .D .二、填空题13.命题“∀x ∈R ,x 2﹣2x ﹣1>0”的否定形式是 . 14.已知点E 、F 分别在正方体 的棱上,且, ,则面AEF 与面ABC 所成的二面角的正切值等于 .15.刘老师带甲、乙、丙、丁四名学生去西安参加自主招生考试,考试结束后刘老师向四名学生了解考试情况.四名学生回答如下:甲说:“我们四人都没考好.” 乙说:“我们四人中有人考的好.” 丙说:“乙和丁至少有一人没考好.” 丁说:“我没考好.”结果,四名学生中有两人说对了,则这四名学生中的 两人说对了.16.等比数列{a n }的公比q=﹣,a 6=1,则S 6= .17.已知[2,2]a ∈-,不等式2(4)420x a x a +-+->恒成立,则的取值范围为__________. 18.函数y=1﹣(x ∈R )的最大值与最小值的和为 2 .三、解答题19.已知函数,.(Ⅰ)求函数的最大值;(Ⅱ)若,求函数的单调递增区间.20.已知函数f(x)=ax2+blnx在x=1处有极值.(1)求a,b的值;(2)判断函数y=f(x)的单调性并求出单调区间.21.在△ABC中,角A,B,C所对的边分别为a,b,c.已知b2+c2=a2+bc.(Ⅰ)求A的大小;(Ⅱ)如果cosB=,b=2,求a的值.22.已知定义在区间(0,+∞)上的函数f(x)满足f()=f(x1)﹣f(x2).(1)求f(1)的值;(2)若当x>1时,有f(x)<0.求证:f(x)为单调递减函数;(3)在(2)的条件下,若f(5)=﹣1,求f(x)在[3,25]上的最小值.23.已知f (x )=x 3+3ax 2+bx 在x=﹣1时有极值为0. (1)求常数 a ,b 的值;(2)求f (x )在[﹣2,﹣]的最值.24.(本小题满分16分)给出定义在()+∞,0上的两个函数2()ln f x x a x =-,()g x x =- (1)若()f x 在1=x 处取最值.求的值;(2)若函数2()()()h x f x g x =+在区间(]0,1上单调递减,求实数的取值范围; (3)试确定函数()()()6m x f x g x =--的零点个数,并说明理由.昌平区第二中学2018-2019学年高三上学期11月月考数学试卷含答案(参考答案)一、选择题1.【答案】C【解析】解:命题p:“∀x∈R,e x>0”,是真命题,命题q:“∃x0∈R,x0﹣2>x02”,即﹣x0+2<0,即:+<0,显然是假命题,∴p∨q真,p∧q假,p∧(¬q)真,p∨(¬q)假,故选:C.【点评】本题考查了指数函数的性质,解不等式问题,考查复合命题的判断,是一道基础题.2.【答案】C【解析】解:不等式(m+1)x2﹣(m﹣1)x+3(m﹣1)<0对一切x∈R恒成立,即(m+1)x2﹣(m﹣1)x+3(m﹣1)<0对一切x∈R恒成立若m+1=0,显然不成立若m+1≠0,则解得a.故选C.【点评】本题的求解中,注意对二次项系数的讨论,二次函数恒小于0只需.3.【答案】A4.【答案】C【解析】解:由f′(x)=3x2﹣3=3(x+1)(x﹣1)=0得到x1=1,x2=﹣1(舍去)∵函数的定义域为[0,2]∴函数在(0,1)上f′(x)<0,(1,2)上f′(x)>0,∴函数f(x)在区间(0,1)单调递减,在区间(1,2)单调递增,则f(x)min=f(1)=m﹣2,f(x)max=f(2)=m+2,f(0)=m由题意知,f(1)=m﹣2>0 ①;f(1)+f(1)>f(2),即﹣4+2m>2+m②由①②得到m>6为所求.故选C【点评】本题以函数为载体,考查构成三角形的条件,解题的关键是求出函数在区间[0,2]上的最小值与最大值5. 【答案】A 【解析】试题分析:42731,1i i i i i ==-∴==-,因为复数满足71i i z +=,所以()1,1i i i i z i z+=-∴=-,所以复数的虚部为,故选A.考点:1、复数的基本概念;2、复数代数形式的乘除运算. 6. 【答案】B 【解析】考点:直线方程的形式.【方法点晴】本题主要考查了直线方程的表示形式,对于直线的点斜式方程只能表示斜率存在的直线;直线的斜截式方程只能表示斜率存在的直线;直线的饿两点式方程不能表示和坐标轴平行的直线;直线的截距式方程不能表示与坐标轴平行和过原点的直线,此类问题的解答中熟记各种直线方程的局限性是解答的关键.111] 7. 【答案】B【解析】解:函数f (x )=﹣lnx 的零点个数等价于函数y=与函数y=lnx 图象交点的个数, 在同一坐标系中,作出它们的图象:由图象可知,函数图象有1个交点,即函数的零点个数为1 故选B8. 【答案】A【解析】考点:1、函数零点问题;2、利用导数研究函数的单调性及求函数的最小值.【方法点晴】本题主要考查函数零点问题、利用导数研究函数的单调性、利用导数研究函数的最值,属于难题.利用导数研究函数()f x 的单调性进一步求函数最值的步骤:①确定函数()f x 的定义域;②对()f x 求导;③令()0f x '>,解不等式得的范围就是递增区间;令()0f x '<,解不等式得的范围就是递减区间;④根据单调性求函数()f x 的极值及最值(若只有一个极值点则极值即是最值,闭区间上还要注意比较端点处函数值的大小).9. 【答案】D【解析】解:根据直线在平面外是指:直线平行于平面或直线与平面相交, ∴直线在平面外,则直线与平面最多只有一个公共点. 故选D .10.【答案】D【解析】解:原式=1﹣(1﹣)÷=1﹣(1﹣)÷=1﹣(1﹣4)×=1﹣(﹣3)×=1+=.故选:D.【点评】本题考查了根式与分数指数幂的运算问题,解题时应细心计算,是易错题.11.【答案】D【解析】解:设|PF1|=t,∵|PF1|=|PQ|,∠F1PQ=60°,∴|PQ|=t,|F1Q|=t,由△F1PQ为等边三角形,得|F1P|=|F1Q|,由对称性可知,PQ垂直于x轴,F2为PQ的中点,|PF2|=,∴|F1F2|=,即2c=,由椭圆定义:|PF1|+|PF2|=2a,即2a=t=t,∴椭圆的离心率为:e===.故选D.12.【答案】C【解析】解:易证所得三棱锥为正四面体,它的棱长为1,故外接球半径为,外接球的体积为,故选C.【点评】本题考查球的内接多面体,球的体积等知识,考查逻辑思维能力,是中档题.二、填空题13.【答案】.【解析】解:因为全称命题的否定是特称命题所以,命题“∀x ∈R ,x 2﹣2x ﹣1>0”的否定形式是:.故答案为:.14.【答案】【解析】延长EF 交BC 的延长线于P ,则AP 为面AEF 与面ABC 的交线,因为,所以为面AEF 与面ABC 所成的二面角的平面角。
2018年北京市昌平区高考数学二模试卷(理科)(解析版)

2018年北京市昌平区高考数学二模试卷(理科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集U=R,集合A={x|x<﹣1或x>1},则∁U A=()A.(﹣∞,﹣1)∪(1,+∞)B.(﹣∞,﹣1]∪[1,+∞)C.(﹣1,1)D.[﹣1,1]2.(5分)若复数z=cosθ+i sinθ,当时,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限3.(5分)已知等比数列{a n}中,a1=27,a4=a3a5,则a7=()A.B.C.D.34.(5分)设,b=log23,c=2﹣0.3,则()A.b>c>a B.a>b>c C.b>a>c D.a>c>b 5.(5分)若满足条件的整点(x,y)恰有12个,其中整点是指横、纵坐标都是整数的点,则整数a的值为()A.﹣3B.﹣2C.﹣1D.06.(5分)设x,y∈R,则“x2+y2≤2“是“|x|≤1且|y|≤1“的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件7.(5分)某四棱锥的三视图如图所示,则该四棱锥的所有面中最大面的面积是()A.4B.C.2D.8.(5分)2011年7月执行的《中华人民共和国个人所得税法》规定:公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累进计算:某调研机构数据显示,纳税人希望将个税免征额从3500元上调至7000元.若个税免征额上调至7000元(其它不变),某人当月少交纳此项税款332元,则他的当月工资、薪金所得介于()A.5000~6000元B.6000~8000元C.8000~9000元D.9000~16000元二、填空题共6小题,每小题5分,共30分.9.(5分)在二项式的展开式中,第四项的系数是.(用数字作答)10.(5分)在△ABC中,,,AC=1,则BC=.11.(5分)已知双曲线C:的渐近线方程为,则双曲线C的离心率是.12.(5分)执行如图所示的程序框图,若输入x值满足﹣2<x≤4,则输出y值的取值范围是.13.(5分)向量,在边长为1的正方形网格中的位置如图所示,则向量,所成角的余弦值是;向量,所张成的平行四边形的面积是.14.(5分)已知函数f(x)=①当x<1时,若函数f(x)有且只有一个极值点,则实数a的取值范围是;②若函数f(x)的最大值为1,则a=.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知函数.(I)求函数f(x)的最小正周期;(II)求函数f(x)在区间上的最值及相应的x值.16.(13分)为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A,B两地区一年的数据中随机抽取了相同20天的观测数据,得到A,B两地区的空气质量指数(AQI)如图所示:根据空气质量指数,将空气质量状况分为以下三个等级:(Ⅰ)试估计A地区当年(365天)的空气质量状况“优良”的天数;(Ⅱ)假设两地区空气质量状况相互独立,记事件C:“A地区空气质量等级优于B地区空气质量等级”.根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件C的概率.(Ⅲ)若从空气质量角度选择生活地区居住,你建议选择A,B两地区哪个地区.(只需写出结论)17.(14分)如图1,在边长为2的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1D⊥BE,如图2.(I)求证:A1E⊥平面BCDE;(II)求二面角E﹣A1D﹣B的余弦值;(III)在线段BD上是否存在点P,使平面A1EP平面A1BP?若存在,求出的值;若不存在,说明理由.18.(14分)已知椭圆E:(a>b>0)的经过点(0,1),且离心率为.(I)求椭圆E的标准方程;(II)过右焦点F的直线l(与x轴不重合)与椭圆交于A,B两点,线段AB 的垂直平分线交y轴于点M(0,m),求实数m的取值范围.19.(13分)已知函数f(x)=ax2+ax﹣xe x,a>1.(I)若曲线f(x)在点(0,f(0))处的切线方程为y=x,求a的值;(II)证明:当x<0时,函数f(x)存在唯一的极小值点为x0,且.20.(13分)已知正项数列{a n}中,若存在正实数p,使得对数列{a n}中的任意一项a k,也是数列{a n}中的一项,称数列{a n}为“倒置数列”,p是它的“倒置系数”.(I)若数列:1,4,9,x(x>9)是“倒置系数”为p的“倒置数列”,求x 和p的值;(II)若等比数列{a n}的项数是m,数列{a n}所有项之积是T,求证:数列{a n}是“倒置数列”,并用m和T表示它的“倒置系数”p;(III)是否存在各项均为整数的递增数列{a n},使得它既是等差数列,又是“倒置数列”,如果存在,请写出一个满足条件的数列,如果不存在,请说明理由.2018年北京市昌平区高考数学二模试卷(理科)参考答案与试题解析一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.(5分)已知全集U=R,集合A={x|x<﹣1或x>1},则∁U A=()A.(﹣∞,﹣1)∪(1,+∞)B.(﹣∞,﹣1]∪[1,+∞)C.(﹣1,1)D.[﹣1,1]【解答】解:∁U A=[﹣1,1].故选:D.2.(5分)若复数z=cosθ+i sinθ,当时,则复数z在复平面内对应的点位于()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:当时,复数z=cos+i sin=﹣﹣i,则复数z在复平面内对应的点位于第三象限.故选:C.3.(5分)已知等比数列{a n}中,a1=27,a4=a3a5,则a7=()A.B.C.D.3【解答】解:∵等比数列{a n}中,a1=27,a4=a3a5,∴27q3=27q2•27q4,解得q=,∴a7=27q6==.故选:A.4.(5分)设,b=log23,c=2﹣0.3,则()A.b>c>a B.a>b>c C.b>a>c D.a>c>b【解答】解:∵,且2﹣0.2<20=1,而b=log23>log22=1.∴b>a>c.故选:C.5.(5分)若满足条件的整点(x,y)恰有12个,其中整点是指横、纵坐标都是整数的点,则整数a的值为()A.﹣3B.﹣2C.﹣1D.0【解答】解:作出满足条件的平面区域,如图:要使整点(x,y)恰有12个,即为(0,0)、(1,0)、(﹣1,﹣1)、(0,﹣1),(1,﹣1)、(2,﹣1)、(﹣2,﹣2)、(﹣1,﹣2)、(0,﹣2),(1,﹣2)、(2,﹣2)、(3,﹣2).故整数a的值为﹣2.故选:B.6.(5分)设x,y∈R,则“x2+y2≤2“是“|x|≤1且|y|≤1“的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【解答】解:由|x|≤1且|y|≤1⇒x2+y2≤2,反之不成立,例如x=0,y=.∴x2+y2≤2“是“|x|≤1且|y|≤1“的必要不充分条件.故选:B.7.(5分)某四棱锥的三视图如图所示,则该四棱锥的所有面中最大面的面积是()A.4B.C.2D.【解答】解:由三视图可知几何体为四棱锥,作出直观图如图所示,其中底面ABCD是长方形,AB=2,AD=1,侧面P AB⊥底面ABCD,且∠P AB=90°,P A=2,=2×1=2,,,则S四边形ABCD,.∴该四棱锥的所有面中最大面的面积是.故选:B.8.(5分)2011年7月执行的《中华人民共和国个人所得税法》规定:公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累进计算:某调研机构数据显示,纳税人希望将个税免征额从3500元上调至7000元.若个税免征额上调至7000元(其它不变),某人当月少交纳此项税款332元,则他的当月工资、薪金所得介于()A.5000~6000元B.6000~8000元C.8000~9000元D.9000~16000元【解答】解:设该人当月工资、薪金所得为x元,由题意得:1500×3%+3000×10%+(x﹣8000)×20%﹣(x﹣7000)×3%=332,整理,得:0.17x=1377,解得x=8100.故选:C.二、填空题共6小题,每小题5分,共30分.9.(5分)在二项式的展开式中,第四项的系数是20.(用数字作答)【解答】解:的展开式的第四项为,∴第四项的系数是C63=20.故答案为:20.10.(5分)在△ABC中,,,AC=1,则BC=1或.【解答】解:由题意可得:sin A=,化为sin A=,解得A=或.∴BC2=﹣2cos A,可得BC2=1或7,解得BC=1或.故答案为:1或.11.(5分)已知双曲线C:的渐近线方程为,则双曲线C的离心率是.【解答】解:根据题意,双曲线C:的渐近线方程为,则有=,即a=2,则双曲线的方程为﹣y2=1,其中a=2,b=1,则c==,则双曲线的离心率e==;故答案为:.12.(5分)执行如图所示的程序框图,若输入x值满足﹣2<x≤4,则输出y值的取值范围是[﹣3,2].【解答】解:根据输入x值满足﹣2<x≤4,故:利用函数的定义域,分成两部分:即:﹣2<x<2和2≤x≤4,当﹣2<x<2时,执行y=x2﹣3的关系式,故:﹣3≤y<1,当2≤x≤4时,执行y=log2x的关系式,故:1≤y≤2.综上所述:y∈[﹣3,2],故答案为:[﹣3,2]13.(5分)向量,在边长为1的正方形网格中的位置如图所示,则向量,所成角的余弦值是;向量,所张成的平行四边形的面积是3.【解答】解:如图所示,建立直角坐标系,不妨取=(2,1),=(1,2),则===.向量,所张成的平行四边形的面积S=••sin=×=5×=3.故答案分别为:,3.14.(5分)已知函数f(x)=①当x<1时,若函数f(x)有且只有一个极值点,则实数a的取值范围是a<1;②若函数f(x)的最大值为1,则a=±1.【解答】解:①x<1时,f(x)=﹣x2+2ax,f′(x)=﹣2x+2a=﹣2(x﹣a),由f′(x)=0,解得x=a.∵函数f(x)有且只有一个极值点,∴a<1.则实数a的取值范围是(﹣∞,1).②a=0时,f(x)=,此时f(x)max=0≠1,舍去.a<0时,x≥1时,f(x)=≤0.x<1时,f(x)=﹣(x﹣a)2+a2,x=a 时,函数f(x)取得最大值,f(a)=a2,令a2=1,a<0,解得a=﹣1.a>0时,x≥1时,f(x)=,f′(x)=,可得函数f(x)在[1,e)内单调递增,在(e,+∞)内单调递减.f(x)max=f(e)=.x<1时,f(x)=﹣(x﹣a)2+a2,x=a时,函数f(x)取得最大值,f(x)max =f(a)=a2,当,即a时,令a2=1,解得a=1.当a2,即0<a<时,令=1,解得a=e.舍去.综上可得:a=±1.故答案为:±1.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(13分)已知函数.(I)求函数f(x)的最小正周期;(II)求函数f(x)在区间上的最值及相应的x值.【解答】解:(Ⅰ)==,∴f(x)的最小正周期是π;(Ⅱ)∵,∴0≤2x≤π,∴,当时,f(x)max=2.当时,f(x)min=﹣1.16.(13分)为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A,B两地区一年的数据中随机抽取了相同20天的观测数据,得到A,B两地区的空气质量指数(AQI)如图所示:根据空气质量指数,将空气质量状况分为以下三个等级:(Ⅰ)试估计A地区当年(365天)的空气质量状况“优良”的天数;(Ⅱ)假设两地区空气质量状况相互独立,记事件C:“A地区空气质量等级优于B地区空气质量等级”.根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件C的概率.(Ⅲ)若从空气质量角度选择生活地区居住,你建议选择A,B两地区哪个地区.(只需写出结论)【解答】(共13分)解:(Ⅰ)从A地区选出的20天中随机选出一天,这一天空气质量状况为“优良”的频率为1﹣=0.75,估计A地区当年(365天)的空气质量状况“优良”的频率为0.75,A地区当年(365天)的空气质量状况“优良”的天数约为365×0.75≈274天.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(Ⅱ)记A1表示事件:“A地区空气质量等级为优良”,A2表示事件:“A地区空气质量等级为轻中度污染”,B1表示事件:“B地区空气质量等级为轻中度污染”,B2表示事件:“B地区空气质量等级为重度污染”,则A1与B1独立,A2与B2独立,B1与B2互斥,C=A1B1∪A1B2∪A2B2.所以P(C)=P(A1B1∪A1B2∪A2B2)=P(A1B1)+P(A1B2)+P(A2B2)=P (A1)P(B1)+P(A1)P(B2)+P(A2)P(B2).由所给数据得A1,A2,B1,B2发生的频率分别为,,,.故,,,,所以事件C的概率P(C)==0.2925.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)(Ⅲ)从空气质量角度,建议选择A地区居住.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(13分)17.(14分)如图1,在边长为2的菱形ABCD中,∠BAD=60°,DE⊥AB于点E,将△ADE沿DE折起到△A1DE的位置,使A1D⊥BE,如图2.(I)求证:A1E⊥平面BCDE;(II)求二面角E﹣A1D﹣B的余弦值;(III)在线段BD上是否存在点P,使平面A1EP平面A1BP?若存在,求出的值;若不存在,说明理由.【解答】(共14分)证明:(I)因为DE⊥AB,所以BE⊥DE.又因为BE⊥A1D,DE∩A1D=D,所以BE⊥平面A1DE.因为A1E⊂平面A1DE,所以A1E⊥BE.又因为A1E⊥DE,BE∩DE=E,所以A1E⊥平面BCDE.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)解:(II)因为A1E⊥平面BCDE,BE⊥DE,所以以E为原点,分别以EB,ED,EA1为x,y,z轴,建立空间直角坐标系,则B(1,0,0),D(0,,0),A1(0,0,1).所以=(﹣1,0,1),=(﹣1,,0).设平面A1BD的法向量=(x,y,z),由,令y=1,得=().因为BE⊥平面A 1DE,所以平面A1DE的法向量,所以cos<,>===.因为所求二面角为锐角,所以二面角E﹣A1D﹣B的余弦值为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(10分)(III)假设在线段BD上存在一点P,使得平面A1EP⊥平面A1BD.设P(x,y,z),=(0≤λ≤1),则(x﹣1,y,z)=λ(﹣1,,0).所以P(1﹣λ,,0).所以=(0,0,1),=(1﹣λ,,0).设平面A1EP的法向量=(x,y,z),由,得,令x=,得=().因为平面A1EP⊥平面A1BD,所以=3λ+λ﹣1=0,解得∈[0,1],所以在线段BD上存在点P,使得平面A1EP⊥平面A1BD,且=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)18.(14分)已知椭圆E:(a>b>0)的经过点(0,1),且离心率为.(I)求椭圆E的标准方程;(II)过右焦点F的直线l(与x轴不重合)与椭圆交于A,B两点,线段AB 的垂直平分线交y轴于点M(0,m),求实数m的取值范围.【解答】(共14分)解:(Ⅰ)由题意,得b=1,椭圆的离心率e===,解得.所以椭圆E的标准方程:.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分)(II)(1)当直线AB⊥x轴时,m=0符合题意.(2)当直线AB与x轴不垂直时,设直线AB的方程为y=k(x﹣1),由,得(1+2k2)x2﹣4k2x+2(k2﹣1)=0,由△=(﹣4k2)2﹣8(1+2k2)(k2﹣1)>0,得k∈R.设A(x1,y1),B(x2,y2),则.所以,所以线段AB中点C的坐标为(,﹣).由题意可知,k≠0,故直线MC的方程为y+=﹣(x﹣),令x=0,,即当k>0时,得,当且仅当时“=”成立.同理,当k<0时,,当且仅当时“=”成立.综上所述,实数m的取值范围为.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(14分)19.(13分)已知函数f(x)=ax2+ax﹣xe x,a>1.(I)若曲线f(x)在点(0,f(0))处的切线方程为y=x,求a的值;(II)证明:当x<0时,函数f(x)存在唯一的极小值点为x0,且.【解答】解:(I)因为f(x)=ax2+ax﹣xe x,得f′(x)=2ax+a﹣e x﹣xe x,所以f′(0)=a﹣1.因为曲线在点(0,f(0))处的切线方程为y=x,所以f′(0)=a﹣1=1,即a=2;(II)证明:设h(x)=2ax+a﹣e x﹣xe x,则h′(x)=2a﹣2e x﹣xe x=2a﹣(x+2)e x.因为x<0,所以x+2<2,e x<1.又因为a>1,所以h′(x)>0,故h(x)=a(2x+1)﹣e x(1+x)在(﹣∞,0)上为增函数.又因h(0)=a﹣1>0,h(﹣)=﹣e<0,由零点存在性定理,存在唯一的,有h(x0)=0.当x∈(﹣∞,x0)时,h(x)=f′(x)<0,即f(x)在(﹣∞,x0)上为减函数,当x∈(x0,0)时,h(x)=f′(x)>0,即f(x)在(﹣∞,x0)上为增函数,所以x0为函数f(x)的极小值点.20.(13分)已知正项数列{a n}中,若存在正实数p,使得对数列{a n}中的任意一项a k,也是数列{a n}中的一项,称数列{a n}为“倒置数列”,p是它的“倒置系数”.(I)若数列:1,4,9,x(x>9)是“倒置系数”为p的“倒置数列”,求x 和p的值;(II)若等比数列{a n}的项数是m,数列{a n}所有项之积是T,求证:数列{a n}是“倒置数列”,并用m和T表示它的“倒置系数”p;(III)是否存在各项均为整数的递增数列{a n},使得它既是等差数列,又是“倒置数列”,如果存在,请写出一个满足条件的数列,如果不存在,请说明理由.【解答】解:(I)因为数列:1,4,9,x(x>9)是“倒置系数”为p的“倒置数列”.所以也是该数列的项,且.故,即x=p=36.(II)因为数列{a n}是项数为m项的有穷正项等比数列,取p=a1•a m>0,对数列{a n}中的任意一项a i(1≤i≤m),也是数列{a n}中的一项,由“倒置数列”的定义可知,数列{a n}是“倒置数列”;又因为数列{a n}所有项之积是T,所以即.(III)假设存在这样的等差数列{a n}为“倒置数列”,设它的公差为d(d>0),“倒置系数”为p.因为数列{a n}为递增数列,所以a1<a2<a3<…<a n<…则又因为数列{a n}为“倒置数列”,则正整数也是数列{a n}中的一项(i=1,2,…),故数列{a n}必为有穷数列,不妨设项数为n项,则p=a i•a n+1(1≤i≤n﹣1)﹣i则a1a n=a2a n﹣1,得a1a n=(a1+d)(a n﹣d),即(n﹣2)d2=0由n≥3,故d=0,与d>0矛盾.所以,不存在满足条件的数列{a n},使得它既是等差数列,又是“倒置数列”.。
2018年北京市昌平区高考数学二模试卷(文科)

2018年北京市昌平区高考数学二模试卷(文科)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1. 已知全集U=R,集合A={x|x<−1或x>1},则∁U A=()A.(−∞, −1)∪(1, +∞)B.(−∞, −1]∪[1, +∞)C.(−1, 1)D.[−1, 1]【答案】D【考点】补集及其运算【解析】进行补集的运算即可.【解答】∁U A=[−1, 1].2. 下列函数中,在定义域上既是奇函数又是增函数的是()A.y=1xB.y=x3C.y=sinxD.y=lgx【答案】B【考点】函数奇偶性的性质【解析】根据题意,依次分析选项中函数的奇偶性与单调性,综合即可得答案.【解答】根据题意,依次分析选项:对于A,y=1x为反比例函数,在其定义域上为奇函数,但不是增函数,不符合题意;对于B,y=x3为幂函数,在其定义域上为奇函数,且是增函数,符合题意;对于C,y=sinx为正弦函数,在其定义域上为奇函数,但不是增函数,不符合题意;对于D,y=lgx为对数函数,其定义域为(0, +∞),不是奇函数,不符合题意;3. 在平面直角坐标系中,不等式组{x−y≥0x+y−1≤0y≥0,表示的平面区域的面积是()A.1B.12C.14D.18【答案】C【考点】简单线性规划【解析】先作出不等式组对应的平面区域,然后根据区域确定面积即可.【解答】作出不等式组对应的平面区域如图:由{x =y x +y =1 得A(12, 12),则三角形的面积S =12×1×12=14,4. 设a =(12)0.2,b =log 23,c =2−0.3,则( )A.b >c >aB.a >b >cC.b >a >cD.a >c >b 【答案】C【考点】 对数值大小的比较【解析】把a ,c 化为同底数,再由指数函数与对数函数的单调性比较大小.【解答】∵ a =(12)0.2=2−0.2>2−0.3=c ,且2−0.2<20=1,而b =log 23>log 22=1.∴ b >a >c .5. 执行如图所示的程序框图,若输入x 值满足−2<x ≤4,则输出y 值的取值范围是( )A.[−3, 2]B.[1, 2]C.[−4, 0)D.[−4, 0)∪[1, 2]【答案】A【考点】程序框图【解析】直接利用程序框图和分段函数求出结果.【解答】解:当−2<x <2时,−3≤y <1,当2≤x ≤4时,1≤y ≤2,得:−3≤y ≤2,即:y ∈[−3, 2].故选A .6. 设x ,y ∈R ,则“|x|≤1且|y|≤1“是“x 2+y 2≤2“的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【考点】必要条件、充分条件与充要条件的判断【解析】“|x|≤1且|y|≤1“⇒x2+y2≤2,反之不成立,例如取x=0,y=√2.即可判断出结论.【解答】“|x|≤1且|y|≤1“⇒x2+y2≤2,反之不成立,例如取x=0,y=√2.∴ “|x|≤1且|y|≤1“是“x2+y2≤2“的充分不必要条件.7. 某四棱锥的三视图如图所示,则该四棱锥的所有面中最大面的面积是()A.4B.√5C.2D.√2【答案】B【考点】由三视图求体积【解析】几何体为侧放的四棱锥,作出直观图,代入数据计算四个侧面的面积及底面面积,则答案可求.【解答】由三视图可知几何体为四棱锥,作出直观图如图所示,其中底面ABCD是长方形,AB=2,AD=1,侧面PAB⊥底面ABCD,且∠PAB=90∘,PA=2,则S四边形ABCD=2×1=2,S△PAD=12×2×1=1,S△PAB=12×2×2=2,S△PBC=12×2√2×1=√2,S PDC=12×2×√5=√5.∴该四棱锥的所有面中最大面的面积是√5.8. 2011年7月执行的《中华人民共和国个人所得税法》规定:公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累进计算:某调研机构数据显示,希望将个税免征额从元上调至元.若个税免征额上调至7000元(其它不变),某人当月工资、薪金所得8500元,则此人当月少缴纳此项税款()A.45元B.350元C.400元D.445元【答案】C【考点】函数解析式的求解及常用方法【解析】根据列表即可分别求出个税免征额为3500元和7000元时,此人当月所缴纳的税款,进而即可得出此人当月少缴纳此项税款的值.【解答】根据表格,个税免征额为3500元时,此人当月所缴纳的税款为:1500×3100+3000×10100+500×20100=445(元);当个税免征额为7000元时,此人当月的所缴纳的税款为:1500×3100=45(元);∴此人当月少缴纳此项税款为445−45=400(元).二、填空题共6小题,每小题5分,共30分.在复平面内,复数1+ii对应的点的坐标为________.【答案】(1, −1)【考点】复数的运算【解析】直接利用复数代数形式的乘除运算化简得答案.【解答】∵1+ii =(1+i)(−i)−i2=1−i,∴复数1+ii对应的点的坐标为(1, −1).若抛物线x2=12y,则焦点F的坐标是________.【答案】(0, 3)【考点】抛物线的性质【解析】根据题意,由抛物线的标准方程分析可得其焦点位置以及p的值,由焦点坐标公式计算可得答案.【解答】根据题意,抛物线x2=12y,其焦点在y轴的正半轴上,且p=6,则其焦点坐标为(0, 3);在△ABC 中,a =2,b =2√63,A =π3,则C =________. 【答案】5π12【考点】正弦定理【解析】根据正弦定理与三角形内角和定理求出B 的值,再求C 的大小.【解答】△ABC 中,a =2,b =2√63,A =π3, ∴a sinA =b sinB , 2sin π3=2√63sinB ,∴ sinB =√22, 又a >b ,∴ 0<B <π2,解得B =π4,∴ C =π−A −B =π−π3−π4=5π12.能够说明命题“设a ,b ,c 是任意实数,若a >b >c ,则2a +b >c ”是假命题的一组整数a ,b ,c 的值依次为________.【答案】−1,−2,−3【考点】命题的真假判断与应用【解析】令整数a ,b ,c 的值依次为−1,−2,−3,可得命题“设a ,b ,c 是任意实数,若a >b >c ,则2a +b >c ”是假命题.【解答】令整数a ,b ,c 的值依次为−1,−2,−3,此时a >b >c ,且2a +b <c ,即命题“设a ,b ,c 是任意实数,若a >b >c ,则2a +b >c ”是假命题,向量a →,b →在边长为1的正方形网格中的位置如图所示,则向量a →,b →所成角的余弦值是________;向量a →,b →所张成的平行四边形的面积是________.【答案】45,3【考点】向量的三角形法则【解析】如图所示,建立直角坐标系,不妨取a →=(2, 1),b →=(1, 2),利用向量夹角公式、数量积运算性质、平行四边形面积计算公式即可得出.【解答】如图所示,建立直角坐标系,不妨取a →=(2, 1),b →=(1, 2),则cos <a →,b →>=a →⋅b →|a →|⋅|b →|=√5⋅√5=45. 向量a →,b →所张成的平行四边形的面积S =|a →|⋅|b →|⋅sin <a →,b →>=√5×√5×√1−(45)2=5×35=(3)已知函数f(x)={−x 2+2ax,x <1alnxx ,x ≥1①当a =1时,函数f(x)极大值是________;②当x <1时,若函数f(x)有且只有一个极值点,则实数a 的取值范围是________.【答案】1e ,a <1【考点】利用导数研究函数的极值【解析】①当a =1时,函数f(x)={−x 2+2x,x <1lnx x,x ≥1 ,f′(x)={−2x +2,x <11−lnx x 2,x ≥1 ,分析各个区间上导函数的符号,进而可得函数f(x)极大值;②当x <1时,若函数f(x)有且只有一个极值点,则函数的对称轴在x =1的左侧,进而得到答案.【解答】①当a =1时,函数f(x)={−x 2+2x,x <1lnx x,x ≥1 , f′(x)={−2x +2,x <11−lnx x 2,x ≥1 , 当x <1时,f′(x)>0,函数为增函数,当1≤x <e 时,f′(x)>0,函数为增函数,当x >e 时,f′(x)<0,函数为减函数,故当x =e 时,函数f(x)极大值是1e ;②当x <1时,若函数f(x)有且只有一个极值点,则函数的对称轴在x =1的左侧,即x =a <1,三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.已知函数f(x)=2sin(π4−x)cos(π4−x)+√3sin2x .(I)求函数f(x)的最小正周期;(II)求函数f(x)在区间[0,π2brack 上的最值及相应的x 值.【答案】(Ⅰ)f(x)=sin(π2−2x)+√3sin2x =cos2x +√3sin2x =2sin(2x +π6),∴ f(x)的最小正周期是π;(Ⅱ)∵ 0≤x ≤π2,∴ 0≤2x ≤π,∴ π6≤2x +π6≤7π6, 当x =π6时,f(x)max =(2)当x =π2时,f(x)min =−(1)【考点】正弦函数的周期性诱导公式三角函数的最值【解析】(I )直接利用二倍角公式变形,再由辅助角公式化积即可求函数f(x)的最小正周期;(II)结合已知条件求出π6≤2x +π6≤7π6,进而可求出函数f(x)在区间[0,π2brack 上的最值及相应的x 值.【解答】(Ⅰ)f(x)=sin(π2−2x)+√3sin2x =cos2x +√3sin2x =2sin(2x +π6),∴ f(x)的最小正周期是π;(Ⅱ)∵ 0≤x ≤π2,∴ 0≤2x ≤π,∴ π6≤2x +π6≤7π6, 当x =π6时,f(x)max =(2)当x =π2时,f(x)min =−(1)已知数列{a n }满足a 1=1,a 2=12,数列{b n }是公差为2的等差数列,且b n a n+1+a n+1=na n .(I)求数列{b n }的通项公式;(II)求数列{a n }前n 项的和S n .【答案】(Ⅰ)因为 b n a n+1+a n+1=na n ,所以 b 1a 2+a 2=a 1.又因为a 1=1,a 2=12,所以b 1=(1)所以数列{b n }的通项公式是b n =2n −(1)(Ⅱ) 由(Ⅰ)知b n =2n −1,且b n a n+1+a n+1=na n .所以(2n −1)a n+1+a n+1=na n ,得到 a n+1a n =12(常数).所以数列{a n }是以1为首项,12为公比的等比数列.那么数列{a n }前n 项和:S n =1−(12)n 1−12=2−21−n .【考点】数列的求和数列递推式【解析】(Ⅰ)直接利用递推关系式求出数列的通项公式.(Ⅱ)根据(Ⅰ)的结论,进一步求出数列的通项公式,最后求出数列的前n 项和.【解答】(Ⅰ)因为 b n a n+1+a n+1=na n ,所以 b 1a 2+a 2=a 1.又因为a 1=1,a 2=12,所以b 1=(1)所以数列{b n }的通项公式是b n =2n −(1)(Ⅱ) 由(Ⅰ)知b n =2n −1,且b n a n+1+a n+1=na n .所以(2n −1)a n+1+a n+1=na n ,得到 a n+1a n =12(常数).所以数列{a n }是以1为首项,12为公比的等比数列.那么数列{a n }前n 项和:S n =1−(12)n 1−12=2−21−n .为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A ,B 两地区分别随机抽取了20天的观测数据,得到A ,B 两地区的空气质量指数(AQI),绘制如下频率分布直方图:根据空气质量指数,将空气质量状况分为以下三个等级:( II)若分别在A 、B 两地区上述20天中,且空气质量指数均不小于150的日子里随机各抽取一天,求抽到的日子里空气质量等级均为“重度污染”的概率.【答案】(Ⅰ)从A 地区选出的20天中随机选出一天,这一天空气质量状况“优良”的频率为(0.008+0.007)×50=0.75,估计A 地区当年(365天)的空气质量状况“优良”的频率为0.75,A 地区当年(365天)的空气质量状况“优良”的天数约为365×0.75≈274天.——————–(Ⅱ)A 地20天中空气质量指数在[150, 200)内,为20×0.003×50=3个,设为a 1,a 2,a 3,空气质量指数在[200, 250)内,为20×0.001×50=1个,设为a 4,B 地20天中空气质量指数在[150, 200)内,为20×0.002×50=2个,设为b 1,b 2,空气质量指数在[200, 250)内,为20×0.003×50=3个,设为b 3,b 4,b 5,设“A ,B 两地区的空气质量等级均为“重度污染””为C ,则基本事件空间:Ω={a 1b 1, a 1b 2, a 1b 3, a 1b 4, a 1b 5, a 2b 1, a 2b 2, a 2b 3, a 2b 4, a 2b 5, a 3b 1, a 3b 2, a 3b 3, a 3b 4, a 3b 5, a 1b 1,a 4b 2,a 4b 3,a 4b ,基本事件个数为n =20,C ={a 4b 3, a 4b 4, a 4b 5},包含基本事件个数为m =3,所以A ,B 两地区的空气质量等级均为“重度污染”的概率为P(C)=320.——————–【考点】古典概型及其概率计算公式【解析】(Ⅰ)从A 地区选出的20天中随机选出一天,这一天空气质量状况“优良”的频率为0.75,由估计A地区当年(365天)的空气质量状况“优良”的频率为0.75,从而能求出A地区当年(365天)的空气质量状况“优良”的天数.(Ⅱ)A地20天中空气质量指数在[150, 200)内为3个,设为a1,a2,a3,空气质量指数在[200, 250)内为1个,设为a4,B地20天中空气质量指数在[150, 200)内为2个,设为b1,b2,空气质量指数在[200, 250)内为3个,设为b3,b4,b5,设“A,B两地区的空气质量等级均为“重度污染””为C,利用列举法能求出A,B两地区的空气质量等级均为“重度污染”的概率.【解答】(Ⅰ)从A地区选出的20天中随机选出一天,这一天空气质量状况“优良”的频率为(0.008+0.007)×50=0.75,估计A地区当年(365天)的空气质量状况“优良”的频率为0.75,A地区当年(365天)的空气质量状况“优良”的天数约为365×0.75≈274天.——————–(Ⅱ)A地20天中空气质量指数在[150, 200)内,为20×0.003×50=3个,设为a1,a2,a3,空气质量指数在[200, 250)内,为20×0.001×50=1个,设为a4,B地20天中空气质量指数在[150, 200)内,为20×0.002×50=2个,设为b1,b2,空气质量指数在[200, 250)内,为20×0.003×50=3个,设为b3,b4,b5,设“A,B两地区的空气质量等级均为“重度污染””为C,则基本事件空间:Ω={a1b1, a1b2, a1b3, a1b4, a1b5, a2b1, a2b2, a2b3, a2b4, a2b5, a3b1, a3b2, a3b3, a3b4, a3b5, a1b1,a4b2,a4b3,a4b ,基本事件个数为n=20,C={a4b3, a4b4, a4b5},包含基本事件个数为m=3,.——————–所以A,B两地区的空气质量等级均为“重度污染”的概率为P(C)=320如图,四边形ABCD是正方形,平面ABCD⊥平面ABE,AF // BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求证:AC // 平面DEF;(III)求三棱锥D−FEB的体积.【答案】(Ⅰ)证明:∵四边形ABCD是正方形,∴AC⊥BD.又∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AB⊥BE,BE⊂平面ABEF,∴BE⊥平面ABCD.又∵AC⊂平面ABCD.∴BE⊥AC,又BE∩BD=B,∴AC⊥平面BDE;(Ⅱ)证明:取DE的中点G,连结OG,FG,∵四边形ABCD为正方形,∴O为BD的中点.则OG // BE,且OG=12BE.由已知AF // BE,且AF=12BE,则AF // OG且AF=OG,∴四边形AOGF为平行四边形,则AO // FG,即AC // FG.∵AC平面DEF,FG⊂平面DEF,∴AC // 平面DEF;(Ⅲ)∵平面ABCD⊥平面ABEF,四边形ABCD是正方形,平面ABEF∩平面ABCD=AB,∴AD // BC,AD⊥AB.由(Ⅰ)知,BE⊥平面ABCD,AD⊂平面ABCD,∴BE⊥AD∴AD⊥平面BEF.∴V D−BEF=13×S△BEF×AD=13×12×BE×AB×AD=43.【考点】柱体、锥体、台体的体积计算【解析】(Ⅰ)由四边形ABCD是正方形,可得AC⊥BD.再由已知结合面面垂直的性质可得BE⊥平面ABCD,则BE⊥AC,由线面垂直的判定可得AC⊥平面BDE;(Ⅱ)取DE的中点G,连结OG,FG,可证明四边形AOGF为平行四边形,则AO // FG,再由线面平行的判定可得AC // 平面DEF;(Ⅲ)由平面ABCD⊥平面ABEF,四边形ABCD是正方形,可得AD // BC,AD⊥AB.由(Ⅰ)知,BE⊥平面ABCD,则BE⊥AD,即有AD⊥平面BEF,然后利用棱锥体积公式求解.【解答】(Ⅰ)证明:∵四边形ABCD是正方形,∴AC⊥BD.又∵平面ABEF⊥平面ABCD,平面ABEF∩平面ABCD=AB,AB⊥BE,BE⊂平面ABEF,∴BE⊥平面ABCD.又∵AC⊂平面ABCD.∴BE⊥AC,又BE∩BD=B,∴ AC ⊥平面BDE ;(Ⅱ)证明:取DE 的中点G ,连结OG ,FG ,∵ 四边形ABCD 为正方形,∴ O 为BD 的中点. 则OG // BE ,且OG =12BE .由已知AF // BE ,且AF =12BE ,则AF // OG 且AF =OG , ∴ 四边形AOGF 为平行四边形,则AO // FG , 即AC // FG .∵ AC 平面DEF ,FG ⊂平面DEF , ∴ AC // 平面DEF ;(Ⅲ)∵ 平面ABCD ⊥平面ABEF ,四边形ABCD 是正方形, 平面ABEF ∩平面ABCD =AB , ∴ AD // BC ,AD ⊥AB .由(Ⅰ)知,BE ⊥平面ABCD ,AD ⊂平面ABCD , ∴ BE ⊥AD∴ AD ⊥平面BEF .∴ V D−BEF =13×S △BEF ×AD =13×12×BE ×AB ×AD =43.已知椭圆E:x 2a 2+y 2b 2=1(a >b >0)的经过点(0, 1),且离心率为√22.( I)求椭圆E 的标准方程;( II)过右焦点F 的直线l (与x 轴不重合)与椭圆交于A ,B 两点,线段AB 的垂直平分线交y 轴于点M(0, m),求实数m 的取值范围. 【答案】(1)由题意,得b =1,椭圆的离心率e =c a =√1−b 2a 2=√22,解得 {a =√2b =1.所以椭圆E 的标准方程:x 22+y 2=1.——————-(2)(1)当直线AB ⊥x 轴时,m =0符合题意.(2)当直线AB 与x 轴不垂直时,设直线AB 的方程为y =k(x −1), 由{y =k(x −1)x 2+2y 2−2=0 ,得(1+2k 2)x 2−4k 2x +2(k 2−1)=0, 由△=(−4k 2)2−8(1+2k 2)(k 2−1)>0,得k ∈R . 设A(x 1, y 1),B(x 2, y 2),则x 1+x 2=4k 21+2k 2,x 1⋅x 2=2(k 2−1)1+2k 2.所以y 1+y 2=k(x 1+x 2−2)=−2k1+2k 2,所以线段AB 中点C 的坐标为(2k 21+2k 2, −k1+2k 2).由题意可知,k ≠0,故直线MC 的方程为y +k 1+2k 2=−1k(x −2k 21+2k 2),令x =0,y =k 1+2k 2,即m =k1+2k 2 当k >0时,得0<m =k 1+2k 2=11k+2k ≤√24,当且仅当k =√22时“=”成立. 同理,当 k <0时,0>m =k1+2k 2=11k+2k ≥−√24,当且仅当k=−√22时“=”成立. 综上所述,实数m 的取值范围为[−√24,√24].——————–【考点】 椭圆的离心率 【解析】(Ⅰ)由题意可知:b =1,根据椭圆的离心率公式,即可求得a 的值,即可求得椭圆方程;(II)分类讨论,当直线AB 与x 轴不垂直时,设直线AB 的方程,代入椭圆方程,利用韦达定理及中点坐标求得AB 中点C 坐标,求得MC 的方程,分类讨论,根据基本不等式的性质,即可求得实数m 的取值范围. 【解答】(1)由题意,得b =1,椭圆的离心率e =c a =√1−b 2a 2=√22,解得 {a =√2b =1.所以椭圆E 的标准方程:x 22+y 2=1.——————-(2)(1)当直线AB ⊥x 轴时,m =0符合题意.(2)当直线AB 与x 轴不垂直时,设直线AB 的方程为y =k(x −1), 由{y =k(x −1)x 2+2y 2−2=0 ,得(1+2k 2)x 2−4k 2x +2(k 2−1)=0, 由△=(−4k 2)2−8(1+2k 2)(k 2−1)>0,得k ∈R . 设A(x 1, y 1),B(x 2, y 2),则x 1+x 2=4k 21+2k 2,x 1⋅x 2=2(k 2−1)1+2k 2.所以y 1+y 2=k(x 1+x 2−2)=−2k1+2k 2, 所以线段AB 中点C 的坐标为(2k 21+2k2, −k 1+2k 2).由题意可知,k ≠0,故直线MC 的方程为y +k1+2k 2=−1k (x −2k 21+2k 2), 令x =0,y =k 1+2k 2,即m =k1+2k 2 当k >0时,得0<m =k 1+2k 2=11k+2k ≤√24,当且仅当k =√22时“=”成立. 同理,当 k <0时,0>m =k1+2k 2=11k+2k ≥−√24,当且仅当k=−√22时“=”成立. 综上所述,实数m 的取值范围为[−√24,√24].——————–设函数f(x)=x 3+c ,g(x)=8x 2−20x ,方程f(x)=g(x)有三个不同实根x 1,x 2,x 3(x 1<x 2<x 3).(I)求曲线y =f(x)在点(1, f(1))处的切线方程; (II)求c 的取值范围;(III)求证:x 1+x 2>4. 【答案】(1)f ′(x)=3x 2,f′(1)=3,又f(1)=c +1,则曲线y =f(x)在点(1, f(1))处的切线方程为:y =3x +c −2; (2)设ℎ(x)=x 3−8x 2+20x +c ,ℎ′(x)=3x 2−16x +20, 令f′(x)=0,则x =2,或x =103,当x 变化时,ℎ′(x)与ℎ(x)的变化情况如下表:所以,当c +16>0,且c +40027<0时,因为ℎ(0)=c <0,ℎ(4)=16+c >0, 故存在x 1∈(0, 2),x 2∈(2,103),x 3∈(103,4), 使得ℎ(x 1)=ℎ(x 2)=ℎ(x 3)=0, 由ℎ(x)的单调性知,当且仅当c ∈(−16,−40027)时,函数ℎ(x)有三个不同的零点,即当且仅当c ∈(−16,−40027)时,方程f(x)=g(x)有三个不同实根.(3)证明:由(Ⅱ)知x 1∈(0, 2),x 2∈(2,103),4−x 2∈(23,2)⊆(0,2), ℎ(x)在(0, 2)上单调递增,则x 1+x 2>4⇔4−x 2<x 1⇔ℎ(4−x 2)<ℎ(x 1)=ℎ(x 2)=0 ⇔u(x 2)=ℎ(x 2)−ℎ(4−x 2)>0,x 2∈(2,103),由ℎ(4−x 2)=(4−x 2)3−8(4−x 2)2+20(4−x 2)+c =−x 23+4x 22−4x 2+c +16,u(x 2)=ℎ(x 2)−ℎ(4−x 2)=(x 23−8x 22+20x 2+c)−(−x 23+4x 22−4x 2+c +16) =2(x 23−6x 22+12x 2−8),设u(x)=2x 3−12x 2+24x −16,则u ′(x)=6(x −2)2所以当x ∈(2,103)时,u ′(x)>0,即u(x)在(2,103)上单调递增,而u(2)=0 所以当x ∈(2,103)时,u(x)>u(2)=0,所以u(x 2)>0,x 2∈(2,103), 所以x 1+x 2>(4) 【考点】利用导数研究曲线上某点切线方程 【解析】(Ⅰ)求得f(x)的导数,可得切线 的斜率和切点,由点斜式方程可得切线的方程;(Ⅱ)设ℎ(x)=x 3−8x 2+20x +c ,求得导数和单调区间、极值,即可得到所求范围; (III)由ℎ(x)的单调性,x 1+x 2>4⇔4−x 2<x 1⇔ℎ(4−x 2)<ℎ(x 1)=ℎ(x 2)=0,设u(x)=2x 3−12x 2+24x −16,求得导数和单调性,即可得证. 【解答】(1)f ′(x)=3x 2,f′(1)=3,又f(1)=c +1,则曲线y =f(x)在点(1, f(1))处的切线方程为:y =3x +c −2; (2)设ℎ(x)=x 3−8x 2+20x +c ,ℎ′(x)=3x 2−16x +20, 令f′(x)=0,则x =2,或x =103,当x 变化时,ℎ′(x)与ℎ(x)的变化情况如下表:所以,当c +16>0,且c +40027<0时,因为ℎ(0)=c <0,ℎ(4)=16+c >0, 故存在x 1∈(0, 2),x 2∈(2,103),x 3∈(103,4), 使得ℎ(x 1)=ℎ(x 2)=ℎ(x 3)=0, 由ℎ(x)的单调性知,当且仅当c ∈(−16,−40027)时,函数ℎ(x)有三个不同的零点,即当且仅当c ∈(−16,−40027)时,方程f(x)=g(x)有三个不同实根.(3)证明:由(Ⅱ)知x 1∈(0, 2),x 2∈(2,103),4−x 2∈(23,2)⊆(0,2), ℎ(x)在(0, 2)上单调递增,则x 1+x 2>4⇔4−x 2<x 1⇔ℎ(4−x 2)<ℎ(x 1)=ℎ(x 2)=0 ⇔u(x 2)=ℎ(x 2)−ℎ(4−x 2)>0,x 2∈(2,103),由ℎ(4−x 2)=(4−x 2)3−8(4−x 2)2+20(4−x 2)+c =−x 23+4x 22−4x 2+c +16,u(x 2)=ℎ(x 2)−ℎ(4−x 2)=(x 23−8x 22+20x 2+c)−(−x 23+4x 22−4x 2+c +16) =2(x 23−6x 22+12x 2−8),设u(x)=2x 3−12x 2+24x −16,则u ′(x)=6(x −2)2所以当x ∈(2,103)时,u ′(x)>0,即u(x)在(2,103)上单调递增,而u(2)=0 所以当x ∈(2,103)时,u(x)>u(2)=0,所以u(x 2)>0,x 2∈(2,103), 所以x 1+x 2>(4)。
最新-北京昌平区2018年高三数学第二学期统一练习(二)

昌平区2018-2018学年第二学期高三年级第二次统一练习数学(文科)试卷考生注意事项:1、本试卷共6页,分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分,满分150分,考试时间 120分钟。
2、答题前,考生务必将学校、姓名、考试编号填写清楚。
答题卡上第一部分(选择题)必须用2B 铅笔作答,第二部分(非选择题)必须用黑色字迹的签字笔作答,作图时可以使用2B 铅笔。
3、修改时,选择题用塑料橡皮擦干净,不得使用涂改液。
请保持卡面整洁,不要折叠、折皱、破损。
不得在答题卡上作任何标记。
4、请按照题号顺序在各题目的答题区域内作答,未在对应的答题区域作答或超出答题区域的作答均不得分。
第Ⅰ卷(选择题 共40分)一、选择题(本大题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.)1.已知集合{}{}3,1,2,3,4A x x B =≥=,则A B =A .{4}B .{3,4}C .{2,3,4}D .{1,2,3,4}2.设条件0:2>+a a p , 条件0:>a q ; 那么q p 是的A .充分但不必要条件B .必要但不充分条件C .充要条件D .既不充分也不必要条件3. 数列{}n a 对任意*N n ∈ ,满足13n n a a +=+,且38a =,则10S 等于 A .155B . 160C .172D .2404. 若b a b a >是任意实数,且、,则下列不等式成立的是 A .22b a > B .1<ab C .0)lg(>-b a D .b a )31()31(<5.已知一个空间几何体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,根据图中标出的尺寸 (单位:cm ),可得这个几何体的体积是 A .πcm 3B .34πcm 3C .35πcm 3 D .2π cm 3俯视图6. 已知3log ,2321==b a ,则输出的值为A.22B.2C. 212- D. 212+7、已知ABC ∆中,,10,4,3===BC AC AB 则∙等于 A .596- B. 215- C. 215 D. 2968、如图AB 是长度为定值的平面α的斜线段,点A 为斜足,若点P 在平面α内运动,使得ABP ∆的面积为定值,则动点P 的轨迹是A.圆B.椭圆 C 一条直线 D 两条平行线第Ⅱ卷(非选择题 共110分)二、填空题(本大题共6小题,每小题5分,共30分.)9.i-12= 10.一个正方形的内切圆半径为2,向该正方形内随机投一点P,点P 恰好落在圆内的概率是__________11.《中华人民共和国道路交通安全法》 规定:车辆驾驶员血液酒精浓度在20~80 mg/100mL (不含80)之间,属于酒后驾车;血液酒精浓度在80mg/100mL (含80)以上时,属醉酒驾车。
昌平高三二模理科数学

则输出y值的取值范围是.
?
13.向量a,b在边长为1的正方形网格中的位置如图所示,
则向量a,b所成角的余弦值是_________;向量a,b所张成的平行四边形的面积是__________.
14.已知函数
①当 时,若函数 有且只有一个极值点,则实数 的取值范围是;
昌平高三二模理科数学精选文档
昌平区2018年高三年级第二次统一练习
数学试卷(理科)
本试卷共5页,共150分.考试时长120分钟.考生务必将答案作答在答题卡上,在试卷上作答无效.
第一部分(选择题共40分)
一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.
1.已知全集 R,集合A={x∣x< 或x> 1},则
(Ⅲ)若从空气质量角度选择生活地区居住,你建议选择A,B两地区哪个地区.(只需写出结论)
17.(本小题14分)
如图1,在边长为2的菱形 中, , 于点 ,将 沿 折起到 的位置,使 ,如图2.
(I)求证: 平面 ;
(II)求二面角 的余弦值;
(III)在线段 上是否存在点 ,使平面 平面 若存在,求出 的值;若不存在,说明理由.
A. B. C. D.
2.若复数 ,当 时,则复数 在复平面内对应的点位于
A.第一象限B.第二象限C.第三象限D.第四象限
3.已知等比数列 中, ,则 =
A. B. C. D.
4.设 , , ,则
A. B. C. D.
5.若满足条件 的整点 恰有12个,其中整点是指横、纵坐标都是整数的点,则整数 的值为
20.(本小题13分)
已知正项数列 中,若存在正实数 ,使得对数列 中的任意一项 , 也是数列 中的一项,称数列 为“倒置数列”, 是它的“倒置系数”.
昌平区第二高级中学2018-2019学年高三上学期11月月考数学试卷含答案(1)

昌平区第二高级中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1. “x ≠0”是“x >0”是的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件2. 已知函数y=x 3+ax 2+(a+6)x ﹣1有极大值和极小值,则a 的取值范围是( )A .﹣1<a <2B .﹣3<a <6C .a <﹣3或a >6D .a <﹣1或a >23. 若偶函数f (x )在(﹣∞,0)内单调递减,则不等式f (﹣1)<f (lg x )的解集是( )A .(0,10)B .(,10)C .(,+∞)D .(0,)∪(10,+∞)4. 若复数z 满足iz=2+4i ,则在复平面内,z 对应的点的坐标是( )A .(2,4)B .(2,﹣4)C .(4,﹣2)D .(4,2)5. 下面茎叶图表示的是甲、乙两个篮球队在3次不同比赛中的得分情况,其中有一个数字模糊不清,在图中以m 表示.若甲队的平均得分不低于乙队的平均得分,那么m 的可能取值集合为()A .B .C .D .6. 已知圆的半径为1,为该圆的两条切线,为两切点,那么O ,PA PB ,A B PA PB ∙u u u r u u u r的最小值为A 、B 、C 、D 、4-3-4-+3-+7. 若()f x 是定义在(),-∞+∞上的偶函数,[)()1212,0,x x x x ∀∈+∞≠,有()()21210f x f x x x -<-,则()A .()()()213f f f -<<B .()()()123f f f <-<C .()()()312f f f <<D .()()()321f f f <-<8. 复数z=(m ∈R ,i 为虚数单位)在复平面上对应的点不可能位于()A .第一象限B .第二象限C .第三象限D .第四象限9. 已知数列{a n }满足a 1=1,a 2=2,a n+2=(1+cos 2)a n +sin 2,则该数列的前10项和为()A .89B .76C .77D .3510.某几何体的三视图如下(其中三视图中两条虚线互相垂直)则该几何体的体积为()班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________A. B .483C.D .16320311.圆锥的高扩大到原来的 倍,底面半径缩短到原来的,则圆锥的体积12( )A.缩小到原来的一半B.扩大到原来的倍C.不变D.缩小到原来的1612.对任意的实数k ,直线y=kx+1与圆x 2+y 2=2的位置关系一定是( )A .相离B .相切C .相交但直线不过圆心D .相交且直线过圆心二、填空题13.如果椭圆+=1弦被点A (1,1)平分,那么这条弦所在的直线方程是 .14.已知实数,满足,目标函数的最大值为4,则______.x y 2330220y x y x y ≤⎧⎪--≤⎨⎪+-≥⎩3z x y a =++a =【命题意图】本题考查线性规划问题,意在考查作图与识图能力、逻辑思维能力、运算求解能力.15.函数的单调递增区间是 .16.如图,在矩形中,,点为线段(含端点)上一个动点,且,ABCD AB =Q CD DQ QC λ=u u u r u u u rBQ交于,且,若,则 .AC P AP PC μ=u u u r u u u rAC BP ⊥λμ-=17.已知是数列的前项和,若不等式对一切恒成立,则的取值范围是n S 1{}2n n -n 1|12n n nS λ-+<+|n N *∈λ___________.【命题意图】本题考查数列求和与不等式恒成立问题,意在考查等价转化能力、逻辑推理能力、运算求解能力.18.已知命题p :∃x ∈R ,x 2+2x+a ≤0,若命题p 是假命题,则实数a 的取值范围是 .(用区间表示)三、解答题19.如图,在底面是矩形的四棱锥P ﹣ABCD 中,PA ⊥平面ABCD ,PA=AB=2,BC=2,E 是PD 的中点.A B C DPQ(1)求证:平面PDC ⊥平面PAD ;(2)求二面角E ﹣AC ﹣D 所成平面角的余弦值.20.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,已知sinA ﹣sinC (cosB+sinB )=0.(1)求角C 的大小; (2)若c=2,且△ABC 的面积为,求a ,b 的值.21.已知函数()f x =121x a +-(1)求的定义域.()f x (2)是否存在实数,使是奇函数?若存在,求出的值;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
俯视图 左视图昌平区2018年高三年级第二次统一练习 数学试卷(理科) 2018.5本试卷共5页,共150分.考试时长120分钟.考生务必将答案作答在答题卡上,在试卷上作答无效.第一部分(选择题 共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项. 1.已知全集U R ,集合A ={x ∣x <1或x > 1},则UA =A .(,1)(1,)-∞-+∞ B .(,1][1,)-∞-+∞ C .(1,1)- D .[1,1]-2.若复数cos isin z θθ=+,当4=π3θ时,则复数z 在复平面内对应的点位于 A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.已知等比数列{}n a 中,143527,a a a a ,则7a =A .127B .19 C .13D .3 4.设0.212a ⎛⎫= ⎪⎝⎭,2log 3b =,0.32c -=,则A .b c a >>B .a b c >>C .b a c >>D .a c b >>5.若满足条件010x y x y y a -≥⎧⎪+-≤⎨⎪≥⎩的整点(,)x y 恰有12个,其中整点是指横、纵坐标都是整数的点,则整数a 的值为A .3-B .2-C .1-D .06.设,x y ∈R ,则22+2x y ≤“”是||1||1x y ≤≤“且”的A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 7.某四棱锥的三视图如图所示,则该四棱锥的所有面中最大面的面积是 A .4 BC . 2 D主视图8.2011年7月执行的《中华人民共和国个人所得税法》规定:公民全月工资、薪金所得不超过3500元的部分不必纳税,超过3500元的部分为全月应纳税所得额.此项税款按下表分段累进计算:全月应纳税所得额(含税级距)税率(%) 不超过1500元3 超过1500元至4500元的部分 10 超过4500元至9000元的部分20 ……某调研机构数据显示,纳税人希望将个税免征额从3500元上调至7000元.若个税免征额上调至7000元(其它不变),某人当月少交纳此项税款332元,则他的当月工资、薪金所得介于A .5000~6000元B .6000~8000元C .8000~9000元D .9000~16000元第二部分(非选择题 共110分)二、填空题共6小题,每小题5分,共30分.9.在二项式6(1)x +的展开式中,第四项的系数是 .(用数字作答)10.在ABC ∆中,34ABC S ∆=,3AB =,1AC =,则BC = . 11.已知双曲线C :2221(0)x y a a -=>的渐近线方程为12y x =±,则双曲线C 的离心率是 .12.执行如图所示的程序框图,若输入 x 值满足24x -<≤, 则输出y 值的取值范围是 .13.向量a ,b 在边长为1的正方形网格中的位置如图所示,则向量a ,b 所成角的余弦值是_________;向量a ,b 所张成的平行四边形的面积是__________.a b2log y x=2x <23y x =-是否x输入输出y结束开始14.已知函数()22,1ln 1.x ax x f x a x x x ⎧-+<⎪=⎨≥⎪⎩‚‚① 当1x <时,若函数()f x 有且只有一个极值点,则实数a 的取值范围是 ; ② 若函数()f x 的最大值为1,则a = .三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程. 15.(本小题13分)已知函数()2sin()cos()244f x x x x =--+ππ. (I )求函数()f x 的最小正周期;(II )求函数()f x 在区间[0,]2π上的最值及相应的x 值.16.(本小题13分)为评估大气污染防治效果,调查区域空气质量状况,某调研机构从A,B两地区一年的数据中随机抽取了相同20天的观测数据,得到A,B两地区的空气质量指数(AQI)如下图所示:(Ⅰ)试估计A地区当年(365天)的空气质量状况“优良”的天数;(Ⅱ)假设两地区空气质量状况相互独立,记事件C:“A地区空气质量等级优于B地区空气质量等级”. 根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件C的概率.(Ⅲ)若从空气质量角度选择生活地区居住,你建议选择A,B两地区哪个地区.(只需写出结论)17.(本小题14分)如图1,在边长为2的菱形ABCD 中,60BAD ∠=,DE AB ⊥于点E ,将ADE ∆沿DE 折起到1A DE ∆的位置,使1A D BE ⊥,如图2.(I )求证:1A E ⊥平面BCDE ; (II )求二面角1E A D B --的余弦值;(III )在线段BD 上是否存在点P ,使平面1A EP ⊥平面1A BD ?若存在,求出BPBD的值;若不存在,说明理由.ABCDE 图1A 1BCDE图218.(本小题14分)已知椭圆()2222:10x y E a b a b+=>>经过点(0,1),且离心率为2.(I )求椭圆E 的标准方程;(II )过右焦点F 的直线l (与x 轴不重合)与椭圆交于,A B 两点,线段AB 的垂直平分线交y 轴于点(0,)M m ,求实数m 的取值范围.已知函数2()e x f x ax ax x =+-,1a >.(I )若曲线()f x 在点(0,(0))f 处的切线方程为y x =,求a 的值; (II) 证明:当0x <时,函数()f x 存在唯一的极小值点为0x ,且0102x -<<.数列{}n a为“倒置数列”,p是它的“倒置系数”.x x 是“倒置系数”为p的“倒置数列”,求x和p的值;(I)若数列:1,4,9,(9)(II)若等比数列{}n a的项数是m,数列{}n a所有项之积是T,求证:数列{}n a是“倒置数列”,并用m和T表示它的“倒置系数”p;(III)是否存在各项均为整数的递增数列{}n a,使得它既是等差数列,又是“倒置数列”,如果存在,请写出一个满足条件的数列,如果不存在,请说明理由.昌平区2018年高三年级第二次统一练习数学试卷(理科)参考答案一、选择题(共8小题,每小题5分,共40分)二、填空题(共6小题,每小题5分,共30分)9.20 10.1 1112.[3,2]- 13.45; 3 14.1a <;1-三、解答题(共6小题,共80分) 15.(共13分)解:(I )π()sin(2)22f x x x =-cos22x x=+π2sin(2)6x =+所以()f x 的最小正周期是π. -------------------8分 (II )因为 π02x ≤≤, 所以 02πx ≤≤,所以 ππ7π2666x ≤≤+,当π6x =时,max ()2f x =. 当π2x =时,m ()1in -f x =. --------------------13分16.(共13分)解:(Ⅰ)从A 地区选出的20天中随机选出一天,这一天空气质量状况为“优良”的频率为510.7520-=,估计A 地区当年(365天)的空气质量状况“优良”的频率为0.75,A 地区当年(365天)的空气质量状况“优良”的天数约为3650.75274⨯≈天. -----------4分(Ⅱ)记1A 表示事件:“A 地区空气质量等级为优良”;2A 表示事件:“A 地区空气质量等级为轻中度污染”; 1B 表示事件:“B 地区空气质量等级为轻中度污染”;2B 表示事件:“B 地区空气质量等级为重度污染”, 则1A 与1B 独立,2A 与2B 独立,1B 与2B 互斥,111222C A B A B A B =.所以111222()()P C P A B A B A B =111222()()()P A B P A B P A B =++111222()()()()()()P A P B P A P B P A P B =++.由所给数据得1A ,2A ,1B ,2B 发生的频率分别为34,15,15,320. 故13()4P A =,21()5P A =,11()5P B =,23()20P B =, 所以31313()()0.2925.4520520P C =⨯++⨯= --------------------10分(Ⅲ)从空气质量角度,建议选择A 地区居住 . --------------------13分17.(共14分)证明:(I )因为DE AB ⊥,所以BE DE ⊥.又因为1BE A D ⊥,1DE A D D =,所以BE ⊥平面1A DE . 因为1A E ⊂平面1A DE , 所以1A E BE ⊥. 又因为1A E DE ⊥,BEDE E =,所以1A E ⊥平面BCDE .--------------------5分 (II )因为1A E ⊥平面BCDE ,BE DE ⊥,所以以E 为原点,分别以EB ,ED ,EA 1为x ,y ,z 轴,建立空间直角坐标系,则(1,0,0)B,D ,1(0,0,1)A .所以1(1,0,1)BA =-,(BD =-. 设平面1A BD 的法向量(,,)x y z =n ,由100BA x z BD x ⎧⋅=-+=⎪⎨⋅=-=⎪⎩n n,得x zx =⎧⎪⎨=⎪⎩令1y =,得=n .因为BE ⊥平面1A DE ,所以平面1A DE 的法向量(1,0,0)EB =,所以321cos ,77EB EB EB ⋅===⋅n n n . 因为所求二面角为锐角,所以二面角1E A D B --的余弦值为217. -------------------10分 (III )假设在线段BD 上存在一点P ,使得平面1A EP ⊥平面1A BD .设(,,)P x y z ,(01)BP BD λλ=≤≤,则(1,,)(1,3,0)x y z λ-=-. 所以(1,3,0)P λλ-.所以1(0,0,1)EA =,(1,3,0)EP λλ=-. 设平面1A EP 的法向量(,,)x y z =m ,由10(1)30EA z EP x y λλ⎧⋅==⎪⎨⋅=-+=⎪⎩m m ,得0(1)3z x y λλ=⎧⎪⎨-=-⎪⎩, 令3x λ=,得(3,1,0)λλ=-m .因为平面1A EP ⊥平面1A BD ,所以310λλ⋅=+-=m n ,解得[]10,14λ=∈, 所以在线段BD 上存在点P ,使得平面1A EP ⊥平面1A BD ,且14BP BD =.--------------------14分 18.(共14分)(Ⅰ)由题意,得222122b c e a a b c =⎧⎪⎪==⎨⎪⎪=+⎩, 解得 21a b ⎧=⎪⎨=⎪⎩. 所以椭圆E 的标准方程是2212x y +=. -------------------5分 (II )(1)当直线x AB ⊥轴时,m = 0符合题意.(2)当直线AB 与x 轴不垂直时,设直线AB 的方程为()1y k x =-, 由22(1)220y k x x y =-⎧⎨+-=⎩,得()()2222124210k x k x k +-+-=, 由2222(4)8(12)(1)0k k k ∆=--+->,得k ∈R .设()11,x y A ,()22,x y B ,则2212122242(1)1212k k x x x x k k-+=⋅=++,. 所以121222(2)12k y y k x x k -+=+-=+, 所以线段AB 中点C 的坐标为2222,1212k k k k ⎛⎫- ⎪++⎝⎭. 由题意可知,0k ≠,故直线C M 的方程为222121212k k y x k k k ⎛⎫+=-- ⎪++⎝⎭, 令x = 0, 212k y k =+,即212k m k =+ 当k > 0时,,得210=11242k m k k k<=≤++,当且仅当2k =时“=”成立. 同理,当 k < 0时,210=1122k m k k k >=≥++,当且仅当k =时“=”成立. 综上所述,实数m的取值范围为44⎡-⎢⎣⎦.--------------------14分 19.(共13分)解:(I )因为2()e x f x ax ax x =+-,得()2e e x x f x ax a x '=+--,所以(0)1f a '=-.因为曲线在点(0,(0))f 处的切线方程为y x =,所以(0)11f a '=-=,即2a =. --------------------5分(II) 设()2e e x x h x ax a x =+--,则()22e e 2(2)e x x x h x a x a x '=--=-+. 因为0x <,所以22x +<,e 1x<.又因为1,a >所以 ()0h x '>,故()(21)e (1)x h x a x x =+-+在(,0)-∞上为增函数. 又因(0)10h a =->,1211()e 022h --=-<,由零点存在性定理,存在唯一的01(,0)2x ∈-,有0()0h x =. 当0(,)x x ∈-∞时,()()0h x f x ='<,即()f x 在0(,)x -∞上为减函数,当0(,0)x x ∈时,()()0h x f x ='>,即()f x 在0(,)x -∞上为增函数, 所以0x 为函数()f x 的极小值点. --------------------13分 20.(共13分)故1,49x ==, 即36x p ==. --------------------3分 31211)()()m m m m m m a a a a a a a --==)假设存在这样的等差数列{}n a 为“倒置数列”,设它的公差为为递增数列,所以123n a a a a <<<<< n p a >>>为“倒置数列”,则正整数也是数列{}n a 中的一项(1,2,),必为有穷数列,不妨设项数为。
