高等数学试卷2017-2018-1试卷 - 副本
2017年-2018年普通高等学校招生全国统一考试数学试题文(天津卷,含答案)

高考衣食住用行衣:高考前这段时间,提醒同学们出门一定要看天气,否则淋雨感冒,就会影响考场发挥。
穿着自己习惯的衣服,可以让人在紧张时产生亲切感和安全感,并能有效防止不良情绪产生。
食:清淡的饮食最适合考试,切忌吃太油腻或者刺激性强的食物。
如果可能的话,每天吃一两个水果,补充维生素。
另外,进考场前一定要少喝水!住:考前休息很重要。
好好休息并不意味着很早就要上床睡觉,根据以往考生的经验,太早上床反而容易失眠。
考前按照你平时习惯的时间上床休息就可以了,但最迟不要超过十点半。
用:出门考试之前,一定要检查文具包。
看看答题的工具是否准备齐全,应该带的证件是否都在,不要到了考场才想起来有什么工具没带,或者什么工具用着不顺手。
行:看考场的时候同学们要多留心,要仔细了解自己住的地方到考场可以坐哪些路线的公交车?有几种方式可以到达?大概要花多长时间?去考场的路上有没有修路堵车的情况?考试当天,应该保证至少提前20分钟到达考场。
绝密★启用前2017年普通高等学校招生全国统一考试(天津卷)数学(文史类)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷1至2页,第Ⅱ卷3至5页。
答卷前,考生务必将自己的姓名、准考号填写在答题考上,并在规定位置粘贴考试用条形码。
答卷时,考生务必将答案涂写在答题卡上,答在试卷上的无效。
考试结束后,将本试卷和答题卡一并交回。
祝各位考生考试顺利!第Ⅰ卷注意事项:1.每小题选出答案后,用铅笔将答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
2.本卷共8小题,每小题5分,共40分。
参考公式:·如果事件A ,B 互斥,那么P (A ∪B )=P (A )+P (B ).·棱柱的体积公式V =Sh . 其中S 表示棱柱的底面面积,h 表示棱柱的高. ·球的体积公式34π3V R =.其中R 表示球的半径. 一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设集合{1,2,6},{2,4},{1,2,3,4}A B C ===,则()A B C =U I (A ){2}(B ){1,2,4}(C ){1,2,4,6}(D ){1,2,3,4,6} (2)设x ∈R ,则“20x -≥”是“|1|1x -≤”的(A )充分而不必要条件(B )必要而不充分条件 (C )充要条件(D )既不充分也不必要条件 (3)有5支彩笔(除颜色外无差别),颜色分别为红、黄、蓝、绿、紫.从这5支彩笔中任取2支不同颜色的彩笔,则取出的2支彩笔中含有红色彩笔的概率为 (A )45(B )35(C )25(D )15(4)阅读右面的程序框图,运行相应的程序,若输入N 的值为19,则输出N 的值为(A )0 (B )1(C )2(D )3(5)已知双曲线22221(0,0)x y a b a b-=>>的左焦点为F ,点A 在双曲线的渐近线上,OAF △是边长为2的等边三角形(O 为原点),则双曲线的方程为(A )221412x y -=(B )221124x y -=(C )2213x y -=(D )2213y x -= (6)已知奇函数()f x 在R 上是增函数.若0.8221(log ),(log 4.1),(2)5a fb fc f =-==,则,,a b c 的大小关系为(A )a b c <<(B )b a c <<(C )c b a <<(D )c a b << (7)设函数()2sin(),f x x x ωϕ=+∈R ,其中0,||πωϕ><.若5π11π()2,()0,88f f ==且()f x 的最小正周期大于2π,则 (A )2π,312ωϕ==(B )211π,312ωϕ==-(C )111π,324ωϕ==-(D )17π,324ωϕ== (8)已知函数||2,1,()2, 1.x x f x x x x +<⎧⎪=⎨+≥⎪⎩设a ∈R ,若关于x 的不等式()||2x f x a ≥+在R 上恒成立,则a 的取值范围是(A )[2,2]-(B)[2]-(C)[2,-(D)[-第Ⅱ卷注意事项:1.用黑色墨水的钢笔或签字笔将答案写在答题卡上。
【精品】吉林省近两年(2017,2018)高考理科数学试卷以及答案(word解析版)

绝密★启用前吉林省2017年高考理科数学试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整,笔迹清楚3.请按照题号顺序在答题卡各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试卷上答题无效4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5.保持卡面清洁,不要折叠、不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.31ii+=+( ) A .12i + B .12i - C .2i + D .2i -2. 设集合{}1,2,4A =,{}240B x x x m =-+=.若{1}AB =,则B =( )A .{}1,3-B .{}1,0C .{}1,3D .{}1,53. 我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )A .1盏B .3盏C .5盏D .9盏4. 如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A . 90πB .63πC .42πD .36π5. 设x ,y 满足约束条件2330233030x y x y y +-≤⎧⎪-+≥⎨⎪+≥⎩,则2z x y =+的最小值是( )A .15-B .9-C .1D .96. 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的安排方式共有( )A .12种B .18种C .24种D .36种7. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩.老师说:你们四人中有2位优秀,2位良好,我现在给甲看乙、丙的成绩,给乙看丙的成绩,给丁看甲的成绩.看后甲对大家说:我还是不知道我的成绩.根据以上信息,则( )A .乙可以知道四人的成绩B .丁可以知道四人的成绩C .乙、丁可以知道对方的成绩D .乙、丁可以知道自己的成绩 8. 执行右面的程序框图,如果输入的1a =-,则输出的S =( )A .2B .3C .4D .59. 若双曲线C :22221x y a b-=(0a >,0b >)的一条渐近线被圆()2224x y -+=所截得的弦长为2,则C 的离心率为( )A .2 BC10. 已知直三棱柱111ABC A B C -中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1CB所成角的余弦值为( ) A.2 B.5 C.5D.3 11. 若2x =-是函数21`()(1)x f x x ax e -=+-的极值点,则()f x 的极小值为( )A.1-B.32e --C.35e -D.112. 已知ABC ∆是边长为2的等边三角形,P 为平面ABC 内一点,则()PA PB PC ⋅+的最小值是( )A.2-B.32-C. 43- D.1- 二、填空题:本题共4小题,每小题5分,共20分。
2017-2018-1《高等数学 ( I ) 》期末考试试卷A

北京化工大学2017——2018学年第一学期《高等数学(I )》期终考试试卷A班级: 姓名: 学号: 分数:一、填空题(3分×6=18分)1.若0x →时,1cos x -与kx 为同阶无穷小,则k = ;2. 1x =为函数 sin ()1xf x x π=-的 间断点;3.设231()1x xf x dt t=+⎰,则(1)f '=; 4.曲线ln(y x =在点(0,0)处的曲率k = ; 5.120171(x dx-+=⎰;6.微分方程 20y y y '''-+= 的通解为 。
二、解答题(6分×7=42分) 1. 求极限 0sin 22sin limtan x x xx x→--2. 设函数()y y x =由方程lncos sec x t y a t=⎧⎨=⎩确定,若()y y x =为微分方程x dyy e dx -=+的解,求常数a 的值。
3. 求不定积分ln(1dx +⎰4. 将函数()arctan f x x = 展开为带有拉格朗日型余项的3阶麦克劳林公式。
5.求曲线24(1)y x =--与22(2)y x =-- 围成的平面图形的面积。
6.求曲线22ln 1yx x =+-上拐点处的切线方程。
7. 计算曲线3sin ,(0)3a a θρ=>相应于03θπ≤≤的一段弧的长度。
三.解答题(7分×5=35分)1. 设101()10x xx xf x x e e -⎧≥⎪⎪+=⎨⎪<⎪+⎩,计算2(1)f x dx -∞-⎰。
2. 求微分方程cos y y x x ''+=+的通解。
3. 求由曲线sin ,cos ,(0)2y x y x x π==≤≤及直线0,2x x π==围成的平面图形绕x 轴旋转一周而成的旋转体的体积。
4. 设21sin ()x tf x dt t=⎰,求10()xf x dx ⎰。
湖北汽车工业学院制卷模板(A4)

2
3
4
5
6
7
8
9
10
三.判断题(共20分,每题2分)
1.
四.简答题(共20分,每题2分)
1.
2.
。。。。。。
答题区域:(答题不得超出答题区域)
五.综合题(共20分,每题2分)
1.
2.
1.答题区域由任课教师根据试卷进行设计。
2.试题部分和答题部分的每道题均应标注总分和分项得分。
3.试卷批改结束后,只装订答题卡。
湖北汽车工业学院2017-2018(1)学期考试试卷(题)
课程编号
课程名称
考试日期
考试形式
□闭卷□开卷
考试时长
□120分钟□100分钟分钟
试题内容:
一.填空题(共10分,每空1分)
1.
2.
二.单选题(共20分,每题2分)
1.
三.判断题(共10分,每题1分)
1.
四.简答题(共10分,每题1分)
1.
2.
五.综合题(共10分,每题1分)
。。。。。。
共2页,第1页
湖北汽车工业学院2017-2018(1)学期考试试卷(题)
高等数学(课程编号:150014)试卷答题纸
学号
姓名
班级
座位号
题号
一
二
三
四
五
六
七
八
九
十
得分
阅卷
答题区域:(答题不得超出答题区域)
一.填空题(共10分,每空1分)
1.,Leabharlann 2.,二.单选题(共20分,每题2分)
东北大学文科类高数期末试卷练习题 (3)

A ];
…
(A) 5 / 2 ; (B) 2 ; (C) 2; (D) 3 .
x (et2 1)dt
解 lim 2 x0 x sin x ln(1 x)
…
… 线 …
5.向量组 1
1 1
,2
1
1
,3
1 2
,4
2
1
的最大无关组是[
D ];
… …
(A) 1,2,3 ; (B ) 1,3,4 ; (C) 1,2 ; (D) 1,3 .
0 不可能是
封 …
函数 f (x) 的 [ B ];
得分:
三.计算题 (每题 3 分,共 15 分)
… …
(A) 可去间断点; (B ) 无穷间断点;
… …
(C ) 跳跃间断点; (D ) 连续点.
x (et2 1)dt
1. 求极限. lim 2 x0 x sin x ln(1 x)
○ …
2
4. |1 2x | dx [ 0
7 3
2 4
的代数余子式
A23
___ 4 ____ .
6 1 2 3
5,齐次线性方程组
x1 2 x1
2 x2 4 x2
x3 0 3x3 0
有非零解,则
______
2
________
.
3x1 2x2 x3 0
… …
3.设 lim x0
f
(
x)
k1,
lim
x0
f (x)
k2 ,其中 k1, k2 是确定的常数,则点 x
一.单项选择题(每题 2 分,共 10 分)
2. 函数 f (x) 2x3 9x2 12x 1 在区间____[1, 2]___单调减少.
大学高等数学习题答案17-18-1-高数1-1A答案

贵州大学2017-2018学年第一期学期考试试卷A《高等数学1-1》参考答案与评分标准一、选择题(每小题3分,共12分) 1. C 2. A 3. D 4.B二、填空题(每小题3分,共18分) 1.31e -+ 2.=a 1- 3. 1y ex =+ 4. π235. dx x x 21sin 2+6.21 三、求下列极限(每小题5分,共15分)1. 解:x xx x x xx x x x 22sin cos 2cos sin lim 2cos cos 1lim 020+=-→→ ……………….. 2分 =x x x x x 2)cos 4(cos sin lim 20+→ ……………….. 3分 =)2cos 4cos (sin lim20x x x x x +→=25……………….. 5分 2. 解:x x x 2tan)1(lim 1π-→=x xx x 2cos2sin)1(lim1ππ-→ ……………….. 1分xx x x x 2sin22cos2)1(2sin lim1πππππ-⨯-+-=→=2π……………….. 5分 四、求下列导数(每题6分,共12分)1. 解:2sin 2cos21222222x x x x x y ⨯+---='=2cot 2)1(222x x x +-- …………….. 4分 2csc 2122)1(22422222x x x x x x x y ----⨯+--='' 2csc 212)2()3(22222xx x x x ----=…………….. 6分2. 解:dt dx dt dydx dy ==ttee --1=t t e e 2--- ……………….. 3分 dt dx dt dx dy d dxy d )(22= =t t t e e e ---22= t t e e 232--- ……………….. 6分五、求下列积分(每题6分,共24分)1. 解:⎰+dx x xcos 2sin 3=x d x x x d x x cos cos 234cos )cos (cos 2cos 122⎰⎰++-=-+- ………….. 3分 =x d x x cos cos 232cos ⎰⎥⎦⎤⎢⎣⎡++- ……………4分 =21cos 2cos 3ln(2cos )2x x x c -+++ ………….. 6分2. 解:dx xx x xx dx x ⎰⎰+-⨯-=221111arctan 1arctan …………….. 3分 =dx x xx x ⎰++211arctan …………….. 4分C x x x ++++=)1ln(211arctan 2 ………….. 6分3. 解:令x t 45-=,则dt tdx t x 2, 452-=-= 于是⎰--1145dx xx =⎰-⨯-1 3 2)2(45dt t t t ……………….. 3分 =⎰-31 285dt t ………………..4分 =3133124185t t -=16……………….. 6分4. 解:2sin ,2cos ,2,002x t dx tdt x t x t π======令时时原式222016sin cos t tdt π=⎰………………………………………………..……3分242013116sin sin 16().22422t tdt ππππ=-=⋅-⋅=⎰…………………………..6分4、解: 六、(10分)解:所求面积 11ln ln 111 =⨯-==⎰⎰dx xx x x xdx A eee…………….. 5分旋转体体积dx x xx x x dx x V e ee x ⎰⎰⨯-==1122 1 ln 12)(ln )(ln πππ=(2)e π- ………….. 10分七、(8分)解: 如图建立坐标系,则在水深[0 , 5]上任取区间],[dz z z +, 对应的体积元素2(25)dV z dzπ=-…………..2分将水吸到z 处所做的功元素2(25)dW g z z dzρπ=-………….. 5分故所求功为 24 5250 025625(25)[]().244z z W g z z dz g g J ρπρπρπ=-=-=⎰………….. 8分八、证明题(6分)证明:据罗尔定理,在(,)a b 内至少存在一点1ξ,使得0)(1='ξf …………….. 2分对导函数)(x f '分别在],[1ξa 与],[1b ξ上应用拉格朗日中值定理:0)()()()(1112<-'-=-'-'=''a a f a a f f f ξξξξ (12ξξ≤<a ) …………….. 3分0)()()()(1113>-'=-'-'=''ξξξξb b f b f b f f (b ≤<31ξξ) …………….. 4分由闭区间上连续函数的介质定理:在23(,)ξξ内至少存在一点ξ,有0)(=''ξf b a <≤≤<32ξξξ. …………….. 6分。
2017-2018学年度高一第一学期期末考试试卷以及答案

2018-2018学年度期末考试试卷高一数学第Ⅰ卷<选择题 共50分)一、选择题<本大题共10小题,每小题5分,共50分,每题只有一个正确答案,请把你认为正确的答案填在答题卡上,答在试卷上的一律无效。
)Ke4U17Jcyx 1. 若{}9,6,3,1=P {}8,6,4,2,1=Q ,那么=⋂Q P < C ) A.{1} B.{6} C. {1,6} D. 1,62.下列函数中哪个与函数y x =是同一个函数 < B )A.2)(x y =B. 33x y = C . xx y 2=D.2x y =3.图<1)是由哪个平面图形旋转得到的< A )图<1) A B CDKe4U17Jcyx 4.下列函数中有两个不同零点的是< D )A .lg y x =B .2x y =C .2y x =D .1y x =-5.函数()12f x x=-的定义域是< A ) A .[)()+∞⋃-,22,1B .[)+∞-,1C .()()+∞⋃∞-,22,D . 1 22 -⋃+∞(,)(,)6.已知直线m ⊥平面α,直线n ⊂平面β,下面有三个命题:①//m n αβ⇒⊥;②//m n αβ⊥⇒;③//m n αβ⇒⊥;则真命题的个数为< B )A .0B .1C .2D .37.若10x -<<,那么下列各不等式成立的是< D )A .220.2x x x -<<B .20.22x x x -<<C .0.222x x x -<<D .220.2x x x -<< 8. 过2 3A -(,) ,2 1B (,) 两点的直线的斜率是< C )A .12B .12-C .2-D .29. 已知函数)31(12)(≤≤+=x x x f ,则< B ) A .)1(-x f =)20(22≤≤+x xB . )1(-x f =)42(12≤≤-x xC . )1(-x f =)20(22≤≤-x xD . )1(-x f =)42(12≤≤+-x x10..已知)(x f 是偶函数,当0<x 时,)1()(+=x x x f ,则当0>x 时,()f x 的值为< A )A .)1(-x xB .)1(--x xC .)1(+x xD .)1(+-x x第Ⅱ卷<非选择题 共100分)二、填空题<本大题共4小题,每小题5分,共20分. 请把你认为正确的答案填在答题卡上,答在试卷上的一律无效。
高数2017-2018年第1学期第1学期期末考试试卷
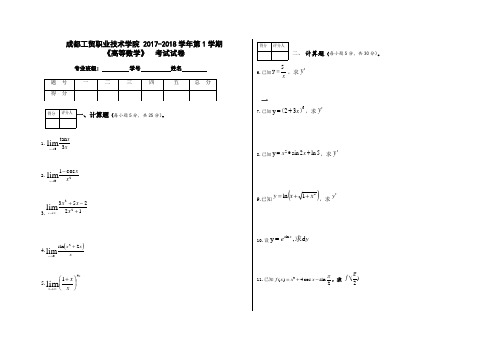
得分评分人得分评分人成都工贸职业技术学院 2017-2018学年第1学期《高等数学》 考试试卷专业班级: 学号 姓名一一、计算题(每小题5分,共25分)。
1.x xx 3tan lim 0→2.2cos 1lim x xx -→3.1225322lim +-+∞→x x x x4.()x xx x 2sin 20lim +→5.xx x x 41lim ⎪⎭⎫ ⎝⎛+∞→二、 计算题(每小题5分,共30分)。
6.已知x5y =,求'y7.已知632y )(x +=,求'y8.已知5ln 2sin y 2+∙=x x ,求'y9.已知()21ln x x y ++=,求'y10.设y e x d ,y sin 求=11.已知3()4cos sin2f x x x π=+-,求)2('πf得分评分人得分评分人得分评分人三、计算题(每小题5分,共20分)。
12. ()dx x x⎰+-32213.dx x x⎰+12214.dx xx ⎰+2ln15.dx x x⎰+1四、应用题(15分)。
16.已知函数()233+-=x x x f .定义区间[]3,2-。
(每小题5分,共15分)(1)求()x f 的极值; (2)求()x f 的单调性与最值; (3)求()x f 的凹凸性。
五、应用题(10分)。
17.在一条河的同旁有甲,乙两城,甲城位于河岸边,乙城离岸40km ,乙城到岸的垂足与甲城相距50km ,两城在河边合建一水厂取水,从水厂到甲城和乙城的水管费用分别为每公里3万元和5万元,问此水厂应该建在河边的何处才能使水管费用最少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017-2018学年第1学期考试试题
课程名称 高等数学A1、B1 任课教师签名 王志宏等
出题教师签名 题库抽题 审题教师签名
考试方式 (闭)卷 适用专业 全校17级 工科本科各专业 考试时间 (120)分钟
一、判断题(共10分,每题2分) 1. 2
arctan lim π
=
∞
→x x . ( )
2. 当0→x 时x x tan 1sin 1--+与x arcsin 是等价无穷小. ( )
3. 函数在某点可导,则必在该点连续. ( )
4. 若c x F dx x f +=⎰)()(,则c x F dx x f +=
⎰)2(2
1
)2(. ( ) 5.
()⎰b a
dx x f 表示以曲线()x f y =为曲边的曲边梯形的面积. ( )
二、填空题(共15分,每小题3分)
1. 若22
lim 2
22=--++→x x b
ax x x , 则a = b = . 2. 设)(x f 可导,且满足()()
12311lim 0
-=--→x
x f f x ,则)1(f '= .
3. 设()x x
x f 2cos 2
sin
+=,则()()π27f = .
4. 若C x dx x
x f +=⎰
arctan )
(,则⎰
=dx x f )( . 5.
(2
1
1
x dx -+
⎰
= .
三、选择题(共15分,每小题3分,在每小题给出的四个选项内,只
有一项是符合题目要求的) 1.设当0→x 时,()()x x βα,都是无穷小()()0≠x β,则当0→x 时,下列表达式中不一定为无穷小的是 ( )
A 、()()()x x βα⋅+1ln
B 、()()x
x x 1sin 22
βα
+
C 、 ()()
x x βα2 D 、()()x x βα+
2.设()x ϕ在a x =连续,()()x a x x F ϕ-=,则( )
A 、)(x F 在a x =点间断
B 、)(x F 在a x =点连续但不可导
C 、)(x F 在a x =点可导
D 、)(x F 在a x =点的可导性与()a ϕ有关 3. 在区间]1,0[上,满足罗尔定理全部条件的函数为 ( )
A 、⎪⎪⎩⎪⎪⎨⎧
≥-<=21
12
1)(x x x x x f B 、 ⎩⎨⎧≥<=111)(x x x x f
C 、⎪⎪⎩⎪⎪⎨⎧≥<-=1411)2
1()(2x x
x x x f D 、⎩⎨⎧≥<=101)(2x x x x f
4. 设)(x F 为偶函数)(x f 的一个原函数,则 ( ) A 、)()(x F x F -= B 、c x F x F +-=-)()( C 、c x F x F +-=)()( D 、)()(x F x F -=-
5. 下列命题中不正确的是 ( )
A 、若0x 为)(x f 的可导的极值点,则0)('0=x f ;
B 、若0)('0=x f ,0x 一定是)(x f 的极值点;
C 、连续函数从左到右,单调性改变的点是极值点,凹凸性改变的点
))(,(00x f x 是拐点;
D 、若0)(''0=x f ,则))(,(00x f x 不一定为曲线的拐点.
四、计算题(共48分,每小题6分)
1. ()()3
2
d cos ln lim
x
t
t t x
x ⎰+→.
2. ⎪⎭⎫
⎝
⎛--→x x x ln 111lim 1. 3. x x
e e
y cos cos +=, 求y '.
4. 求由参数方程2ln(1)
arctan x t y t t
ì=+ïí=-ïî所确定函数的二阶导数2
2dx y d . 5. 设1
2
+=
x x y , 求dy .
6. 计算不定积分
⎰
-+.922
dx x
x
7. 设21,0
()ln(1),0
x x f x x x ⎧+<=⎨+≥⎩,计算31
(2)d f x x -⎰.
8. 求⎰
∞+++0
2
8
4x x dx
.
五、综合题(共12分,每小题6分)
1.设函数()x f 在闭区间[]b a ,上连续,且()0>x f ,证明方程
()()
01
=+⎰
⎰
dt t f dt t f x
b
x a
在开区间()b a ,内有唯一的根。
2. 设有抛物线2
:(0,0)L y a bx a b =->>,试确定常数a ,b 的值,使得
(1)L 与直线1y x =-+相切;
(2)L 与x 轴所围图形绕y 轴旋转所得旋转体的体积最大。
