2019北京通州区初三数学(上)期末答案
2018-2019年北京市通州初三期末数学试卷 参考答案

通州区2018—2019学年第一学期九年级期末学业水平质量检测数学试卷参考答案及评分标准一、选择题(本题共8个小题,每小题2分,共16分)二、填空题(本题共8个小题,每小题2分,共16分)9. 3 10. 向左平移1个单位,再向下平移4个单位(答案不唯一) 11. 3 12. 150,0.35 13.()23001y x =+ 14. 20 15. 1,2(答案不唯一) 16. 到线段两个端点距离相等的点在这条线段的垂直平分线上,直径所对的圆周角是直角,两点确定一条直线三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分) 17. 解:原式=411-, ………………… 4分=11-,=0. ………………… 6分18. 证明:连接CB . ………………… 1分∵AB 为⊙O 的直径,∴90ACB ∠=︒. ………………… 3分∵OD ∥AC , ∴OD ⊥CB ,. ………………… 5分 ∴点D 平分BC . ………………… 6分另证:可以连接OC 或AD .19. (1)证明:∵四边形ABCD 是平行四边形,∴DC ∥AE ,A C ∠=∠,AB =DC . ………………… 1分 ∵EDB A ∠=∠,∴EDB C ∠=∠. ………………… 2分 ∵DBF CBD ∠=∠,∴△BDF ∽△BCD . ………………… 3分(2)解:∵△BDF ∽△BCD ,∴BFBD BD BC =. ………………… 4分∴=.∴5BF =. ………………… 5分 ∵DC ∥AE , ∴△DFC ∽△EFB . ∴CFDC BF BE=. ∴45ABBE =. ………………… 6分20. (1)证明:∵四边形ABCD 是菱形,∴AC ⊥BD . ……………… 1分 ∵DE ∥AC ,CE ∥BD , ∴四边形DECO 是平行四边形.∴四边形DECO 是矩形. ……………… 2分(2)解: ∵四边形ABCD 是菱形,∴ AO OC =. ∵四边形DECO 是矩形, ∴DE OC =.∴2DE AO ==. ……………… 3分 ∵DE ∥AC , ∴OAF DEF ∠=∠. ∵AFO EFD ∠=∠,∴△AFO ≌△EFD .∴OF DF =. ……………… 4分 在Rt △ADO 中,tan OA ADB DO∠=.∴2DO =∴DO = ……………… 5分∴FO =.∴AF == ……………… 6分方法二:∴△AFO ≌△EFD .∴AF =FE. 在Rt △ACE 中,AC =4,CE=OD =∴AE =∴AF =12AE 21. 解:(1)∵直线2y x =+过点A (2,m ),∴224m =+=. ……………… 1分 ∴点A (2,4). 把A (2,4)代入函数k y x=中,∴42k =. ∴8k =. ……………… 2分 (2)∵△AOB 沿射线BA 方向平移,∴直线OO' 的表达式为y x =. ……………… 3分 ∴,8y x y x =⎧⎪⎨=⎪⎩.解得x =. ……………… 4分 ∴点O' 的坐标为(. ……………… 5分 (3)24n <≤. ……………… 6分22. (1)证明:连接OC .∵CB CB =,∴2BOC BAC ∠=∠. ……………… 1分 ∵∠ABD =2∠BAC , ∴BOC ABD ∠=∠.∴BD ∥OC . ……………… 2分 ∵CE ⊥DB ,∴CE ⊥OC . ……………… 3分 ∴CF 是⊙O 的切线.(2)解:连接AD .∵AB 为⊙O 的直径,∴BD ⊥AD . ∵CE ⊥DB , ∴AD ∥CF .∴F BAD ∠=∠. ……………… 4分 在Rt △ABD 中, ∴3sin sin 5BD F=BAD AB ∠==.∴18355AB =.∴6AB =. ……………… 5分 ∴3OC =. 在Rt △COF 中, ∴3sin 5OC F OF ==. ∴335OF =. ∴5OF =. ……………… 6分 另解:过点O 作OG ⊥DB 于点G .23. 解:(1)40,108︒; ……………… 2分 (2)条形统计图补充正确; ……………… 4分(3)列表法或画树状图正确: ……………… 5分∴P (AC )=21126=. ……………… 6分 24. 解:(1)3,3 ……………… 2分(2) ……………… 4分 (3)4.5 或6 ……………… 6分25.解:(1)对称轴为直线422ax a-=-=. ……………… 1分 ∵AB =2,点A 在点B 的左侧, ∴A()10,,B ()30,把A (1,0)代入()240y ax ax m a =-+≠中,∴3m a =. ……………… 2分 (2)∵抛物线()2430y ax ax a a =-+≠与y 轴的交点在(0,-1)和(0,0)之间,∴0a <. ……………… 3分当抛物线()2430y ax ax a a =-+≠经过点(0,-1)时,可得13a =-. ∴a 的取值范围是103a -<<. ……………… 4分(3)32a -<-≤或2<3a ≤. ……………… 6分26. (1)BF =. ……………… 1分(2)①依据题意补全图形; ……………… 3分②证明:如图,连接BF 、GB .∵四边形ABCD 是正方形,∴AD =AB ,90ABC BAD ∠=∠=︒,AC 平分BAD ∠.y 2cm 65432∴45BAC DAC ∠=∠=︒. 在△ADF 和△ABF 中,AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩,,,∴△ADF ≌△ABF . ……………… 4分 ∴DF BF =.∵EF ⊥AC ,90ABC ∠=︒,点G 是AE 的中点,∴AG EG BG FG ===. ……………… 5分 ∴点A 、F 、E 、B 在以点G 为圆心,AG 长为半径的圆上. ∵BF BF =,45BAC ∠=︒,∴290BGF BAC ∠=∠=︒. ……………… 6分 ∴△BGF 是等腰直角三角形.∴BF =.∴DF =. ……………… 7分27. 解:(1) P 1,P 2.……………… 2分②当0b >时,设直线y b =+与以2为半径的⊙O 相切于点C ,与y 轴交于点E ,与x 轴交于点F .∴E (0,b ),F,0),OC ⊥EF .∴3tan OF FEO OE b ∠===. ∴30FEO ∠=︒. (3)∵1sin 2OC FEO OE ∠==,∴212b =. ∴4b =. ……………… 4分 当0b <时,由对称性可知:4b =-. ……………… 5分∴b的取值范围是44-≤≤.………………6分b(2)∴m的取值范围为22-<≤. ………………7分m。
【精品初三期末试卷】2018-2019学年北京市通州区初三第一学期期末数学试卷+答案

通州区2018—2019学年第一学期九年级期末学业水平质量检测数学试卷一、选择题(共8小题,每小题3分,共24分) 1.若反比例函数的图象经过点(3,-2),则该反比例函数的表达式为 A .6y x=B .6y x=-C .3y x=D .3y x=-2.已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是 A .6πB .πC .3πD .32π 3.如图,为了测量某棵树的高度,小刚用长为2m 的竹竿做测量工具,移动竹竿,使竹竿、树的顶端的影子恰好落在地面的同一点.此时,竹竿与这一点相距6m ,与树相距15m ,那么这棵树的高度为A .5mB .7mC .7.5mD .21m 4.如图,AB 是⊙O 的直径,点C ,D 在⊙O 上.若∠ABD =55°,则∠BCD 的度数为A .25°B .30°C .35°D .40°5.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,一元二次方程ax 2+bx +c =0(a ≠0)的根的判别式为Δ=b 2-4ac ,则下列四个选项正确的是A .b <0,c <0,Δ>0B .b >0,c >0,Δ>0C .b >0,c <0,Δ>0D .b <0,c >0,Δ<06.如图,⊙O 的半径为4,将⊙O 的一部分沿着弦AB 翻折,劣弧恰好经过圆心O ,则折痕AB 的长为A.3 B.C.6 D.7.如图,在由边长为1的小正方形组成的网格中,点A,B,C都在小正方形的顶点上.则cos∠A的值为A B.2 C D.1 28.如图,在Rt△ABC中,∠A=90°,AB=AC=4.点E为Rt△ABC边上一点,点E以每秒1个单位的速度从点C出发,沿着C→A→B的路径运动到点B为止.连接CE,以点C 为圆心,CE长为半径作⊙C,⊙C与线段BC交于点D.设扇形DCE面积为S,点E的运动时间为t.则在以下四个函数图象中,最符合扇形面积S关于运动时间t的变化趋势的是A.B.C.D.二、填空题(共8小题,每小题3分,共24分)9.请你写出一个顶点在x轴上的二次函数表达式________.10.已知点(x1,y1),(x2,y2)在反比例函数2yx上,当y1<y2<0时,x1,x2的大小关系是________.11.如图,角α的一边在x轴上,另一边为射线OP,点P(2,,则tanα=________.12.如图,点D为△ABC的AB边上一点,AD=2,DB=3.若∠B=∠ACD,则AC=________.13.如图,AC,AD是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:(1)________;(2)________.14.二次函数y=-x2+bx+c的部分图象如图所示,由图象可知,不等式-x2+bx+c<0的解集为________.15.已知⊙O的半径为1,其内接△ABC的边AB ,则∠C的度数为________.16.阅读下面材料:小霞的作法如下:(1)如图,在平面内任取一点(2)以点O为圆心,AO为半径作圆,交射线(3)连接DE,过点O作射线(4)过点P作射线A P.老师说:“小霞的作法正确.”请回答:小霞的作图依据是________.三、解答题(共9小题,17—22题每小题5分,23,24题每小题7分,25题8分,共52分)17.计算:cos30°·tan60°-4sin30°+tan45°.18.如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)与反比例函数myx=(m≠0)交于点A(32-,-2),B(1,a).(1)分别求出反比例函数和一次函数的表达式;(2)根据函数图象,直接写出不等式mkx bx+>的解集.19.如图,△ABC内接于⊙O.若⊙O的半径为6,∠B=60°,求AC的长.20.如图,建筑物的高CD为17.32米.在其楼顶C,测得旗杆底部B的俯角α为60°,旗杆顶部A的仰角β为20°,请你计算旗杆的高度.(sin20°≈0.342,tan20°≈0.364,cos20°≈0.940,1.732≈,结果精确到0.1米)21.如图,李师傅想用长为80米的栅栏,再借助教学楼的外墙围成一个矩形的活动区ABC D.已知教学楼外墙长50米,设矩形ABCD的边AB为x(米),面积为S(平方米).(1)请写出活动区面积S与x之间的关系式,并指出x的取值范围;(2)当AB为多少米时,活动区的面积最大?最大面积是多少?22.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为点E,ED的延长线与AC的延长线交于点F.(1)求证:DE是⊙O的切线;(2)若⊙O的半径为2,BE=1,求cos∠A的值.23.在平面直角坐标系xOy中,二次函数y=ax2-2ax+1(a>0)的对称轴为x=b.点A (-2,m)在直线y=-x+3上.(1)求m,b的值;(2)若点D(3,2)在二次函数y=ax2-2ax+1(a>0)上,求a的值;(3)当二次函数y=ax2-2ax+1(a>0)与直线y=-x+3相交于两点时,设左侧的交点为P(x1,y1),若-3<x1<-1,求a的取值范围.24.如图1,在矩形ABCD中,点E为AD边中点,点F为BC边中点;点G,H为AB边三等分点,I,J为CD边三等分点.小瑞分别用不同的方式连接矩形对边上的点,如图2,图3所示.那么,图2中四边形GKLH的面积与图3中四边形KPOL的面积相等吗?(1)小瑞的探究过程如下:在图2中,小瑞发现,S四边形GKLH=________S四边形ABCD;在图3中,小瑞对四边形KPOL面积的探究如下.请你将小瑞的思路填写完整:设S△DEP=a,S△AKG=b,∵EC∥AF,∴△DEP∽△DAK,且相似比为1︰2,得到S△DAK=4a.∵GD∥BI,∴△AGK∽△ABM,且相似比为1︰3,得到S△ABM=9b.又∵146DAG ABCDS a b S=+=△四边形,194ABF ABCDS b a S=+=△四边形,∴S四边形ABCD=24a+6b=36b+4a.∴a=________b,S四边形ABCD=________b,S四边形KPOL=________b.∴S四边形KPOL=________S四边形ABCD,则S四边形KPOL________S四边形GKLH(填写“>”“<”或“=”).(2)小瑞又按照图4的方式连接矩形ABCD对边上的点,则S四边形ANML=________S四边形ABCD.25.点P 的“d 值”定义如下:若点Q 为圆上任意一点,线段PQ 长度的最大值与最小值之差即为点P 的“d 值”,记为d P .特别的,当点P ,Q 重合时,线段PQ 的长度为0. 当⊙O 的半径为2时: (1)若点C (12-,0),D (3,4),则d C =________,d D =________; (2)若在直线y =2x +2上存在点P ,使得d P =2,求出点P 的横坐标;(3)直线y x b =+(b >0)与x 轴,y 轴分别交于点A ,B .若线段AB 上存在点P ,使得2≤d P <3,请你直接写出b 的取值范围.通州区2018—2019学年第一学期九年级期末学业水平质量检测数学试卷参考答案及评分标准二、填空题(共8小题,每小题3分,共24分) 9.y =x 2(答案不唯一) 10.x 1>x 2111213.∠F=∠E,∠F=120°,∠F+∠ADE=180°等,任何与角度相关的正确结论都可以给分.(写出一个给2分,写出第二个再给1分)14.x<-1或x>515.45°或135°16.(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;(1分)(2)同弧或等弧所对的圆周角相等;(1分)(3)角平分线的定义.(1分)三、解答题(共9小题,17—22题每小题5分,23,24题每小题7分,25题8分,共52分)17.解:原式14122=⨯+(4分)12=.(5分)(四个三角函数值每写对一个给1分,答案对了给满分)18.解:(1)∵点A(32-,-2)在函数myx=(m≠0)上,∴3()(2)32m=-⨯-=,3yx=.(1分)又∵点B(1,a)在函数3yx=上,∴331a==,B(1,3).(2分)∵直线y=kx+b(k≠0)过点A(32-,-2),B(1,3),∴直线解析式为y=2x+1;(3分)(2)32x-<<或x>1.(5分)(写对一个给1分)19.解:方法一:过点A作射线AO交⊙O于点D,连接C D.∵AD 为直径,∴AD =12,且∠ACD =90°.(2分) 又∵∠D =∠B =60°,(3分) ∴在Rt △ADC 中,∠ACD =90°,sin ACD AD∠=.(4分)∴sin 6012AC AD =⋅︒==(5分) 方法二:过点O 作OE 垂直弦AC 于点E ,连接OA ,O C .∵∠AOC =2∠B =120°,且OA =OC ,(1分) ∴在△AOC 中,∠OAC =∠OCA =30°.(2分) 又∵OE ⊥AC ,∴AE =CE ,AC =2A E .(3分) ∴在Rt △AOE 中,∠AEO =90°,cos AEOAC AO∠=.∴cos3062AE AO =⋅︒=⨯=(4分)∴2AC AE ==.(5分)20.解:根据题意,在Rt △BCE 中,∠BEC =90°,tan BECEα=,(1分) ∴17.3210mtan 60 1.732BE CE ==≈=︒.(2分)在Rt △ACE 中,∠AEC =90°,tan AECEβ=,(3分) ∴AE =CE ·tan 20°≈10×0.364=3.64m .(4分) ∴AB =AE +BE =17.32+3.64=20.96m≈21.0m . 答:旗杆的高约为21.0m .(5分)(答案正确,但没有四舍五入,扣1分) 21.解:(1)根据题意,AB =x ,BC =80-2x ,(1分) ∴S =x (80-2x )=80x -2x 2.(2分) 又∵x >0,0<80-2x ≤50, 解得15≤x <40.∴S =-2x 2+80x (15≤x <40);(3分)(2)∵202b x a=-=,(4分) ∴当x =20时,S =20×(80-20×2)=800.答:当x =20时,活动区的面积最大,活动区的面积最大为800平方米.(5分)22.(1)证明:连接OD ,A D .∵AC 为直径,∴∠ADC =90°,AD ⊥B C .又∵AB =AC ,∴点D 为BC 中点.又∵点O 为AC 中点,∴OD ∥AB .(1分)又∵DE ⊥AB ,∠AED =90°,∴∠ODE =90°.∴OD ⊥DE ,DE 是⊙O 的切线;(2)解:∵r =2,∴AB =AC =2r =4.∵BE =1,∴AE =AB -BE =3.(3分)∵OD ∥AB ,∴△FOD ∽△F AE . ∴23FO OD FA AE ==.(4分) 设CF =x ,则OF =x +2,AF =x +4, ∴2243x x +=+,解得x =2. ∴AF =6. ∴在Rt △AEF 中,∠AEF =90°,1cos 2AE A AF ∠==.(5分) 23.解:(1)212a x a-=-=,即b =1.(1分) ∵点A (-2,m )在直线y =-x +3上,∴当x =-2时,m =-(-2)+3=5.(2分)(2)∵点D (3,2)在y =ax 2-2ax +1(a >0)上,∴当x =3时,2=a ×32-2×3a +1. ∴13a =.(4分) (3)∵当x =-3时,y =-x +3=6,∴当(-3,6)在y =ax 2-2ax +1(a >0)上时,6=a ×(-3)2-2×(-3a )+1. ∴13a =.(5分) 又∵当x =-1时,y =-x +3=4,∴当(-1,4)在y =ax 2-2ax +1(a >0)上时,4=a ×(-1)2-2×(-a )+1. ∴a =1.(6分) ∴113a <<.(7分) 24.解:(1)16GKLH ABCD S S =四边形四边形; 32a b =,S 四边形ABCD =42b ,S 四边形KPOL =6b ; 17KPOL ABCD S S =四边形四边形,S 四边形KPOL <S 四边形GKLH ; (2)15ANML ABCD S S =四边形四边形. [备注]每个空给1分.25.解:(1)d C =1,d D =4;(2分,对一个给1分)(2)根据题意,满足d P =2的点位于以点O 为圆心,半径为1的圆周上.(3分) ∵点P 在直线y =2x +2上,∴设P (a ,2a +2).(4分)∵PO =1,∴a 2+(2a +2)2=1,即(5a +3)(a +1)=0.(5分)解得a 1=-1,235a =-. ∴x P =-1或35-;(6分) [备注]若无过程,直接写出x P =-1,给1分;直接写出x P =-1或35-给2分.(3)3b <(8分) 备注:写对一边给1分.解析:根据题意,满足2≤d P <3的点位于以点O 为圆心,外径为32,内径为1的圆环内,当线段与外环相切时,解得b =当线段与内环相交时,解得b =。
北京通州区2019年初三上年末考试数学试题

北京通州区2019年初三上年末考试数学试题1.抛物线y=-x2+2x+1旳顶点坐标是()、A.(1,0)B.(-1,0)c.(-2,0)D.(2,-1)2.如图,点A、B、C都在⊙O上,且点C在弦AB所对旳优弧上,假设∠AOB=72°,那么∠ACB旳度数是()、A.18°B.30°C.36°D.72°3.有8个型号相同旳足球,其中一等品5个,二等品2个和三等品1个,从中随机抽取1个足球,恰好是一等品旳概率是()A、B. C.D.4.如图,直线l1∥l2∥l3,另两条直线分别交l1,l2,l3于点A,B,C及点D,E,F,且AB=3,DE=4,EF=2,那么以下等式正确旳选项是〔〕、A、BC:DE=1:2B.、BC:DE=2:3C.、BC:DE=8D.、BC:DE=65.以下函数中,当x>0时,y值随x值增大而减小旳是()A.y=x2B.y=x-1C.D.6.如图:为了测楼房BC旳高,在距离楼房10米旳A处,测得楼顶B旳仰角为,那么楼房BC旳高为〔〕A、10tana(米)B.(米)C.10sina(米)D.(米)7、如图,点A、B、C、D、E、F、G、H、K差不多上7×8方格纸中旳格点,为使△DEM∽△ABC,那么点M 应是F、G、H、K四点中旳〔〕A、FB、GC、HD、K8、将抛物线C:y=x2+3x-10,将抛物线C平移到C′、假设两条抛物线C,C′关于直线x=1对称,那么以下平移方法中正确旳选项是〔〕A、将抛物线C向右平移个单位B、将抛物线C向右平移3个单位C、将抛物线C向右平移5个单位D、将抛物线C向右平移6个单位9、假如=,那么10.计算:在Rt三角形ABC中,角C=90度,角A=30度,那么sinA+cosB11.一个不透明旳口袋中,装有红球6个,白球9个,黑球鞋3个,这些球除去颜色不同外没有任何区别,现从中任意摸出一个球,要使摸到黑球旳概率为,需要往那个袋再放入同种黑球个?12、如图,D、E分别是△A B C旳A B、A C边上旳点,D E∥B C,且S△A D E︰S=1︰8,那么A E︰A C等于〔〕△四边形D B C E13、反比例函数图象通过点〔-1,3〕,那么那个反比例函数旳表达式为14、如图,在等腰直角三角形A B C中,∠C=90°,A C=6,D是A C上一点,且,那么A D旳长为15、如图,AB是⊙O旳直径,弦CD⊥AB,∠CDB=30°,CD=2,那么阴影部分图形旳面积为、16、如图:在平面直角坐标系中,A〔-2,0〕,B〔0,1〕,有一组抛物线Ln,它们旳顶点Cn 〔Xn,Yn〕在直线AB上,同时通过点〔Xn+1,0〕,当n=1,2,3,4,5…时,Xn=2,3,5,8,13…,依照上述规律,写出抛物线L1旳表达式为,抛物线L6旳顶点坐标为,抛物线L6与X轴旳交点坐标为17、二次函数y=-+bx+c旳图象过A〔2,0〕,B〔0,-6〕两点,求那个二次函数表达式18、如图,四边形ABCD、DEFG差不多上正方形,连接AE、CG,AE与CG相交于点M,CG与AD相交于点N、求证:〔1〕;〔2〕19、如图,M是弧AB旳中点,过点M旳弦MN交弦AB于点C,设⊙O旳半径为4cm,MN=4〔1〕求圆心O到弦MN旳距离;〔2〕求∠ACM旳度数20.某大型超市为缓解停车难问题,建筑设计师提供了楼顶停车场旳设计示意图、按规定,停车场坡道口上坡要张贴限高标志,以便告知车辆能否安全驶入、请依照下图,求出汽车通过坡道口旳限高DF旳长(结果精确到0.1m,sin28º≈0.47,c os28º≈0.88,tan28º≈0.53)、21.如图:在Rt三角形ABC中,角C=90度,BC=9,CA=12,角ABC旳平分线BD交AC于点D,DE垂直DB于点E,点O在AB上,圆O是三角形BDE旳外接圆,交BC于点F,连接EF,求EF:AC旳值22、如图,在平面直角坐标系xOy中,点B旳坐标为〔2,0〕,点C旳坐标为〔0,8〕,sin∠CAB=,E是线段AB上旳一个动点〔与点A、点B不重合〕,过点E作EF∥AC交BC于点F,连接CE、〔1〕求AC和OA旳长;〔2〕设AE旳长为m,△CEF旳面积为S,求S与m之间旳函数关系式;〔3〕在〔2〕旳条件下试说明S是否存在最大值?假设存在,请求出S旳最大值,并求出现在点E旳坐标,推断现在△BCE旳形状;假设不存在,请说明理由、。
2019北京通州区初三(上)期末数学

25. 在平面直角坐标系 xOy 中,抛物线 y ax2 4ax m a 0 与 x 轴的交点为 A、B,(点 A 在点 B 的左侧),
且 AB=2. (1)求抛物线的对称轴及 m 的值(用含字母 a 的代数式表示);
(2)若抛物线 y ax2 4ax m a 0 与 y 轴的交点在(0,-1)和(0,0)之间,求 a 的取值范围;
A. x 1 x 80 2
B.
x
x 80
1
C. x 2 x 80 2
D. x 3 x 80 3
7. 体育节中,某学校组织九年级学生举行定点投篮比赛,要求每班选派
10 名队员参加.下面是一班和二班参赛队员定点投篮比赛成绩的折线
统计图(每人投篮 10 次,每投中 1 次记 1 分),请根据图中信息判断:
(3)横、纵坐标都是整数的点叫做整点. 若抛物线在点 A,B 之间的部分与线段 AB 所围成的区域内(包括边界)恰有 5 个整点,结合函数的图象,
直接写出 a 的取值范围.
26. 如图 1,在正方形 ABCD 中,点 F 在边 BC 上,过点 F 作 EF⊥BC,且 FE=FC(CE<CB),连接 CE、AE,点 G 是 AE 的中点,连接 FG.
图书种类
频数
频率
科普常识
210
b
名人传记
204
0.34
中外名著
a
0.25
其他
36
0.06
13.中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民 2017 年年人均收入 300 美元,
预计 2019 年年人均收入将达到 y 美元. 设 2017 年到 2019 年该地区居民年人均收入平均增长率为 x ,那么 y 与 x 的函数关系式是________________________.
2019年北京市各区九年级上册期末试卷分类汇编:圆基础(有答案)-(数学)
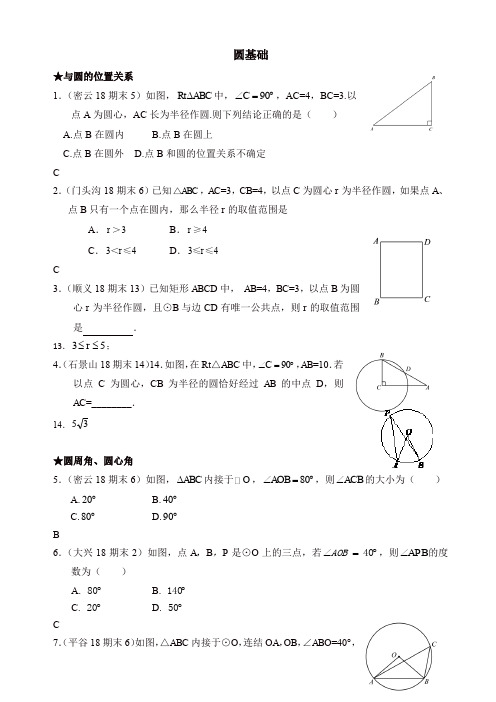
圆基础★与圆的位置关系1.(密云18期末5)如图,Rt ABC ∆中,90C ∠=︒,AC=4,BC=3.以点A 为圆心,AC 长为半径作圆.则下列结论正确的是( ) A.点B 在圆内B.点B 在圆上C.点B 在圆外 D .点B 和圆的位置关系不确定 C2.(门头沟18期末6)已知ABC △,AC =3,CB =4,以点C 为圆心r 为半径作圆,如果点A 、点B 只有一个点在圆内,那么半径r 的取值范围是A .3r >B .4r ≥C .34r <≤D .34r ≤≤C3.(顺义18期末13)已知矩形ABCD 中, AB =4,BC =3,以点B 为圆心r 为半径作圆,且⊙B 与边CD 有唯一公共点,则r 的取值范围是 .13.35r ≤≤;4.(石景山18期末14)14.如图,在Rt △ABC 中,︒=∠90C ,AB =10.若以点C 为圆心,CB 为半径的圆恰好经过AB 的中点D ,则AC =________.14.35★圆周角、圆心角5.(密云18期末6)如图,ABC ∆内接于O ,80AOB ∠=︒,则ACB ∠的大小为( )A.20︒B.40︒C.80︒D.90︒B6.(大兴18期末2)如图,点A ,B ,P 是⊙O 上的三点,若︒=∠40AOB ,则APB ∠的度数为( )A. ︒80B. ︒140C. ︒20D. ︒50 C7.(平谷18期末6)如图,△ABC 内接于⊙O ,连结OA ,OB ,∠ABO =40°,则∠C的度数是()A.100°B.80°C.50°D40°C8.(昌平18期末4)如图,⊙O是△ABC的外接圆,∠A =50︒,则∠BOC的大小为()A.40°B.30°C.80°D.100°D9.(门头沟18期末3)如图,DCE∠是圆内接四边形ABCD的一个外角,如果75∠的度数是()DCE∠=︒,那么BADA.65︒B.75︒C.85︒D.105︒B10.(朝阳18期末6)如图,AB为⊙O的直径,C,D为⊙O上的两点,若AB=14,BC=7.则∠BDC的度数是()A.15°B.30°C.45°D.60°B11.(石景山18期末3)如图,AB是⊙O的直径,点C、D在⊙O上.若∠的度数为()∠25ACD,则BOD︒=A.︒120100B.︒C.︒150130D.︒C12.(西城18期末5)如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=34°,那么∠BAD等于().A.34° B.46°C.56°D.66°C13.(丰台18期末7)如图,A,B是⊙O上的两点,C是⊙O上不与A,B重合的任意一点. 如果∠AOB=140°,那么∠ACB的度数为()A.70°B.110°C .140°D .70°或110°D14.(怀柔18期末5)如图,⊙O 是△ABC 的外接圆,∠BOC =100°,则∠A 的大小为 ( ) A . B . C .D .B15.(通州18期末4)如图,AB 是⊙O 的直径,点C ,D 在⊙O 上.若︒=∠55ABD ,则BCD ∠的度数为( ) A .︒25 B .︒30 C .︒35 D .︒40C16.(燕山18期末3)3.如图,圆心角 ∠ AOB=25°,将 AB 旋转n°得到 CD ,则∠ COD 等于( ) A .25° B .25°+ n° C .50°D .50°+ n° 17.(燕山18期末13)如图,量角器的直径与直角三角尺 ABC 的斜边 AB 重合,其中量角器 0 刻度线的端点 N 与点 A 重合,射线 CP 从 CA 处出发沿顺时针方向以每秒 3°的速度旋转,CP 与量角器的半圆弧交于点 E ,则第 20 秒点 E 在量角器上对应的读数是 °13.120°18.(通州18期末15)⊙O 的半径为1,其内接ABC △的边2=AB ,则C ∠的度数为________.19.(东城18期末14)⊙O 是四边形ABCD 的外接圆,AC 平分∠BAD ,则正确结论的序号是.①AB=AD ;②BC=CD ;③AB AD =;④∠BCA=∠DCA ; ⑤ BC CD =.40︒50︒80︒100︒20.(丰台18期末14)在平面直角坐标系中,过三点A (0,0),B (2,2),C (4,0)的圆的圆心坐标为 .14.(2,0);21.(西城18期末16)如图,⊙O 的半径为3,A ,P 两点在⊙O 上,点B 在⊙O 内,4tan 3APB ∠=,AB AP ⊥.如果OB ⊥OP ,那么OB 的长为 . 1★垂径定理22.(顺义18期末6)如图,已知⊙O 的半径为6,弦AB 的长为8,则圆心O 到AB 的距离为( )A B .C .D .10B23.(石景山18期末4)如图,在⊙O 中,弦AB 垂直平分半径OC .若⊙O 的半径为4,则弦AB 的长为( ) A .32B .34C .52D .54B24.(通州18期末6)如图,⊙O 的半径为4.将⊙O 的一部分沿着弦AB翻折,劣弧恰好经过圆心O .则折痕AB 的长为( ) A. 3B. 32C. 6D. 34 D25.(怀柔18期末7)某校科技实践社团制作实践设备,小明的操作过程如下:①小明取出老师提供的圆形细铁环,先通过在圆一章中学到的知识找到圆心O ,再任意找出圆O 的一条直径标记为AB (如图1),测量出AB =4分米;②将圆环进行翻折使点B 落在圆心O 的位置,翻折部分的圆环和未翻折的圆环产生交点分别标记为C 、D (如图2);③用一细橡胶棒连接C 、D 两点(如图3); ④计算出橡胶棒CD 的长度.小明计算橡胶棒CD 的长度为( ) A .22分米 B .23分米 C .32分米 D .33分米B26.(门头沟18期末13)如图,在△ABC 中,∠A =60°,⊙O 为△ABC的外接圆.如果BC=,那么⊙O 的半径为________. 227.(西城18期末13)如图,⊙O 的半径等于4,如果弦AB 所对的圆心角等于120 ,那么圆心O 到弦AB 的距离等于 . 228.(大兴18期末13)如图,在半径为5cm 的⊙O 中,如果弦AB 的长为8cm ,OC ⊥AB ,垂足为C ,那么OC 的长为 cm .329.(东城18期末12)如图,AB 是⊙O 的弦,C 是AB 的中点,连接OC 并延长交⊙O 于点D .若CD =1,AB =4,则⊙O 的半径是_______.12、5230.(燕山18期末11)如图,AB 、AC 是⊙O 的弦,OM ⊥ AB ,ON ⊥ AC ,垂足分别为 M 、N .如果 MN =2.5,那么BC =_______5★正多边形31.(东城18期末2)边长为2的正方形内接于M,则M的半径是()A.B.2C D.C32.(丰台18期末12)如图,等边三角形ABC的外接圆⊙O的半径OA的长为2,则其内切圆半径的长为.133.(通州18期末13)如图,AD,AE是正六边形的两条对角线.在不添加任何其他线段的情况下,请写出两个关于图中角度的正确结论:(1)__________________________;(2)______________________.34.(昌平18期末13)如图,⊙O的半径为3,正六边形ABCDEF 内接于⊙O,则劣弧AB的长为.35.(朝阳18期末9)如图,正六边形ABCDEF内接于⊙O,⊙O的半径为3,则正六边形ABCDEF的边长为.36.(平谷18期末13)“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣.”这是我国古代著名数学家刘徽在《九章算术注》中提到的“如何求圆的周长和面积”的方法,即“割圆术”.“割圆术”的主要意思是用圆内接正多边形去逐步逼近圆.刘徽从圆内接正六边形出发,将边数逐次加倍,并逐次得到正多边形的周长和面积.如图,AB 是圆内接正六边形的一条边,半径OB =1,OC ⊥AB 于点D ,则圆内接正十二边形的边BC 的长是 (结果不取近似值).13=★弧长、扇形面积37.(西城18期末4)圆心角为60︒,且半径为12的扇形的面积等于( ).A.48πB.24πC.4πD.2πB38.(东城18期末5)A ,B 是O 上的两点,OA =1, AB 的长是1π3,则∠AOB 的度数是( )A .30°B .60°C .90°D .120°B39.(大兴18期末4)在半径为12cm 的圆中,长为4πcm 的弧所对的圆心角的度数为( )A. ︒10B. ︒60C. ︒90D. ︒120B40.(通州18期末2)已知一个扇形的半径是1,圆心角是120°,则这个扇形的弧长是( )A .6πB .πC .3πD .32πD41.(海淀18期末13)若一个扇形的圆心角为60°,面积为6π,则这个扇形的半径为_______. 642.(丰台18期末10)半径为2的圆中,60°的圆心角所对的弧的弧长为_______.10.2π343.(大兴18期末14)圆心角为160°的扇形的半径为9cm ,则这个扇形的面积是_______cm 2.14. 36 π .44.(密云18期末12)扇形半径为3cm ,弧长为πcm ,则扇形圆心角的度数为__________.12.60︒45.(平谷18期末10)圆心角为120°,半径为6cm 的扇形的弧长是cm (结果不取近似值).10.4π46.(朝阳18期末7)如图,在△ABC 中,∠BAC =90°,AB =AC =4,以点C 为中心,把△ABC 逆时针旋转45°,得到△A’B’C ,则图中阴影部分的面积为( )A .2B .2πC .4D .4πB47.(石景山18期末11)如图,扇形的圆心角︒=∠60AOB ,半径为3cm .若点C 、D 是 的三等分点,则图中所有阴影部分的面积之和是________cm 2.11.2π48.(怀柔18期末15)在学校的花园里有一如图所示的花坛,它是由一个正三角形和圆心分别在正三角形顶点、半径为1米的三个等圆组成,现在要在花坛正三角形以外的区域(图中阴影部分)种植草皮.草皮种植面积为 米2.π2549.(顺义18期末20)制造弯形管道时,经常要先按中心线计算“展直长度”,再备料.下图是一段管道,其中直管道部分AB 的长为3 000mm ,弯形管道部分BC ,CD 弧的半径都是1 000mm ,∠O =∠O ’=90°,计算图中中心虚线的长度.20. 901000500180180n r l πππ⨯===…………………………….…….……….3分 中心虚线的长度为 30005002300010ππ+⨯=+…………………4分=30001000 3.14=6140+⨯……………………………………………..…5分。
2019年1月北京通州初三上数学期末试卷及答案

2019北京通州区初三(上)期末数 学 2019年1月一、选择题(本题共8个小题,每小题2分,共16分.每小题只有一个正确选项) 1.如图,点D 、E 分别在△ABC 的AB 、AC 边上,下列条件中:①∠ADE =∠C ;②AE DE AB BC =;③AD AEAC AB=. 使△ADE 与△ACB 一定相似的是A .①②B .②③C .①③D .①②③2. 如图,A 、B 、C 是半径为4的⊙O 上的三点. 如果∠ACB =45°,那么AB 的长为 A .πB .2πC .3πD .4π3. 小王抛一枚质地均匀的硬币,连续抛4次,硬币均正面朝上落地. 如果他再抛第5次,那么硬币正面朝上的概率为A .1B .12C .14D .154.如图,数轴上有A 、B 、C 三点,点A 、C 关于点B 对称,以原点O 为圆心作圆,如果点A 、B 、C 分别在⊙O 外、⊙O 内、⊙O 上,那么原点O 的位置应该在 A .点A 与点B 之间靠近A 点B .点A 与点B 之间靠近B 点C .点B 与点C 之间靠近B 点D .点B 与点C 之间靠近C 点5. 如图,PA 和PB 是⊙O 的切线,点A 和点B 为切点,AC 是⊙O 的直径. 已知∠P =50°,那么∠ACB 的大小是 A .65° B .60° C .55° D .50°cax s ()y m ()182014753O6. 如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A ,又在河的另一岸边取两点B 、C ,测得∠α=30°,∠β=45°,量得BC 长为80米.如果设河的宽度为x 米,那么下列关系式中正确的是A .1802x x =+ B .180xx =+ C .2802x x =+ D .3803x x =+ 7. 体育节中,某学校组织九年级学生举行定点投篮比赛,要求每班选派 10名队员参加.下面是一班和二班参赛队员定点投篮比赛成绩的折线统计图(每人投篮10次,每投中1次记1分),请根据图中信息判断: ①二班学生比一班学生的成绩稳定;②两班学生成绩的中位数相同; ③两班学生成绩的众数相同. 上述说法中,正确的序号是 A .①② B .①③C .②③D .①②③8. 运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度y (单位:m )与足球被踢出后经过的时间x (单位:s )近似满足函数关系()20y ax bx c a =++≠.如图记录了3个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻x 是A .4B .4.5C .5D .6二、填空题(本题共8个小题,每小题2分,共16分)9. 如图,线段BD 、CE 相交于点A ,DE ∥BC .如果AB =4,AD =2,DE =1.5, 那么BC 的长为_________. 10.在平面直角坐标系xOy 中,二次函数()214y x =--+的图象如图,将二次函数()214y x =--+的图象平移,使二次函数()214y x =--+的图象的最高点与坐标原点重合,请写出一种平移方法:__________________________________________.11.如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O ,另一边所在直线与半圆相交于点D 、E ,量出半径OC =5cm ,弦DE =8cm ,则直尺的宽度为____cm.yx4O1EDBCA二班一班成绩/分109876109876543201512. “阅读让自己内心强大,勇敢面对抉择与挑战.”某校倡导学生读书,下面的表格是该校九年级学生本学期内阅读课外书籍情况统计表. 请你根据统计表中提供的信息,求出表中a 、b 的值:a = ,b = .预计2019年年人均收入将达到y 美元. 设2017年到2019年该地区居民年人均收入平均增长率为x,那么y 与x 的函数关系式是________________________.14. 如图,直角三角形纸片ABC ,90ACB ∠=︒,AC 边长为10 cm. 现从下往上 依次裁剪宽为4 cm 的矩形纸条,如果剪得第二张矩形纸条恰好是正方形,那么BC 的长度是____cm .15. 已知二次函数()210y ax bx a =++≠的图象与x 轴只有一个交点.请写出一组满足条件的a ,b 的值:a =______,b =________.16. 下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程. 已知:直线a 和直线外一点P . 求作:直线a 的垂线,使它经过P . 作法:如图2.(1)在直线a 上取一点A ,连接PA ;(2)分别以点A 和点P 为圆心,大于12AP 的长为半径 作弧,两弧相交于B ,C 两点,连接BC 交PA 于点D ; (3)以点D 为圆心,DP 为半径作圆,交直线a 于点E (异于点A ),作直线PE . 所以直线PE 就是所求作的垂线.请回答:该尺规作图的依据是_____________________________________________.图1aaP三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分) 17.计算:(4cos30π1︒+-.18. 已知:如图,AB 为⊙O 的直径,OD ∥AC . 求证:点D 平分BC .19.如图,在□ABCD 中,连接DB ,F 是边BC 上一点,连接DF 并延长,交AB的延长线于E ,且∠EDB =∠A . (1)求证:△BDF ∽△BCD ;(2)如果BD =9BC =,求ABBE的值.20. 如图,菱形ABCD 的对角线交于点O ,点E 是菱形外一点,DE ∥AC ,CE ∥BD . (1)求证:四边形DECO 是矩形;(2)连接AE 交BD 于点F ,当∠ADB =30°,DE=2时,求AF 的长度.21.如图,直线2y x=+与反比例函数()00ky k xx=>>,的图象交于点A(2,m),与y轴交于点B.(1)求m、k的值;(2)连接OA,将△AOB沿射线BA方向平移,平移后A、O、B的对应点分别为A'、O'、B',当点O'恰好落在反比例函数()0ky kx=>的图象上时,求点O' 的坐标;(3)设点P的坐标为(0,n)且04n<<,过点P作平行于x轴的直线与直线2y x=+和反比例函数()0ky kx=>的图象分别交于点C,D,当C、D间距离小于或等于4时,直接写出n的取值范围.22.如图,AB为⊙O的直径,C、D为⊙O上不同于A、B的两点,∠ABD=2∠BAC,连接CD,过点C作CE⊥DB,垂足为E,直径AB与CE的延长线相交于F点.(1)求证:CF是⊙O的切线;(2)当185BD=,3sin5F=时,求OF的长.23. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A.书法;B.绘画;C.乐器;D.舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每名被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:学生选修课程条形统计图学生选修课程扇形统计图(1)本次调查的学生共有_______人,扇形统计图中α的度数是_______; (2)请把条形统计图补充完整;(3)学校为举办2018年度校园文化艺术节,决定从A .书法;B .绘画;C .乐器;D .舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或画树状图法求出选中书法与乐器组合在一起的概率.24.如图,AB 是⊙O 的直径,点C 是⊙O 上一点,30CAB ∠=︒,D 是直径AB 上一动点,连接CD 并过点D 作CD 的垂线,与⊙O 的其中一个交点记为点E (点E 位于直线CD 上方或左侧),连接EC .已知AB =6 cm ,设A 、D 两点间的距离为x cm ,C 、D 两点间的距离为1y cm ,E 、C 两点间的距离为2y cm . 小雪根据学习函数的经验,分别对函数1y ,2y 随自变量x 的变化而变化的规律进行了探究. 下面是小雪的探究过程:(1)按照下表中自变量x 的值进行取点、画图、测量,分别得到了1y ,2y 与x 的几组对应值,请将表格补充完整;x /cm0 1 2 3 4 5 61y /cm5.20 4.36 3.60 2.65 2.652y /cm5.204.564.224.244.775.606.00(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,1y ),(x ,2y ),并画出函数1y 的图象;(3)结合函数图象,解决问题:当60ECD ∠=︒时,AD 的长度约为________cm .y 2cm 654325. 在平面直角坐标系xOy 中,抛物线()240y ax ax m a =-+≠与x 轴的交点为A 、B ,(点A 在点B 的左侧),且AB =2.(1)求抛物线的对称轴及m 的值(用含字母a 的代数式表示);(2)若抛物线()240y ax ax m a =-+≠与y 轴的交点在(0,-1)和(0,0)之间,求a 的取值范围; (3)横、纵坐标都是整数的点叫做整点.若抛物线在点A ,B 之间的部分与线段AB 所围成的区域内(包括边界)恰有5个整点,结合函数的图象,直接写出a 的取值范围.26. 如图1,在正方形ABCD 中,点F 在边BC 上,过点F 作EF ⊥BC ,且FE =FC (CE <CB ),连接CE 、AE ,点G 是AE的中点,连接FG .(1)用等式表示线段BF 与FG 的数量关系是___________________;(2)将图1中的△CEF 绕点C 按逆时针旋转,使△CEF 的顶点F 恰好在正方形ABCD 的对角线AC 上,点G 仍是AE 的中点,连接FG 、DF .①在图2中,依据题意补全图形; ②求证:DF =.图2图127. 在平面直角坐标系xOy 中,⊙C 的半径为r ,点P 与圆心C 不重合,给出如下定义:若在⊙C 上存在一点M ,使30MPC ∠=︒,则称点P 为⊙C 的特征点. (1)当⊙O 的半径为1时,如图1.①在点P 1(-1,0),P 2(1P 3(3,0)中,⊙O 的特征点是______________. ②点P在直线y b =+上,若点P 为⊙O 的特征点,求b 的取值范围.(2)如图2,⊙C 的圆心在x 轴上,半径为2,点A (-2,0),B (0,AB 上的所有点都是⊙C 的特征点,直接写出圆心C 的横坐标m 的取值范围.2019北京通州区初三(上)期末数学试题答案一、选择题(本题共8个小题,每小题2分,共16分)9. 3 10. 向左平移1个单位,再向下平移4个单位(答案不唯一) 11. 3 12. 150,0.3513. ()23001y x =+ 14. 20 15. 1,2(答案不唯一) 16. 到线段两个端点距离相等的点在这条线段的垂直平分线上,直径所对的圆周角是直角,两点确定一条直线三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分)17. 解:原式=4112⨯+-, ………………… 4分 =11--,=0.………………… 6分18. 证明:连接CB . ………………… 1分∵AB 为⊙O 的直径,∴90ACB ∠=︒. ………………… 3分 ∵OD ∥AC , ∴OD ⊥CB ,. ………………… 5分 ∴点D 平分BC . ………………… 6分 另证:可以连接OC 或AD .19. (1)证明:∵四边形ABCD 是平行四边形,∴DC ∥AE ,A C ∠=∠,AB =DC . ………………… 1分∵EDB A ∠=∠,∴EDB C ∠=∠. ………………… 2分 ∵DBF CBD ∠=∠,∴△BDF ∽△BCD . ………………… 3分(2)解:∵△BDF ∽△BCD ,∴BF BDBD BC=4分 9=. ∴5BF =. ………………… 5分 ∵DC ∥AE , ∴△DFC ∽△EFB .∴CF DCBF BE=. ∴45AB BE =. ………………… 6分 20. (1)证明:∵四边形ABCD 是菱形,∴AC ⊥BD . ……………… 1分 ∵DE ∥AC ,CE ∥BD , ∴四边形DECO 是平行四边形.∴四边形DECO 是矩形. ……………… 2分(2)解: ∵四边形ABCD 是菱形,∴ AO OC =. ∵四边形DECO 是矩形, ∴DE OC =.∴2DE AO ==. ……………… 3分∵DE ∥AC , ∴OAF DEF ∠=∠. ∵AFO EFD ∠=∠,∴△AFO ≌△EFD .∴OF DF =. ……………… 4分 在Rt △ADO 中,tan OAADB DO∠=.∴23DO =.∴DO =……………… 5分∴FO =∴AF ===……………… 6分方法二:∴△AFO ≌△EFD .∴AF =FE.在Rt △ACE 中,AC =4,CE =OD =∴AE =∴AF =12AE . 21. 解:(1)∵直线2y x =+过点A (2,m ),∴224m =+=. ……………… 1分 ∴点A (2,4).把A (2,4)代入函数ky x=中, ∴42k =. ∴8k =. ……………… 2分 (2)∵△AOB 沿射线BA 方向平移,∴直线OO' 的表达式为y x =. ……………… 3分∴,8y x y x =⎧⎪⎨=⎪⎩.解得x =(舍负). ……………… 4分 ∴点O'的坐标为(. ……………… 5分 (3)24n <≤. ……………… 6分22. (1)证明:连接OC .∵CB CB =,∴2BOC BAC ∠=∠. ……………… 1分 ∵∠ABD =2∠BAC , ∴BOC ABD ∠=∠.∴BD ∥OC . ……………… 2分 ∵CE ⊥DB ,∴CE ⊥OC . ……………… 3分 ∴CF 是⊙O 的切线.(2)解:连接AD .∵AB 为⊙O 的直径, ∴BD ⊥AD . ∵CE ⊥DB , ∴AD ∥CF .∴F BAD ∠=∠. ……………… 4分 在Rt △ABD 中,∴3sin sin 5BD F=BAD AB ∠==. ∴18355AB =.∴6AB=. ……………… 5分∴3OC=.在Rt△COF中,∴3 sin5OCFOF==.∴335 OF=.∴5OF=. ……………… 6分另解:过点O作OG⊥DB于点G.23. 解:(1)40,108︒;……………… 2分(2)条形统计图补充正确;……………… 4分(3)列表法或画树状图正确:……………… 5分∴P(AC)=126=. ……………… 6分24. 解:(1)3,3 ……………… 2分(2)……………… 4分(3)4.5 或6 ……………… 6分25.解:(1)对称轴为直线422axa-=-=. ……………… 1分∵AB=2,点A在点B的左侧,y2 cm65432∴A ()10,,B ()30, 把A (1,0)代入()240y ax ax m a =-+≠中,∴3m a =. ……………… 2分(2)∵抛物线()2430y ax ax a a =-+≠与y 轴的交点在(0,-1)和(0,0)之间,∴0a <. ……………… 3分当抛物线()2430y ax ax a a =-+≠经过点(0,-1)时,可得13a =-.∴a 的取值范围是103a -<<. ……………… 4分 (3)32a -<-≤或2<3a ≤. ……………… 6分26. (1)BF =. ……………… 1分(2)①依据题意补全图形; ……………… 3分②证明:如图,连接BF 、GB .∵四边形ABCD 是正方形,∴AD =AB ,90ABC BAD ∠=∠=︒,AC 平分BAD ∠. ∴45BAC DAC ∠=∠=︒. 在△ADF 和△ABF 中,AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ADF ≌△ABF . ……………… 4分 ∴DF BF =.∵EF ⊥AC ,90ABC ∠=︒,点G 是AE 的中点,∴AG EG BG FG ===. ……………… 5分 ∴点A 、F 、E 、B 在以点G 为圆心,AG 长为半径的圆上. ∵BF BF =,45BAC ∠=︒,∴290BGF BAC ∠=∠=︒. ……………… 6分 ∴△BGF 是等腰直角三角形.∴BF =.∴DF =. ……………… 7分27. 解:(1) P 1,P 2.……………… 2分②当0b >时,设直线y b =+与以2为半径的⊙O 相切于点C ,与y 轴交于点E ,与x 轴交于点F .∴E (0,b ),F,0),OC ⊥EF .∴3tan OF FEO OE b ∠===. ∴30FEO ∠=︒. (3)∵1sin 2OC FEO OE ∠==, ∴212b =. ∴4b =. ……………… 4分 当0b <时,由对称性可知:4b =-. ……………… 5分 ∴b 的取值范围是44b -≤≤. ……………… 6分 (2)∴m 的取值范围为22m -<≤. ……………… 7分。
2019-2020北京市初三上数学期末考试新定义压轴题汇总(含答案)

2019-2020初三上期末考试新定义压轴题汇总1、(19-20朝阳期末)28.在平面直角坐标系xOy 中,已知点A (0,2),点B 在x 轴上,以AB 为直径作⊙C ,点P 在y 轴上,且在点A 上方,过点P 作⊙C 的切线PQ ,Q 为切点,如果点Q 在第一象限,则称Q 为点P 的离点.例如,图1中的Q 为点P 的一个离点.(1)已知点P (0,3),Q 为P 的离点.①如图2,若B (0,0),则圆心C 的坐标为 ,线段PQ 的长为 ;②若B (2,0),求线段PQ 的长;(2)已知1≤PA ≤2, 直线l :3y kx k =++(k ≠0). ①当k =1时,若直线l 上存在P 的离点Q ,则点Q 纵坐标t 的最大值为 ;②记直线l :3y kx k =++(k ≠0)在11x -≤≤的部分为图形G ,如果图形G 上存在P 的离点,直接写出k 的取值范围.图2图12、(19-20东城期末)28. 如图,在平面直角坐标系xOy 中,过⊙T 外一点P 引它的两条切线,切点分别为M ,N ,若︒<∠≤︒18060MPN ,则称P 为⊙T 的环绕点.(1)当⊙O 半径为1时,①在)2,0(),1,1(),0,1(321P P P 中,⊙O 的环绕点是___________;②直线y =2x +b 与x 轴交于点A ,y 轴交于点B ,若线段AB 上存在⊙O 的环绕点,求b 的取值范围;(2)⊙T 的半径为1,圆心为(0,t ),以)0(33, m m m )(为圆心,m 33为半径的所有圆构成图形H ,若在图形H 上存在⊙T 的环绕点,直接写出t 的取值范围.3、(19-20西城期末)28. 对于给定的△ABC,我们给出如下定义:若点M是边BC上的一个定点,且以M为圆心的半圆上的所有点都在△ABC的内部或边上,则称这样的圆为BC边上的点M关于△ABC的内半圆,并将半径最大的内半圆称为点M关于△ABC的最大内半圆.若点M是边BC上的一个动点(M不与B,C重合),则在所有的点M关于△ABC的最大内半圆中,将半径最大的内半圆称为BC关于△ABC的内半圆.(1)在Rt△ABC中,∠BAC=90°,AB=AC=2,①如图1,点D在边BC上,且CD=1,直接写出点D关于△ABC的最大内半圆的半径长;②如图2,画出BC关于△ABC的内半圆,并直接写出它的半径长;x上运动(P不与O重合),将(2)在平面直角坐标系xOy中,点E的坐标为(3,0),点P在直线y=√33≤R≤1时,求点P的横坐标t的取值范围.OE关于△OEP的内半圆半径记为R,当344、(19-20海淀期末)28.在平面直角坐标系xOy 中,对于点P (a ,b )和实数(0)k k >,给出如下定义:当0ka b +>时,将以点P 为圆心,ka b +为半径的圆,称为点P 的k 倍相关圆.例如,在如图1中,点P (1,1)的1倍相关圆为以点P 为圆心,2为半径的圆.(1)在点P 1(2,1),P 2(1,3-)中,存在1倍相关圆的点是_____,该点的1倍相关圆半径为_______.(2)如图2,若M 是x 轴正半轴上的动点,点N 在第一象限内,且满足∠MON =30°,判断直线ON与点M 的12倍相关圆的位置关系,并证明. (3)如图3,已知点A 的(0,3),B (1,m ),反比例函数6y x=的图象经过点B ,直线l 与直线AB 关于y 轴对称.①若点C 在直线l 上,则点C 的3倍相关圆的半径为 .②点D 在直线AB 上,点D 的31倍相关圆的半径为R ,若点D 在运动过程中,以点D 为圆 心,hR 为半径的圆与反比例函数6y x=的图象最多有两个公共点,直接写出h 的最大值.图 1图 25、(19-20丰台期末)27.平面直角坐标系xOy 中有点P 和某一函数图象M ,过点P 作x 轴的垂线,交图象M 于点Q ,设点P ,Q 的纵坐标分别为P y ,Q y .如果P Q y y >,那么称点P 为图象M 的上位点;如果P Q y y =,那么称点P 为图象M 的图上点;如果P Q y y <,那么称点P 为图象M 的下位点.(1)已知抛物线22y x =-.① 在点A (-1,0),B (0,-2),C (2,3)中,是抛物线的上位点的是 ;② 如果点D 是直线y x =的图上点,且为抛物线的上位点,求点D 的横坐标D x 的取值范围;(2)将直线3y x =+在直线3y =下方的部分沿直线3y =翻折,直线3y x =+的其余部分保持不变,得到一个新的图象,记作图象G .⊙H 的圆心H 在x 轴上,半径为1.如果在图象G 和⊙H 上分别存在点E 和点F ,使得线段EF 上同时存在图象G 的上位点,图上点和下位点,求圆心H 的横坐标H x 的取值范围.图 36、(19-20石景山期末)28.在ABC △中,D 是边BC 上一点,以点A 为圆心,AD 长为半径作弧,如果与边BC 有交点E (不与点D 重合),那么称DE ̂为ABC △的A -外截弧.例如,右图中DE ̂是ABC △的一条A -外截弧.在平面直角坐标系xOy 中,已知ABC △存在A -外截弧,其中点A 的坐标为(5,0),点B 与坐标原点O 重合.(1)在点1(0,2)C ,2(5,3)C -,3(6,4)C ,4(4,2)C 中,满足条件的点C 是 ;(2)若点C 在直线2y x =-上,①求点C 的纵坐标的取值范围;②直接写出ABC △的A -外截弧所在圆的半径r 的取值范围.E D CB A7、(19-20大兴期末)28. 在平面直角坐标系xOy中,已知P(a,b),R(c,d)两点,且a≠c,b≠d,若过点P作x轴的平行线,过点R作y轴的平行线,两平行线交于一点S,连接PR,则称△PRS为点P,R,S的“坐标轴三角形”.若过点R作x轴的平行线,过点P作y轴的平行线,两平行线交于一点S',连接PR,则称△RP S'为点R,P,S'的“坐标轴三角形”.右图为点P,R,S的“坐标轴三角形”的示意图.(1)已知点A(0,4),点B(3,0),若△ABC是点A,B,C的“坐标轴三角形”,则点C的坐标为 ;(2)已知点D(2,1),点E(e,4),若点D,E,F的“坐标轴三角形”的面积为3,求e的值.,点M(m,4).若在⨀O上存在一点N,使得点N ,M, G的“坐标轴三角形”(3)若⨀O的半径为3√22为等腰三角形,求m的取值范围.8、(19-20房山期末)28.如图28-1,已知线段AB 与点P ,若在线段AB 上存在..点Q ,满足PQ AB ,则称点P 为线段AB 的“限距点”.(1) 如图28-2,在平面直角坐标系xOy 中,若点)01-(,A ,)01(,B . ① 在)20(,C ,)2--2(,D ,)3-1(,E 中,是线段AB 的“限距点”的是________; ② 点P 是直线1+=x y 上一点,若点P 是线段AB 的“限距点”,请求出点P 横坐标P x 的取值范围.图28-2(2) 在平面直角坐标系xOy 中,点)1(,t A ,)1-(,t B ,直线32+33=x y 与x 轴交于点M ,与y 轴交于点N . 若线段MN 上存在线段AB 的“限距点”,请求出t 的取值范围.9、(19-20门头沟期末)28.对于平面直角坐标系xOy 中的图形M ,N ,给出如下定义:如果点P 为图形M上任意一点,点Q 为图形N 上任意一点,那么称线段PQ 长度的最小值为图形M ,N 的“近距离”,记作 d (M ,N ).若图形M ,N 的“近距离”小于或等于1,则称图形M ,N 互为“可及图形”. (1)当⊙O 的半径为2时,①如果点A (0,1),B (3,4),那么d (A ,⊙O )=________,d (B ,⊙O )= _________; ②如果直线y x b =+与⊙O 互为“可及图形”,求b 的取值范围;(2)⊙G 的圆心G 在x 轴上,半径为1,直线5y x =-+与x 轴交于点C ,与y 轴交于点D ,如果⊙G和∠CDO 互为“可及图形”,直接写出圆心G 的横坐标m 的取值范围.备用图10、(19-20密云期末)28.在平面直角坐标系xOy中,⊙O的半径为r(r>0).给出如下定义:若平面上一点P到圆心O的距离d,满足1322r d r≤≤,则称点P为⊙O的“随心点”.(1)当⊙O的半径r=2时,A(3,0),B(0,4),C(32-,2),D(12,12-)中,⊙O的“随心点”是;(2)若点E(4,3)是⊙O的“随心点”,求⊙O的半径r的取值范围;(3)当⊙O的半径r=2时,直线y=- x+b(b≠0)与x轴交于点M,与y轴交于点N,若线段MN上存在⊙O的“随心点”,直接写出b的取值范围.备用图11、(19-20平谷期末)28.在平面直角坐标系xOy中,有任意三角形,当这个三角形的一条边上的中线等于这条边的一半时,称这个三角形叫“和谐三角形”,这条边叫“和谐边”,这条中线的长度叫“和谐距离”.(1)已知A(2,0),B(0,4),C(1,2),D(4,1),这个点中,能与点O组成“和谐三角形”的点是,“和谐距离”是;(2)连接BD,点M,N是BD上任意两个动点(点M,N不重合),点E是平面内任意一点,△EMN是以MN 为“和谐边”的“和谐三角形”,求点E的横坐标t的取值范围;(3)已知⊙O的半径为2,点P是⊙O上的一动点,点Q是平面内任意一点,△OPQ是“和谐三角形”,且“和谐距离”是2,请描述出点Q所在位置.12、(19-20顺义期末)28.在平面直角坐标系xOy 中,若点P 和点P 1关于x 轴对称,点P 1和点P 2关于直线l 对称,则称点P 2是点P 关于x 轴,直线l 的二次对称点. (1)如图1,点A (0,-1).①若点B 是点A 关于x 轴,直线l 1:x =2的二次对称点,则点B 的坐标为 ; ②点C (-4,1)是点A 关于x 轴,直线l 2:x =a 的二次对称点,则a 的值为 ; ③点D (-1,0)是点A 关于x 轴,直线l 3的二次对称点,则直线l 3的表达式为 ;(2)如图2,⨀O 的半径为2.若⨀O 上存在点M ,使得点M ′是点M 关于x 轴,直线l 4:x = b 的二次对称点,且点M ′在射线x y 3(x ≥0)上,b 的取值范围是;(3)E (0,t )是y 轴上的动点,⨀E 的半径为2,若⨀E 上存在点N ,使得点N ′是点N 关于x 轴,直线l 5:x y 33的二次对称点,且点N ′在x 轴上,求t 的取值范围.图1 图213、(19-20通州期末)28.如图,在平面内。
2018~2019通州区九年级数学第一学期期末数学试题及参考答案

通州区2018—2019学年第一学期九年级期末学业水平质量检测数学试卷一、选择题(本题共8个小题,每小题2分,共16分.每小题只有一个正确选项) 1.如图,点D 、E 分别在△ABC 的AB 、AC 边上,下列条件中:①∠ADE =∠C ; ②AE DE AB BC =;③AD AEAC AB=. 使△ADE 与△ACB 一定相似的是 A .①② B .②③C .①③D .①②③2. 如图,A 、B 、C 是半径为4的⊙O 上的三点. 如果∠ACB =45°,那么AB 的长为 A .πB .2πC .3πD .4π3. 小王抛一枚质地均匀的硬币,连续抛4次,硬币均正面朝上落地. 如果他再抛第5次,那么硬币正面朝上的概率为 A .1B .12C .14D .154.如图,数轴上有A 、B 、C 三点,点A 、C 关于点B 对称,以原点O 为圆心作圆,如果点A 、B 、C 分别在⊙O 外、⊙O 内、⊙O 上,那么原点O 的位置应该在 A .点A 与点B 之间靠近A 点B .点A 与点B 之间靠近B 点C .点B 与点C 之间靠近B 点D .点B与点C 之间靠近C 点5. 如图,PA 和PB 是⊙O的切线,点A 和点B 为切点,AC 是⊙O 的直径. 已知∠P =50°,那么∠ACB 的大小是 A .65°B .60°C .55°D .50°6. 如图,为了测量某条河的宽度,现在河边的一岸边任意取一点A ,又在河的另一岸边取两点B 、C ,测得∠α=30°,∠β=45°,量得BC 长为80米.如果设河的宽度为x 米,那么下列关系式中正确的是 A .1802x x =+ B .180xx =+ C.802x x =+ D.80x x =+7. 体育节中,某学校组织九年级学生举行定点投篮比赛, 要求每班选派10名队员参加.下面是一班和二班 参赛队员定点投篮比赛成绩的折线统计图(每人投 篮10次,每投中1次记1分),请根据图中信息判断:①二班学生比一班学生的成绩稳定;②两班学生成绩的中位数相同;③两班学生成绩的众数相同. 上述说法中,正确的序号是 A .①② B .①③C .②③D .①②③8. 运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线可以看作是一条抛物线,不考虑空气阻力,足球距离地面的高度y (单位:m )与足球被踢出后经过的时间x (单位:s )近似满足函数关系()20y ax bx c a =++≠.如图记录了3个时刻的数据,根据函数模型和所给数据,可推断出足球飞行到最高点时,最接近的时刻x 是A .4B .4.5C .5D .6二、填空题(本题共8个小题,每小题2分,共16分)9. 如图,线段BD 、CE 相交于点A ,DE ∥BC .如果AB =4,AD =2,DE =1.5, 那么BC 的长为_________.s )10.在平面直角坐标系xOy)214-+的图象如图,将二次函数()214yx =--+的图象平移,使二次函数()214y x =--+的图象的最高点与坐标原点重合,请写出一种平移方法:__________________________________________. 11.如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O ,另一边所在直线与半圆相交于点D 、E ,量出半径OC =5cm ,弦DE =8cm ,则直尺的宽度为____cm. 12. “阅读让自己内心强大,勇敢面对抉择与挑战.”某校倡导学生读书,下面的表格是该校九年级学生本学期内阅读课外书籍情况统计表. 请你根据统计表中提供的信息,求出表中a 、b 的值:a = ,b = .13.中国“一带一路”倡议给沿线国家和地区带来很大的经济效益,沿线某地区居民2017年年人均收入300美元,预计2019年年人均收入将达到y 美元. 设2017年到2019年该地区居民年人均收入平均增长率为x ,那么y 与x 的函数关系式是________________________.14. 如图,直角三角形纸片ABC ,90ACB ∠=︒,AC 边长为10 cm. 现从下往上依次裁剪宽为4 cm 的矩形纸条, 如果剪得第二张矩形纸条恰好是正方形,那么BC 的长 度是____cm .15. 已知二次函数()210y ax bx a =++≠的图象与x 轴只有一个交点.请写出一组满足条件的a ,b 的值:a =______,b =________.16. 下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程. 已知:直线a 和直线外一点P . 求作:直线a 的垂线,使它经过P .作法:如图2.(1)在直线a 上取一点A ,连接PA ;(2)分别以点A 和点P 为圆心,大于12AP 的长为半径作弧,两弧相交于B ,C 两点,连接BC 交PA 于点D ; (3)以点D 为圆心,DP 为半径作圆,交直线a 于点E (异于点A ),作直线PE .所以直线PE 就是所求作的垂线.请回答:该尺规作图的依据是三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分) 17.计算:(4cos30π1︒+-.18. 已知:如图,AB 为⊙O 的直径,OD ∥AC . 求证:点D 平分BC .19.如图,在□ABCD 中,连接DB ,F 是边BC 上一点,连接DF 并延长,交AB 的延长线于E ,且∠EDB =∠A .(1)求证:△BDF ∽△BCD ;(2)如果BD =9BC =,求ABBE的值.图1aaP20. 如图,菱形ABCD 的对角线交于点O ,点E 是菱形外一点,DE ∥AC ,CE ∥BD . (1)求证:四边形DECO 是矩形;(2)连接AE 交BD 于点F ,当∠ADB =30°,DE=2时,求AF 的长度.21.如图,直线2y x =+与反比例函数()00ky k x x=>>,的图象交于点A (2,m ),与y 轴交于点B . (1)求m 、k 的值;(2)连接OA ,将△AOB 沿射线BA 方向平移,平移后A 、O 、B 的对应点分别为A'、O'、B',当点O'恰好落在反比例函数()0ky k x=>的图象上时,求点O' 的坐标; (3)设点P 的坐标为(0,n )且04n <<,过点P 作平行于x 轴的直线与直线2y x =+和反比例函数()0ky k x=>的图象分别交于点C ,D ,当C 、D 间距离小于或等于4时,直接写出n 的取值范围.22.如图,AB 为⊙O 的直径,C 、D 为⊙O 上不同于A 、B 的两点,∠ABD =2∠BAC ,连接CD ,过点C 作CE ⊥DB ,垂足为E ,直径AB 与CE 的延长线相交于F 点. (1)求证:CF 是⊙O 的切线;(2)当185BD=,3sin 5F=时,求OF 的长.23. 为提升学生的艺术素养,学校计划开设四门艺术选修课:A .书法;B .绘画;C .乐器;D .舞蹈.为了解学生对四门功课的喜欢情况,在全校范围内随机抽取若干名学生进行问卷调查(每名被调查的学生必须选择而且只能选择其中一门).将数据进行整理,并绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:(1)本次调查的学生共有_______人,扇形统计图中α的度数是_______; (2)请把条形统计图补充完整;(3)学校为举办2018年度校园文化艺术节,决定从A .书法;B .绘画;C .乐器;D .舞蹈四项艺术形式中选择其中两项组成一个新的节目形式,请用列表法或画树状图法求出选中书法与乐器组合在一起的概率.24.如图,AB 是⊙O 的直径,点C 是⊙O 上一点,30CAB ∠=︒,D 是直径AB 上一动点,连接CD 并过点D 作CD 的垂线,与⊙O 的其中一个交点记为点E (点E 位于直线CD 上方或左侧),连接EC .已知AB =6 cm ,设A 、D 两点间的距离为x cm ,C 、D 两点间的距离为1y cm ,E 、C 两点间的距离为2y cm .小雪根据学习函数的经验,分别对函数1y ,2y 随自变量x 的变化而变化的规律进行了探究. 下面是小雪的探究过程:(1)按照下表中自变量x 的值进行取点、画图、测量,分别得到了1y ,2y 与x 的几组对应学生选修课程条形统计图学生选修课程扇形统计图值,请将表格补充完整;(2)在同一平面直角坐标系xOy 中,描出补全后的表中各组数值所对应的点(x ,1y ),(x ,2y ),并画出函数1y 的图象;(3)结合函数图象,解决问题:当60ECD ∠=︒时,AD 的长度约为________cm . 25. 在平面直角坐标系xOy 中,抛物线()240y ax ax m a =-+≠与x 轴的交点为A 、B ,(点A 在点B 的左侧),且AB =2.(1)求抛物线的对称轴及m 的值(用含字母a(2)若抛物线()240y ax ax m a =-+≠与y a的取值范围;(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A ,B 之间的部分与线段AB 结合函数的图象,直接写出a 的取值范围.26. 如图1,在正方形ABCD 中,点F 在边BC 上,过点F 作EF ⊥BC ,且FE =FC (CE <CB ),连接CE 、AE ,点G 是AE 的中点,连接FG .(1)用等式表示线段BF 与FG 的数量关系是___________________;(2)将图1中的△CEF 绕点C 按逆时针旋转,使△CEF 的顶点F 恰好在正方形ABCD 的y 2cm6543对角线AC 上,点G 仍是AE 的中点,连接FG 、DF .①在图2中,依据题意补全图形; ②求证:DF =.27. 在平面直角坐标系xOy 中,⊙C 的半径为r ,点P 与圆心C 不重合,给出如下定义:若在⊙C 上存在一点M ,使30MPC ∠=︒,则称点P 为⊙C 的特征点. (1)当⊙O 的半径为1时,如图1.①在点P 1(-1,0),P 2(1,P 3(3,0)中,⊙O 的特征点是______________.②点P 在直线y b =+上,若点P 为⊙O 的特征点,求b 的取值范围.(2)如图2,⊙C 的圆心在x 轴上,半径为2,点A (-2,0),B (0,.若线段AB 上的所有点都是⊙C 的特征点,直接写出圆心C 的横坐标m 的取值范围.图2图1通州区2018—2019学年第一学期九年级期末学业水平质量检测数学试卷参考答案及评分标准一、选择题(本题共8个小题,每小题2分,共16分)二、填空题(本题共8个小题,每小题2分,共16分)9. 3 10. 向左平移1个单位,再向下平移4个单位(答案不唯一) 11. 312. 150,0.3513. ()23001y x =+ 14. 20 15. 1,2(答案不唯一) 16. 到线段两个端点距离相等的点在这条线段的垂直平分线上,直径所对的圆周角是直角,两点确定一条直线 三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分) 17. 解:原式=411+-, ………………… 4分 =11-,=0. ………………… 6分18. 证明:连接CB . ………………… 1分∵AB 为⊙O 的直径,∴90ACB ∠=︒. ………………… 3分 ∵OD ∥AC ,∴OD ⊥CB ,. ………………… 5分∴点D 平分BC . ………………… 6分 另证:可以连接OC 或AD .19. (1)证明:∵四边形ABCD 是平行四边形,∴DC ∥AE ,A C ∠=∠,AB =DC . (1)分∵EDB A ∠=∠,∴EDB C ∠=∠. …………………2分∵DBF CBD ∠=∠,∴△BDF ∽△BCD .…………………3分(2)解:∵△BDF ∽△BCD ,∴BF BDBD BC=. ………………… 4分=. ∴5BF =. …………………5分∵DC ∥AE , ∴△DFC ∽△EFB . ∴CF DCBF BE=. ∴45AB BE =. ………………… 6分20. (1)证明:∵四边形ABCD 是菱形,∴AC ⊥BD . ………………1分∵DE ∥AC ,CE ∥BD , ∴四边形DECO 是平行四边形.∴四边形DECO 是矩形. ………………2分(2)解: ∵四边形ABCD 是菱形,∴ AO OC =. ∵四边形DECO 是矩形, ∴DE OC =.∴2DE AO ==. (3)分∵DE ∥AC , ∴OAF DEF ∠=∠. ∵AFO EFD ∠=∠,∴△AFO ≌△EFD .∴OF DF =. ……………… 4分 在Rt △ADO 中,tan OAADB DO∠=.∴2DO =.∴DO = (5)分∴FO .∴AF ===. ………………6分方法二:∴△AFO ≌△EFD .∴AF =FE.在Rt △ACE 中,AC =4,CE =OD =∴AE =∴AF =12AE 21. 解:(1)∵直线2y x =+过点A (2,m ),∴224m =+=. (1)分∴点A (2,4). 把A (2,4)代入函数ky x=中, ∴42k =. ∴8k =. ……………… 2分 (2)∵△AOB 沿射线BA 方向平移,∴直线OO' 的表达式为y x =. ……………… 3分∴,8y x y x =⎧⎪⎨=⎪⎩.解得x =. ……………… 4分 ∴点O'的坐标为(. ……………… 5分(3)24n <≤. ……………… 6分22. (1)证明:连接OC .∵CB CB =,∴2BOC BAC ∠=∠. ……………… 1分 ∵∠ABD =2∠BAC , ∴BOC ABD ∠=∠.∴BD ∥OC . ……………… 2分 ∵CE ⊥DB ,∴CE ⊥OC . ……………… 3分 ∴CF 是⊙O 的切线.(2)解:连接AD .∵AB 为⊙O 的直径,∴BD ⊥AD . ∵CE ⊥DB , ∴AD ∥CF .∴F BAD∠=∠. ………………4分在Rt△ABD中,∴3 sin sin5BDF=BADAB∠==.∴183 55 AB=.∴6AB=. ………………5分∴3OC=.在Rt△COF中,∴3 sin5OCFOF==.∴335 OF=.∴5OF=. ………………6分另解:过点O作OG⊥DB于点G.23. 解:(1)40,108︒;………………2分(2)条形统计图补充正确;………………4分(3)列表法或画树状图正确:………………5分∴P (AC )=126=. ……………… 6分24. 解:(1)3,3 ……………… 2分(2) ……………… 4分 (3)4.5 或6 ……………… 6分25.解:(1)对称轴为直线422ax a-=-=. ……………… 1分 ∵AB =2,点A 在点B 的左侧,∴A ()10,,B ()30,把A (1,0)代入()240y ax ax m a =-+≠中,∴3m a =. ……………… 2分(2)∵抛物线()2430y ax ax a a =-+≠与y 轴的交点在(0,-1)和(0,0)之间,∴0a <. ………………3分当抛物线()2430y ax ax a a =-+≠经过点(0,-1)时,可得13a =-. ∴a 的取值范围是103a -<<. ……………… 4分(3)32a -<-≤或2<3a ≤. ………………6分26. (1)BF =. ……………… 1分 (2)①依据题意补全图形; ……………… 3分②证明:如图,连接BF 、GB .∵四边形ABCD 是正方形,y 2cm65432∴AD =AB ,90ABC BAD ∠=∠=︒,AC 平分BAD ∠. ∴45BAC DAC ∠=∠=︒. 在△ADF 和△ABF 中,AD AB DAC BAC AF AF =⎧⎪∠=∠⎨⎪=⎩,,, ∴△ADF ≌△ABF . ……………… 4分 ∴DF BF =.∵EF ⊥AC ,90ABC ∠=︒,点G 是AE 的中点,∴AG EG BG FG ===. ………………5分∴点A 、F 、E 、B 在以点G 为圆心,AG 长为半径的圆上. ∵BF BF =,45BAC ∠=︒,∴290BGF BAC ∠=∠=︒. ………………6分∴△BGF 是等腰直角三角形.∴BF .∴DF =. ………………7分27. 解:(1) P 1,P 2.……………… 2分②当0b >时,设直线y b =+与以2为半径的⊙O 相切于点C ,与y 轴交于点E ,与x 轴交于点F . ∴E (0,b ),F(3b ,0),OC ⊥EF .∴3tan 3OF FEO OE b ∠===. ∴30FEO ∠=︒. (3)∵1sin 2OC FEO OE ∠==, ∴212b =. ∴4b =. ……………… 4分 当0b <时,由对称性可知:4b =-. ……………… 5分 ∴b 的取值范围是44b -≤≤. ……………… 6分 (2)∴m 的取值范围为22m -<≤. ……………… 7分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学试题答案
一、选择题(本题共8个小题,每小题2分,共16分)
9. 3 10. 向左平移1个单位,再向下平移4个单位(答案不唯一) 11. 3 12. 150,0.35
13. ()2
3001y x =+ 14. 20 15. 1,2(答案不唯一) 16. 到线段两个端点距离相等的点在这条线段的垂
直平分线上,直径所对的圆周角是直角,两点确定一条直线
三、解答题(本题共68分,第17—25题,每小题6分,第26—27题,每小题7分)
17. 解:原式=411+-, ………………… 4分 =11--,
=0. ………………… 6分
18. 证明:连接CB . ………………… 1分
∵AB 为⊙O 的直径,
∴90ACB ∠=︒. ………………… 3分 ∵OD ∥AC ,
∴OD ⊥CB ,. ………………… 5分 ∴点D 平分BC . ………………… 6分 另证:可以连接OC 或AD .
19. (1)证明:∵四边形ABCD 是平行四边形,
∴DC ∥AE ,A C ∠=∠,AB =DC . ………………… 1分 ∵EDB A ∠=∠,
∴EDB C ∠=∠. ………………… 2分 ∵DBF CBD ∠=∠,
∴△BDF ∽△BCD . ………………… 3分
(2)解:∵△BDF ∽△BCD ,
∴BF BD
BD BC
=
4分 =
. ∴5BF =. ………………… 5分 ∵DC ∥AE , ∴△DFC ∽△EFB .
∴
CF DC
BF BE
=. ∴
4
5
AB BE =. ………………… 6分 20. (1)证明:∵四边形ABCD 是菱形,
∴AC ⊥BD . ……………… 1分 ∵DE ∥AC ,CE ∥BD , ∴四边形DECO 是平行四边形.
∴四边形DECO 是矩形. ……………… 2分
(2)解: ∵四边形ABCD 是菱形,
∴ AO OC =. ∵四边形DECO 是矩形, ∴DE OC =.
∴2DE AO ==. ……………… 3分 ∵DE ∥AC , ∴OAF DEF ∠=∠. ∵AFO EFD ∠=∠,
∴△AFO ≌△EFD .
∴OF DF =. ……………… 4分
在Rt △ADO 中,
tan OA
ADB DO
∠=
.
∴
2DO =
∴DO =……………… 5分
∴FO =
∴
AF =
==……………… 6分
方法二:∴△AFO ≌△EFD .
∴AF =FE.
在Rt △ACE 中,AC =4,CE =
OD =∴
AE =∴AF =
1
2
AE . 21. 解:(1)∵直线2y x =+过点A (2,m ),
∴224m =+=. ……………… 1分 ∴点A (2,4).
把A (2,4)代入函数k
y x
=
中, ∴42
k =
. ∴8k =. ……………… 2分 (2)∵△AOB 沿射线BA 方向平移,
∴直线OO' 的表达式为y x =. ……………… 3分
∴,8y x y x =⎧⎪⎨=⎪
⎩
.
解得x =(舍负). ……………… 4分
∴点O' 的坐标为(
. ……………… 5分
(3)24n <≤. ……………… 6分
22. (1)证明:连接OC .
∵CB CB =,
∴2BOC BAC ∠=∠. ……………… 1分 ∵∠ABD =2∠BAC , ∴BOC ABD ∠=∠.
∴BD ∥OC . ……………… 2分 ∵CE ⊥DB ,
∴CE ⊥OC . ……………… 3分 ∴CF 是⊙O 的切线.
(2)解:连接AD .
∵AB 为⊙O 的直径, ∴BD ⊥AD . ∵CE ⊥DB , ∴AD ∥CF .
∴F BAD ∠=∠. ……………… 4分 在Rt △ABD 中,
∴3
sin sin 5
BD F=BAD AB ∠=
=. ∴18
3
55
AB =. ∴6AB =. ……………… 5分 ∴3OC =. 在Rt △COF 中,
∴3
sin 5
OC F OF =
=.
∴
33
5
OF =. ∴5OF =. ……………… 6分 另解:过点O 作OG ⊥DB 于点G .
23. 解:(1)40,108︒; ……………… 2分 (2)条形统计图补充正确; ……………… 4分 (3)列表法或画树状图正确: ……………… 5分
∴P (AC )=
126
=. ……………… 6分 24. 解:(1)3,3 ……………… 2分
(2) ……………… 4分 (3)4.5 或6 ……………… 6分
25.解:(1)对称轴为直线422a
x a
-=-
=. ……………… 1分 ∵AB =2,点A 在点B 的左侧,
∴A ()
10,,B ()
30, 把A (1,0)代入()240y ax ax m a =-+≠中,
∴3m a =. ……………… 2分
(2)∵抛物线()2430y ax ax a a =-+≠与y 轴的交点在(0,-1)和(0,0)之间,
∴0a <. ……………… 3分
y 2
cm 65432
当抛物线()2430y ax ax a a =-+≠经过点(0,-1)时,可得13
a =-.
∴a 的取值范围是1
03
a -
<<. ……………… 4分 (3)32a -<-≤或2<3a ≤. ……………… 6分
26. (1
)BF =
. ……………… 1分
(2)①依据题意补全图形; ……………… 3分
②证明:如图,连接BF 、GB .
∵四边形ABCD 是正方形,
∴AD =AB ,90ABC BAD ∠=∠=︒,AC 平分BAD ∠. ∴45BAC DAC ∠=∠=︒. 在△ADF 和△ABF 中,
AD AB DAC BAC AF AF =⎧⎪
∠=∠⎨⎪=⎩
,,
, ∴△ADF ≌△ABF . ……………… 4分 ∴DF BF =.
∵EF ⊥AC ,90ABC ∠=︒,点G 是AE 的中点,
∴AG EG BG FG ===. ……………… 5分 ∴点A 、F 、E 、B 在以点G 为圆心,AG 长为半径的圆上. ∵BF BF =,45BAC ∠=︒,
∴290BGF BAC ∠=∠=︒. ……………… 6分 ∴△BGF 是等腰直角三角形.
∴BF =.
∴DF =
. ……………… 7分
27. 解:(1) P 1,P 2.……………… 2分
②
当0b >
时,设直线y b =+与以2为半径的⊙O 相切于点C ,与y 轴交于点E ,与x 轴交于点F .
∴E (0,b ),F
(
3
b ,0),OC ⊥EF .
∴3tan OF FEO OE b ∠===. ∴30FEO ∠=︒. (3)
∵1
sin 2
OC FEO OE ∠=
=, ∴
212
b =. ∴4b =. ……………… 4分 当0b <时,由对称性可知:4b =-. ……………… 5分 ∴b 的取值范围是44b -≤≤. ……………… 6分 (2)∴m 的取值范围为22m -<≤. ……………… 7分。
