(完整版)立体几何初步知识点(很详细的).doc
立体几何复习知识点汇总(全)

立体几何知识点汇总(全)1.平面平面的基本性质:掌握三个公理及推论,会说明共点、共线、共面问题。
(1).证明点共线的问题,一般转化为证明这些点是某两个平面的公共点(依据:由点在线上,线在面内,推出点在面内),这样可根据公理2证明这些点都在这两个平面的公共直线上。
(2).证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线。
(3).证共面问题一般先根据一部分条件确定一个平面,然后再证明其余的也在这个平面内,或者用同一法证明两平面重合2. 空间直线.(1). 空间直线位置关系三种:相交、平行、异面. 相交直线:共面有且仅有一个公共点;平行直线:共面没有公共点;异面直线:不同在任一平面内,无公共点[注]:①两条异面直线在同一平面内射影一定是相交的两条直线.(×)(也可能两条直线平行,也可能是点和直线等)②直线在平面外,指的位置关系是平行或相交③若直线a、b异面,a平行于平面α,b与α的关系是相交、平行、在平面α内.④两条平行线在同一平面内的射影图形是一条直线或两条平行线或两点.⑤在平面内射影是直线的图形一定是直线.(×)(射影不一定只有直线,也可以是其他图形)⑥在同一平面内的射影长相等,则斜线长相等.(×)(并非是从平面外一.点.向这个平面所引的垂线段和斜线段)⑦ba,是夹在两平行平面间的线段,若a,的位置关系为相交或平行或异面.a=,则bb⑧异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)(2). 平行公理:平行于同一条直线的两条直线互相平行.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
(直线与直线所成角]90,0[︒︒∈θ)(向量与向量所成角])180,0[ ∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.(3). 两异面直线的距离:公垂线段的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.[注]:21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)3. 直线与平面平行、直线与平面垂直.(1). 空间直线与平面位置分三种:相交、平行、在平面内.(2). 直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)[注]:①直线a 与平面α内一条直线平行,则a ∥α. (×)(平面外一条直线)②直线a 与平面α内一条直线相交,则a 与平面α相交. (×)(平面外一条直线)③若直线a 与平面α平行,则α内必存在无数条直线与a 平行. (√)(不是任意一条直线,可利用平行的传递性证之)④两条平行线中一条平行于一个平面,那么另一条也平行于这个平面. (×)(可能在此平面内)⑤平行于同一个平面的两直线平行.(×)(两直线可能相交或者异面) ⑥直线l 与平面α、β所成角相等,则α∥β.(×)(α、β可能相交)(3). 直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)(4). 直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直. ● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理),● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质:如果两条直线同垂直于一个平面,那么这两条直线平行.(5)a.垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上。
(完整版)立体几何知识点总结完整版

立体几何知识点【考纲解读】1、平面的概念及平面的表示法,理解三个公理及三个推论的内容及作用,初步掌握性质与推论的简单应用。
2、 空间两条直线的三种位置关系,并会判定。
3、 平行公理、等角定理及其推论,了解它们的作用,会用它们来证明简单的几何问题,掌握证明空间两直线 平行及角相等的方法。
4、 异面直线所成角的定义,异面直线垂直的概念,会用图形来表示两条异面直线,掌握异面直线所成角的范 围,会求异面直线的所成角。
5•理解空间向量的概念,掌握空间向量的加法、减法和数乘;了解空间向量的基本定理,理解空间向量坐标的概念,掌握空间向量的坐标运算 ;掌握空间向量的数量积的定义及其性质,掌握用直角坐标计算空间向量数量积公式.6•了解多面体、凸多面体、正多面体、棱柱、棱锥、球的概念•掌握棱柱,棱锥的性质,并会灵活应用,掌握球的表面积、体积公式;能画出简单空间图形的三视图, 能识别上述的三视图所表示的立体模型, 会用斜二测法画出它们的直观图•7•空间平行与垂直关系的论证 •8.掌握直线与平面所成角、二面角的计算方法,掌握三垂线定理及其逆定理,并能熟练解决有关问题 ,进一步掌握异面直线所成角的求解方法,熟练解决有关问题9•理解点到平面、直线和直线、直线和平面、平面和平面距离的概念会用求距离的常用方法(如:直接法、转 化法、向量法)•对异面直线的距离只要求学生掌握作出公垂线段或用向量表示的情况)和距离公式计算距离。
【知识络构建】<— 翅MJL 何体的峯构特征一袞间几何怀的表面锲和体枳 —I 吩间儿何体的三视图和吒现图 空何向話的槪念线性运算空间向园数呈积理和坐标运算【重点知识整合】1. 空间几何体的三视图专间儿何体空问点仁n线、平面ft置关系宀VIHI向虽与<体儿何(1) 正视图:光线从几何体的前面向后面正投影得到的投影图;(2) 侧视图:光线从几何体的左面向右面正投影得到的投影图;(3) 俯视图:光线从几何体的上面向下面正投影得到的投影图.几何体的正视图、侧视图和俯视图统称为几何体的三视图.2. 斜二测画水平放置的平面图形的基本步骤(1) 建立直角坐标系,在已知水平放置的平面图形中取互相垂直的Ox, Oy,建立直角坐标系;(2) 画出斜坐标系,在画直观图的纸上(平面上)画出对应的Ox', Oy',使/ x Oy = 45。
高中立体几何基础知识点全集(图文并茂)
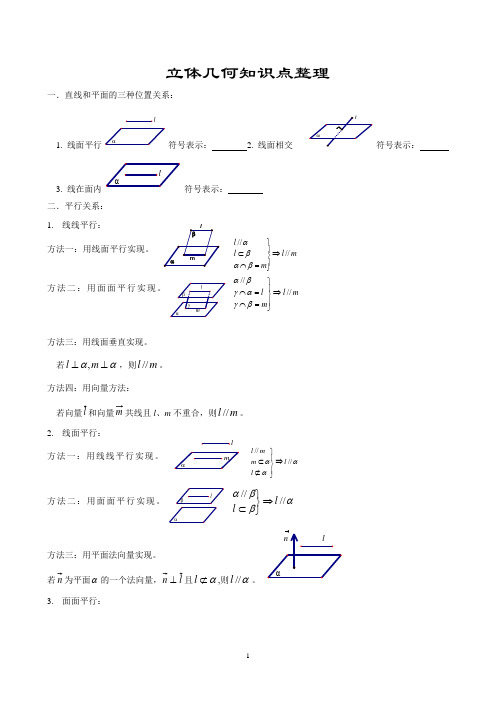
立体几何知识点整理一.直线和平面的三种位置关系:1. 线面平行l符号表示: 2. 线面相交符号表示:3. 线在面内符号表示:二.平行关系: 1. 线线平行:ml m l l ////⇒⎪⎭⎪⎬⎫=⋂⊂βαβα方法一:用线面平行实现。
m l m l ////⇒⎪⎭⎪⎬⎫=⋂=⋂βγαγβα 方法二:用面面平行实现。
方法三:用线面垂直实现。
若αα⊥⊥m l ,,则m l //。
方法四:用向量方法:若向量和向量共线且l 、m 不重合,则m l //。
2. 线面平行:ααα////l l m m l ⇒⎪⎭⎪⎬⎫⊄⊂方法一:用线线平行实现。
αββα////l l ⇒⎭⎬⎫⊂ 方法二:用面面平行实现。
方法三:用平面法向量实现。
若为平面α的一个法向量,⊥且α⊄l ,则α//l 。
3. 面面平行:lβαβαα//,////⇒⎪⎭⎪⎬⎫⊂且相交m l m l 用线面平行实现。
三.垂直关系: 1. 线面垂直:αα⊥⇒⎪⎪⎭⎪⎪⎬⎫⊂=⋂⊥⊥l AB AC A AB AC AB l AC l , 方法一:用线线垂直实现。
αββαβα⊥⇒⎪⎭⎪⎬⎫⊂⊥=⋂⊥l l m l m , 方法二:用面面垂直实现。
2. 面面垂直:βαβα⊥⇒⎭⎬⎫⊂⊥l l 方法一:用线面垂直实现。
方法二:计算所成二面角为直角。
3. 线线垂直:m l m l ⊥⇒⎭⎬⎫⊂⊥αα 方法一:用线面垂直实现。
方法二:三垂线定理及其逆定理。
PO l OA l PA l αα⊥⎫⎪⊥⇒⊥⎬⎪⊂⎭方法三:用向量方法:若向量l 和向量m 的数量积为0,则ml ⊥。
三.夹角问题。
(一) 异面直线所成的角: (1) 范围:]90,0(︒︒(2)求法: 方法一:定义法。
步骤1:平移,使它们相交,找到夹角。
步骤2:解三角形求出角。
(常用到余弦定理)余弦定理:abc b a 2cos 222-+=θ(计算结果可能是其补角)方法二:向量法。
转化为向量的夹角 (计算结果可能是其补角):=θcos(二) 线面角(1)定义:直线l 上任取一点P (交点除外),作PO ⊥α于O,连结AO ,则AO 为斜线PA 在面α内的射影,PAO ∠(图中θ)为直线l 与面α所成的角。
(完整版)立体几何初步(知识点梳理),推荐文档

春季高考立体几何部分知识点梳理及历年试题一.线面之间空间关系及证明方法A.线//线的证明方法1.将两条直线放到一个平面内(或者转移到同一平面内)利用平行四边形或者三角形的中位线来证明2. 一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.(线//面→线//线)3. 如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
(面//面→线//线)4.垂直于同一个平面的两条直线平行。
B.线⊥线的证明方法1.异面直线平移到一个平面内证明垂直2. 一条直线垂直于一个平面,则这条直线与平面内任意直线垂直.(线⊥面→线⊥线)C.线//面的证明方法1. 平面外一直线与平面内一直线平行,则该直线与此平面平行. (线//线→线//面)2. 如果两个平面平行,那么其中一平面内的任一直线平行于另一平面(面//面→线//面)D. 线⊥面的证明方法1.一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直(线⊥线→线⊥面)2. 两平面垂直,则一个平面内垂直于交线的直线垂直于另一个平面(面⊥面→线⊥面)E. 面//面的证明方法1.一个平面内有两条相交直线与另一个平面平行,则这两平面平行(线//面→面//面)2. 如果一个平面内的两条相交直线和另一个平面内的两条相交直线分别平行,那么这两个平面平行(线//线→面//面)3.垂直于同一条直线的两个平面平行。
4.平行于同一个平面的两个平面平行。
F. 面⊥面的证明方法1. 如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直(线⊥面→面⊥面)二.各几何体的体积公式柱体(圆柱,棱柱)V=s h 其中s 为底面积,h 为高∙椎体(圆柱,棱柱)V= 其中s 为底面积,h 为高13s ∙ℎ球体 体积V= 表面积S=443πr 3πr22012年春考真题23.已知空间四边形ABCD 中,E ,F ,G ,H 分别是边AB ,BC ,CD ,DA 的中点,给出下列四个命题:1.AC 与BD 是相交直线2.AB//DC3.四边形EFGH 是平行四边形4.EH//平面BCD 其中真命题的个数是A. 4B.3C.2D.1解析:如图AC 与BD 没有相交,是异面直线。
立体几何基础知识

立体几何基础知识1.平面的概念:平面是没有厚薄的,可以无限延伸,这是平面最基本的属性2.平面的画法及其表示方法:①常用平行四边形表示平面通常把平行四边形的锐角画成45 ,横边画成邻边的两倍画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分画成虚线或不画②一般用一个希腊字母、、来表示,还可用平行四边形的对角顶点的字母来表示如平面AC .3.空间图形是由点、线、面组成的点、线、面的基本位置关系如下表所示:图形符号语言文字语言(读法)Aa A a点 A 在直线a上A aA a点 A 不在直线a上A A点 A在平面内A A点 A 不在平面内A baa b A直线 a 、b交于A点a a直线 a 在平面内aa //直线 a 与平面平行aA a A直线a与平面交于点Al平面、相交于直线l注意:直线与平面平行( a //)和直线与平面相交(a A )两种情形,统称为直线在平面外,记为 a.4.平面的基本性质(1)公理 1: 如果一条直线的两点在一个平面内,那么这条直线上的所有点都在这个平面内B符号表示:A, B a.如图示: A应用:是判定直线是否在平面内的依据,也可用于验证一个面是否是平面.公理 1 说明了平面与曲面的本质区别.通过直线的“直”来刻划平面的“平”,通过直线的“无限延伸”来描述平面的“无限延展性” ,它既是判断直线在平面内,又是检验平面的方法.(2) 公理2: 如果两个平面有一个公共点, 那么它们还有其他公共点, 且所有这些公共点的集合是一条过这个公共点的直线A符号表示:l 且A l 且 l 唯一如图示:A应用:①确定两相交平面的交线位置;②判定点在直线上公理 2 揭示了两个平面相交的主要特征,是判定两平面相交的依据,提供了确定两个平面交线的方法.(3)公理 3: 经过不在同一条直线上的三点,有且只有一个平面推理模式: A, B, C 不共线存在唯一的平面,使得 A, B, C应用:①确定平面;②证明两个平面重合注意 : “有且只有一个”的含义分两部分理解,“有”说明图形存在,但不唯一,“只有一个”说明图形如果有顶多只有一个,但不保证符合条件的图形存在,“有且只有一个”既保证了图形的存在性,又保证了图形的唯一性.在数学语言的叙述中,“确定一个” ,“可以作且只能作一个”与“有且只有一个”是同义词,因此,在证明有关这类语句的命题时,要从“存在性”和“唯一性”两方面来论证.(4)推论 1 : 经过一条直线和直线外的一点有且只有一个平面推理模式: A a存在唯一的平面,使得A,l(5)推论 2: 经过两条相交直线有且只有一个平面推理模式: a b P存在唯一的平面,使得a,b(6)推论 3 : 经过两条平行直线有且只有一个平面推理模式: a // b存在唯一的平面,使得a,b5.平面图形与空间图形的概念 : 如果一个图形的所有点都在同一个平面内,则称这个图形为平面图形,否则称为空间图形特别注意空间四边形是平面图形而不是平面图形.6.空间两直线的位置关系(1)相交——有且只有一个公共点;(2)平行——在同一平面内,没有公共点;(3)异面——不在任何一个平面内,没有公共点;..7.公理 4 :平行于同一条直线的两条直线互相平行推理模式: a // b, b // c a // c .8.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等9.等角定理的推论: 如果两条相交直线和另两条相交直线分别平行, 那么这两条直线所成的锐角( 或直角 ) 相等10.空间两条异面直线的画法a b babaD1C1A1B1DCA B11.异面直线判定定理:连结平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线推理模式:A, B, l, B l AB 与 l 是异面直线12. 异面直线所成的角:已知两条异面直线a, b ,经过空间任一点O 作直线 a // a, b // b,a , b所成的角的大小与点 O 的选择无关,把 a , b 所成的锐角(或直角)叫异面直线a, b 所成的角(或夹角).为了简便,点 O 通常取在异面直线的一条上注 : 异面直线所成的角的范围:(0,]213.异面直线垂直:如果两条异面直线所成的角是直角,则叫两条异面直线垂直.两条异面直线a,b垂直,记作 a b.14.求异面直线所成的角的方法:通过平移,把两条异面直线所成的角转化成两条相交直线所成的角.15.两条异面直线的公垂线、距离和两条异面直线都垂直相交的直线,我们称之为异面直线的公垂线....理解:因为两条异面直线互相垂直时,它们不一定相交,所以公垂线的定义要注意“相交”的含义.两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离.注意 : 两条异面直线的公垂线有且只有一条16.直线和平面的位置关系( 1)直线在平面内(无数个公共点);符号表示为:a;( 2)直线和平面相交(有且只有一个公共点);符号表示为:a A ,( 3)直线和平面平行(没有公共点); 符号表示为 : a //.17.线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行.推理模式:a,b, a // b a //.18.线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.推理模式: a // , a,b a // b .19.平行平面:如果两个平面没有公共点,那么这两个平面互相平行.20.图形表示:画两个平面平行时,通常把表示这两个平面的平行四边形的相邻两边分别画成平行的.21.平行平面的判定定理:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面互相平行.推理模式:: a,b,a b P , a //,b ////.22.平行平面的判定定理推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面互相平行.推理模式:a //a' ,b//b' ,,,b,a'b''a',b'//.a b o a o23.平行平面的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.推理模式:// ,a,b a // b .24.面面平行的另一性质:如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.推理模式:// , a a //.25.线面垂直定义:如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面互相垂直其中直线叫做平面的垂线,平面叫做直线的垂面交点叫做垂足直线与平面垂直简称线面垂直,记作:a⊥ α26.直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面27.直线和平面垂直的性质定理 :如果两条直线同垂直于一个平面, 那么这两条直线平行28.两个平面垂直的定义:两个相交成直二面角的两个平面互相垂直;相交成直二面角的两个平面叫做互相垂直的平面29.两平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直推理模式: a ?,a.30.两平面垂直的性质定理:若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面推理模式:,l , a, a l a31.异面直线所成的角:已知两条异面直线a, b ,经过空间任一点O 作直线 a // a, b // b,a , b所成的角的大小与点 O 的选择无关,把 a , b 所成的锐角(或直角)叫异面直线a, b 所成的角(或夹角).为了简便,点 O 通常取在异面直线的一条上注 : 异面直线所成的角的范围:(0,]232.求异面直线所成的角的方法:ab′b O33.直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角一直线垂直于平面,所成的角是直角注: ①一直线平行于平面或在平面内,所成角为0 角②直线和平面所成角范围:0,2(2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角34.二面角:平面内的一条直线把平面分为两个部分,其中的每一部分叫做半平面;从一条直线出发的两个半平面所组成的图形叫做二面角,这条直线叫做二面角的棱,每个半平面叫做二面角的面若棱为 l ,两个面分别为,的二面角记为l;35.二面角的平面角:( 1)过二面角的棱上的一点O 分别在两个半平面内作棱的两条垂线OA, OB ,则AOB 叫做二面角l的平面角2l的棱l,且与两半平面交线分别为OA, OB, O 为垂足,则AOB也()一个平面垂直于二面角是l的平面角说明:①二面角的平面角范围是[0 ,180 ] ;②二面角的平面角为直角时,则称为直二面角,组成直二面角的两个平面互相垂直36.求二面角的射影公式: cos S,S其中各个符号的含义是:S 是二面角的一个面内图形 F 的面积,S是图形 F 在二面角的另一个面内的射影,是二面角的大小37.点到平面的距离:已知点 P 是平面外的任意一点,过点 P 作 PA,垂足为 A ,则 PA 唯一,则 PA是点 P 到平面的距离即一点到它在一个平面内的正射影的距离叫做这一点到这个平面的距离结论:连结平面外一点 P与内一点所得的线段中,垂线段PA 最短38.异面直线的公垂线:和两条异面直线都垂直相交的直线叫做异面直线的公垂线.39.公垂线唯一:任意两条异面直线有且只有一条公垂线40.两条异面直线的公垂线段:两条异面直线的公垂线夹在异面直线间的部分,叫做两条异面直线的公垂线段;41.公垂线段最短:两条异面直线的公垂线段是分别连结两条异面直线上两点的线段中最短的一条;42.两条异面直线的距离:两条异面直线的公垂线段的长度说明:两条异面直线的距离AB 即为直线a到平面过另一条直线且与这条直线平行的平面的距离的距离即两条异面直线的距离等于其中一条直线到43.直线到与它平行平面的距离:( 转化为点面距离)一条直线上的任一点到与它平行的平面的距离, 叫做这条直线到平面的距离44.两个平行平面的公垂线、公垂线段:(1)两个平面的公垂线:和两个平行平面同时垂直的直线,叫做两个平面的公垂线(2)两个平面的公垂线段:公垂线夹在平行平面间的的部分,叫做两个平面的公垂线段(3)两个平行平面的公垂线段都相等(4)公垂线段小于或等于任一条夹在这两个平行平面间的线段长45.两个平行平面的距离:两个平行平面的公垂线段的长度叫做两个平行平面的距离46.七种距离:点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离,点到平面的距离有时用“体积法”来求47.多面体的概念:由若干个多边形围成的空间图形叫多面体;每个多边形叫多面体的面,两个面的公共边叫多面体的棱,棱和棱的公共点叫多面体的顶点,连结不在同一面上的两个顶点的线段叫多面体的对角线48.棱柱的概念:有两个面互相平行,其余每相邻两个面的交线互相平行,这样的多面体叫棱柱两个互相平行的面叫棱柱的底面(简称底);其余各面叫棱柱的侧面;两侧面的公共边叫棱柱的侧棱;两底面所在平面的公垂线段叫棱柱的高(公垂线段长也简称高)49.棱柱的分类:侧棱不垂直于底面的棱柱叫斜棱柱侧棱垂直于底面的棱柱叫直棱柱底面的是正多边形的直棱柱叫正棱柱棱柱的底面可以是三角形、四边形、五边形这样的棱柱分别叫三棱柱、四棱柱、五棱柱50.棱柱的性质(1)棱柱的侧棱相等,侧面都是平行四边形;直棱柱侧面都是矩形;正棱柱侧面都是全等的矩形;(2)棱柱的两个底面与平行于底面的截面是对应边互相平行的全等的多边形;(3)过棱柱不相邻的两条侧棱的截面都是平行四边形51.直棱柱:52.正棱柱:53.长方体的性质 : 长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和54.棱锥的概念:有一个面是多边形,其余各面是有一个公共顶点的三角形,这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面;多边形叫棱锥的底面或底;各侧面的公共顶点( S) ,叫棱锥的顶点,顶点到底面所在平面的垂线段(SO) ,叫棱锥的高(垂线段的长也简称高).55.棱锥的表示:棱锥用顶点和底面各顶点的字母,或用顶点和底面一条对角线端点的字母来表示例如五棱锥可表示为S ABCDE ,或 S AC .56.棱锥的分类:(按底面多边形的边数)分别称底面是三角形,四边形,五边形的棱锥为三棱锥,四棱锥,五棱锥57.棱锥的性质:定理:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比.中截面:经过棱锥高的中点且平行于底面的截面,叫棱锥的中截面58.正棱锥:底面是正多边形,顶点在底面上的射影是底面的中心的棱锥叫正棱锥.(1)正棱锥的各侧棱相等,各侧面是全等的等腰三角形,各等腰三角形底边上的高相等(叫正棱锥的斜高).(2)正棱锥的高、斜高、斜高在底面上的射影组成一个直角三角形;正棱锥的高、侧棱、侧棱在底面上的射影也组成一个直角三角形59.球的概念:与定点距离等于或小于定长的点的集合,叫做球体,简称球定点叫球心,定长叫球的半径与定点距离等于定长的点的集合叫做球面一个球或球面用表示它的球心的字母表示,例如球 O 60.球的截面:用一平面去截一个球 O ,设 OO是平面的垂线段, O 为垂足,且 OO d ,所得的截面是以球心在截面内的射影为圆心,以r R2 d 2为半径的一个圆,截面是一个圆面注 : 球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆61. 表面积、体积公式( 1)直棱柱的侧面积: S ch ;( 2)圆柱的侧面积: S cl2 r l ( 其中 c 为底面圆的周长 ) ; ( 3)正棱锥的侧面积 : S1ch ( 其中 h 为斜高 );1 24Sclrl (其中 c 为底面圆的周长 );( )圆锥的侧面积:2( 5)圆台的侧面积 :S1(c c )l( r r )l ;2 ( 6)球的表面积: S 4 R 2;( 7)柱体的体积 : V Sh ;( 8)锥体的体积: V1Sh ;3( 9)台体的体积: V1(SS S S)h ;3( 10)球的体积公式: V4 R 33R ,而在实际问题中常给出球的外径(直径)注意 : ①在应用球体积公式时要注意公式中给出的是球半径②球与其它几何体的切接问题,要仔细观察、分析、弄清相关元素的位置关系和数量关系,选择最佳角度作出截面,以使空间问题平面化。
(完整版)立体几何初步知识点(很详细的)

立体几何初步1、 柱、锥、台、球的结构特征(1) 棱柱:几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行 于底面的截面是与底面全等的多边形。
(2) 棱锥几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与 高的比的平方。
(3) 棱台:几何特征:①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点(4) 圆柱:定义:以矩形的一边所在的直线为轴旋转 ,其余三边旋转所成几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直; ④侧面展开图是一个矩形。
(5) 圆锥:定义:以直角三角形的一条直角边为旋转轴 ,旋转一周所成几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6) 圆台:定义:以直角梯形的垂直与底边的腰为旋转轴 ,旋转一周所成几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
(7) 球体:定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体几何特征:①球的截面是圆;②球面上任意一点到球心的距离等于半径。
2、 空间几何体的三视图定义三视图:正视图(光线从几何体的前面向后面正投影) ;侧视图(从左向右)、俯视图(从上向下)注:正视图反映了物体的高度和长度;俯视图反映了物体的长度和宽度;侧视图反映了物体的高度和宽 度。
3、 空间几何体的直观图一一斜二测画法斜二测画法特点: ①原来与x 轴平行的线段仍然与 x 平行且长度不变;② 原来与y 轴平行的线段仍然与 y 平行,长度为原来的一半。
4、 柱体、锥体、台体的表面积与体积(1)几何体的表面积为几何体各个面的面积的和。
(2)特姝儿何体表面积公式(、c 为底面周长, h 为高, h 为斜高, l 为母线)s 直棱柱侧面积 ch s ®柱侧 2 rh s 正棱锥侧面积 -ch' 2 S 圆锥侧面积 rls 正棱台侧面积1 尹 Q )h' s 圆台侧面积 (r R) ls 圆柱表 2 r r l S i 锥表 r r l s 圆台表 r rl Rl R 2(3) 柱体、 锥体、台体的体积公式V 柱 Sh 2V 圆柱 Sh r h V 锥 ’Sh 3 1 2V 圆锥-r h 3 V 台 S 'S S)h V I 台 3(s .S 'S S)h 12 2 -(r 2rR R 2)h3 (4)球体的表面积和体积公式: V 球=4 R 3 ; S 求面=4 R 234、空间点、直线、平面的位置关系公理1:如果一条直线的两点在一个平面内,那么这条直线是所有的点都在这个平面内。
立体几何初步知识点全总结

立体几何初步知识点全总结一、空间几何体的结构。
1. 棱柱。
- 定义:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的多面体叫做棱柱。
- 分类:- 按底面多边形的边数分为三棱柱、四棱柱、五棱柱等。
- 直棱柱:侧棱垂直于底面的棱柱。
正棱柱:底面是正多边形的直棱柱。
- 性质:- 侧棱都相等,侧面是平行四边形。
- 两个底面与平行于底面的截面是全等的多边形。
- 过不相邻的两条侧棱的截面(对角面)是平行四边形。
2. 棱锥。
- 定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥。
- 分类:- 按底面多边形的边数分为三棱锥、四棱锥、五棱锥等。
- 正棱锥:底面是正多边形,且顶点在底面的射影是底面正多边形的中心的棱锥。
- 性质:- 正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高)。
- 棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。
3. 棱台。
- 定义:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫做棱台。
- 分类:由三棱锥、四棱锥、五棱锥等截得的棱台分别叫做三棱台、四棱台、五棱台等。
- 性质:- 棱台的各侧棱延长后交于一点。
- 棱台的上下底面是相似多边形,侧面是梯形。
4. 圆柱。
- 定义:以矩形的一边所在直线为轴旋转,其余三边旋转所成的曲面所围成的几何体叫做圆柱。
- 性质:- 圆柱的轴截面是矩形。
- 平行于底面的截面是与底面全等的圆。
5. 圆锥。
- 定义:以直角三角形的一条直角边所在直线为轴旋转,其余两边旋转所成的曲面所围成的几何体叫做圆锥。
- 性质:- 圆锥的轴截面是等腰三角形。
- 平行于底面的截面是圆,截面半径与底面半径之比等于顶点到截面距离与圆锥高之比。
6. 圆台。
- 定义:用一个平行于圆锥底面的平面去截圆锥,底面与截面之间的部分叫做圆台。
高一数学立体几何初步知识点总结

高一数学立体几何初步知识点总结高一数学知识点总结:立体几何初步1、柱、锥、台、球的结构特征(1)棱柱:定义:有两个面互相平行,其余各面都是四边形,且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱柱、四棱柱、五棱柱等。
表示:用各顶点字母,如五棱柱或用对角线的端点字母,如五棱柱。
几何特征:两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
(2)棱锥定义:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的几何体。
分类:以底面多边形的边数作为分类的标准分为三棱锥、四棱锥、五棱锥等表示:用各顶点字母,如五棱锥几何特征:侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方。
(3)棱台:定义:用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分。
分类:以底面多边形的边数作为分类的标准分为三棱态、四棱台、五棱台等表示:用各顶点字母,如五棱台几何特征:①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点(4)圆柱:定义:以矩形的一边所在的直线为轴旋转,其余三边旋转所成的曲面所围成的几何体。
几何特征:①底面是全等的圆;②母线与轴平行;③轴与底面圆的半径垂直;④侧面展开图是一个矩形。
(5)圆锥:定义:以直角三角形的一条直角边为旋转轴,旋转一周所成的曲面所围成的几何体。
几何特征:①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
(6)圆台:定义:用一个平行于圆锥底面的平面去截圆锥,截面和底面之间的部分几何特征:①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
(7)球体:定义:以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体几何特征:①球的截面是圆;②球面上任意一点到球心的距离等于半径。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
- 1 -
立体几何初步
1、柱、锥、台、球的结构特征 ( 1)棱柱:
几何特征 :两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形。
( 2)棱锥
几何特征 :侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与
高的比的平方。
( 3)棱台:
几何特征 :①上下底面是相似的平行多边形 ②侧面是梯形 ③侧棱交于原棱锥的顶点 ( 4)圆柱:定义 :以矩形的一边所在的直线为轴旋转 ,其余三边旋转所成 几何特征 :①底面是全等的圆; ②母线与轴平行; ③轴与底面圆的半径垂直; ④侧面展开图是一个矩形。
( 5)圆锥:定义 :以直角三角形的一条直角边为旋转轴,旋转一周所成
几何特征 :①底面是一个圆;②母线交于圆锥的顶点;③侧面展开图是一个扇形。
( 6)圆台:定义: 以直角梯形的垂直与底边的腰为旋转轴,旋转一周所成
几何特征: ①上下底面是两个圆;②侧面母线交于原圆锥的顶点;③侧面展开图是一个弓形。
( 7)球体:定义: 以半圆的直径所在直线为旋转轴,半圆面旋转一周形成的几何体几何特征: ①球的截面是圆;②球面上任意一点到球心的距离等于半径。
2、空间几何体的三视图
定义三视图:正视图(光线从几何体的前面向后面正投影) ;侧视图(从左向右) 、俯视图(从上向下)
注:正视图反映了物体的高度和长度;俯视图反映了物体的长度和宽度;侧视图反映了物体的高度和宽度。
3、空间几何体的直观图——斜二测画法
斜二测画法特点: ①原来与 x 轴平行的线段仍然与 x 平行且长度不变;
②原来与 y 轴平行的线段仍然与 y 平行,长度为原来的一半。
4、柱体、锥体、台体的表面积与体积
( 1)几何体的表面积为几何体各个面的面积的和。
( 2)特殊几何体表面积公式( c 为底面周长, h 为高, h ' 为斜高, l 为母线)
S
直棱柱侧面积
ch
S
圆柱侧
2 rh
S 正棱锥侧面积
1 ch' S
rl
圆锥侧面积
1
2
S 正棱台侧面积
( c 1 c 2 )h' S 圆台侧面积 (r
R) l
2
2
2
S
圆柱表 2
r r
l
圆锥表
r r
l S 圆台表
r
rl Rl
R
S
( 3)柱体、锥体、台体的体积公式
V 柱 Sh
V 圆
柱
Sh
r 2
h
V 锥 1
Sh
V
圆
锥
1 r 2h
1 (S '
3
1
3
V 台 1 (S '
S '
S S)h
V
圆台
S ' S S)h
(r 2 rR R 2 )h
3 3
3
( 4)球体的表面积和体积公式: V 球 =4 R 3 ; S 球面 =4 R 2
3
4、空间点、直线、平面的位置关系
公理 1:如果一条直线的两点在一个平面内,那么这条直线是所有的点都在这个平面内。
应用: 判断直线是否在平面内
用符号语言表示公理
1: A l ,B
l , A ,B l
公理 2:如果两个不重合的平面有一个公共点
,那么它们有且只有一条过该点的公共直线
符号: 平面α和β相交,交线是 a ,记作α∩β= a 。
符号语言: P AI B
AI B
l ,P l
公理 2 的作用:
①它是判定两个平面相交的方法。
②它说明两个平面的交线与两个平面公共点之间的关系:交线必过公共点。
1
- 2 -
③它可以判断点在直线上,即证若干个点共线的重要依据。
公理 3:经过不在同一条直线上的三点,有且只有一个平面。
推论:一直线和直线外一点确定一平面;两相交直线确定一平面;两平行直线确定一平面。
公理 3 及其推论作用:①它是空间内确定平面的依据②它是证明平面重合的依据
公理 4:平行于同一条直线的两条直线互相平行
空间直线与直线之间的位置关系
① 异面直线定义:不同在任何一个平面内的两条直线
② 异面直线性质:既不平行,又不相交。
③ 异面直线判定:过平面外一点与平面内一点的直线与平面内不过该店的直线是异面直线
④ 异面直线所成角:作平行,令两线相交,所得锐角或直角,即所成角。
两条异面直线所成角的范围
是( 0°, 90° ],若两条异面直线所成的角是直角,我们就说这两条异面直线互相垂直。
求异面直线所成角步骤:
A、利用定义构造角,可固定一条,平移另一条,或两条同时平移到某个特殊的位置,顶点选在特殊的
位置上。
B、证明作出的角即为所求角C、利用三角形来求角
(7)等角定理:如果一个角的两边和另一个角的两边分别平行,那么这两角相等或互补。
(8)空间直线与平面之间的位置关系
直线在平面内——有无数个公共点.
三种位置关系的符号表示:aαa∩α= A a∥α
(9)平面与平面之间的位置关系:平行——没有公共点;α∥β
相交——有一条公共直线。
α∩β=b
5、空间中的平行问题
( 1)直线与平面平行的判定及其性质
线面平行的判定定理:平面外一条直线与此平面内一条直线平行,则该直线与此平面平行。
线线平行线面平行
线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,
那么这条直线和交线平行。
线面平行线线平行
(2)平面与平面平行的判定及其性质
两个平面平行的判定定理
(1)如果一个平面内的两条相交直线都平行于另一个平面,那么这两个平面平行
(线面平行→面面平行),
(2)如果在两个平面内,各有两组相交直线对应平行,那么这两个平面平行。
(线线平行→面面平行),
(3)垂直于同一条直线的两个平面平行,
两个平面平行的性质定理
( 1)如果两个平面平行,那么某一个平面内的直线与另一个平面平行。
(面面平行→线面平行)
( 2)如果两个平行平面都和第三个平面相交,那么它们的交线平行。
(面面平行→线线平行)
7、空间中的垂直问题
(1)线线、面面、线面垂直的定义①两条异面直线的垂直:如果两条异面直线所成的角是直角,就说
这两条异面直线互相垂直。
②线面垂直:如果一条直线和一个平面内的任何一条直线垂直,就说这条直
线和这个平面垂直。
③平面和平面垂直:如果两个平面相交,所成的二面角(从一条直线出发的两个半
平面所组成的图形)是直二面角(平面角是直角),就说这两个平面垂直。
(2)垂直关系的判定和性质定理
①线面垂直判定定理和性质定理
判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
②面面垂直的判定定理和
性质定理
判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。
2。
