《信号与系统》第七章 北京理工大学
北京理工大学信号和系统实验报告材料

本科实验报告实验名称:信号与系统实验实验一信号的时域描述与运算一、实验目的①掌握信号的MATLAB表示及其可视化方法。
②掌握信号基本时域运算的MATLAB实现方法。
③利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形常用的信号产生函数2.连续时间信号的时域运算-1-0.8-0.6-0.4-0.200.20.40.60.81Time(seconds)图1 利用向量表示连续时间信号-1-0.50.51t图 2 利用符号对象表示连续时间信号sin(t)对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
1)相加和相乘信号相加和相乘指两信号对应时刻的值相加和相乘,对于两个采用向量表示的可以直接使用算术运算的运算符“+”和“*”来计算,此时要求表示两信号的向量时间范围和采样间隔相同。
北京理工大学信号与系统实验报告7 连续时间系统的建模与仿真
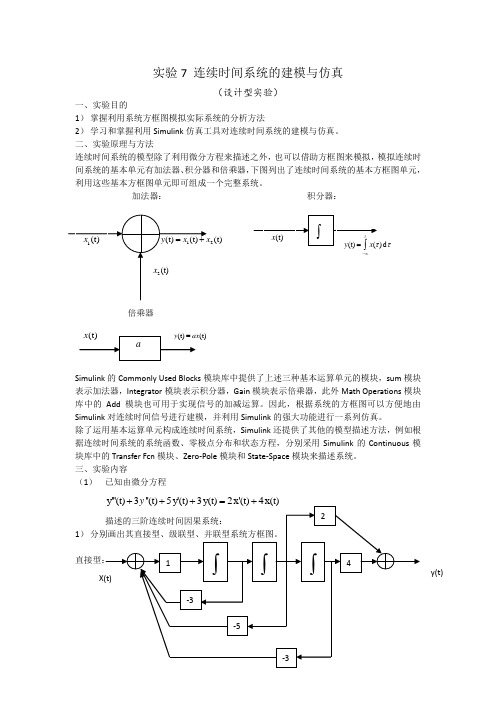
实验7 连续时间系统的建模与仿真(设计型实验)一、实验目的1) 掌握利用系统方框图模拟实际系统的分析方法2) 学习和掌握利用Simulink 仿真工具对连续时间系统的建模与仿真。
二、实验原理与方法连续时间系统的模型除了利用微分方程来描述之外,也可以借助方框图来模拟,模拟连续时间系统的基本单元有加法器、积分器和倍乘器,下图列出了连续时间系统的基本方框图单元,利用这些基本方框图单元即可组成一个完整系统。
加法器: 积分器:倍乘器Simulink 的Commonly Used Blocks 模块库中提供了上述三种基本运算单元的模块,sum 模块表示加法器,Integrator 模块表示积分器,Gain 模块表示倍乘器,此外Math Operations 模块库中的Add 模块也可用于实现信号的加减运算。
因此,根据系统的方框图可以方便地由Simulink 对连续时间信号进行建模,并利用Simulink 的强大功能进行一系列仿真。
除了运用基本运算单元构成连续时间系统,Simulink 还提供了其他的模型描述方法,例如根据连续时间系统的系统函数、零极点分布和状态方程,分别采用Simulink 的Continuous 模块库中的Transfer Fcn 模块、Zero-Pole 模块和State-Space 模块来描述系统。
三、实验内容(1) 已知由微分方程1)2(t)2)根据上述3种系统框图,分别采用Simulink的基本运算单元的模块创建系统的模型,并仿真实现系统的单位阶跃响应。
直接型级联型并联型(2) 已知一个三阶连续时间因果系统的系统函数为3257(s)554s H s s s +=+++,根据系统函数,采用simulink 创建系统模型,并仿真实现对输入(t)u(t 3)u(t)x =--的响应。
四、实验心得通过本次实验掌握了利用Simulink 仿真工具对连续时间系统进行建模、仿真的基本方法。
北理工信号课程设计

北理工信号课程设计一、课程目标知识目标:1. 理解并掌握信号与系统的基本概念,包括信号分类、基本信号及其性质;2. 学会使用数学工具描述和分析信号与系统的特性,如傅里叶变换、拉普拉斯变换等;3. 掌握线性时不变系统的特性,理解卷积积分及其在信号处理中的应用。
技能目标:1. 能够运用所学知识对实际信号进行处理和分析,如滤波、调制等;2. 能够设计简单的信号处理算法,并使用计算机仿真实现;3. 培养良好的实际操作能力,包括使用信号发生器、示波器等实验设备。
情感态度价值观目标:1. 培养学生对信号与系统学科的兴趣,激发学生探索未知、解决问题的热情;2. 培养学生的团队合作精神,提高沟通与协作能力;3. 增强学生的国防意识,使其认识到信号与系统在国防科技领域的重要应用。
本课程针对北理工高年级本科生,结合课程性质、学生特点和教学要求,将目标分解为具体的学习成果。
在教学过程中,注重理论与实践相结合,以培养学生实际操作能力和创新精神为核心。
通过本课程的学习,使学生能够熟练运用所学知识解决实际问题,为后续相关课程和未来从事相关工作奠定坚实基础。
二、教学内容1. 信号与系统基本概念:信号分类、基本信号及其性质、信号的运算与变换;教材章节:第一章 信号与系统概述2. 数学工具描述与分析:傅里叶级数、傅里叶变换、拉普拉斯变换、Z变换;教材章节:第二章 傅里叶级数与变换,第三章 拉普拉斯变换与Z变换3. 线性时不变系统:系统的性质、卷积积分、差分方程;教材章节:第四章 线性时不变系统4. 信号处理与分析:滤波器设计、调制与解调、采样与重建;教材章节:第五章 信号处理技术,第六章 采样与重建5. 实践环节:使用信号发生器、示波器等设备进行信号处理实验;教材章节:第七章 信号与系统实验教学内容安排与进度:第一周:信号与系统基本概念第二周:傅里叶级数与傅里叶变换第三周:拉普拉斯变换与Z变换第四周:线性时不变系统第五周:滤波器设计与调制解调第六周:采样与重建第七周:实践环节第八周:复习与考核本教学内容根据课程目标,结合教材内容,科学系统地组织与安排。
北京理工大学信号与系统实验实验报告

北京理工大学信号与系统实验实验报告信号与系统实验报告姓名:肖枫学号:1120111431班号:05611102专业:信息对抗技术学院:信息与电子学院12实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB实现方法。
3. 利用MATLAB分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB并不能处理连续时间信号,在MATLAB中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10;>> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t);>> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形10.80.60.40.2-0.2-0.4-0.6-0.8-1012345678910Time(seconds)图1 利用向量表示连续时间信号3sin(t)10.5-0.5-1-6-4-20246t图 2 利用符号对象表示连续时间信号常用的信号产生函数函数名功能函数名功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波 sinc sinc函数 sawtooth 周期锯齿波或三角波 exp 指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
北京理工大学信号与系统信号的频域分析

x(t ) a0 ak cos kw0t bk sin kw0t
k 1 k 1
(3)
其中:
a0
1 2 2 T0 x(t )dt , ak T x(t ) cos kw0tdt , bk T x(t ) sin kw0tdt 0 T0 T0 T0 0
(4)
4、离散非周期时间信号的频域分析
非周期序列 x( n) 可以表示成一组复指数序列的连续和
x ( n)
其中
1 2
X (e
2
j
)e jn d
(15)
X (e j )
n
x ( n )e
jn
(16)
式(16)称为 x( n) 的离散时间傅里叶变换,式(15)和式(16)确立了非周期离散时 间信号 x( n) 及其离散时间傅里叶变换 X (e 称为频谱函数,且 X (e
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
N=20;T=1;a=0.5;A=1;
1 .2
1
0 .8
0 .6
0 .4
0 .2
0
-0 .2 -1 .5
-1
-0 .5
0
0 .5
1
1 .5
③利用 MATLAB 绘出周期矩形脉冲信号的频谱,观察参数 T 和变 化时对频谱波形的影响。
Answer:频谱包络形状不变,过零点不变,普贤间隔随着 T 变大而缩小。
2、已知 x(t)是如图所示的矩形脉冲信号。 ①求该信号的傅里叶变换; ②利用 MATLAB 绘出矩形脉冲信号的频谱,观察矩形脉冲信号宽 度变化时对频谱波形的影响; ③让矩形脉冲信号的面积始终等于 1,改变矩形脉冲宽度,观察 矩形脉冲信号时域波形和频谱随矩形脉冲宽度的变化趋势。
陈后金《信号与系统》(第2版)配套题库【名校考研真题+课后习题+章节题库+模拟试题】(上册)

图2-2
3.有一离散时间信号
(1)画出
(2)求序列 学]
使之满足
解:(1)
又 比较上述两式可得: 故如图2-3所示。
[电子科技大
图2-3
4.已知 如图2-4(a),画出
和
的波形。[北
京理工大学]
解:将 反转得 如图2-4(b)所示,将它们相加、减得 ,波形如图2-4(c)、(d)所示。
图2-4 5.已知f(t)的波形如图2-5所示,令r(t)=tu(t)。
大学]
图1-2 解:因为:
故:
y2(t)的波形如图1-3所示。
图1-3 3.将如图1-4(a)、(b)所示的连续信号展成如下形式:
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解:(a)该信号可分为两段:
和
可化简为
故
,即:
(b)该信号可分为三段: 可化简为 故
,即
4.求
的值。[北京航空航天大学2006研]
,应该与齐次解有关,即系统的特征根为-1和-3,故特征方程应为 ,即a0=4,a1=3。
(2)设系统对激励 rzs(t),则
的零输入响应和零状态响应分别为rzi(t)和
由于
,则由线性时不变系统的微分特性可知
同时,设系统的单位冲激响应为h(t),则由线性时不变系统的叠加性 可知
由式(1)、式(2),并设
陈后金《信号与系统》(第2版)配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1.方程 天大学2007研] A.线性时不变 B.非线性时不变 C.线性时变 D.非线性时变 E.都不对 【答案】B
描述的系统是( )。[北京航空航
《信号与系统》第七章 北京理工大学

求响应y(t)。
解:
1 s Y (s) 3sY (s) 2Y (s) Re{s} 1 s 1 分解 1 1 1 Y ( s) s 2 s 1 ( s 1) 2
2
反变换
y(t ) (e t e 2t tet )u(t )
7.6.3 非零状态系统的S域分析
1
线性性质
ax1 (t ) bx2 (t ) aX1 (s) bX 2 (s), ROC R1 R2
2
时域平移
x(t t0 ) est 0 X (s) ROC R
3 S域平移
e s0t x(t ) X (s s0 ) ROC R Re(s0 )
4
时间尺度变换
1 s x(at) X ( ) ROC aR a a
例
5
时域卷积定理
x1 (t ) x2 (t ) X 1 (s) X 2 (s), ROC包括R1 R2
6 时域微分性质
7 单边拉氏变换的时域微分性质
8 时域积分性质
9 单边拉氏变换的时域积分性质
10 S域微分
指数阶函数:对于 x (t ) ,若能找到实数 , ,并满足
t
lim e t x(t ) 0,
t
lim e t x(t ) 0
则 x (t )为指数阶函数。
拉氏变换的收敛域
1)如果x(t)是有限持续期的信号,其收敛域是整个S域
无论,选择任何值,x(t )的象函数都是收敛的 收敛域是整个S全平面
P284 表7-1
习题
1.
的拉氏变换及其收敛域为( )
)
2. x(t)=tu(t-1) 的拉氏变换为(
北京理工大学信号与系统实验实验报告材料
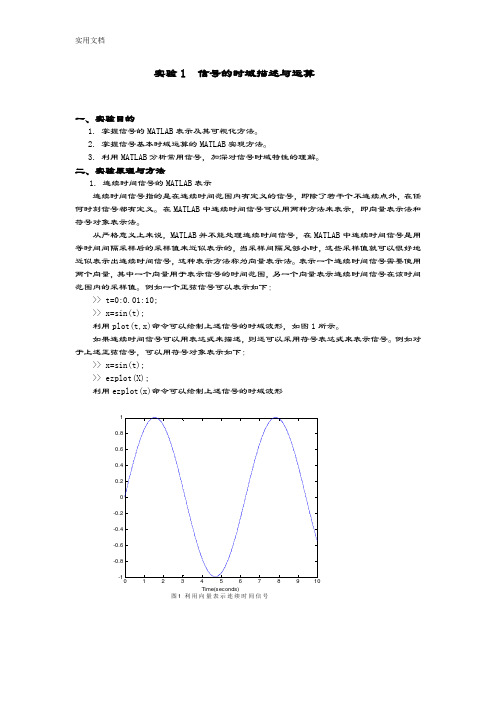
实验1 信号的时域描述与运算一、实验目的1. 掌握信号的MATLAB 表示及其可视化方法。
2. 掌握信号基本时域运算的MATLAB 实现方法。
3. 利用MATLAB 分析常用信号,加深对信号时域特性的理解。
二、实验原理与方法1. 连续时间信号的MATLAB 表示连续时间信号指的是在连续时间范围内有定义的信号,即除了若干个不连续点外,在任何时刻信号都有定义。
在MATLAB 中连续时间信号可以用两种方法来表示,即向量表示法和符号对象表示法。
从严格意义上来说,MATLAB 并不能处理连续时间信号,在MATLAB 中连续时间信号是用等时间间隔采样后的采样值来近似表示的,当采样间隔足够小时,这些采样值就可以很好地近似表示出连续时间信号,这种表示方法称为向量表示法。
表示一个连续时间信号需要使用两个向量,其中一个向量用于表示信号的时间范围,另一个向量表示连续时间信号在该时间范围内的采样值。
例如一个正弦信号可以表示如下:>> t=0:0.01:10; >> x=sin(t);利用plot(t,x)命令可以绘制上述信号的时域波形,如图1所示。
如果连续时间信号可以用表达式来描述,则还可以采用符号表达式來表示信号。
例如对于上述正弦信号,可以用符号对象表示如下:>> x=sin(t); >> ezplot(X);利用ezplot(x)命令可以绘制上述信号的时域波形012345678910-1-0.8-0.6-0.4-0.200.20.40.60.81Time(seconds)图1 利用向量表示连续时间信号-6-4-20246-1-0.50.51t图 2 利用符号对象表示连续时间信号sin(t)常用的信号产生函数 函数名 功能 函数名 功能 heaviside 单位阶跃函数 rectpuls 门函数 sin 正弦函数 tripuls 三角脉冲函数 cos 余弦函数 square 周期方波sinc sinc 函数 sawtooth 周期锯齿波或三角波 exp指数函数2.连续时间信号的时域运算对连续时间信号的运算包括两信号相加、相乘、微分、积分,以及位移、反转、尺度变换(尺度伸缩)等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例
推广
11 时域乘积
1 1 x1 (t ) x2 (t ) [ X 1 ( s) X 2 ( s)] 2j 2j
j
j
X 1 ( p) X 2 ( s p)dp
12 初值定理
用途
注意
13 终值定理
2
表7-1
7.4
常用函数的拉氏变换
1 单边右向信号的拉氏变换
v (s) I R (s) R R v L ( s ) i L (0 ) I L (s) sL s I C ( s ) sCvC ( s ) CvC (0 )
v R ( s) RIR ( s) v L ( s) Ls I L ( s) LiL (0 ) 1 1 vC ( s) I C ( s) vC (0 ) sC s
e at u (t ) 1 Re{s} a sa u (t ) 1 Re{s} 0 s
B根据S域的微分性质 C冲激信号
t n1 1 u (t ) n Re{s} 0 (n 1)! s
(t ) 1 ROC 为s平面 (t ) s ROC 为s平面
P284 表7-1
习题
1.
的拉氏变换及其收敛域为( )
)
2. x(t)=tu(t-1) 的拉氏变换为(
3. x(t)=(t+1)u(t+1) 的单边拉氏变换为( ) 4. x(t ) (3t ) u(3t ) 的拉氏变换及其收敛域为( )
7.5
拉普拉斯反变换
u (t ) x(t ) 2j
第七章 拉普拉斯变换 复频域分析
7.1 引言
连续时间系统的
1)应用傅氏变换,信号要绝对可积;
2)拉氏变化是另一种求解系统响应的办法,运算简单, 能同时求出系统的零输入响应和零状态响应; 3)能直观表示出系统具有的复频域特性。
7.2 拉普拉斯变换
引入衰减因子 e t ,定义 s j 则
j
j
X ( s )e st ds
拉氏反变换共有三种方法:
1 根据性质直接查表计算法 2 部分分式展开法 3 留数定理
1 围线积分法 (留数法)
以最右极点画出一条直线A,B,以原 点为圆心R为半径,构成一闭合曲线, 它包含全部的极点。
st 则x(t) 为曲线中被积函数 X ( s)e 所有极点的函数之和
1 Re{ s} a A 指数信号 sa 1 u (t ) Re{s} 0 B阶跃信号 s s cos 0t u (t ) 2 Re{s} 0 C余弦信号 2 s 0 sin 0t u (t ) 2 0 2 Re{s} 0 D正弦信号 s 0 sa e at cos 0t u (t ) Re{ s} a 2 E指数调制的余弦和正弦信号 ( s a ) 2 0 e at u (t )
的拉氏变换
y(t ) [6(e 1/ 2t e t ) e 3t ]u(t )
7.6系统函数
定义:一个连续时间LTI系统的系统函数定义为系统的零状态响应的拉 氏变换与激励的拉氏变换之比,是该系统单位冲激响应的拉氏变换。
H ( s) Y ( s) / X ( s)
H(s)是系统的时域模型h(t)对s域的映射,与输入无关。 H(s)是系统的基本特征,LTI系统的许多性质,如因果性、稳定性、系 统的频率响应等,与H(s)的零极点分布和收敛域有关。
2)如果x(t)是一个右边信号,则X(s) 的收敛域求法:
Re[s] 0 左
t
lim x(t )e t 0, 左为收敛域左边界
3)如果x(t)是一个左边信号,则X(s) 的收敛域求法:
t
lim x(t )e t 0, 右为收敛域右边界
R, SL,
1 SC
例:求如图所示的RC电路的S域模型。已知输入为阶跃电压u(t), 电容的断电压v(0)
v R (s) SRC v( s) SRC 1
7.6.2 零状态系统的S域分析
例:设某因果性LTI系统的微分方程描述为 d2 d y (t ) 3 y (t ) 2 y (t ) e t u (t ), y (0) y (0) 0 2 dt dt
e at sin 0t u (t )
F根据S域的微分性质
t n1 at 1 e u (t ) Re{s} a (n 1)! ( s a) n
2 ( s a ) 2 0
0
Re{ s} a
7.4常用函数的拉氏变换
2 单边左向信号的拉氏变换 A 指数信号
得
X ( s)
x(t )e st dt
拉普拉斯正变换
所以,
1 x(t ) 2j
j
j
X ( s)e st ds
拉普拉斯 反变换
拉普拉斯变换对
1 正变换公式
象函数
X ( s)
2 反变换公式
x(t )e st dt
一对拉氏变换对
原函数
1 x (t ) 2j
罗斯判据
j
j
X ( s )e st ds
单边拉氏变换公式
X ( s) x(t )e st dt
0
u (t ) j x(t ) X ( s)e st ds 2j j
拉氏变换和傅氏变换的区别:
1) 分解为 e
j t
和 e 的和;
st
2) 傅氏是从 ,而拉氏是从 j j
2 由输入的拉氏变换和系统的S域模型,进行简单的代数运算, 得到输出的拉氏变换式;
3取输出的拉氏变换式的反变换,得到系统的输出。 系统的S域模型: 可通过将时域微分模型两边拉氏变化获得 可通过电路元件的S域特性获得。
7.6.1 电路的S域模型
将电路的时域模型转换为S域模型,并运用计算电阻电路所用的全部定 律、方法和计算公式于S域电路模型,经过简单的代数运算,便可得到 输出的拉氏变换。 对于R,L,C,它们的S域表达式为:
2 例: d y (t ) 3 d y (t ) 1 y (t ) 5e 3t u (t ), y (0) 1, y ' (0) 0 2 dt 2 dt 2 求响应y(t)。
解: 微分方程各项进行单边拉氏变换,有 3 1 5 2 ' [s Y (s) sy(0) y (0)] [sY (s) y(0)] y(s) 2 2 s 3 5 3 初始条件 s s3 2 零输入响应 Y ( s) 3 1 3 1 的拉氏变换 s2 s s s2 2 2 2 2 零状态响应 反变换
例7-1 设 x(t ) e t u (t ) 求其拉氏变换的收敛域
解
L[ x(t )] e
0
t
e dt e ( s )t dt
st 0
e ( s )t 1 |0 s s
极点为s , Re[s]
例7-2 设 x(t ) e t u (t ) 求其拉氏变换的收敛域
1
线性性质
ax1 (t ) bx2 (t ) aX1 (s) bX 2 (s), ROC R1 R2
2
时域平移
x(t t0 ) est 0 X (s) ROC R
3 S域平移
e s0t x(t ) X (s s0 ) ROC R Re(s0 )
解
L[ x(t )] e
t
u (t )e dt e ( s )t dt
st
0
e ( s )t 0 1 | s s
极点为s , Re[s]
见 p275, 例7-3
7.3
拉氏变换的性质
求响应y(t)。
解:
1 s Y (s) 3sY (s) 2Y (s) Re{s} 1 s 1 分解 1 1 1 Y ( s) s 2 s 1 ( s 1) 2
2
反变换
y(t ) (e t e 2t tet )u(t )
7.6.3 非零状态系统的S域分析
求反变换的运算 转换为被积函数各 极点上的函数
P286
例7-10
2 部分分式法
由拉氏变换的性质或直接查表得到
讨论:
其中
P287 例 7-12
长除法
7.6连续时间系统的复频域分析法
系统的复频域分析法的步骤: 1 取输入信号和系统时域模型的拉氏变换,得到输入的拉氏 变换式和系统的S域模型;
Re[s] 0 右
拉氏变换的收敛域
4)当f(t)是一个双边信号时, 左 Re[s] 右 ,当ROC边界不满 足 左 右,则信号不存在双边拉氏变换。
5)X(s)的收敛域内不含极点,收敛域的边界由极点决定。
注意: 1 同一个象函数,如收敛域不一样,则对应的时间函数不一 样。 2 当象函数为有理函数,收敛域的边界是由系统的极点所决 定的。
4
时间尺度变换
1 s x(at) X ( ) ROC aR a a
例
5
时域卷积定理
x1 (t ) x2 (t ) X 1 (s) X 2 (s), ROC包括R1 R2
6 时域微分性质
7 单边拉氏变换的时域微分性质
8 时域积分性质
9 单边拉氏变换的时域积分性质
10 S域微分
指数阶函数:对于 x (t ) ,若能找到实数 , ,并满足
t
lim e t x(t ) 0,
