三角函数与圆
三角函数和圆的关系
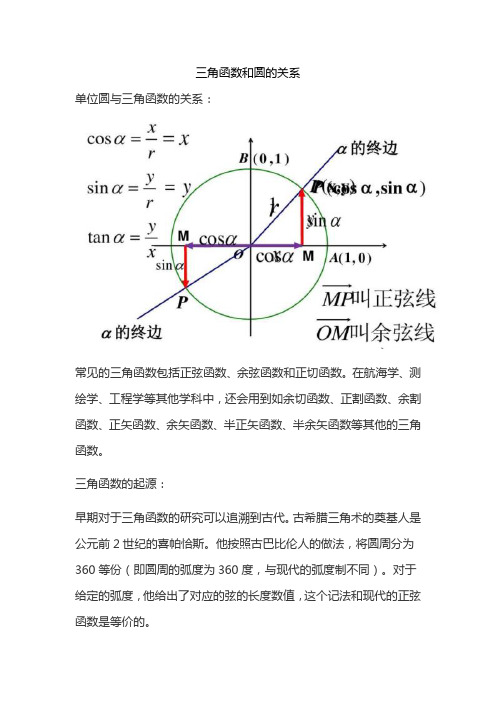
三角函数和圆的关系
单位圆与三角函数的关系:
常见的三角函数包括正弦函数、余弦函数和正切函数。
在航海学、测绘学、工程学等其他学科中,还会用到如余切函数、正割函数、余割函数、正矢函数、余矢函数、半正矢函数、半余矢函数等其他的三角函数。
三角函数的起源:
早期对于三角函数的研究可以追溯到古代。
古希腊三角术的奠基人是公元前2世纪的喜帕恰斯。
他按照古巴比伦人的做法,将圆周分为360等份(即圆周的弧度为360度,与现代的弧度制不同)。
对于给定的弧度,他给出了对应的弦的长度数值,这个记法和现代的正弦函数是等价的。
喜帕恰斯实际上给出了最早的三角函数数值表。
然而古希腊的三角学基本是球面三角学。
这与古希腊人研究的主体是天文学有关。
梅涅劳斯在他的著作《球面学》中使用了正弦来描述球面的梅涅劳斯定理。
三角函数与单位圆

三角函数与单位圆在数学中,三角函数是研究角度和三角形关系的重要工具之一。
而单位圆则是三角函数中的一个重要概念,它与三角函数之间存在着密切的关系。
一、三角函数的基本定义及公式三角函数包括正弦函数、余弦函数、正切函数等。
它们的定义如下:1. 正弦函数(sin):在直角三角形中,对于一个角,正弦值等于对边与斜边长度的比值。
2. 余弦函数(cos):在直角三角形中,对于一个角,余弦值等于邻边与斜边长度的比值。
3. 正切函数(tan):在直角三角形中,对于一个角,正切值等于对边与邻边长度的比值。
这些三角函数在单位圆中也有对应的定义及公式。
单位圆是以圆心为原点、半径为1的圆,在坐标系中可以表示为x^2 + y^2 = 1。
对于单位圆上的任意一点P(x, y),可以定义其对应的角度为A,单位圆上的点与角度之间存在着一一对应的关系。
二、三角函数与单位圆的关系在单位圆中,以圆心为起点,与圆上任意一点P(x, y)连接,这条线段与圆的半径的夹角即为角A。
根据三角函数的定义,在单位圆中,可以得到以下关系:1. 正弦函数:sin(A) = y2. 余弦函数:cos(A) = x3. 正切函数:tan(A) = y/x利用这些关系,可以得到三角函数在单位圆中的图形。
正弦函数在单位圆中的图形表现为一个周期为2π的正弦波,其振幅为1。
余弦函数与正弦函数相位相差π/2,也表现为一个周期为2π的正弦波。
而正切函数在单位圆中的图形是一个以原点为渐近线的周期为π的函数。
三、三角函数在解决问题中的应用三角函数在数学中有着广泛的应用,特别是在解决与角度和三角形相关的问题时。
1. 几何问题:三角函数可以用于求解直角三角形的边长、角度等问题。
例如,已知一个角的正弦值,可以通过反正弦函数求解角度值;已知两个边长,可以利用正弦定理或余弦定理求解另外一个角度或边长。
2. 物理问题:三角函数在解决物理问题中也有广泛应用。
例如,通过正弦函数可以描述周期性的振动现象;借助于正切函数可以求解斜面上物体的滑动问题。
圆周运动与三角函数

圆周运动与三角函数圆周运动是物体沿着圆周运动的运动,是日常生活中最为常见的物理运动,如风车的转动、电转、轮子的旋转等。
圆周运动的主要特征就是物体一直沿着同一圆心,顺时针或逆时针运动,其角度随时间发生变化。
三角函数是数学中常用的一类函数,是表达由角度或者弧度来描述物体在圆周运动中的位置。
它们把圆周运动的角度转换成实数,由此可以计算出物体的位置和速度。
圆周运动与三角函数的关系是密不可分的,在数学、物理等学科中应用非常广泛。
在物理运动中,所有的圆周运动包括定位和机械的移动,都可以用三角函数来描述。
它们可以用来描述物体在圆周运动过程中的角度随时间的变化,也可以应用到位置、速度以及加速度计算中。
比如可以用正弦函数来描述物体在圆周运动中沿着x轴和y轴的位置变化,也可以用余弦函数来描述物体沿着y轴方向的速度变化,以此类推,其它的三角函数也同样有此作用。
此外,圆周运动与三角函数还可以用来解决一些比较复杂的有关圆周运动的数学问题。
比如可以用正弦函数来表示物体在圆周运动中沿着x轴和y轴的惯性力,还可以用余弦函数来表示圆周运动中沿着y轴方向的加速度变化,以此类推,其它的三角函数也可以应用到物体在圆周运动中各种力学运动中去。
同时,三角函数也可以用来解决一些切线、正切和几何等数学问题。
此外,圆周运动与三角函数在更多的学科领域中也有着重要的作用,例如在天文学方面,它们可以用来研究行星的轨道、星系的形状等;在物理中,可以用来研究物体的旋转运动;在工程中,可以用来计算齿轮传送系统的传动效率;在振动力学中,可以用来分析振动系统的运动方式等。
总之,圆周运动和三角函数是数学中最为基本的概念,在解决各种复杂的物理问题中备受青睐,应用到物理、数学、天文学、工程和振动力学等学科中,它们都起着至关重要的作用。
本文对圆周运动和三角函数作出了简要的介绍,并对它们之间的密切关系进行了讨论。
它们在物理、数学和其它学科中的应用也被详细地说明,表明它们是解决复杂物理学问题的重要工具。
三角函数和圆的知识点总结

三角函数和圆的知识点总结在圆的知识中,圆是一种简单的几何图形,它有着许多有趣的性质和应用,比如圆周率和圆的面积、弧长等。
下面我们将对三角函数和圆的知识点进行详细的总结。
一、三角函数1. 正弦函数正弦函数是一种周期性的函数,它的图像是一条波浪线。
正弦函数在几何学中常用来描述角的正弦值,它定义为一个直角三角形中对边与斜边的比值。
在代数学中,正弦函数可以用于描述周期性变化的现象,比如声音的波动、天体运动等。
正弦函数的性质包括:- 周期性:正弦函数的周期是2π,即f(x+2π) = f(x)。
- 增减性:在一个周期内,正弦函数是先增后减的。
- 奇函数:正弦函数是奇函数,即f(-x) = -f(x)。
2. 余弦函数余弦函数也是一种周期性的函数,它的图像是一条波浪线,但与正弦函数的波形相位差π/2。
余弦函数描述了一个角的余弦值,它定义为一个直角三角形中邻边与斜边的比值。
在代数学中,余弦函数可以描述一些对称变化的现象,比如振动、波动等。
余弦函数的性质包括:- 周期性:余弦函数的周期也是2π,即f(x+2π) = f(x)。
- 增减性:在一个周期内,余弦函数是先减后增的。
- 偶函数:余弦函数是偶函数,即f(-x) = f(x)。
3. 正切函数正切函数是斜率的函数,它描述了一个角的正切值,定义为一个直角三角形中对边与邻边的比值。
在几何学中,正切函数用于求解三角形的角度和边长;在物理学和工程学中,正切函数可以描述力和速度的关系。
正切函数的性质包括:- 周期性:正切函数的周期是π,即f(x+π) = f(x)。
- 增减性:在一个周期内,正切函数是先增后减或者先减后增的。
- 奇函数:正切函数是奇函数,即f(-x) = -f(x)。
4. 反正弦函数、反余弦函数、反正切函数除了正弦函数、余弦函数和正切函数之外,三角函数还有反函数,分别是反正弦函数arcsin(x)、反余弦函数arccos(x)、反正切函数arctan(x)。
圆和三角函数的知识点总结

圆和三角函数的知识点总结一、圆的基本概念1. 圆的定义圆是由平面上到一点距离等于定值的所有点的集合所构成的图形。
这个定值称为圆的半径,记作R。
圆的中心是到圆上任意一点的距离都等于半径的点。
2. 圆的性质(1)圆的直径是经过圆心并且两端点在圆上的线段,其长度等于半径的两倍,即2R。
(2)圆的周长是圆的边界长度,等于2πR。
(3)圆的面积是圆的内部面积,等于πR²。
3. 圆的相关公式(1)周长的计算公式:C = 2πR(2)面积的计算公式:A = πR²4. 圆的图形圆的图形一般用于图像的绘制、工程设计和数学证明等方面,其圆心和半径都是图形的重要参数。
二、三角函数的基本概念1. 三角函数的定义三角函数是一类反映角度和三角形边长关系的函数,包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数等。
其中,最基本的三角函数是正弦函数和余弦函数。
2. 三角函数的性质(1)正弦函数的性质:周期性、奇偶性、单调性等。
(2)余弦函数的性质:周期性、偶偶性、单调性等。
(3)其他三角函数的性质:正切函数、余切函数、正割函数和余割函数的性质。
3. 三角函数的公式三角函数有一系列的常用公式,如和差公式、倍角公式、半角公式、和角公式等,这些公式能够简化三角函数的计算。
4. 三角函数的图形正弦函数和余弦函数的图形是三角函数中最为常见的图形,它们在数学和物理学中有着广泛的应用。
在图像上,正弦函数是一个周期函数,其图像呈现正弦波形;余弦函数也是一个周期函数,其图像呈现余弦波形。
三、圆和三角函数的关系1. 弧度制和角度制圆和三角函数之间的关系在很大程度上依赖于角度的度量方式。
弧度制是一种更为自然的角度度量方式,而角度制是较为常见的角度度量方式。
弧度制和角度制的关系为:1弧度= 180°/π度。
2. 弧长和扇形面积正弦函数和余弦函数的定义涉及到圆的弧长和扇形面积,它们与三角函数之间有着密切的关系。
三角函数圆的知识点总结

三角函数圆的知识点总结1. 正弦函数和余弦函数正弦函数和余弦函数是三角函数中最基本的两个函数之一。
它们的定义来自于单位圆。
单位圆是一个半径为1的圆,我们可以以圆心为原点建立直角坐标系,这样单位圆的边界就可以表示为坐标为$(\cos \theta, \sin \theta)$的点。
这里$\theta$表示与$x$轴正方向的夹角,即角度。
正弦函数$\sin \theta$在单位圆上对应点的纵坐标,而余弦函数$\cos \theta$在单位圆上对应点的横坐标。
这样,我们可以得到正弦函数和余弦函数的定义:$$\sin \theta = \frac{\text{对边}}{\text{斜边}} = \frac{y}{r}$$$$\cos \theta = \frac{\text{邻边}}{\text{斜边}} = \frac{x}{r}$$其中$r$为单位圆的半径。
正弦函数和余弦函数的图像都是周期性的,周期为$2\pi$(或$360^{\circ}$),并且它们都是偶函数。
正弦函数和余弦函数的图像都是连续的,且在定义域内都是单调递增的。
它们的最大值和最小值都是1和-1。
2. 正切函数正切函数是另一个基本的三角函数,定义为$\tan \theta = \frac{\sin \theta}{\cos \theta}$。
可以从正弦函数和余弦函数的定义中得到正切函数的等价定义:$\tan \theta =\frac{y}{x}$。
正切函数的图像是周期性的,周期同样是$2\pi$(或$360^{\circ}$)。
它是一个奇函数,即$\tan (-\theta) = -\tan \theta$。
正切函数在定义域内有无穷多个间断点,因为$\cos \theta = 0$时,$\tan \theta$无定义。
在这些点处,正切函数的图像会有无限大的正向或负向趋向。
正切函数的图像在$(-\frac{\pi}{2}, \frac{\pi}{2})$上是单调递增的,在$(\frac{\pi}{2}, \frac{3\pi}{2})$上是单调递减的。
三角函数与圆周率的关系

三角函数与圆周率的关系1 引言圆周率和三角函数之间有着密不可分的关系。
圆周率是指弧长和圆周之比,它可以将圆周这个曲线参数化从而表示其特性。
而三角函数则是一类有回旋特性的函数,它几乎可以描述宇宙中的任何曲线形状。
圆的周长与半径r的关系是圆周率pi*2r,三角函数sin,cos,tan可以等价地表示为sinθ=y/r,cosθ=x/r,tanθ=y/x,所以可知圆周率与三角函数有着密不可分的关系。
2 圆周率与极坐标圆周率和极坐标记法也有一定的关联。
通常我们可以用一个坐标轴描述一条直线;而极坐标轴系则可以很好地描述一个圆,它把圆分成了辐条来表示,根据此原理,我们可以用一个角度α表示圆的圆周,用半径r表示弧长l,把l与2π的关系写成就可以得出它们之间的关系。
3 三角函数三角函数是一类有回旋特性的函数。
它可以描述宇宙中的任何曲线形状,因此用它可以计算圆周率。
比如cos、sin和tan函数,它们都可以通过r, α来表示,比如cosθ=x/r,sinθ=y/r,tanθ=y/x,这里x,y是坐标轴上的实际值。
4 莎士比亚公式莎士比亚公式(Arquimedes' Formula)是用来计算圆周率的最古老的方法之一。
它利用了圆周率和三角函数之间的关系,用来计算圆周率。
为了得出莎士比亚公式,他们把半径r内的圆分成n个等宽的三角形,称为当量三角形,积聚这些当量三角形就可以形成一个近似的圆,再用n*sin(α)的关系就可以得出π即圆周率。
5 结论通过本文我们知道,圆周率与三角函数具有密不可分的关系。
可以用极坐标轴来表示圆,角度α可以表示圆的圆周,半径r可以表示圆周率pi*2r,三角函数等价于sinθ=y/r,cosθ=x/r,tanθ=y/x,这些关系可以用莎士比亚公式来计算圆周率。
三角函数圆圈

三角函数圆圈三角函数之圆在数学中,三角函数是研究角和三角形的函数,其中最基本的三角函数有正弦函数、余弦函数和正切函数。
这些函数在数学的各个分支中起着非常重要的作用,尤其在几何、物理和工程学中经常被使用。
三角函数与圆圈之间存在着密切的关系。
正弦函数和余弦函数可以被看作是一个圆上点在x轴和y轴上的投影,而正切函数则可以被看作是一个圆上点与x轴的切线斜率。
这种圆与三角函数的联系可追溯到几百年前的古代希腊数学家。
首先,我们需要知道一个重要的概念,那就是单位圆。
单位圆是一个半径为1的圆,圆心位于坐标原点(0,0)。
这个圆的方程是x^2 + y^2 = 1。
这个单位圆在数学中起到了非常重要的作用,因为它可以帮助我们理解三角函数的性质。
正弦函数是一个周期函数,它的周期是2π。
在单位圆上,正弦函数的值可以通过一个圆上点的y坐标来表示。
例如,在点(π/6,1/2)处,正弦函数的值是1/2。
我们可以将这个点连接到坐标原点,形成一个直角三角形。
其中,直角边的长度等于点的y坐标,斜边的长度等于1(因为是单位圆),而邻边的长度则可以通过勾股定理计算得到。
这样,我们就可以计算出正弦函数的值。
余弦函数与正弦函数非常相似,只不过它的值是通过一个圆上点的x坐标来表示。
在同样的例子中,我们可以通过点(π/6,√3/2)来计算余弦函数的值。
同样地,我们可以将这个点连接到坐标原点,形成一个直角三角形。
这样,我们就可以计算出余弦函数的值。
正切函数也是一个周期函数,它的周期是π。
在单位圆上,正切函数的值可以通过斜边与直角边的比值来表示。
例如,在点(π/4,1)处,正切函数的值是1。
我们可以将这个点连接到坐标原点,形成一个直角三角形。
其中,直角边的长度等于点的y 坐标,斜边的长度等于点的x坐标,而邻边的长度则可以通过勾股定理计算得到。
这样,我们就可以计算出正切函数的值。
除了正弦函数、余弦函数和正切函数之外,还有很多其他的三角函数,如余割函数、正割函数和余切函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:(1)D(0,-4),B(2,0),C(8,0) ∴解析式为:y=-1/4x2+5/2x-4 ∴y=-(x-5)2+9/4 (2)由垂径定理,作BC中点H, 可证∠BDC=∠BAH,∴tan ∠BDC=tan ∠BAH=3/4.
(3)求直线PC的解析式:y=-3/4x+6 设I为直线PC与y轴的交点,则I的坐标为(0,6) ∴ID=IC=10∴∠ICD=∠IDC ∴∠ICA=∠IDA=∠IDC+∠CDA=90° ∴∠ICO=∠BDC=∠PFD ∴∠CGF=∠GDF+1/2∠PFD=∠GDF+1/2∠BDC=∠HDF=45°
4
课时训练
1.如图所示,C是⊙O外一点,由C作⊙O的两条切线,切点 为B、D,BO的延长线交⊙O于E,交CD的延长线于A,若 AE=2,AB=23 求:(1)BE的长;(2)sin A的值. 解: (1)BE=AB-AE=2(3-1) (2)连OD,则OD=3-1 ∵CD为⊙O的切线∴OD⊥CD
4. 如图所示,抛物线 y=ax2-3x+c 交 x 轴正方向于 A、B 两点, 交y轴正方向于C点,过A、B、C三点作⊙D,若⊙D与y轴相 切. (1)求a、c满足的关系式; (2)设∠ACB=α ,求tan α ; (3)设抛物线顶点为P,判断直线PA与⊙D的位置关系,并 证明.
解:(1)A、B的横坐标是方程ax2-3x+c=0 的两根,设为x1,x2(x2>x1),C的纵坐标为c 又∵y轴与⊙D相切, ∴OA·OB=OC2∴x1·x2=c2, 又由方程ax2-3x+c=0和已知x1·x2= c a c 2 ∴c = 即ac=1.
解:(1)连结AC∵AC=CE∴∠CEA=∠CAE ∵∠CEA=∠CBA∴∠CBA=∠CAE ∵AB是直径∴∠ACB=90° ∵CP⊥AB∴∠CBA=∠ACP ∴∠CAE=∠ACP∴AD=CD (2)∵∠ACB=90°∠CAE=∠ACP ∴∠DCF=∠CFD∴AD=CD=DF=5/4 ∵∠ECB=∠DAP,tan ∠ECB=3/4 ∴tan ∠DAP=DPPA=3/4 ∵DP2+PA2=DA2 ∴DP=3/4 PA=1∴CP=2 ∵∠ACB=90°,CP⊥AB ∴△APC∽△CPB
15 4
【例5】(2003年·河南省)已知:如图所示,AB是⊙O的直 径,O为圆心,AB=20,DP与⊙O相切于点D,DP⊥PB,垂足 为P,PB与⊙O交于点C,PD=8 (1)求BC的长; (2)连结DC,求tan ∠PCD的值; (3)以A为原点,直线AB为x轴建立平面直角坐标系,求 直线BD的解析式.
3 5 , 2a 4a
)
5 又∵a>0∴在Rt△PAE中,PE= 4 a
PE 5 ∴tan β = AE 2
∴tanβ =tan α ∴β =α ∴∠PAE=∠ADE ∵∠ADE+∠DAE=90°∴∠PAE+∠DAE=90° 即∠PAD=90°∴PA和⊙D相切.
5.(2003年·深圳市)如图所示,已知A(5,-4),⊙A与x轴 分别相交于点B、C,⊙A与y轴相切于点D, (1)求过D、B、C三点的抛物线的解析式; (2)连结BD,求tan ∠BDC的值; (3)点P是抛物线顶点,线段DE是直径,直线PC与直线DE相 交于点F,∠PFD的平分线FG交DC于G,求sin ∠CGF的值.
【解析】 (1)过O作OE⊥BC,垂足为E,则BE=EC,连结OD,则OD⊥DP 又∵DP⊥PB,∴四边形OEPD为矩形 ∴ OE=PD=8 ∵OB=1/2*AB=1/2×20=10 在Rt△OEB中,EB2=OB2-OE2=102-82=36 ∴EB=6,∴BC=2EB=12
(2)∵PB=PE+EB=DO+EB=16 ∴PC=PB-BC=16-12=4 在Rt△PCD中, DP=8, PC=4 8 ∴tan ∠PCD=PD/PC= =2
第二部分第四课时:
三角函数与圆
思想方法提炼 感悟、渗透、应用 课时训练
思想方法提炼
三角函数是与角密切相关的函数,而圆中常会出 现与角有关的求解问题,尤其会出现一些非特殊角求 其三角函数值的问题,或已知三角函数值求圆中的有 关线段长等问题.三角函数与圆的综合应用也是中考 中的热点问题之一.
a
(2)连结PD,交x轴于E,直线PD必为抛物线的对称轴, 连结AD、BD, 1 1 ∴AE= 2 AB,∠ACB= ∠ADB=∠ADE=α 2 ∵a>0,x2>x1
∴AB=x2-x1=
9 4ac 5 a a
∴AE=
5 2a
又ED=OC=c,∴tan α =
AE 5 DE 2
(3)设∠PAB=β ,∵P点坐标为(
解:(1)∵DC为⊙O的直径∴DE⊥EC 2 2 DC DE 64 15 =7 ∵DC=8,DE= 15 ∴EC= 设EM=x,由于M为OB的中点∴BM=2,AM=6 ∴AM·MB=x·(7-x) 即6×2=x(7-x),x2-7x+12=0 ∴x1=3,x2=4∵EM>MC∴EM=4 (2)∵OE=EM=4∴△OEM为等腰三角形 过E作EF⊥OM,垂足为F,则OF=1 ∴EF= OE 2 OF 2 16 1 15 ∴sin ∠EOB=
感悟、渗透、应用
【例1 】如图所示,已知AB 为⊙O 的直径,C 为AB延长线上 的点,以OC为直径的圆交⊙O于D,连结AD,BD,CD. (1)求证:CD是⊙O的切线; (2)若AB=BC=2,求tan ∠A的值.
【解析】 (1)证∠CDO=90°即可,理由OC为圆的直径. (2)利用△BCD∽△DCA得到BD8DA的比值
AP PC ∴ PC PB
∴PB=4
【例 4 】 (2003 年 · 河南省 ) 已知如图所示,在半径为 4 的 ⊙O中,AB、CD是两条直径,M为OB的中点,CM的延长线交 ⊙O于点E,且EM>MC,连结DE,DE= 15 . (1)求EM的长; (2)求sin ∠EOB的值.
【分析】 (1)用勾股定理求EC长,再用相交弦定理求EM的长. (2)构造Rt△EOF,利用三角函数求正弦值.
sin A sin B sin A cos A 2m 5 m5 sin A sin B sin A cos A 12 ( 2m 5 ) 2 24 m5 m5 m5
①2-②×2得(sin A+cos A)2-2sin A·cos A 消去sin A和cos A,得m2-18m-40=0 解之得m=20或m=-2
BD 2 ∠A= DA 2
【例 2 】 (2004 年 · 甘肃省 ) 已知:如图,四边形 ABCD 内接 于⊙O,AB是⊙O的直径,CE切⊙O于C,AE⊥CE, 交⊙O于D. (1)求证:DC=BC; (2)若DC:AB=3:5, 求sin∠CAD的值.
证明: 连接 BD.∵AB是⊙ O 的直径,∴∠ADB=90°. 又∠AEC=90°. ∴BD//EC.∴∠ECD=∠BDC.∴BC=CD 又∠CAD=∠CAB ∴sin∠CAD=sin∠CAB=BC/AB=DC/AB= 3/5.
OD 3 1 3 1 4 2 3 2 3 ∴sin A= OA ( 3 1 ) 2 3 1 2
3. △ ABC 中, AB=10,外接圆 O 的面积为 25 π ,sin A,sin B是方程(m+5)x2-(2m-5)x+12=0的个两根,其中m≠-5. (1)求m的值;(2)求△ABC的内切圆的半径.
(2)当m=20时, 方程化为:25x2-35x+12=0 解之得 x=3/5,x=4/5 则sin A=3/5,sin B=45或sin A=4/5,sin B=3/5 即: AC=AB·sin B=10×4/5=8 BC=AB·sin A=10×3/5=6或AC=6,BC=8 于是内切圆半径r=1/2(a+b-c)= 1/2(8+6-10)=2 当m=-2时,方程化为x2+3x+4=0 ∵此方程无实根 ∴m=-2应舍去 ∴m=20,r=2
∵DA=AH=半径∴sin ∠CGF=sin 45°=
2 . 2
解:(1)连结OD,∵OC为直径 ∴∠CDO=90° 又∵OD为⊙O的半径∴CD是⊙O的切线
(2)由切割线定理有:CD2=CB·CA=8∴CD=22 ∵∠BDC=∠A,∠BCD=∠DCA∴△BCD∽△DCA
BD DB=90°∴tan
【例3】(2003年·湖北省黄冈市)已知:如图Z4-3,C为 半圆上一点, AC=CE,过点 C 作直径 AB 的垂线 CP,P 为垂足, 弦AE分别交PC,CB于点D,F, (1)求证:AD=CD; (2)若DF=5/4,tan ∠ECB =3/4,求PB的长.
【分析】 (1)证△ACD为等腰三角形即可得. (2)先证明 CD=AD=FD,在Rt△ADP中再利用勾股定理及tan ∠DAP=tan ∠ECB=3/4, 求 出 DP、PA、CP, 最 后 利 用 △APC∽△CPB求PB的长.
