第13章 习题解答
范里安-微观经济学现代观点-第8版-第八版-ch13-风险资产(含全部习题解答)-东南大学曹乾

Intermediate Microeconomics:A Modern Approach (8th Edition)Hal R. Varian范里安中级微观经济学:现代方法(第8版)完美中文翻译版)含全部习题详细解答)第13章:风险资产(含全部习题详细解答风险资产(曹乾译(东南大学caoqianseu@)13风险资产在上一章,我们分析了不确定性情形下的个人行为模型,以及保险市场和股票市场这两种经济制度的作用。
在本章我们进一步分析股票市场如何分散风险的。
为做此事,最好从一个简化的不确定性行为模型进行分析。
13.1均值—方差效用在上一章我们分析了不确定性情形下的选择问题,我们是用期望效用函数进行分析的。
这样的问题还有另外一类分析方法,即用一些参数(parameters )描述选择的目标,然后将效用函数视为这些参数的函数。
这类方法中最为流行的就是均值..—.方差模型....(mean-variance model )。
在均值—方差方法中,我们不再认为消费者的偏好取决于他的财富在每种可能结果上的整个概率分布,而是假设他的偏好可用几个关于他财富概率分布的统计量进行描述。
令随机变量w 取值s w 的概率为s π(其中S s ,...,2,1=)。
w 概率分布的均值..(mean )就是它的加权平均值:s Ss s w w ∑==1πµ.上式就是加权平均值的计算公式:每个结果s w 以它自身发生的概率s π作为权重(即s s w π),然后全部相加(一)。
w 概率分布的方差..(variance )是2)(w u w −的加权平均值: 212)(w S s s wu w −=∑=πσ. 方差衡量分布的“分散性”,因此可用来衡量风险。
还有一种相近的衡量方法,称为标准差...(standard deviation ),用w σ表示,它是方差的平方根:2w w σσ=.概率分布的均值衡量它的加权平均值,即这些分布围绕着的那个数值。
工程光学课后答案(12 13 15章)

1λ十二 十三 十五第十二章 习题及答案1。
双缝间距为1mm ,离观察屏1m ,用钠灯做光源,它发出两种波长的单色光 =589.0nm 和2λ=589.6nm ,问两种单色光的第10级这条纹之间的间距是多少?解:由杨氏双缝干涉公式,亮条纹时:d Dm λα=(m=0, ±1, ±2···)m=10时,nmx 89.511000105891061=⨯⨯⨯=-,nmx 896.511000106.5891062=⨯⨯⨯=- m x x x μ612=-=∆2。
在杨氏实验中,两小孔距离为1mm ,观察屏离小孔的距离为50cm ,当用一片折射率 1.58的透明薄片帖住其中一个小孔时发现屏上的条纹系统移动了0.5cm ,试决定试件厚度。
21r r l n =+∆⋅22212⎪⎭⎫⎝⎛∆-+=x d D r 22222⎪⎭⎫⎝⎛∆++=x d D r x d x d x d r r r r ∆⋅=⎪⎭⎫⎝⎛∆--⎪⎭⎫ ⎝⎛∆+=+-222))((221212mm r r d x r r 2211210500512-=⨯≈+⋅∆=-∴ ,mm l mm l 2210724.110)158.1(--⨯=∆∴=∆- 3.一个长30mm 的充以空气的气室置于杨氏装置中的一个小孔前,在观察屏上观察到稳定的干涉条纹系。
继后抽去气室中的空气,注入某种气体,发现条纹系移动了25个条纹,已知照明光波波长λ=656.28nm,空气折射率为000276.10=n 。
试求注入气室内气体的折射率。
0008229.10005469.0000276.1301028.6562525)(600=+=⨯⨯=-=-∆-n n n n n l λ4。
垂直入射的平面波通过折射率为n 的玻璃板,透射光经透镜会聚到焦点上。
玻璃板的厚度沿着C 点且垂直于图面的直线发生光波波长量级的突变d,问d 为多少时焦点光强是玻璃板无突变时光强的一半。
03 电磁学:第12、13章 习题课及部分习题解答-修订补充版
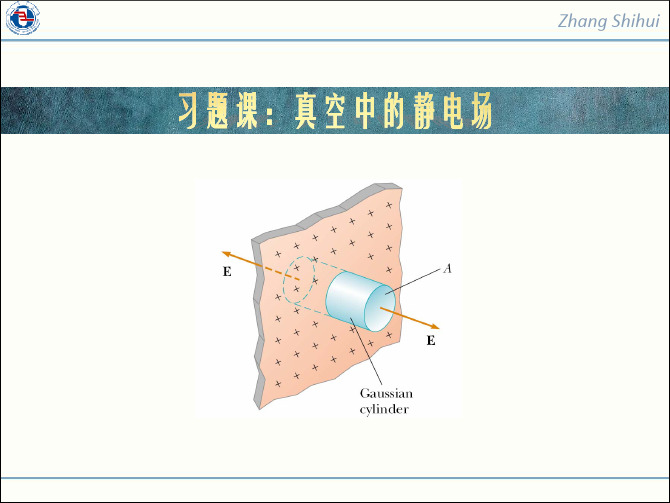
R
∫
S
E ⋅ dS ⇒2πrlE =
R
q
ε0
r l
q=∫
0
2 Ar ⋅ 2πrldr = πAlR 3 3
3
AR E= 3ε 0 r
(r > R)
目录·电势的计算
作业册·第十三章 电势·第8题
Zhang Shihui
③ 内外电势分布 内部电势 U =
∫
L
r R
Edr Ar AR dr + ∫ dr R 3ε r 3ε 0 0
dl = Rdθ
λ dl cos θ dEx = dE cos θ = 2 4πε 0 a
q q cos θ dθ = cos θ ⋅ adθ = 2 4πε 0 a θ 0 a 4πε 0 a 2θ 0 1
θ0
2
θ
−
θ0
2
θ0
2
dE
x
q 2 沿x正 E = ∫ θ0 dEx = (sin + sin ) = − 4πε 0 a 2θ 0 2 2 2πε 0 a 2θ 0 方向 2
均匀带电细棒垂面上场强
2.电势的计算
Zhang Shihui
① 叠加原理,取微 U = 元,直接求电势 ② 先利用高斯定理 求场强,再求电势
∑ 4πε r
0
qi
i
,U =∫
b a
dq 4πε 0 r
作业册 第13章电势 第1题 第8题 第2题
V
∫
S
E ⋅ dS =
Q
ε0
, U a = ∫ E ⋅ dl
ΔS
O
ΔS
x
ρd = 2ε 0
−x
截面放大后
[嵌入式系统设计(基于STM32F4)][徐灵飞][习题解答] (13)
![[嵌入式系统设计(基于STM32F4)][徐灵飞][习题解答] (13)](https://img.taocdn.com/s3/m/0755cfde4a7302768f993970.png)
《嵌入式系统设计(基于STM32F429)》第13章课后题参考答案1.常用的DAC电路结构有哪些?答:权电阻网络DAC、R–2R倒T形电阻网络DAC、电流型网络DAC2.分辨率为12位,参考电压为3.3V的DAC,想要输出1.2V的电压,请问输出这一电压对应的数字信号是多少?答:(1.2/3.3)*4095 = 14893.STM32F429微控制器的DAC有哪些触发方式(转换启动方式)?答:(1)、软件触发:通过写DAC的数据保持寄存器触发DAC转换(2)、硬件信号触发:通过定时器TRGO 事件或外部中断线9触发。
4.请问寄存器DHR和DOR之间有什么关系?答:DHR:数据保持寄存器。
可读写。
DOR:数据输出寄存器。
只读。
程序一般操作的是DHR寄存器。
5.DAC单通道的数据格式有哪些?答:(1)对于DAC单通道x,有三种可能的方式。
8位右对齐:软件必须将数据加载到DAC_DHR8R x[7:0]位(存储到DHR x[11:4]位)。
12位左对齐:软件必须将数据加载到DAC_DHR12L x[15:4]位(存储到DHR x[11:0]位)。
12位右对齐:软件必须将数据加载到DAC_DHR12R x[11:0]位(存储到DHR x[11:0]位)。
(2)对于DAC双通道,有以下可能的方式。
8位右对齐:将DAC通道1的数据加载到DAC_DHR8RD[7:0]位(存储到DHR1[11:4]位),将DAC通道2的数据加载到DAC_DHR8RD[15:8]位(存储到DHR2[11:4]位)。
12位左对齐:将DAC通道1的数据加载到DAC_DHR12RD[15:4]位(存储到DHR1[11:0]位),将DAC通道2的数据加载到DAC_DHR12RD[31:20]位(存储到DHR2[11:0]位)。
12位右对齐:将DAC通道1的数据加载到DAC_DHR12RD[11:0]位(存储到DHR1[11:0]位),将DAC通道2的数据加载到DAC_DHR12RD[27:16]位(存储到DHR2[11:0]位)。
工程光学-郁道银-第13章光的衍射课后习题答案
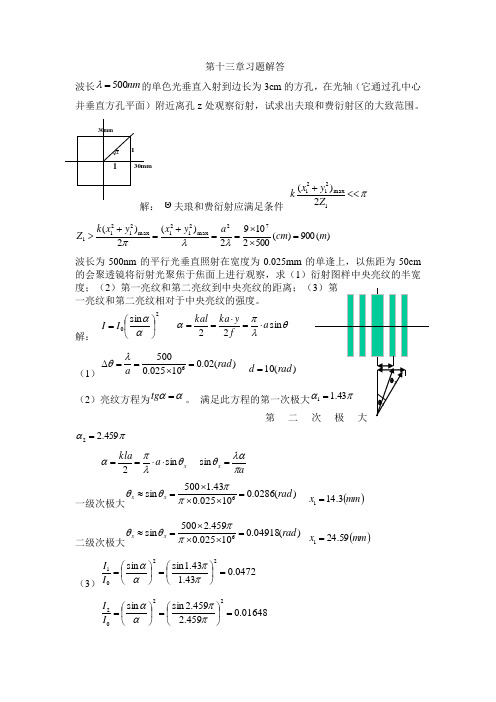
1θ2θ2mm3011mm 30第十三章习题解答波长nm 500=λ的单色光垂直入射到边长为3cm 的方孔,在光轴(它通过孔中心并垂直方孔平面)附近离孔z 处观察衍射,试求出夫琅和费衍射区的大致范围。
解: 夫琅和费衍射应满足条件 π<<+1max 21212)(Z y x k)(900)(50021092)(2)(72max 2121max 21211m cm a y x y x k Z =⨯⨯==+=+>λλπ波长为500nm 的平行光垂直照射在宽度为0.025mm 的单逢上,以焦距为50cm的会聚透镜将衍射光聚焦于焦面上进行观察,求(1)衍射图样中央亮纹的半宽度;(2)第一亮纹和第二亮纹到中央亮纹的距离;(3)第一亮纹和第二亮纹相对于中央亮纹的强度。
解: 20sin ⎪⎭⎫⎝⎛=ααI I θλπαs i n 22a f y ka kal ⋅=⋅==(1))(02.010025.05006rad a=⨯==∆λθ )(10rad d =(2)亮纹方程为αα=tg 。
满足此方程的第一次极大πα43.11= 第二次极大πα459.22=x a k l a θλπαs i n 2⋅⋅==a x πλαθ=sin 一级次极大)(0286.010025.043.1500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 3.141=二级次极大)(04918.010025.0459.2500sin 6rad x x =⨯⨯⨯=≈ππθθ ()mm x 59.241=(3)0472.043.143.1sin sin 2201=⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I01648.0459.2459.2s i n s i n 2202=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=ππααI I10.若望远镜能分辨角距离为rad 7103-⨯的两颗星,它的物镜的最小直径是多少?同时为了充分利用望远镜的分辨率,望远镜应有多大的放大率?解:D λθ22.10= )(24.21031055022.179m D =⨯⨯⨯=--⨯-=⨯⨯⨯⨯⨯=''=Γ969310180606060067πϕ11. 若要使照相机感光胶片能分辨m μ2线距,(1)感光胶片的分辨率至少是没毫米多少线;(2)照相机镜头的相对孔径f D至少是多大?(设光波波长550nm ) 解:)(50010213mm N 线=⨯=-3355.01490=≈'NfD12. 一台显微镜的数值孔径为0。
汽车 离合器复习题

148第13章离合器13。
1 习题13.1。
1 选择题1。
汽车离合器安装于( )。
A。
发动机与变速器之间 B.变速器与后驱动轴之间C。
皮带轮与变速器之间 D。
分动器与变速器之间*2。
汽车离合器的主要作用有()。
A。
保证汽车怠速平稳 B。
使换档时工作平顺C。
防止传动系过载 D。
增加变速比3.下列不属于汽车离合器部分的是()。
A。
分离轴承 B。
曲轴C.皮带轮D.从动盘*4.下列哪些方法能够提高汽车离合器的转矩容量().A。
提高摩擦因数 B。
增加飞轮的质量C.减小离合器摩擦面单位压力D.增加摩擦面数5。
在正常情况下,发动机工作,汽车离合器踏板处于自由状态时().A。
发动机的动力不传给变速器 B.发动机的动力传给变速器C。
离合器分离杠杆受力 D.离合器的主动盘与被动盘分离*6.下列说法正确的是( ).A.汽车离合器操作要领要求是分离时要迅速、彻底,结合时要平顺、柔和B。
汽车离合器有摩擦式、液力耦合式和带式等几种C.离合器从动盘有带扭转减振器和不带扭转减振器两种结构形式D.离合器的压盘压力越大越好*7。
下列说法正确的是()A.从动盘体与摩擦片之间加铆波浪形弹性钢片的目的是为了提高接合的柔顺性B.摩擦片要求具有较小的摩擦因数、良好的耐磨性、耐热性和适当的弹性C.离合器从动盘与发动机曲轴相连接D膜片弹簧离合器中的膜片弹簧起到压紧弹簧和分离杠杆的双重作用**8.下列说法正确的是( )。
A。
离合器机械式操纵机构有杆式传动和绳索式传动两种形式B。
压式离合器操纵机构在大修加油后不用进行排空就可工作C.离合踏板没有自由行程148149D.带扭转减振器的离合器可避免传动系统的共振9。
请指出图13—1中汽车离合器的标号()A。
4 B. 3C. 2D. 1图13-110.学生a说:汽车在紧急制动时,要马上踩住离合器,防止传动系过载而使发动机的机件损坏。
学生b说:汽车在紧急制动时不用踩住离合器,离合器有传动系过载保护功能。
他们说法正确的是( )。
最优化设计 课后习题答案

最优化方法-习题解答张彦斌计算机学院2014年10月20日Contents1第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、412第二章线搜索算法-P27习题2、4、643第三章最速下降法和牛顿法P41习题1,2,374第四章共轭梯度法P51习题1,3,6(1)105第五章拟牛顿法P73-2126第六章信赖域方法P86-8147第七章非线性最小二乘问题P98-1,2,6188第八章最优性条件P112-1,2,5,6239第九章罚函数法P132,1-(1)、2-(1)、3-(3),62610第十一章二次规划习题11P178-1(1),5291第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、4 1.验证下列各集合是凸集:(1)S={(x1,x2)|2x1+x2≥1,x1−2x2≥1};需要验证:根据凸集的定义,对任意的x(x1,x2),y(y1,y2)∈S及任意的实数λ∈[0,1],都有λx+(1−λ)y∈S.即,(λx1+(1−λ)y1,λx2+(1−λ)y2)∈S证:由x(x1,x2),y(y1,y2)∈S得到,{2x1+x2≥1,x1−2x2≥12y1+y2≥1,y1−2y2≥1(1)1把(1)中的两个式子对应的左右两部分分别乘以λ和1−λ,然后再相加,即得λ(2x1+x2)+(1−λ)(2y1+y2)≥1,λ(x1−2x2)+(1−λ)(y1−2y2)≥1(2)合并同类项,2(λx1+(1−λ)y1)+(λx2+(1−λ)y2)≥1,(λx1+(1−λ)y1)−2(λx2+(1−λ)y2)≥1(3)证毕.2.判断下列函数为凸(凹)函数或严格凸(凹)函数:(3)f(x)=x21−2x1x2+x22+2x1+3x2首先二阶导数连续可微,根据定理1.5,f在凸集上是(I)凸函数的充分必要条件是∇2f(x)对一切x为半正定;(II)严格凸函数的充分条件是∇2f(x)对一切x为正定。
王镜岩_徐长法_朱圣庚_主编,生物化学_第三版_课后习题解答全__上册1-13章,下册

生物化学王镜岩(第三版)课后习题解答全 (上册1-13章,下册19-40章)第一章糖类糖类是四大类生物分子之一,广泛存在于生物界,特别是植物界。
糖类在生物体内不仅作为结构成分和主要能源,复合糖中的糖链作为细胞识别的信息分子参与许多生命过程,并因此出现一门新的学科,糖生物学。
多数糖类具有(CH2O)n 的实验式,其化学本质是多羟醛、多羟酮及其衍生物。
糖类按其聚合度分为单糖,1个单体;寡糖,含2-20 个单体;多糖,含20 个以上单体。
同多糖是指仅含一种单糖或单糖衍生物的多糖,杂多糖指含一种以上单糖或加单糖衍生物的多糖。
糖类与蛋白质或脂质共价结合形成的结合物称复合糖或糖复合物。
单糖,除二羟丙酮外,都含有不对称碳原子(C*)或称手性碳原子,含C*的单糖都是不对称分子,当然也是手性分子,因而都具有旋光性,一个C*有两种构型D-和L-型或R-和S-型。
因此含n个C*的单糖有2n个旋光异构体,组成2n-1对不同的对映体。
任一旋光异构体只有一个对映体,其他旋光异构体是它的非对映体,仅有一个C*的构型不同的两个旋光异构体称为差向异构体。
单糖的构型是指离羧基碳最远的那个C*的构型,如果与D-甘油醛构型相同,则属D系糖,反之属L系糖,大多数天然糖是D系糖Fischer E论证了己醛糖旋光异构体的立体化学,并提出了在纸面上表示单糖链状立体结构的Fischer 投影式。
许多单糖在水溶液中有变旋现象,这是因为开涟的单糖分子内醇基与醛基或酮基发生可逆亲核加成形成环状半缩醛或半缩酮的缘故。
这种反应经常发生在C5羟基和C1醛基之间,而形成六元环吡喃糖(如吡喃葡糖)或C5经基和C2酮基之间形成五元环呋喃糖(如呋喃果糖)。
成环时由于羰基碳成为新的不对称中心,出现两个异头差向异构体,称a和B异头物,它们通过开链形式发生互变并处于平衡中。
在标准定位的Hsworth式中D-单糖异头碳的羟基在氧环面下方的为a异头物,上方的为B异头物,实际上不像Haworth式所示的那样氧环面上的所有原子都处在同一个平面,吡喃糖环一般采取椅式构象,呋喃糖环采取信封式构象。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B X1
X1 C
P
L
CD杆: N1 X 1 P AD杆: N 2 X 1 P
AB杆: N3 X1
BC杆: N 4 X 1 CA杆: N5 2( P X1 ) BD杆: N6 2 X1
A
L
D
解法一:利用卡氏定理。 先求约束反力:YA P(), X D P(), YD P()
B
PLh2 () 2 EI L M ( x ) M ( x ) h M ( x ) M ( x ) 1 1 2 2 A dx1 dx2 0 0 EI m f EI m f
令mf=0
h 1 L { ( Px1 )( 1)dx1 ( PL )( 1)dx2 } 0 F=0 EI 0
P2 R3 2 2 P 2 R 3 sin d 2 EI 0 8EI
南昌航空大学科技学院
1
13.4 z y
80N.m
1000N
解:计算简图为
360N
作内力图 x
80N.m
80N.m
M2 T2 U dx dx l 2 EI l 2GI P
2
(T) (My)
36N.m
(2)求A处转角,受力图如图所示
x , M( x AB段: M ( 1) Px 1 1) 1
x1 x3 D RD=P x2 C
x BC段: M ( x 2) Ph, M ( 2) 1
P A
B
x2 L
x , M( CD段: M ( x 3 ) Px 3 3) 0
南昌航空大学科技学院
15
例题、 如图所示,桁架各杆材料相同,横截面积相等,试求各 杆的内力。
B C
P
L
B X1
X1 C
P
L
A
L
D
A
L
D
解:一次内力静不定问题。 以BD杆为多余约束,假想地把它截开,并代以多余约束 反力,得到相当系统。 问题转化为:在切口两侧相对位移Δ1 =0的条件下,计算X1
南昌航空大学科技学院
-P L
1
A L
D
A
D
1 L
解法二:利用莫尔积分。 基本静定系在P作用下,各杆的轴力如图所示。 基本静定系在单位力作用下,各杆的轴力如图所示。
变形协调方程: 1 11 X 1 1P 0
南昌航空大学科技学院
19
物理方程:1P
Ni Ni 2(1 2 ) PL Li EA EA i 1
PL ( L 2h ) 2 EI
( )
9
南昌航空大学科技学院
13.14(b) 试求截面A的水平位移和转角。
B x2 C
(1)求水平位移,受力图如图所示
, M( x AB段: M (x 1) - Px 1 1) -x 1
BC段: M (x x 2) - Ph, M ( 2) -h 由对称性,得到:
0.2
2 2 My Mz
0
0.2
2 EI
T2 dx 0.2 2GI P
0.4
2
0
(180x) 2 (500x) 2 2 EI
802 dx 0.2 2GI P
0.4
28.537 31.83 64.4( N .mm)
(Mz)
100N.m 南昌航空大学科技学院
2
13.8(a) 试求截面B的转角和挠度。 解:虚加力偶 mf mf M ( x) Px m f x M ( x ) M ( x ) x, 1 P m f
2P B P
C
P
L
2P
B
P
C
Q
F
P-Q-F D
-2P
2(P F )
0
A
L
D
P-F A 3P-F
P-Q-F
解:C处虚加F和Q,求出约束反力。 使用节点法,求出各杆的轴力,并标出在图上。
南昌航空大学科技学院
12
应用卡氏定理,求出C点的位移。 5 N N xC i i Li (F=Q=0) i 1 EA F
M ( xi ) M ( xi ) dxi l EI F i 1 i 令mf=0 1 h { ( Pb )( x2 )dx 2 } F=0,Q=0 EI 0 Pbh2 () 2 EI xA
3
x3
h
x2
南昌航空大学科技学院
4
Q FA
a
b
Pm x1 C
M ( x1 ) m f Px1
再求出各杆的轴力。 变形协调方程: 1 0 6 L N N 物理方程: 1 i i Li 4(1 2 ) X 1 2(1 2 ) P EA i 1 EA X 1
南昌航空大学科技学院
17
由变形协调方程和物理方程得到补充方程:
4(1 2 ) X1 2(1 2 ) P 0 P X1 解得: 2 因此,各杆的内力为: CD杆: N1 X 1 P P / 2 AD杆: N 2 X 1 P P / 2
5
13.9(b) 刚架中各杆的EI皆相等,试求截面A、B的位移。 解:A处仅有铅直方向的位移,B处仅有水平方向位移。 (1)计算A处铅直位移,虚加集中力F。
q F
x2
A
h
x1 B ql+F 2 ql+F 2
可利用对称性简化计算。 ql F q 2 M ( x1 ) 0, M ( x2 ) x2 x2 2 2 2 M ( xi ) M ( xi ) y A 2 dxi li EI F i 1 令F=0 2 l / 2 ql q 2 x2 ( x2 x2 )( )dx 2 0 EI 2 2 2
令P=0
M ( x1 ) Px1,
2 EI
l /2
0
ql q 2 ( x2 x2 )( h )dx2 2 2
ql3h ( ) 12EI
南昌航空大学科技学院
7
13.9(c) 刚架中各杆的EI皆相等,试求截面A的水平位移、 铅直位移和转角。 解:虚加F与力偶 mf P m M ( x1 ) m f Px1 L AC段:
C
x2
h
x1 A F
f
BC段:
M ( x2 ) m f PL Fx2
yA
B 令mf=0
L
0
h M ( x ) M ( x ) M ( x1 ) M ( x1 ) 2 2 dx1 dx2 0 EI P EI P
h 1 L { ( Px1 )( x1 )dx1 ( PL )( L)dx 2 } 0 F=0 EI 0
PL3 ( L 3h)() 3EI
南昌航空大学科技学院
8
C
L
P
x2
h
x1
A
mf
F
h M ( x ) M ( x ) M ( x1 ) M ( x1 ) 2 2 xA dx1 dx2 0 0 EI F EI F L h 令mf=0 1 { ( Px1 )( 0)dx1 ( PL )( x2 )dx2 } 0 F=0 EI 0 L
5ql4 () 384EI
南昌航空大学科技学院
6
q x2 A
(2)计算B处水平位移,在B处虚加水平力P。 可利用对称性简化计算。
h x1
P ql 2 B ql 2 P
ql q 2 M ( x2 ) Ph x2 x2 2 2 2 M ( xi ) M ( xi ) xB 2 dxi l EI P i 1 i
f
x3
h
M ( x2 ) m f Pb Fx2 Qa
M ( x3 ) Qx3
yA
i 1 3 li
x2
M ( xi ) M ( xi ) dxi EI Q
1 F=0,Q=0 EI
令mf=0
h
0
Pabh ( Pb ) adx 2 ( ) 刚架中各杆的EI皆相等,试求截面A的水平位移、 铅直位移和截面C的转角。 解:虚加F、Q与力偶 mf Q FA
M ( x1 ) m f Px1
M ( x3 ) Qx3
a
b
Pm x1 C
f
M ( x2 ) m f Pb Fx2 Qa
6 6
Ni Ni 4(1 2 ) PL 11 Li EA EA i 1
解得:
P X1 2
南昌航空大学科技学院
20
13.17 如图所示,桁架各杆材料相同,横截面积相等,试求节 点B与D间的相对位移。 2
M(x1 ) M(x1 ) M(x2 ) M(x2 ) A dx 1 dx 2 EI1 EI2 0 0
Ph h L ( ) ( 2E I1 I 2
h
L
x1 1 A RA=1/L
x3 D RD=1/L
)
南昌航空大学科技学院
11
13.16 如图所示,桁架各杆材料相同,横截面积相等,试求节 点C处的水平位移和垂直位移。
令mf=0
F=0,Q=0
M ( xi ) M ( xi ) C dxi l EI m f i 1 i h 1 b Pbh { ( Px1 )( 1)dx1 ( Pb )( 1)dx2 } (b 2h )( ) 0 EI 0 2 EI
3
南昌航空大学科技学院
P
2P
B
P
C
Q F
P-Q-F
D
