模糊数学学习心得
模糊数学的读后心得

模糊數學的讀後心得
我們這一組看的是有關於〝步兵分隊城市作戰效能分析與與模糊總合評價〞,研究內容是在評估步兵分隊城市作戰效能的諸因素評估指標體系,運用層次分析法確定各效能指標權重系數。
採用模糊綜合評價方法將子效能加權聚合成裝備體系效能,其要素包括測評因素集、評判集及因素集與評判集間的模糊關系矩陣,由此實現步兵分隊城市作戰效能的定量化評估。
最後以城市作戰步兵分隊 3 種裝備編配方案為例加以驗証。
他也應用多層次模糊綜合評判法的步兵分隊作戰效能評估法,是分隊武器裝備体系研究中應用模糊數學的嘗試,是在子效能無法用效用函數等方法進行聚集時的可行辦法。
該方法不僅用于步兵分隊單個編配方案作戰效能的評估,且可對多個編配方案作戰效能進行比較。
藉由這一個研究我們可以清楚看到,並且去分析那一種戰力對於作戰才能達到最有高效能的戰鬥,也可以分析那一項最適合在哪裡作戰,雖然對於些許的運算不太了解,但是可以清楚看到,他運算到後來,效能最高的做戰方式,也很清楚了解如何運用不一樣的兵種及方式去作戰,這對於作戰有很大的幫助。
而也看到很多關於模糊數學運用在其他方面,可以知道,模糊數學可以用的非常的廣泛。
組員: 493310624 鄭孟津493310363 張根源492310093 李永德493310052 胡凱文493310179 林冠仲492310225 曹榮昇。
学习《离散数学》心得体会模板(三篇)

学习《离散数学》心得体会模板学习《离散数学》的过程中,我深深感受到了它的重要性和广泛应用的意义。
离散数学作为一门重要的数学基础课程,不仅能够培养我们的逻辑思维能力,还可以为我们理解和解决实际问题提供很多方法和工具。
在学习过程中,我积累了不少心得体会,今天我将分享给大家。
首先,我认为《离散数学》这门课程非常重要的一点就是培养了我的逻辑思维能力。
在学习过程中,我们需要学习和掌握数理逻辑、集合论、函数与关系、图论等一系列的基本概念和方法。
这些内容都是以形式化的推理和证明为基础的,要求我们对问题进行严密的思考和分析。
通过解题和习题训练,我逐渐掌握了一些基本的证明技巧和思考方法,提高了我的逻辑思维和分析能力。
其次,学习《离散数学》让我深刻理解了数学与现实世界的联系。
离散数学的理论和方法广泛应用于计算机科学、信息科学、通信工程、物理学等领域。
学习离散数学的过程,不仅让我学到了一些基本的数学知识,还让我了解到这些知识在实际应用中的重要性和作用。
比如在计算机网络中,我们需要用到图论的知识来解决网络路由问题;在密码学中,我们需要用到数论的知识来解决加密算法的设计;在数据库中,我们需要用到集合论和关系代数的知识来进行数据查询和操作。
通过学习《离散数学》,我对数学与实际问题的联系有了更深的认识。
另外,学习《离散数学》还让我锻炼了一种系统性的学习方法。
离散数学的内容非常广泛而且抽象,需要我们建立起一个完整的知识体系。
在学习过程中,我发现只有把每个概念、定理等都串起来,形成一个完整的知识链条,才能更好地理解和掌握。
因此,我养成了先学习基本概念和定理,再进行习题训练和实战演练的学习方法。
这种方法让我更加系统地掌握了离散数学的核心内容,提高了我的学习效率。
除此之外,学习《离散数学》还对我培养了一种严谨的学术态度和方法。
离散数学是一门严谨而抽象的学科,要求我们在处理问题时要严肃认真,不能有丝毫马虎。
在解题和习题训练中,我不断反思自己的解题思路和方法,发现解题中的错误和不足之处,不断调整和改进,直至找到正确的答案。
2024年蒙氏数学学习心得体会(3篇)

2024年蒙氏数学学习心得体会蒙氏数学是一种在中国流行的数学教育方法,以培养学生的数学思维能力和逻辑推理能力为核心。
2024年我开始接触蒙氏数学,通过一年的学习,我深深感受到了它对我的影响,不仅在数学学习上有所提升,更在思维方式和学习态度上有了积极的变化。
以下,我将总结我在蒙氏数学学习中所得到的心得体会。
首先,蒙氏数学注重培养学生的思维能力。
在传统的数学教学中,我们往往只注重知识点的灌输和运算技巧的训练。
而在蒙氏数学中,通过一系列的思维训练和启发性的问题,激发了我们思考的欲望和能力。
蒙氏数学的教材和练习题目设置合理,给出的问题涉及到多个数学概念之间的联系和推理过程。
通过解决这些问题,我们不仅可以加深对知识点的理解,还可以培养我们的逻辑思维和问题解决能力。
在学习过程中,我逐渐养成了分析问题、思考解决方法、推理过程的习惯,这对我的数学学习和其他学科的学习都产生了积极的影响。
其次,蒙氏数学注重培养学生的自主学习能力。
在传统的数学课堂中,老师通常是主导者,学生被动接受知识。
而在蒙氏数学中,我们需要自己独立思考和解决问题。
蒙氏数学的教材和练习题目给出了提示和引导,但并不提供具体的解题方法,需要我们自己去探索和发现。
这样的学习方式让我们从被动的接受者变成主动的学习者,培养了我们的学习兴趣和学习动力。
通过自主学习,我们可以加深对数学知识的理解和掌握,并且更加自信和独立地解决问题。
在蒙氏数学学习中,我逐渐学会了自主思考和学习,这对我今后的学习和工作都有着深远的影响。
再次,蒙氏数学注重培养学生的实践能力。
在蒙氏数学中,我们不仅要通过纸上的计算和推理来解决问题,还要通过实际操作和观察来加深对数学概念的理解。
蒙氏数学的练习题和活动往往与实际生活相结合,引导我们去观察和体验数学的应用。
通过这种实践,我们可以更加直观地理解和掌握数学知识,同时也培养了我们的观察力和实践能力。
在蒙氏数学学习中,我经常进行实际操作和观察,例如使用积木拼装、运用量杯测量等,这让我对数学的学习更加有趣和有效。
模糊数学综合评价总结

模糊数学综合评价总结第一篇:模糊数学综合评价总结模糊综合评判1、概念及基本知识1965年,美国著名自动控制专家查德(L.A.Zadeh)教授提出了模糊(fuzzy)的概念,并发表了第一篇用数学方法研究模糊现象的论文“模糊集合”(fuzzy set)。
他提出用“模糊集合”作为表现模糊事物的数学模型。
并在“模糊集合”上逐步建立运算、变换规律,开展有关的理论研究,就有可能构造出研究现实世界中的大量模糊的数学基础,能够对看来相当复杂的模糊系统进行定量的描述和处理的数学方法。
而模糊综合评价是根据模糊数学的隶属度理论把定性评价转化为定量评价的一种综合评价方法。
它具有结果清晰,系统性强的特点,能较好地解决模糊的、难以量化的问题,适合各种非确定性问题的解决。
在决策中,对于方案、人才、成果的评价,人们的考虑往往是从多种因素出发的,而且这些考虑一般只能用模糊语言来描述。
例如,评价者从考虑问题的诸因素出发,参照有关的数据和情况,根据他们的判断对复杂问题分别作出“大、中、小”;“高、中、低”;“优、良、可、劣”;“好、较好、一般、较差、差”等程度的模糊评价。
然后通过模糊数学提供的方法进行运算,就能得出定量的综合评价结果。
2、模糊综合评价的基本原理首先确定被评价对象的因素(指标)集合评价(等级)集;再分别确定各个因素的权重及它们的隶属度向量,获得模糊评判矩阵;最后把模糊评判矩阵与因素的权向量进行模糊运算并进行归一化,得到模糊综合评价结果。
其特点在于评判逐对象进行,对被评价对象有唯一的评价值,不受被评价对象所处对象集合的影响。
综合评价的目的是要从对象集中选出优胜对象,所以还需要将所有对象的综合评价结果进行排序。
3、模糊综合评判方法步骤1、确定评价对象的因素论域2、确定评语等级论域3、进行单因素评价,建立模糊关系矩阵R4、确定评价因素的模糊权向量5、多因素模糊评价6、对模糊综合评价结果进行分析答案二:模糊综合评价的一般步骤如下:ϖ(1)确定评价对象的因素集ϖ(2)确定评语集;ϖ(3)作出单因素评价ϖ(4)综合评价1、确定评价对象的因素集U={u1,u2,L,um}1也就是说有m个评价指标,表明我们对被评价对象从哪些方面来进行评判描述。
模糊数学要点
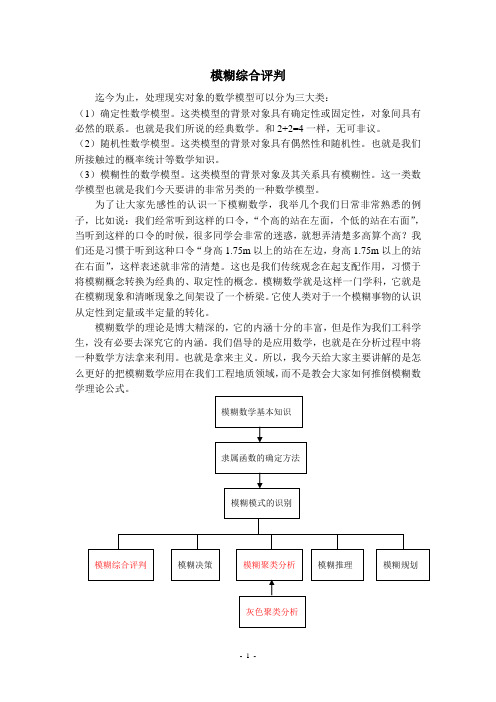
模糊综合评判迄今为止,处理现实对象的数学模型可以分为三大类:(1)确定性数学模型。
这类模型的背景对象具有确定性或固定性,对象间具有必然的联系。
也就是我们所说的经典数学。
和2+2=4一样,无可非议。
(2)随机性数学模型。
这类模型的背景对象具有偶然性和随机性。
也就是我们所接触过的概率统计等数学知识。
(3)模糊性的数学模型。
这类模型的背景对象及其关系具有模糊性。
这一类数学模型也就是我们今天要讲的非常另类的一种数学模型。
为了让大家先感性的认识一下模糊数学,我举几个我们日常非常熟悉的例子,比如说:我们经常听到这样的口令,“个高的站在左面,个低的站在右面”,当听到这样的口令的时候,很多同学会非常的迷惑,就想弄清楚多高算个高?我们还是习惯于听到这种口令“身高1.75m以上的站在左边,身高1.75m以上的站在右面”,这样表述就非常的清楚。
这也是我们传统观念在起支配作用,习惯于将模糊概念转换为经典的、取定性的概念。
模糊数学就是这样一门学科,它就是在模糊现象和清晰现象之间架设了一个桥梁。
它使人类对于一个模糊事物的认识从定性到定量或半定量的转化。
模糊数学的理论是博大精深的,它的内涵十分的丰富,但是作为我们工科学生,没有必要去深究它的内涵。
我们倡导的是应用数学,也就是在分析过程中将一种数学方法拿来利用。
也就是拿来主义。
所以,我今天给大家主要讲解的是怎么更好的把模糊数学应用在我们工程地质领域,而不是教会大家如何推倒模糊数学理论公式。
我们在学习模糊数学之前,我先给大家说一下模糊数学在我们工程地质领域的应用方向。
到目前为止,模糊数学可以用来分析:湖水的安全评价,地表水(河水、湖水等)的水质评价、边坡稳定性的模糊综合评判、膨胀土涨缩等级的模糊综合评判、岩体质量的模糊综合评判、海水入侵地下水水质评价、岩溶塌陷稳定性评价等。
一、理论基础模糊综合评判可以分为:一级综合评判和多级综合评判。
我们用的最多的还是一级综合评判,无论是我们将来发表小论文还是撰写毕业论文,主要用的还是一级综合评判,对于多极综合评判如果大家有兴趣,可以看一下相关的书籍,目前,我们只要知道有这么一个概念就可以。
浅谈模糊数学

浅谈模糊数学在日常生活中,我们遇到的概念不外乎两类。
一类是清晰的概念,对象是否属于这个概念是明确的。
例如;人、自然数、正方形等等。
要么是人,要么不是人、要么是自然数、要么不是自然数、要么是正方形,要么不是正方形。
另一类概念对象从属的界限是模糊的,随判断人的思维而定。
例如:美不美?早不早?“便宜不便宜?等等。
西施是我国古代公认的美女,有道是“情人眼里出西施”,这就是说,在一些人看来未必那么美的人,在另一些人眼里,却美得可以与西施相比拟。
可见,“美”与“不美”是不存在一个精确的界限的。
再说“早”与“不早”,清晨五点,对于为都市“梳妆打扮”的清洁工人来说可能算是迟了,但对大多数小学生说,却是很早很早的。
至于便宜不便宜,那更是随人的感觉而异了!在客观世界中,诸如上述的模糊概念要比清晰概念多得多。
对于这类模糊现象,过去已有的数学模型难以适用,需要形成新的理论和方法,即在数学和模糊现象之间架起一座桥梁。
它,就是我们要讲的“模糊数学”。
加速这座桥梁架设的是计算机科学的迅速发展。
大家知道,人的大脑具有非凡的判别和处理模糊事物的能力。
就拿一个孩子识别自己的母亲为例,即使这位母亲更换了新衣,改变了发式,她的孩子依然会从高矮、胖瘦、音容、姿态等迅速地作出准确判断。
如果这件事让计算机来干,那就非得把这位母亲的身高、体重、行走速度、外形曲线等等,全都计算到小数点后的十几位,然后才能着手判断。
这样的“精确”实在是事与愿违,走到了事物的反面。
说不定就因为这位母亲脸上一时长了一个小疖,该部位的平均高度,比原来高了零点零几毫米,而使计算机作出“拒绝接受”的判断呢?难怪模糊数学的创始人,美国加利福尼亚大学教授、自控专家扎德(L.A.Za-deh)说:“所面对的系统越复杂,人们对它进行有意义的精确化能力就越低。
”他生动地举了一个停车问题的例子,他说:要把汽车停在拥挤停车场的已有两辆汽车之间的空地上,这对有经验的司机来说,并非什么难事。
模糊数学论文

模糊数学学校开设了模糊中数学,本着对数学的钟情和同学的介绍,我修了这门课程。
现在课已经结束了,但我对这门课有了特殊的感觉,让我对数学更加热爱了,不知是老师的原因,还是因为所设的课程,或者说是共同的原因吧。
在所学的知识中,我不仅只学了这门课程,就想许多人所说的,数学跟很多课程是有联系的,这次我深刻的体会到了,现在老师讲模糊集合的场景好像是昨天发生的,是老师讲的精彩,还是在知识对我以后的所学的专业有用了,想在我都不知是那个缘故,下面是我体会到模糊中的数学在我所学专业中的应用。
“民以食为天”,食品安全人民健康的根本保障。
当每次3.15来临,揭发很多关于食品的事件,如“三鹿事件”,“地沟油”等危害人们健康的事件的曝光,人们开始越来越关心食品安全,越来越重视食品的检测。
也是我专业所关心的事实之一。
传统的检测方法只是提取食品的各项指标,然后与标准指标进行比对,如果有超过一定数目的指标超标,则认为这类食品时不合格的。
诚然,因为传统方法的简单易操作,它曾经带给人们很多便利。
但是随着食品检测的不断发展以及人们对食品安全的重视程度的提高,传统方法的弊端不断的显现出来。
首先在传统方法中没有区分主次因素,对所有指标都一视同仁,这就直接导致了食品检测中的准确度降低。
其次,因为传统检测方法的最终结果只有合格与不合格两种等级,这也就引起了分类结果的不精确。
因为在合格里面也有质量好与质量不很好之分,把它们归于一类不但会对消费者的利益产生危害,也直接影响了生产者的积极性。
最后,因为食品检测的指标之间是相互影响的,传统的检测方法可能会多提取了指标。
模糊数学的诞生,得益于用机器去模拟人脑的科学——人工智能。
当用计算机去模拟人脑时,经典数学在很大程度上显得无能为力。
现代电子计算机对模糊性语言和信息的处理能力甚至不及一个婴儿。
例如,一个二、三岁的小孩能在一堆苹果中迅速、准确地挑出最大的那个,而不需作任何度量。
这一点要计算机做,却非常困难。
模糊数学学习心得

《模糊数学》学习心得姓名:李书纲学号:200805050303专业:信息与计算科学老师;黄晓昆地点:文鼎楼502《模糊数学》学习心得在大四的上学期,我们数学学院给我们开了黄晓昆老师的《模糊数学》这门课,这是继《近世代数基础》后黄老师给我们上的第二门比较抽象的课程。
“模糊数学”这个词一听上去就很抽象,翻开课本是感觉更“模糊”。
但在学习了半个学期后,对这门课程有了一定的了解,并学到了一部分知识,也积累了一点自己的学习心得体会。
先说说什么是“模糊数学”。
模糊数学是相对于精确数学而言的,在较长时间里,精确数学及随机数学在描述自然界多种事物的运动规律中,获得显著效果。
但在日常生活中,经常遇到许多模糊事物,没有分明的数量界限,要使用一些模糊的词句来形容、描述。
比如,比较年轻、高个、大胖子、好、漂亮、善、热、远……。
在人们的工作经验中,往往也有许多模糊的东西。
例如,要确定一炉钢水是否已经炼好,除了要知道钢水的温度、成分比例和冶炼时间等精确信息外,还需要参考钢水颜色、沸腾情况等模糊信息。
因此,为了研究这些与模糊概念相关的东西,“模糊数学”就产生了。
1965年,美国控制论专家、数学家查德发表了论文《模糊集合》,标志着模糊数学这门学科的诞生。
模糊数学的研究内容主要有:第一,研究模糊数学的理论,以及它和精确数学、随机数学的关系。
查德以精确数学集合论为基础,并考虑到对数学的集合概念进行修改和推广。
他提出用“模糊集合”作为表现模糊事物的数学模型。
并在“模糊集合”上逐步建立运算、变换规律,开展有关的理论研究,就有可能构造出研究现实世界中的大量模糊的数学基础,能够对看来相当复杂的模糊系统进行定量的描述和处理的数学方法。
在模糊集合中,给定范围内元素对它的隶属关系不一定只有“是”或“否”两种情况,而是用介于0和1之间的实数来表示隶属程度,还存在中间过渡状态。
比如“老人”是个模糊概念,70岁的肯定属于老人,它的从属程度是 1,40岁的人肯定不算老人,它的从属程度为 0,按照查德给出的公式,55岁属于“老”的程度为0.5,即“半老”,60岁属于“老”的程度0.8。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《模糊数学》学习心得
姓名:李书纲
学号:200805050303
专业:信息与计算科学
老师;黄晓昆
地点:文鼎楼502
《模糊数学》学习心得
在大四的上学期,我们数学学院给我们开了黄晓昆老师的《模糊数学》这门课,这是继《近世代数基础》后黄老师给我们上的第二门比较抽象的课程。
“模糊数学”这个词一听上去就很抽象,翻开课本是感觉更“模糊”。
但在学习了半个学期后,对这门课程有了一定的了解,并学到了一部分知识,也积累了一点自己的学习心得体会。
先说说什么是“模糊数学”。
模糊数学是相对于精确数学而言的,在较长时间里,精确数学及随机数学在描述自然界多种事物的运动规律中,获得显著效果。
但在日常生活中,经常遇到许多模糊事物,没有分明的数量界限,要使用一些模糊的词句来形容、描述。
比如,比较年轻、高个、大胖子、好、漂亮、善、热、远……。
在人们的工作经验中,往往也有许多模糊的东西。
例如,要确定一炉钢水是否已经炼好,除了要知道钢水的温度、成分比例和冶炼时间等精确信息外,还需要参考钢水颜色、沸腾情况等模糊信息。
因此,为了研究这些与模糊概念相关的东西,“模糊数学”就产生了。
1965年,美国控制论专家、数学家查德发表了论文《模糊集合》,标志着模糊数学这门学科的诞生。
模糊数学的研究内容主要有:第一,研究模糊数学的理论,以及它和精确数学、随机数学的关系。
查德以精确数学集合论为基础,并考虑到对数学的集合概念进行修改和推广。
他提出用“模糊集合”作为表现模糊事物的数学模型。
并在“模糊集合”上逐步建立运算、变换规律,开展有关的理论研究,就有可能构造出研究现实世界中的大量模糊的数学基础,能够对看来相当复
杂的模糊系统进行定量的描述和处理的数学方法。
在模糊集合中,给定范围内元素对它的隶属关系不一定只有“是”或“否”两种情况,而是用介于0和1之间的实数来表示隶属程度,还存在中间过渡状态。
比如“老人”是个模糊概念,70岁的肯定属于老人,它的从属程度是 1,40岁的人肯定不算老人,它的从属程度为 0,按照查德给出的公式,55岁属于“老”的程度为0.5,即“半老”,60岁属于“老”的程度0.8。
查德认为,指明各个元素的隶属集合,就等于指定了一个集合。
当隶属于0和1之间值时,就是模糊集合。
第二,研究模糊语言学和模糊逻辑。
人类自然语言具有模糊性,人们经常接受模糊语言与模糊信息,并能做出正确的识别和判断。
为了实现用自然语言跟计算机进行直接对话,就必须把人类的语言和思维过程提炼成数学模型,才能给计算机输入指令,建立和是的模糊数学模型,这是运用数学方法的关键。
查德采用模糊集合理论来建立模糊语言的数学模型,使人类语言数量化、形式化。
如果我们把合乎语法的标准句子的从属函数值定为1,那么,其他文法稍有错误,但尚能表达相仿的思想的句子,就可以用以0到1之间的连续数来表征它从属于“正确句子”的隶属程度。
这样,就把模糊语言进行定量描述,并定出一套运算、变换规则。
第三,研究模糊数学的应用。
模糊数学是以不确定性的事物为其研究对象的。
模糊集合的出现是数学适应描述复杂事物的需要。
查德的功绩在于用模糊集合的理论找到解决模糊性对象加以确切化,从而使研究确定性对象的数学与不确定性对象的数学沟通起来。
过去精确
数学随机数学描述感到不足之处就能得到弥补。
对于我们刚学习这门课程的来说,现在还没有完全入门,只学到了一点基础的东西。
对于其具体的研究方法,还有待我们继续深入的学习。
