第5章 树与二叉树习题参考答案
第五章-树-练习-答案
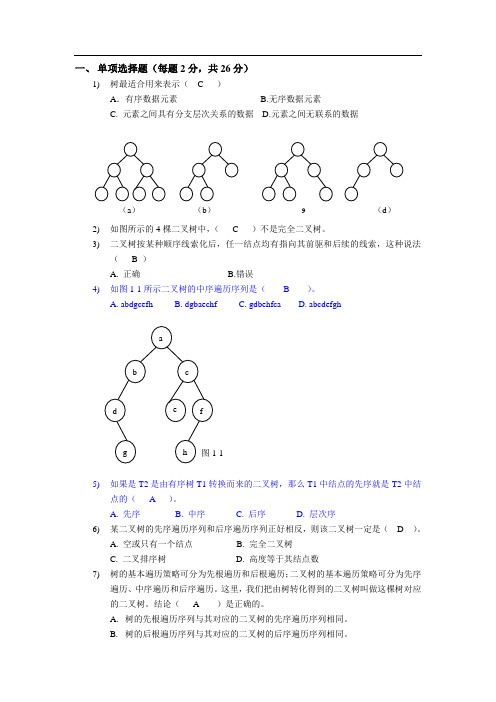
一、 单项选择题(每题2分,共26分)1) 树最适合用来表示( C )A .有序数据元素 B.无序数据元素C. 元素之间具有分支层次关系的数据D.元素之间无联系的数据2) 如图所示的4棵二叉树中,( C )不是完全二叉树。
3) 二叉树按某种顺序线索化后,任一结点均有指向其前驱和后续的线索,这种说法( B )A. 正确B.错误4) 如图1-1所示二叉树的中序遍历序列是( B )。
A. abdgcefhB. dgbaechfC. gdbehfcaD. abcdefgh5) 如果是T2是由有序树T1转换而来的二叉树,那么T1中结点的先序就是T2中结点的( A )。
A. 先序B. 中序C. 后序D. 层次序6) 某二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树一定是( D )。
A. 空或只有一个结点B. 完全二叉树C. 二叉排序树D. 高度等于其结点数7) 树的基本遍历策略可分为先根遍历和后根遍历;二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。
这里,我们把由树转化得到的二叉树叫做这棵树对应的二叉树。
结论( A )是正确的。
A. 树的先根遍历序列与其对应的二叉树的先序遍历序列相同。
B. 树的后根遍历序列与其对应的二叉树的后序遍历序列相同。
(a ) (b ) 9 (d )C. 树的先根遍历序列与其对应的二叉树的中序遍历序列相同。
D. 以上都不对8) 如图所示的T2是由森林T1转换而来的二叉树,那么森里T1有( C )个叶子结点。
A. 4B. 5C. 6D. 79) 深度为5的二叉树至多有( C )个结点。
A. 16B. 32C. 31D. 1010) 在一非空二叉树的中序遍历序列中,根结点的右边( A )。
A. 只有右子树上的所有结点B. 只有右子树的部分结点C. 只有左子树上的部分结点D. 只有左子树上的所有结点11) 设n ,m 为一棵二叉树上的两个结点,在中序遍历时,n 在m 前的条件是( C )。
树和二叉树习题及答案

一、填空题1. 不相交的树的聚集称之为森林。
2. 从概念上讲,树与二叉树是两种不同的数据结构,将树转化为二叉树的基本目的是_树可采用孩子-兄弟链表(二叉链表)做存储结构,目的是利用二叉树的已有算法解决树的有关问题。
3. 深度为k的完全二叉树至少有2 k-1个结点。
至多有2 k-1个结点,若按自上而下,从左到右次序给结点编号(从1开始),则编号最小的叶子结点的编号是2 k-2+1。
4. 在一棵二叉树中,度为零的结点的个数为n,度为2的结点的个数为n2,则有n= n2+1。
5. 一棵二叉树的第i(i≥1)层最多有2 i-1个结点;一棵有n(n>0)个结点的满二叉树共有(n+1)/2个叶子和(n-1) /2个非终端结点。
6.现有按中序遍历二叉树的结果为abc,问有5种不同形态的二叉树可以得到这一遍历结果。
7. 哈夫曼树是带权路径最小的二叉树。
8. 前缀编码是指任一个字符的编码都不是另一个字符编码的前缀的一种编码方法,是设计不等长编码的前提。
9. 以给定的数据集合{4,5,6,7,10,12,18}为结点权值构造的Huffman树的加权路径长度是 165 。
10. 树被定义为连通而不具有回路的(无向)图。
11. 若一棵根树的每个结点最多只有两个孩子,且孩子又有左、右之分,次序不能颠倒,则称此根树为二叉树。
12. 高度为k,且有个结点的二叉树称为二叉树。
2k-1 满13. 带权路径长度最小的二叉树称为最优二叉树,它又被称为树。
Huffman14. 在一棵根树中,树根是为零的结点,而为零的结点是结点。
入度出度树叶15. Huffman树中,结点的带权路径长度是指由到之间的路径长度与结点权值的乘积。
结点树根16. 满二叉树是指高度为k,且有个结点的二叉树。
二叉树的每一层i上,最多有个结点。
2k-12i-1二、单选题1. 具有10个叶结点的二叉树中有 (B) 个度为2的结点。
(A)8 (B)9 (C)10 (D)112.对二叉树的结点从1开始进行连续编号,要求每个结点的编号大于其左右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,则可采用_(3)次序的遍历实现编号。
数据结构第五章参考答案

习题51.填空题(1)已知二叉树中叶子数为50,仅有一个孩子的结点数为30,则总结点数为(___________)。
答案:129(2)3个结点可构成(___________)棵不同形态的二叉树。
答案:5(3)设树的度为5,其中度为1~5的结点数分别为6、5、4、3、2个,则该树共有(___________)个叶子。
答案:31(4)在结点个数为n(n>1)的各棵普通树中,高度最小的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
高度最大的树的高度是(___________),它有(___________)个叶子结点,(___________)个分支结点。
答案:2 n-1 1 n 1 n-1(5)深度为k的二叉树,至多有(___________)个结点。
答案:2k-1(6)(7)有n个结点并且其高度为n的二叉树的数目是(___________)。
答案:2n-1(8)设只包含根结点的二叉树的高度为0,则高度为k的二叉树的最大结点数为(___________),最小结点数为(___________)。
答案:2k+1-1 k+1(9)将一棵有100个结点的完全二叉树按层编号,则编号为49的结点为X,其双亲PARENT (X)的编号为()。
答案:24(10)已知一棵完全二叉树中共有768个结点,则该树中共有(___________)个叶子结点。
答案:384(11)(12)已知一棵完全二叉树的第8层有8个结点,则其叶子结点数是(___________)。
答案:68(13)深度为8(根的层次号为1)的满二叉树有(___________)个叶子结点。
答案:128(14)一棵二叉树的前序遍历是FCABED,中序遍历是ACBFED,则后序遍历是(___________)。
答案:ABCDEF(15)某二叉树结点的中序遍历序列为ABCDEFG,后序遍历序列为BDCAFGE,则该二叉树结点的前序遍历序列为(___________),该二叉树对应的树林包括(___________)棵树。
《数据结构及其应用》笔记含答案 第五章_树和二叉树

第5章树和二叉树一、填空题1、指向结点前驱和后继的指针称为线索。
二、判断题1、二叉树是树的特殊形式。
()2、完全二叉树中,若一个结点没有左孩子,则它必是叶子。
()3、对于有N个结点的二叉树,其高度为。
()4、满二叉树一定是完全二叉树,反之未必。
()5、完全二叉树可采用顺序存储结构实现存储,非完全二叉树则不能。
()6、若一个结点是某二叉树子树的中序遍历序列中的第一个结点,则它必是该子树的后序遍历序列中的第一个结点。
()7、不使用递归也可实现二叉树的先序、中序和后序遍历。
()8、先序遍历二叉树的序列中,任何结点的子树的所有结点不一定跟在该结点之后。
()9、赫夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
()110、在赫夫曼编码中,出现频率相同的字符编码长度也一定相同。
()三、单项选择题1、把一棵树转换为二叉树后,这棵二叉树的形态是(A)。
A.唯一的B.有多种C.有多种,但根结点都没有左孩子D.有多种,但根结点都没有右孩子解释:因为二叉树有左孩子、右孩子之分,故一棵树转换为二叉树后,这棵二叉树的形态是唯一的。
2、由3个结点可以构造出多少种不同的二叉树?(D)A.2 B.3 C.4 D.5解释:五种情况如下:3、一棵完全二叉树上有1001个结点,其中叶子结点的个数是(D)。
A.250 B. 500 C.254 D.501解释:设度为0结点(叶子结点)个数为A,度为1的结点个数为B,度为2的结点个数为C,有A=C+1,A+B+C=1001,可得2C+B=1000,由完全二叉树的性质可得B=0或1,又因为C为整数,所以B=0,C=500,A=501,即有501个叶子结点。
4、一个具有1025个结点的二叉树的高h为(C)。
A.11 B.10 C.11至1025之间 D.10至1024之间解释:若每层仅有一个结点,则树高h为1025;且其最小树高为⎣log21025⎦ + 1=11,即h在11至1025之间。
第5章树和二叉树习题答案

第5章树和⼆叉树习题答案第6章树和⼆叉树⼀.选择题(1)由3 个结点可以构造出多少种不同的⼆叉树?( D )A.2 B.3 C.4 D.5(2)⼀棵完全⼆叉树上有1001个结点,其中叶⼦结点的个数是(D )。
A.250 B. 500 C.254 D.501(3)⼀个具有1025个结点的⼆叉树的⾼h为( C )。
A.11 B.10 C.11⾄1025之间 D.10⾄1024之间(4)深度为h的满m叉树的第k层有( A )个结点。
(1=A.mk-1 B.mk-1 C.mh-1 D.mh-1(5)对⼆叉树的结点从1开始进⾏连续编号,要求每个结点的编号⼤于其左、右孩⼦的编号,同⼀结点的左右孩⼦中,其左孩⼦的编号⼩于其右孩⼦的编号,可采⽤( C )遍历实现编号。
A.先序 B. 中序 C. 后序 D. 从根开始按层次遍历(6)若⼆叉树采⽤⼆叉链表存储结构,要交换其所有分⽀结点左、右⼦树的位置,利⽤( D )遍历⽅法最合适。
A.前序 B.中序 C.后序 D.按层次(7)⼀棵⾮空的⼆叉树的先序遍历序列与后序遍历序列正好相反,则该⼆叉树⼀定满⾜( B )。
A.所有的结点均⽆左孩⼦ B.所有的结点均⽆右孩⼦C.只有⼀个叶⼦结点 D.是任意⼀棵⼆叉树(8)某⼆叉树的前序序列和后序序列正好相反,则该⼆叉树⼀定是( C )的⼆叉树。
A.空或只有⼀个结点 B.任⼀结点⽆左⼦树C.⾼度等于其结点数 D.任⼀结点⽆右⼦树(9)若X是⼆叉中序线索树中⼀个有左孩⼦的结点,且X不为根,则X的前驱为( C )。
A.X的双亲 B.X的右⼦树中最左的结点C.X的左⼦树中最右结点 D.X的左⼦树中最右叶结点(10)引⼊⼆叉线索树的⽬的是( A )。
A.加快查找结点的前驱或后继的速度 B.为了能在⼆叉树中⽅便的进⾏插⼊与删除C.为了能⽅便的找到双亲 D.使⼆叉树的遍历结果唯⼀⼆.简答题(1)试找出满⾜下列条件的⼆叉树①先序序列与后序序列相同②中序序列与后序序列相同③先序序列与中序序列相同④中序序列与层次遍历序列相同答:(1)若先序序列与后序序列相同,则或为空树,或为只有根结点的⼆叉树(2)若中序序列与后序序列相同,则或为空树,或为任⼀结点⾄多只有左⼦树的⼆叉树.(3)若先序序列与中序序列相同,则或为空树,或为任⼀结点⾄多只有右⼦树的⼆叉树.(4)若中序序列与层次遍历序列相同,则或为空树,或为任⼀结点⾄多只有右⼦树的⼆叉树2. 试写出如图所⽰的⼆叉树分别按先序、中序、后序遍历时得到的结点序列。
数据结构第5章作业参考答案

第5章树和二叉树一、单项选择题1.以下说法错误的是(B )。
A. 存在这样的二叉树,对其采用任何次序的遍历其结点访问序列均相同B. 二叉树是树的特殊情形C. 满二叉树中所有叶结点都在同一层上D. 在二叉树只有一棵子树的情况下,也要指出是左子树还是右子树2.树最适合用来表示( C)。
A.有序数据元素B.无序数据元素C.元素之间具有分支层次关系的数据D.元素之间无联系的数据3.下列叙述正确的是(C )。
A. 二叉树是度为2的有序树B. 完全二叉树一定存在度为1的结点C. 深度为k的二叉树中结点总数≤2k-1D. 对于有n个结点的二叉树,其高度为⎣log2n⎦+14.按照二叉树的定义,具有三个节点的二叉树有( C )种。
A.3B.4C.5D.65.下列叙述中正确的是(C )。
A. 二叉树是度为2的有序树B. 二叉树中的结点只有一个孩子时无左右之分C. 二叉树中每个结点最多只有两棵子树,并且有左右之分D. 二叉树若存在两个结点,则必有一个为根,另一个为左孩子6.设某二叉树中度数为0的结点数为N0,度数为1的结点数为N l,度数为2的结点数为N2,则下列等式成立的是( C )。
A.N0=N1+1 B.N=Nl+N2C.N=N2+1 D.N=2N1+17.设按照从上到下、从左到右的顺序从1开始对完全二叉树进行顺序编号,则编号为i结点的左孩子结点的编号为( B )。
A. 2i+1B.2iC.i/2D.2i-18.有100个结点的完全二叉树由根开始从上到下从左到右对结点进行编号,根结点的编号为1,编号为46的结点的右孩子的编号为( C )A.50 B.92 C.93 D.869.若一棵有n个结点的树,则该树中的度之和为(C )。
A. n+1B. nC. n-1D. 不确定10.已知完全二叉树有90个结点,则整个二叉树有( B )个度为1的结点。
A 0B 1C 2D 不确定11.一棵完全二叉树上有1001个结点,其中叶子结点的个数是(C )。
树和二叉树习题及答案
一、填空题1. 不相交的树的聚集称之为森林。
2. 从概念上讲,树与二叉树是两种不同的数据结构,将树转化为二叉树的基本目的是_树可采用孩子-兄弟链表(二叉链表)做存储结构,目的是利用二叉树的已有算法解决树的有关问题。
3. 深度为k的完全二叉树至少有2 k-1个结点。
至多有2 k-1个结点,若按自上而下,从左到右次序给结点编号(从1开始),则编号最小的叶子结点的编号是2 k-2+1。
4. 在一棵二叉树中,度为零的结点的个数为n,度为2的结点的个数为n2,则有n= n2+1。
5. 一棵二叉树的第i(i≥1)层最多有2 i-1个结点;一棵有n(n>0)个结点的满二叉树共有(n+1)/2个叶子和(n-1) /2个非终端结点。
6.现有按中序遍历二叉树的结果为abc,问有5种不同形态的二叉树可以得到这一遍历结果。
7. 哈夫曼树是带权路径最小的二叉树。
8. 前缀编码是指任一个字符的编码都不是另一个字符编码的前缀的一种编码方法,是设计不等长编码的前提。
9. 以给定的数据集合{4,5,6,7,10,12,18}为结点权值构造的Huffman树的加权路径长度是 165 。
10. 树被定义为连通而不具有回路的(无向)图。
11. 若一棵根树的每个结点最多只有两个孩子,且孩子又有左、右之分,次序不能颠倒,则称此根树为二叉树。
12. 高度为k,且有个结点的二叉树称为二叉树。
2k-1 满13. 带权路径长度最小的二叉树称为最优二叉树,它又被称为树。
Huffman14. 在一棵根树中,树根是为零的结点,而为零的结点是结点。
入度出度树叶15. Huffman树中,结点的带权路径长度是指由到之间的路径长度与结点权值的乘积。
结点树根16. 满二叉树是指高度为k,且有个结点的二叉树。
二叉树的每一层i上,最多有个结点。
2k-1 2i-1二、单选题1. 具有10个叶结点的二叉树中有 (B) 个度为2的结点。
(A)8 (B)9 (C)10 (D)112.对二叉树的结点从1开始进行连续编号,要求每个结点的编号大于其左右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,则可采用_(3)次序的遍历实现编号。
第5章+树与二叉树习题解析(答)
习题五树与二叉树一、选择题1、一棵非空的二叉树的先序遍历序列与后序遍历序列正好相反,则该二叉树一定满足。
A、所有的结点均无左孩子B、所有的结点均无右孩子C、只有一个叶子结点D、是任意一棵二叉树2、一棵完全二叉树上有1001个结点,其中叶子结点的个数是。
A、250B、500C、254D、505E、以上答案都不对3、以下说法正确的是。
A、若一个树叶是某二叉树前序遍历序列中的最后一个结点,则它必是该子树后序遍历序列中的最后一个结点B、若一个树叶是某二叉树前序遍历序列中的最后一个结点,则它必是该子树中序遍历序列中的最后一个结点C、在二叉树中,具有两个子女的父结点,在中序遍历序列中,它的后继结点最多只能有一个子女结点D、在二叉树中,具有一个子女的父结点,在中序遍历序列中,它没有后继子女结点4、以下说法错误的是。
A、哈夫曼树是带权路径长度最短得数,路径上权值较大的结点离根较近B、若一个二叉树的树叶是某子树中序遍历序列中的第一个结点,则它必是该子树后序遍历序列中的第一个结点C、已知二叉树的前序遍历和后序遍历并不能唯一地确定这棵树,因为不知道树的根结点是哪一个D、在前序遍历二叉树的序列中,任何结点其子树的所有结点都是直接跟在该结点之后的5、一棵有124个叶结点的完全二叉树,最多有个结点。
A、247B、248C、249D、250E、2516、任何一棵二叉树的叶结点在前(先)序、中序和后序遍历序列中的相对次序。
A、不发生变化B、发生变化C、不能确定7、设a、b为一棵二叉树上的两个结点。
在中序遍历时,a在b前面的条件是。
A、a在b的右方B、a在b的左方C、a是b的祖先D、a 是b的子孙8、设深度为k的二叉树上只有度为0和度为2的结点,则这类二叉树上所含的结点总数为。
A、不确定B、2kC、2k-1D、2k+19、设有13个值,用它们组成一棵哈夫曼树,则该哈夫曼树共有个结点。
A、13B、12C、26 D、2510、下面几个符号串编码集合中,不是前缀编码的是。
第5章 树与二叉树习题参考答案
习题五参考答案一、选择题1.对一棵树进行后根遍历操作与对这棵树所对应的二叉树进行( B )遍历操作相同。
A.先根 B. 中根 C. 后根 D. 层次2.在哈夫曼树中,任何一个结点它的度都是( C )。
B.0或1 B. 1或2 C. 0或2 D. 0或1或23.对一棵深度为h的二叉树,其结点的个数最多为( D )。
A.2h B. 2h-1 C. 2h-1 D. 2h-14.一棵非空二叉树的先根遍历与中根遍历正好相同,则该二叉树满足( A )A.所有结点无左孩子 B. 所有结点无右孩子C. 只有一个根结点D. 任意一棵二叉树5.一棵非空二叉树的先根遍历与中根遍历正好相反,则该二叉树满足( B )B.所有结点无左孩子 B. 所有结点无右孩子C. 只有一个根结点D. 任意一棵二叉树6.假设一棵二叉树中度为1的结点个数为5,度为2的结点个数为3,则这棵二叉树的叶结点的个数是( C )A.2 B. 3 C. 4 D. 57.若某棵二叉树的先根遍历序列为ABCDEF,中根遍历序列为CBDAEF,则这棵二叉树的后根遍历序列为( B )。
A.FEDCBA B. CDBFEA C. CDBEFA D. DCBEFA8.若某棵二叉树的后根遍历序列为DBEFCA,中根遍历序列为DBAECF,则这棵二叉树的先根遍历序列为( B )。
A.ABCDEF B. ABDCEF C. ABCDFE D. ABDECF9.根据以权值为{2,5,7,9,12}构造的哈夫曼树所构造的哈夫曼编码中最大的长度为( B )A.2 B. 3 C. 4 D. 510.在有n个结点的二叉树的二叉链表存储结构中有( C )个空的指针域。
A.n-1 B. n C. n+1 D. 0二、填空题1.在一棵度为m的树中,若度为1的结点有n1个,度为2的结点有n2个,……,度为m的结点有n m个,则这棵树中的叶结点的个数为1+n2+2n3+3n4+…+(m-1)n m。
数据结构与算法第5章课后答案
page: 1The Home of jetmambo - 第 5 章树和二叉树第 5 章树和二叉树(1970-01-01) -第 5 章树和二叉树课后习题讲解1. 填空题⑴树是n(n≥0)结点的有限集合,在一棵非空树中,有()个根结点,其余的结点分成m (m>0)个()的集合,每个集合都是根结点的子树。
【解答】有且仅有一个,互不相交⑵树中某结点的子树的个数称为该结点的(),子树的根结点称为该结点的(),该结点称为其子树根结点的()。
【解答】度,孩子,双亲⑶一棵二叉树的第i(i≥1)层最多有()个结点;一棵有n(n>0)个结点的满二叉树共有()个叶子结点和()个非终端结点。
【解答】2i-1,(n+1)/2,(n-1)/2【分析】设满二叉树中叶子结点的个数为n0,度为2的结点个数为n2,由于满二叉树中不存在度为1的结点,所以n=n0+n2;由二叉树的性质n0=n2+1,得n0=(n+1)/2,n2=(n-1)/2。
⑷设高度为h的二叉树上只有度为0和度为2的结点,该二叉树的结点数可能达到的最大值是(),最小值是()。
【解答】2h -1,2h-1【分析】最小结点个数的情况是第1层有1个结点,其他层上都只有2个结点。
⑸深度为k的二叉树中,所含叶子的个数最多为()。
【解答】2k-1【分析】在满二叉树中叶子结点的个数达到最多。
⑹具有100个结点的完全二叉树的叶子结点数为()。
【解答】50【分析】100个结点的完全二叉树中最后一个结点的编号为100,其双亲即最后一个分支结点的编号为50,也就是说,从编号51开始均为叶子。
⑺已知一棵度为3的树有2个度为1的结点,3个度为2的结点,4个度为3的结点。
则该树中有()个叶子结点。
【解答】12【分析】根据二叉树性质3的证明过程,有n0=n2+2n3+1(n0、n2、n3分别为叶子结点、度为2的结点和度为3的结点的个数)。
⑻某二叉树的前序遍历序列是ABCDEFG,中序遍历序列是CBDAFGE,则其后序遍历序列是()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题五参考答案备注: 红色字体标明的是与书本内容有改动的内容一、选择题1.对一棵树进行后根遍历操作与对这棵树所对应的二叉树进行( B )遍历操作相同。
A.先根 B. 中根 C. 后根 D. 层次2.在哈夫曼树中,任何一个结点它的度都是( C )。
B.0或1 B. 1或2 C. 0或2 D. 0或1或23.对一棵深度为h的二叉树,其结点的个数最多为( D )。
A.2h B. 2h-1 C. 2h-1 D. 2h-14.一棵非空二叉树的先根遍历与中根遍历正好相同,则该二叉树满足( A )A.所有结点无左孩子 B. 所有结点无右孩子C. 只有一个根结点D. 任意一棵二叉树5.一棵非空二叉树的先根遍历与中根遍历正好相反,则该二叉树满足( B )B.所有结点无左孩子 B. 所有结点无右孩子C. 只有一个根结点D. 任意一棵二叉树6.假设一棵二叉树中度为1的结点个数为5,度为2的结点个数为3,则这棵二叉树的叶结点的个数是( C )A.2 B. 3 C. 4 D. 57.若某棵二叉树的先根遍历序列为ABCDEF,中根遍历序列为CBDAEF,则这棵二叉树的后根遍历序列为( B )。
A.FEDCBA B. CDBFEA C. CDBEFA D. DCBEFA8.若某棵二叉树的后根遍历序列为DBEFCA,中根遍历序列为DBAECF,则这棵二叉树的先根遍历序列为( B )。
A.ABCDEF B. ABDCEF C. ABCDFE D. ABDECF9.根据以权值为{2,5,7,9,12}构造的哈夫曼树所构造的哈夫曼编码中最大的长度为( B )A.2 B. 3 C. 4 D. 510.在有n个结点的二叉树的二叉链表存储结构中有( C )个空的指针域。
A.n-1 B. n C. n+1 D. 0二、填空题1.在一棵度为m的树中,若度为1的结点有n1个,度为2的结点有n2个,……,度为m的结点有n m个,则这棵树中的叶结点的个数为1+n2+2n3+3n4+…+(m-1)n m。
2.一棵具有n个结点的二叉树,其深度最多为 n ,最少为 [log2n]+1 。
3.一棵具有100个结点的完全二叉树,其叶结点的个数为 50 。
4.以{5,9,12,13,20,30}为叶结点的权值所构造的哈夫曼树的带权路径长度是 217 。
5.有m个叶结点的哈夫曼树中,结点的总数是 2m-1 。
6.若一棵完全二叉树的第4层(根结点在第0层)有7个结点,则这棵完全二叉树的结点总数是 11 。
7.在深度为k的完全二叉树中至少有 k个结点,至多有 2k-1 个结点。
8.对一棵树转换成的二叉树进行先根遍历所得的遍历序列为ABCDEFGH,则对这棵树进行先根遍历所得的遍历序列为 ABCDEFGH 。
9.二叉树常用的存储结构是二叉链式存储结构,树常用的存储结构是孩子兄弟链表存储结构。
10.对森林进行后根遍历操作等同于从左到右对森林中的每一棵树进行后根遍历操作,并且对森林的后根遍历序列与对森林所对应的二叉树的中根遍历序列相同。
四、算法设计题1.编写一个基于二叉树类的统计叶结点数目的成员函数。
参考答案:public int countLeafNode(BiTreeNode T) {// 统计叶结点数目int count = 0;if (T != null) {if (T.getLchild() == null && T.getRchild() == null) {++count;// 叶结点数增1} else {count += countLeafNode(T.getLchild()); // 加上左子树上叶结点数count += countLeafNode(T.getRchild());// 加上右子树上的叶结点数}}return count;}2.编写一个基于二叉树类的查找二叉树结点的成员函数。
参考答案:public BiTreeNode searchNode(BiTreeNode T,Object x) {// 在以T为根结点的二叉树中查找值为x的结点,若找到,则返回该结点,否则返回空值if (T != null) {if (T.getData().equals(x))return T;else {BiTreeNode lresult= searchNode(T.getLchild(),x); // 在左子树上查找return (lresult!=null?lresult:searchNode(T.getRchild(),x)) ;// 若左子树上没找到,则到右子树上找}}return null;}3.编写算法求一棵二叉树的根结点root到一个指定结点p之间的路径并输出。
参考答案:// 求根结点到指定结点的路径过程中,采用了后跟遍历的思想,最终求得的路径保存在一个链栈中,其中根结点处于栈顶位置,指定结点处于栈底位置。
//下面用到的二叉树结点类BiTreeNode在书中第5章中已给出public LinkStack getPath(BiTreeNode root, BiTreeNode p) {BiTreeNode T = root;LinkStack S = new LinkStack();// 构造链栈if (T != null) {S.push(T); // 根结点进栈Boolean flag;// 访问标记BiTreeNode q = null;// q指向刚被访问的结点while (!S.isEmpty()) {while (S.peek() != null)// 将栈顶结点的所有左孩子结点入栈S.push(((BiTreeNode) S.peek()).getLchild());S.pop(); // 空结点退栈while (!S.isEmpty()) {T = (BiTreeNode) S.peek();// 查看栈顶元素if (T.getRchild() == null || T.getRchild() == q) {if (T.equals(p)) {// 对栈S进行倒置,以保证根结点处于栈顶位置LinkStack S2 = new LinkStack();while (!S.isEmpty())S2.push(S.pop());return S2;}S.pop();// 移除栈顶元素q = T;// q指向刚被访问的结点flag = true;// 设置访问标记} else {S.push(T.getRchild());// 右孩子结点入栈flag = false;// 设置未被访问标记}if (!flag)break;}}}return null;}4.编写算法统计树(基于孩子兄弟链表存储结构)的叶子数目。
参考答案://下面用到的孩子兄弟链表结构中的结点类CSTreeNode在书中第5章中已给出public int countLeafNode(CSTreeNode T) {int count = 0;if (T != null) {if (T.getFirstchild() == null)++count;// 叶结点数增1elsecount += countLeafNode(T.getFirstchild()); // 加上孩子上叶结点数count += countLeafNode(T.getNextsibling());// 加上兄弟上叶结点数}return count;}5.编写算法计算树(基于孩子兄弟链表存储结构)的深度。
参考答案:public int treeDepth(CSTreeNode T) {if (T != null) {int h1= treeDepth(T.getFirstchild());int h2= treeDepth(T.getNextsibling());return h1+1>h2?h1+1:h2;}return 0;}四、上机实践题1.编写一个程序实现:先建立两棵以二叉链表存储结构表示的二叉树,然后判断这两棵二叉树是否相等并输出测试结果。
参考答案:package ch05Exercise;import ch05.BiTreeNode;//教材第5章中有此类的描述public class Exercise5_4_1 {public boolean isEqual(BiTreeNode T1, BiTreeNode T2) {//判断两棵树是否相等,若相等则返回true,否则返回falseif (T1 == null && T2 == null)// 同时为空return true;if (T1 != null && T2 != null) // 同时非空进行比较if (T1.getData().equals(T2.getData()))// 根结点数据元素是否相等if (isEqual(T1.getLchild(), T2.getLchild())) // 左子树是否相等if (isEqual(T1.getRchild(), T2.getRchild()))// 右子树是否相等return true;return false;}//测试主方法public static void main(String[] args) {// 创建根结点为T1的二叉树BiTreeNode D1 = new BiTreeNode('D');BiTreeNode G1 = new BiTreeNode('G');BiTreeNode H1 = new BiTreeNode('H');BiTreeNode E1 = new BiTreeNode('E', G1, null);BiTreeNode B1 = new BiTreeNode('B', D1, E1);BiTreeNode F1 = new BiTreeNode('F', null, H1);BiTreeNode C1 = new BiTreeNode('C', F1, null);BiTreeNode T1 = new BiTreeNode('A', B1, C1);// 创建根结点为T2的二叉树BiTreeNode D2 = new BiTreeNode('D');BiTreeNode G2 = new BiTreeNode('G');BiTreeNode H2= new BiTreeNode('H');BiTreeNode E2 = new BiTreeNode('E', G2, null);BiTreeNode B2 = new BiTreeNode('B', D2, E2);BiTreeNode F2 = new BiTreeNode('F', null, H2);BiTreeNode C2 = new BiTreeNode('C', F2, null);BiTreeNode T2 = new BiTreeNode('A', B2, C2);// 创建根结点为T3的二叉树BiTreeNode E3= new BiTreeNode('E');BiTreeNode F3 = new BiTreeNode('F');BiTreeNode D3= new BiTreeNode('D',F3,null);BiTreeNode B3 = new BiTreeNode('B', null, D3);BiTreeNode C3 = new BiTreeNode('C', null, E3);BiTreeNode T3 = new BiTreeNode('A', B3, C3);Exercise5_4_1 e = new Exercise5_4_1();if (e.isEqual(T1, T2))System.out.println("T1、T2两棵二叉树相等!");elseSystem.out.println("T1、T2两棵二叉树不相等!");if (e.isEqual(T1, T3))System.out.println("T1、T3两棵二叉树相等!");elseSystem.out.println("T1、T3两棵二叉树不相等!");}}运行结果:2.编写一个程序实现:先建立一棵以孩子兄弟链表存储结构表示的树,然后输出这棵树的先根遍历序列和后根遍历序列。
