求正弦交流电的有效电流值的微积分证明

交流电有效值的计算(微课课件)

I2RTI12RT 2I22RT 2
即 I2 521( 5)21
2 22
解得
I5 3A 2
3.思考练习
如图实线所示的交变电流，最大值为Im，周期为T，则下
列有关该交变电流的有效值I，判断正确的是（ B ）来自A.I Im 2
B. I I m 2
C. I I m
2
再见！
2-5.非对称性矩形脉冲交流电有效值
分析：从t＝0开始的任意一个周期内，前半周期是大小不变的直流电，为
I1 5A ，后半周期是有效值为
I2
5 A 的交变电流。
2
设所求交变电流的有效值为I，根据有效值的定义，选择一个周期的时间，利用在相同时间内通过相同的电阻所产生的热量相等，由焦耳定律得
交流电有效值的计算(微课课件)
1.有效值的计算
有效值：是根据电流的热效应来规定的。
将交流电与一直流电加在阻值相同的电阻上，如果相等时间内所发热量相等，则这一直流电的值叫交流电的有效值。
2-1.正弦交流电的有效值
电动势：
E
Em 2
0.707Em
e（i）
电
压：
UUm 2
0.70U 7m
QI12RT 3I22R23T62RT 332R2 3 T1R 8T
设该交变电流的有效值为I，则上述热量
QI2RT
联立上两式，可得有效值为 I 3 2A
2-4-3.矩形脉冲电流的有效值
由U2 T Um2 t
Um
RR
0
得U
t T
U
m
当t 1时，U
T2
2 2 Um
0
t
电
流：
I

正弦交流电有效值推导过程

正弦交流电有效值推导过程说到正弦交流电的有效值，嘿，这可是个非常有趣的话题哦。

想象一下你在一个阳光明媚的日子里，和朋友们在公园里野餐，带着冰凉的饮料，四周都是欢声笑语。

可是，突然间，你听到了一个噼里啪啦的声音，回头一看，哎呀，原来是电器在作怪。

没错，交流电就像你耳边的风，时而温柔，时而强烈，而它的有效值就是我们用来衡量这种电的“实力”的一个小秘密。

说到这里，先来聊聊什么是有效值。

你可能会想，有效值是不是个复杂的术语？其实并不，简单来说，有效值就是电流或电压在交流电中表现出来的“相当于”直流电的能力。

想象一下，你在比赛中，有些选手一看就很强，但实际跑起来可能没你快。

这就是有效值，它给我们一个更准确的评判标准。

要是没有这个，有时候你可能会被表面现象迷惑。

然后，我们来个简单的数学小把戏，别害怕，咱们不算什么复杂的数字。

正弦波的电流或电压可以用一个简单的公式来表示。

想象一下，一条光滑的波浪，起起伏伏，正弦波就是这样的形状。

在计算有效值的时候，我们需要把这条波形“平衡”一下。

哎，听上去有点复杂吧？其实不然。

只需要把波形的平方取平均，再开方就好。

就像把你的各种情绪混合一下，最后得到一个“平衡”的你。

好啦，接下来再深入一点。

正弦波的方程式看起来可能有点吓人，其实就是个简单的事情。

设想一下，一个电流的变化可以表示成 ( I(t) = I_m sin(omega t) )，这里的( I_m ) 是最大值，而 ( omega ) 则是频率。

要计算有效值，咱们首先把这个正弦波平方，再取平均。

平方后的波形，看起来就像是在做一场舞蹈，每个点都在展现自己的魅力。

然后，把这个平均值开方，哇，最终得到的就是有效值，听起来是不是挺神奇的？而这个有效值的计算公式其实是个很经典的结果：( I_{rms = frac{I_m{sqrt{2 )。

是不是觉得很简单？就像你去超市买菜，看到那个促销的标签，原来有效值就是那个隐藏的折扣，能让你买到更划算的东西。

交流电有效值计算方法

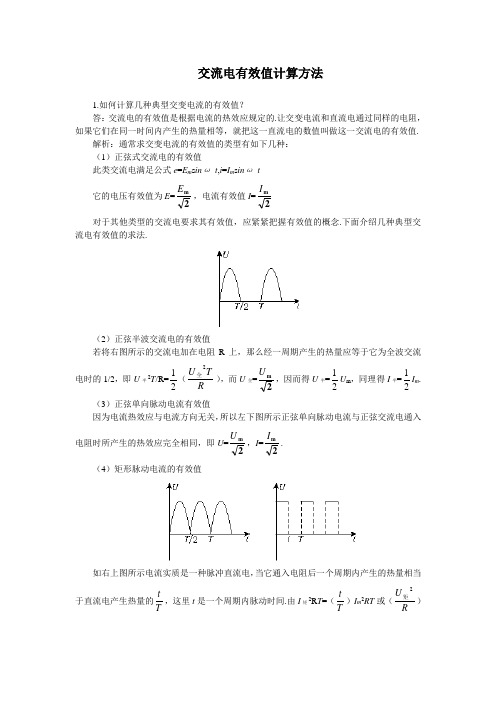
交流电有效值计算方法1.如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值. 解析：通常求交变电流的有效值的类型有如下几种：（1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ，电流有效值I =2mI对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全），而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m . （3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2m U ，I =2m I .（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或（R U 2矩）T =T t （R u 2m ）T ,得I 矩=T t I m ，U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m . （5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同，则V 252,)2/(022===U U t R U t R U o 所以 3.在图示电路中，已知交流电源电压u=200s in 10πt V ，电阻R=10 Ω，则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为 u =2200V=141 V ，电流值i =R U =102200⨯ A=14.1 A.答案：B。

求交流电有效值的方法

求交流电有效值的方法
交流电的有效值是根据电流的热效应规定的。

在求交流电的有效值时，通常采用以下几种方法：
直接计算法：对于已知波形的交流电，如正弦波、方波、三角波等，可以根据其波形特点直接计算出有效值。

例如，对于正弦波交流电，其有效值等于峰值除以根号2。

积分法：对于任意波形的交流电，可以通过积分的方式计算其有效值。

具体步骤是，将交流电在一个周期内的瞬时值进行平方，然后对时间进行积分，最后取平方根即可得到有效值。

这种方法需要知道交流电的瞬时值表达式或者采样数据。

仪表测量法：在实际应用中，通常使用电表来测量交流电的有效值。

电表内部采用了专门的电路和算法来计算有效值，可以直接显示出测量结果。

需要注意的是，不同类型的电表可能采用不同的计算方法，因此测量结果可能存在一定的误差。

需要注意的是，在求交流电的有效值时，需要明确所求的是电压有效值还是电流有效值，并且要注意单位的一致性。

此外，对于非正弦波形的交流电，其有效值并不能简单地用峰值除以根号2来计算，而需要根据其波形特点进行具体分析。

总之，求交流电的有效值需要根据具体情况选择合适的方法，并且要注意测量误差和单位的一致性。

在实际应用中，还需要考虑交流电的频率、波形等因素对有效值的影响。

正弦式交流电有效值的四种证明方法

正弦式交流电有效值的四种证明方法正弦交流电的有效值与其最大值之间关系高中书本中没有给出证明方法，只是直接给出了正弦交流电的有效值与最大值之间的关系：在大学物理中用到了微积分来证明，在高中若直接绕过不讲，总觉得对对我们理科生有点不尊重，有没有啥方法利初等数学及物理知识证明这一关系。

我们知道交流电的有效值是根据电流的热效应来规定的，让交流和直流通过相同阻值的电阻，如果它们在相同的时间内产生的热量相等，就把这一直流的数值叫做这一交流的有效值。

由于正弦函数具有对称性和周期性，据此可以证明如下：方法一：叠加法假设有两个交变电压，其变化规律如图所示，它们的最大值与周期都相同，它们的瞬时表达式分别为u1=Umsinωt，u2=Umcosωt，其中ω=2兀/T把它们分别加在两个阻值相同的电阻上，设电阻的阻值为R，由于电流的热效应与电流的方向及先后作用的时间顺序无关，故在一个周期内两个交流电产生的焦耳热相同，设都为Q，产生的总的焦耳热Q=2Q。

设它们交流电压的有效值为为U，在任一时刻t，这两个电阻上的热功率分别为两个电阻总的发热功率为可以看出：两个电阻上总的发热功率是一定值与时刻t无关，所以两个电阻在一个周期内两个电阻上总的发热量为：用一个恒定电压为U的电源，分别给两个相同的电阻R供电，在相同时间T内，每个电阻产生的热量是两个电阻产生的总热量为Q总’=2Q,由热效应的等效Q总’=Q而这个恒定电R的电压U就是正弦交变电流的电压的有效值。

电流的有效值可同法证得。

方法二：平均功率法设流过定值电阻R的电流按正弦规律变化，即i=Imsinωt，交流电的瞬时功率为上式中，后一项在一个周期内平均值为零，因此在一个周期内交流电平均功率为：如果考虑一个恒定电流I与其等效，即P=I² R就有因焦耳热等于平均功率和时间的成积，所以得证。

方法三：图像法设通过电阻R的正弦交流电电流表达式为i=Imsinωt,则交流电的瞬时功率为p=i²R=Im ²Rsin²ωt，作出交流电的P—t图象如下图所示由微元方法可知曲线与时间轴所包围的面积表示交流电在一个周期内产生的热量.利用割补法或“移峰填谷”的方法，将斜线所画部分截下，倒过来恰好可以填充在“谷”里.从图象可以很直观地发现：曲线与横轴所包围的面积，正好等于高为Im ²R/2，宽为T的矩形面积，此矩形面积在数值上又恰等于该交流电在一个周期内产生的热量。

求正弦交流电的有效电流值的微积分证明

求正弦交流电的有效电流值的微积分证明首先，正弦交流电的有效值是指与它做功能力等效的直流电的数值。

即在相同时间内,一个直流电压和电流和一个交流电压和电流在同一电阻上产生的热量相等时,我们就把这个直流电压和电流称为对应的交流电压和电流的有效值.所以，此问题应从做功角度去推导。

设有一个纯电阻电路,电阻为R,正弦交流电的电压瞬时值为u=Um*sinωt，电流瞬时值为i=Im*sinωt。

1、求瞬时功率，功率p=u*u/R=Um*Um*sinωt*sinωt/R=1/2*Um*Um*（1-cos2ωt)/R。

2、计算此式在一个周期T的时间内所做的功：假如时间变化一个无限小增量dt,我们得到在dt时间内交流电所做的功为:dw=p*dt=Um*Um*sinωt*sinωt*dt/R=1/2*Um*Um/R*（1-cos2ωt)*dt;再求交流电在一个周期T内所做的功:dw对时间积分,下限是0,上限是T得:功W=int(0-T)p*dt=int(0-T)(1/2*Um*Um*（1-cos2ωt)*dt)/R=1/2R*Um*Um*int(0-T)dt+1/2R*Um*Um*int(0-T)cos2ωt*dt;其中，int表示积分，（0-T）为积分限。

此式右边积分为零，我们得到：W=1/2R * Um*Um*T。

此式的物理意义是：1/2*Um*Um是一个常数，在电学上就是一个直流分量，而交流分量在一个周期内的积分是零，是因为波形上下对称。

3、求平均功率，就得到与它等效的直流电,即电压有效值和电流有效值了：P=W/T=1/2R * Um*Um。

令：U为对应的等效直流电压，即U*U/R=1/2*Um*Um/R。

所以我们得到:U=√2/2 * Um；同理，P=i*i*R=Im*Im*R*sinωt*sinωt=1/2*Im*Im*R*(1-cos2ωt);W=int(0-t)P*dt=1/2*Im*Im*R*T平均功率P=W/T=1/2*Im*Im*R。

交流电有效值证明

2 m
R
T
U2
2T
U
2 m
T
R
R
U Um 2
正弦交流电有效值的证明
u Um sin(t)
方法3：
Q
T 0
(U m
sin(t))2
R
dt
Q Um2 T sin2 (t)dt R0
Q
U
2 m
T
U
2 有
T
2R
R
Q Um2 T 1 cos(2t) dt R0 2
Q Um2 (t sin(2t)) T
Q总
U2 R
2T
在任一时刻t，这两个电阻上的热功率分别为：
P1
u12 R
(U m
sin t)2
R
P2
u22 R
(U m
cos t )2
R
P
P1
P2
U
2 mΒιβλιοθήκη (sin2t
R
cos2
t)
U
2 m
R
可以看出：两个电阻上总的发热功率是一定值，与时刻
t无关。所以在一个周期内两个电阻上总的发热量为：
Q总
PT
U
方法2：
u1 U m sin t
u2 U m cost
把它们分别加在两个阻值相同的电阻上，设电阻的阻值
为R，由于电流的热效应与电流的方向及先后作用的时
间顺序无关，故在一个周期内两个交流电产生的焦耳热
相同，设都为Q，产生的总的焦耳热Q总=2Q。设它们交流电压的有效值为U，则有：
Q U2 T R
2R
2 0
U有
Um 2
Q Um2 T 2R
正弦交流电有效值的证明

交流电有效值的计算

交流电有效值的计算交流电有效值的计算是指通过测量或计算得出交流电信号在一定时间内的平均能量大小。

在交流电中，电流和电压都是随时间变化的，因此不能直接使用最大值或峰值来表示电流或电压的大小。

有效值的概念旨在提供一个与直流电相同功率的参考值。

要计算交流电的有效值，可以使用以下三种方法：平均值法、功率法和积分法。

1. 平均值法：交流电的有效值可通过将电流或电压的平方信号取平均并开方来计算。

假设电流的波形为I(t)，则交流电的有效值表示为Irms，可用以下公式计算：Irms = √(1/T ∫[0 to T] I(t)²dt)其中，T表示一个完整的周期。

例如，如果电流的波形是正弦波，那么该方法可以简化为使用最大峰值电流的70.71%：Irms = Imax/√22.功率法：根据交流电功率的定义，可以使用功率计来测量电流和电压之间的功率输出。

根据功率的平方等于电流和电压乘积的平均值，可以将交流电的有效值表示为：Irms = √(Pavg/Vrms)其中，Pavg表示平均功率输出，Vrms表示电压的有效值。

这种方法适用于通过功率计间接测量交流电的有效值。

3.积分法：通过将电流或电压信号与一个参考信号进行积分，并将结果除以积分时间来计算有效值。

该方法需要使用一些数学和信号处理技术，通常在数字信号处理领域使用。

这些方法可以适用于各种交流电信号的有效值计算。

但需要注意的是，对于非线性或非周期性的波形，这些方法可能不适用。

在这种情况下，可以借助计算机和数值计算技术进行数值模拟和数据处理。

除了计算交流电的有效值，也可以使用示波器等检测设备来显示电流和电压的波形，并通过与标准波形进行比较来估计有效值。

交流电有效值计算在电力系统分析、电路设计和实际应用中具有重要意义。

它能够描述交流电信号的实际能量，为电力传输、电能计量和电气设备的设计和使用提供准确的参考值。

有效值计算也是交流电工程中一项基本的测量和分析技术。

例谈正弦交流电的有效值和平均值

例谈正弦交流电的有效值和平均值〔关键词〕物理教学；正弦交流电；有效值；平均值；计算；应用一、交流电的有效值和平均值的意义有效值是根据电流的热效应来规定的.让交流和直流电通过阻值相等的电阻，如果在相同的时间内产生的热量相同，那么这一直流的数值就叫做该交流电的有效值，有效值是交流电的几何平均值.交流电的平均值是指在某一段时间内产生的交变电流对时间的平均值，是交流电的算术平均值，其值大小表示单位时间内通过的电量平均值，在交流图象中波形对横轴所围“面积”与时间的比值.二、正弦交流电的有效值和平均值计算公式（1）正弦交流电的有效值积分法。

根据有效值的意义，在一个周期内，交流电流i通过电阻R产生的热量与稳恒电流I通过同一个电阻R产生的热量相等.即交流电i与稳恒电流I等效.稳恒电流I，在时间T内通过电阻R产生的热量为：Q=I2RT交流电i=Imsin？棕t，在一个周期T内通过电阻R产生的热量为：Q=iRdt=IRsin？棕tdt=IR[dt-cos？棕tdt]=IRT则：IRT=IRT 解得：I=同理得：E= U=（2）正弦交流电的平均值方法一：根据正弦交流电的对称性，正弦交流电在T内的平均值等于T内的平均值；利用法拉第电磁感应定律，线圈在匀强磁场中绕垂直于磁场方向的轴从中心面开始转动T的过程中的平均电动势为：E====可见：对于正弦交流电有：E=I= U=方法二：正弦交流电在T内的平均值等于T时间内的平均值.用积分法得：I=idt=Imsin？棕tdt=sin？棕td？棕t= 即：I=三、应用举例例1：某正弦交流电电压u=50sin100？仔tV，加在一氖管的两端，已知当氖管的两端的电压达到25V时才能发光，则此氖管一个周期内发光的总时间为：（A）0.02s （B）0.0025s （C）0.01s （D）0.005s分析：由交流电电压的表达式u=50sin100？仔tV得：25=50sin100？仔tV解得：t=T，一个周期内发光的时间为tT=T=0.01s，（C）选项正确.例2：求如图所示的交变电流的有效值，其中，每个周期的前半周期的图象为正弦曲线，后半周期为稳恒电流.分析：从t=0开始的任意一个周期内，前半周期电流的有效值为I1=A，后半周期是大小不变的稳恒电流I2=5A由有效值的意义得：I2RT=I12R+I22R解得：I=A。

交流电有效值的计算

交流电有效值的计算江苏省新海高级中学崔晓霞 222006交变电流的大小和方向随时间作周期性变化。

为方便研究交变电流的特性，根据电流的热效应引入了有效值这一物理量。

一、正弦交流电有效值表达式的推导：交流电的有效值是用它的热效应规定的，因此设法求出正弦交流电的热效应，才能求出其有效值，正弦交流电电压的瞬时值u =U m ·sin ωt ，如果把这加在负载电阻R 上，它的瞬时电功率22cos 1sin 2222t R U t R U R u P m m ⋅-⋅=⋅==ωω 其图像如图1所示．由微元法可知，P-t 图线和t 轴之间所包围的面积就是功（图中打斜条的部分）．不难看出，图中有斜条打△的部分和无斜条打△的部分面积是相同的，因此打斜条部分的面积就是P =U 2m /2R 线和t 轴之间的面积．设正弦交流电电压的有效值是U ，根据有效值的定义：RU R U m 222= 可得：2/m U U = 同理可得：2/m I I =；2/m E E =此关系式仅适用于正弦交流电，那么非正弦交流电的有效值又该如何求解呢？二、非正弦交流电有效值的计算例1. 如图2甲乙所示分别表示交变电流随时间变化的图象，则这两个交流电的有效值分别是 V 和 A 。

解析：对于图甲，该交变电流在每个周期T 内都可看作两个阶段的直流电流：前T /3中，U 1=100V ，后2T /3中，U 2=50V 。

在一个周期中，该交变电流在电阻R 上产生的热量为：32503100323222221T R T R T R U T R U Q ⋅+⋅=+⋅= ① 设该交流电电压的有效值为U ，则上述热量T Q ⋅=RU 2②联立①、②两式，可得有效值为V 250=U 对于图乙，从t ＝0开始的任意一个周期内，前半周期是大小不变的直流电，为I A 15=，图1图2 甲乙后半周期是有效值为I A 252=的交变电流。

设所求交变电流的有效值为I ，根据有效值的定义，选择一个周期的时间，利用在相同时间内通过相同的电阻所产生的热量相等，由焦耳定律得I RT I R T I R T 2122222=+ 即I 2225125212=⨯+⨯() 解得I A =532 点评：对于非正弦交流电，要从有效值从定义出发，根据热效应求解。

交流电有效值计算方法

交流电有效值计算方法1.如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值. 解析：通常求交变电流的有效值的类型有如下几种：（1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ，电流有效值I =2mI对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全），而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m . （3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2m U ，I =2m I .（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或（R U 2矩）T =T t （R u 2m ）T ,得I 矩=T t I m ，U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m . （5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同，则V 252,)2/(022===U U t R U t R U o 所以 3.在图示电路中，已知交流电源电压u=200s in 10πt V ，电阻R=10 Ω，则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为 u =2200V=141 V ，电流值i =R U =102200⨯ A=14.1 A.答案：B。

交流电有效值推导公式

交流电有效值推导公式
交流电有效值指的是一个变化周而复始的电流或电压定义该信号的均值。

它在一种规律交流电路中比平均值大一倍，它是交流电路中最重要的参数之一。

对电流而言，有效值是指在钟形电流谱图的钟的半径，而电压的有效值则是指在正弦波电压谱图的正弦曲线的半峰值。

由此可见，有效值是很重要的概念，有效值推导公式旨在揭示这一概念使得其在实际应用中更加可视化和实现。

有效值推导公式的一般形式如下：对于任何有形式为f(t)的波形，其有效值可以写为：
f_eff=\frac{1}{T}\int^T_0 (f(t))^2dt
其中，T是波形的周期。

另一种经典形式则是：
f_eff=\sqrt{\frac{2}{pi}P_o}
其中，po是波形的功率。

不论是上述的哪种形式推导出的有效值，其准确性都要求波形信号完全遵从数学形状，不能存在任何外部干扰和异常断裂现象。

交流电的有效值推导公式可以应用到实际的日常生活中，例如汽车电子设备检测时需要测量电压和电流的有效值。

有效值推导公式能够更准确地表征出其实际特性，从而让维修工程师对电子设备进行更加科学的维护。

有效值推导公式对我们熟知的交流电有着重要的影响，已经运用到许多实际应用场景中去了，它能够更加有效地处理多种交流电相关的应用场景，提高维修效率以及增加研究发展的潜力。

正弦交变电流有效值计算公式的推导

中学教学参考
2018··6 中旬
2018
物理·教学研究
要的结论，但课本没有给出推导过程，而是直接给出：I=
Im
Um
，U=
。
2
2
本文用微积分法、平均值法、三角函数法对推导法
物理学科与数学学科有着密切的联系，在运用物理
知识解题时，一般要进行数学推理和运算。同时新课改
物理·教学研究
正弦交变电流有效值计算公式的推导
广西贺州高级中学（542800）毛亮
［摘
要］对交流电有效值定义的理解和应用以及各种交流电的有效值的计算是高考对学生知识和能力考查的内容之一。人民
教育出版社出版的普通高中课程标准实验教科书物理选修 3-2 中，
正弦交变电流的电压和电流的有效值是一个重要的结论，
以来，数学教材已经发生了变化，在高中阶段已经引入
了导数和微积分的内容，而微积分的引入对高中物理的
教学是有促进作用的，虽说学习起来有点难，但是有利
于进入高校后的学习。
现有一正弦交变电流，
如图 1 ，它的瞬时表达式为
i1=Imsinωt。
交流电的电流、电压及功
图1
率都是随时间变化的，其中电
一门科学，更是一门艺术，是科学与艺术的综合。物理
课堂精准教学需要做到优化、独到；教师的教学热情与
教态可以激发教学活力；学生的学习要做到自主、深刻；
评价要做到科学、激励；借助信息技术要做到恰当、有
效。只有这样才能把精准教学落到实处。
［参考文献］
［1］彭红超，祝智庭 . 面向智慧学习的精准教学活动生成性设
学后教，当堂练习，个性教学，合作学习”这些都是符合
新课程理念与新时代要求的。

正弦交变电流有效值计算公式的推导

正弦交变电流有效值计算公式的推导作者：毛亮来源：《中学教学参考·理科版》2018年第06期[摘要]对交流电有效值定义的理解和应用以及各种交流电的有效值的计算是高考对学生知识和能力考查的内容之一。

人民教育出版社出版的普通高中课程标准实验教科书物理选修3-2中，正弦交变电流的电压和电流的有效值是一个重要的结论，但课本没有给出推导过程，而是直接给出了结论。

文章用微积分法、平均值法、三角函数法对正弦交变电流的有效值进行推导，学生可以根据自己的情况选择。

[关键词]交变电流；有效值；公式推导[中图分类号] G633.7 [文献标识码] A [文章编号] 1674-6058（2018）17-0047-02交变电流是高中物理选修3-2的内容，是指电流的大小和方向都随时间作周期性变化的电流，在生活中运用最广的是有效值，如：1.计算与电流热效应相关的量（如功率、热量）；2.交流电表的测量值；3.电气设备标注的额定电流.4.保险丝的熔断电流。

对交流电的有效值定义的理解和应用及各种交流电的有效值的计算也是高考对学生知识和能力考查的内容。

那么怎样计算正弦交变电流的有效值呢？交流电的有效值是根据电热效应来规定的，简称“三同”，即让交流和直流通过相同阻值的电阻，经过相同的时间，产生相同的热量，就把这一直流的数值叫作这一交流电的有效值，即用与交变电流有相同热效应的直流电流来等效替代交变电流在能量方面所产生的平均效果。

人教版实验教科书物理选修3-2中，正弦交变电的电压和电流的有效值是一个重要的结论，但课本没有给出推导过程，而是直接给出：I=[Im2]，U=[Um2]。

本文用微积分法、平均值法、三角函数法对正弦交变电流的有效值进行推导，以便学生理解掌握。

一、微积分推导法物理学科与数学学科有着密切的联系，在运用物理知识解题时，一般要进行数学推理和运算。

同时新课改以来，数学教材已经发生了变化，在高中阶段已经引入了导数和微积分的内容，而微积分的引入对高中物理的教学是有促进作用的，虽说学习起来有点难，但是有利于进入高校后的学习。

正弦式交变电流有效值的两种推导方法

作者：杨梅芬李维兵
作者机构：江苏省南通高等师范学校,江苏省南通市226100
出版物刊名：物理教学探讨：中学教学教研专辑
页码： 50-51页
年卷期： 2011年第3期
主题词：交变电流有效值推导方法正弦人民教育出版社数学运算实验教科书物理学
摘要：物理学是一门精确科学,与数学有密切关系,在应用物理知识解决实际问题时,一般都要进行数学运算、进行数学推理,因此数学是物理学的基础。

在现行普通高中课程标准实验教科书·物理选修3？2（人民教育出版社,2006年12月第2版）中,作为正弦式交变电流的电流、电压的有效值这样一个重要的结论,。

交流电有效值计算方法

交流电有效值计算方法1.如何计算几种典型交变电流的有效值？答：交流电的有效值是根据电流的热效应规定的.让交变电流和直流电通过同样的电阻，如果它们在同一时间内产生的热量相等，就把这一直流电的数值叫做这一交流电的有效值. 解析：通常求交变电流的有效值的类型有如下几种：（1）正弦式交流电的有效值此类交流电满足公式e =E m s in ω t ,i =I m s in ω t它的电压有效值为E =2mE ，电流有效值I =2mI对于其他类型的交流电要求其有效值，应紧紧把握有效值的概念.下面介绍几种典型交流电有效值的求法.（2）正弦半波交流电的有效值若将右图所示的交流电加在电阻R 上，那么经一周期产生的热量应等于它为全波交流电时的1/2，即U 半2T /R=21（R T U 2全），而U 全=2m U ，因而得U 半=21U m ，同理得I 半=21I m . （3）正弦单向脉动电流有效值因为电流热效应与电流方向无关，所以左下图所示正弦单向脉动电流与正弦交流电通入电阻时所产生的热效应完全相同，即U =2m U ，I =2m I .（4）矩形脉动电流的有效值如右上图所示电流实质是一种脉冲直流电，当它通入电阻后一个周期内产生的热量相当于直流电产生热量的T t ，这里t 是一个周期内脉动时间.由I 矩2R T =（T t ）I m 2RT 或（R U 2矩）T =T t （R u 2m ）T ,得I 矩=T t I m ，U 矩=T t U m .当T t =1/2时，I 矩=21I m ，U 矩=21U m . （5）非对称性交流电有效值假设让一直流电压U 和如图所示的交流电压分别加在同一电阻上，交变电流在一个周期内产生的热量为Q 1=222221T R U T R U ⋅+⋅，直流电在相等时间内产生的热量 Q 2=R U 2T ，根据它们的热量相等有 RU T R U 2212=⋅T 得 U =)(212221U U +，同理有I =)(212221I I +. 2.一电压U 0=10 V 的直流电通过电阻R 在时间t 内产生的热量与一交变电流通过R/2时在同一时间内产生的热量相同，则该交流电的有效值为多少？解：根据t 时间内直流电压U 0在电阻R 上产生的热量与同一时间内交流电压的有效值U 在电阻R /2上产生的热量相同，则V 252,)2/(022===U U t R U t R U o 所以 3.在图示电路中，已知交流电源电压u=200s in 10πt V ，电阻R=10 Ω，则电流表和电压表读数分别为A.14.1 A,200 VB.14.1 A,141 VC.2 A,200 VD.2 A,141 V分析：在交流电路中电流表和电压表测量的是交流电的有效值，所以电压表示数为 u =2200V=141 V ，电流值i =R U =102200⨯ A=14.1 A.答案：B。

正弦交流电的有效值

正弦交流电的有效值
正弦交流电
正弦交流电是指大小和方向都随时间按正弦规律作周期性变化的电流（或电压），也叫简谐交流电。

我们日常用的电都是正弦交流电，它是各种形式的交流电中最为基本和重要的。

由数学可知，一个正弦量与时间的函数关系可以用它的频率、初相位和振幅三个量来表示它的基本特征，这三个量叫正弦量的三要素。

对于一个正弦交流电来说，也可以由这三要素来唯一决定。

一个正弦交流电流，这个是数学表达式。

式中i表示交流电流的瞬时大小，称为瞬时值。

Im表示正弦电流振幅的大小，称为最大值。

ω表示正弦电流的角频率，φ0表示正弦电流的初相位。

ω、φ0及Im是表示正弦交流电的三要素，也是区分不同正弦电流的依据。

正弦交流电的有效值
一个交流电流的作功能力相当于某一数值的直流电流的作功能力，这个直流电流的数值就是该交流电的有效值。

如图所示，在同一个电阻R中分别通以交流电和直流电，在相同的时间内产生的热量相同，我们就说这两个电流等效，这个直流电流的数值就是该交流电流的有效值。

即交流电的有效值就是与它平均耗能相等的直流电的值。

通常用英文大写字母不加下标表示，如用I、U、E分别表示交流电流、电压和电动势的有效值。

根据焦耳定律，交流电流在一个周期内产生的热量为
直流电流在一个周期内产生的热量为
根据有效值的定义，两种电流产生的热量相等，即
由此得交流电流的有效值
设交流电流为i=Imsinωt，代入上式，得
在电工测量中，常用的交流电压表、电流表测得的数值都是有效值，交流电设备铭牌上标注的也是有效值。