函数极限与连续的MATLAB求解
高等数学问题的MATLAB解法

第5章 高等数学问题的MATLAB解法
图 5-3 摆线的绘制
第5章 高等数学问题的MATLAB解法
5.1.3 曲线族的绘制 【例5-1-3】 三次曲线的方程为y=ax3+cx,试探讨参数a和c
对其图形的影响。 解: ◆ 建模 因为函数比较简单, 因此可以直接写入绘图语句中,用循环
语句来改变参数。注意坐标的设定方法,以得到适于观察的图形。 给出的程序不是唯一的,例如也可用fplot函数等。读者可自行探 索其他编法。
xvalues=w*exp(-4*tvalues).*sin(w*tvalues + pi/3);
第5章 高等数学问题的MATLAB解法
◆ 程序运行结果 运行这两种程序都得到图5-1所示的曲线。为了节省篇幅,我 们没有显示y的数据。以后的各例中还将省略绘图时的标注语句。 从本例看,第二种方法似乎更麻烦一些,但它具备模块化的特点。 当程序中要反复多次调用此函数,而且输入不同的自变量时,利 用函数文件可大大简化编程。我们应该掌握这种方法。两次应用 diff函数或用diff(y,2)可以求y的二次导数,读者可自行实践。
【例5-1-4】 极限的定义和判别。 解: ◆ 建模 对于函数y=f(x),当任意给定一个正数ε时,有一个对应的正数
δ 0<|xc-x|<δ
时, |A-f(x)|<ε
其中,A是f(x)在x→xc时的极限,如果找不到这样的δ,A就不是 它的极限。只考虑左极限时,因为xc-x必为正数,所以可去掉绝 对值符号。
ezplot(′(1-cos(x))./x./sin(x)′) grid on 运行程序得出图5-5。从图上可见,此函数在x0=±π处有间断 点。在间断点左右,函数f(x)分别趋向于±∞。现在尝试用数组方 法计算以下三个特征点的值,令 x1=[-pi,0,pi] y1=(1-cos(x1))./x1./sin(x1) 得到警告: Warning: Divide by zero及 y1=1.0e+015 *[5.1984, NaN, 5.1984]
实验报告

实验课程: 数学分析 专业: 数学与应用数学 班级: 09级数本一班 学号: 2009403078 姓名: 王h实验一 函数极限(黑体三号)【实验目的】1.掌握使用Matlab 求极限的方法2.通过Matlab 实验理解掌握极限的定义。
【实验内容】1.求函数极限 2. 求数列极限 3. 了解函数在某点连续【实验所使用的仪器设备与软件平台】实验使用MATLAB 软件【实验方法与步骤】(阐述实验的原理、方案、方法及完成实验的具体步骤等,对于必须编写计算机程序的实验,要附上编写的程序)一、 实验原理:1.运用数列极限的定义。
2.函数极限的定义。
3.函数)(x f 在0x 点连续的定义。
4.运用极限)(limx f 与)(lim x f 存在的充要条件。
二、 实验方案与方法:首先了解极限的定义,然后运用Matlab 软件编写程序求极限。
在使用Matlab 时要会运用声明符号变量syms,并且针对函数求极限的情况(左极限或右极限以及趋近于某点的左右极限等不同情况)编写相应的程序。
三、 实验步骤: 1. 先确定函数极限求∞→n limnn,)1ln(cos 1lim+-→x e x xx ,22)2(sin ln lim x x x -→ππ,xx arctan lim ∞→,xx xx 2)1(lim +∞→2. 以第一个为例编写程序如下:3.再求数列极限618.0215lim1≈-=+∞→n n n F F (其中已知数列])251()251[(51F 11++--+=n n n【实验结果】【结果分析与讨论】。
matlab计算函数极值,如何用MATLAB求函数的极值点和最大值

matlab计算函数极值,如何⽤MATLAB求函数的极值点和最⼤值两种⽅法:1、求导的⽅法:syms x y;>>y=x^3+x^2+1>>diff(y)ans =3*x^2 + 2*x>>solve(ans)ans=-2/3极值有两点。
同时也是最值;2、直接⽤最⼩值函数:求最⼤值,既求-y的最⼩值:>>f=@(x)(-x^3-x^2-1)f =@(x)(-x^3-x^2-1)>>x=fminunc(f,-3,3)%在-3;-3范围内找Warning: Gradient must be provided fortrust-region method; using line-search methodinstead. > In fminunc at354Optimization terminated: relative infinity-norm of gradient lessthan options.TolFun.x =-0.6667>> f(x)ans =-1.1481在规定范围内的最⼤值是1.1481由于函数的局限性,求出的极值可能是局部最⼩(⼤)值。
求全局最值要⽤遗传算法。
例⼦:syms xf=(200+5*x)*(0.65-x*0.01)-x*0.45;s=diff(f);%⼀阶导数s2=diff(f,2);%⼆阶导数h=double(solve(s));%⼀阶导数为零的点可能就是极值点,注意是可能,详情请见⾼数课本fori=1:length(h)ifsubs(s2,x,h(i))<0disp(['函数在' num2str(h(i))'处取得极⼤值,极⼤值为' num2str(subs(f,x,h(i)))])elseifsubs(s2,x,h(i))>0disp(['函数在' num2str(h(i))'处取得极⼩值,极⼩值为'num2str(subs(f,x,h(i)))])elsedisp(['函数在' num2str(h(i))'处⼆阶导数也为0,故在该点处函数可能有极⼤值、极⼩值或⽆极值'])%%%详情见⾼数课本endend。
高等数学:MATLAB实验

MATLAB实验
2.fplot绘图命令 fplot绘图命令专门用于绘制一元函数曲线,格式为:
fplot('fun',[a,b]) 用于绘制区间[a,b]上的函数y=fun的图像.
MATLAB实验 【实验内容】
MATLAB实验
由此可知,函数在点x=3处的二阶导数为6,所以f(3)=3为 极小值;函数在点x= 1处的二阶导数为-6,所以f(1)=7为极大值.
MATLAB实验
例12-10 假设某种商品的需求量q 是单价p(单位:元)的函 数q=12000-80p,商 品的总成本C 是需求量q 的函数 C=25000+50q.每单位商品需要纳税2元,试求使销售 利润达 到最大的商品单价和最大利润额.
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验 实验九 用 MATLAB求解二重积分
【实验目的】 熟悉LAB中的int命令,会用int命令求解简单的二重积分.
MATLAB实验
【实验M步A骤T】 由于二重积分可以化成二次积分来进行计算,因此只要
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
MATLAB实验
实验七 应用 MATLAB绘制三维曲线图
【实验目的】 (1)熟悉 MATLAB软件的绘图功能; (2)熟悉常见空间曲线的作图方法.
【实验要求】 (1)掌握 MATLAB中绘图命令plot3和 mesh的使用; (2)会用plot3和 mesh函数绘制出某区间的三维曲线,线型
matlab求曲线极值程序,matlab函数求极值matlab函数求极值.ppt

matlab求曲线极值程序,matlab函数求极值matlab函数求极值.pptmatlab函数求极值matlab函数求极值* * 函数的极值 1、⼀元函数的极值 函数命令:fminbnd 调⽤格式:[x,feval,exitflag,output]=fminbnd(fun,x1,x2,options) %求fun在区间(x1,x2)上的极值. 返回值: x:函数fun在(x1,x2)内的极值点 feval:求得函数的极值 exitflag: exitflag>0,函数收敛于解x处 exitflag=0,已达最⼤迭代次数 exiflag<0,函数在计算区间内不收敛. 例1:求函数 在 上的极⼩值. fun=inline('(x+pi)*exp(abs(sin(x+pi)))')[x,feval,exitflag,output]=fminbnd(fun,-pi/2,pi/2) fun = Inline function: fun(x) = (x+pi)*exp(abs(sin(x+pi))) x = -1.2999e-005 feval = 3.1416 exitflag = 1 output = iterations: 21 funcCount: 22 algorithm: 'golden section search, parabolic interpolation' message: [1x112 char] xx=-pi/2:pi/200:pi/2; yxx=(xx+pi).*exp(abs(sin(xx+pi))); plot(xx,yxx) xlabel('x'),grid on % 可以⽤命令[xx,yy]=ginput(1) 从局部图上取出极值点及相应函数值 例2:求解函数humps的极⼩值. type humps %humps 是⼀个Matlab提供的M 函数⽂件 function [out1,out2] = humps(x) %HUMPS A function used by QUADDEMO, ZERODEMO and FPLOTDEMO. % Y = HUMPS(X) is a function with strong maxima near x = .3 % and x = .9. % % [X,Y] = HUMPS(X) also returns X. With no input arguments, % HUMPS uses X = 0:.05:1. % % Example: % plot(humps) % % See QUADDEMO, ZERODEMO and FPLOTDEMO. % Copyright 1984-2002 The MathWorks, Inc. % $Revision: 5.8 $ $Date: 2002/04/15 03:34:07 $ if nargin==0, x = 0:.05:1; end y = 1 ./ ((x-.3).^2 + .01) + 1 ./ ((x-.9).^2 + .04) - 6; if nargout==2, out1 = x; out2 = y; else out1 = y; end[x,y]=fminbnd(@humps,0.5,0.8) x = 0.6370 y = 11.2528 xx=0:0.001:2; yy=humps(xx); plot(xx,yy) 例3:求 在(0,1)内的极⼩值. type myfunmin1 %显⽰M⽂件内容 function f=myfunmin1(x) f=x.^x; [x,y]=fminbnd(@myfunmin1,0,1) x = 0.3679 y =0.6922 xx=0:0.001:1; yy=myfunmin1(xx); plot(xx,yy) [x,y]=fminbnd('x.^x',0,1) x = 0.3679 y = 0.6922 2、 多元函数的极值 函数命令:fminsearch 调⽤格式:[x,feval,exitflag,output]=fminsearch(fun,x0,optipons) % 求在x0附近的极值 例4:求 的极⼩值. type myfunmin2 function f=myfunmin2(v) x=v(1); y=v(2); f=100*(y-x.^2).^2+(1-x).^2;[sx,sfeval]=fminsearch(@myfunmin2,[1 1]) sx。
实验三 用matlab求极限和导数
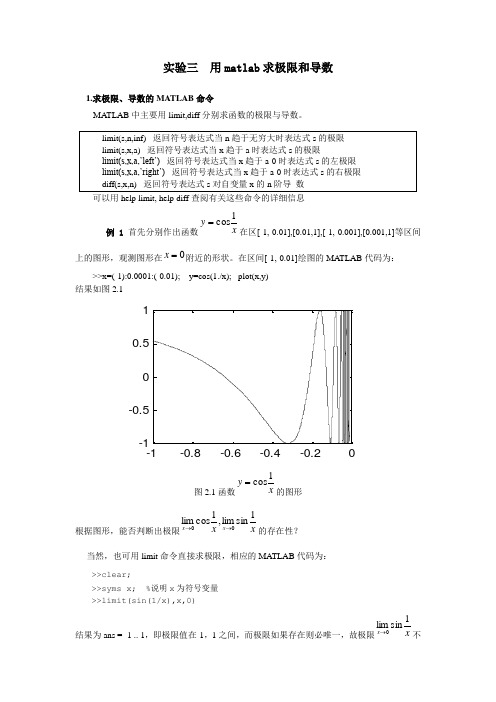
实验三 用matlab 求极限和导数1.求极限、导数的MATLAB 命令MATLAB 中主要用limit,diff 分别求函数的极限与导数。
可以用help limit, help diff 查阅有关这些命令的详细信息例1首先分别作出函数x y 1cos=在区[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=cos(1./x); plot(x,y) 结果如图2.1图2.1函数x y 1cos=的图形根据图形,能否判断出极限x x x x 1sinlim ,1cos lim 00→→的存在性? 当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear;>>syms x; %说明x 为符号变量>>limit(sin(1/x),x,0)结果为ans = -1 .. 1,即极限值在-1,1之间,而极限如果存在则必唯一,故极限x x 1sinlim 0→不存在,同样,极限x x 1coslim 0→也不存在。
例2 首先分别作出函数x xy sin =在区间[-1,-0.01],[0.01,1],[-1,-0.001],[0.001,1]等区间上的图形,观测图形在0=x 附近的形状。
在区间[-1,-0.01]绘图的MA TLAB 代码为: >>x=(-1):0.0001:(-0.01); y=sin(x)./x; plot(x,y) 结果如图2.2图2.2 函数x xy sin =的图形根据图形,能否判断出极限1sin lim0=→x xx 的正确性?当然,也可用limit 命令直接求极限,相应的MATLAB 代码为:>>clear; >>syms x;>>limit(sin(x)/x,x,0) 结果为ans =1.例3 观测当n 趋于无穷大时,数列n n n a )11(+=和1)11(++=n n n A 的变化趋势。
matlab多项式运算及求极限、复杂函数求极限

文章主题:深入探讨MATLAB中的多项式运算及求极限、复杂函数求极限MATLAB(Matrix Laboratory)是一款强大的数学软件,广泛应用于工程、科学、经济等领域。
在MATLAB中,多项式运算及求极限、复杂函数求极限是常见且重要的数学问题,对于提高数学建模和计算能力具有重要意义。
本文将从简到繁地探讨MATLAB中的多项式运算及求极限、复杂函数求极限,以帮助读者深入理解这一主题。
一、MATLAB中的多项式运算多项式是数学中常见的代数表达式,通常以系数的形式表示。
在MATLAB中,可以使用多种方法进行多项式的运算,如加法、减法、乘法、除法等。
对于两个多项式f(x)和g(x),可以使用“+”、“-”、“*”、“/”等运算符进行运算。
在实际应用中,多项式的运算往往涉及到多项式系数的提取、多项式的乘方、多项式的符号变化等操作。
MATLAB提供了丰富的函数和工具箱,如polyval、polyfit、roots等,可以帮助用户进行多项式的运算。
通过这些工具,用户可以方便地进行多项式的求值、拟合、求根等操作。
二、MATLAB中的多项式求极限求多项式的极限是微积分中常见的问题,对于研究函数的性质和图像具有重要意义。
在MATLAB中,可以通过lim函数来求多项式的极限。
lim函数可以接受不同的输入参数,如函数、变量、极限点等,从而计算多项式在某一点的极限值。
在进行多项式求极限时,需要注意的是对极限的性质和运算规则。
MATLAB中的lim函数遵循了标准的极限计算规则,如极限的四则运算法则、极限的有界性、极限的夹逼定理等。
用户可以通过lim函数灵活地进行多项式求极限的计算和分析。
三、MATLAB中的复杂函数求极限除了多项式,复杂函数在工程和科学中也具有广泛的应用。
MATLAB提供了丰富的函数和工具箱,如syms、limit、diff等,可以帮助用户进行复杂函数的求导、求极限等操作。
对于复杂函数的极限计算,需要综合运用代数运算、微分计算、极限性质等技巧。
Matlab系列教辅(4)-极限、导数和积分

小综合练习
问题:老张在银行存入1000元,复利率为 问题:老张在银行存入 元 每年10%, %,分别以按年结算和按连续复 每年 %,分别以按年结算和按连续复 利结算两种方式计算10年后老张在银行 利结算两种方式计算 年后老张在银行 的存款额。 注 按复利计算, 的存款额。(注:按复利计算,若每年结 算m次,则每个结算周期的复利率为 / 次 则每个结算周期的复利率为r/ m,r为年利润 。 , 为年利润)。 为年利润
分析: 表示n年后的存款额 年后的存款额, 分析:令 Pn 表示 年后的存款额, r 表示 年利率,用 P 表示本金,则 年利率, 表示本金, 按年结算,; 10 (1)按年结算,;P = P(1+ r)10 (2)按复利结算,设每年结算m次,则 按复利结算,设每年结算 次 每个结算周期的复利率为r/m,所以10 每个结算周期的复利率为r/m,所以10 r ) ,而我们所说的是 p (1 + 年后的存款额为 m 按连续复利计算,即一年结算无数次, 按连续复利计算,即一年结算无数次,所 以按连续复利计算的10 10年后的存款额应 以按连续复利计算的10年后的存款额应 为: P = lim p (1 + r )
符号微积分(求导)
例:求
1 d −2x (e cos(3x 2 )) dx
syms x y f=sym('exp(cos(3 x^(1 f=sym('exp(-2*x) * cos(3 * x^(1/2))') diff(f,x) 运行
符号微积分(求导)
例:求 ∂ f(x, y, g(x, y)), ∂x
问题:近年来, 问题:近年来,世界范围内每年的石油 消耗率呈指数增长, 消耗率呈指数增长,增长指数大约为 0.07。1970年初,消耗率大约为每年 年初, 。 年初 161亿桶 161亿桶.设 R(t) 表示从1970年起第年 亿桶. 表示从1970年起第年 的石油消耗率, 亿桶)。 的石油消耗率,则R(t ) = 161e0.07t (亿桶 。试 亿桶 用此式估计从1970年到 年到1990年间石油 用此式估计从 年到 年间石油 消耗的总量。 消耗的总量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
另一种是描述法,若集合 是由具有某种性质 的元素 的全体所组成的是两个非空集合,如果存在一个法则 ,使得对 中每个元素 ,按法则 ,在 中有 唯一确定的元素 与之对应,则称 为从 到 的映射,记作 其中 称为元素 在映射 下的像,并记作 ,即 ,即 ; 中所
第6章 函数、极限与连续的MATLAB求解
编者
Outline
6.1 6.2 6.3 6.4 6.5
映射与函数 数列的极限 函数的极限 函数的连续性与间断点 闭区间上连续函数的性质
6.1
1.集合
映射与函数
集合是数学中的一个基本概念,所谓集合是指具有某种特定性质的对象的总体,组成 这个集合的每一个体称为该集合的元素。如果 是集合 的元素,就说 属于 ,记作 , 否则就说 不属于 ,记作 或 。一个集合,若它只含有限个元素,则称为有限集; 否则称为无限集。 表示集合的方法通常有以下两种:一种是列举法,就是把集合的全体元素一一列举出 来表示。例如,由元素 组成的集合 可表示成
如果 使得 ,则 称为函数 设函数 在闭区间 上连续,且 内至少有一点 ,使 的零点。 与 异号(即
),那么在开区间
从几何上看,上述定理(称为零点定理)表示:如果连续曲线弧 的两个端点位于 轴的不同侧,那么这段曲线弧与 轴至少有一个交点。 将上述零点定理稍加推广可得到介值定理:设函数 在闭区间 上连续,且在这区间的 端点取不同的函数值 及 那么,对于 与 之间的任意一个数 ,在开区间 内至少有一点 ,使
谢谢大家!
6.4 函数的连续性与间断点
1.函数的连续性
设函数 在点 的某一邻域内有定义,如果
那么就称函数 在点 连续。 述函数的连续性定义利用程序语句的形式来描述可以编写函数文件FunContinuity.m。
运行结果如图所示。
图
函数连续性的图形直观表示
2.函数的间断点
设函数 在点 的某去心邻域内有定义,在此前提下,如果函数 有下列三种 情形之一: (1)在 没有定义; (2)虽在 有定义,但 不存在; (3)虽在 有定义,且 存在,但 , 则函数 在点 为不连续,而点 称为函数 的不连续点或间断点。 间断点的几种常见类型有:无穷间断点、振荡间断点、可去间断点和跳跃间断点等。 若根据函数的左极限与右极限是否存在分类还可以将间断点分为两类:如果 是函数 的 间断点,但左极限 及右极限 都存在,那么 称为函数 的的第一类间断点,不是 第一类间断点的任何间断点均成为第二类间断点。可去间断点和跳跃间断点属于第一类间 断点,而无穷间断点和振荡间断点属于第二类间断点。
3.常用数学函数
在我们所研究的函数关系中,有几类最基本的常见函数,这就是常值函数、幂函数、指 数函数、对数函数、三角函数和反三角函数,这几类函数称为基本初等函数。 MATLAB只提供了底为 的对数求解函数,对于一般情形,可根据换底公式:
6.2
数列的极限
1.数列极限的定义
设 为一数列,如果存在常数 ,对于任意给定的正数 (不论它多么小),总存 在正整数 ,使得当 时,不等式 都成立,那么就称常量 是数列 的极限,或者称数列 或 收敛于 ,记为
6.5
闭区间上连续函数的性质
上有定义的函数 ,如果存在 ,使得对于任一 都有
1.有界性与最大值最小值定理
对于在区间
则称 是函数 在区间 上的最大值(最小值)。 根据该定义,我们可以给出有界性与最大值最小值定理:在闭区间上连续的函数在该 区间上有界且一定能取到它的最大值和最小值。
2.零点定理与介值定理
)
函数极限的MATLAB符号求解
数列可以看成一种特殊的函数,所以求函数的极限仍然采用limit函数,此时其调用格式为: L=limit(fx, x, x0) L=limit(fx, x, x0, 'left') L=limit(fx, x, x0, 'right') 运行结果如图所示。
图
函数极限的图形直观表示
2.数列极限的MATLAB符号求解
在MATLAB中,提供了limit函数来求取数列的极限,其调用格式为: L=limit(xn, n, inf) L=limit(xn, inf)
运行结果如图所示。
图
数列极限的图形直观表示
6.3
函数的极限
函数极限的定义
1. 自变量趋于有限值时的函数极限 设函数 在点 的某一去心邻域内有定义,如果存在常数 ,对于任意给定的正数 ( 不论它多么小),总存在正数 ,使得当 满足不等式 时,对应的函数值 都 满足不等式 那么常数 就叫做函数 当 时的极限,记作 或 (当 ) 2. 自变量趋于无穷大时的极限 设函数 当 大于某一正数时有定义,如果存在常数 ,对于任意给定的正数 (不论 它多么小),总存在正数 ,使得当 满足不等式 时,对应的函数值 都满足不等式 那么常数 就叫做函数 当 时的极限,记作 或 (当
而元素 称为元素 在映射 下的原像;集合 称为映射 的定义域,记作 有元素的像所组成的集合称为映射 的值域,记作 或 ,即 设数集 ,则称映射 为定义在 上的函数,通常简记为
其中 称为自变量, 称为因变量, 称为定义域。
2. 反函数与复合函数
设函数 的定义域为 ,值域为 。如果对于任意数值 ,在 中都有唯一确定的值 , 使得 ,则得到以 为自变量, 为因变量的新函数,这个新函数叫做函数 的反函数,记作 ,其 定义域为 ,值域为 。
