曲面立体的截交线新
合集下载
《工程制图》第十章-曲面立体的截交线

三、 圆柱截交线例题
12
例题1 求圆柱截交线
1' 2'3'
4'5'
6'7'
8'
5
3
2
3" 5"
7"
1" 8"
解题步骤
2"
1 分析 截交线的水平投影为椭
圆,侧面投影为圆;
2 求出截交线上的特殊点Ⅰ、 Ⅳ、 Ⅴ、 Ⅷ;
4" 3 求出若干个一般点Ⅱ、Ⅲ、
Ⅵ、Ⅶ;
4 光滑且顺次地连接各点,作
6"
出截交线,并且判别可见性;
2 转向点 曲线上处于曲面投影转向线上的点,它们是区分 曲线可见与不可见部分的分界点。
3 特征点 曲线本身具有特征的点,如椭圆长短轴上四个端 点。
4 结合点 截交线由几部分不同线段(曲线、直线)组成时 结合处的那些点。
对于特殊点,根据现有的知识凡是能求出来的都应求出来 。
7
五、 作图步骤
1 根据截平面位置与曲面立体表面的性质、判别截交线的形 状和性质。
5 整理轮廓线。
Ⅲ
Ⅰ
Ⅱ
Ⅶ
Ⅳ
Ⅷ
Ⅵ
13
例题2 求圆柱截交线
解题步骤 1 分析 截交线的水平投影为椭 圆的一部分,侧面投影为圆的 一部分; 2 求出截交线上的特殊点Ⅰ、Ⅳ 、 Ⅴ; 3 求出若干个一般点Ⅱ、Ⅲ ; 4 光滑且顺次地连接各点,作出 截交线,并且判别可见性; 5 整理轮廓线。
14
例题6 想象出物体及其侧面投影的形状
18
§ 10-3 平面与 圆锥相交
一、平面与圆锥相交所得截交线形状 二、 圆锥截交线的求法 三、 圆锥截交线例题
第6章 曲面立体及截交线
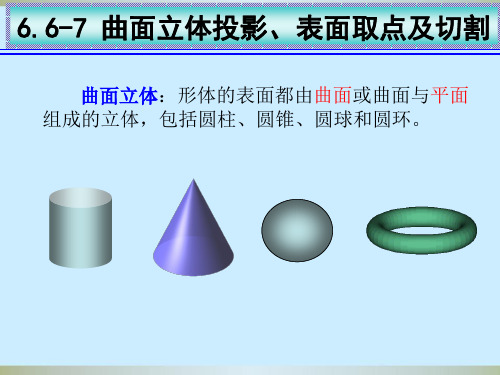
截平面位置 立 体 图 与V面平行 与H面平行 与V面垂直
投 影 图
六、圆球体切割
例5-11 圆球被一正垂面截切,完成其水平投影和侧 例5-11 求圆球被正垂面截切的截交线 面投影。 绘图步骤: (1)截交线的投影为椭圆,投 影椭圆上短轴的两个端点Ⅰ、 Ⅱ与长轴的两个端点Ⅲ 、 Ⅳ; (2)求截交线与轮廓线的交点 Ⅴ 、Ⅵ ; (3)求截交线与轮廓线的交点 Ⅶ 、Ⅷ ; (4)依次光滑连接各点; (5)检查并加粗可见轮廓线。 点击播放视频
c
a
例5-5 圆柱表面取点
a” (c”) b”
b
二、圆锥的投影及表面取点
圆锥的形成 圆锥是由一直母线绕与它相交的轴线旋转一周形 成的,具有一个底面和一个回转面(圆锥面)。 圆锥面上所有素线相交于锥顶,所有纬圆平行。
锥顶 圆锥面 母线 底面 轴线 素线 纬圆
(a) 圆锥面的形成 点击图片播放视频
(b) 圆锥的结构特征 圆锥的特征
s’
例5-6 圆锥表面取点
s”
a”
e’
e”
s
a e
素线法
二、圆锥的投影及表面取点
2、表面取点
例5-6 圆锥表面取点
例5-6 如图所示,已知点 A在圆锥表面上,并知它 的正面投影a’,可采用下 列两种方法求出点A的水 平投影a和侧面投影a” 。
s’
s”
a”
s a
纬圆法
三、圆球的投影及表面取点
圆球的形成 一圆周绕自身的一直径旋转一周即形成圆球, 形成的回转面称为圆球面。平面与球面的交线为 一个圆,称为纬圆。
(c) 圆锥面的结构特征
二、圆锥的投影及表面取点
1、投影分析 圆锥面的轮廓素线 圆锥的轴线垂直 SA、SB将圆柱面分成可 于H面。圆锥底圆为水 见的前半部分与不可见 平面,水平投影反映实 的后半部分。 形,其正面和侧面投影 轮廓素线SC、SD将 积聚为水平直线。 圆柱面分成可见的左半 圆锥面的水平投影 部分与不可见的右半部 为圆,其正面和侧面投 分。 影为三角形。
投 影 图
六、圆球体切割
例5-11 圆球被一正垂面截切,完成其水平投影和侧 例5-11 求圆球被正垂面截切的截交线 面投影。 绘图步骤: (1)截交线的投影为椭圆,投 影椭圆上短轴的两个端点Ⅰ、 Ⅱ与长轴的两个端点Ⅲ 、 Ⅳ; (2)求截交线与轮廓线的交点 Ⅴ 、Ⅵ ; (3)求截交线与轮廓线的交点 Ⅶ 、Ⅷ ; (4)依次光滑连接各点; (5)检查并加粗可见轮廓线。 点击播放视频
c
a
例5-5 圆柱表面取点
a” (c”) b”
b
二、圆锥的投影及表面取点
圆锥的形成 圆锥是由一直母线绕与它相交的轴线旋转一周形 成的,具有一个底面和一个回转面(圆锥面)。 圆锥面上所有素线相交于锥顶,所有纬圆平行。
锥顶 圆锥面 母线 底面 轴线 素线 纬圆
(a) 圆锥面的形成 点击图片播放视频
(b) 圆锥的结构特征 圆锥的特征
s’
例5-6 圆锥表面取点
s”
a”
e’
e”
s
a e
素线法
二、圆锥的投影及表面取点
2、表面取点
例5-6 圆锥表面取点
例5-6 如图所示,已知点 A在圆锥表面上,并知它 的正面投影a’,可采用下 列两种方法求出点A的水 平投影a和侧面投影a” 。
s’
s”
a”
s a
纬圆法
三、圆球的投影及表面取点
圆球的形成 一圆周绕自身的一直径旋转一周即形成圆球, 形成的回转面称为圆球面。平面与球面的交线为 一个圆,称为纬圆。
(c) 圆锥面的结构特征
二、圆锥的投影及表面取点
1、投影分析 圆锥面的轮廓素线 圆锥的轴线垂直 SA、SB将圆柱面分成可 于H面。圆锥底圆为水 见的前半部分与不可见 平面,水平投影反映实 的后半部分。 形,其正面和侧面投影 轮廓素线SC、SD将 积聚为水平直线。 圆柱面分成可见的左半 圆锥面的水平投影 部分与不可见的右半部 为圆,其正面和侧面投 分。 影为三角形。
曲面立体的截交线、贯穿点、相贯线.

1
d
f
e
29
平面体与曲面立体相交 交线 (相贯线)
共性
交线为二表面所共有线 求交线的本质 求二表面的共有点
本节重点讨论:求交线的基本方法
30
求交线的基本方法
作图步骤看动画演示
31
求交线的基本方法
例
此段外形轮廓线消失
(直线)构成的封 交线投影分析 实质是求平面体 闭的空间折线 交线的投影作图 各表面与回转体 H、 W投影已知 求V投影 求截交 的交线
特殊点 外形轮廓线 中间点 终止点 光滑连接曲线 截交线投影 虚实分界点 交线可见性
11
例 圆锥被水平面截切,求出截交线的另外两个投影。
3’
2’ 1’5”4” (4’)(5’)
3” 2” 1”
具体步骤如下: (1)先求特殊点。 (2)再求一般点。 (3)依次光滑连接各点。
5 4 3 2 1 4 5
内、外交线分别求解 注意检查 孔的外形轮廓线投影 截平面与孔的交线
7
4、平面与圆锥体相交 平面P与圆锥面的交线
P
P
P轴线 交线为圆
P∠轴线 > 交线为椭圆
8
平面P与圆锥面的交线
P
P
P ∠轴线 = 交线为抛物线
P ∠轴线 0 < 交线为双曲线
9
平面P与圆锥面的交线
P
归纳
P轴线 交线为圆 P∠轴线 > 交线为椭圆 P∠ 轴线 = 交线为抛物线 P∠轴线 0< 交线为双曲线 P过锥顶 交线为直线
10
P过锥顶 交线为直线
例 求截交线
椭圆短轴的投影 是什么点?
P
P
椭圆画法
4-2 曲面立体-截交线

例3 完成圆柱切口的水平投影和侧面投影。
1'(4') 4” 1” 2”
2'(3')
3”
圆弧侧 面投影 可见 最前、最后的 素线被截切到, 已不完整 作图:
Ⅳ Ⅲ Ⅰ Ⅱ
4(3)
(1)标记截交线的顶点; (2)求侧平面的水平投影; (3)求ⅠⅡ、ⅢⅣ的侧面投影; (4)求圆弧及水平面的侧面投影;
1(2)
1、平面切割圆柱体
例5 完成带切口圆筒的水平投影和侧面投影。
Ⅷ 1'(4')(5')(8') 8” 5” 4” 1” 2” Ⅶ Ⅴ Ⅵ Ⅳ Ⅰ Ⅲ Ⅱ
6” 2'(3') (6')(7')
7” 3”
作图:
8(7) 5(6) 4(3) 1(2)
§4-2 截交线
(1)标记截交线的顶点; (2)求侧平面的水平投影; (3)求直线ⅠⅡ、ⅢⅣ、ⅤⅥ和 ⅦⅧ 的侧面投影; (4)求圆弧及水平面的侧面投影; (5)完成作图。
短轴
a'b' e'(f')
中点
a' PV f” d”
a” e” c” b” F D
A E C B
c'(d')
b'
作图:
d f a c e
§4-2 截交线
长轴
b
(1)特殊点:最高点A、最低点B、最 前点C、最后点D ; (2)特殊点:转向轮廓线上的点E、F ; (3)一般点;
2、平面切割圆锥体
例6 求正垂面与直立正圆锥体的截交线。
2、平面切割圆锥体
平面与圆锥体表面的交线,因平面与圆锥轴线的相对位置 不同而有不同的形状,可能的情况有五种。
1'(4') 4” 1” 2”
2'(3')
3”
圆弧侧 面投影 可见 最前、最后的 素线被截切到, 已不完整 作图:
Ⅳ Ⅲ Ⅰ Ⅱ
4(3)
(1)标记截交线的顶点; (2)求侧平面的水平投影; (3)求ⅠⅡ、ⅢⅣ的侧面投影; (4)求圆弧及水平面的侧面投影;
1(2)
1、平面切割圆柱体
例5 完成带切口圆筒的水平投影和侧面投影。
Ⅷ 1'(4')(5')(8') 8” 5” 4” 1” 2” Ⅶ Ⅴ Ⅵ Ⅳ Ⅰ Ⅲ Ⅱ
6” 2'(3') (6')(7')
7” 3”
作图:
8(7) 5(6) 4(3) 1(2)
§4-2 截交线
(1)标记截交线的顶点; (2)求侧平面的水平投影; (3)求直线ⅠⅡ、ⅢⅣ、ⅤⅥ和 ⅦⅧ 的侧面投影; (4)求圆弧及水平面的侧面投影; (5)完成作图。
短轴
a'b' e'(f')
中点
a' PV f” d”
a” e” c” b” F D
A E C B
c'(d')
b'
作图:
d f a c e
§4-2 截交线
长轴
b
(1)特殊点:最高点A、最低点B、最 前点C、最后点D ; (2)特殊点:转向轮廓线上的点E、F ; (3)一般点;
2、平面切割圆锥体
例6 求正垂面与直立正圆锥体的截交线。
2、平面切割圆锥体
平面与圆锥体表面的交线,因平面与圆锥轴线的相对位置 不同而有不同的形状,可能的情况有五种。
§4.2 平面与立体相交求截交线

1
s 2
3
(3)连接各点同面投影即等截交 线的三个投影
(4)补全棱线投影
求作四棱锥被截切后的水平投影和侧面投影。
分析:截平面为正垂面 截交线的正面投影积聚 为直线。截平面与四条 棱线相交,从正面可直 接找出交点。 作出各对应点的投影, 4• 1 2
•
1'
(4') 2'
3'
4"
3"
2"
1"
依次连接各点。 3 补全棱锥体的外形投影。
3 1
2
a
3
2
[例题5]
分析并想象出圆锥穿孔后的投影
主要内容
4.2.1 圆柱截交线 4.2.2 圆锥截交线
4.2.3 圆球截交线
一.面与圆球相交所得截交线
圆
二.求圆球截交线上点
平行圆画法:在圆球表面上取若干个平行于投
影面的平行圆,求这些平行圆与截平面的交点;
三.圆球截交线
[例题1]求圆球截交线
ο
截平面与圆锥轴线
倾斜,倾角θ>α 截交线为椭圆。
Pv
Pv
Pv
截平面与圆锥轴线 倾斜面,倾角θ=α 截交线为抛物线。
截平面与圆锥轴线 平行或倾角θ<α, 截交线为双曲线。
截平面过锥顶截 交线为三角形。
特殊点 一般点 b'
a'
a''
c'
b''
c''
整理加深
S
由点连线
P
b
c
a
Ⅰ
解题步骤 1 分析 截交线的水 平投影和侧面投影已 知,正面投影为双曲 线并反映实形; 2 求出截交线上的特 殊点A、C; 3 求出一般点B ; 4 光滑且顺次地连接 各点,作出截交线, 并且判别可见性; 5 整理轮廓线。
第10章 曲面立体的截交线

第十章曲面立体的截交线基本要求§10-1 概述§10-2 平面与圆柱相交§10-3 平面与圆锥相交§10-4 平面与圆球相交§10-5 综合题基本要求§10-1 概述一、截交线的性质二、截交线的类型及形状三、求作截交线的方法四、截交线上的特殊点五、作图步骤一、曲面立体截交线的性质二、截交线的类型及形状三、求作截交线的方法四、特殊点五、作图步骤§10-2 平面与圆柱相交一、平面与圆柱相交所得截交线形状二、求圆柱截交线上点的方法三、例题一、平面与圆柱相交所得截交线形状圆矩形椭圆二、求圆柱截交线上点的方法三、例题11'1"5"4" 8' 8"83254ⅦⅢⅡ ⅣⅤⅠ4'5' 2'3' 2" 3" 解题步骤1.分析 截平面为正垂面,截交线的侧面投影为圆,水平投影为椭圆;2.求出截交线上的特殊点Ⅰ、Ⅳ、 Ⅴ、 Ⅷ;3.求出若干个一般点Ⅱ、Ⅲ、 Ⅵ、Ⅶ;4.光滑且顺次地连接各点,作出截交线,并且判别可见性; 5.整理轮廓线。
7 66'7'6"7"解题步骤1.分析侧面投影为圆的一部分,截交线的水平投影为椭圆的一部分; 2.求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ ;3.求出若干个一般点Ⅳ、 Ⅴ ; 4.光滑且顺次地连接各点,作出截交线,并且判别可见性; 5 整理轮廓线。
3453'3"4'5'5' 4'1'2'2"1"122' 1'4'3'[例题3] 求圆柱截交线解题步骤1.分析 截交线的水平投影为直线和部分圆,侧面投影为矩形;2.求出截交线上的特殊点Ⅰ、Ⅱ、Ⅲ、Ⅳ; 3.顺次地连接各点,作出截交线并判别可见性; 4.整理轮廓线。
4-1 立体的截交线
平面与曲面立体的交线一般为封闭的平面曲线。 平面与曲面立体的交线一般为封闭的平面曲线 。 截交线上的点是曲面上的素线与截平面的交点。 截交线上的点是曲面上的素线与截平面的交点 。 曲面体截交线的性质: 曲面体截交线的性质: 截交线的性质 1、封闭的平面图形(曲、平线围成)。 封闭的平面图形( 封闭的平面图形 平线围成)。 2、截交线为立体表面和截平面的共有线。 截交线为立体表面和截平面的共有线。 截交线为立体表面和截平面的共有线 3、截交线上的点为立体表面和截平面的共有点。 截交线上的点为立体表面和截平面的共有点。 截交线上的点为立体表面和截平面的共有点 求曲面体的截交线的方法: 求曲面体的截交线的方法: 截交线的方法 依 找出立体表面和平面上的若干共有点, 找出立体表面和平面上的若干共有点,然后 次连线。 次连线。
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。
截交线投影分析 截交线投影分析: 投影分析
截平面
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。
截交线空间及投 截交线空间及投 影分析: 影分析
截交线的正面投影
水平投影和侧面 投影是小于原形 的类似形
截平面是正垂面, 截平面是正垂面, 截交线在正立面内 积聚为一线 截平面
截交线空间是三边形
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。 s' s" 3' 2´ 1' a' a b' 1 Ⅲ s 2 b 3 c A Ⅰ Ⅱ B c' a" S
1. 找出有积聚性的投影 2. 从已知投影开始, 从已知投影开始, 确定各棱线的交点1` 确定各棱线的交点 2`3`。 3. 用线上取点的方法求 C 得其余各投影。 得其余各投影。 4. 连接棱面上的交线并 判断可见性。 判断可见性。
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。
截交线投影分析 截交线投影分析: 投影分析
截平面
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。
截交线空间及投 截交线空间及投 影分析: 影分析
截交线的正面投影
水平投影和侧面 投影是小于原形 的类似形
截平面是正垂面, 截平面是正垂面, 截交线在正立面内 积聚为一线 截平面
截交线空间是三边形
例4-1 :求三棱锥被正垂面截切截交线的投影。 求三棱锥被正垂面截切截交线的投影。 s' s" 3' 2´ 1' a' a b' 1 Ⅲ s 2 b 3 c A Ⅰ Ⅱ B c' a" S
1. 找出有积聚性的投影 2. 从已知投影开始, 从已知投影开始, 确定各棱线的交点1` 确定各棱线的交点 2`3`。 3. 用线上取点的方法求 C 得其余各投影。 得其余各投影。 4. 连接棱面上的交线并 判断可见性。 判断可见性。
第4章 平面与曲面立体相交、两曲面立体相交

图4-7 辅助平面法作图原理
例:求作如图所示部分球体与圆锥台的相贯线。
(1) 空间分析及投影分析:
部分球体为 1/4 球前后对称地切去两块而成,圆锥台的轴 线垂直于水平面但不通过球心,其相贯线为前后对称的封闭空 间曲线。因为球与锥台的各投影都没有积聚性 , 故需用辅助平 面法求作相贯线。
(2) 作图:
② 作一般位置点。 在点I、III的高度范围 内 , 选取水平面 R 为辅助平 面,平面R与球及圆锥台的截 交线分别是以r2、r3为半径 的圆弧, 它们的交点Ⅴ、Ⅵ 就是相贯线上的点。先求出 水 平 投 影 5 、 6, 然 后 找 到 5′、 6′和 5" 、 6", 如图 (d)所示。
③ 依次光滑连接各点的 投影, 并判别可见性, 完 成相贯线的投影。最后 注意,圆锥台左视轮廓 素线画到2"、4"两点, 球体左视轮廓素线上有 一段虚线, 如图 (e)所示。
① 辅助平面法的实质, 是求辅助平面分别截两立 体所得截交线的交点。
② 辅助平面位置选取的原则,是使辅助平面分别 截两立体所得截交线的形状最简单(直线和圆),以便用 工具作图。
例:求轴线正交的水平圆柱与直立圆锥的相贯线。
解题步骤:
1'
4' 3'
1"
PV1 PV2
PV3
2" y y
4" PW1
PW2
g"(h")
c"
y
d e a g c h f b
y
2、利用辅助平面法求相贯线
作图原理 :
如图,为了求作部分球 体与圆锥台相交的表面共有 点,假想用一平面P (称为 辅助平面)截切两立体。平 面P 与部分球体的截交线为 一个圆LA,平面P 与圆锥台 的截交线也为一个圆LB。 LA 与LB的交点K1和K2 即为辅助 平面P、球体和圆锥台三个表 面的共有点,因此也是相贯 线上的点。 这种利用三面共点的原 理求相贯线上的点的方法叫 做辅助平面法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3'' 5'' 7''
8
6
4
7
5
3
是什么立体?属于截切的 低点、最前点、最后点、最左点、最 那种情况? 右点、转向轮廓线上的点(可见与不 截交线的水平投影 可见的分界点),椭圆长短轴上的点。 截交线的侧面投影 2、找一般点(至少一对) 3、将点的投影光滑连线 4、加粗可见的轮廓线
1、找截交线的特殊点:最高点、最 分析:截交线的正面投影
一、平面与圆柱相交
截交线的形状有几种?
矩形 圆 椭圆
一、平面与圆柱相交
5'
(6‘) (7‘) 4' 3' 2' 6 '' 7 '' 8 '' 5'' 4'' 3'' 1 '' 2 ''
(8‘) 1'
7 8 1
6
5
2 3
4
是什么立体?属于截切的 低点、最前点、最后点、最左点、最 那种情况? 右点、转向轮廓线上的点(可见与不 截交线的水平投影 可见的分界点)。 截交线的侧面投影 2、找一般点(至少一对) 3、将点的投影光滑连线 4、加粗可见的轮廓线
§2-3 平面与回转体表面相交
曲面立体截交线的性质
1. 曲面立体的截交线通常是封闭的平面曲线,或是由曲线和 直线所围成的平面图形或多边形;
2. 曲面立体的截交线为曲面立体表面和截平面的共有线; 3. 曲面立体截交线上的点为立体表面和截平面的共有点。 4. 截交线的形状与立体的形状及截平面的相对位置有关。
1、找截交线的特殊点:最高点、最 分析:截交线的正面投影
一、平面与圆柱相交
1'( 2' ) 2 ''
1 ''
3 ''
3 ' (4')
4 ''
4 2
31
例1 完成立体被截切后投影
1' (2')
2 ''
1 ''
3 ' (4')
4 ''
3 ''
2 4
1 3
〔例2〕完成圆柱体左边被切凹槽,右边被切凸台后的水 平投影
a' b'
a"( b" )
A
B
a
b
例3 已知空心缺口圆柱的正面投影和水平投影, 作出 空心圆柱被切后的侧面投影。
1 ' (2') 3 ' (4')
Ⅰ Ⅲ
Ⅱ Ⅳ
4
2
31
二、平面与圆锥相交
截交线的形状有几种?
圆
三角形
椭圆
双曲线
抛物线
二、平面与圆锥相交
5 ' (4') (6') 7' (8')
3'
4'' 6'' 8''
判断 各截 平面 形状
截平 面为 圆或 者多 边形
找关 键点 用圆 规和 直尺 作图
判断 可见 性并 补全 投影
检查 结果
曲面立体截切部分结束
P
4 3 2 5 6
7 8
Q
1 10
9
〔例8 〕 完成组合立体被截切后的投影
(5')2' (3') 1' 4' 3" 5" 4" 2"
1"
3
5 1 4 2
求曲面立体截交线的步骤
求曲面立体截交线的步骤:
截平 面为 曲线 图形
找若 干特 殊点 和一 般点 光滑 连接
确定 截切 前基 本体 形状
判断 截平 面数 量及 位置
1' 2' 5' (4') 7' (6') (8') 3'
r' q '
P
8
6
4
1 7 5
2 3
〔例7 〕 求作圆锥被Q与P平面截切以后,所截交线的 四、立体组合截切 投影
有两个以上的基本体便可构成组合体,平面与组 8 8' 合体截切一般会产生几段不同的交线,相邻两段交线 9' 7" 9" 10' 1' 3' " 2' 的分界点必在组合体的分界线上。因此,作组合截切 (7' 5" 1" (4') (5')(6') ) (6") 4" 3" 2" (10") 时应先确定各立体的形状,及确定相邻立体间的分界 线,然后分别作出各自的截交线。
〔例4〕求作圆锥被Q与P平面截切以后,所截交线的投影
p
7' 6"
7"
q
5' 3' (6') (4') 1' (2')
Hale Waihona Puke 4"2"
5" 3"
1"
Q
Ⅺ
Ⅻ Ⅹ Ⅲ Ⅰ
2 4
P
6 7
Ⅳ
Ⅱ
1 3
5
三、平面与球相交
圆
〔例5〕 作出半圆球被切口以后交线的投影
〔例6〕 完成圆球被正垂面截切以后的水平投影
p '
