2006中考压轴题精选
2006年全国中考数学压轴题全析全解(二)

2006年全国中考数学压轴题全析全解(二)8、(2006吉林长春)如图,在平面直角坐标系中,两个函数621,+-==x y x y 的图象交于点A 。
动点P 从点O 开始沿OA 方向以每秒1个单位的速度运动,作PQ ∥x 轴交直线BC 于点Q ,以PQ 为一边向下作正方形PQMN ,设它与△OAB 重叠部分的面积为S 。
(1)求点A 的坐标。
(2)试求出点P 在线段OA 上运动时,S 与运动时间t (秒)的关系式。
(3)在(2)的条件下,S 是否有最大值?若有,求出t 为何值时,S 有最大值,并求出最大值;若没有,请说明理由。
(4)若点P 经过点A 后继续按原方向、原速度运动,当正方形PQMN 与△OAB 重叠部分面积最大时,运动时间t 满足的条件是____________。
解:(1)由⎪⎩⎪⎨⎧+-==,621,x y x y 可得⎩⎨⎧==.4,4y x ∴A (4,4)。
(2)点P 在y = x 上,OP = t ,则点P 坐标为).22,22(t t 点Q 的纵坐标为t 22,并且点Q 在621+-=x y 上。
∴t x x t 212,62122-=+-=, 即点Q 坐标为)22,212(t t -。
t PQ 22312-=。
当t t 2222312=-时,23=t 。
当时230≤<t , .2623)22312(222t t t t S +-=-=当点P 到达A 点时,24=t ,当2423<t<时, 2)22312(t S -= 144236292+-=t t 。
(3)有最大值,最大值应在230≤<t 中, ,12)22(2312)824(232623222+--=++--=+-=t t t t t S当22=t 时,S 的最大值为12。
(4)212≥t 。
9、(2006湖南常德)把两块全等的直角三角形ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中90ABC DEF ∠=∠=,45C F ∠=∠=,AB=DE=4,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q 。
2006年到2012年嘉兴中考压轴题汇总

2006年到2012年嘉兴中考压轴题汇总一、选择题10.(2006)已知函数5-=x y,令21=x、1、23、2、25、3、27、4、29、5,可得函数图象上的十个点.在这十个点中随机取两个点),(11y x P 、),(22y x Q ,则P 、Q 两点在同一反比例函数图象上的概率是( ) (A )91 (B )454 (C )457 (D )5210.(2007)给出三个命题:①点P (b ,a )在抛物线y =x 2+1上;②点A (1,3)能在抛物线y =ax 2+bx +1上;③点B (-2,1)能在抛物线y =ax 2-bx +1上.若①为真命题,则( ) (A )②③都是真命题 (B )②③都是假命题(C )②是真命题,③是假命题(D )②是假命题,③是真命题10.(2008)一个函数的图象如图,给出以下结论: ①当0x =时,函数值最大;②当02x <<时,函数y 随x 的增大而减小; ③存在001x <<,当0x x =时,函数值为0. 其中正确的结论是( ) A .①② B .①③ C .②③ D .①②③10.(2009)如图,等腰△ABC 中,底边aBC=,︒=∠36A,ABC ∠的平分线交AC 于D ,BCD ∠的平分线交BD 于E ,设215-=k ,则=DE( )A .a k 2B .a k 3C .2kaD .3ka10.(2010)如图,已知C 是线段AB 上的任意一点(端点除外),分别以AC 、BC 为斜边并且在AB 的同一侧作等腰直角△ACD 和△BCE ,连结AE 交CD 于M ,连结BD 交CE 于N .给出以下三个结论:①ABMN //;②BCAC MN111+=;③ABMN41≤.其中正确结论的个数是( ) (A )0(B )1(C )2(D )310.(2011)如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH (不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm 2,四边形ABCD 面积是11cm 2,则①②③④四个平行四边形周长的总和为( )(第10题)ADC EB (第10题) ABCDEMN(第10题)(A )48cm (B )36cm (C )24cm(D )18cm10.(2012)如图,正方形ABCD 的边长为a ,动点P 从点A 出发,沿折线A →B →D →C →A 的路径运 动,回到点A 时运动停止.设点P 运动的路程长为长为x ,AP 长为y ,则y 关于x 的函数图象大致是( )A .B .C .D .二、填空题 16.(2006)定义一种对正整数n 的“F 运算”:①当n 为奇数时,结果为53+n;②当n 为偶数时,结果为kn 2(其中k 是使kn 2为奇数的正整数),并且运算重复进行.例如,取26=n,则:若449=n,则第449次“F 运算”的结果是 .16.(2007)如图,AB 是⊙O 的直径,CD 是圆上的两点(不与A 、B 重合),已知BC =2,tan ∠ADC =54,则AB =__________.16.(2008)定义1:与四边形四边都相切的圆叫做四边形的内切圆. 定义2:一组邻边相等,其他两边也相等的凸四边形叫做筝形. 探究:任意筝形是否一定存在内切圆?答案: .(填“是”或“否”)16.(2009)如图,在直角坐标系中,已知点)0,3(-A ,)4,0(B ,对△OAB 连续作旋转变换,依次得到三角形①、②、③、④…,则三角形⑩的直角顶点的坐标为 .(第10题)FABCDHEG①②③④⑤F ②F ①F ②…第1次 第2次 第3次D 2007年16题16.(2010)在直角坐标系中,横坐标和纵坐标都是整数的点称为格点.已知一个圆的圆心在原点、半径等于5,那么这个圆上的格点有 个.16.(2011)如图,AB 是半圆直径,半径OC ⊥AB 于点O ,AD 平分∠CAB 分别交OC 于点E ,交弧BC 于点D ,连结CD 、OD ,给出以下四个结论:①S △AEC =2S △DEO ;②AC=2CD ;③线段OD 是DE 与DA 的比例中项;④ABCE CD⋅=22.其中正确结论的序号是 .16.(2012)如图,在Rt △ABC 中,∠ABC=90°,BA=BC .点D 是AB 的中点,连接CD ,过点B 作BG 丄CD ,分别交GD 、CA 于点E 、F ,与过点A 且垂直于的直线相交于点G ,连接DF .给出以下四个结论: ①;②点F 是GE 的中点;③AF=AB ;④S △ABC =S △BDF ,其中正确的结论序号是 .三、23题 23.(2006)如图,已知△ABC ,6==BC AC ,︒=∠90C .O 是AB 的中点,⊙O 与AC 相切于点D 、与BC 相切于点E .设⊙O 交OB 于F ,连DF 并延长交CB 的延长线于G . (1)BFG ∠与BGF ∠是否相等?为什么? (2)求由DG 、GE 和弧ED23.(2007)解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.(1)设A =3x x -2-xx +2,B =x 2-4x ,求A 与B 的积;(2)提出(1)的一个“逆向”问题,并解答这个问题. 23.(2008)小丽参加数学兴趣小组活动,提供了下面3个有联系的问题,请你帮助解决:(第16题)A BDCOEA(1)如图1,正方形A B C D 中,作A E 交B C 于E ,D F A E ⊥交A B 于F ,求证:A E D F =; (2)如图2,正方形A B C D 中,点E F ,分别在A D B C ,上,点G H ,分别在A B C D ,上,且E F G H ⊥,求E F G H的值;(3)如图3,矩形A B C D 中,A B a =,B C b =,点E F ,分别在A D B C ,上,且E F G H ⊥,求E F G H的值.23.(2009)如图,已知一次函数bkx y+=的图象经过)1,2(--A ,)3,1(B 两点,并且交x 轴于点C ,交y轴于点D ,(1)求该一次函数的解析式; (2)求OCD∠tan的值;(3)求证:︒=∠135AOB .23.(2010)如图,已知⊙O 的半径为1,PQ 是⊙O 的直径,n 个相同的正三角形沿PQ 排成一列,所有正三角形都关于PQ 对称,其中第一个111C B A △的顶点1A 与点P 重合,第二个222C B A △的顶点2A 是11C B 与PQ 的交点,…,最后一个n n n C B A △的顶点n B 、n C 在圆上.(1)如图1,当1=n时,求正三角形的边长1a ;(第23题图1) (第23题图2)(第23题图3)Q1(第23题 图1)Q(第23题 图2)Qn n(第23题)(2)如图2,当2=n时,求正三角形的边长2a ;(3)如题图,求正三角形的边长n a (用含n 的代数式表示).23.(2011)以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH .(1)如图1,当四边形ABCD 为正方形时,我们发现四边形EFGH 是正方形;如图2,当四边形ABCD为矩形时,请判断:四边形EFGH 的形状(不要求证明);(2)如图3,当四边形ABCD 为一般平行四边形时,设∠ADC =α(0°<α<90°),① 试用含α的代数式表示∠HAE ; ② 求证:HE =HG ;③ 四边形EFGH 是什么四边形?并说明理由.四、24题23.(2012嘉兴)将△ABC 绕点A 按逆时针方向旋转θ度,并使各边长变为原来的n 倍,得△AB ′C ′,即如图①,我们将这种变换记为[θ,n].(1)如图①,对△ABC 作变换[60°,]得△AB ′C ′,则S △AB ′C ′:S △ABC = 3 ;直线BC 与直线B ′C ′所夹的锐角为 60 度;(2)如图②,△ABC 中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B 、C 、C ′在同一直线上,且四边形ABB'C'为矩形,求θ和n 的值;(4)如图③,△ABC 中,AB=AC ,∠BAC=36°,BC=l ,对△ABC 作变换[θ,n]得△AB ′C ′,使点B 、C 、B ′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n 的值.四、24题 24.(2006)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC 由同一平面内的两段ABCDHEF G (第23题图2) EBFGDHAC(第23题图3)(第23题图1) A BCDHEF G抛物线组成,其中AB 所在的抛物线以A 为顶点、开口向下,BC 所在的抛物线以C 为顶点、开口向上.以过山脚(点C )的水平线为x 轴、过山顶(点A )的铅垂线为y 轴建立平面直角坐标系如图(单位:百米).已知AB 所在抛物线的解析式为8412+-=xy,BC 所在抛物线的解析式为2)8(41-=x y,且已知)4,(m B .(1)设),(y x P 是山坡线AB 上任意一点,用y 表示x ,并求点B 的坐标;(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图). ①分别求出前三级台阶的长度(精确到厘米); ②这种台阶不能一直铺到山脚,为什么?(3)在山坡上的700米高度(点D )处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E 处,1600=OE (米).假设索道DE 可近似地看成一段以E 为顶点、开口向上的抛物线,解析式为2)16(281-=x y.试求索道的最大悬空..高度.24.(2007)如图,已知A (8,0),B (0,6),两个动点P 、Q 同时在△OAB 的边上按逆时针方向(→O→A →B →O →)运动,开始时点P 在点B 位置,点Q 在点O 位置,点P 的运动速度为每秒2个单位,点Q 的运动速度为每秒1个单位.(1)在前3秒内,求△OPQ 的最大面积;(2)在前10秒内,求P 、Q 两点之间的最小距离,并求此时点P 、Q 的坐标;(3)在前15秒内,探究PQ 平行于△OAB24.(2008)如图,直角坐标系中,已知两点(00)(20)O A ,,,,点B 在第一象限且O A B △为正三角形,O A B △的外接圆交y 轴的正半轴于点C ,过点C 的圆的切线交x 轴于点D .(1)求B C ,两点的坐标; (2)求直线C D 的函数解析式;(3)设E F ,分别是线段A B A D ,上的两个动点,且E F 平分四边形A B C D 的周长. 试探究:A E F △的最大面积?24.(2009)如图,已知A 、B 是线段MN 上的两点,4=MN,1=MA,1>MB .以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设xAB =.(1)求x 的取值范围;(2)若△ABC 为直角三角形,求x 的值; (3)探究:△ABC 的最大面积?24.(2010)如图,已知抛物线4212++-=x xy交x 轴的正半轴于点A ,交y 轴于点B .(1)求A 、B 两点的坐标,并求直线AB 的解析式; (2)设),(y x P (0>x)是直线xy=上的一点,Q 是OP 的中点(O 是原点),以PQ 为对角线作正方形PEQF .若正方形PEQF 与直线AB 有公共点,求x 的取值范围;(3)在(2)的条件下,记正方形PEQF 与△OAB 公共部分的面积为S ,求S 关于x 的函数解析式,并探究S 的最大值.24.(2011浙江省嘉兴,24,14分)已知直线3+=kx y (k<0)分别交x 轴、y 轴于A 、B 两点,线段OA 上有一动点P 由原点O 向点A 运动,速度为每秒1个单位长度,过点P 作x 轴的垂线交直线AB(第24题) (第24题)OABPEQF x y (第24题)于点C ,设运动时间为t 秒. (1)当1-=k时,线段OA 上另有一动点Q 由点A 向点O 运动,它与点P 以相同速度同时出发,当点P 到达点A 时两点同时停止运动(如图1). ① 直接写出t =1秒时C 、Q 两点的坐标;② 若以Q 、C 、A 为顶点的三角形与△AOB 相似,求t 的值. (2)当43-=k时,设以C 为顶点的抛物线nm x y++=2)(与直线AB 的另一交点为D (如图2),① 求CD 的长;② 设△COD 的OC 边上的高为h ,当t 为何值时,h 的值最大?24.(2012嘉兴)在平面直角坐标系xOy 中,点P 是抛物线:y=x 2上的动点(点在第一象限内).连接 OP ,过点0作OP 的垂线交抛物线于另一点Q .连接PQ ,交y 轴于点M .作PA 丄x 轴于点A ,QB 丄x 轴于点B .设点P 的横坐标为m . (1)如图1,当m= 时,①求线段OP 的长和tan ∠POM 的值;②在y 轴上找一点C ,使△OCQ 是以OQ 为腰的等腰三角形,求点C 的坐标; (2)如图2,连接AM 、BM ,分别与OP 、OQ 相交于点D 、E . ①用含m 的代数式表示点Q 的坐标;②求证:四边形ODME 是矩形.(第24题图2)(第24题图1)。
上海中考物理压轴题精选[1]
![上海中考物理压轴题精选[1]](https://img.taocdn.com/s3/m/a0cc30571ed9ad51f11df229.png)
上海中考物理压轴题精选1.(2006年上海中考第17题)在图l1(a)所示的电路中,电源电压为6伏且不变,滑动变阻器R 2上标有“50Ω 2A ”字样。
闭合电键S ,移动滑片P 到某位置时,电压表、电流表的示数分别为2伏和0.2安。
求:(1)滑动变阻器R 2接入电路的阻值。
(2)电阻R 1的阻值。
(3)在移动滑片P 的过程中,通过电阻R 1的最大电流I 最大。
(4)改变滑片P 的位置,使电压表、电流表指针偏离零刻度线的角度恰好相同,如图10(b)和(c)所示,此时滑动变阻器R 2接入电路的阻值。
2.(2007年上海中考第17题)如图 11 所示,边长分别为 0.2 米和 0.1 米的实心正方体 A 、B 放置在水平地面上,ρA 为 0.l×l03 千克/米 3, ρB 为 0.8×l03 千克/米 3。
求:(1) 物体 A 的质量m A 。
(2) 物体 B 对地面的压力F B 。
(3) 小明和小华两位同学设想在正方体 A 、B 上部沿水平方向分别截去一定的厚度后,通 过计算比较A 、B 剩余部分对地面压强的大小关系。
小明设想在 A 、B 的上部均截去 0.09 米,小华设想在 A 、B 的上部均截去 0.05 米,他们的计算过程及得出的结论分别如下表所示:①请判断:就他们设想截去的厚度而言,小明的结论是 的,小华的结论是 的。
(均选填“正确”或“错误”)②是否有可能存在某一厚度h ,沿水平方向截去 h 后使 A 、B 剩余部分对地面的压强相等?若有可能,求出 h 的值;若没有可能,说明理由。
3.(2008年上海中考第17题)在图10所示的电路中,电源电压为15伏且不变,滑动变阻器R 2上标有“20Ω 2A ”字样。
闭合电键S 后,电流表的示数为0.2安,电压表的示数为2伏。
图10AB图11图(a )求 :(1)滑动变阻器 R 2 连入电路的阻值。
(2)电阻R 1消耗的电功率 P 1。
2006年全国中考数学压轴题全解全析(完整版第一辑)

2006年全国中考数学压轴题全解全析(完整版第一辑)一年一度的中考结束了,中考数学中的压轴题向来是广大师生非常关注的,因为这些试题往往在很大程度上决定了考分的高下,为了帮助大家迎接明年的中考,特别制作了此资料,希望能对大家有一定的帮助。
1、(北京课改B 卷)我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形.请解答下列问题:(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;(2)探究:当等对角线四边形中两条对角线所夹锐角为60时,这对60角所对的两边之和与其中一条对角线的大小关系,并证明你的结论.[解] (1)答案不唯一,如正方形、矩形、等腰梯形等等.(2)结论:等对角线四边形中两条对角线所夹锐角为60时,这对60角所对的两边之和大于或等于一条对角线的长.已知:四边形ABCD 中,对角线AC ,BD 交于点O ,AC BD =,且60AOD ∠=.求证:BC AD AC +≥.证明:过点D 作DF AC ∥,在DF 上截取DE ,使DE AC =. 连结CE ,BE .故60EDO ∠=,四边形ACED 是平行四边形. 所以BDE △是等边三角形,CE AD =. 所以DE BE AC ==.①当BC 与CE 不在同一条直线上时(如图1), 在BCE △中,有BC CE BE +>. 所以BC AD AC +>.②当BC 与CE 在同一条直线上时(如图2), 则BC CE BE +=. 因此BC AD AC +=.综合①、②,得BC AD AC +≥.即等对角线四边形中两条对角线所夹角为60时,这对60角所对的两边之和大于或等于其中一条对角线的长.[点评]本题是一道探索题,是近年来中考命题的热点问题,在第2小题中要求学生先猜想可能的结论,再进行证明,这对学生的确有较高的能力要求,而在探索结论前可以自己先画几个草图,做到心中有数再去努力求证;很多学生往往会忽略特殊情况没有进行讨论,应当予以关注,总之这是一道新课标形势下的优秀压轴题。
2006中考压轴题汇编

2006华师大版中考压轴题精选及解析1、(2006 广东省实验区)如图所示,在平面直角坐标系中,四边形OABC 是等腰梯形,BC OA ∥,7460OA AB COA === ,,∠,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合.连结CP ,过点P 作PD 交AB 于点D . (1)求点B 的坐标;(2)当点P 运动什么位置时,OCP △为等腰三角形,求这时点P 的坐标; (3)当点P 运动什么位置时,使得CPD OAB =∠∠,且58BD AB =,求这时点P 的坐标.1、解:(1)过B 点作BE OA ⊥,垂足是点E , 四边形OABC 是等腰梯形,60OC AB BAO COA ∴===,∠∠, 在Rt BAE △中,s i n 60c o s 604B E A E AB AB AB===,,,144222BE AE =⨯==⨯=. 725O E O A A E =-=-=,B ∴点的坐标(5,, (2)60COA =∠ ,OCP △为等腰三角形, O C P∴△为等边三角形. 4O C O P P C ∴===, P 点是在x 轴上,P ∴点的坐标(40),或(40)-,。
(3)58BD AB =,且342AD BD AB AB AD +==∴=,,. 60CPD OAB COA ===∠∠∠,x1201806012O C PC P O C P O A PD +=+=-=,∠∠∠∠,O C P D P A =∠∠.O C P A P D ∴△∽△ O P O C A D A P ∴=,设7OP x AP x ==-,,即4372x x =-. 21276016x x x x -+===,, 这时P 点的坐标(10)(60),,,.2、(2006江苏省宿迁市)设边长为2a 的正方形的中心A 在直线l 上,它的一组对边垂直于直线l ,半径为r 的⊙O 的圆心O 在直线l 上运动..,点A 、O 间距离为d . (1)如图①,当r <a 时,根据d 与a 、r 之间关系,将⊙O 与正方形的公共点个数填所以,当r <a 时,⊙O 与正方形的公共点的个数可能有个;(2)如图②,当r =a 时,根据d 与a 、r 之间关系,将⊙O 与正方形的公共点个数填入下所以,当r =a 时,⊙O 与正方形的公共点个数可能有个;(3)如图③,当⊙O 与正方形有5个公共点时,试说明r =54a ;(4)就r >a 的情形,请你仿照“当……时,⊙O 与正方形的公共点个数可能有个”的形式,至少给出一个关于“⊙O 与正方形的公共点个数”的正确结论.l(题图①)l(题图②)(题图③)解: (1)所以,当r <a 时,⊙O 与正方形的公共点的个数可能有0、1、2个; (2)所以,当r =a 时,⊙O 与正方形的公共点个数可能有0、1、2、4个; (3)如图所示,连结OC .则OE =OC =r ,OF =EF -OE =2a -r .在Rt △OCF 中,由勾股定理得:OF 2+FC 2=OC 2即(2a -r )2+a 2=r 24a 2-4ar +r 2+a 2=r 25a 2=4ar5a =4r ∴r =54a .3、(2006 长沙市)如图1,已知直线12y x =-与抛物线2164y x =-+交于AB ,两点. (1)求AB ,两点的坐标; (2)求线段AB 的垂直平分线的解析式;(3)如图2,取与线段AB 等长的一根橡皮筋,端点分别固定在AB ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动,动点P 将与AB ,构成无数个三角形,ll l 图②这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.3、解:依题意得216412y x y x⎧=-+⎪⎪⎨⎪=-⎪⎩解之得12126432x x y y ==-⎧⎧⎨⎨=-=⎩⎩(63)(42A B ∴--,,, ···························································································· 3分 (2)作AB 的垂直平分线交x 轴,y 轴于C D ,两点,交AB 于M (如图1) 由(1)可知:OA OB ==AB ∴=122OM AB OB ∴=-= 过B 作BE x ⊥轴,E 为垂足由BEO OCM △∽△,得:54OC OM OC OB OE =∴=,,同理:55500242OD C D ⎛⎫⎛⎫=∴- ⎪ ⎪⎝⎭⎝⎭,,,, 设CD 的解析式为(0)y kx b k =+≠52045522k k b b b ⎧==+⎧⎪⎪⎪∴∴⎨⎨=-⎪⎪-=⎩⎪⎩AB ∴的垂直平分线的解析式为:522y x =-.图2 图1图1第3题(3)若存在点P 使APB △的面积最大,则点P 在与直线AB 平行且和抛物线只有一个交点的直线12y x m =-+上,并设该直线与x 轴,y 轴交于G H ,两点(如图2). 212164y x m y x ⎧=-+⎪⎪∴⎨⎪=-+⎪⎩2116042x x m ∴-+-= 抛物线与直线只有一个交点,2114(6)024m ⎛⎫∴--⨯-= ⎪⎝⎭,2523144m P ⎛⎫∴=∴ ⎪⎝⎭, 在直线12524GH y x =-+:中, 25250024G H ⎛⎫⎛⎫∴ ⎪ ⎪⎝⎭⎝⎭,,,GH ∴=设O 到GH 的距离为d ,112211252524224GH d OG OH d d AB GH ∴=∴⨯=⨯⨯∴= ,∥P ∴到AB 的距离等于O 到GH 的距离d 。
2006-2019安徽中考数学压轴题集锦
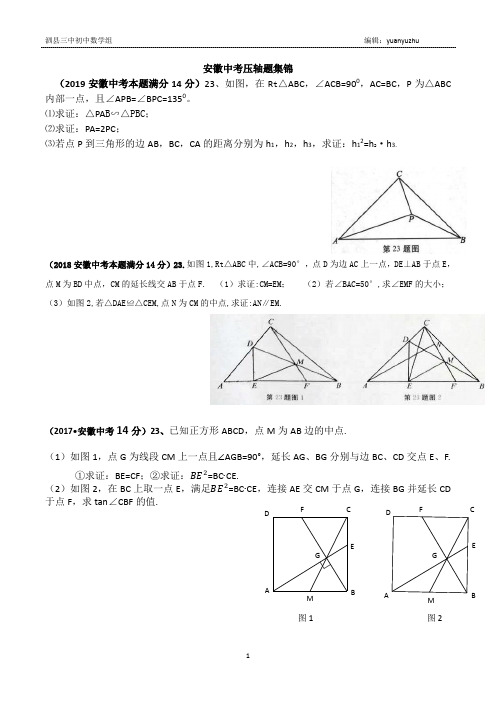
安徽中考压轴题集锦(2019安徽中考本题满分14分)23、如图,在R t △ABC ,∠ACB=900,AC=BC ,P 为△ABC 内部一点,且∠APB=∠BPC=1350。
⑴求证:△PA B ∽△PBC ; ⑵求证:PA=2PC ;⑶若点P 到三角形的边AB ,BC ,CA 的距离分别为h 1,h 2,h 3,求证:h 12=h 2·h 3.(2018安徽中考本题满分14分)23.如图1,Rt △ABC 中,∠ACB=90°,点D 为边AC 上一点,DE ⊥AB 于点E ,点M 为BD 中点,CM 的延长线交AB 于点F. (1)求证:CM=EM ; (2)若∠BAC=50°,求∠EMF 的大小; (3)如图2,若△DAE ≌△CEM,点N 为CM 的中点,求证:AN ∥EM.(2017•安徽中考14分)23、已知正方形ABCD ,点M 为AB 边的中点.(1)如图1,点G 为线段CM 上一点且∠AGB=90°,延长AG 、BG 分别与边BC 、CD 交点E 、F. ①求证:BE=CF ;②求证: =BC CE.(2)如图2,在BC 上取一点E ,满足 =BC CE ,连接AE 交CM 于点G ,连接BG 并延长CD 于点F ,求tan ∠CBF 的值.ABCD EF GMMGF ED C BA图1 图2(2016安徽中考)23.(14分)如图1,A ,B 分别在射线OA ,ON 上,且∠MON 为钝角,现以线段OA ,OB 为斜边向∠MON 的外侧作等腰直角三角形,分别是△OAP ,△OBQ ,点C ,D ,E 分别是OA ,OB ,AB 的中点.(1)求证:△PCE ≌△EDQ ; (2)延长PC ,QD 交于点R .①如图1,若∠MON=150°,求证:△ABR 为等边三角形; ②如图3,若△ARB ∽△PEQ ,求∠MON 大小和的值.(安徽2015本题满分14分)23.如图1,在四边形ABCD 中,点E 、F 分别是AB 、CD 的中点,过点E作AB 的垂线,过点F 作CD 的垂线,两垂线交于点G ,连接AG 、BG 、CG 、DG ,且∠AGD =∠BGC . (1)求证:AD =BC ; (2)求证:△AGD ∽△EGF ;(3)如图2,若AD 、BC 所在直线互相垂直,求 ADEF的值.(2014安徽,本题满分14分)23、如图1,正六边形ABCDEF 的边长为a ,P 是BC 边上一动点,过P 作PM ∥AB 交AF 于M ,作PN ∥CD 交DE 于N , (1) ①∠MPN =②求证:3PM PN a +=(2)如图2,点O 是AD 的中点,连接OM 、ON 。
20062012北京中考压轴题汇...
2006-2012北京中考压轴题汇编2006北京08.将如右图所示的圆心角为90°的扇形纸片AOB 围成圆锥形纸帽,使扇形的两条半径OA 与OB 重合(接缝粘贴部分忽略不计),则围成的圆锥形纸帽是 M 、N 分别是AB 、AC 的中点,D 、E 为BC 上的点,连结DN 、EM 。
若AB =13cm ,,则图中阴影部分的面积为 cm 2。
22.请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图①,请把它们分割后拼接成一个新的正方形。
要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。
小东同学的做法是:设新正方形的边长为x (x >0)。
依题意,割补前后图形的面积相等,有x 2=5,解得x =5。
由此可知新正方形得边长等于两个小正方形组成得矩形对角线得长。
于是,画出如图②所示的分割线,拼出如图③所示的新正方形。
请你参考小东同学的做法,解决如下问题:现有10个边长为1的正方形,排列形式如图④,请把它们分割后拼接成一个新的正方形。
要求:在图④中画出分割线,并在图⑤的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形。
23.如图①,OP 是∠MON 的平分线,请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。
请你参考这个作全等三角形的方法,解答下列问题:(1)如图②,在△ABC 中,∠ACB 是直角,∠B =60°,AD 、CE 分别是∠BAC 、∠BCA 的平分线,AD 、CE 相交于点F 。
请你判断并写出FE 与FD 之间的数量关系;(第12题图)BD E(第22题图)图①图②图③图⑤图④(2)如图③,在△ABC 中,如果∠ACB 不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
24.已知抛物线y =ax 2+bx +c 与y 轴交于点A (0,3),与x 轴分别交于B (1,0)、C (5,0)两点。
2006年全国中考数学压轴题全析全解(2)
2006年全国中考数学压轴题全解全析11、(河北卷)如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD ∥AB ?若存在,求出t 的值;若不存在,请说明理由; (4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB ?若存在,请估计t 的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由. [解] (1)由题意知 CQ =4t ,PC =12-3t , ∴S △PCQ =t t CQ PC 246212+-=⋅. ∵△PCQ 与△PDQ 关于直线PQ 对称, ∴y=2S △PCQ t t 48122+-=. (2)当CQCP CA CB=时,有PQ ∥AB ,而AP 与BQ 不平行,这时四边形PQBA 是梯形, ∵CA =12,CB =16,CQ =4t , CP =12-3t , ∴16412312tt =-,解得t =2. ∴当t =2秒时,四边形PQBA 是梯形.(3)设存在时刻t ,使得PD ∥AB ,延长PD 交BC 于点M ,如图2,若PD ∥AB ,则∠QMD =∠B ,又∵∠QDM =∠C =90°,∴Rt △QMD ∽Rt △ABC ,从而ACQDAB QM =, ∵QD =CQ =4t ,AC =12, AB20, ∴QM =203t . 若PD ∥AB ,则CP CMCA CB=,得20412331216t t t +-=, 解得t =1211. ∴当t =1211秒时,PD ∥AB .(4)存在时刻t ,使得PD ⊥AB .P图2图7D 时间段为:2<t ≤3.[点评]这是一道非常典型的动态几何问题,考查相似形、图形变换等知识,难度比起2005年河北非课改区的那道压轴题略有降低,但仍保留了足够的区分度,在解第3小题时应当先假设结论存在,再根据已知求解,若出现矛盾,则说明结论不存在,第4小题应该通过画图来判断时间段。
2006年全国中考数学压轴题全析全解2
2006年全国中考数学压轴题全解全析31、(辽宁沈阳卷)如图,在平面直角坐标系中,直线13y x =-+分别与x 轴,y 轴交于点A ,点B .(1)以AB 为一边在第一象限内作等边ABC △及ABC △的外接圆M (用尺规作图,不要求写作法,但要保留作图痕迹);(2)若M 与x 轴的另一个交点为点D ,求A ,B ,C ,D 四点的坐标;(3)求经过A ,B ,D 三点的抛物线的解析式,并判断在抛物线上是否存在点P ,使AD P △的面积等于ADC △的面积?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.[解] (1)如图,正确作出图形,保留作图痕迹(2)由直线13y x =-+,求得点A的坐标为),点B 的坐标为()01,∴在Rt AOB △中,OA =1OB =2AB ∴=,tan OAOBA OB==∠60OBA ∴=∠9030OAB OBA ∴=-=∠∠ ABC △是等边三角形 2CA AB ∴==,60CAB =∠90CAD CAB OAB ∴=+=∠∠∠∴点C的坐标为),连结BMABC △是等边三角形 1302MBA ABC ∴==∠∠90OBM OBA MBA ∴=+=∠∠∠ OB BM ∴⊥∴直线OB 是M 的切线2OB OD OA ∴=213OD ∴=OD ∴=∴点D 的坐标为0⎫⎪⎪⎝⎭(3)设经过A ,B ,D 三点的抛物线的解析式是(y a x x ⎛= ⎝⎭把()01B ,代入上式得1a =∴抛物线的解析式是21y x =+ 存在点P ,使ADP △的面积等于ADC △的面积点P 的坐标分别为123P ⎛⎫⎪ ⎪⎝⎭,,223P ⎛⎫⎪ ⎪⎝⎭,. [点评]本题是一道综合性很强的压轴题,主要考查二次函数、一次函数、圆、几何作图等大量知识,第3小题是比较常规的结论存在性问题,运用方程思想和数形结合思想可解决。
32、(山东滨州卷)已知:抛物线2:(1)(2)M y x m x m =+-+-与x 轴相交于12(0)(0)A x B x ,,,两点,且12x x <.(Ⅰ)若120x x <,且m 为正整数,求抛物线M 的解析式; (Ⅱ)若1211x x <>,,求m 的取值范围;(Ⅲ)试判断是否存在m ,使经过点A 和点B 的圆与y 轴相切于点(02)C ,,若存在,求出m 的值;若不存在,试说明理由;(Ⅳ)若直线:l y kx b =+过点(07)F ,,与(Ⅰ)中的抛物线M 相交于P Q ,两点,且使12PF FQ =,求直线l 的解析式. [解] (Ⅰ)解法一:由题意得, 1220x x m =-<. 解得,2m <.m 为正整数,1m ∴=.21y x ∴=-.解法二:由题意知,当0x =时,20(1)0(2)0y m m =+-⨯+-<.(以下同解法一) 解法三:22(1)4(2)(3)m m m ∆=---=-,12(1)(3)122m m x x x m --±-∴=∴=-=-,,.又122020x x x m <∴=->,.2m ∴<.(以下同解法一.)解法四:令0y =,即2(1)(2)0x m x m +-+-=,12(1)(2)012x x m x x m∴++-=∴=-=-,,.(以下同解法三.) (Ⅱ)解法一:1212111010x x x x <>∴-<->,,,.12(1)(1)0x x ∴--<,即1212()10x x x x -++<.1212(1)2x x m x x m +=--=-,, (2)(1)10m m ∴-+-+<.解得 1m <.m ∴的取值范围是1m <.解法二:由题意知,当1x =时,1(1)(2)0y m m =+-+-<.解得:1m <.m ∴的取值范围是1m <.解法三:由(Ⅰ)的解法三、四知,1212x x m =-=-,.121121x x m <>∴->,,,1m ∴<.m ∴的取值范围是1m <. (Ⅲ)存在.解法一:因为过A B ,两点的圆与y 轴相切于点(02)C ,,所以A B ,两点在y 轴的同侧,120x x ∴>.由切割线定理知,2OC OA OB =, 即2122x x =.124x x ∴=,12 4.x x ∴=2 4.6m m ∴-=∴=.解法二:连接O B O C '',.圆心所在直线11222b m m x a --=-=-=, 设直线12mx -=与x 轴交于点D ,圆心为O ', 则122mO D OC O C OD -''====,.2132ABAB x x m BD =-==-=,, 32m BD -∴=.在Rt O DB '△中, 222O D D B O B ''+=.即22231222m m --⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭.解得 6m =.(Ⅳ)设1122()()P x y Q x y ,,,,则22112211y x y x =-=-,.过P Q ,分别向x 轴引垂线,垂足分别为112(0)(0)P x Q x ,,,.则11PP FO QQ ∥∥.所以由平行线分线段成比例定理知,11PO PF OQ FQ=.因此,120102x x -=-,即212x x =-. 过P Q ,分别向y 轴引垂线,垂足分别为2122(0)(0)P y Q y ,,,, 则22PP QQ ∥.所以22FP P FQ Q △∽△.22P F FPFQ FQ∴=. 127172y y -∴=-.12212y y ∴-=.22122211212(1) 1.2324 1.x x x x ∴--=-∴-=-21142x x ∴=∴=,,或12x =-.当12x =时,点(23)P ,.直线l 过(23)(07)P F ,,,,7032.k b k b =⨯+⎧∴⎨=⨯+⎩, 解得72.b k =⎧⎨=-⎩,当12x =-时,点(23)P -,.直线l 过(23)(07)P F -,,,,703(2).k b k b =⨯+⎧∴⎨=⨯-+⎩, 解得72.b k =⎧⎨=⎩,故所求直线l 的解析式为:27y x =+,或27y x =-+.[点评]本题对学生有一定的能力要求,涉及了初中数学的大部分重点章节的重点知识,是一道选拔功能卓越的好题。
06年全国中考数学压轴题集锦
06年全国中考数学压轴题集锦1、(2006浙江金华)如图,平面直角坐标系中,直线AB与某轴,y轴分别交于A(3,0),B(0,3)两点,,点C为线段AB上的一动点,过点C作CD⊥某轴于点D.(1)求直线AB的解析式;(2)若S梯形OBCD=43,求点C的坐标;3(3)在第一象限内是否存在点P,使得以P,O,B为顶点的三角形与△OBA相似.若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.[解](1)直线AB解析式为:y=(2)方法一:设点C坐标为(某,3某+3.333某+3),那么OD=某,CD=某+3.3332某3.6∴S梯形OBCD =OBCDCD=2由题意:3243某3=,解得某12,某24(舍去)633)3133433,S梯形OBCD=,∴SACD.OAOB2236∴C(2,方法二:∵SAOB由OA=3OB,得∠BAO=30°,AD=3CD.∴SACD=1333CD2=CD某AD=.可得CD=.2263∴AD=1,OD=2.∴C(2,(3)当∠OBP=Rt∠时,如图3).3①若△BOP∽△OBA,则∠BOP=∠BAO=30°,BP=3OB=3,∴P1(3,3).33OB=1.3②若△BPO∽△OBA,则∠BPO=∠BAO=30°,OP=∴P2(1,3).当∠OPB=Rt∠时③过点P作OP⊥BC于点P(如图),此时△PBO∽△OBA,∠BOP=∠BAO=30°过点P作PM⊥OA于点M.方法一:在Rt△PBO中,BP=133OB=,OP=3BP=.222∵在Rt△PMO中,∠OPM=30°,∴OM=1333333OP=;PM=3OM=.∴P3(,).24444方法二:设P(某,33某+3),得OM=某,PM=某+333由∠BOP=∠BAO,得∠POM=∠ABO.∵tan∠POM==PM=OM3某3OA3,tan∠ABOC==3.某OB∴33333某+3=3某,解得某=.此时,P3(,).4434④若△POB∽△OBA(如图),则∠OBP=∠BAO=30°,∠POM=30°.∴PM=33OM=.3433,)(由对称性也可得到点P4的坐标).44∴P4(当∠OPB=Rt∠时,点P在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:P1(3,333333),P2(1,3),P3(,),P4(,).4434422、(2006重庆)如图1所示,一张三角形纸片ABC,∠ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪成AC1D1和BC2D2两个三角形(如图2所示).将纸片AC1D1沿直线D2B(AB)方向平移(点A,D1,D2,B始终在同一直线上),当点D1于点B重合时,停止平移.在平移过程中,C1D1与BC2交于点E,AC1与C2D2、BC2分别交于点F、P.(1)当AC1D1平移到如图3所示的位置时,猜想图中的D1E与D2F的数量关系,并证明你的猜想;(2)设平移距离D2D1为某,AC1D1与BC2D2重叠部分面积为y,请写出y与某的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的某的值,使重叠部分的面积等于原ABC面积的若存在,求某的值;若不存在,请说明理由.C1C2CABADD1D2图1图21.4C1PFED1C2BAD2B图3AP[解](1)D1ED2F.因为C1D,∥C2D12所以C1AFD2.又因为ACB90,CD是斜边上的中线,所以,DCDADB,即C1D1C2D2BD2AD1所以,C1A,所以AFD2A所以,AD2D2F.同理:BD1D1E.又因为AD1BD2,所以AD2BD1.所以D1ED2F(2)因为在RtABC中,AC8,BC6,所以由勾股定理,得AB10.即AD1BD2C1D1C2D25又因为D2D1某,所以D1EBD1D2FAD25某.所以C2FC1E某3CQDB在BC2D2中,C2到BD2的距离就是ABC的AB边上的高,为24.5设BED1的BD1边上的高为h,由探究,得BC2D2∽BED1,所以h5某.2455所以h24(5某)112(5某)2.SBED1BD1h25225又因为C1C290,所以FPC290.43,coB.5534162某所以PC2某,PF某,SFC2PPC2PF552251126(5某)2某2而ySBC2D2SBED1SFC2PSABC2252518224某某(0某5)所以y255118224某某6(3)存在.当ySABC时,即425552整理,得3某20某250.解得,某1,某25.351即当某或某5时,重叠部分的面积等于原ABC面积的.34又因为C2B,inB3、(2006山东济南)如图1,已知Rt△ABC中,CAB30,BC5.过点A作AE⊥AB,且AE15,连接BE交AC于点P.(1)求PA的长;(2)以点A为圆心,AP为半径作⊙A,试判断BE与⊙A是否相切,并说明理由;(3)如图2,过点C作CD⊥AE,垂足为D.以点A为圆心,r为半径作⊙A;以点C为圆心,R为半径作⊙C.若r和R的大小是可变化的,并且在变化过程中保持⊙A和⊙C相.切,且使D点在⊙A的内部,B点在⊙A的外部,求r和R的变化范围..EEPCDAABPCB[解]图1图24(1)在Rt△ABC中,CAB30,BC5,AC2BC10.AE∥BC,△APE∽△CPB.PA:PCAE:BC3:1.PA:AC3:4,PA(2)BE与⊙A相切.在Rt△ABE中,AB53,AE15,tanABE31015.42AE153,ABE60.AB53APB90,又PAB30,ABEPAB90,BE与⊙A相切.(3)因为AD5,AB53,所以r的变化范围为5r53.当⊙A与⊙C外切时,Rr10,所以R的变化范围为1053R5;当⊙A与⊙C内切时,Rr10,所以R的变化范围为15R1053.4、(2006浙江嘉兴)某旅游胜地欲开发一座景观山.从山的侧面进行堪测,迎面山坡线ABC由同一平面内的两段抛物线组成,其中AB所在的抛物线以A为顶点、开口向下,BC所在的抛物线以C为顶点、开口向上.以过山脚(点C)的水平线为某轴、过山顶(点A)的铅垂线为y轴建立平面直角坐标系如图(单位:百米).已知AB所在抛物线的解121某8,BC所在抛物线的解析式为y(某8)2,且已知B(m,4).44(1)设P(某,y)是山坡线AB上任意一点,用y表示某,并求点B的坐标;析式为y(2)从山顶开始、沿迎面山坡往山下铺设观景台阶.这种台阶每级的高度为20厘米,长度因坡度的大小而定,但不得小于20厘米,每级台阶的两端点在坡面上(见图).①分别求出前三级台阶的长度(精确到厘米);②这种台阶不能一直铺到山脚,为什么?(3)在山坡上的700米高度(点D)处恰好有一小块平地,可以用来建造索道站.索道的起点选择在山脚水平线上的点E处,OE1600(米).假设索道DE可近似地看成一段以E为顶点、开口向上的抛物线,解析式为y高度.1(某16)2.试求索道的最大悬空..28长度高度y7AD4B上山方向5 [解](1)∵P(某,y)是山坡线AB上任意一点,∴y12某8,某0,4∴某24(8y),某28y∵B(m,4),∴m284=4,∴B(4,4)(2)在山坡线AB上,某28y,A(0,8)①令y08,得某00;令y180.0027.998,得某120.0020.08944∴第一级台阶的长度为某1某00.08944(百米)894(厘米)同理,令y2820.002、y3830.002,可得某20.12649、某30.15492∴第二级台阶的长度为某2某10.03705(百米)371(厘米)第三级台阶的长度为某3某20.02843(百米)284(厘米)②取点B(4,4),又取y40.002,则某23.9983.99900∵43.999000.0010.002∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚(注:事实上这种台阶从山顶开始最多只能铺到700米高度,共500级.从100米高度到700米高度都不能铺设这种台阶.解题时取点具有开放性)②另解:连接任意一段台阶的两端点P、Q,如图∵这种台阶的长度不小于它的高度∴PQR45当其中有一级台阶的长大于它的高时,PQR45PRQ在题设图中,作BHOA于H则ABH45,又第一级台阶的长大于它的高∴这种台阶不能从山顶一直铺到点B,从而就不能一直铺到山脚6y(3)AB4O4D(2,7)、E(16,0)、B(4,4)、C(8,0)上山方向CE某由图可知,只有当索道在BC上方时,索道的悬空高度才有可能取最大值..索道在BC上方时,悬空高度y..11(某16)2(某8)228413208(3某240某96)(某)2141433当某208时,yma某33800∴索道的最大悬空高度为米...325、(2006山东烟台)如图,已知抛物线L1:y=某-4的图像与某有交于A、C两点,(1)若抛物线l2与l1关于某轴对称,求l2的解析式;(2)若点B是抛物线l1上的一动点(B不与A、C重合),以AC为对角线,A、B、C三点为顶点的平行四边形的第四个顶点定为D,求证:点D在l2上;(3)探索:当点B分别位于l1在某轴上、下两部分的图像上时,平行四边形ABCD的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2006中考压轴题精选1、(2006 广东省实验区)如图所示,在平面直角坐标系中,四边形OABC 是等腰梯形,BC OA ∥,7460OA AB COA === ,,∠,点P 为x 轴上的一个动点,点P 不与点O 、点A 重合.连结CP ,过点P 作PD 交AB 于点D . (1)求点B 的坐标;(2)当点P 运动什么位置时,OCP △为等腰三角形,求这时点P 的坐标;且58BD AB =,求(3)当点P 运动什么位置时,使得CPD OAB =∠∠,这时点P 的坐标.2、(2006江苏省宿迁市)设边长为2a 的正方形的中心A 在直线l 上,它的一组对边垂直于直线l ,半径为r 的⊙O 的圆心O 在直线l 上运动..,点A 、O 间距离为d . (1)如图①,当r <a 时,根据d 与a 、r 之间关系,将⊙O 与正方形的公共点个数填 入下表:所以,当r <a 时,⊙O 与正方形的公共点的个数可能有个;(2O 与正方形的公共点个数填入下表:所以,当r =a 时,⊙O 与正方形的公共点个数可能有 个;l(题图①)l(题图②)54a ; (3)如图③,当⊙O 与正方形有5个公共点时,试说明r =(4)就r >a 的情形,请你仿照“当……时,⊙O 与正方形的公共点个数可能有 个”的形式,至少给出一个关于“⊙O 与正方形的公共点个数”的正确结论.3、(2006 长沙市)如图1,已知直线12y x =-与抛物线2164y x =-+交于A B ,两点. (1)求A B ,两点的坐标;(2)求线段AB 的垂直平分线的解析式;(3)如图2,取与线段AB 等长的一根橡皮筋,端点分别固定在A B ,两处.用铅笔拉着这根橡皮筋使笔尖P 在直线AB 上方的抛物线上移动,动点P 将与A B ,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P 点的坐标;如果不存在,请简要说明理由.4、(2006 福建南平市)如图,正方形ABCD 的边长为1,点E 是AD 边上的动点,从点A 沿AD 向D 运动..,以BE 为边,在BE 的上方作正方形BEFG ,连接CG 。
请探究:(1)线段AE 与CG 是否相等?请说明理由:(题图③)图2图1(2)若设x AE =,y DH =,当x 取何值时,y 最大?(3)连接BH ,当点E 运动到AD 的何位置时,△BEH ∽△BAE ? 5、(2006 福建泉州市)一条隧道的截面如图所示,它的上部是一个以AD 为直径的半圆O ,下部是一个矩形ABCD . (1)当AD=4米时,求隧道截面上部半圆O 的面积; (2)已知矩形ABCD 相邻两边之和为8米,半圆O 的半径为r 米. ①求隧道截面的面积S (米2)关于半径r (米)的函数关系式(不要求写出r 的取值范围);②若2米≤CD ≤3米,利用函数图象求隧道截面的面积S 的最大值(π取3.14,结果精确到0.1米)6、(2006南阳油田)如图,等边三角形ABC 的边长为8,点P 由点B 开始沿BC 以每秒1个单位长的速度作匀速运动,到点C 后停止运动;点Q 由点C 开始沿C-A-B 以每秒2个单位长的速度作匀速运动,到点B 后停止运动.若点P ,Q 同时开始运动,运动的时间为t(秒)(t >0).(1)指出当t =4秒时,点P,Q 的位置,此时直线PQ 有何特点? (2)当点Q 在AC 边上运动时,求△PCQ 的面积S 1与t 的函数关系式. (3)当点Q 在AB 边上运动时(点Q 与点B 不重合),求四边形PCAQ 的面积S 2与t的函数关系式,并指出自变量t 的取值范围.7、(2006山东枣庄市)半径为2.5的⊙O 中,直径AB 的不同侧有定点C 和动点P .已知BC :CA =4 : 3,点P 在AB 上运动,过点C 作CP 的垂线,与PB 的延长线交于点O. (l )当点P 与点C 关于AB 对称时,求CQ 的长; (2)当点P 运动AB 到的中点时,求CQ 的长;(3)当点P 运动到什么位置时,CQ 取到最大值?求此时CQ 的长.D(第23题)BP8、(2006年潍坊市)已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数1y kx=+的图象与二次函数的图象交于A B,两点(A在B的左侧),且A点坐标为()44-,.平行于x轴的直线l过()01-,点.(1)求一次函数与二次函数的解析式;(2)判断以线段AB为直径的圆与直线l的位置关系,并给出证明;(3)把二次函数的图象向右平移2个单位,再向下平移t个单位()0t>,二次函数的图象与x轴交于M N,两点,一次函数图象交y轴于F点.当t为何值时,过F M N,,三点的圆的面积最小?最小面积是多少?9、(2006 伊春市)如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程x2-18x+72=0的两个根,点C是线段AB的中点,点D在线段OC上,OD=2CD.(1)求点C的坐标;(2)求直线AD的解析式;(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.10、(2006四川省内江)如图所示,一张三角形纸片ABC,∠成11AC D∆和ACB=90°,AC=8,BC=6.沿斜边AB的中线CD把这张纸片剪22BC D∆两个三角形(如图28-2所示).将纸片11AC D∆沿直线2D B(AB)方向平移(点12,,,A D D B始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.(1) 当11AC D ∆平移到如图28-3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想; (2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3) 对于(2)中的结论是否存在这样的x 的值,重叠部分的面积等于原ABC ∆面积的14.若不存在,请说明理由.11、(2006贵阳市)如图,在平面直角坐标系中,以坐标原点O 为圆心,2为半径画⊙O ,P 是⊙O 上一动点,且P 在第一象限内,过点P 作⊙O 的切线与x 轴相交于点A ,与y 轴相交于点B 。
(1)点P 在运动时,线段AB 的长度页在发生变化,请写出线段AB 长度的最小值,并说明理由;(2)在⊙O 上是否存在一点Q ,使得以Q 、O 、A 、P 为顶点的四边形时平行四边形?若存在,请求出Q 点的坐标;若不存在,请说明理由。
12、(2006贵阳市)某商场购进一种单价为40元的篮球,如果以单价50元出售,那么每月可售出500个,根据销售经验,售价每提高1元,销售量相应减少10个; (1)假设销售单价提高x 元,那么销售每个篮球所获得的利润是 元;这种篮球每月的销售量是 个;(用含x 的代数式表示)(4分)(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?(8分)13、(2006北京海淀区) 如图,已知⊙O 的直径AB 垂直于弦CD于E ,连结AD 、BD 、OC 、CB D A 28-1图12228-3图 C 2D 2C 1B D 1A 28-2图OD ,且OD =5。
(1)若sin ∠BAD =35,求CD 的长; (2)若 ∠ADO :∠EDO =4:1,求扇形OAC (阴影部分)的面积(结果保留π)。
14、(2006锦州市)如图,在平面直角坐标系中,四边形OABC 为菱形,点C 的坐标为(4,0),∠AOC=60°,垂直于x 轴的直线l 从y 轴出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线l 与菱形OABC 的两边分别交于点M 、N(点M 在点N 的上方).(1)求A 、B 两点的坐标;(2)设△OMN 的面积为S ,直线l 运动时间为t 秒(0≤t≤6), 试求S 与t 的函数表达式;(3)在题(2)的条件下,t 为何值时,S 的面积最大?最大面积是多少?15、(2006西江南昌)已知抛物线2y ax bx c =++,经过点A (0,5)和点B (3 ,2)(1)求抛物线的解析式:(2)现有一半径为l ,圆心P 在抛物线上运动的动圆,问⊙P 在运动过程中,是否存在⊙P与坐标轴相切的情况?若存在,请求出圆心P 的坐标:若不存在,请说明理由; (3)若⊙ Q 的半径为r ,点Q 在抛物线上、⊙Q 与两坐轴都相切时求半径r 的值 16、(2006山东青岛市)如图①,有两个形状完全相同的直角三角形ABC 和EFG 叠放在一起(点A 与点E 重合),已知AC =8cm ,BC =6cm ,∠C =90°,EG =4cm ,∠EGF =90°,O 是△EFG 斜边上的中点.如图②,若整个△EFG 从图①的位置出发,以1cm/s 的速度沿射线AB 方向平移,在△EFG 平移的同时,点P 从△EFG 的顶点G 出发,以1cm/s 的速度在直角边GF 上向点F 运动,当点P 到达点F 时,点P 停止运动,△EFG 也随之停止平移.设运动时间为x (s ),FG 的延长线交 AC 于H ,四边形OAHP 的面积为y (cm 2)(不考虑点P 与G 、F 重合的情况). (1)当x 为何值时,OP ∥AC ?(2)求y 与x 之间的函数关系式,并确定自变量x 的取值范围.(3)是否存在某一时刻,使四边形OAHP 面积与△ABC 面积的比为13∶24?若存在,求出x 的值;若不存在,说明理由.(参考数据:1142 =12996,1152 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)17、(2006 烟台市)如图,已知抛物线L 1: y=x 2-4的图像与x 有交于A 、C 两点.(1)若抛物线l 2与l 1关于x 轴对称,求l 2的解析式; (2)若点B 是抛物线l 1上的一动点(B 不与A 、C 重合),以AC 为对角线,A 、B 、C 三点为顶点的平行四边形的第四个顶点定为D ,求证:点D 在l 2上; (3)探索:当点B 分别位于l 1在x 轴上、下两部分的图像上时,平行四边形ABCD 的面积是否存在最大值和最小值?若存在,判断它是何种特殊平行四边形,并求出它的面积;若不存在,请说明理由。
18、(2006 湖南常德市)把两块全等的直角三角形ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中90ABC DEF ∠=∠= ,45C F ∠=∠= ,4AB DE ==,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图9,当射线DF 经过点B ,即点Q 与点B 重合时,易证APD CDQ △∽△.此时,AP CQ =· .(2)将三角板DEF 由图9所示的位置绕点O 沿逆时针方向旋转,设旋转角为α.其中090α<< ,问AP CQ ·的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ x =,两块三角板重叠面积为y ,求y 与x 的函数关系式.(图10,图11供解题用)19(2006 临安市)如图,△OAB是边长为2O 是坐标原点,顶点B 在y 轴正方向上,将△OAB 折叠,使点A 落在边OB 上,记为A ′,折痕为EF. (1)当A ′E//x 轴时,求点A ′和E 的坐标; (2)当A ′E//x 轴,且抛物线216y x bx c =-++经过点A ′和E 时,求抛物线与x 轴的交点的坐标;(3)当点A ′在OB 上运动,但不与点O 、B 重合时,能否使△A ′EF 成为直角三角形?若能,请求出此时点A ′的坐标;若不能,请你说明理由.20、(2006南通市)如图,在平面直角坐标系中,O 为坐标原点为,B (5,0),M 为等腰梯形OBCD 底边OB 上一点,OD =BC =2,∠DMC=∠DOB =60°.(1)求直线CB 的解析式; (2)求点M 的坐标;(3)∠DMC 绕点M 顺时针旋转α (30°<α<60°)后,得到∠D 1MC 1(点D 1,C 1依次与点D ,C 对应),射线MD 1交直线DC 于点E ,射线MC1交直线CB 于点F ,设DE =m ,BF =n .求m 与 n 的函数关系式.BEE 图9 图10图11。
