最新初中数学几何作图综合测试卷含答案

合集下载

人教版九年级数学上册圆几何综合单元测试卷(含答案解析)

人教版九年级数学上册圆几何综合单元测试卷（含答案解析）一、初三数学圆易错题压轴题（难）1．已知圆O 的半径长为2，点A 、B 、C 为圆O 上三点，弦BC=AO ，点D 为BC 的中点，(1)如图，连接AC 、OD ，设∠OAC=α，请用α表示∠AOD ；(2)如图，当点B 为AC 的中点时，求点A 、D 之间的距离： (3)如果AD 的延长线与圆O 交于点E ，以O 为圆心，AD 为半径的圆与以BC 为直径的圆相切，求弦AE 的长．【答案】（1）1502AOD α∠=︒-；（2）7AD =3）33133122or 【解析】【分析】（1）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOC 等于30°，OA=OC 可得∠ACO=∠CAO=α，利用三角形的内角和定理即可表示出∠AOD 的值.（2）连接OB 、OC ，可证△OBC 是等边三角形，根据垂径定理可得∠DOB 等于30°，因为点D 为BC 的中点，则∠AOB=∠BOC=60°，所以∠AOD 等于90°，根据OA=OB=2,在直角三角形中用三角函数及勾股定理即可求得OD 、AD 的长.（3）分两种情况讨论：两圆外切，两圆内切.先根据两圆相切时圆心距与两圆半径的关系，求出AD 的长，再过O 点作AE 的垂线，利用勾股定理列出方程即可求解.【详解】(1)如图1：连接OB 、OC.∵BC=AO∴OB=OC=BC∴△OBC 是等边三角形∴∠BOC=60°∵点D 是BC 的中点∴∠BOD=1302BOC ∠=︒ ∵OA=OC∴OAC OCA ∠=∠=α∴∠AOD=180°-α-α-30︒=150°-2α(2)如图2：连接OB、OC、OD.由（1）可得：△OBC是等边三角形，∠BOD=130 2BOC∠=︒∵OB=2，∴OD=OB∙cos30︒=3∵B为AC的中点，∴∠AOB=∠BOC=60°∴∠AOD=90°根据勾股定理得：AD=227AO OD+=（3）①如图3.圆O与圆D相内切时：连接OB、OC，过O点作OF⊥AE∵BC是直径，D是BC的中点∴以BC为直径的圆的圆心为D点由（2）可得：3D的半径为1∴31设AF=x 在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=-+- 解得：331x 4+= ∴AE=3312AF +=②如图4.圆O 与圆D 相外切时：连接OB 、OC ，过O 点作OF ⊥AE∵BC 是直径，D 是BC 的中点∴以BC 为直径的圆的圆心为D 点由（2）可得：3D 的半径为1∴31在Rt △AFO 和Rt △DOF 中，2222OA AF OD DF -=-即()2222331x x -=-解得：331x 4-= ∴AE=3312AF -=【点睛】本题主要考查圆的相关知识：垂径定理，圆与圆相切的条件，关键是能灵活运用垂径定理和勾股定理相结合思考问题，另外需注意圆相切要分内切与外切两种情况.2．已知：在△ABC中，AB=6，BC=8，AC=10，O为AB边上的一点，以O为圆心，OA长为半径作圆交AC于D点，过D作⊙O的切线交BC于E.（1）若O为AB的中点(如图1)，则ED与EC的大小关系为：ED EC（填“”“”或“”）（2）若OA<3时（如图2），（1）中的关系是否还成立？为什么？（3）当⊙O过BC中点时（如图3），求CE长.【答案】（1）ED=EC；（2）成立；（3）3【解析】试题分析：（1）连接OD，根据切线的性质可得∠ODE=90°，则∠CDE+∠ADO=90°，由AB=6，BC=8，AC=10根据勾股定理的逆定理可证得∠ABC=90°，则∠A+∠C=90°，根据圆的基本性质可得∠A=∠ADO，即可得到∠CDE=∠C，从而证得结论；（2）证法同（1）；（3）根据直角三角形的性质结合圆的基本性质求解即可.（1）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（2）连接OD∵DE为⊙O的切线∴∠ODE=90°∴∠CDE+∠ADO=90°∵AB=6，BC=8，AC=10∴∠ABC=90°∴∠A+∠C=90°∵AO=DO∴∠A=∠ADO∴∠CDE=∠C∴ED=EC；（3）CE=3.考点：圆的综合题点评：此类问题综合性强，难度较大，在中考中比较常见，一般作为压轴题，题目比较典型．3．如图，△ABC内接于⊙O，AB是直径，过点A作直线MN，且∠MAC＝∠ABC．（1）求证：MN是⊙O的切线．（2）设D是弧AC的中点，连结BD交AC于点G，过点D作DE⊥AB于点E，交AC于点F．①求证：FD＝FG．②若BC＝3，AB＝5，试求AE的长．【答案】（1）见解析；（2）①见解析；②AE＝1【解析】【分析】（1）由AB为直径知∠ACB＝90°，∠ABC+∠CAB＝90°．由∠MAC＝∠ABC可证得∠MAC+∠CAB＝90°，则结论得证；（2）①证明∠BDE＝∠DGF即可．∠BDE＝90°﹣∠ABD；∠DGF＝∠CGB＝90°﹣∠CBD．因为D是弧AC的中点，所以∠ABD＝∠CBD．则问题得证；②连接AD、CD，作DH⊥BC，交BC的延长线于H点．证明Rt△ADE≌Rt△CDH，可得AE＝CH．根据AB＝BH可求出答案．【详解】（1）证明：∵AB是直径，∴∠ACB＝90°，∴∠CAB+∠ABC＝90°；∵∠MAC＝∠ABC，∴∠MAC+∠CAB＝90°，即MA⊥AB，∴MN是⊙O的切线；（2）①证明：∵D是弧AC的中点，∴∠DBC＝∠ABD，∵AB是直径，∴∠CBG+∠CGB＝90°，∵DE⊥AB，∴∠FDG+∠ABD＝90°，∵∠DBC ＝∠ABD ，∴∠FDG ＝∠CGB ＝∠FGD ，∴FD ＝FG ；②解：连接AD 、CD ，作DH ⊥BC ，交BC 的延长线于H 点．∵∠DBC ＝∠ABD ，DH ⊥BC ，DE ⊥AB ，∴DE ＝DH ，在Rt △BDE 与Rt △BDH 中，DH DE BD BD=⎧⎨=⎩， ∴Rt △BDE ≌Rt △BDH （HL ），∴BE ＝BH ，∵D 是弧AC 的中点，∴AD ＝DC ，在Rt △ADE 与Rt △CDH 中，DE DH AD CD =⎧⎨=⎩， ∴Rt △ADE ≌Rt △CDH （HL ）．∴AE ＝CH ．∴BE ＝AB ﹣AE ＝BC+CH ＝BH ，即5﹣AE ＝3+AE ，∴AE ＝1．【点睛】本题是圆的综合题，考查了切线的判定，圆周角定理，全等三角形的判定与性质，等腰三角形的判定，正确作出辅助线来构造全等三角形是解题的关键．4．如图，在平面直角坐标系中，O 为坐标原点，△ABC 的边BC 在y 轴的正半轴上，点A 在x 轴的正半轴上，点C 的坐标为（0，8），将△ABC 沿直线AB 折叠，点C 落在x 轴的负半轴D （−4，0）处．（1）求直线AB 的解析式；（2）点P 从点A 出发以每秒5AB 方向运动，过点P 作PQ ⊥AB ，交x 轴于点Q ，PR ∥AC 交x 轴于点R ，设点P 运动时间为t （秒），线段QR 长为d ，求d 与t 的函数关系式（不要求写出自变量t 的取值范围）；（3）在（2）的条件下，点N 是射线AB 上一点，以点N 为圆心，同时经过R 、Q 两点作⊙N ，⊙N 交y 轴于点E ，F ．是否存在t ，使得EF =RQ ？若存在，求出t 的值，并求出圆心N 的坐标；若不存在，说明理由．【答案】（1）132y x =-+（2）d =5t （3）故当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）．【解析】试题分析：（1）由C （0，8），D （-4，0），可求得OC ，OD 的长，然后设OB=a ，则BC=8-a ，在Rt △BOD 中，由勾股定理可得方程：（8-a ）2=a 2+42,解此方程即可求得B 的坐标，然后由三角函数的求得点A 的坐标，再利用待定系数法求得直线AB 的解析式；（2）在Rt △AOB 中，由勾股定理可求得AB 的长，继而求得∠BAO 的正切与余弦，由PR//AC 与折叠的性质，易证得RQ=AR ，则可求得d 与t 的函数关系式；（3）首先过点分别作NT ⊥RQ 于T ，NS ⊥EF 于S ，易证得四边形NTOS 是正方形，然后分别从点N 在第二象限与点N 在第一象限去分析求解即可求解;试题解析：（1）∵C （0，8），D （-4，0），∴OC=8，OD=4，设OB=a ，则BC=8-a ，由折叠的性质可得：BD=BC=8-a ，在Rt △BOD 中，∠BOD=90°，DB 2=OB 2+OD 2，则（8-a ）2=a 2+42，解得：a=3，则OB=3，则B （0，3），tan ∠ODB=34OB OD = ，在Rt △AOC 中，∠AOC=90°，tan ∠ACB=34OA OC = ，则OA=6，则A （6，0），设直线AB 的解析式为：y=kx+b ，则60{3k bb+==，解得：1{23kb=-=，故直线AB的解析式为：y=-12x+3；（2）如图所示：在Rt△AOB中，∠AOB=90°，OB=3，OA=6，则22135,tan2OBOB OA BAOOA+=∠==，255OAcos BAOAB∠==，在Rt△PQA中，905APQ AP t∠=︒=，则AQ=10cosAPtBAO=∠,∵PR∥AC，∴∠APR=∠CAB，由折叠的性质得：∠BAO=∠CAB，∴∠BAO=∠APR，∴PR=AR，∵∠RAP+∠PQA=∠APR+∠QPR=90°，∴∠PQA=∠QPR，∴RP=RQ，∴RQ=AR，∴QR=12AQ=5t,即d=5t;（3）过点分别作NT⊥RQ于T，NS⊥EF于S，∵EF=QR，∴NS=NT，∴四边形NTOS是正方形，则TQ=TR=1522QR t=，∴1115151022224NT AT AQ TQ t t t==-=-=（）（），分两种情况，若点N 在第二象限，则设N （n ，-n ），点N 在直线132y x =-+ 上，则132n n -=-+ ，解得：n=-6，故N （-6，6），NT=6，即1564t = ，解得：85t = ; 若点N 在第一象限，设N （N ，N ），可得：132n n =-+ , 解得：n=2，故N （2，2），NT=2，即1524t =, 解得：t=815∴当 t =85，或815，时，QR =EF ，N （-6，6）或（2，2）。

新人教版初中数学七年级数学上册第四单元《几何图形初步》检测(含答案解析)

一、选择题1．如图所示，已知直线AB 上有一点O ，射线OD 和射线OC 在AB 同侧，∠AOD ＝42°，∠BOC ＝34°，OM 是∠AOD 的平分线，则∠MOC 的度数是（）A ．125°B ．90°C ．38°D ．以上都不对 2．将如图所示的直角三角形绕直线l 旋转一周，得到的立体图形是（）A ．B ．C ．D ． 3．如图所示，90AOC ∠=︒，COB α∠=，OD 平分AOB ∠，则COD ∠的度数为（）A ．2αB ．45α︒-C ．452α︒- D ．90α︒- 4．α∠和β∠的顶点和一边都重合,另一边都在公共边的同侧,且αβ∠>∠,那么α∠的另一半落在β∠的( )A ．另一边上B ．内部;C ．外部D ．以上结论都不对 5．如图，O 是直线AC 上一点，OB 是一条射线，OD 平分∠AOB ，OE 在∠BOC 内，且∠DOE ＝60°，∠BOE ＝13∠EOC ，则下列四个结论正确的个数有（） ①∠BOD ＝30°；②射线OE 平分∠AOC ；③图中与∠BOE 互余的角有2个；④图中互补的角有6对．A ．1个B ．2个C ．3个D ．4个6．如图∠AOC=∠BOD=90︒，4位同学观察图形后分别说了自己的观点.甲：∠AOB=∠COD ；乙：图中小于平角的角有6个；丙：∠AOB+∠COD =90︒；丁：∠BOC+∠AOD = 180︒ .其中正确的结论有（）.A ．4个B ．3个C ．2个D ．1个7．“枪挑一条线，棍扫一大片”，从数学的角度解释为（）．A ．点动成线，线动成面B ．线动成面，面动成体C ．点动成线，面动成体D ．点动成面，面动成线 8．计算：135333030306︒︒''''⨯-÷的值为（） A ．335355︒'''B ．363355︒'''C ．63533︒'''D ．53533︒''' 9．如图，C ，D 是线段AB 上的两点，E 是AC 的中点，F 是BD 的中点，若EF ＝m ，CD ＝n ，则AB ＝（）A ．m ﹣nB ．m +nC ．2m ﹣nD ．2m +n 10．如图，在数轴上有A ，B ，C ，D 四个整数点(即各点均表示整数)，且2AB ＝BC ＝3CD ，若A ，D 两点表示的数分别为-5和6，点E 为BD 的中点，在数轴上的整数点中，离点E 最近的点表示的数是（）A ．2B ．1C ．0D ．-111．已知α∠和β∠互补，且αβ∠>∠，则有下列式子：①90β︒-∠；②90α∠-︒；③()12αβ∠+∠；④()12αβ∠-∠；⑤()1902α∠-︒；其中，表示β∠的余角的式子有( ) A ．4个 B ．3个 C ．2个 D ．1个12．小陆制作了一个如图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的表面展开图可能是（）A．B．C．D．二、填空题13．硬币在桌面上快速地转动时，看上去象球，这说明了_________________．14．如图，记以点A为端点的射线条数为x，以点D为其中一个端点的线段的条数为y，-的值为________．则x y15．如图所示，填空：∠=∠+_________；（1）AOB AOC∠=∠-_________=_________-_________；（2）COB COD∠+∠-∠=_________.（3）AOB COD AOD16．如图所示，观察下列图形，在横线上写出几何体的名称及截面形状.（1）①的名称是________，截面形状________；（2）②的名称是________，截面形状是________；（3）③的名称是________，截面形状是________；（4）④的名称是________，截面形状是________；17．已知点B 在直线AC 上，AB=6cm ，AC=10cm ，P 、Q 分别是AB 、AC 的中点，则PQ=_____18．如图，线段AB 被点C ，D 分成2:4:7三部分，M ，N 分别是AC ，DB 的中点，若17MN cm =，则BD =__cm ．19．如图，C 岛在A 岛的北偏东60°方向，在B 岛的北偏西45°方向，则从C 岛看A 、B 两岛的视角∠ACB ＝_______.20．如图，90AOC BOD ∠=∠=︒，70AOB ∠=︒，在∠AOB 内画一条射线OP 得到的图中有m 对互余的角，其中AOP x ∠=︒，且满足050x <<，则m =_______．三、解答题21．已知：如图，在∠AOB 的内部从O 点引3条射线OC ，OD ，OE ，图中共有多少个角？若在∠AOB 的内部，从O 点引出4条，5条，6条，…，n 条不同的射线，可以分别得到多少个不同的角？22．如图，已知OE 是∠AOB 的平分线，C 是∠AOE 内的一点，若∠BOC ＝2∠AOC ，∠AOB ＝114°，则求∠BOC ，∠EOC 的度数．23．已知：如图AB ∥CD ，EF 交AB 于G ，交CD 于F ，FH 平分∠EFD ，交AB 于H ，∠AGE ＝50°，求：∠BHF 的度数．24．如图，一个五棱柱的盒子(有盖)，有一只蚂蚁在A处发现一只虫子在D处，立刻赶去捕捉，你知道它怎样去的吗?请在图中画出它的爬行路线，如果虫子正沿着DI方向爬行，蚂蚁预想在点I处将它捕捉，应沿着什么方向?请在图中画出它的爬行路线.25．如图，有一只蚂蚁想从A点沿正方体的表面爬到G点，走哪一条路最近？(1)请你利用部分平面展开图画出这条最短的路线，并说明理由．(2)探究若这只蚂蚁在正方体上爬行的最短路线，请你找出所有的最短路线，并画出示意. 26．如图，直角三角形ABC的两条直角边AB和BC分别长4厘米和3厘米，现在以斜边AC为轴旋转一周．求所形成的立体图形的体积．【参考答案】***试卷处理标记，请不要删除一、选择题1．A解析：A【分析】由OM是∠AOD的平分线，求得∠AOM＝21°，利用∠BOC＝34°，根据平角的定义求出答案．【详解】∵OM是∠AOD的平分线，∴∠AOM＝21°．又∵∠BOC＝34°，∴∠MOC＝180°－21°－34°＝125°．故选：A．【点睛】此题考查角平分线的有关计算，几何图形中角度的和差计算，根据图形掌握各角之间的关系是解题的关键．2．B解析：B【分析】根据题意作出图形，即可进行判断．【详解】将如图所示的直角三角形绕直线l旋转一周，可得到圆锥，故选B．【点睛】此题考查了点、线、面、体，重在体现面动成体：考查学生立体图形的空间想象能力及分析问题，解决问题的能力．3．C解析：C【分析】先利用角的和差关系求出∠AOB的度数，根据角平分线的定义求出∠BOD的度数，再利用角的和差关系求出∠COD的度数．【详解】解：∵∠AOC=90°，∠COB=α，∴∠AOB=∠AOC+∠COB=90°+α．∵OD平分∠AOB，∴∠BOD=12（90°+α）=45°+12α，∴∠COD=∠BOD-∠COB=45°-12α，故选：C.【点睛】本题综合考查了角平分线的定义及角的和差关系，熟练掌握是解题的关键.4．C解析：C【分析】根据题意画出图形，利用数形结合即可得出结论.【详解】解：如图所示：．故选C.【点睛】本题考查的是角的大小比较，能根据题意画出图形是解答此题的关键.5．D解析：D【分析】根据题意首先计算出∠AOD的度数，再计算出∠AOE、∠EOC、∠BOE、∠BOD的度数，然后再分析即可．【详解】解：由题意设∠BOE=x，∠EOC=3x，∵∠DOE＝60°，OD平分∠AOB，∴∠AOD＝∠BOD =60°-x，根据题意得：2（60°-x）+4x=180°，解得x=30°，∴∠EOC=∠AOE＝90°，∠BOE＝30°，∴∠BOD=∠AOD＝30°，故①正确；∵∠BOD＝∠AOD＝30°，∴射线OE平分∠AOC，故②正确；∵∠BOE＝30°，∠AOB＝60°，∠DOE＝60°，∴∠AOB+∠BOE＝90°，∠BOE+∠DOE＝90°，∴图中与∠BOE互余的角有2个，故③正确；∵∠AOE＝∠EOC＝90°，∴∠AOE+∠EOC＝180°，∵∠EOC＝90°，∠DOB＝30°，∠BOE＝30°，∠AOD＝30°，∴∠COD+∠AOD＝180°，∠COD+∠BOD＝180°，∠COD+∠BOE＝180°，∠COB+∠AOB＝180°，∠COB+∠DOE＝180°，∴图中互补的角有6对，故④正确，正确的有4个，故选：D ．【点睛】本题主要考查角平分线以及补角和余角，解答的关键是正确计算出图中各角的度数． 6．B解析：B【分析】根据余角的性质，补角的性质，可得答案．【详解】解：甲∠AOB+∠BOC=∠BOC+∠COD=90°，∠AOB=∠COD ，故甲正确；乙∠AOB ，∠AOC ，∠AOD ，∠BOC ，∠BOD ，∠COD ，故乙正确；丙∠AOB=∠COD ，故丙错误；丁：∠BOC+∠AOD=∠BOC+∠AOB+∠BOD=∠AOC+∠BOD=180°，故丁正确；故选：B ．【点睛】本题考查了余角、补角的定义和角的有关推理的应用，能正确进行推理是解此题的关键，难度适中．7．A解析：A【分析】根据从运动的观点来看点动成线，线动成面进行解答即可．【详解】“枪挑”是用枪尖挑，枪尖可看作点，棍可看作线，故这句话从数学的角度解释为点动成线，线动成面．故选A ．【点睛】本题考查了点、线、面得关系，难度不大，注意将生活中的实物抽象为数学上的模型． 8．B解析：B【分析】先进行度、分、秒的乘法除法计算，再算减法．【详解】135333030306︒︒''''⨯-÷4139555︒︒''''=-386415055︒︒''''-''='''363355︒=．故选：B ．【点睛】本题考查了度、分、秒的四则混合运算，是角度计算中的一个难点，注意以60为进制即可．9．C解析：C【分析】由已知条件可知，EC+FD=m-n，又因为E是AC的中点，F是BD的中点，则AE+FB=EC+FD，故AB=AE+FB+EF可求．【详解】解：由题意得，EC+FD=m-n∵E是AC的中点，F是BD的中点，∴AE+FB=EC+FD=EF-CD=m-n又∵AB=AE+FB+EF∴AB=m-n+m=2m-n故选：C．【点睛】利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时，灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．10．A解析：A【分析】根据A、D两点在数轴上所表示的数，求得AD的长度，然后根据2AB=BC=3CD，求得AB、BD的长度，从而找到BD的中点E所表示的数．【详解】解：如图：∵|AD|=|6-（-5）|=11，2AB=BC=3CD，∴AB=1.5CD，∴1.5CD+3CD+CD=11，∴CD=2，∴AB=3，∴BD=8，∴ED=1BD=4，2∴|6-E|=4，∴点E所表示的数是：6-4=2．∴离线段BD的中点最近的整数是2．故选：A．【点睛】本题考查了数轴、比较线段的长短．灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．11．B解析：B【分析】根据余角和补角的概念进行角度的计算即可得解.【详解】∵9090ββ︒-∠+∠=︒，∴①正确；∵α∠和β∠互补，∴180αβ∠+∠=︒，∴901809090αβ∠-︒+∠=︒-︒=︒，∴②正确，⑤错误； ∵()11180909022αββββ∠+∠+∠=⨯︒+∠=︒+∠≠︒， ∴③错误； ∵()()11118090222αββαβ∠-∠+∠=∠+∠=⨯︒=︒， ∴④正确；∴①②④正确，故选：B.【点睛】本题主要考查了余角和补角的含义，熟练掌握相关角度的计算是解决本题的关键. 12．A解析：A【分析】对面图案均相同的正方体礼品盒，则两个相同的图案一定不能相邻，据此即可判断．【详解】解：根据分析，图A 折叠成正方体礼盒后，心与心相对，笑脸与笑脸相对，太阳与太阳相对，即对面图案相同；图B 、图C 和图D 中对面图案不相同；故选A ．【点睛】本题考查了正方体的展开图，注意正方体的空间图形，从相对面入手，分析及解答问题．二、填空题13．面动成体【分析】本题是面动成体的原理在现实中的具体表现根据面动成体原理解答即可【详解】硬币在桌面上快速地转动时看上去象球这说明了面动成体故答案为面动成体【点睛】本题考查了点线面体掌握面动成体原理是解解析：面动成体【分析】本题是面动成体的原理在现实中的具体表现，根据面动成体原理解答即可.【详解】硬币在桌面上快速地转动时，看上去象球，这说明了面动成体，故答案为面动成体.【点睛】本题考查了点、线、面、体，掌握面动成体原理是解题的关键.14．【分析】先根据射线和线段的定义求出xy 的值再代入求解即可【详解】以点为端点的射线有射线AC 和射线AB 共两条故点为其中一个端点的线段有线段ADODBDCD 共四条故将代入中原式故答案为：【点睛】本题考查解析：2-【分析】先根据射线和线段的定义求出x ，y 的值，再代入求解即可．【详解】以点A 为端点的射线有射线AC 和射线AB ，共两条，故2x =点D 为其中一个端点的线段有线段AD 、OD 、BD 、CD ，共四条，故4y =将2x =，4y =代入x y -中原式242=-=-故答案为：2-．【点睛】本题考查了代数式的运算，掌握射线和线段的定义是解题的关键．15．∠BOC 【分析】根据图中各角的和与差的关系进行运算即可完成解答；【详解】（1）；（2）=∠AOB-∠AOC （3）====∠BOC 【点睛】此题主要考查角的和差关系解答的关键在于在图形中寻找角的和差关系解析：BOC ∠ BOD ∠ AOB ∠ AOC ∠ ∠BOC【分析】根据图中各角的和与差的关系进行运算，即可完成解答；【详解】（1）AOB AOC ∠=∠+BOC ∠；（2）COB COD ∠=∠-BOD ∠=∠AOB-∠AOC（3）AOB COD AOD ∠+∠-∠=()AOB COD AOB BOD ∠+∠-∠+∠=AOB COD AOB BOD ∠+∠-∠-∠=COD BOD ∠-∠=∠BOC【点睛】此题主要考查角的和差关系，解答的关键在于在图形中寻找角的和差关系.16．（1）①正方体长方形；（2）②圆锥等腰三角形；（3）③圆柱圆；（4）④正方体长方形【解析】【分析】首先观察图形先判断出各个几何体的名称然后根据平面截几何体的方向和角度判断出截面的形状【详解】(1)图解析：（1）①正方体，长方形；（2）②圆锥，等腰三角形；（3）③圆柱，圆；（4）④正方体，长方形.【解析】【分析】首先观察图形，先判断出各个几何体的名称，然后根据平面截几何体的方向和角度，判断出截面的形状.【详解】(1)图中几何体是正方体,截面垂直正方体底面,故截面是长方形;(2)图中几何体是圆锥,截面垂直圆锥底面,故截面是等腰三角形;(3)图中几何体是圆柱,截面平行圆柱底面,故截面是圆;(4)图中几何体是正方体,截面垂直正方体底面,故截面是长方形.故答案为：（1）①正方体，长方形；（2）②圆锥，等腰三角形；（3）③圆柱，圆；（4）④正方体，长方形.【点睛】此题考查判断几何体的名称以及截面形状，需要利用常见几何体的特征和截面的知识进行解答.17．2或8【分析】本题没有给出图形在画图时应考虑到ABC三点之间的位置关系的多种可能再根据正确画出的图形解题【详解】解：如图：当点BC在点A 的不同侧时∴AP=AB=3cmAQ=AC=5cm∴PQ=AQ+解析：2或8【分析】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系的多种可能，再根据正确画出的图形解题．【详解】解：如图：当点B、C在点A的不同侧时，∴AP=12AB=3cm，AQ=12AC=5cm，∴PQ=AQ+AP=5+3=8cm．当点B、C在点A的同一侧时，∴AP=12AB=3cm ， ∴AQ=12AC=5cm ， PQ=AQ-AP=5-3=2cm ．故答案为8cm 或2cm ．【点睛】在未画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性．在今后解决类似的问题时，要防止漏解．18．14【分析】线段AB 被点CD 分成2：4：7三部分于是设AC=2xCD=4xBD=7x 由于MN 分别是ACDB 的中点于是得到CM=AC=xDN=BD=x 根据MN=17cm 列方程即可得到结论【详解】解：线解析：14【分析】线段AB 被点C ，D 分成2：4：7三部分，于是设AC=2x ，CD=4x ，BD=7x ，由于M ，N 分别是AC ，DB 的中点，于是得到CM=12AC=x ，DN=12BD=72x ，根据MN=17cm 列方程，即可得到结论．【详解】解：线段AB 被点C ，D 分成2:4:7三部分， ∴设2AC x =，4CD x =，7BD x =， M ，N 分别是AC ，DB 的中点，12CM AC x ∴==，1722DN BD x ==， 17MN cm =，74172x x x ∴++=， 2x ∴=，14BD ∴=．故答案为：14．【点睛】本题考查了两点间的距离，利用了线段的和差，利用中点性质转化线段之间的倍分关系是解题的关键．19．【分析】先求出∠CAB 及∠ABC 的度数再根据三角形内角和是180°即可进行解答【详解】∵C 岛在A 岛的北偏东60°方向在B 岛的北偏西45°方向∴∠CAB+∠ABC=180°﹣（60°+45°）=75°解析：【分析】先求出∠CAB 及∠ABC 的度数，再根据三角形内角和是180°即可进行解答．【详解】∵C岛在A岛的北偏东60°方向，在B岛的北偏西45°方向，∴∠CAB+∠ABC=180°﹣（60°+45°）=75°，∵三角形内角和是180°，∴∠ACB=180°﹣∠CAB﹣∠ABC=180°﹣30°﹣45°=105°．故答案为105．【点睛】此题主要考查了方向角的概念和三角形的内角和定理，根据题意得到∠CAB和∠ABC的度数是解题关键.20．3或4或6【分析】分三种情况下：①∠AOP＝35°②∠AOP＝20°③0＜x ＜50中的其余角根据互余的定义找出图中互余的角即可求解【详解】①∠AOP ＝∠AOB=35°时∠BOP=35°∴互余的角有∠解析：3或4或6【分析】分三种情况下：①∠AOP＝35°，②∠AOP＝20°，③0＜x＜50中的其余角，根据互余的定义找出图中互余的角即可求解．【详解】①∠AOP＝12∠AOB =35°时，∠BOP=35°∴互余的角有∠AOP与∠COP，∠BOP与∠COP，∠AOB与∠COB，∠COD与∠COB，一共4对；②∠AOP＝90°-∠AOB =20°时，∴互余的角有∠AOP与∠COP，∠AOP与∠AOB，∠AOP与∠COD，∠COD与∠COB，∠AOB与∠COB，∠COP与∠COB，一共6对；③0＜x＜50中35°与20°的其余角，互余的角有∠AOP与∠COP，∠AOB与∠COB，∠COD 与∠COB，一共3对．则m＝3或4或6．故答案为：3或4或6．【点睛】本题考查了余角和补角：如果两个角的和等于90°（直角），就说这两个角互为余角．即其中一个角是另一个角的余角．三、解答题21．角的个数分别为10，15，21，28，…，(2)(1)2n n++．【分析】1、在锐角∠AOB的内部以O为顶点作3条射线,由此你能得到以O为顶点的射线共有多少条吗?2、根据以一条射线为边,以其余n+1条射线为另一边可作n+1个角,相信你能求得5条射线共多少个锐角；3、由于任意两射线所得的角都多计一次,所以当在∠AOB的内部从O点引3条射线共有1452⨯⨯个角；4、结合作3条射线得到的角的个数,可以推出以O为顶点共有n条射线时,得到的角的个数为(1)(2)2n n++，继而将n=5、6、7代入即可．【详解】解：顺时针数，与射线OA构成的角有4个，与射线OC构成的角有3个，与射线OD构成的角有2个，与射线OE构成的角有1个，故共有角4＋3＋2＋1＝10(个). 类似地，引4条射线有角5＋4＋3＋2＋1＝15(个)，引5条射线有角6＋5＋4＋3＋2＋1＝21(个)，引6条射线有角7＋6＋5＋4＋3＋2＋1＝28(个)，…，以此类推，引n条射线有角(n＋1)＋n＋(n－1)＋…＋2＋1＝(1)(2)2n n++(个) ．【点睛】本题中,根据以点O为顶点的射线有n+2条,再求这n+2条射线可形成的角的个数.要求同学们能够准确利用题目中的已知信息,灵活运用所学知识进行解答.本题还可以采用顺序枚举法进行解答,按一定顺序,把所有元素一一列举出来,要做到不重不漏,适合元素(射线)个数较少情况,如果图中有n条射线这时无法逐一列举,可用规律归纳法.22．∠BOC＝76°，∠EOC＝19°．【分析】由∠BOC＝2∠AOC，则∠AOB=∠BOC+∠AOC=3∠AOC，即∠BOC=23∠AOB，然后求解即可;再根据OE是∠AOB的平分线求得∠BOE，最后根据角的和差即可求得∠EOC．【详解】解：∵∠BOC＝2∠AOC，∠AOB＝114°，∴∠BOC＝23∠AOB =23×114°＝76°，∵OE是∠AOB的平分线，∠AOB＝114°，∴∠BOE＝12∠AOB ＝12×114°＝57°.∴∠EOC＝∠BOC－∠BOE＝19°．【点睛】本题主要考查了角平分线的定义以及角的和差运算，掌握数形结合思想成为解答本题的关键．23．∠BHF=115° .【分析】由AB∥CD得到∠AGE=∠CFG，由此根据邻补角定义可得∠GFD的度数，又FH平分∠EFD，由此可以先后求出∠GFD，∠HFD，继而可求得∠BHF的度数．【详解】∵AB∥CD，∴∠CFG=∠AGE=50°，∴∠GFD=130°；又FH平分∠EFD，∠EFD=65°；∴∠HFD=12∵AB∥CD，∴∠BHF=180°-∠HFD=115°．【点睛】本题考查了平行线的性质，角平分线的定义，邻补角等知识，两直线平行时，应该想到它们的性质；由两直线平行的关系可以得到角之间的数量关系，从而达到解决问题的目的．24．第一问：如图沿线段AD爬行；第二问取线段E J的中点M，连结AM和MI，此路线为蚂蚁爬行的路线．【分析】根据两点之间线段最短，结合图形得出蚂蚁爬行的路线．【详解】解：第一问：如图沿线段AD爬行；第二问取线段E J的中点M，连结AM和MI，此路线为蚂蚁爬行的路线．理由都是：两点之间线段最短．【点睛】本题考查了几何体的展开图与两点之间线段最短，利用展开图的性质得出答案是解题的关键．25．如图①，（1）见解析，理由：两点之间线段最短；（2）见解析.【分析】（1）先把正方体展开，根据两点之间线段最短，即可得出由A爬到G的最短途径．（2）分情况讨论，作图解答即可.【详解】（1）如图①，理由：两点之间线段最短．（2）如图②，这种最短路线有4条．【点睛】本题考查了几何体的展开图和最短路线问题，把几何体展开为平面图形是解决“怎样爬行最近”这类问题的关键．26．6π立方厘米【解析】试题分析：先根据勾股定理求出斜边为5厘米，再用“3×4÷5=2.4厘米”求出斜边上的高，绕斜边旋转一周后所得到的就是两个底面半径为2.4厘米，高的和为5厘米的圆锥体，由此利用圆锥的体积公式求得这两个圆锥的体积之和即可．试题过B作BD⊥AC，∵直角边AB和BC分别长4厘米和3厘米，∴AC=2234=5（厘米），斜边上的高为“3×4÷5=2.4（厘米），所形成的立体图形的体积：132.42 5 =9.6π（立方厘米）．。

初中数学几何综合-含答案

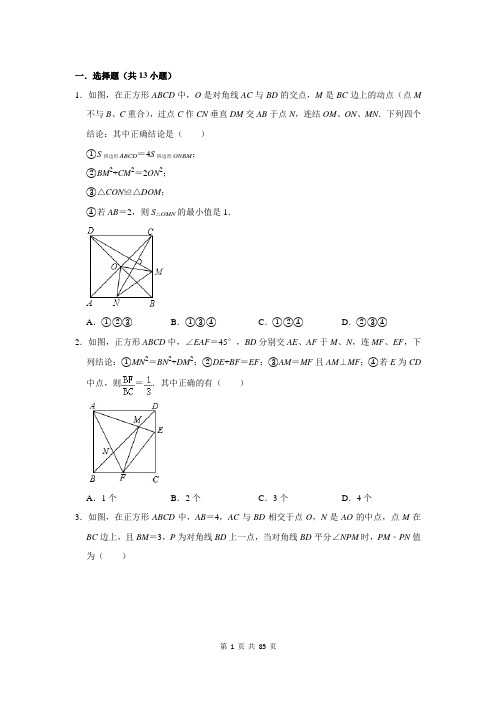
一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．45．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或27．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE ⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF＝BE，正确的有（）A．2个B．3个C．4个D．5个11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有（填番号）．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝．三．解答题（共24小题）17．如图，在直线l上将正方形ABCD和正方形ECGF的边CD和边CE靠在一起，连接DG，过点A作AH∥DG，交BG于点H．连接HF，AF，其中FH交DG于点M．（1）求证：△AHF为等腰直角三角形．（2）若AB＝3，EC＝4，求DM的长．18．如图，已知正方形ABCD的面积是8，连接AC、BD交于点O，CM平分∠ACD交BD 于点M，MN⊥CM，交AB于点N，（1）求∠BMN的度数；（2）求BN的长．19．如图示，正方形ABCD的对角线交于点O，点E、F分别在AB，BC的延长线上，且∠EOF＝90°，OE与BC交于点M，连接EF，G是EF的中点，连接OG．（1）求证：OE＝OF（2）若∠BOG＝65°，求∠BOE的度数；（3）是否存在点M是BC中点，且使（1）的结论成立，若存在，请给予证明；若不存在，请说明理由．20．如图，正方形ABCD中，AB＝，在边CD的右侧作等腰三角形DCE，使DC＝DE，记∠CDE为α（0°＜α＜90°），连接AE，过点D作DG⊥AE，垂足为G，交EC的延长线于点F，连接AF．（1）求∠DEA的大小（用α的代数式表示）；（2）求证：△AEF为等腰直角三角形；（3）当CF＝时，求点E到CD的距离．21．如图1，在正方形ABCD中，点E在边CD上（不与点C，D重合），AE交对角线BD 于点G，GF⊥AE交BC于点F．（1）求证：AG＝FG．（2）若AB＝10，BF＝4，求BG的长．（3）如图2，连接AF，EF，若AF＝AE，求正方形ABCD与△CEF的面积之比．22．在正方形ABCD中，点E是DC上一点，连结AC，AE．（1）如图1，若AC＝8，AE＝10，求△ACE的面积．（2）如图2，EF⊥AC于点F，连结BF．求证：AE＝BF．23．如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．（1）求证：△BCG≌△DCE；（2）如图2，连接BD，若，求BG的长．24．如图，在正方形ABCD中，对角线AC、BD相交于点O，E为OC上动点（不与O、C 重合），作AF⊥BE，垂足为G，分别交BC、OB于F、H，连接OG、CG．（1）求证：△AOH≌△BOE；（2）求∠AGO的度数；（3）若∠OGC＝90°，BG＝，求△OGC的面积．25．如图，O为正方形ABCD对角线的交点，E为AB边上一点，F为BC边上一点，△EBF 的周长等于BC的长．（1）若AB＝24，BE＝6，求EF的长；（2）求∠EOF的度数；（3）若OE＝OF，求的值．26．如图，正方形ABCD中，E为BC上一点，过B作BG⊥AE于G，延长BG至点F使∠CFB＝45°（1）求证：∠BAG＝∠CBF；（2）求证：AG＝FG；（3）若GF＝2BG，CF＝，求AB的长．27．如图1，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且P A＝PE，PE交CD于点F，（1）证明：PC＝PE；（2）求∠CPE的度数；（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC＝120°，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．28．如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E．（1）试说明EO＝FO；（2）当点O运动到何处时，四边形AECF是矩形并证明你的结论；（3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论．29．如图，已知平行四边形ABCD中，对角线AC、BD交于点O，E是DB延长线上一点，且△ACE是等边三角形．（1）求证：四边形ABCD是菱形；（2）若∠AEB＝2∠EAB，求证：四边形ABCD是正方形．30．如图1，在正方形ABCD中，G为线段BD上一点，连接AG，过G作AG⊥GE交BC 于E，连接AE．（1）求证：BG＝DG+BE；（2）如图2，AB＝4，E为BC中点，P，Q分别为线段AB，AE上的动点，满足QE＝AP，则在P，Q运动过程中，当以PQ为对角线的正方形PRQS的一边恰好落在△ABE的某一边上时，直接写出正方形PRQS的面积．31．如图，在平行四边形ABCD中，AC⊥AD，延长DA于点E，使得DA＝AE，连接BE．（1）求证：四边形AEBC是矩形；（2）过点E作AB的垂线分别交AB，AC于点F，G，连接CE交AB于点O，连接OG，若AB＝6，∠CAB＝30°，求△OGC的面积．32．如图，在四边形ABCD中，AD∥BC，AB＝BC，对角线AC、BD交于点O，BD平分∠ABC，过点D作DE⊥BC，交BC的延长线于点E，连接OE．（1）求证：四边形ABCD是菱形；（2）若DC＝2，AC＝4，求OE的长．33．如图，在菱形ABCD中，对角线AC、BD交于点O，过点A作AE⊥BC于点E，延长BC至F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）若BF＝8，DF＝4，求CD的长．34．已知：如图，点E为▱ABCD对角线AC上的一点，点F在线段BE的延长线上，且EF ＝BE，线段EF与边CD相交于点G．（1）求证：DF∥AC；（2）如果AB＝BE，DG＝CG，联结DE、CF，求证：四边形DECF是矩形．35．如图，▱ABCD的对角线AC，BD交于点O，过点D作DE⊥BC于E，延长CB到点F，使BF＝CE，连接AF，OF．（1）求证：四边形AFED是矩形．（2）若AD＝7，BE＝2，∠ABF＝45°，试求OF的长．36．如图，平行四边形ABCD中，AC⊥BC，过点D作DE∥AC交BC的延长线于点E，点M为AB的中点，连接CM．（1）求证：四边形ADEC是矩形；（2）若CM＝5，且AC＝8，求四边形ADEC的周长．37．如图，已知△OAB中，OA＝OB，分别延长AO、BO到点C、D．使得OC＝AO，OD ＝BO，连接AD、DC、CB．（1）求证：四边形ABCD是矩形；（2）以OA、OB为一组邻边作▱AOBE，连接CE，若CE⊥BD，求∠AOB的度数．38．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．（1）求证：四边形AEFD是矩形；（2）连接OE，若AD＝10，EC＝4，求OE的长度．39．如图，在平行四边形BPCD中，点O为BD中点，连接CO并延长交PB延长线于点A，连接AD、BC，若AC＝CP，（1）求证：四边形ABCD为矩形；（2）在BA的延长线上取一点E，连接OE交AD于点F，若AB＝9，BC＝12，AE＝3，则AF的长为．40．如图，菱形ABCD中，AC与BD交于点O，DE∥AC，DE＝AC．（1）求证：四边形OCED是矩形；（2）连结AE，交OD于点F，连结CF，若CF＝CE＝1，求AC长．2021年01月06日杨莲莲的初中数学组卷参考答案与试题解析一．选择题（共13小题）1．如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点（点M 不与B、C重合），过点C作CN垂直DM交AB于点N，连结OM、ON、MN．下列四个结论：其中正确结论是（）①S四边形ABCD＝4S四边形ONBM；②BM2+CM2＝2ON2；③△CON≌△DOM；④若AB＝2，则S△OMN的最小值是1．A．①②③B．①③④C．①②④D．②③④【分析】根据正方形的性质，依次判定△CNB≌△DMC，△AON≌△BOM，根据全等三角形的性质以及勾股定理进行计算即可得出结论．【解答】解：∵四边形ABCD是正方形，∴AC⊥BD，AO＝AC，BO＝BD，AC＝BD，∴AO＝BO，∠OAN＝∠OBM＝45°，∠AOB＝90°，∵CN⊥DM，∴∠MCN+∠CMD＝∠CMD+∠CDM＝90°，∴∠CDM＝∠BCN，∵CD＝BC，∠DCM＝∠CBN，∴△CDM≌△BCN（AAS），∴CM＝BN，∴AN＝BM，∴△AON≌△BOM（SAS），∴S△AON＝S△BOM，∴S四边形ONBM＝S△AOB＝S正方形ABCD，∴S四边形ABCD＝4S四边形ONBM；故①正确；∵△AON≌△BOM，∴ON＝OM，∠AON＝∠BOM，∴∠NOM＝∠AOB＝90°，∴△NOM是等腰直角三角形，∴MN2＝2ON2，∵BN2+BM2＝MN2，∴CM2+BM2＝2ON2，故②正确；∵∠MON＝∠COD＝90°，∴∠NOC＝∠MOD，∵OD＝OC，ON＝OM，∴△CON≌△DOM（SAS），故③正确；∵AB＝2，∴S正方形ABCD＝4，∵△AON≌△BOM，∴四边形BMON的面积＝△AOB的面积＝1，即四边形BMON的面积是定值1，∴当△MNB的面积最大时，△MNO的面积最小，设BN＝x＝CM，则BM＝2﹣x，∴△MNB的面积＝x（2﹣x）＝﹣x2+x＝﹣（x﹣1）2+，∴当x＝1时，△MNB的面积有最大值，此时S△OMN的最小值是1﹣＝，故④不正确，故选：A．【点评】本题主要考查了正方形的性质、全等三角形的判定与性质，二次函数的最值以及勾股定理的综合应用，解题时注意二次函数的最值的运用．2．如图，正方形ABCD中，∠EAF＝45°，BD分别交AE、AF于M、N，连MF、EF，下列结论：①MN2＝BN2+DM2；②DE+BF＝EF；③AM＝MF且AM⊥MF；④若E为CD 中点，则＝．其中正确的有（）A．1个B．2个C．3个D．4个【分析】①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，易证△ADM≌△ABH，△AHN≌△AMN，得MN＝HN，最后根据勾股定理可作判断；②延长CB，截取BI＝DE，连接AI，如图，易证△ADE≌△ABI，△AIF≌△AEF，得IF＝EF，即DE+BF＝EF，成立．③作辅助线，则可证△AFJ为等腰直角三角形，CK＝BF＝KJ，证明∠JCK＝45°，推出四边形BCJK为平行四边形，所以GJ＝BC＝AD，可证△GJM≌△DAM，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，CF＝2a﹣x，CE＝a，由勾股定理可知：3x＝2a，则＝＝，成立．【解答】解：①过B作BD的垂线，截取BH＝MD，连接AH，HN，如图，∵四边形ABCD是正方形，∴AD＝AB，∠ADB＝∠ABD＝45°，∠BAD＝90°，∴∠ABH＝45°＝∠ADM，在△ADM和△ABM中，∵，∴△ADM≌△ABH（SAS），∴∠DAM＝∠BAH，AM＝AH，∵∠EAF＝45°，∠BAD＝90°，∴∠DAM+∠BAN＝∠BAH+∠BAN＝45°，∴∠MAN＝∠HAN＝45°，在△AHN和△AMN中，∵，∴△AHN≌△AMN（SAS），∴MN＝HN，Rt△BHN中，HN2＝BH2+BN2，∴MN2＝BN2+DM2，成立．②延长CB，截取BI＝DE，连接AI，如图，在△ADE和△ABI中，∵∴△ADE≌△ABI（SAS），同理得△AIF≌△AEF（SAS），∴IF＝EF，即DE+BF＝EF，成立；③如图，过F作FJ⊥AF交AE的延长线于J，过J作JK⊥BC于K，连接CJ，过J作JG ∥BC交BD于G，∴∠AFJ＝∠AFB+∠JFK＝90°，∵∠AFB+∠BAF＝90°，∴∠BAF＝∠JFK，∵∠EAF＝45°，∠AFJ＝90°，∴△AFJ是等腰直角三角形，在△ABF和△FKJ中，∵，∴△ABF≌△FKJ（SAS），∴AB＝FK＝BC，BF＝KJ，∴CK＝BF＝KJ，∴∠JCK＝45°，∴∠DBC＝∠JCK，∴BG∥CJ，∵JG∥BC，∴四边形BCJK为平行四边形，∴GJ＝BC＝AD，∵AD∥BC∥GJ，∴∠DAM＝∠MJK，在△GJM和△DAM中，∵，∴△GJM≌△DAM（AAS），∴AM＝MJ，则M为AJ的中点，又∠AFJ＝90°，故AM＝MF且AM⊥MF，成立．④延长CB，截取BL＝DE，连接AL，可设DE＝a，BF＝x，则EF＝LF＝a+x，∵E为CD中点，∴CD＝BC＝2a，∴CF＝2a﹣x，CE＝a，在Rt△EFC中，由勾股定理得：EF2＝CE2+CF2∴（a+x）2＝a2+（2a﹣x）2解得：3x＝2a，则＝＝，成立．故选：D．【点评】本题考查了正方形的性质，全等三角形的判定和性质，勾股定理，正确的作出辅助线是解题的关键．3．如图，在正方形ABCD中，AB＝4，AC与BD相交于点O，N是AO的中点，点M在BC边上，且BM＝3，P为对角线BD上一点，当对角线BD平分∠NPM时，PM﹣PN值为（）A．1B．C．2D．【分析】作以BD为对称轴作N的对称点N'，连接MN'，PN'，根据PM﹣PN＝PM﹣PN'≤MN'，当P，M，N'三点共线时，取“＝”，再证得△MCN'∽△BCA，从而推得△MCN'为等腰直角三角形，结合BM＝3．正方形的边长为4，求得CM，即为MN'，问题可解．【解答】解：如图所示，∵对角线BD平分∠NPM，∴作以BD为对称轴N的对称点N'，连接MN'，PN'，根据轴对称性质可知，PN＝PN'，∠NPO＝N′PO，NO＝N′O∵在正方形ABCD中，AB＝4∴AC＝AB＝4，∵O为AC中点∴OA＝OC＝2∵N为OA的中点∴ON＝∴ON'＝CN'＝∴AN'＝3∵BM＝3∴CM＝4﹣3＝1∴＝＝∵∠MCN'＝∠BCA∴△MCN'∽△BCA∴∠CMN'＝∠ABC＝90°∵∠MCN'＝45°∴△MCN'为等腰直角三角形∴MN'＝CM＝1∴PM﹣PN的值为1．故选：A．【点评】本题主要考查了正方形的性质，明确正方形的相关性质及相似三角形的判定、勾股定理等知识点，是解题的关键．4．如图，在正方形ABCD内一点E连接BE、CE，过C作CF⊥CE与BE延长线交于点F，连接DF、DE．CE＝CF＝1，DE＝，下列结论中：①△CBE≌△CDF；②BF⊥DF；③点D到CF的距离为2；④S四边形DECF＝+1．其中正确结论的个数是（）A．1B．2C．3D．4【分析】根据正方形的性质、全等三角形的判定和性质、勾股定理等知识逐项判断即可．【解答】解：∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∵CF⊥CE，∴∠ECF＝∠BCD＝90°，∴∠BCE＝∠DCF，在△BCE与△DCF中，，∴△BCE≌△DCF（SAS），故①正确；∵△BCE≌△DCF，∴∠CBE＝∠CDF，∴∠DFB＝∠BCD＝90°，∴BF⊥DF，故②正确，过点D作DM⊥CF，交CF的延长线于点M，∵∠ECF＝90°，FC＝EC＝1，∴∠CFE＝45°，∵∠DFM+∠CFB＝90°，∴∠DFM＝∠FDM＝45°，∴FM＝DM，∴由勾股定理可求得：EF＝，∵DE＝，∴由勾股定理可得：DF＝2，∵EF2+BE2＝2BE2＝BF2，∴DM＝FM＝，故③错误，∵△BCE≌△DCF，∴S△BCE＝S△DCF，∴S四边形DECF＝S△DCF+S△DCE＝S△ECF+S△DEF＝+，故④错误，故选：B．【点评】本题考查四边形的综合问题，涉及正方形的性质、全等三角形的性质与判定、勾股定理、三角形面积公式等知识内容，综合程度高，需要学生灵活运用知识解答．5．如图，已知E，F分别为正方形ABCD的边AB，BC的中点，AF与DE交于点M．则下列结论：①∠AME＝90°，②∠BAF＝∠EDB，③AM＝MF，④ME+MF＝MB．其中正确结论的有（）A．4个B．3个C．2个D．1个【分析】根据正方形的性质可得AB＝BC＝AD，∠ABC＝∠BAD＝90°，再根据中点定义求出AE＝BF，然后利用“边角边”证明△ABF和△DAE全等，根据全等三角形对应角相等可得∠BAF＝∠ADE，然后求出∠ADE+∠DAF＝∠BAD＝90°，从而求出∠AMD ＝90°，再根据邻补角的定义可得∠AME＝90°，得出①正确；根据中线的定义判断出∠ADE≠∠EDB，然后求出∠BAF≠∠EDB，判断出②错误；设正方形ABCD的边长为2a，利用勾股定理列式求出AF，再根据似三角形对应边成比例求出AM，然后求出MF，消掉a即可得到AM＝MF，判断出③正确；过点M作MN⊥AB于N，由相似三角形的性质得出＝＝，解得MN＝a，AN＝a，得出NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得BM＝a，求出ME+MF＝+a＝a，MB＝a，得出ME+MF＝MB，故④正确．于是得到结论．【解答】解：在正方形ABCD中，AB＝BC＝AD，∠ABC＝∠BAD＝90°，∵E、F分别为边AB，BC的中点，∴AE＝BF＝BC，在△ABF和△DAE中，，∴△ABF≌△DAE（SAS），∴∠BAF＝∠ADE，∵∠BAF+∠DAF＝∠BAD＝90°，∴∠ADE+∠DAF＝∠BAD＝90°，∴∠AMD＝180°﹣（∠ADE+∠DAF）＝180°﹣90°＝90°，∴∠AME＝180°﹣∠AMD＝180°﹣90°＝90°，故①正确；∵DE是△ABD的中线，∴∠ADE≠∠EDB，∴∠BAF≠∠EDB，故②错误；设正方形ABCD的边长为2a，则BF＝a，在Rt△ABF中，AF＝＝＝a，∵∠BAF＝∠MAE，∠ABC＝∠AME＝90°，∴△AME∽△ABF，∴＝，即＝，解得：AM＝a，∴MF＝AF﹣AM＝a﹣a＝a，∴AM＝MF，故③正确；如图，过点M作MN⊥AB于N，则MN∥BC，∴△AMN∽△AFB，∴＝＝，即＝＝，解得MN＝a，AN＝a，∴NB＝AB﹣AN＝2a﹣a＝a，根据勾股定理得：BM＝＝＝a，∵ME+MF＝+a＝a，MB＝a，∴ME+MF＝MB，故④正确．综上所述，正确的结论有①③④共3个．故选：B．【点评】本题考查了正方形的性质，全等三角形的判定与性质，相似三角形的判定与性质，勾股定理等知识；仔细分析图形并作出辅助线构造出直角三角形与相似三角形是解题的关键．6．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，EH与CF交于点O．则HE的长为（）A．2B．C．2D．或2【分析】利用直角三角形斜边上的中线等于斜边的一半，分别求得HO和OE的长后即可求得HE的长．【解答】解：∵AC、CF分别是正方形ABCD和正方形CGFE的对角线，∴∠ACD＝∠GCF＝45°，∴∠ACF＝90°，又∵H是AF的中点，∴CH＝HF，∵EC＝EF，∴点H和点E都在线段CF的中垂线上，∴HE是CF的中垂线，∴点H和点O是线段AF和CF的中点，∴OH＝AC，在Rt△ACD和Rt△CEF中，AD＝DC＝1，CE＝EF＝3，∴AC＝，∴CF＝3，又OE是等腰直角△CEF斜边上的高，∴OE＝，∴HE＝HO+OE＝2．故选：C．【点评】本题考查了正方形的性质、直角三角形的性质及勾股定理的知识，综合性较强，难度较大．7．如图，在正方形ABCD中，E为BC上一点，过点E作EF∥CD，交AD于F，交对角线BD于G，取DG的中点H，连结AH，EH，FH．下列结论：①FH∥AE；②AH＝EH且AH⊥EH；③∠BAH＝∠HEC；④△EHF≌△AHD；⑤若，则．其中哪些结论是正确（）A．①②④⑤B．②③④C．①②③D．②③④⑤【分析】①根据正方形对角线互相垂直、过一点有且只有一条直线与已知直线垂直即可得结论；②根据矩形的判定和性质、直角三角形的性质，证明三角形全等即可得结论；③根据全等三角形性质、矩形的性质进行角的计算即可得结论；④根据边边边证明三角形全等即可得结论；⑤根据割补法求四边形的面积，再求等腰直角三角形的面积，即可得结论．【解答】证明：①在正方形ABCD中，∠ADC＝∠C＝90°，∠ADB＝45°，∵EF∥CD∴∠EFD＝90°，得矩形EFDC．在Rt△FDG中，∠FDG＝45°，∴FD＝FG，∵H是DG中点，∴FH⊥BD∵正方形对角线互相垂直，过A点只能有一条垂直于BD的直线，∴AE不垂直于BD，∴FH与AE不平行．所以①不正确．②∵四边形ABEF是矩形，∴AF＝EB，∠BEF＝90°，∵BD平分∠ABC，∴∠EBG＝∠EGB＝45°，∴BE＝GE，∴AF＝EG．在Rt△FGD中，H是DG的中点，∴FH＝GH，FH⊥BD，∴∠AFH＝∠AFE+∠GFH＝90°+45°＝135°，∠EGH＝180°﹣∠EGB＝180°﹣45°＝135°，∴∠AFH＝∠EGH，∴△AFH≌△EGH，∴AH＝EH，∠AHF＝∠EHG，∴∠AHF+AHG＝∠EHG+∠AHG，即∠FHG＝∠AHE＝90°，∴AH⊥EH．所以②正确．③∵△AFH≌△EGH，∴∠F AH＝∠GEH，∵∠BAF＝CEG＝90°，∴∠BAH＝∠HEC．所以③正确．④∵EF＝AD，FH＝DH，EH＝AH，∴△EHF≌△AHD所以④正确．⑤如图，过点H作HM⊥AD于点M，设EC＝FD＝FG＝x，则BE＝AF＝EG＝2x，∴BC＝DC＝AB＝AD＝3x，HM＝x，AM＝x，∴AH2＝（x）2+（x）2＝x2，S四边形DHEC＝S梯形EGDC﹣S△EGH＝（2x+3x）•x﹣×＝2x2S△AHE＝AH•EH＝AH2＝x2∴＝＝．所以⑤不正确．故选：B．【点评】本题考查了正方形的性质、矩形的判定和性质、全等三角形的判定和性质、直角三角形的性质、三角形和梯形的面积等内容，解题关键是综合利用以上知识解决问题．8．如图，在正方形ABCD中，AC、BD相交于点O，E、F分别为BC、CD上的两点，BE ＝CF，AE、BF分别交BD、AC于M、N两点，连OE、OF．下列结论：①AE＝BF；②AE⊥BF；③CE+CF＝BD；④S四边形OECF＝S正方形ABCD，其中正确的是（）A．①②B．①④C．①②④D．①②③④【分析】①易证得△ABE≌△BCF（ASA），则可证得结论①正确；②由△ABE≌△BCF，可得∠FBC＝∠BAE，证得AE⊥BF，选项②正确；③证明△BCD是等腰直角三角形，求得选项③错误；④证明△OBE≌△OCF，根据正方形被对角线将面积四等分，即可得出选项④正确．【解答】解：①∵四边形ABCD是正方形，∴AB＝BC，∠ABE＝∠BCF＝90°，在△ABE和△BCF中，∵，∴△ABE≌△BCF（SAS），∴AE＝BF，故①正确；②由①知：△ABE≌△BCF，∴∠FBC＝∠BAE，∴∠FBC+∠ABF＝∠BAE+∠ABF＝90°，∴AE⊥BF，故②正确；③∵四边形ABCD是正方形，∴BC＝CD，∠BCD＝90°，∴△BCD是等腰直角三角形，∴BD＝BC，∴CE+CF＝CE+BE＝＝BC，故③错误；④∵四边形ABCD是正方形，∴OB＝OC，∠OBE＝∠OCF＝45°，在△OBE和△OCF中，∵，∴△OBE≌△OCF（SAS），∴S△OBE＝S△OCF，∴S四边形OECF＝S△COE+S△OCF＝S△COE+S△OBE＝S△OBC＝S正方形ABCD，故④正确；故选：C．【点评】此题属于四边形的综合题．考查了正方形的性质，全等三角形的判定与性质、勾股定理以及等腰直角三角形的性质．注意掌握全等三角形的判定与性质是解此题的关键．9．如图，在正方形ABCD中，M是对角线BD上的一点，点E在AD的延长线上，连接AM、EM、CM，延长EM交AB于点F，若AM＝EM，∠E＝30°，则下列结论：①FM＝ME；②BF＝DE；③CM⊥EF；④BF+MD＝BC，其中正确的结论序号是（）A．①②③B．①②④C．②③④D．①②③④【分析】①证明△AFM是等边三角形，可判断；②③证明△CBF≌△CDE（ASA），可作判断；④设MN＝x，分别表示BF、MD、BC的长，可作判断．【解答】解：①∵AM＝EM，∠AEM＝30°，∴∠MAE＝∠AEM＝30°，∴∠AMF＝∠MAE+∠AEM＝60°，∵四边形ABCD是正方形，∴∠F AD＝90°，∴∠F AM＝90°﹣30°＝60°，∴△AFM是等边三角形，∴FM＝AM＝EM，故①正确；②连接CE、CF，∵四边形ABCD是正方形，∴∠ADB＝∠CDM，AD＝CD，在△ADM和△CDM中，∵，∴△ADM≌△CDM（SAS），∴AM＝CM，∴FM＝EM＝CM，∴∠MFC＝∠MCF，∠MEC＝∠ECM，∵∠ECF+∠CFE+∠FEC＝180°，∴∠ECF＝90°，∵∠BCD＝90°，∴∠DCE＝∠BCF，在△CBF和△CDE中，∵，∴△CBF≌△CDE（ASA），∴BF＝DE；故②正确；③∵△CBF≌△CDE，∴CF＝CE，∵FM＝EM，∴CM⊥EF，故③正确；④过M作MN⊥AD于N，设MN＝x，则AM＝AF＝2x，AN＝x，DN＝MN＝x，∴AD＝AB＝x+x，∴DE＝BF＝AB﹣AF＝x+x﹣2x＝x﹣x，∴BF+MD＝（x﹣x）+x＝x，∵BC＝AD＝x+x x，故④错误；所以本题正确的有①②③；故选：A．【点评】本题考查了正方形的性质，全等三角形的判定与性质，等腰三角形的性质和判定，熟记正方形的性质确定出△AFM是等边三角形是解题的关键．【点评】此题考查的是正方形的性质，等腰直角三角形的性质和判定以及菱10．如图，在正方形ABCD中，对角线AC，BD交于点O，AG平分∠BAC交BD于G，DE⊥AG于点H．下列结论：①AD＝2AE：②FD＝AG；③CF＝CD：④四边形FGEA是菱形；⑤OF ＝BE，正确的有（）A．2个B．3个C．4个D．5个【分析】①根据正方形的性质和角平分线的定义得：∠BAG＝∠CAG＝22.5°，由垂直的定义计算∠AED＝90°﹣22.5°＝67.5°，∠EAD＝∠EAD＝22.5°，得ED是AG的垂直平分线，则AE＝EG，△BEG是等腰直角三角形，则AD＝AB＞2AE，可作判断；②证明△DAF≌△ABG（ASA），可作判断；③分别计算∠CDF＝∠CFD＝67.5°，可作判断；④根据对角线互相平分且垂直的四边形是菱形可作判断；⑤设BG＝x，则AF＝AE＝x，表示OF和BE的长，可作判断．【解答】解：①∵四边形ABCD是正方形，∴∠BAD＝90°，∠BAC＝45°，∵AG平分∠BAC，∴∠BAG＝∠CAG＝22.5°，∵AG⊥ED，∴∠AHE＝∠EHG＝90°，∴∠AED＝90°﹣22.5°＝67.5°，∴∠ADE＝22.5°，∵∠ADB＝45°，∴∠EDG＝22.5°＝∠ADE，∵∠AHD＝∠GHD＝90°，∴∠DAG＝∠DGA，∴AD＝DG，AH＝GH，∴ED是AG的垂直平分线，∴AE＝EG，∴∠EAG＝∠AGE＝22.5°，∴∠BEG＝45°＝∠ABG，∴∠BGE＝90°，∴AE＝EG＜BE，∴AD＝AB＞2AE，故①不正确；②∵四边形ABCD是正方形，∴AD＝AB，∠DAF＝∠ABG＝45°，∵∠ADF＝∠BAG＝22.5°，∴△DAF≌△ABG（ASA），∴DF＝AG，故②正确；③∵∠CDF＝45°+22.5°＝67.5°，∠CFD＝∠AFE＝90°﹣22.5°＝67.5°，∴∠CDF＝∠CFD，∴CF＝CD，故③正确；④∵∠EAH＝∠F AH，∠AHE＝∠AHF，∴∠AEF＝∠AFE，∴AE＝AF，∴EH＝FH，∵AH＝GH，AG⊥EF，∴四边形FGEA是菱形；故④正确；⑤设BG＝x，则AF＝AE＝x，由①知△BEG是等腰直角三角形，∴BE＝x，∴AB＝AE+BE＝x+x＝（+1）x，∴AO＝＝，∴OF＝AO﹣AF＝﹣x＝，∴＝＝，∴OF＝BE；故⑤正确；本题正确的结论有：②③④⑤；故选：C．形的判定与性质等知识．此题综合性较强，难度较大，注意掌握正方形的性质，注意数形结合思想的应用．11．如图，以正方形ABCD的顶点A为圆心，以AD的长为半径画弧，交对角线AC于点E，再分别以D，E为圆心，以大于DE的长为半径画弧，两弧交于图中的点F处，连接AF并延长，与BC的延长线交于点P，则∠P＝（）A．90°B．45°C．30°D．22.5°【分析】根据正方形的性质得到∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC ＝22.5°，根据三角形的内角和即可得到结论．【解答】解：∵四边形ABCD是正方形，∴∠DAC＝∠ACD＝45°，由作图知，∠CAP＝∠DAC＝22.5°，∴∠P＝180°﹣∠ACP﹣∠CAP＝22.5°，故选：D．【点评】本题考查了正方形的性质，角平分线定义，正确的理解题意是解题的关键．12．如图，正方形ABCD中，点E在边CD上，连接AE，过点A作AF⊥AE交CB的延长线于点F，连接EF，AG平分∠F AE，AG分别交BC，EF于点G，H，连接EG，DH．则下列结论中：①AF＝AE；②∠EGC＝2∠BAG；③DE+BG＝EG；④AD+DE＝DH；⑤若DE＝CE，则CE：CG：EG＝3：4：5，其中正确的结论有（）A．2个B．3个C．4个D．5个【分析】①正确．证明△ADE≌△ABF（ASA）可得结论．②正确．证明△AGF≌△AGE（SAS），推出∠AGF＝∠AGE＝90°﹣∠BAG，推出∠EGF ＝180°﹣2∠BAG可得结论．③正确．证明△GAF≌△GAE，推出GF＝GE可得结论．④正确．过点H作HM⊥AD于M，HN⊥CD于N，证明△HMA≌△HNE（AAS），推出AM＝EN，HM＝HN，再证明四边形HMDN是正方形可得结论．⑤正确．当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，利用勾股定理构建方程求出x即可解决问题．【解答】解：∵四边形ABCD是正方形，∴AB＝AD，∠ABC＝∠ABF＝∠ADE＝∠BAD＝90°，∵AE⊥AF，∴∠EAF＝∠BAD＝90°，∴∠BAF＝∠DAE，∴△ADE≌△ABF（ASA），∴AE＝AF，故①正确，∵AG平分∠EAF，∴∠GAF＝∠GAE，∵AF＝AE，AG＝AG，∴△AGF≌△AGE（SAS），∴∠AGF＝∠AGE＝90°﹣∠BAG，∴∠EGF＝180°﹣2∠BAG，∵∠EGF＝180°﹣∠EGC，∴∠EGC＝2∠BAG，故②正确，∵△ADE≌△ABF，∴DE＝BF，∵△GAF≌△GAE，∴GF＝GE，∵FG＝BF+BG＝DE+BG，∴EG＝BG+DE，故③正确，过点H作HM⊥AD于M，HN⊥CD于N，∵AE＝AF，∠EAF＝90°，AH平分∠EAF，∴AH⊥EF，HF＝HE，∴HA＝HE＝HF，∵∠ADE+∠AHE＝180°，∴∠HAD+∠DEH＝180°，∵∠DEH+∠HEN＝180°，∴∠HAM＝∠HEN，∵∠AMH＝∠ENH＝90°，∴△HMA≌△HNE（AAS），∴AM＝EN，HM＝HN，∵∠HMD＝∠HND＝∠MDN＝90°，∴四边形HMDN是矩形，∵HM＝HN，∴四边形HMDN是正方形，∴DM＝DN＝HM＝HN，DH＝DM，∴DA+DE＝DM+AM+DN﹣EN＝2DM＝DH，故④正确，当DE＝EC时，设DE＝EC＝a，BG＝x，则EG＝a+x，GC＝2a﹣x，在Rt△ECG中，∵EG2＝EC2+CG2，∴（x+a）2＝a2+（2a﹣x）2，解得x＝a，∴CG＝a，EG＝a，∴CE：CG：EG＝a：a：＝3：4：5，故⑤正确，故选：D．【点评】本题考查正方形的性质，全等三角形的判定和性质，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，学会利用参数构建方程解决问题，属于中考选择题中的压轴题．13．如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB、CD交于点E、F，连接BF交AC于点M，连接DE、BO．若∠COB＝60°，FO＝FC＝2，则下列结论：①FB⊥OC；②△EOB≌△CMB；③四边形EBFD是菱形；④MB＝2．其中正确结论的个数是（）A．1个B．2个C．3个D．4个【分析】连接BD，先证明△BOC是等边三角形，得FO＝FC，BO＝BC，故①正确；因为△EOB≌△FOB≌△FCB，故△EOB不会全等于△CBM，故②错误；再证明四边形EBFD是平行四边形，由OB⊥EF推出四边形EBFD是菱形故③正确，先判断出CM＝，再由∠CBM＝30°，判断出BC＝2，进而判断出④，由此不难得到答案．【解答】解：连接BD，∵四边形ABCD是矩形，∴AC＝BD，AC、BD互相平分，∵O为AC中点，∴BD也过O点，∴OB＝OC，∵∠COB＝60°，OB＝OC，∴△OBC是等边三角形，∴OB＝BC＝OC，∠OBC＝60°，在△OBF与△CBF中，，∴△OBF≌△CBF（SSS），∴△OBF与△CBF关于直线BF对称，∴FB⊥OC，OM＝CM；∴①正确，∵∠OBC＝60°，∴∠ABO＝30°，∵△OBF≌△CBF，∴∠OBM＝∠CBM＝30°，∴∠ABO＝∠OBF，∵AB∥CD，∴∠OCF＝∠OAE，∵OA＝OC，∠AOE＝∠FOC∴△AOE≌△COF（ASA），∴OE＝OF，∴OB⊥EF，∴四边形EBFD是菱形，∴③正确，∵△EOB≌△FOB≌△FCB，∴△EOB≌△CMB错误．∴②错误；∵FO＝FC＝2，FM⊥OC，∠FCM＝30°，∴CM＝，∵∠CBM＝30°，∴BC＝2，∴BM＝3，∴④错误．综上可知其中正确结论的个数是2个，故选：B．【点评】本题属于四边形的综合题，考查矩形的性质、等边三角形的判定和性质．全等三角形的判定和性质、菱形的判定、勾股定理等知识，解题的关键是灵活运用这些知识解决问题，属于中考常考题型．二．填空题（共3小题）14．如图，点E为正方形ABCD外一点，且ED＝CD，连接AE，交BD于点F．若∠CDE ＝40°，则∠DFC的度数为110°．【分析】根据正方形性质和已知得：AD＝DE，利用等腰三角形性质计算∠DAE＝25°，由三角形的内角和定理得：∠AFD＝110°，证明△ADF≌△CDF（SAS），∠DFC＝∠AFD ＝110°．【解答】解：∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∴∠ADB＝∠BDC＝45°，∵DC＝DE，∴AD＝DE，∴∠DAE＝∠DEA，∵∠ADE＝90°+40°＝130°，∴∠DAE＝＝25°，∴∠AFD＝180°﹣25°﹣45°＝110°，在△ADF和△CDF中，∵，∴△ADF≌△CDF（SAS），∴∠DFC＝∠AFD＝110°，故答案为：110°．【点评】本题考查了正方形的性质、三角形全等的性质和判定、等腰三角形的性质、三角形内角和定理，属于基础题，熟练掌握正方形的性质是关键．15．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE＝AD，DF＝BD，连接BF分别交CD，CE于H，G，下列结论：①EC＝2DG；②∠GDH＝∠GHD；③S△CDG＝S四边形DHGE；④图中只有8个等腰三角形．其中正确的有②③（填番号）．【分析】根据正方形的性质和已知推出四边形DECB是平行四边形，得到BD＝CE，BD ∥CE，无法证出G为CE的中点；得到BD∥CE，推出∠DCG＝∠BDC＝45°，求出∠BGC＝∠GBC，得到BC＝CG＝CD，求出∠CDG＝∠DHG即可；根据三角形的面积公式推出△CDG和四边形DHGE的面积相等；可得有9个等腰三角形．【解答】解：∵正方形ABCD，DE＝AD，∴AD∥BC，DE＝BC，∠EDC＝90°，∴四边形DECB是平行四边形，∴BD＝CE，BD∥CE，∵DE＝BC＝AD，∴∠DCE＝∠DEC＝45°，要使CE＝2DG，只要G为CE的中点即可，但DE＝DC，DF＝BD，∴EF≠BC，即△EFG和△BCG不全等，∴G不是CE中点，∴①错误；∵∠ADB＝45°，DF＝BD，∴∠F＝∠DBH＝∠ADB＝22.5°，∴∠DHG＝180°﹣90°﹣22.5°＝67.5°，∵BD∥CE，∴∠DCG＝∠BDC＝45°，∵∠DHG＝67.5°，∴∠HGC＝22.5°，∠DEC＝45°，∵∠BGC＝180°﹣22.5°﹣135°＝22.5°＝∠GBC，∴BC＝CG＝CD，∴∠CDG＝∠CGD＝（180°﹣45°）＝67.5°＝∠DHG，∴②正确；∵CG＝DE＝CD，∠DCE＝∠DEC＝45，∠HGC＝22.5°，∠GDE＝90﹣∠CDG＝90﹣67.5＝22.5°，∴△DEG≌△CHG，要使△CDG和四边形DHGE的面积相等，只要△DEG和△CHG的面积相等即可，根据已知条件△DEG≌△CHG，∴③S△CDG＝S四边形DHGE；正确，等腰三角形有△ABD，△CDB，△BDF，△CDE，△BCG，△DGH，△EGF，△CDG，△DGF；∴④错误；故答案为：②③．【点评】本题主要考查对三角形的内角和定理，等腰三角形的性质和判定，正方形的性质，平行四边形的性质和判定等知识．综合运用这些性质进行推理是解此题的关键．16．如图，在正方形ABCD中，P为AB的中点，BE⊥PD的延长线于点E，连接AE、BE、F A⊥AE交DP于点F，连接BF，FC．若AE＝2，则FC＝2．【分析】根据正方形的性质可得AB＝AD，再求出∠BAE＝∠DAF，∠ABE＝∠ADF，然后利用“角边角”证明△ABE和△ADF全等，根据全等三角形对应边相等可得AE＝AF，从而判断出△AEF是等腰直角三角形，根据AE的长度求出EF，过点A作AH⊥EF于H，连接BH，根据等腰直角三角形的性质可得AH＝EH＝FH，利用“角边角”证明△APH 和△BPE全等，根据全等三角形对应边相等可得BE＝AH，然后求出△BEH是等腰直角三角形，根据等腰直角三角形的性质可得∠EHB＝45°，然后求出∠AHB＝∠FHB，再利用“边角边”证明△ABH和△FBH全等，根据全等三角形对应边相等可得AB＝BF，再根据全等三角形对应边相等求出BE＝DF，全等三角形对应角相等求出∠BAH＝∠BFE，然后求出∠BFE＝∠ADF，根据等角的余角相等求出∠EBF＝∠FDC，再利用“边角边”证明△BEF和△DFC全等，根据全等三角形对应边相等可得FC＝EF．【解答】解：在正方形ABCD中，AB＝AD，∠BAD＝90°，∵F A⊥AE，∴∠EAF＝90°，∴∠BAE＝∠DAF，∵∠ABE+∠BPE＝∠ADF+∠APD＝90°，∴∠ABE＝∠ADF，在△ABE和△ADF中，，∴△ABE≌△ADF（ASA），∴AE＝AF，BE＝DF，∵F A⊥AE，∴△AEF是等腰直角三角形，∴EF＝AE＝2，过点A作AH⊥EF于H，连接BH，。

初中数学中考复习尺规作图题专项练习及答案解析(专题试卷50道)

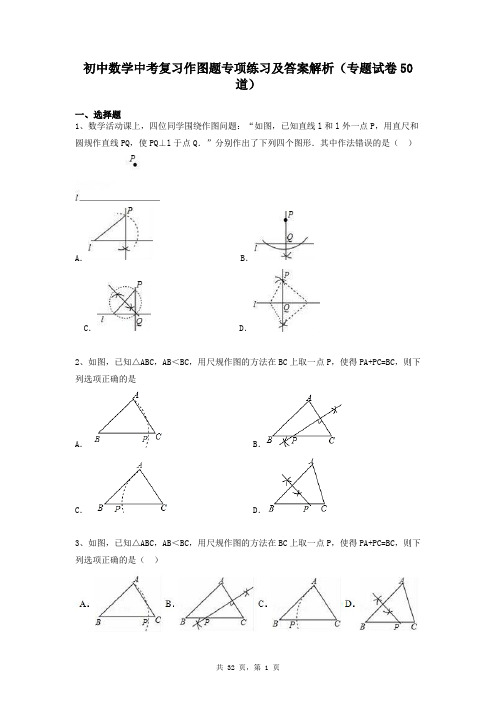
初中数学中考复习作图题专项练习及答案解析（专题试卷50道）一、选择题1、数学活动课上，四位同学围绕作图问题：“如图，已知直线l和l外一点P，用直尺和圆规作直线PQ，使PQ⊥l于点Q．”分别作出了下列四个图形．其中作法错误的是（）A．B．C．D．2、如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是A．B．C．D．3、如图，已知△ABC，AB＜BC，用尺规作图的方法在BC上取一点P，使得PA+PC=BC，则下列选项正确的是（）4、下列尺规作图，能判断AD是△ABC边上的高是（）A．B．C．D．5、任意一条线段EF，其垂直平分线的尺规作图痕迹如图所示．若连接EH、HF、FG，GE，则下列结论中，不一定正确的是（）A．△EGH为等腰三角形B．△EGF为等边三角形C．四边形EGFH为菱形D．△EHF为等腰三角形6、用直尺和圆规作一个以线段AB为边的菱形，作图痕迹如图所示，能得到四边形ABCD是菱形的依据是（）A．一组邻边相等的四边形是菱形B．四边相等的四边形是菱形C．对角线互相垂直的平行四边形是菱形D．每条对角线平分一组对角的平行四边形是菱形7、如图，在▱ABCD中，AB＞AD，按以下步骤作图：以点A为圆心，小于AD的长为半径画弧，分别交AB、AD于点E、F；再分别以点E、F为圆心，大于EF的长为半径画弧，两弧交于点G；作射线AG交CD于点H，则下列结论中不能由条件推理得出的是（）A. AG平分∠DABB. AD=DHC. DH=BCD. CH=DH8、如图，已知钝角三角形ABC，依下列步骤尺规作图，并保留作图痕迹.步骤1：以点C为圆心，CA为半径画弧①；步骤2：以点B为圆心，BA为半径画弧②，交弧①于点D；步骤3：连接AD，交BC的延长线于点H.下列叙述正确的是：A．BH垂直平分线段AD B．AC平分∠BADC．S△ABC=BC·AH D．AB=AD二、填空题9、阅读下面材料：在数学课上，老师提出如下问题：所以PB和PC就是所求的切线．请回答：小涵的作图依据是．10、如图，在△ABC中，∠ACB=80°，∠ABC=60°．按以下步骤作图：①以点A为圆心，小于AC的长为半径画弧，分别交AB、AC于点E、F；②分别以点E、F为圆心，大于EF 的长为半径画弧，两弧相交于点G；③作射线AG交BC于点D．则∠ADB的度数为°．11、如图，在△ABC中，∠C=90°，∠CAB=60°，按以下步骤作图：①分别以A，B为圆心，以大于AB的长为半径做弧，两弧相交于点P和Q．②作直线PQ交AB于点D，交BC于点E，连接AE．若CE=4，则AE= ．12、如图，在△ABC中，AB＞AC．按以下步骤作图：分别以点B和点C为圆心，大于BC一半的长为半径作圆弧，两弧相交于点M和点N；作直线MN交AB于点D；连结CD．若AB=6，AC=4，则△ACD的周长为．三、计算题13、如图，已知线段a和h．求作：△ABC，使得AB=AC，BC=a，且BC边上的高AD=h．要求：尺规作图，不写作法，保留作图痕迹．14、如图所示，点C、D是∠AOB内部的两点．（1）作∠AOB的平分线OE；（2）在射线OE上，求作一点P，使PC=PD．（要求用尺规作图，保留作图痕迹）四、解答题15、如图，已知等腰直角△ABC，∠A=90°．（1）利用尺规作∠ABC的平分线BD，交AC于点D（保留作图痕迹，不写作法）；（2）若将（1）中的△ABD沿BD折叠，则点A正好落在BC边上的A1处，当AB=1时，求△A1DC的面积．16、（8分）如图，在Rt△ABC中，∠ACB=90°．（1）用尺规在边BC上求作一点P，使PA=PB（不写作法，保留作图痕迹）；（2）连结AP，若AC=4，BC=8时，试求点P到AB边的距离．17、已知△ABC，用直尺和圆规作△ABC的角平分线CD和高AE．（不写画法，保留作图痕迹）18、数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线.根据以上情境，解决下列问题：(1)李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________.(2)小聪的作法正确吗？请说明理由.(3)请你帮小颖设计用刻度尺作角平分线的方法.（要求：作出图形，写出作图步骤，不予证明）19、如图，∠AOB=30°，OA表示草地边，OB表示河边，点P表示家且在∠AOB内．某人要从家里出发先到草地边给马喂草，然后到河边喂水，最后回到家里．（1）请用尺规在图上画出此人行走的最短路线图（保留作图痕迹，不写作法和理由）．（2）若OP=30米，求此人行走的最短路线的长度．20、如图，在△ABC中，AB=AC=8cm，∠BAC=120°.（1）作△ABC的外接圆（只需作出图形，并保留作图痕迹）；（2）求它的外接圆半径.21、某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．（1）请找出截面的圆心；（不写画法，保留作图痕迹．）（2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．22、如图，已知△ABC，用直尺和圆规求作一直线AD，使直线过顶点A，且平分△ABC的面积（不需写作法，保留作图痕迹）23、高致病性禽流感是比SARS传染速度更快的传染病．为防止禽流感蔓延，政府规定：离疫点3km范围内为扑杀区；离疫点3km～5km范围内为免疫区，对扑杀区与免疫区内的村庄、道路实行全封闭管理．现有一条笔直的公路AB通过禽流感病区，如图，在扑杀区内公路CD长为4km．（1）请用直尺和圆规找出疫点O（不写作法，保留作图痕迹）；（2）求这条公路在免疫区内有多少千米？24、作图题：如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1）、（2，1）．（1）以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；（2）分别写出B、C两点的对应点B′、C′的坐标．25、如图，⊙O为△ABC的外接圆，直线l与⊙O相切与点P，且l∥BC．（1）请仅用无刻度的直尺，在⊙O中画出一条弦，使这条弦将△ABC分成面积相等的两部分（保留作图痕迹，不写作法）；（2）请写出证明△ABC被所作弦分成的两部分面积相等的思路．26、如图，107国道OA和302国道OB在甲市相交于点O，在∠AOB的内部有工厂C和D，现要修建一个货站P，使P到OA，OB的距离相等，且使PC=PD，试确定出点P的位置．（不写作法，保留作图痕迹，写出结论）27、用尺规作图从△ABC（CB＜CA）中裁出一个以AB为底边的等腰△ABD，并使得△ABD的面积尽可能大（保留作图痕迹，不要求写作法、证明）28、如图，已知△ABC，利用尺规完成下列作图（不写画法，保留作图痕迹）．（1）作△ABC的外接圆；（2）若△ABC所在平面内有一点D，满足∠CAB=∠CDB，BC=BD，求作点D．29、如图，点A是半径为3的⊙O上的点，（1）尺规作图：作⊙O的内接正六边形ABCDEF；（2）求（1）中的长．30、已知，如图，直线AB与直线BC相交于点B，点D是直线BC上一点，直线DE∥AB，且点E到B，D两点的距离相等．（1）用尺规作图作出点E；（不写作法，保留作图痕迹）（2）连接BE，求证：BD平分∠ABE．31、如图，BC是⊙O的一个内接正五边形的一边，请用等分圆周的方法，在⊙A中用尺规作图作出一个⊙A的内接正五边形（请保留作图痕迹）．32、已知：如图，在△ABC中，∠A=30°，∠B=60°．（1）作∠B的平分线BD，交AC于点D；作AB的中点E（要求：尺规作图，保留作图痕迹，不必写作法和证明）；（2）连接DE，求证：△ADE≌△BDE．33、如图，已知△ABC，用直尺（没有刻度）和圆规在平面上求作一个点P，使P到∠B两边的距离相等，且PA=PB．（不要求写作法，但要保留作图痕迹）34、如图，在△ABC中，AB=AC=8cm，∠BAC=120°.（1）作△ABC的外接圆（只需作出图形，并保留作图痕迹）；（2）求它的外接圆半径.35、如图，已知等腰直角△ABC，∠A=90°．（1）利用尺规作∠ABC的平分线BD，交AC于点D（保留作图痕迹，不写作法）；（2）若将（1）中的△ABD沿BD折叠，则点A正好落在BC边上的A1处，当AB=1时，求△A1DC的面积．36、如图，△ABC中，∠C=90°，小王同学想作一个圆经过A、C两点，并且该圆的圆心到AB、AC距离相等，请你利用尺规作图的办法帮助小王同学确定圆心D．（不写作法，保留作图痕迹）．37、如图，将矩形ABCD沿对角线AC折叠，点B落在点E处，请用尺规作出点E．（不写画法，保留作图痕迹）38、如图，在等腰直角△ABC中，∠ACB=90°，AC=1．（1）作⊙O，使它过点A、B、C（要求：尺规作图，保留作图痕迹，不写作法）．（2）在（1）所作的圆中，求出劣弧BC的长．39、如图，在△ABC中，∠C=90°，∠B=30°．（1）作∠CAB的平分线，交BC边于点D（用尺规作图，保留作图痕迹，不要求写作法和证明）；（2）求S△ACD：S△ABC的值．40、如图，某地有两所大学和两条交叉的公路．图中点M，N表示大学，OA，OB表示公路，现计划修建一座物资仓库，希望仓库到两所大学的距离相同，到两条公路的距离也相同，你能确定出仓库P应该建在什么位置吗？请在图中画出你的设计．（尺规作图，不写作法，保留作图痕迹）41、如图，AE∥BF，AC平分∠BAE，交BF于C．（1）尺规作图：过点B作AC的垂线，交AC于O，交AE于D，（保留作图痕迹，不写作法）；（2）在（1）的图形中，找出两条相等的线段，并予以证明．42、▱ABCD中，点E在AD上，DE=CD，请仅用无刻度的直尺，按要求作图（保留作图痕迹，不写作法）（1）在图1中，画出∠C的角平分线；（2）在图2中，画出∠A的角平分线．43、如图，两条公路OA和OB相交于O点，在∠AOB的内部有工厂C和D，现要修建一个货站P，使货站P到两条公路OA、OB的距离相等，且到两工厂C、D的距离相等，用尺规作出货站P的位置．（要求：不写作法，保留作图痕迹，写出结论）44、从△ABC（CB＜CA）中裁出一个以AB为底边的等腰△ABD，并使得△ABD的面积尽可能大．（1）用尺规作图作出△ABD．（保留作图痕迹，不要求写作法、证明）（2）若AB=2m，∠CAB=30°，求裁出的△ABD的面积．45、如图，在中，.（1）利用直尺和圆规按下列要求作图，并在图中标明相应的字母.（保留作图痕迹，不写作法）①作的垂直平分线，交于点，交于点；②以为圆心，为半径作圆，交的延长线于点.⑵在⑴所作的图形中，解答下列问题.①点与的位置关系是_____________；（直接写出答案）②若，，求的半径.46、在数轴上作出表示的点（保留作图痕迹，不写作法）．47、△ABC在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位长度．按要求作图：①画出△ABC关于原点O的中心对称图形△A1B1C1；②画出将△ABC绕点C顺时针旋转90°得到△A2B2C．48、如图，某村庄计划把河中的水引到水池M中，怎样开的渠最短，为什么（保留作图痕迹，不写作法和证明）理由是：．49、如图，已知线段a和b，a＞b，求作直角三角形ABC，使直角三角形的斜边AB=a，直角边AC=b．（用尺规作图，保留作图痕迹，不要求写作法）50、如图，已知⊙O，用尺规作⊙O的内接正四边形ABCD．（写出结论，不写作法，保留作图痕迹，并把作图痕迹用黑色签字笔描黑）参考答案1、A．2、D3、D4、B5、B．6、B7、D8、A9、直径所对的圆周角是直角．10、100.11、8.12、10．13、见解析14、见解析15、(1)详见解析；（2）．16、(1)、答案见解析；(2)、5.17、答案见解析18、(1)SSS；(2)、理由见解析；(3)、答案见解析19、(1)、答案见解析；(2)、30m.20、(1)、答案见解析；(2)、r=8cm 21、（1）见试题解析；（2）这个圆形截面的半径是10cm．22、答案见解析23、(1)作图详见解析；(2)（﹣4）千米．24、(1)图形详见解析；(2) B′（﹣6，2），C′（﹣4，﹣2）．25、26、作图详见解析.27、28、（1）作图见解析（2）作图见解析29、(1)见试题解析；（2）2π．30~33、详见解析.34、(1)、答案见解析；(2)、r=8cm35、(1)、答案见解析；(2)、36、作图参见解析.37、作图参见解析.38、（1）作图参见解析；（2）π.39、（1）作图见解析（2）1:340、答案见解析41、（1）作图见解解析；（2）AB=AD=BC．42、作图参见解析.43、44、（1）如图；（2）m245、（1）作图见解析；（2）①点B在⊙O上；②5.46、47、见解析48、见解析49、见解析50、答案见解析．答案详细解析【解析】1、试题分析：A、根据作法无法判定PQ⊥l；B、以P为圆心大于P到直线l的距离为半径画弧，交直线l，于两点，再以两点为圆心，大于它们的长为半径画弧，得出其交点，进而作出判断；C、根据直径所对的圆周角等于90°作出判断；D、根据全等三角形的判定和性质即可作出判断．故选：A．考点：作图—基本作图．2、试题分析：由PB+PC=BC和PA+PC=BC易得PA=PB，根据线段垂直平分线定理的逆定理可得点P在AB的垂直平分线上，于是可判断D选项正确．故选D．考点：作图—复杂作图3、试题分析：∵PB+PC=BC，而PA+PC=BC，∴PA=PB，∴点P在AB的垂直平分线上，即点P为AB的垂直平分线与BC的交点．故选D．考点：基本作图4、试题分析：过点A作BC的垂线，垂足为D，故选B．考点：作图—基本作图．5、试题分析：根据线段垂直平分线的性质可得EG=EH=FH=GF，由此可得选项A正确，选项B错误，选项C、正确，选项D正确．故答案选B．考点：线段垂直平分线的性质．6、试题分析：根据作图的痕迹以及菱形的判定方法解答．解：由作图痕迹可知，四边形ABCD的边AD=BC=CD=AB，根据四边相等的四边形是菱形可得四边形ABCD是菱形．故选B．7、试题分析：由角平分线的作法，依题意可知AG平分∠DAB，A正确；∠DAH＝∠BAH，又AB∥DC，所以∠BAH＝∠ADH，所以，∠DAH＝∠ADH，所以，AD＝DH，又AD＝BC，所以，DH ＝BC，B、C正确，故答案选D.考点：平行四边形的性质；平行线的性质.8、试题分析：由作法可得BH为线段AD的垂直平分线，故答案选A.考点：线段垂直平分线的性质.9、试题分析：∵OP是⊙A的直径，∴∠PBO=∠PCO=90°，∴OB⊥PB，OC⊥PC，∵OB、OC是⊙O的半径，∴PB、PC是⊙O的切线；则小涵的作图依据是：直径所对的圆周角是直角．故答案为：直径所对的圆周角是直角．【考点】切线的判定；作图—复杂作图．10、试题解析：根据已知条件中的作图步骤知，AG是∠CAB的平分线，∵∠ACB=80°，∠ABC=60°，∴∠CAB=40°，∴∠BAD=20°；在△ADC中，∠B=60°，∠CAD=20°，∴∠ADB=100°，考点：作图—基本作图．11、试题解析：由题意可得出：PQ是AB的垂直平分线，∴AE=BE，∵在△ABC中，∠C=90°，∠CAB=60°，∴∠CBA=30°，∴∠EAB=∠CAE=30°，∴CE=AE=4，∴AE=8．考点：1.作图—复杂作图；2.线段垂直平分线的性质；3.含30度角的直角三角形．12、试题分析：∵分别以点B和点C为圆心，以大于BC一半的长为半径画弧，两弧相交于点M和N，作直线MN．直线MN交AB于点D，连结CD，∴直线MN是线段BC的垂直平分线，∴BD=CD，∴BD+AD=CD+AD=AB，∵AB=6，AC=4，∴△ADC的周长=（CD+AD）+AC=AB+AC=6+4=10．故答案为：10．考点：线段垂直平分线的性质．13、解：如图所示．△ABC就是所求的三角形．14、试题分析：（1）根据赔付风险的画法画出图形即可．（2）画出作线段CD的垂直平分线MN，即可解决问题．解：（1）∠AOB的平分想如图所示，（2）作线段CD的垂直平分线MN与射线OE交于点P．点P就是所求的点．15、试题分析：（1）利用尺规作出∠ABC的平分线BD即可．（2）首先利用勾股定理求出BC，再求出A1C，根据△A1DC的面积=•A1C•A1D计算即可．试题解析：（1）∠ABC的平分线BD，交AC于点D，如图所示，（2）在RT△ABC中，∵∠A=90°，AC=BC=1，∴BC=，∵AB=A1B=AC=1，∴A1C=，∵∠C=45°，∠DA1C=90°，∴∠C=∠A1DC=45°∴△A1DC是等腰直角三角形，∴．考点：翻折变换（折叠问题）；作图—基本作图．16、试题分析：(1)、做出线段AB的中垂线得出答案；(2)、设BP=x，则AP=x，CP=BC﹣PB=8﹣x，然后根据Rt△ACP的勾股定理得出答案.试题解析：(1)、如图，点P为所作；(2)、设BP=x，则AP=x，CP=BC﹣PB=8﹣x，在Rt△ACP中，∵PC2+AC2=AP2，∴（8﹣x）2+42=x2，解得x=5，即BP的长为5．考点：勾股定理17、试题分析：根据角平分线的作法以及过直线外一点向直线最垂线的作法得出即可．试题解析：如图所示：CD，AE即为所求．考点：作图—复杂作图．18、试题分析：(1)、本题都是作线段相等，则根据SSS来判定三角形全等；(2)、根据垂直得出∠OMP=∠ONP=90°，然后结合OP=OP，OM=ON得出直角三角形全等；(3)、根据三角形全等的性质得出角平分线.试题解析：(1)、SSS(2)、小聪的作法正确理由：∵PM⊥OM , PN⊥ON ∴∠OMP=∠ONP=90°在Rt△OMP和Rt△ONP中∵OP="OP" ,OM=ON∴Rt△OMP≌Rt△ONP（HL）∴∠MOP=∠NOP ∴OP平分∠AOB(3)、如图所示.步骤：①利用刻度尺在OA、OB上分别截取OG=OH. ②连结GH，利用刻度尺找出GH的中点Q.③作射线OQ.则OQ为∠AOB的平分线.考点：角平分线的做法.19、试题分析：(1)、利用轴对称最短路线求法得出P点关于OA，OB的对称点，进而得出行走路线；(2)、利用等边三角形的判定方法以及其性质得出此人行走的最短路线长为P′P″进而得出答案．试题解析：(1)、如图所示：此人行走的最短路线为：PC→CD→DP；(2)、连接OP′，OP″，由题意可得：OP′=OP″，∠P′OP″=60°，则△P′OP″是等边三角形，∵OP=30米，∴PC+CD+DP=P′P″=30（m），考点：(1)、作图—应用与设计作图；(2)、轴对称-最短路线问题．20、试题分析：(1)、分别作AB和AC的中垂线，他们的交点就是圆心；(1)、连接AO、BO，根据∠BAC的度数以及等腰三角形的性质得出△ABO为等边三角形，然后求出半径. 试题解析：(1)、如图所示：⊙O即为所求的△ABC的外接圆；(2)、连接AO，BO，∵AB=AC=8cm，∠BAC=120°，∴∠BAO=∠CAO=60°，∵AO=BO，∴△ABO是等边三角形，∴AO=AB=8cm，即它的外接圆半径为8cm．考点：(1)、三角形外接圆的作法；(2)、等边三角形的判定与性质21、试题分析：（1）根据尺规作图的步骤和方法做出图即可；（2）先作辅助线，利用垂径定理求出半径，再根据勾股定理计算．试题解析：（1）如图所示；（2）如图，OE⊥AB交AB于点D，则DE=4cm，AB=16cm，AD=8cm，设半径为Rcm，则OD=OE﹣DE=R﹣4，由勾股定理得，OA2=AD2+OD2，即R2=82+（R﹣4）2，解得R=10．故这个圆形截面的半径是10cm．【考点】作图—应用与设计作图；垂径定理的应用．22、试题分析：首先作出BC的垂直平分线，可确定BC的中点记作D，再根据三角形的中线平分三角形的面积画出直线AD即可．试题解析：如图所示：，直线AD即为所求．考点：作图—复杂作图．23、试题分析：（1）在内圆（或外圆）任意作出两条弦，分别作出者两条弦的垂直平分线，它们的交点就是疫点（即圆心O）；（2）利用垂径定理求出AB、CD的长度，问题解决．试题解析：（1）作图如下：（2）如图：连接OA、OC，过点O作OE⊥AB于点E，∴CE=CD=2km，AE=AB，在Rt△OCE中，OE==km，在Rt△OAE中，AE==km，∴AB=2AE=km，因此AC+BD=AB﹣CD=﹣4（km）．答：这条公路在免疫区内有（﹣4）千米．考点：作图—应用与设计作图．24、试题分析：（1）延长BO到B′，使OB′=2OB，则B′就是B的对应点，同样可以作出C的对称点，则对应的三角形即可得到；（2）根据（1）的作图即可得到B′、C′的坐标．试题解析：（1）△OB′C′是所求的三角形；（2）B′的坐标是（﹣6，2），C′的坐标是（﹣4，﹣2）．考点：作图-位似变换．25、试题分析：（1）连结PO并延长交BC于E，过点A、E作弦AD即可；（2）由于直线l与⊙O相切于点P，根据切线的性质得OP⊥l，而l∥BC，则PE⊥BC，根据垂径定理得BE=CE，所以弦AE将△ABC分成面积相等的两部分．试题解析：（1）如图所示：（2）∵直线l与⊙O相切与点P，∴OP⊥l，∵l∥BC，∴PE⊥BC，∴BE=CE，∴弦AE将△ABC分成面积相等的两部分．【考点】作图—复杂作图；三角形的外接圆与外心．26、试题分析：作∠AOB的平分线与线段CD的垂直平分线，两线相交于点P，点P即为所求．试题解析：点P即为所求．考点：作图——应用与设计作图．27、试题分析：利用△ABD是以AB为底边的等腰三角形，则点D在AB的垂直平分线上，于是作AB的垂直平分线交AC于D，则△ABD满足条件．试题解析：如图，△ABD为所作．考点：作图﹣复杂作图．28、试题分析：（1）作出BD、BC的垂直平分线，两线的交点就是⊙O的圆心O的位置，然后以O为圆心AO长为半径画圆即可；（2）以B为圆心，BC长为半径化弧，交⊙O于点D，再连接BD，CD即可．试题解析：（1）如图所示：⊙O即为所求；（2）如图所示：点D即为所求．考点：1、作图—复杂作图；2、圆周角定理；3、三角形的外接圆与外心29、试题分析：（1）由正六边形ABCDEF的中心角为60°，可得△OAB是等边三角形，继而可得正六边形的边长等于半径，则可画出⊙O的内接正六边形ABCDEF；（2）由（1）可求得∠AOC=120°，继而求得（1）中的长．试题解析：（1）首先连接OA，然后以A为圆心，OA长为半径画弧，交⊙O于B，F，再分别以B，F为圆心，OA长为半径画弧，交⊙O于点E，C，在以C为圆心，OA长为半径画弧，交⊙O于点D，则正六边形ABCDEF即为所求；（2）∵正六边形ABCDEF是⊙O的内接正六边形∴∠AOC=120°，∵⊙O的半径为3，∴的长为：=2π．【考点】正多边形和圆；弧长的计算；作图—复杂作图．30、试题分析：(1)、直接利用作一角等于已知角的作法结合线段垂直平分线的作法得出符合题意的图形；(2)、直接利用平行线的性质以及结合线段垂直平分线的性质得出答案．试题解析：(1)、如图所示：点E即为所求；(2)、∵DE∥AB，∴∠ABD=∠BDE，又∵EB=ED，∴∠EBD=∠EDB，∴∠ABD=∠EBD，即BD平分∠ABE．考点：(1)、作图—复杂作图；(2)、平行线的性质；(3)、线段垂直平分线的性质．31、试题分析：如图，①作∠EAF=∠BOA．②在⊙A上截取，则五边形EFGHL即为所求．试题解析：如图，①作∠EAF=∠BOA．②在⊙A上截取．五边形EFGHL即为所求．考点：1、作图—复杂作图；2、正多边形和圆32、试题分析：（1）①以B为圆心，任意长为半径画弧，交AB、BC于F、N，再以F、N为圆心，大于FN长为半径画弧，两弧交于点M，过B、M画射线，交AC于D，线段BD就是∠B的平分线；②分别以A、B为圆心，大于AB长为半径画弧，两弧交于X、Y，过X、Y画直线与AB交于点E，点E就是AB的中点；（2）首先根据角平分线的性质可得∠ABD的度数，进而得到∠ABD=∠A，根据等角对等边可得AD=BD，再加上条件AE=BE，ED=ED，即可利用SSS证明△ADE≌△BDE．试题解析：（1）作出∠B的平分线BD；作出线段AB垂直平分线交AB于点E，点E是线段AB的中点．（2）证明：∵∠ABD=×60°=30°，∠A=30°，∴∠ABD=∠A，∴AD=BD，在△ADE和△BDE中∴△ADE≌△BDE（SSS）．考点：作图—复杂作图；全等三角形的判定．33、试题分析：分别作∠B的平分线BE和线段AB的垂直平分线MN，利用角平分线的性质以及线段垂直平分线的性质得出即可．试题解析：如图，点P即为所求点．考点：作图——基本作图；角平分线的性质．34、试题分析：(1)、分别作AB和AC的中垂线，他们的交点就是圆心；(1)、连接AO、BO，根据∠BAC的度数以及等腰三角形的性质得出△ABO为等边三角形，然后求出半径. 试题解析：(1)、如图所示：⊙O即为所求的△ABC的外接圆；(2)、连接AO，BO，∵AB=AC=8cm，∠BAC=120°，∴∠BAO=∠CAO=60°，∵AO=BO，∴△ABO是等边三角形，∴AO=AB=8cm，即它的外接圆半径为8cm．考点：(1)、三角形外接圆的作法；(2)、等边三角形的判定与性质35、试题分析：(1)、利用尺规作出∠ABC的平分线BD即可；(2)、首先利用勾股定理求出BC，再求出A1C，根据△A1DC的面积=•A1C•A1D计算即可．试题解析：(1)、∠ABC的平分线BD，交AC于点D，如图所示，(2)、在RT△ABC中，∵∠A=90°，AC=BC=1，∴BC=，∵AB=A1B=AC=1，∴A1C=-1，∵∠C=45°，∠DA1C=90°，∴∠C=∠A1DC=45°∴△A1DC 是等腰直角三角形，∴S=．考点：(1)、翻折变换（折叠问题）；(2)、作图—基本作图．36、试题分析：根据角平分线的性质定理和线段垂直平分线的性质定理，先作∠BAC的平分线AE，再作AC的垂直平分线m交AE于点D，则点D满足条件．试题解析：如图，先作∠BAC的平分线AE，再作AC的垂直平分线m交AE于点D，点D为所作．考点：作图—复杂作图．37、试题分析：以点A为圆心以AB长为半径作弧，以C为圆心以BC长为半径作弧，两弧相交于点E．试题解析：以点A为圆心以AB长为半径作弧，以C为圆心以BC长为半径作弧，如图所示：两弧相交于点E．则点E即为所求.考点：1.翻折变换（折叠问题）；2.矩形的性质．38、试题分析：（1）先找到圆心，作线段AB的垂直平分线交AB于O点，然后以O为圆心，OA为半径画圆即可；（2）先利用等腰直角三角形的性质求出AB的长，那么OB=OA=AB，又∠BOC=90°，将它们代入弧长公式计算即可．试题解析：（1）如图，作线段AB的垂直平分线交AB于O点，然后以O为圆心，OA为半径画圆，⊙O即为所作；（2）∵在等腰直角△ABC中，∠ACB=90°，AC=1，∴AB=AC=，∵线段AB的垂直平分线交AB于O点，∴∠BOC=90°，OB=OA=AB=，∴劣弧BC的长=π．考点：1.弧长的计算；2.作图—复杂作图．39、试题分析：（1）根据角平分线的基本作图画图即可；（2）根据角平分线的性质的到边之间的关系，然后根据三角形的面积公式计算即可.试题解析：（1）如图所示，AD为所求的角平分线；（2）∵∠C=90°，∠B=30°，∴∠CAB =60°，∵AD平分∠CAB，∴∠CAD ="∠DAB" =30°，∵∠ACD=90°，∴AD=2CD，∵∠B=30°，∴∠B=∠DAB，∴AD= BD，∴BD=2CD，∴BC=3CD，∵，，∴．考点：角平分线40、试题分析：作∠AOB的角平分线和线段MN的中垂线，两条直线的交点就是点P的位置.试题解析：如图所示：点P就是所求的点.考点：(1)、角平分线的作法；(2)、线段的中垂线的作法41、试题分析：（1）利用基本作图作BO⊥AC即可；（2）先利用平行线的性质得∠EAC=∠BCA，再根据角平分线的定义和等量代换得到∠BCA=∠BAC，则BA=BC，然后根据等腰三角形的判定方法由BD⊥AO，AO平分∠BAD得到AB=AD，所以AB=AD=BC．试题解析：（1）如图，BO为所作；（2）AB=AD=BC．证明如下：∵AE∥BF，∴∠EAC=∠BCA，∵AC平分∠BAE，∴∠EAC=∠BAC，∴∠BCA=∠BAC，∴BA=BC，∵BD⊥AO，AO平分∠BAD，∴AB=AD，∴AB=AD=BC．考点：作图—基本作图；作图题．42、试题分析：（1）连结CE，由DE=DC得到∠DEC=∠DCE，由AD∥BC得∠DEC=∠BCE，则∠DCE=∠BCE，即CE平分∠BCD；（2）连结AC、BD，它们相交于点O，延长EO交BC于F，则AF为所作．试题解析：（1）如图1，由DE=DC得到∠DEC=∠DCE，由AD∥BC得∠DEC=∠BCE，则∠DCE=∠BCE，即CE平分∠BCD.CE为所求作；（2）如图2，连结AC、BD，它们相交于点O，延长EO交BC于F，则AF为所作.因为三角形BOF和三角形DOE全等，导出BF=DE=AB=CD,从而得出∠BAF=∠BFA=∠FAD，则AF是所求作的角平分线.考点：1.基本作图；2.三角形全等的判定与性质；3.平行四边形的性质.43、试题分析：根据点P到∠AOB两边距离相等，到点C、D的距离也相等，点P既在∠AOB的角平分线上，又在CD垂直平分线上，即∠AOB的角平分线和CD垂直平分线的交点处即为点P．解：如图所示：作CD的垂直平分线，∠AOB的角平分线的交点P即为所求，此时货站P到两条公路OA、OB的距离相等．P和P1都是所求的点．点评：此题主要考查了线段的垂直平分线和角平分线的作法．这些基本作图要熟练掌握，注意保留作图痕迹．44、试题分析：（1）直接利用线段垂直平分线的性质作出AB的垂直平分线，交AC于点D，进而得出△ABD；（2）利用锐角三角形关系得出DE的长，进而利用三角形面积求法得出答案．试题解析：（1）如图所示：△ABD即为所求；（2）∵MN垂直平分AB，AB=2m，∠CAB=30°，∴AE=1m，则tan30°=，解得：DE=．故裁出的△ABD的面积为：×2×=（m2）．考点：作图—复杂作图．45、试题分析：（1）先作AC的垂直平分线，然后作⊙O；（2）①通过证明OB=OA来判断点在⊙O上；②设⊙O的半径为r，在Rt△AOD中利用勾股定理得到r2=42+（r-2）2，然后解方程求出r 即可．试题解析：（1）如图所示；。

初中数学几何综合题及答案

最新初中数学几何综合题及答案1、已知：如图，四边形ABCD为平行四边形，以CD为直径作⊙O，⊙O与边BC相交于点F，⊙O的切线DE与边AB相交于点E，且AE=3EB．（1）求证：△ADE∽△CDF；（2）当CF：FB=1：2时，求⊙O与▱ABCD的面积之比．解:（1）证明：∵CD是⊙O的直径，∴∠DFC=90°，∵四边形ABCD是平行四边形，∴∠A=∠C，AD∥BC，∴∠ADF=∠DFC=90°，∵DE为⊙O的切线，∴DE⊥DC，∴∠EDC=90°，∴∠ADF=∠EDC=90°，∴∠ADE=∠CDF，∵∠A=∠C，∴△ADE∽△CDE；（2）解：∵CF：FB=1：2，∴设CF=x，FB=2x，则BC=3x，∵AE=3EB，∴设EB=y，则AE=3y，AB=4y，∵四边形ABCD是平行四边形，∴AD=BC=3x，AB=DC=4y，∵△ADE∽△CDF，∴=，∴=，∵x、y均为正数，∴x=2y，∴BC=6y，CF=2y，在Rt△DFC中，∠DFC=90°，由勾股定理得：DF===2y，∴⊙O的面积为π•（DC）2=π•DC2=π（4y）2=4πy2，四边形ABCD的面积为BC•DF=6y•2y=12y2，∴⊙O与四边形ABCD的面积之比为4πy2：12y2=π：3．2、半径为2cm的⊙O与边长为2cm的正方形ABCD在水平直线L的同侧，⊙O与L相切于点F，DC在L上.（1）过点B作⊙O的一条切线BE，E为切点.①填空：如图1，当点A在⊙O上时，∠EBA的度数是；②如图2，当E，A，D三点在同一直线上时，求线段OA的长；（2）以正方形ABCD的边AD与OF重合的位置为初始位置．．．．，向左移动正方形（图3），至边BC与OF重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围.解：（1）①∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O上时，过点B作的一条切线BE，E为切点，∴OB=4，EO=2，∠OEB=90°，∴∠EBA的度数是：30°；②如图2，∵直线l与⊙O相切于点F，∴∠OFD=90°，∵正方形ADCB中，∠ADC=90°，∴OF∥AD，∵OF=AD=2，∴四边形OFDA为平行四边形，∵∠OFD=90°，∴平行四边形OFDA为矩形，∴DA⊥AO，∵正方形ABCD中，DA⊥AB，∴O，A，B三点在同一条直线上；∴EA⊥OB，∵∠OEB=∠AOE，∴△EOA∽△BOE，∴=，∴OE2=OA•OB，∴OA（2+OA）=4，解得：OA=﹣1±，∵OA＞0，∴OA=﹣1；方法二：在Rt△OAE中，cos∠EOA==，在Rt△EOB中，cos∠EOB==，∴=，解得：OA=﹣1±，∵OA＞0，∴OA=﹣1；方法三：∵OE⊥EB，EA⊥OB，∴由射影定理，得OE2=OA•OB，∴OA（2+OA）=4，解得：OA=﹣1±，∵OA＞0，∴OA=﹣1；（2）如图3，设∠MON=n°，S扇形MON=×22=n（cm2），S随n的增大而增大，∠MON取最大值时，S扇形MON最大，当∠MON取最小值时，S扇形MON最小，过O点作OK⊥MN于K，∴∠MON=2∠NOK，MN=2NK，在Rt△ONK中，sin∠NOK==，∴∠NOK随NK的增大而增大，∴∠MON随MN的增大而增大，∴当MN最大时∠MON最大，当MN最小时∠MON最小，①当N，M，A分别与D，B，O重合时，MN最大，MN=BD，∠MON=∠BOD=90°，S扇形MON最大=π（cm2），②当MN=DC=2时，MN最小，∴ON=MN=OM，∴∠NOM=60°，S扇形MON最小=π（cm2），∴π≤S扇形MON≤π．故答案为：30°．3、如图，在直角梯形ABCD中，AD∥BC，∠ABC=90°．点E为底AD上一点，将△ABE沿直线BE折叠，点A落在梯形对角线BD上的G 处，EG的延长线交直线BC于点F．（1）点E可以是AD的中点吗？为什么？（2）求证：△ABG∽△BFE；（3）设AD=a，AB=b，BC=c①当四边形EFCD为平行四边形时，求a，b，c应满足的关系；②在①的条件下，当b=2时，a的值是唯一的，求∠C的度数．解：（1）不是．据题意得：AE=GE，∠EGB=∠EAB=90°，∴Rt△EGD中，GE＜ED，∴AE＜ED，故，点E不可以是AD的中点；（注：大致说出意思即可；反证法叙述也可）（2）方法一：证明：∵AD∥BC，∴∠AEB=∠EBF，∵△EAB≌△EGB，∴∠AEB=∠BEG，∴∠EBF=∠BEF，∴FE=FB，∴△FEB为等腰三角形．∵∠ABG+∠GBF=90°，∠GBF+∠EFB=90°，∴∠ABG=∠EFB，在等腰△ABG和△FEB中，∠BAG=（180°﹣∠ABG）÷2，∠FBE=（180°﹣∠EFB）÷2，∴∠BAG=∠FBE，…5分∴△ABG∽△BFE，方法二：∠ABG=∠EFB（见方法一），证得两边对应成比例：，由此可得出结论．（3）①方法一：∵四边形EFCD为平行四边形，∴EF∥DC，证明两个角相等，得△ABD∽△DCB，∴，即，∴a2+b2=ac；…8分方法二：如图，过点D作DH⊥BC，∵四边形EFCD为平行四边形∴EF∥DC，∴∠C=∠EFB，∵△ABG∽△BFE，∴∠EFB=∠GBA，∴∠C=∠ABG，∵∠DAB=∠DHC=90°，∴△ABD∽△HCD，∴，∴，∴a2+b2=ac；方法三：证明△ABD∽△GFB，则有，∴，则有BF=，∵四边形EFCD为平行四边形，∴FC=ED=c﹣，∵ED∥BC，∴△EDG∽△FBG，∴，∴，∴a2+b2=ac；…8分方法一②：解关于a的一元二次方程a2﹣ac+22=0，得：a1=，a2=由题意，△=0，即c2﹣16=0，∵c＞0，∴c=4，∴a=2…10分∴H为BC的中点，且ABHD为正方形，DH=HC，∠C=45°；方法二：设关于a的一元二次方程a2﹣ac+22=0两根为a1，a2，a1+a2=c＞0，a1•a2=4＞0，∴a1＞0，a2＞0，…9分由题意，△=0，即c2﹣16=0，∵c＞0，∴c=4，∴a=2，…10分∴H为BC的中点，且ABHD为正方形，DH=HC，∠C=45°．4、如图1，Rt△ABC两直角边的边长为AC＝1，BC＝2．图1Z O YXC BAP 1（1）如图2，⊙O 与Rt △ABC 的边AB 相切于点X ，与边CB 相切于点Y ．请你在图2中作出并标明⊙O 的圆心O ；（用尺规作图，保留作图痕迹，不写作法和证明）（2）P 是这个Rt △ABC 上和其内部的动点,以P 为圆心的⊙P 与Rt △ABC 的两条边相切．设⊙的面积为s ，你认为能否确定s 的最大值？若能，请你求出s 的最大值;若不能,请你说明不能确定s 的最大值的理由．解：(1看见垂足为Y （X ）的一条垂线 (或者∠ABC 的平分线)即评1分，(2)①当⊙P 与Rt △ABC 的边 AB 和BC 相切时，由角平分线的性质，动点P 是∠ABC 的平分线BM 上的点.如图1，在∠ABC 的平分线BM 上任意确定点P 1 (不为∠ABC 的顶点)，∵ OX ＝BOsin ∠ABM, P 1Z ＝BP 1sin ∠ABM ．当 BP 1＞BO 时，P 1Z ＞OX,即P 与B 的距离越大，⊙P 的面积越大．这时，BM 与AC 的交点P 是符合题意的、BP 长度最大的点. 如图2，∵∠BPA ＞90°，过点P 作PE ⊥AB ，垂足为E ，则E 在边AB 上.∴以P 为圆心、PC 为半径作圆，则⊙P 与边CB 相切于C ，与边第23题图2图1YXC BC AA图2E图3DA AB 相切于E ，即这时的⊙P 是符合题意的圆. 这时⊙P 的面积就是S 的最大值.∵∠A ＝∠A ，∠BCA ＝∠AEP ＝90°,∴ Rt △ABC ∽Rt △APE ， ∴BCPEAB PA =. ∵AC ＝1，BC ＝2，∴AB ＝5.设PC ＝x ，则PA ＝AC －PC ＝1－x, PC ＝PE ，∴251x x =-， ∴x ＝522+ ． ②如图3，同理可得：当⊙P 与Rt △ABC 的边AB 和AC 相切时，设PC ＝y ，则152y y =-， ∴y=512+. （7分）21世纪教育网③如图4，同理可得：当⊙P 与Rt △ABC 的边BC 和AC 相切时，设PF ＝z ，则122z z =-， ∴z=32. （8分）由①，②，③可知：∵ 5 ＞2，∴ 5＋2＞5＋1＞3，∵当分子、分母都为正数时，若分子相同，则分母越小，这个分数越大， (或者:∵x=522+=25-4, y=512+ =215- 5,∴y-x=24549->0, ∴y>x. ∵z-y=645721532-=-->0)∴52251232+>+>2，（9分，没有过程直接得出酌情扣1分）∴ z ＞y ＞x. ∴⊙P 的面积S 的最大值为π94.5、如图①，P 是△ABC 边AC 上的动点，以P 为顶点作矩形PDEF ，顶点D,E 在边BC 上，顶点F 在边AB 上；△ABC 的底边BC 及BC 上的高的长分别为a , h,且是关于x 的一元二次方程20mx nx k ++=的两个实数根，设过D,E,F 三点的⊙O 的面积为O S ๏,矩形PDEF 的面积为PDEF S 矩形。

初中数学几何综合试题1及答案

初中数学几何综合试题班级____ 学号____ 姓名____ 得分____一、单选题(每道小题 3分共 9分 )1. 下列各式中正确的是[ ]A.sin12=30 B.tg1=45C.tg30=3D.cos60=122. 如图,已知AB 和CD 是⊙O 中两条相交的直径,连AD 、CB 那么α和β的关系是 [ ]A B C D ....αββαβαβα=><=121223. 在一个四边形中，如果两个内角是直角，那么另外两个内角可以 [ ] A ．都是钝角 B ．都是锐角C ．一个是锐角一个是直角D ．都是直角或一个锐角一个钝角二、填空题(第1小题 1分, 2-7每题 2分, 8-9每题 3分, 10-14每题 4分, 共 39分)1. 人们从实践经验中总结出来的图形的基本性质,我们把它叫做_______．2. 小于直角的角叫做______;大于直角而小于平角的角叫做________．3. 已知正六边形外接圆的半径为R , 则这个正六边形的周长为_______．4. 在中若则Rt ABC ,C =90,cosB =23,sinA =∆∠ .5. 如果圆的半径R 增加10% , 则圆的面积增加_____________．6. cos sin cos sin .45306030-+=7. 已知∠a=60°,∠AOB=3∠a,OC 是∠AOB 的平分线,则∠a=___∠AOC ．8. 等腰Rt △ABC, 斜边AB 与斜边上的高的和是12厘米, 则斜边AB= 厘米．9. 已知：如图△ABC 中AB=AC, 且EB=BD=DC=CF, ∠A=40°, 则∠EDF 的度数为________．10. 在同一个圆中, 当圆心角不超过180°时, 圆心角越大, 所对的弧______;所对的弦_______, 所对弦的弦心距_______．11. 如图，在直角三角形ABC 中，∠C=90°，D 、E 分别是AB 、AC 中点， AC=7，BC=4，若以C 为圆心，BC 为半径做圆，则ED 与⊙o 的位置关系是：D 在______, E 在_____．12. 在△ABC 中,∠C=90°若a=5,则S △ABC =12.5,则c=_________,∠A=_________13. 如图：CB ⊥AB,CE 平分∠BCD,DE 平分∠CDA,∠1+∠2=90° 求证：DA ⊥AB证明：∵∠1+∠2=90°(已知)∠2=∠4,∠1=∠3(角平分线定义) ∴∠3+∠4=90°(等量代换)∴∠ADC+∠BCD=180°(等量代换) AD ∥BC( )∵BC ⊥AB(已知)∴AD ⊥AB( )14. 圆外切四边形ABCD 中，如果AB=2，BC=3，CD=8，那么 AD= ．三、计算题(第1小题 4分, 2-3每题 6分, 共 16分)1. 求值：cos 245°+tg30°sin60°2. 已知正方形ABCD ，E 是BC 延长线上一点，AE 交CD 于F ，如果AC=CE ，求∠AFC 的度数．3. 如图：AB 是半圆的直径，O 为圆心，C 是AB 延长线上的一点，CD 切半圆于，于，已知：，，求之长．D DE AB E EB AB CD BC ⊥==152四、解答题(1-2每题 4分, 第3小题 6分, 第4小题 7分, 共 21分)1. 在△Rt △ABC 中,∠C=90°,AB+AC=a,∠B=a,求AC.2. 如图：铁路的路基的横截面是等腰梯形斜坡的坡度为为米基面宽米求路基的高，基底的宽及坡角的度数答案可带根号,AB 13,33,AD 2,AE BEC B .():BE3. 如图,某厂车间的人字屋架为等腰三角形,跨度AB=12米,∠A=30°,求中柱CD 和上弦AC 的长(答案可带根号)4. 如图：已知AB∥CD , ∠BAE=40°, ∠ECD=62°, EF平分∠AEC , 则∠AEF是多少度?五、证明题(第1小题 4分, 2-4每题 7分, 共 25分)1. 已知：如图 , AB=AC , ∠B=∠C．BE、DC交于O点．求证：BD=CE2. 已知：如图，PA=PB，PA切⊙O于A，BCD交⊙O于C、D，PC延长交⊙O于E，连结BE交⊙O于F．求证：DF∥PB．3. 如图：EG∥AD , ∠BFG=∠E.求证：AD平分∠BAC.4. 已知：如图 , 在∠AOB的两边OA , OB上分别截取OQ=OP , OT=OS , PT 和QS相交于点C．求证：OC平分∠AOB六、画图题(第1小题 2分, 2-3每题 4分, 共 10分)1. 已知：如图, ∠AOB求作：射线OC, 使∠AOC=∠BOC．(不写作法)2. 已知：两角和其中一个角的对边 ,求作：三角形ABC(写出已知 , 求作 , 画图,写作法)3. 如图, 要在河边修建一个水泵站, 分别向张村, 李村送水．修在河边什么地方, 可使所用的水管最短?(写出已知, 求作, 并画图)初中数学模拟考试题答案一、单选题1. D2. D3. D二、填空题1. 公理2. 锐角,钝角3. 6R4. 2 35. 0.21πR26. 21 27. 2 38. 89. 70°10. 越长, 越长, 越短11. 在圆外，在圆内12. 5245,13. 同旁内角互补,两直线平行；一条直线和两条平行线中的一条垂直,也和另一条垂直14. 7三、计算题1. 解：原式=+⨯=+=()2233321212122. 解：∵AC=CE 则∠1=∠2 又∵∠ACE=135°∴∠1=(180°-135°)÷2=22.5°故∠AFC=180°-(45°+22.5°)=112.5°3. 解：如图，连结、，为直径∴又∵，∽∴·同理·而，∴··∴：：∵切半圆于，∽，：：：AD DB ABADBDE AB ADE ABDADABAEADAD AE ABBD BE AB BE ABADBDAE ABBE ABC CAD BDCD D CDB A ADC DBC DC BC AD BD CDBC∠=⊥======∠=∠=∠=∠====︒9015412121212222∆∆∆∆四、解答题1. 解：在中则即即Rt ABC CACABAC ABACaACACa∆∠==+=+=+=+∴90111sinsinsinsinsinsinsinααααααα2. 解：米米AEAEBCB3313326330===+∠=∴()()()3. CDAC为米为米2343解：过E作EG∥AB∵∠BAE=40°∴∠AEG=40°同理∠CEG=62°∴∠AEC=102°又∵EF平分∠AEC ∴∠AEF=51°五、证明题4.1. 证：∵∠A=∠A , AB=AC , ∠B=∠C．∴△ADC≌△AEB(ASA)∴AD=AE∵AB=AC,∴BD=CE．2. 证明：如图，切⊙于，交⊙于、，又的公用∽又∥PA O A BCD O C DAP PC PEPA PB PB PC PEPBPCPEPBBPC PBC PEBEE BDF BDF DF PB∴=⋅=∴=⋅∴=∠∴∴∠=∠∴∠=∠∴∠=∠∴2211∆∆证明：∵∠BFG=∠E=∠EFAEG∥AD∴∠E=∠DAC ∠BFG=∠BAD∴AD平分∠BAC4. 证：作射线OC , 连结TS．在△SOP和△TOQ中 ,OS=OT , OQ=OP , ∠AOB=∠BOA．∴△SOP≌△TOQ(SAS) ∴∠1=∠2．∵OT=OS , ∴∠OST=∠OTS3.∴∠3=∠4 ∴CT=CS∵OC=OC , OS=OT , CT=CS∴△OCS≌△OCT (SSS)∴∠5=∠6∴OC平分∠AOB六、画图题1. 射线OC为所求．2. 已知：∠a、∠b、线段a求作：△ABC使∠A=∠a , ∠B=∠b, BC=a作法：1.作线段BC=a2.在BC的同侧作∠DBC=∠b,∠ECB=180-∠a-∠b,BD和CE交于A, 则△ABC为所求的三角形．3. 已知：直线a和a的同侧两点A、B．求作：点C, 使C在直线a上, 并且AC+BC最小．作法：1.作点A关于直线a的对称点A'．2.连结A'B交a于点C．则点C就是所求的点．证明：在直线a上另取一点C', 连结AC,AC', A'C', C'B．∵直线a是点A, A'的对称轴, 点C, C'在对称轴上∴AC=A'C, AC'=A'C'∴AC+CB=A'C+CB=A'B在△A'C'B中,∵A'B＜A'C'+C'B∴AC+CB＜AC'+C'B即AC+CB最小．。

数学九年级上册圆几何综合单元测试卷(含答案解析)

数学九年级上册圆几何综合单元测试卷（含答案解析）一、初三数学圆易错题压轴题（难）1．在圆O中，C是弦AB上的一点，联结OC并延长，交劣弧AB于点D ，联结AO、BO、AD、BD．已知圆O的半径长为5，弦AB的长为8．（1）如图1，当点D是弧AB的中点时，求CD的长；（2）如图2，设AC=x，ACOOBDSS=y，求y关于x的函数解析式并写出定义域；（3）若四边形AOBD是梯形，求AD的长．【答案】（1）2；（2）2825x x x-+（0＜x＜8）;（3）AD=145或6．【解析】【分析】(1)根据垂径定理和勾股定理可求出OC的长.(2)分别作OH⊥AB，DG⊥AB，用含x的代数式表示△ACO和△BOD的面积，便可得出函数解析式.(3)分OB∥AD和OA∥BD两种情况讨论.【详解】解：（1）∵OD过圆心，点D是弧AB的中点，AB=8，∴OD⊥AB，AC=12AB=4，在Rt△AOC中，∵∠ACO=90°，AO=5，∴22AO AC-，∴OD=5，∴CD=OD﹣OC=2；（2）如图2，过点O作OH⊥AB，垂足为点H，则由（1）可得AH=4，OH=3，∵AC=x，∴CH=|x﹣4|，在Rt△HOC中，∵∠CHO=90°，AO=5，∴22HO HC+223|x4|+-2825x x-+∴CD=OD ﹣OC=5过点DG ⊥AB 于G ， ∵OH ⊥AB ， ∴DG ∥OH ， ∴△OCH ∽△DCG ， ∴OH OCDG CD=， ∴DG=OH CD OC⋅35， ∴S △ACO =12AC ×OH=12x ×3=32x ， S △BOD =12BC （OH +DG ）=12（8﹣x ）×（335）=32（8﹣x ）∴y=ACO OBDS S=()323582x x -（0＜x ＜8）（3）①当OB ∥AD 时，如图3，过点A 作AE ⊥OB 交BO 延长线于点E ，过点O 作OF ⊥AD ，垂足为点F ，则OF=AE ， ∴S=12AB•OH=12OB•AE ， AE=AB OH OB ⋅=245=OF ，在Rt △AOF 中，∠AFO=90°，AO=5，∴75∵OF 过圆心，OF ⊥AD ，∴AD=2AF=145．②当OA ∥BD 时，如图4，过点B 作BM ⊥OA 交AO 延长线于点M ，过点D 作DG ⊥AO ，垂足为点G ，则由①的方法可得DG=BM=245，在Rt △GOD 中，∠DGO=90°，DO=5，∴GO=22DO DG -=75，AG=AO ﹣GO=185，在Rt △GAD 中，∠DGA=90°，∴AD=22AG DG +=6综上得AD=145或6．故答案为（1）2；（2）y=()2825x x x -+（0＜x ＜8）;（3）AD=145或6．【点睛】本题是考查圆、三角形、梯形相关知识，难度大，综合性很强.2．已知：四边形ABCD 内接于⊙O ，∠ADC ＝90°，DE ⊥AB ，垂足为点E ，DE 的锯长线交⊙O 于点F ，DC 的延长线与FB 的延长线交于点G ．（1）如图1，求证：GD ＝GF ；（2）如图2，过点B 作BH ⊥AD ，垂足为点M ，B 交DF 于点P ，连接OG ，若点P 在线段OG 上，且PB ＝PH ，求∠ADF 的大小；（3）如图3，在（2）的条件下，点M 是PH 的中点，点K 在BC 上，连接DK ，PC ，D 交PC 点N ，连接MN ，若AB ＝122，HM +CN ＝MN ，求DK 的长．【答案】（1）见解析；（2）∠ADF ＝45°；（31810【解析】【分析】（1）利用“同圆中，同弧所对的圆周角相等”可得∠A ＝∠GFD ，由“等角的余角相等”可得∠A ＝∠GDF ，等量代换得∠GDF ＝∠GFD ，根据“三角形中，等角对等边”得GD ＝GF ；（2）连接OD 、OF ，由△DPH ≌△FPB 可得：∠GBH ＝90°，由四边形内角和为360°可得：∠G ＝90°，即可得：∠ADF ＝45°；（3）由等腰直角三角形可得AH ＝BH ＝12，DF ＝AB ＝12，由四边形ABCD 内接于⊙O ，可得：∠BCG ＝45°＝∠CBG ，GC ＝GB ，可证四边形CDHP 是矩形，令CN ＝m ，利用勾股定理可求得m ＝2，过点N 作NS ⊥DP 于S ，连接AF ，FK ，过点F 作FQ ⊥AD 于点Q ，过点F 作FR ⊥DK 交DK 的延长线于点R ，通过构造直角三角形，应用解直角三角形方法球得DK ．【详解】解：（1）证明：∵DE ⊥AB ∴∠BED ＝90° ∴∠A +∠ADE ＝90° ∵∠ADC ＝90° ∴∠GDF +∠ADE ＝90° ∴∠A ＝∠GDF ∵BD BD = ∴∠A ＝∠GFD ∴∠GDF ＝∠GFD ∴GD ＝GF （2）连接OD 、OF ∵OD ＝OF ，GD ＝GF ∴OG ⊥DF ，PD ＝PF 在△DPH 和△FPB 中PD PF DPH FPB PH PB =⎧⎪∠=∠⎨⎪=⎩∴△DPH ≌△FPB （SAS ） ∴∠FBP ＝∠DHP ＝90° ∴∠GBH ＝90°∴∠DGF ＝360°﹣90°﹣90°﹣90°＝90° ∴∠GDF ＝∠DFG ＝45° ∴∠ADF ＝45°（3）在Rt △ABH 中，∵∠BAH ＝45°，AB ＝2 ∴AH ＝BH ＝12 ∴PH ＝PB ＝6 ∵∠HDP ＝∠HPD ＝45° ∴DH ＝PH ＝6∴AD ＝12+6＝18，PN ＝HM ＝12PH ＝3，PD ＝2 ∵∠BFE ＝∠EBF ＝45°∴EF ＝BE∵∠DAE ＝∠ADE ＝45° ∴DE ＝AE∴DF ＝AB ＝∵四边形ABCD 内接于⊙O ∴∠DAB +∠BCD ＝180° ∴∠BCD ＝135° ∴∠BCG ＝45°＝∠CBG ∴GC ＝GB又∵∠CGP ＝∠BGP ＝45°，GP ＝GP ∴△GCP ≌△GBP （SAS ） ∴∠PCG ＝∠PBG ＝90° ∴∠PCD ＝∠CDH ＝∠DHP ＝90° ∴四边形CDHP 是矩形∴CD ＝HP ＝6，PC ＝DH ＝6，∠CPH ＝90° 令CN ＝m ，则PN ＝6﹣m ，MN ＝m +3 在Rt △PMN 中，∵PM 2+PN 2＝MN 2 ∴32+（6﹣m ）2＝（m +3）2，解得m ＝2 ∴PN ＝4过点N 作NS ⊥DP 于S ，在Rt △PSN 中，PS ＝SN ＝DS ＝﹣＝SN 1tanDS 2SDN ∠=== 连接AF ，FK ，过点F 作FQ ⊥AD 于点Q ，过点F 作FR ⊥DK 交DK 的延长线于点R 在Rt △DFQ 中，FQ ＝DQ ＝12 ∴AQ ＝18﹣12＝6 ∴tan 1226FQ FAQ AQ ∠=== ∵四边形AFKD 内接于⊙O ， ∴∠DAF +∠DKF ＝180° ∴∠DAF ＝180°﹣∠DKF ＝∠FKR在Rt △DFR 中，∵DF ＝1tan 2FDR ∠=∴,55FR DR ==在Rt △FKR 中，∵FR ＝5tan ∠FKR ＝2∴KR＝6105∴DK＝DR﹣KR＝24106101810555=-=．【点睛】本题是一道有关圆的几何综合题，难度较大，主要考查了圆内接四边形的性质，圆周角定理，全等三角形性质及判定，等腰直角三角形性质，解直角三角形等知识点；解题关键是添加辅助线构造直角三角形．3．如图，矩形ABCD中，BC＝8，点F是AB边上一点（不与点B重合）△BCF的外接圆交对角线BD于点E，连结CF交BD于点G．（1）求证：∠ECG＝∠BDC．（2）当AB＝6时，在点F的整个运动过程中．①若BF＝22时，求CE的长．②当△CEG为等腰三角形时，求所有满足条件的BE的长．（3）过点E作△BCF外接圆的切线交AD于点P．若PE∥CF且CF＝6PE，记△DEP的面积为S1，△CDE的面积为S2，请直接写出12SS的值．【答案】（1）详见解析；（2）①1825；②当BE为10，395或445时，△CEG为等腰三角形；（3）724.【解析】【分析】（1）根据平行线的性质得出∠ABD＝∠BDC，根据圆周角定理得出∠ABD＝∠ECG，即可证得结论；（2）根据勾股定理求得BD ＝10，①连接EF ，根据圆周角定理得出∠CEF ＝∠BCD ＝90°，∠EFC ＝∠CBD ．即可得出sin ∠EFC＝sin ∠CBD ，得出35CE CD CF BD ==，根据勾股定理得到CF ＝CE ； ②分三种情况讨论求得：当EG ＝CG 时，根据等腰三角形的性质和圆周角定理即可得到∠GEC ＝∠GCE ＝∠ABD ＝∠BDC ，从而证得E 、D 重合，即可得到BE ＝BD ＝10；当GE ＝CE 时，过点C 作CH ⊥BD 于点H ，即可得到∠EGC ＝∠ECG ＝∠ABD ＝∠GDC ，得到CG ＝CD ＝6．根据三角形面积公式求得CH ＝245，即可根据勾股定理求得GH ，进而求得HE ，即可求得BE ＝BH ＋HE ＝395；当CG ＝CE 时，过点E 作EM ⊥CG 于点M ，由tan ∠ECM ＝43EM CM =．设EM ＝4k ，则CM ＝3k ，CG ＝CE ＝5k ．得出GM ＝2k ，tan ∠GEM ＝2142GM k EM k ==，即可得到tan ∠GCH ＝GH CH =12．求得HE ＝GH ＝125，即可得到BE ＝BH ＋HE ＝445；（3）连接OE 、EF 、AE 、EF ，先根据切线的性质和垂直平分线的性质得出EF ＝CE ，进而证得四边形ABCD 是正方形，进一步证得△ADE ≌△CDE ，通过证得△EHP ∽△FBC ，得出EH ＝16BF ，即可求得BF ＝6，根据勾股定理求得CF ＝10，得出PE ＝106，根据勾股定理求得PH ，进而求得PD ，然后根据三角形面积公式即可求得结果．【详解】（1）∵AB ∥CD ． ∴∠ABD ＝∠BDC ， ∵∠ABD ＝∠ECG ， ∴∠ECG ＝∠BDC ．（2）解：①∵AB ＝CD ＝6，AD ＝BC ＝8，∴BD ＝10，如图1，连结EF ，则∠CEF ＝∠BCD ＝90°， ∵∠EFC ＝∠CBD ． ∴sin ∠EFC ＝sin ∠CBD ， ∴35CE CD CF BD ==∴CF∴CE②Ⅰ、当EG＝CG时，∠GEC＝∠GCE＝∠ABD＝∠BDC．∴E与D重合，∴BE＝BD＝10．Ⅱ、如图2，当GE＝CE时，过点C作CH⊥BD于点H，∴∠EGC＝∠ECG＝∠ABD＝∠GDC，∴CG＝CD＝6．∵CH＝BC CD24 BD5⋅=，∴GH185 =，在Rt△CEH中，设HE＝x，则x2+（245）2＝（x+185）2解得x＝75，∴BE＝BH+HE＝325+75＝395；Ⅲ、如图2，当CG＝CE时，过点E作EM⊥CG于点M．∵tan∠ECM＝43 EMCM=．设EM＝4k，则CM＝3k，CG＝CE＝5k．∴GM＝2k，tan∠GEM＝2142 GM kEM k==，∴tan∠GCH＝GHCH＝tan∠GEM＝12．∴HE＝GH＝12412 255⨯=，∴BE＝BH+HE＝321244 555+=，综上所述，当BE为10，395或445时，△CEG为等腰三角形；（3）解：∵∠ABC＝90°，∴FC是△BCF的外接圆的直径，设圆心为O，如图3，连接OE、EF、AE、EF，∵PE是切线，∴OE⊥PE，∵PE∥CF，∴OE⊥CF，∵OC＝OF，∴CE＝EF，∴△CEF是等腰直角三角形，∴∠ECF＝45°，EF=2FC，∴∠ABD＝∠ECF＝45°，∴∠ADB＝∠BDC＝45°，∴AB＝AD＝8，∴四边形ABCD是正方形，∵PE∥FC，∴∠EGF＝∠PED，∴∠BGC＝∠PED，∴∠BCF＝∠DPE，作EH⊥AD于H，则EH＝DH，∵∠EHP＝∠FBC＝90°，∴△EHP∽△FBC，∴16 EH PEBF FC==，∴EH＝16 BF，∵AD＝CD，∠ADE＝∠CDE，∴△ADE≌△CDE，∴AE＝CE，∴AE＝EF，∴AF＝2EH＝13 BF，∴13BF+BF＝8，∴BF＝6，∴EH＝DH＝1，CF10，∴PE＝16FC＝53，∴PH4 3 =，∴PD＝47133 +=，∴1277 3824S PDS AD===．【点睛】本题是四边形的综合题，考查了矩形的性质，圆周角定理、三角形的面积以及相似三角形的判定和性质，作出辅助线构建直角三角形是解题的关键．4．如图①，已知Rt △ABC 中，∠ACB ＝90°，AC ＝8，AB ＝10，点D 是AC 边上一点（不与C 重合），以AD 为直径作⊙O ，过C 作CE 切⊙O 于E ，交AB 于F ．（1）若⊙O 半径为2，求线段CE 的长；（2）若AF ＝BF ，求⊙O 的半径；（3）如图②，若CE ＝CB ，点B 关于AC 的对称点为点G ，试求G 、E 两点之间的距离．【答案】（1）CE ＝2；（2）⊙O 的半径为3；（3）G 、E 两点之间的距离为9.6 【解析】【分析】（1）根据切线的性质得出∠OEC=90°，然后根据勾股定理即可求得；（2）由勾股定理求得BC ，然后通过证得△OEC ∽△BCA ，得到OE OC BC BA =，即8610r r-= 解得即可；（3）证得D 和M 重合，E 和F 重合后，通过证得△GBE ∽△ABC ，GB GEAB AC=，即12108GE =，解得即可. 【详解】解：（1）如图①，连接OE ，∵CE切⊙O于E，∴∠OEC＝90°，∵AC＝8，⊙O的半径为2，∴OC＝6，OE＝2，∴CE＝2242OC OE-=；（2）设⊙O的半径为r，在Rt△ABC中，∠ACB＝90°，AB＝10，AC＝8，∴BC＝22AB A C-＝6，∵AF＝BF，∴AF＝CF＝BF，∴∠ACF＝∠CAF，∵CE切⊙O于E，∴∠OEC＝90°，∴∠OEC＝∠ACB，∴△OEC∽△BCA，∴OE OCBC BA=，即8610r r-=解得r＝3，∴⊙O的半径为3；（3）如图②，连接BG，OE，设EG交AC于点M，由对称性可知，CB＝CG，∵CE ＝CG ， ∴∠EGC ＝∠GEC ， ∵CE 切⊙O 于E ， ∴∠GEC +∠OEG ＝90°， ∵∠EGC +∠GMC ＝90°， ∴∠OEG ＝∠GMC ， ∵∠GMC ＝∠OME ， ∴∠OEG ＝∠OME ， ∴OM ＝OE ， ∴点M 和点D 重合， ∴G 、D 、E 三点在同一直线上，连接AE 、BE ， ∵AD 是直径，∴∠AED ＝90°，即∠AEG ＝90°，又CE ＝CB ＝CG ， ∴∠BEG ＝90°，∴∠AEB ＝∠AEG +∠BEG ＝180°， ∴A 、E 、B 三点在同一条直线上， ∴E 、F 两点重合，∵∠GEB ＝∠ACB ＝90°，∠B ＝∠B ， ∴△GBE ∽△ABC ，∴GB GE AB AC = ，即12108GE= ∴GE ＝9.6，故G 、E 两点之间的距离为9.6．【点睛】本题考查了切线的判定，轴的性质，勾股定理的应用以及三角形相似的判定和性质，证得G 、D 、E 三点共线以及A 、E 、B 三点在同一条直线上是解题的关5．已知：图1 图2 图3 （1）初步思考：如图1，在PCB ∆中，已知2PB =，BC=4，N 为BC 上一点且1BN =，试说明：12PN PC =（2）问题提出：如图2，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC +的最小值．（3）推广运用：如图3，已知菱形ABCD 的边长为4，∠B ﹦60°，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC -的最大值．【答案】（1）详见解析；（2）5；（3）最大值DG =【解析】【分析】（1）利用两边成比例，夹角相等，证明BPN ∆∽BCP ∆，得到PN BNPC BP=，即可得到结论成立；（2）在BC 上取一点G ，使得BG=1，由△PBG ∽△CBP ，得到12PG PC =，当D 、P 、G 共线时，12PD PC +的值最小，即可得到答案；（3）在BC 上取一点G ，使得BG=1，作DF ⊥BC 于F ，与（2）同理得到12PG PC =，当点P 在DG 的延长线上时，12PD PC -的值最大，即可得到答案. 【详解】（1）证明：∵2,1,4PB BN BC ===， ∴24,4PB BN BC =⋅=， ∴2PB BN BC =⋅，∴BN BPBP BC =， ∵B B ∠=∠，∴BPN BCP ∆∆∽， ∴12PN BN PC BP ==， ∴12PN PC =；（2）解：如图，在BC 上取一点G ，使得BG=1，∵242,212PB BC BG PB ====， ∴,PB BCPBG PBC BG PB =∠=∠， ∴PBG CBP ∆∆∽， ∴12PG BG PC PB ==， ∴12PG PC =， ∴12PD PC DP PG +=+； ∵DP PG DG +≥， ∴当D 、P 、G 共线时，12PD PC +的值最小， ∴最小值为：22435DG =+=；（3）如图，在BC 上取一点G ，使得BG=1，作DF ⊥BC 于F ，与（2）同理，可证12PG PC =，在Rt △CDF 中，∠DCF=60°，CD=4， ∴DF=CD •sin60°=23CF=2，在Rt △GDF 中，22(23)537+=， ∴12PD PC PD PG DG -=-≤，当点P 在DG 的延长线上时，12PD PC -的值最大， ∴最大值为：37DG = 【点睛】本题考查圆综合题、正方形的性质、菱形的性质、相似三角形的判定和性质、两点之间线段最短等知识，解题的关键是学会构建相似三角形解决问题，学会用转化的思想思考问题，把问题转化为两点之间线段最短解决，题目比较难，属于中考压轴题．6．选做题：从甲乙两题中选作一题，如果两题都做，只以甲题计分题甲：已知矩形两邻边的长、是方程的两根.（1）求的取值范围；（2）当矩形的对角线长为时，求的值；（3）当为何值时，矩形变为正方形？题乙：如图，是直径，于点，交于点，且．（1）判断直线和的位置关系，并给出证明；（2）当，时，求的面积．【答案】题甲（1）（2）（3）题乙：（1）BD是切线；证明所以OB⊥BD，BD是切线（2）S=【解析】试题分析：题甲：（1）、是方程的两根，则其；由得（2）矩形两邻边的长、，矩形的对角线的平方=；矩形两邻边的长、是方程的两根，则；因为，所以；解得由得（3）矩形变为正方形，则a=b；、是方程的两根，所以方程有两个相等的实数根，即，由得题乙：（1）BD是切线；如图所示，是弧AC所对的圆周角，；因为，所以；于点，，所以，，在三角形OBD中，所以OB⊥BD；BD是切线（2），AB是圆的直径，所以OB=5；于点，交于点，F是BC的中点；，BF=4；在直角三角形OBF中由勾股定理得OF=；根据题意，，则，所以，从而，解得DF=，的面积=考点：直线与圆相切，相似三角形点评：本题考查直线与圆相切，相似三角形；解本题的关键是会判断直线与圆是否相切，能判定两个三角形相似7．在平面直角坐标系xOy中，⊙C的半径为r(r＞1)，点P是圆内与圆心C不重合的点，⊙C的“完美点”的定义如下：过圆心C的任意直线CP与⊙C交于点A，B，若满足|PA﹣PB|＝2，则称点P为⊙C的“完美点”，如图点P为⊙C的一个“完美点”．(1)当⊙O的半径为2时①点M(32，0)⊙O的“完美点”，点(﹣3，﹣12)⊙O的“完美点”；(填“是”或者“不是”)②若⊙O的“完美点”P在直线y＝34x上，求PO的长及点P的坐标；(2)设圆心C的坐标为(s，t)，且在直线y＝﹣2x+1上，⊙C半径为r，若y轴上存在⊙C的“完美点”，求t的取值范围．【答案】(1)①不是，是；②PO的长为1，点P的坐标为(45，35)或(﹣45，﹣35)；(2)t的取值范围为﹣1≤t≤3．【解析】【分析】（1）①利用圆的“完美点”的定义直接判断即可得出结论.②先确定出满足圆的“完美点”的OP的长度，然后分情况讨论计算即可得出结论；（2）先判断出圆的“完美点”的轨迹，然后确定出取极值时OC与y轴的位置关系即可得出结论.【详解】解：(1)①∵点M(32，0)，∴设⊙O与x轴的交点为A，B，∵⊙O的半径为2，∴取A(﹣2，0)，B(2，0)，∴|MA﹣MB|＝|(32+2)﹣(2﹣32)|＝3≠2，∴点M不是⊙O的“完美点”，同理：点(﹣3，﹣12)是⊙O的“完美点”．故答案为不是，是．②如图1，根据题意，|PA﹣PB|＝2，∴|OP+2﹣(2﹣OP)|＝2，∴OP＝1．若点P在第一象限内，作PQ⊥x轴于点Q，∵点P在直线y＝34x上，OP＝1，∴43,55 OQ PQ==．∴P(43,55)．若点P在第三象限内，根据对称性可知其坐标为(﹣45，﹣35)．综上所述，PO的长为1，点P的坐标为(43,55)或（43,55--）)．(2)对于⊙C的任意一个“完美点”P都有|PA﹣PB|＝2，∴|CP+r﹣(r﹣CP)|＝2．∴CP＝1．∴对于任意的点P，满足CP＝1，都有|CP+r﹣(r﹣CP)|＝2，∴|PA﹣PB|＝2，故此时点P为⊙C的“完美点”．因此，⊙C的“完美点”是以点C为圆心，1为半径的圆．设直线y＝﹣2x+1与y轴交于点D，如图2，当⊙C移动到与y轴相切且切点在点D的上方时，t的值最大．设切点为E，连接CE，∵⊙C的圆心在直线y＝﹣2x+1上，∴此直线和y轴，x轴的交点D(0，1)，F(12，0)，∴OF＝12，OD＝1，∵CE∥OF，∴△DOF∽△DEC，∴OD OF DE CE=，∴112 DE=，∴DE＝2，∴OE＝3，t的最大值为3，当⊙C移动到与y轴相切且切点在点D的下方时，t的值最小．同理可得t的最小值为﹣1．综上所述，t的取值范围为﹣1≤t≤3．【点睛】此题是圆的综合题，主要考查了新定义，相似三角形的性质和判定，直线和圆的位置关系，解本题的关键是理解新定义的基础上，会用新定义，是一道比中等难度的中考常考题.8．已知ABD △内接于圆O ，点C 为弧BD 上一点，连接BC AC AC 、，交BD 于点E ，CED ABC ∠=∠．（1）如图1，求证：弧AB =弧AD ；（2）如图2，过B 作BF AC ⊥于点F ，交圆O 点G ，连接AG 交BD 于点H ，且222EH BE DH =+，求CAG ∠的度数；（3）如图3，在（2）的条件下，圆O 上一点M 与点C 关于BD 对称，连接ME ，交AB 于点N ，点P 为弧AD 上一点，PQ BG ∥交AD 于点Q ，交BD 的延长线于点R ，AQ BN =，ANE 的周长为20，52DR =，求圆O 半径．【答案】（1）见解析；（2）∠CAG=45°；（3）r=62 【解析】【分析】（1）证∠ABD=∠ACB 可得；（2）如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合，证△ALE ≌△AHE ，利用勾股定理逆定理推导角度；（3）如下图，延长QR 交AB 于点T ，分别过点N 、Q 作BD 的垂线，交于点V ，I ，取QU=AE ，过点U 作UK 垂直BD.先证△AEN ≌△QUD ，再证△NVE ≌△RKU ，可得到NV=KR=DK ，进而求得OB 的长. 【详解】（1）∵∠CED 是△BEC 的外角，∴∠CED=∠EBC+∠BCA ∵∠ABC=∠ABD+∠EBC 又∵∠CED=∠ABC ∴∠ABD=∠ACB ∴弧AB=弧AD（2）如下图，△AHD 绕点A 旋转至△ALE 处，使得点D 与点B 重合∵△ALB是△AHD旋转所得∴∠ABL=∠ADB，AL=AH设∠CAG=a，则∠CBG=a∵BG⊥AC∴∠BCA=90°-a，∴∠ADB=∠ABD=90°-a∴在△BAD中，BAE+∠HAD=180-a-(90°-a)-(90°-a)=a∴∠LAE=∠EAH=a∵LA=AH，AE=AE∴△ALE≌△AHE，∴LE=EH∵HD=LB，222=+EH BE DH∴△LBE为直角三角形∴∠LBE=(90°-a)+(90°-a)=90°，解得：a=45°∴∠CAG=45°（3）如下图，延长QR交AB于点T，分别过点N、Q作BD的垂线，交于点V，I，取QU=AE，过点U作UK垂直BD由（2）得∠BAD=90°∴点O在BD上设∠R=n，则∠SER=∠BEC=∠MEB=90°-n∴∠AEN=2n∵SQ⊥AC∴∠TAS=∠AQS=∠DQR，AN=QD∵QU=AE∴△AEN≌△QUD∴∠QUD=∠AEN=2n∴UD=UR=NE，∵△ANE的周长为20∴QD+QR=20在△DQR中，QD=7∵∠ENR=∠UDK=∠R=n∴△NVE≌△RKU∴NV=KR=DK=52 2∴BN=5∴BD=122，OB=62r=【点睛】本题考查了圆的证明，涉及到全等、旋转和勾股定理，解题关键是结合图形特点，适当构造全等三角形9．如图，已知AB是⊙O的直径，C是⊙O上一点（不与A、B重合），D为的AC中点，过点D作弦DE⊥AB于F，P是BA延长线上一点，且∠PEA＝∠B．（1）求证：PE是⊙O的切线；（2）连接CA与DE相交于点G，CA的延长线交PE于H，求证：HE＝HG；（3）若tan∠P＝512，试求AHAG的值．【答案】（1）证明见解析；（2）证明见解析；（3）1310 AHAG=．【解析】【分析】（1）连接OE，由圆周角定理证得∠EAB+∠B＝90°，可得出∠OAE＝∠AEO，则∠PEA+∠AEO＝90°，即∠PEO＝90°，则结论得证；（2）连接OD，证得∠AOD＝∠AGF，∠B＝∠AEF，可得出∠PEF＝2∠B，∠AOD＝2∠B，可证得∠PEF＝∠AOD＝∠AGF，则结论得证；（3）可得出tan∠P＝tan∠ODF＝512OFDF=，设OF＝5x，则DF＝12x，求出AE，BE，得出23AEBE=，证明△PEA∽△PBE，得出23PAPE=，过点H作HK⊥PA于点K，证明∠P＝∠PAH，得出PH＝AH，设HK＝5a，PK＝12a，得出PH＝13a，可得出AH＝13a，AG＝10a，则可得出答案．【详解】解：（1）证明：如图1，连接OE，∵AB是⊙O的直径，∴∠AEB＝90°，∴∠EAB+∠B＝90°，∵OA＝OE，∴∠OAE＝∠AEO，∴∠B+∠AEO＝90°，∵∠PEA＝∠B，∴∠PEA+∠AEO＝90°，∴∠PEO＝90°，又∵OE为半径，∴PE是⊙O的切线；（2）如图2，连接OD，∵D为AC的中点，∴OD⊥AC，设垂足为M，∴∠AMO＝90°，∵DE⊥AB，∴∠AFD＝90°，∴∠AOD+∠OAM＝∠OAM+∠AGF＝90°，∴∠AOD＝∠AGF，∵∠AEB＝∠EFB＝90°，∴∠B＝∠AEF，∵∠PEA＝∠B，∴∠PEF＝2∠B，∵DE⊥AB，∴AE AD，∴∠AOD＝2∠B，∴∠PEF＝∠AOD＝∠AGF，∴HE＝HG；（3）解：如图3，∵∠PEF＝∠AOD，∠PFE＝∠DFO，∴∠P＝∠ODF，∴tan∠P＝tan∠ODF＝512 OFDF=，设OF＝5x，则DF＝12x，∴OD22OF DF+13x，∴BF＝OF+OB＝5x+13x＝18x，AF＝OA﹣OF＝13x﹣5x＝8x，∵DE⊥OA，∴EF＝DF＝12x，∴AE22AF EF+13，BE22EF BF+13，∵∠PEA＝∠B，∠EPA＝∠BPE，∴△PEA∽△PBE，∴41323613PA AEPE BE===，∵∠P+∠PEF＝∠FAG+∠AGF＝90°，∴∠HEG＝∠HGE，∴∠P＝∠FAG，又∵∠FAG＝∠PAH，∴∠P＝∠PAH，∴PH＝AH，过点H作HK⊥PA于点K，∴PK＝AK，∴13 PKPE=，∵tan∠P＝5 12，设HK＝5a，PK＝12a，∴PH＝13a，∴AH＝13a，PE＝36a，∴HE ＝HG＝36a﹣13a ＝23a ，∴AG ＝GH ﹣AH ＝23a ﹣13a ＝10a ，∴13131010AH a AG a ==．【点睛】本题是圆的综合题，考查了垂径定理，圆周角定理，相似三角形的判定和性质，切线的判定，解直角三角形，勾股定理，等腰三角形的性质等知识，掌握相似三角形的判定定和性质定理及方程思想是解题的关键．10．在O 中，AB 为直径，CD 与AB 相较于点H ，弧AC=弧AD（1）如图1，求证：CD AB ⊥;（2）如图2，弧BC 上有一点E ，若弧CD=弧CE ，求证：3EBA ABD ∠=∠;（3）如图3，在（2）的条件下，点F 在上，连接,//FH FH DE ，延长FO 交DE 于点K ，若165,55FK DB BE ==，求AB ．【答案】（1）证明见解析；（2）证明见解析；（3）1855AB =．【解析】【分析】（1）连接,OC OD ,根据AC AD = 得出COA DOA ∠=再根据OC OD =得出OCD ODC ∠=∠，从而得证；（2）连接,BC BD ,根据AC AD =得出,BC BD BA CD =⊥，CBA ABD ∠=∠，再根据CE CD =,得出CBE CBD ∠=∠,从而得出结论；（3）作,CM DB CN BE ⊥⊥，过点P 作,PT BE PS BD ⊥⊥，,5BE BP a DB a ===先证CDM CEN ∆≅∆，DM EN =，再证,CMB CNB BM BN ∆≅∆=，设DM b =，得出2b a =，再算出,CM CD 得出CPD ∆为等腰三角形，再根据BP 是角平分线利用角平分线定理得出BCP EBP S DP BD S PE BE∆==，从而算出,PE DE ,再根据三角函数值算出BG ,,,,AB r OG OH ，再根据//FH DE 得出HO OF GO OK=，从而计算AB ．【详解】（1）连接OC ，CD因为AC AD=，所以COA DOA∠=∠OC OD=，,OA CD CD AB∴⊥∴⊥;(2)连接BC，,BC BD BA CD=⊥所以AB平分CBD∠，设ABD ABCα∠=∠=2CBDα∴∠=CDCE∴=2CBE CBDα∴∠=∠=，3EBAα∴∠=3EBA ABD∴∠=∠．(3) 2,90EBC BPE PEBαα︒∠=∠=∠=-设,5BE BP a DB a===作,CM DB CN BE⊥⊥，可证：CDM CEN∆≅∆，DM EN=，再证：,CMB CNB BM BN∆≅∆=设,5,2DM EN b a b a b b a==+=-∴=在CBM∆中勾股4CM a=在CDM∆中勾股25CD a=得CPD∆为等腰三角形25DP DC a==因为BP为角平分线，过点P作,PT BE PS BD⊥⊥可证：5BCPEBPS DP BDS PE BE∆===2525,53PE a DE a ∴== 14tan ,tan 223αα== 2555,32BG a AB a ∴== 557535,,4124r a OG a OH a === //FH DE97HO OF GO OK ∴== 995185,16OF KF AB ===【点睛】本题是一道圆的综合题目，难度较大，考查了圆相关的性质以及与三角形综合，掌握相关的线段与角度转化是解题关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

初中数学几何作图综合测试卷含答案
初中数学几何作图综合测试卷
一、单选题(共7道，每道14分)
1.根据下列要求作图:①作线段AB;②作射线AD;③作直线AC;
其中符合要求的是()
A. B.
C. D.
答案：A
试题难度：三颗星知识点：几何作图
2.计划把河水引到水池A中，先引AB⊥CD，垂足为B，然后沿AB开渠，能
使所开的渠道最短，这样设计的依据是（）
A.过直线外一点，有且只有一条直线与已知直线垂直
B.两点之间，线段最短
C.垂线段最短
D.两点确定一条直线
答案：C
解题思路：本题考察的是点到直线的距离，直线外一点与直线上各点连接的所有线段中，垂线段最短，简单记作：垂线段最短。

所以选C
易错点：不清楚垂线段最短和两点之间，线段最短的区别是什么。

误选B
试题难度：一颗星知识点：点到直线的距离
3.如图,为了解决A、B、C、D四个小区的缺水问题,市政府准备投资修建一个水厂P,使之到A、B、C、D四个小区的距离内之和最短,则P的位置应建在
()
A.线段AC的中点
B.线段BD的中点
C.线段AC与线段BD的交点
D.直线AB与直线CD的中点
答案：C
试题难度：三颗星知识点：两点之间线段最短
4.在直线l上任取一点A,截取AB=15cm,再截取AC=8cm,则线段BC的长为()
A.7cm
B.23cm
C.7 cm或23cm
D.7 cm或15cm
答案：C
试题难度：三颗星知识点：分类讨论
5.已知A、B、C三点在同一条直线上,M、N分别为线段AB、BC的中点,且AB=10,BC=6,则MN的长为()
A.2
B.8
C.1或8
D.2或8
答案：D
试题难度：三颗星知识点：分类讨论
6.从O点出发的三条射线OA、OB、OC,若∠AOB=70°,∠AOC为20°,则∠BOC 的度数为()
A.90°
B.50°
C.50°或45°
D.90°或50°
答案：D
试题难度：三颗星知识点：分类讨论
7.已知∠AOB=80°,∠BOC=30°,OM平分∠AOB,ON平分∠BOC,求∠MON的度数()
A.25°或55°
B.55°
C.25°
D.50°或55°
答案：A
试题难度：三颗星知识点：分类讨论。