计量经济学实验四--李子奈
李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解

李子奈《计量经济学》(第4版)笔记和课后习题(含考研真题)详解李子奈《计量经济学》(第4版)笔记和课后习题详解第1章绪论一、计量经济学1计量经济学计量经济学,又称经济计量学,是由经济理论、统计学和数学结合而成的一门经济学的分支学科,其研究内容是分析经济现象中客观存在的数量关系。
2计量经济学模型(1)模型分类模型是对现实生活现象的描述和模拟。
根据描述和模拟办法的不同,对模型进行分类,如表1-1所示。
表1-1 模型分类(2)数理经济模型和计量经济学模型的区别①研究内容不同数理经济模型的研究内容是经济现象各因素之间的理论关系,计量经济学模型的研究内容是经济现象各因素之间的定量关系。
②描述和模拟办法不同数理经济模型的描述和模拟办法主要是确定性的数学形式,计量经济学模型的描述和模拟办法主要是随机性的数学形式。
③位置和作用不同数理经济模型可用于对研究对象的初步研究,计量经济学模型可用于对研究对象的深入研究。
3计量经济学的内容体系(1)根据所应用的数理统计方法划分广义计量经济学根据所应用的数理统计方法包括回归分析方法、投入产出分析方法、时间序列分析方法等;狭义计量经济学所应用的数理统计方法主要是回归分析方法。
需要注意的是,通常所述的计量经济学指的是狭义计量经济学。
(2)根据内容深度划分初级计量经济学的主要研究内容是计量经济学的数理统计学基础知识和经典的线性单方程计量经济学模型理论与方法;中级计量经济学的主要研究内容是用矩阵描述的经典的线性单方程计量经济学模型理论与方法、经典的线性联立方程计量经济学模型理论与方法,以及传统的应用模型;高级计量经济学的主要研究内容是非经典的、现代的计量经济学模型理论、方法与应用。
(3)根据研究目标和研究重点划分理论计量经济学的主要研究目标是计量经济学的理论与方法的介绍与研究;应用计量经济学的主要研究目标是计量经济学模型的建立与应用。
理论计量经济学的研究重点是理论与方法的数学证明与推导;应用计量经济学的研究重点是建立和应用计量模型处理实际问题。
计量经济学试验完整版--李子奈

计量经济学试验——李子奈目录实验一一元线性回归 (5)一实验目的 (5)二实验要求 (5)三实验原理 (5)四预备知识 (5)五实验内容 (5)六实验步骤 (5)1.建立工作文件并录入数据 (5)2.数据的描述性统计和图形统计: (7)3.设定模型,用最小二乘法估计参数: (8)4.模型检验: (8)5.应用:回归预测: (9)实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验 (12)一实验目的: (12)二实验要求 (12)三实验原理 (12)四预备知识 (12)五实验内容 (12)六实验步骤 (13)实验三多元线性回归 (15)一实验目的 (15)三实验原理 (15)四预备知识 (15)五实验内容 (15)六实验步骤 (15)6.1 建立工作文件并录入全部数据 (15)6.2 建立二元线性回归模型 (16)6.3 结果的分析与检验 (16)6.4 参数的置信区间 (17)6.5 回归预测 (17)6.6 置信区间的预测 (19)实验四异方差性 (21)一实验目的 (21)二实验要求 (21)三实验原理 (21)四预备知识 (21)五实验内容 (21)六实验步骤 (21)6.1 建立对象: (21)6.2 用普通最小二乘法建立线性模型 (22)6.3 检验模型的异方差性 (22)6.4 异方差性的修正 (25)实验五自相关性 (29)一实验目地 (29)二实验要求 (29)三实验原理 (29)四预备知识 (29)五实验内容 (29)六实验步骤 (29)6.1 建立Workfile和对象 (30)6.2 参数估计、检验模型的自相关性 (30)6.3 使用广义最小二乘法估计模型 (34)6.4 采用差分形式作为新数据,估计模型并检验相关性 (36)实验六多元线性回归和多重共线性 (38)一实验目的 (38)二实验要求 (38)三实验原理 (38)四预备知识 (38)五实验内容 (38)六实验步骤 (38)6.1 建立工作文件并录入数据 (38)6.2 用OLS估计模型 (38)6.3 多重共线性模型的识别 (39)6.4 多重共线性模型的修正 (40)实验七分布滞后模型与自回归模型及格兰杰因果关系检验 (43)一实验目的 (43)二实验要求 (43)三实验原理 (43)四预备知识 (43)五实验内容 (43)六实验步骤 (43)6.1 建立工作文件并录入数据 (43)6.2 使用4期滞后2次多项式估计模型 (44)6.3 格兰杰因果关系检验 (46)实验八联立方程计量经济学模型 (50)一实验目的 (50)二实验要求 (50)三实验原理 (50)四预备知识 (50)五实验内容 (50)六实验步骤 (51)6.1 分析联立方程模型。
计量经济学李子奈(第3版)例题+习题数据
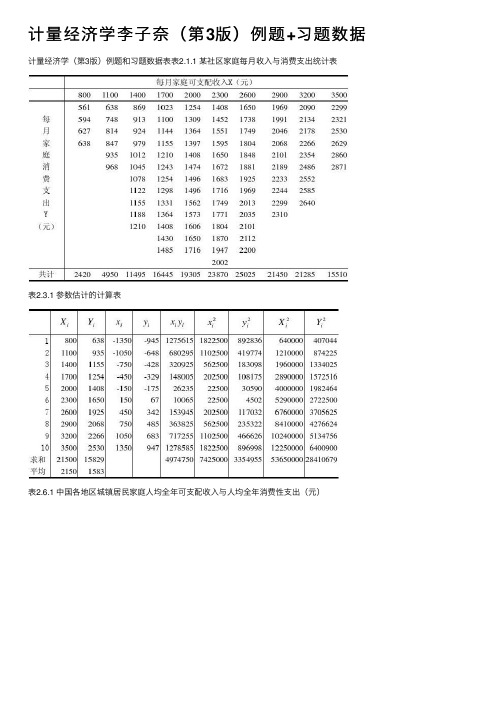
计量经济学李⼦奈(第3版)例题+习题数据计量经济学(第3版)例题和习题数据表表2.1.1 某社区家庭每⽉收⼊与消费⽀出统计表表2.3.1 参数估计的计算表表2.6.1 中国各地区城镇居民家庭⼈均全年可⽀配收⼊与⼈均全年消费性⽀出(元)资料来源:《中国统计年鉴》(2007)。
表2.6.3 中国居民总量消费⽀出与收⼊资料单位:亿元年份GDP CONS CPI TAX GDPC X Y 19783605.6 1759.1 46.21519.28 7802.5 6678.83806.7 19794092.6 2011.5 47.07537.828694.2 7551.64273.2 19804592.9 2331.2 50.62571.70 9073.7 7944.24605.5 19815008.8 2627.951.90629.899651.8 8438.05063.9 19825590.0 2902.9 52.95700.02 10557.3 9235.25482.4 19836216.2 3231.154.00775.5911510.8 10074.65983.2 19847362.7 3742.0 55.47947.35 13272.8 11565.06745.7 19859076.7 4687.460.652040.79 14966.8 11601.77729.2 198610508.5 5302.1 64.572090.37 16273.7 13036.58210.9 198712277.4 6126.1 69.302140.36 17716.3 14627.78840.0 198815388.6 7868.1 82.302390.47 18698.7 15794.09560.5 198917311.3 8812.6 97.002727.40 17847.4 15035.59085.5 199019347.8 9450.9 100.002821.86 19347.8 16525.99450.9 199122577.4 10730.6 103.422990.17 21830.9 18939.610375.8 199227565.2 13000.1 110.033296.91 25053.0 22056.511815.3 199336938.1 16412.1 126.204255.30 29269.1 25897.313004.7 199450217.4 21844.2 156.655126.88 32056.2 28783.413944.2 199563216.9 28369.7 183.416038.04 34467.5 31175.415467.9 199674163.6 33955.9 198.666909.82 37331.933853.717092.5 199781658.5 36921.5 204.218234.04 39988.5 35956.218080.6 199886531.6 39229.3 202.599262.80 42713.1 38140.919364.1 199991125.0 41920.4 199.7210682.58 45625.8 40277.020989.3 200098749.0 45854.6200.5512581.51 49238.0 42964.622863.9 2001108972.4 49213.2 201.9415301.38 53962.5 46385.424370.1 2002120350.3 52571.3 200.3217636.45 60078.0 51274.026243.2 2003136398.8 56834.4 202.7320017.31 67282.2 57408.128035.0 2004160280.4 63833.5 210.6324165.68 76096.3 64623.130306.2 2005188692.1 71217.5 214.4228778.54 88002.1 74580.433214.4 2006221170.5 80120.5 217.6534809.72 101616.3 85623.136811.2资料来源:根据《中国统计年鉴》(2001,2007)整理。
(2024年)完整版李子奈计量经济学版第四版课件

• 三阶段最小二乘法(3SLS):三阶段最小二乘法是对二阶段最小二乘法的改进。 该方法在第二阶段估计时,不仅考虑了残差作为解释变量,还考虑了其他所有 内生变量的估计值作为解释变量。这样可以进一步提高参数估计量的效率。
在社会科学领域,这些方法可用于分析人口 统计数据、经济指标等,揭示社会经济现象 背后的复杂关系。
2024/3/26
30
THANKS
感谢观看
2024/3/26
31
多重共线性的检验
相关系数矩阵法、方差膨胀因子 法、条件指数法等。
14
04
时间序列计量经济学模型
Chapter
2024/3/26
15
时间序列基本概念与性质
01
02
03
时间序列定义
按时间顺序排列的一组数 据,反映现象随时间变化 的发展过程。
2024/3/26
时间序列构成要素
现象所属的时间(年、季、 月、日等)和反映现象在 各个时间上的统计指标数 值。
28
半参数回归分析方法
部分线性模型
模型中既包含参数部分也包含非参数部分,参数部分用于描述主要 影响因素,非参数部分用于捕捉其他未知影响因素。
单指标模型
通过投影寻踪方法将高维数据降维到一维,然后利用非参数方法进 行回归分析。
变系数模型
模型系数随着某个或多个变量的变化而变化,可以灵活捕捉变量间的 动态关系。
不可识别的情况 当联立方程模型中的某个方程不能被任何其他方程所替代 时,该方程就是不可识别的。此时,无法对该方程的参数 进行一致估计。
计量经济学实验操作指导完整李子奈

计量经济学试验 (完整版)——李子奈目录实验一一元线性回归 (4)一实验目的 (4)二实验要求 (4)三实验原理 (4)四预备知识 (4)五实验内容 (4)六实验步骤 (4)1.建立工作文件并录入数据 (4)2.数据的描述性统计和图形统计: (6)3.设定模型,用最小二乘法估计参数: (6)4.模型检验: (7)5.应用:回归预测: (7)实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验9一实验目的: (9)二实验要求 (10)三实验原理 (10)四预备知识 (10)五实验内容 (10)六实验步骤 (10)实验三多元线性回归 (11)一实验目的 (11)三实验原理 (11)四预备知识 (11)五实验内容 (11)六实验步骤 (12)6.1 建立工作文件并录入全部数据 (12)6.2 建立二元线性回归模型 (12)6.3 结果的分析与检验 (12)6.4 参数的置信区间 (12)6.5 回归预测 (13)6.6 置信区间的预测 (13)实验四异方差性 (14)一实验目的 (14)二实验要求 (14)三实验原理 (14)四预备知识 (14)五实验内容 (14)六实验步骤 (14)6.1 建立对象: (14)6.2 用普通最小二乘法建立线性模型 (14)6.3 检验模型的异方差性 (14)6.4 异方差性的修正 (15)实验五自相关性 (16)一实验目地 (16)二实验要求 (16)三实验原理 (16)四预备知识 (16)五实验内容 (16)六实验步骤 (17)6.1 建立Workfile和对象 (17)6.2 参数估计、检验模型的自相关性 (17)6.3 使用广义最小二乘法估计模型 (18)6.4 采用差分形式作为新数据,估计模型并检验相关性 (19)实验六多元线性回归和多重共线性 (20)一实验目的 (20)二实验要求 (20)三实验原理 (20)四预备知识 (20)五实验内容 (20)六实验步骤 (20)6.1 建立工作文件并录入数据 (20)6.2 用OLS估计模型 (20)6.3 多重共线性模型的识别 (20)6.4 多重共线性模型的修正 (21)实验七分布滞后模型与自回归模型及格兰杰因果关系检验 (21)一实验目的 (21)二实验要求 (21)三实验原理 (21)四预备知识 (21)五实验内容 (21)六实验步骤 (22)6.1 建立工作文件并录入数据 (22)6.2 使用4期滞后2次多项式估计模型 (22)6.3 格兰杰因果关系检验 (23)实验八联立方程计量经济学模型 (24)一实验目的 (24)二实验要求 (25)三实验原理 (25)四预备知识 (25)五实验内容 (25)六实验步骤 (25)6.1 分析联立方程模型。
计量经济学实验操作指导(完整版)--李子奈

计量经济学试验(完整版)——李子奈目录实验一一元线性回归 (5)一实验目的 (5)二实验要求 (5)三实验原理 (5)四预备知识 (5)五实验内容 (5)六实验步骤 (5)1.建立工作文件并录入数据 (5)2.数据的描述性统计和图形统计: (7)3.设定模型,用最小二乘法估计参数: (8)4.模型检验: (8)5.应用:回归预测: (9)实验二可化为线性的非线性回归模型估计、受约束回归检验及参数稳定性检验 (12)一实验目的: (12)二实验要求 (12)三实验原理 (12)四预备知识 (12)五实验内容 (12)六实验步骤 (13)实验三多元线性回归 (14)一实验目的 (14)三实验原理 (15)四预备知识 (15)五实验内容 (15)六实验步骤 (15)6.1 建立工作文件并录入全部数据 (15)6.2 建立二元线性回归模型 (15)6.3 结果的分析与检验 (16)6.4 参数的置信区间 (16)6.5 回归预测 (17)6.6 置信区间的预测 (18)实验四异方差性 (20)一实验目的 (20)二实验要求 (20)三实验原理 (20)四预备知识 (20)五实验内容 (20)六实验步骤 (20)6.1 建立对象: (20)6.2 用普通最小二乘法建立线性模型 (21)6.3 检验模型的异方差性 (21)6.4 异方差性的修正 (24)实验五自相关性 (28)一实验目地 (28)二实验要求 (28)三实验原理 (28)四预备知识 (28)五实验内容 (28)六实验步骤 (28)6.1 建立Workfile和对象 (29)6.2 参数估计、检验模型的自相关性 (29)6.3 使用广义最小二乘法估计模型 (33)6.4 采用差分形式作为新数据,估计模型并检验相关性 (35)实验六多元线性回归和多重共线性 (37)一实验目的 (37)二实验要求 (37)三实验原理 (37)四预备知识 (37)五实验内容 (37)六实验步骤 (37)6.1 建立工作文件并录入数据 (38)6.2 用OLS估计模型 (38)6.3 多重共线性模型的识别 (38)6.4 多重共线性模型的修正 (39)实验七分布滞后模型与自回归模型及格兰杰因果关系检验 (41)一实验目的 (41)二实验要求 (41)三实验原理 (41)四预备知识 (41)五实验内容 (41)六实验步骤 (42)6.1 建立工作文件并录入数据 (42)6.2 使用4期滞后2次多项式估计模型 (42)6.3 格兰杰因果关系检验 (45)实验八联立方程计量经济学模型 (49)一实验目的 (49)二实验要求 (49)三实验原理 (49)四预备知识 (49)五实验内容 (49)六实验步骤 (50)6.1 分析联立方程模型。
计量经济学实验四--李子奈
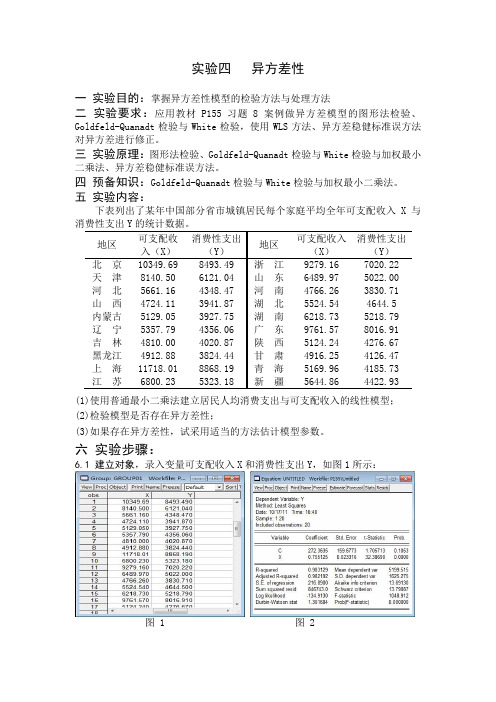
实验四异方差性一实验目的:掌握异方差性模型的检验方法与处理方法二实验要求:应用教材P155习题8案例做异方差模型的图形法检验、Goldfeld-Quanadt检验与White检验,使用WLS方法、异方差稳健标准误方法对异方差进行修正。
三实验原理:图形法检验、Goldfeld-Quanadt检验与White检验与加权最小二乘法、异方差稳健标准误方法。
四预备知识:Goldfeld-Quanadt检验与White检验与加权最小二乘法。
五实验内容:下表列出了某年中国部分省市城镇居民每个家庭平均全年可支配收入X与消费性支出Y的统计数据。
地区可支配收入(X)消费性支出(Y)地区可支配收入(X)消费性支出(Y)北京10349.69 8493.49 浙江9279.16 7020.22 天津8140.50 6121.04 山东6489.97 5022.00 河北5661.16 4348.47 河南4766.26 3830.71 山西4724.11 3941.87 湖北5524.54 4644.5 内蒙古5129.05 3927.75 湖南6218.73 5218.79 辽宁5357.79 4356.06 广东9761.57 8016.91 吉林4810.00 4020.87 陕西5124.24 4276.67 黑龙江4912.88 3824.44 甘肃4916.25 4126.47 上海11718.01 8868.19 青海5169.96 4185.73 江苏6800.23 5323.18 新疆5644.86 4422.93(1)使用普通最小二乘法建立居民人均消费支出与可支配收入的线性模型;(2)检验模型是否存在异方差性;(3)如果存在异方差性,试采用适当的方法估计模型参数。
六实验步骤:6.1 建立对象,录入变量可支配收入X和消费性支出Y,如图1所示:图 1 图 26.2 用普通最小二乘法建立线性模型设定一元线性回归模型为:01Y X ββμ∧=++ 点击主界面菜单Quick\Estimate Equation ,在弹出的对话框中输入Y 、C 、X ,点击确定即可得到回归结果,如图2所示。
李子奈《计量经济学》(第4版)配套题库-选择题考研真题精选(圣才出品)

二、选择题1.设有n 个样本观测点,这些样本观测点的样本回归函数如下:Y i =∧β0+∧β1X i +e i (其中,e i 为残差项)在满足高斯-马尔可夫假设条件时,下列说法正确的是()。
[北航2018研]A.y 的估计值为∧Y,则均值E(∧Y)=E(β0+β1X)B.ˆ0i ie Y =∑C.设ˆˆi i y Y Y =-,则ˆ0i i e y >∑D.普通最小二乘估计量∧β1服从正态分布,其方差与残差项的方差相同【答案】B【解析】满足高斯-马尔科夫条件时,∑e i =0,∑e i X i =0,所以01ˆˆˆ0i i i i i e Y e e X ββ=+=∑∑∑2.对于联立方程计量经济学模型的估计方法,下列说法错误的是()。
[北航2018研]A.间接最小二乘法适用于恰好识别的结构方程的参数估计B.二阶段最小二乘法可适用于过度识别的结构方程的参数估计C.采用二阶段最小二乘法得到结构方程的参数估计量是无偏的D.二阶段最小二乘法是一种工具变量法【答案】C 【解析】A 项,在联立方程计量经济学模型的估计中,间接最小二乘法适用于恰好识别的结构方程的参数估计;BD 两项,二阶段最小二乘法是一种工具变量法,既适用于恰好识别的结构方程的参数估计,又适用于过度识别的结构方程。
C项,采用二阶段最小二乘法得到结构方程的参数估计量在小样本下是有偏的,在大样本下是渐进无偏的。
3.用最小二乘法估计经典线性模型y i=β0+β1X i+u i,则样本回归线通过点()。
[湖南大学2017研]A.(x,y)B.(x,∧y)C.(_x,∧y)D.(_x,_y)【答案】D【解析】普通最小二乘法下的样本回归线必然经过样本均值点(_x,_y)。
4.根据20个观测值估计的结果,一元线性回归模型的D.W.=2.3,在样本容量n=20,解释变量k=1,显著性水平a=0.05时,查得d L=1,d U=1.41,则可以判断()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四异方差性
一实验目的:掌握异方差性模型的检验方法与处理方法
二实验要求:应用教材P155习题8案例做异方差模型的图形法检验、Goldfeld-Quanadt检验与White检验,使用WLS方法、异方差稳健标准误方法对异方差进行修正。
三实验原理:图形法检验、Goldfeld-Quanadt检验与White检验与加权最小二乘法、异方差稳健标准误方法。
四预备知识:Goldfeld-Quanadt检验与White检验与加权最小二乘法。
五实验内容:
下表列出了某年中国部分省市城镇居民每个家庭平均全年可支配收入X与
地区可支配收
入(X)
消费性支出
(Y)
地区
可支配收入
(X)
消费性支出
(Y)
北京10349.69 8493.49 浙江9279.16 7020.22 天津8140.50 6121.04 山东6489.97 5022.00 河北5661.16 4348.47 河南4766.26 3830.71 山西4724.11 3941.87 湖北5524.54 4644.5 内蒙古5129.05 3927.75 湖南6218.73 5218.79 辽宁5357.79 4356.06 广东9761.57 8016.91 吉林4810.00 4020.87 陕西5124.24 4276.67 黑龙江4912.88 3824.44 甘肃4916.25 4126.47 上海11718.01 8868.19 青海5169.96 4185.73 江苏6800.23 5323.18 新疆5644.86 4422.93
(1)使用普通最小二乘法建立居民人均消费支出与可支配收入的线性模型;
(2)检验模型是否存在异方差性;
(3)如果存在异方差性,试采用适当的方法估计模型参数。
六实验步骤:
6.1 建立对象,录入变量可支配收入X和消费性支出Y,如图1所示:
图 1 图 2
6.2 用普通最小二乘法建立线性模型
设定一元线性回归模型为:
01Y X ββμ∧
=++ 点击主界面菜单Quick\Estimate Equation ,在弹出的对话框中输入Y 、C 、X ,点击确定即可得到回归结果,如图2所示。
根据图2中的数据,得到模型的估计结果为
272.360.7551(1.71)(32.39)Y X ∧
=+
20.9831R = 2
0.9822R = .. 1.3017DW =
1048.912F = 846743.0RSS =
估计结果显示,即使在10%的显著性水平下,都不拒绝常数项为零的假设。
6.3 检验模型的异方差性
6.3.1 图形检验法
生成残差序列。
在得到图2结果后,在工作文件中点击Object\Generate Series …,在弹出的窗口中,在主窗口键入命令如下“e2=resid^2”,如图3所示,得到残差平方和序列e2。
图 3 图4
如果存在异方差,则只可能是由于可支配收入X 引起的。
绘制2t e 对t X 的散点图。
按住Ctrl 键,同时选择变量X 与e2,以组对象方式打开,进入数据列表,再点击View\Graph\Scatter\Simple Scatter ,可得散点图,如图4所示。
由图4可以看出,残差平方和2t e 对t X 大致存在递增关系,即存在单调增型异方差。
6.3.2 Goldfeld-Quanadt 检验
对变量取值排序(按递增或递减)。
在工作文件中点击Proc\Scrt Current Page …,在弹出对话框中输入X 即可(默认项是升序),如图5所示。
本列选择升序排列,这时变量Y 将以X 按升序排列。
图 5 图6 构造子样本区间,建立回归模型。
在本题中,样本容量n=20,删除中间1/4的观测值,大约4个数据,余下部分平分得两个样本区间:1-8和13-20,它们的样本个数均是8个,即128n n ==.在工作文件窗口中点击Sample 菜单,在弹出的对话框中输入1 8,将样本期改为1~8,如图6所示。
然后,用OLS 方法求得如图7的结果
图 7 图 8
根据图7中的数据,得到模型的估计结果为:
1277.1610.5541(0.829)
(1.779)Y X ∧=+
20.3454R = 20.2363R = .. 3.0045DW =
3.1659F = 1126528.3RSS =
同样的,在Sample 菜单中,将区间定义为13~20,再利用OLS 方法求得如图8的结果。
根据图8中的数据,得到模型的估计结果为:
212.21180.7619(0.3997)(12.625)Y X ∧
=+
20.9637R = 2
0.9577R = .. 1.723DW =
159.39F = 2615472.0RSS =
计算F统计量:
2
1
615472.0
4.86
126528.3
RSS
F
RSS
===
如果设定显著性水平为5%,那么自由度为(6,6)的F分布的临界值为
0.55
(6,6) 4.28
F=,即有
0.55
4.86 4.28(6,6)
F F
=>=,所以拒绝原假设,表明模型存在异方差性
6.3.3 White检验
由图2的估计结果中,点击View\Residual tests\white heteroskedasticity(no cross terms),进入White检验,进过估计出现White 检验的结果如图9所示。
图 9
由图9中的数据,得到
22
180998.949.428460.02115
( 1.7508)(1.708)( 1.145)
e X X
∧
=-+-
--
20.632606
R=
White统计量2200.63260612.65212
nR=⨯=,该值大于5%显著性水平下自由
度为2的2χ分布的相应临界值2
0.05
(2) 5.99
χ=,(在估计模型中含有两个解释变量,所以自由度为2)因此拒绝同方差性的原假设。
6.4 异方差性的修正
6.4.1 加权最小二乘法
运用OLS方法估计过程中,我们选用权数1/
t t
w e
=。
权数生成过程如下,在图2的情况下,在工作文件中点击Object\Generate Series…,在弹出的窗口中,在Enter equation处输入w=1/@abs(resid).
在工作文件中点击Quick\Estimate Equation,在弹出的画框中输入Y、C、X,如图10所示。
图 10 图 11 然后,在图10中点击Options 选项,选中Weighted LS/TLS 复选框,在Weight 框中输入w ,如图11所示,点击确定,即可得到加权最小二乘法的结果,如图12所示。
图 12
由图12中的数据,得到模型的估计结果:
415.66030.729026(3.55)(32.5)Y X ∧
=+
20.9999R = 2
0.9999R = .. 2.3678DW =
1056.477F = 106856.0RSS =
可以看出,常数项的t 统计量的值有了显著的改进。
下面检验是否经加权的回归的模型已不存在异方差性。
记2e ≈
为加权回归后模型的残差估计的平方和。
在图12中,点击View\Residual tests\white heteroskedasticity(no cross terms),进入White 检验,经过估计出现White 检验结果,如图13所示。
图 13
由图13中的数据,得到
22=6196.4810.1653230.0000048(0.525)(0.050)(0.023)e X X ≈-+-
20.003821R =
White 统计量20.07642nR =,其所对应的伴随概率为0.967983P =,因此在5%的显著性水平下,不能拒绝同方差的假设。
6.4.2 异方差稳健性标准误方法
在图2中,点击Estimate 按钮,出现Spection 窗口(图14),点击Option 按钮,在出现的EstimationOptions 窗口中,选择“Heteroskedasticity ”选项,并选择默认的White 选项(图15),点击按钮退回到Equation Spection 窗口(图
14),再点击OK 按钮,即得到如图16所示的结果。
图14 图 15
图 16
可以看出,估计的参数与普通最小二乘法的结果相同,只是由于参数的标准差得到了修正,从而使得t检验值与普通最小二乘法的结果不同。
