实验十四水塔流量估计建模
数学建模——水塔流量问题

数学建模——⽔塔流量问题实验⼗四⽔塔流量问题【实验⽬的】1.了解有关数据处理的基本概念和原理。
2.初步了解处理数据插值与拟合的基本⽅法,如样条插值、分段插值等。
3.学习掌握⽤MATLAB 命令处理数据插值与拟合问题。
【实验内容】某居民区有⼀供居民⽤⽔的圆形⽔塔,⼀般可以通过测量其⽔位来估计⽔的流量。
但⾯临的困难是,当⽔塔⽔位下降到设定的最低⽔位时,⽔泵⾃动启动向⽔塔供⽔,到设定的最⾼⽔位时停⽌供⽔,这段时间是⽆法测量⽔塔的⽔位和⽔泵的供⽔量。
通常⽔泵每天供⽔⼀两次,每次约两⼩时。
⽔塔是⼀个⾼⽶、直径⽶的正圆柱。
按照设计,⽔塔⽔位降到约⽶时,⽔泵⾃动启动,⽔位升到约⽶时⽔泵停⽌⼯作。
某⼀天的⽔位测量记录如表1所⽰,试估计任何时刻(包括⽔泵正供⽔时)从⽔塔流出的⽔流量,及⼀天的总⽤⽔量。
表1 ⽔位测量启⽰录(0101001111012012)(2x L )(2ξL )(ξf y )(x f n 0x 1x n x 0y 1y n y n n )(x L n )(x L n m x a 011-m x a x a m 1-m a n )(k n x L k y k n )(ξn L )(ξf )(x L n )(x f n m n )(x L n )(x f x )(x L n )(x f a 0x 1x nx b )(x P 11----i i i i y x x x x i i i i y x x x x 11----1-i x x i x i n 0x 0y 1x 1y n x n y a b )(x S k )(x S k )(x S i i y )(x S a b k n i x i y i n i x y )(x f )(x f )(x f )(11x r a )(22x r a )(x r a m m )(x r k k a k m m n k a Q∑=-ni ix f 12i)y )((10t t t t t t t t t dt3;%% ⽤差分计算t(22)和t(23)的流量S 2.8/8.>> t3=[20 t(22) t(23)];% 取第2时段20,两点和第3时段,两点>> xx3=[abs(polyval(a2,t3(1:2))),dht3]; 取第2时段20,两点和第3时段,两点的流量>> c3=polyfit(t3,xx3,3)% 拟合出第2⽔泵供⽔时段的流量函数>> tp3=::24;>> x3=polyval(c3,tp3);% 输出第2供⽔时段(外推到t=24)各时刻的流量求第1、2时段和第1、2供⽔时段流量的积分之和,就是⼀天总⽤⽔量。
估计水塔的水流量
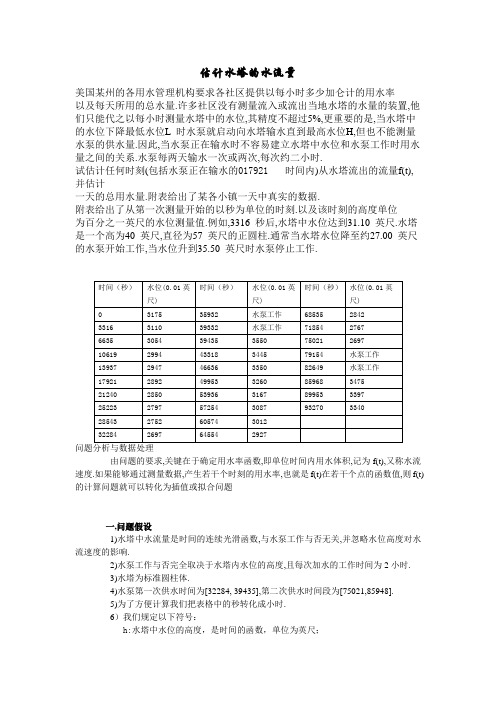
估计水塔的水流量美国某州的各用水管理机构要求各社区提供以每小时多少加仑计的用水率以及每天所用的总水量.许多社区没有测量流入或流出当地水塔的水量的装置,他们只能代之以每小时测量水塔中的水位,其精度不超过5%,更重要的是,当水塔中的水位下降最低水位L 时水泵就启动向水塔输水直到最高水位H,但也不能测量水泵的供水量.因此,当水泵正在输水时不容易建立水塔中水位和水泵工作时用水量之间的关系.水泵每两天输水一次或两次,每次约二小时.试估计任何时刻(包括水泵正在输水的017921 时间内)从水塔流出的流量f(t),并估计一天的总用水量.附表给出了某各小镇一天中真实的数据.附表给出了从第一次测量开始的以秒为单位的时刻.以及该时刻的高度单位为百分之一英尺的水位测量值.例如,3316 秒后,水塔中水位达到31.10 英尺.水塔是一个高为40 英尺,直径为57 英尺的正圆柱.通常当水塔水位降至约27.00 英尺的水泵开始工作,当水位升到35.50 英尺时水泵停止工作.问题分析与数据处理由问题的要求,关键在于确定用水率函数,即单位时间内用水体积,记为f(t),又称水流速度.如果能够通过测量数据,产生若干个时刻的用水率,也就是f(t)在若干个点的函数值,则f(t)的计算问题就可以转化为插值或拟合问题一,问题假设1)水塔中水流量是时间的连续光滑函数,与水泵工作与否无关,并忽略水位高度对水流速度的影响.2)水泵工作与否完全取决于水塔内水位的高度,且每次加水的工作时间为2小时.3)水塔为标准圆柱体.4)水泵第一次供水时间为[32284, 39435],第二次供水时间段为[75021,85948].5)为了方便计算我们把表格中的秒转化成小时.6)我们规定以下符号:h:水塔中水位的高度,是时间的函数,单位为英尺;v:水塔中水的体积,是时间的函数,单位为加仑; t:时间,单位为小时;f:模型估计的水塔水流量,是时间的函数,单位为加仑/小时p:水泵工作时的充水水流量,也是时间的函数,单位为加仑/小时。
水塔流量估计的数学建模

水塔流量估计的数学建模1. 引言水塔是现代城市供水系统中至关重要的组成部分,其作用是通过储存水源来保障城市居民日常用水,并且在有紧急情况时提供应急用水。
为了更好地保障全社会的用水需求,并降低供水系统建设和运营成本,对水塔的流量进行准确的估计和预测具有重要意义。
本文将探讨如何利用数学建模的方法对水塔流量进行估计和预测。
2. 水塔流量的影响因素水塔流量的大小受到多种因素的影响,主要包括以下几个方面:2.1 水塔容积水塔的容积越大,其流量也就越大。
因此,在进行水塔流量估计时,首先需要考虑其容积。
2.2 外部水压水塔的流量受到外部水压的影响。
如果外部水压较大,则水塔的流量也将较大。
2.3 水泵功率水泵功率的大小直接影响到水塔的流量大小。
水泵功率越大,水塔的流量也就越大。
2.4 关阀状态水塔流量还受到管道关阀状态的影响。
如果关阀状态较大,则水塔流量也将减小。
3. 水塔流量的数学建模方法水塔流量的数学建模方法主要包括以下几个步骤:3.1 收集数据收集水塔流量的相关数据,并对其进行初步的整理和分析。
3.2 设计建模方程根据已收集到的数据,设计合适的建模方程。
建模方程需要考虑到水塔容积、外部水压、水泵功率、关阀状态等多种因素。
3.3 参数估计利用已有的数据对建模方程中的参数进行估计。
参数估计是非常重要的一步,其准确性直接影响到模型的准确性和可靠性。
3.4 模型检验和优化使用已有的数据来对所建立的模型进行检验和优化。
检验过程中需要对模型的精度、准确性、鲁棒性等进行评估,如果出现问题,需要进行适当的调整。
4. 案例分析为了说明水塔流量估计的数学建模方法,我们以某市几座水塔为例进行分析。
4.1 收集数据在该市的几座水塔中,我们选取了其中一座水塔进行了数据的收集,主要包括该水塔的容积、水泵功率、外部水压等基本信息。
4.2 设计建模方程根据收集到的数据,我们设计了一个基础的建模方程,其中各项参数分别为:Q为流量,V为水塔容积,P为外部水压,H为水泵的扬程,K为关阀系数。
水塔水流量的估计

水塔水流量的估计一.实验问题某居民区有一供居民用水的圆柱形水塔,一般可以通过测量其水位来估计水的流量。
但面临的困难是,当水塔水位下降到设定的最低水位时,水泵自动启动向水塔供水,到设定的最高水位时停止供水,这段时间无法测量水塔的水位和水泵的供水量。
通常水泵每天供水一次,每次约2h。
水塔是一个高为12.2m,直径为17.4m的正圆柱。
按照设计,水塔水位降至约8.2m时,水泵自动启动,水位升到约10.8m时水泵停止工作。
表1是某一天的水位测量纪录(符号“//”表示水泵启动),试估计任何时刻(包括水泵正供水时)从水塔流出的水流量,及一天的总用水量。
表1 水位测量纪录二.问题分析根据以上数据的形式和以往经验,适合采用线性拟合的方式进行数据处理。
对第1、2、3未供水时段可直接进行用五次多项式进行拟合。
对第1、2供水时段分别在两端各取两个点用前后时刻的流速拟合得到。
结果可以用分段函数表示分为5段,分别是第一未供水时段,第一供水时段,第二未供水时段,第二供水时段,第三未供水时段。
得出流速之后再乘以水塔横截面积即得任何时刻与水塔流出水流量的关系,即流速与时间的关系。
对流速进行分段积分并求和,即得一天的总水流量。
三.程序的设计与求解方法1.数据的单位转换水塔的横截面积为A=(17.4)^2*pi/4=237.0661(平方米)。
2.拟合水位——时间函数(1)对第1未供水时段的数据进行拟合。
t=[0 0.92 1.84 2.90 3.87 4.98 5.90 7.00 7.93 8.97 10.95 12.03 12.95 13.88 14.98 15.90 16.83 17.93 19.04 19.96 20.84 23.88 24.99 25.91]h=[ 9.68 9.48 9.31 9.13 8.98 8.81 8.69 8.52 8.39 8.22 10.82 10.50 10.21 9.94 9.65 9.41 9.18 8.92 8.66 8.43 8.22 10.59 10.35 10.18] f1=polyfit(t(1:10),h(1:10),5); tm1=0:0.1:9.0; y1=polyval(f1,tm1); plot(tm1,y1)01234567898.28.48.68.899.29.49.69.8(2)对第2未供水时段的数据进行拟合。
【精品】水塔水流量的估计建模问题

水塔水流量的估计
美国某州的各用水管理机构要求各社区提供以每小时多少加仑计的用水率以及每天所用的总水量.许多社区没有测量流入或流出水塔的水量装置,他们只能代之以每小时测量水塔中的水位,其误差不超过5%。
更重要的是,当水塔中的水位下降到最低水位L时水泵就启动向水塔输水直到最高水位H,期间不能测量水泵的供水量。
因此,当水泵正在输水时不容易建立水塔中水位和用水量之间的关系。
水泵每天输水一次或两次,每次约二小时.
试估计任何时刻(包括水泵正在输水时间)从水塔流出的水流量f(t),并估计一天的总用水量。
已知该水塔是一个高为40英尺(ft),直径为57英尺(ft)的正圆柱,表12。
1给出了某个小镇一天水塔水位的真实数据,水位降至约27.00ft水泵开始工作,水位升到35。
50ft停止工作。
(注:1英尺(ft)=0.3024米(m))
表12-1某小镇某天水塔水位。
MATLAB数学建模估计水塔的水流量问题Word版

估计水塔的水流量自动化12K2 许杨旸摘要:在估计某地区的用水速度和日总用水量的时候,在已知某时间t下的水位h,以及水塔直径,求出t时刻的水体积,由于没有具体函数,故用差商方法近似求出水体积对时间t的导数即用水速度,再利用三样条插值方法求出不同时刻的用水速度。
最终,通过数值积分方法求出日用水总量I。
符号及含义:t:时刻;h:水位高度;D:水塔直径;V:水体积;dV:水流速度;I:日用水总量。
一、提出问题某地区用水管理机构需要对居民的用水速度(单位时间的用水量)和日总用水量进行估计。
现有一居民区,其自来水是由一个圆柱形水塔提供,水塔高12.2m,塔的直径为17.4m。
水塔是由水泵根据水塔中的水位自动加水,一般水泵每天工作两次,按照设计,当水塔中的水位降至最低水位,约8.2m时,水泵自动启动加水;当水位升高到最高水位,约10.8m时,水泵停止工作。
表2给出的是某一天的测量数据,测量了28个时刻的数据,但由于水泵正向水塔供水,有三个时刻无法测到水位(表中用—表示),试建立数学模型,来估计居民的用水速度和日用水量。
表2 水塔中水位原始数据二、求解问题1、水塔中的水体积计算求解的问题的关键是求解出用水的速度,即单位时间内的用水体积,由于水塔可以近似成圆柱体,所以水塔的体积V可近似成:V=π4D2ℎ式中D为水塔直径D=17.4m,h为水位高度。
其中,在三个无法得到水位的时刻,其水位高度用一个负数表示,即该时刻水位为负值,显然现实当中无法出现这样的情况,现在我们用-1表示其水位。
现在开始计算水塔的体积:输入t=[0 0.921 1.843 2.949 3.871 4.978 5.900 ...7.006 7.928 8.967 9.981 10.925 10.954 12.032 ...12.954 13.875 14.982 15.903 16.826 17.931 19.037 ...19.959 20.839 22.015 22.958 23.880 24.986 25.908];h=[9.677 9.479 9.308 9.125 8.982 8.814 8.686 ...8.525 8.388 8.220 -1 -1 10.820 10.500 ...10.210 9.936 9.653 9.409 9.180 8.921 8.662 ...8.433 8.220 -1 10.820 10.591 10.354 10.180];D=17.4;V=pi/4*D^2*h;最终求得V= [2.3011 2.2540 2.2133 2.16982.1358 2.0959 2.0654 2.0271 1.9946 1.9546-0.2378 -0.2378 2.5729 2.4968 2.42782.3627 2.2954 2.2373 2.1829 2.1213 2.0597 2.0053 1.9546 -0.2378 2.5729 2.5184 2.4620 2.4207]。
数学建模估计水塔的流量用数学软件求解拟合问题

算法设计与编程
1. 拟合第1、2时段的水位,并导出流量
2. 拟合供水时段的流量
3. 估计一天总用水量
4. 流量及总用水量的检验
1. 拟合第1时段的水位,并导出流量 设t,h为已输入的时刻和水位测量记录(水泵启动的4个时刻不输入),第1时段各 时刻的流量可如下得: 1) c1=polyfit(t(1:10),h(1:10),3); %用3次多项式拟合第1时段水位,c1输出3次多项式的系数 2)a1=polyder(c1); % a1输出多项式(系数为c1)导数的系数
m 3 103 L
MATLAB(llgjz)
4. 流量及总用水量的检验
计算出的各时刻的流量可用水位记录的数值微分来检验.用水量y1可用第1时段水位测 量记录中下降高度968-822=146来检验,类似地,y2用1082-822=260检验. 供水时段流量的一种检验方法如下:供水时段的用水量加上水位上升值 260是该时段泵入 的水量,除以时段长度得到水泵的功率(单位时间泵入的水量),而两个供水时段水泵的 功率应大致相等.第1、2时段水泵的功率可计算如下: p1=(y12+260)/2; %第1供水时段水泵的功率 (水量仍以高度计) tp4=20.8:0.1:23; xp2=polyval(c3,tp4); % xp2输出第2供水时段 各时刻的流量 p2=(0.1*trapz(xp2)+260)/2.2; %第2供水时段水泵的功率 (水量仍以高度计) 计算结果:p1=154.5 ,p2=140.1
用非线性最小二乘拟合c(t)-用lsqcurvefit
1. 用M文件curvefun3.m定义函数
function f=curvefun3(x,tdata) d=300 f=(x(1)\d)*exp(-x(2)*tdata) % x(1)=v; x(2)=k
水塔流量估计的数学建模

水塔流量估计的数学建模水塔是城市供水系统中的重要组成部分,它们储存着大量的水资源,为城市居民提供生活用水。
在城市供水系统中,水塔的流量是一个非常重要的参数,它直接影响着供水系统的运行效率和水资源的利用率。
因此,如何准确地估计水塔的流量是一个非常重要的问题。
水塔的流量估计可以通过数学建模来实现。
首先,我们需要了解水塔的基本结构和工作原理。
水塔通常由水箱、进水管、出水管、溢流管等组成。
当水箱内的水位下降时,进水管会自动打开,将外部的水源引入水箱中,同时出水管会自动关闭,防止水箱内的水流失。
当水箱内的水位上升到一定高度时,溢流管会自动打开,将多余的水流出水箱,以保持水箱内的水位稳定。
在水塔的运行过程中,我们可以通过测量进水管和出水管的水流速度来估计水塔的流量。
根据流量的定义,流量等于单位时间内通过某一截面的液体体积。
因此,我们可以通过测量进水管和出水管的截面积和水流速度来计算水塔的流量。
具体地,假设进水管的截面积为A1,出水管的截面积为A2,进水管的水流速度为v1,出水管的水流速度为v2,则水塔的流量Q可以表示为:Q = A1v1 - A2v2其中,A1v1表示进水管的流量,A2v2表示出水管的流量。
由于进水管和出水管的截面积和水流速度可能会随着时间的变化而发生变化,因此我们需要不断地对它们进行测量和调整,以保证水塔的流量估计的准确性。
除了测量进水管和出水管的水流速度外,我们还可以通过其他的方法来估计水塔的流量。
例如,我们可以通过测量水塔内部的水位变化来估计水塔的流量。
具体地,我们可以安装水位传感器在水塔内部,通过测量水位的变化来计算水塔的流量。
这种方法的优点是不需要对进水管和出水管进行测量,但是需要安装水位传感器,成本较高。
水塔流量估计的数学建模是一个非常重要的问题。
通过测量进水管和出水管的水流速度或者测量水塔内部的水位变化,我们可以准确地估计水塔的流量,从而保证城市供水系统的正常运行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
H L
二、问题分析
流量是单位时间内流出水的体积.由于水塔是正圆柱形,截面 面积是常数, 所以,流量很容易根据水位相对时间的变化率算出。 水泵不工作时段的用水量可以由测量记录直接得到: 由表1中 记录的水位下降高度乘以水塔的截面面积就是这一时段的用水量. 这个数值可以用来检验数据插值或拟合结果的准确性。 问题的难点在于:如何估计水泵供水时段的流量。 水泵供水时段的流量只能靠供水 时段前后的流量经插值或拟合得到. 而作为用于插值或拟合的原始数据, 我们希望水泵不工作时段的流量数 据越准确越好. L
数值实验: 下表给出的是21个数据点(x, y), 尝试用MATLAB数学 软件的相关命令进行数据拟合、数据插值实验.
x y x y x y 0 9.01 7 11.18 14 9.15 1 2 3 4 8.95 7.96 7.96 8.02 8 9 10 11 12.26 13.28 13.32 12.61 15 16 17 18 7.90 7.95 8.86 9.81 5 9.05 12 11.29 19 10.80 6 10.13 13 10.22 20 10.93
v( x 0 ) = (3 y 0 − 4 y1 + y 2 ) /( x 2 − x 0 )
v ( x n ) = ( − 3 y n + 4 y n −1 − y n − 2 ) /( x n − x n − 2 )
经过计算,得到时间与流速之间的关系数据表3 表 3
时间(h) 0 0.46 1.38 2.395 3.41 4.425 5.44 6.45 7.465 8.45 8.97 9.98 10.93 10.95 11.49 流速(cm/h) 29.89 21.74 18.48 16.22 16.30 15.32 13.04 15.45 13.98 16.35 19.29 水泵开动 水泵开动 33.50 29.63 时间(h) 12.49 13.42 14.43 15.44 16.37 17.38 18.49 19.50 20.40 20.84 22.02 22.96 23.88 24.43 25.45 25.91 流速(cm/h) 31.52 29.03 26.36 26.09 24.73 23.64 23.42 25.00 23.86 22.17 水泵开动 水泵开动 27.09 21.62 18.48 13.30
2 (4) 水塔截面面积为 (57 × 0.3048) × π = 237.8 平方米。 4
3.2 流量估计方法
由表2给出的数据,用MTALAB软件做出时间—水位散点图1:
11 10.5 10 9.5 9 8.5 8 0 5 10 15 20 25 30
为了计算水箱水流量与时间的关系,最简单的方法就是: 根据给出的散点数据图,将数据分为三段,然后对每一 段数据用数据插值或者数据拟合的方法得到流量与时间的近 似函数关系。
实验十四
水塔水流量的估计
实验十四
实验目的:
水塔水流量的估计
1. 掌握四种经典的插值方法:拉格朗日插值法、牛顿 插值法、分段插值法、三次样条插值法。 2. 学会用MATLAB软件进行数据插值计算. 3. 学会用数据插值、数据拟合方法建立数学模型并求解.
实验内容:
1. 数据插值、数据拟合理论方法. 2. 熟悉使用MATLAB软件进行数据插值,数据拟合. 3. 简单的数据建模实验:水塔水流量的估计.
H
二、问题分析
流量大体上可由两种方法计算: (1) 直接对表1中的用水量用数值插值方法算出各时段的流量, 用它们拟合其它时刻或连续时间的流量; (2)先用表中数据拟合水位--时间函数,求导数即可得到连续 时间的流量. 有了任何时刻的流量,就不难计算一天的总用水量.
H L
三、问题求解
为了表示方便, 将所给表1中的数据全部化为国际标准单位, 时间用小时(h),高度用米(m). 表2 一天内水塔水位记录
数据表3对应的时间--流速散点图如下: 图2 35 30 25 20 15 10 0 5 10 15 20 25 30
11 10.5 10 9.5 9 8.5 8 0
5
10
15点图如下: 图2 35 30 25 20 15 0 5 10 15 20 25 30 (1) 数据插值法 采用拉格朗日、分段线性和三次样条三种数据插值方法。 根据表3的数据,对水泵不工作时段1,2通过采取数据插值 方法可以得到任意时刻的流速,从而知道任意时刻的流量. 对于水泵工作时段1,应用前后时期的流速进行插值。 由于最后水泵工作时段2的数据太少,我们将它与水泵不工 作时段2合并,一同进行数据插值处理(简称混合时段) 10
3.1 模型假设
(1) 流量只取决于水位差,与水位本身无关. (2) Torricelli定律:从小孔流出液体的流速正比于液面高度 的平方根。 在假设出口的水位为零的前提下,题目给出水塔的最低和最 高水位分别是8.1648m(27×0.3024) 和 10.7352m(35.50×0.3024). 因为: sqrt(10.7352/8.1648)=1.1467≈1 所以,可忽略水位对流速的影响。 (3) 流量可以看作是时间的连续函数。因此,为了计算简单, 不妨将流量定义成单位时间流出水的高度,即水位对时间变化率 的绝对值。
以第 1 未供水时段数据为例分别用三种方法算出流量函数和用水 量(用水高度)。 t=[0,0.46,1.38,2.395,3.41,4.425,5.44,6.45,7.465,8.45,8.97]; v=[29.89,21.74,18.48,16.22,16.30,15.32,13.04,15.45,13.98,16.35,19.27]; t0=0:0.1:8.97; lglr=lglrcz(t,v,t0); lglrjf=0.1*trapz(lglr) fdxx=interp1(t,v,t0); fdxxjf=0.1*trapz(fdxx) scyt=interp1(t,v,t0,'spline'); sancytjf=0.1*trapz(scyt) plot(t,v,'*',t0,lglr,'r',t0,fdxx,'g',t0,scyt,'b') gtext('lglr') gtext('fdxx') gtext('scyt')
水塔水流量的估计
一. 实验问题
某一地区的用水管理机构要求各社区提供每小时以加仑计的 用水量以及每天所用水的总量。由于许多社区没有测量流入或流 出水塔的水量装置,所以他们只能通过测量水塔每小时的水位高 度来代替每小时的用水量(误差不超过0.05)。当水塔中的水位下降 到最低水位L (27.00ft)时水泵就自动启动向水塔输水, 当水塔水位 达到限定最高水位H (35.00ft)时,水泵停止供水。水泵供水期间 无法测量水泵的供水量。水泵每天输水一次或两次,每次约二小时。
时间(h) 0 0.92 1.84 2.95 3.87 4.98 5.90 7.00 7.93 8.97 9.98 10.93 10.95 12.03 水位(m) 时间(h) 9.68 12.95 9.45 13.88 9.31 14.98 9.13 15.90 8.98 16.83 8.81 17.93 8.69 19.04 8.52 19.96 8.39 20.84 8.22 22.02 水泵开动 22.96 水泵开动 23.88 10.82 24.99 10.50 25.91 水位(m) 10.21 9.94 9.65 9.41 9.18 8.92 8.66 8.43 8.22 水泵开动 水泵开动 10.59 10.35 10.18
H L
已知某一小镇的水塔是一高为40ft,直径为57ft的正圆柱,下 表记录的是某一天水塔水位的真实数据(1ft=0.3024米(m))。 试估计任何时刻(包括水泵正在输水时间)从水塔流出的水流量 和一天的用水总量 表1 已记录的水位高度
时间/s 水位/0.01ft 0 3175 3316 3110 6635 3054 10619 2994 13937 2947 17921 2892 21240 2850 25223 2795 28543 2752 32284 2697 35932 水泵开动 39332 水泵开动 39435 3550 43318 3445 时间/s 46636 49953 53936 57254 60574 64554 68535 71854 75021 79254 82649 85968 89953 93270 水位/0.01ft 3350 3260 3167 3087 3012 2927 2842 2767 2697 水泵开动 水泵开动 3475 3397 3340
回顾:
数据插值方法:拉格朗日插值法、牛顿插值法 如何用MATLAB软件进行数据插值、数据拟合计算
讲解:
简单的数据建模实验:水塔水流量的估计.
基本理论方法回顾:
x
x0
y0
x1
y1
x2
y2
L
L
xn
yn
y
多项式插值:满足条件 Pn ( x i ) = y i , i = 0 ,1, 2 , L , n
MATLAB软件实现数据插值
yb=interp1(x,y,xb,'method') zb=interp2(x,y,z,xb,yb,'method') vb=interp3(x,y,z,v,xb,yb,zb,'method') yb=spline(x,y,xb) yb=interp1(x,y,xb,'cubic')
2 n
的n次多项式 Pn ( x ) = a 0 + a1 x + a 2 x + L + a n x 唯一存在。 方法: 拉格朗日插值多项式,牛顿插值多项式 数据拟合: 选定基函数 寻找待定参数 充分小。
