算法设计与分析第2讲 渐进性
算法设计与分析王晓东

习题2-1 求下列函数的渐进表达式:3n^2+10n; n^2/10+2n; 21+1/n; logn^3; 10 log3^n 。
解答:3n^2+10n=O(n^2),n^2/10+2^n=O(2^n),21+1/n=O(1),logn^3=O(logn),10log3^n=O(n).习题2-3 照渐进阶从低到高的顺序排列以下表达式:n!,4n^2,logn,3^n,20n,2,n^2/3。
解答:照渐进阶从高到低的顺序为:n!、3^n、4n^2 、20n、n^2/3、logn、2习题2-4(1)假设某算法在输入规模为n时的计算时间为T(n)=3*2^n。
在某台计算机上实现并完成该算法的时间为t秒。
现有另外一台计算机,其运行速度为第一台计算机的64倍,那么在这台新机器上用同一算法在t秒内能解输入规模为多大的问题?(2)若上述算法的计算时间改进为T(n)=n^2,其余条件不变,则在新机器上用t秒时间能解输入规模多大的问题?(3)若上述算法的计算时间进一步改进为,其余条件不变,那么在新机器上用t秒时间能解输入规模多大的问题?解答:(1)设能解输入规模为n1的问题,则t=3*2^n=3*2^n/64,解得n1=n+6(2)n1^2=64n^2得到n1=8n(3)由于T(n)=常数,因此算法可解任意规模的问题。
习题2-5 XYZ公司宣称他们最新研制的微处理器运行速度为其竞争对手ABC公司同类产品的100倍。
对于计算复杂性分别为n,n^2,n^3和n!的各算法,若用ABC公司的计算机能在1小时内能解输入规模为n的问题,那么用XYZ公司的计算机在1小时内分别能解输入规模为多大的问题?解答:n'=100nn'^2=100n^2得到n'=10nn'^3=100n^3得到n'=4.64nn'!=100n!得到n'<n+log100=n+6.64习题2-6对于下列各组函数f(n)和g(n),确定f(n)=O(g(n))或f(n)=Ω(g(n))或f(n)=θ(g(n)),并简述理由。
算法分析与设计第章习题答案

算法分析与设计第章习题答案第一章习题(1-1,1-2,1-3,1-6)1-1 求下列函数的渐进表达式3n2+10n = O(n2)n2/10+2n = O(2n)21+1/n = O(1)logn3 = O(logn)10log3n = O(n)知识点:如果存在正的常数C和自然数N0,使得:当N>=N0时有f(N)<=Cg(N),则称f(N)当N充分大时上有界,且g(N)是它的一个上界,记为f(N)=O(g(N)).这时,可以说f(N)的阶不高于g(N)的阶。
1-2 论O(1)和O(2)的区别O(1)和O(2)差别仅在于其中的常数因子,根据渐进上界记号O的定义可知,O(1)=O(2)。
1-3 从低到高排列以下表达式(按渐进阶排列以下表达式)结果:2 logn n2/320n 4n23n n! 分析:当n>=1时,有logn< n2/3当n>=7时,有3n < n!补充:当n>=4时,有logn> n1/31-6 对于下列各组函数f(n)和g(n),确定f(n)=O(g(n))或f(n)=Ω(g(n))或f(n)=Θ(g(n))。
知识点:f(n)的阶不高于g(n)的阶:f(n)=O(g(n));f(n)的阶不低于g(n)的阶:f(n)=Ω(g(n));f(n)与g(n) 同阶:f(n)=Θ(g(n)) (1)f(n)= logn2 ; g(n)= logn+5f(n)与g(n)同阶,故f(n)=Θ(g(n)) (2) f(n)= logn2 ; g(n)= n1/2当n>=8时,f(n)<=g(n),故f(n)=O(g(n))分析:此类题目不易直接看出阶的高低,可用几个数字代入观察结果。
如依次用n=1, 21, 22, 23, 26, 28, 210 (3) f(n)= n ; g(n)= log2n f(n)=Ω(g(n))(4) f(n)= nlogn+n; g(n)= lognf(n)=Ω(g(n))(5) f(n)= 10 ; g(n)= log10f(n)=Θ(g(n))(6) f(n)= log2n ; g(n)= lognf(n)=Ω(g(n))(7) f(n)= 2n ; g(n)= 100 n2f(n)=Ω(g(n))(8) f(n)= 2n ; g(n)= 3nf(n)=O(g(n))。
算法的渐进复杂度分析

算法优化可以降低算法的渐进复杂度, 从而提高算法的效率。常见的算法优化 方法包括选择更高效的算法、减少重复 计算、使用更有效的数据结构等。
算法优化可以减少算法在处理大规模数据时 的计算量和时间复杂度,从而提高算法的实 用性。
算法优化可以改进算法的并行性和 分布式计算能力,从而更好地利用 多核处理器和分布式计算资源,提 高算法的执行效率。
在游戏开发中的算法选择与渐进复杂度分析
要点一
总结词
要点二
详细描述
游戏开发中,算法的渐进复杂度分析有助于优化游戏性能 和提升用户体验。
游戏开发中,算法的选择直接影响到游戏的运行效率和性 能表现。渐进复杂度分析可以帮助我们评估不同算法在游 戏中的性能表现,从而选择适合的算法来优化游戏性能。 例如,对于游戏物理引擎,可以使用碰撞检测和碰撞响应 算法来提高游戏交互性和真实性;对于游戏渲染,可以采 用光线追踪和阴影渲染等技术来提升画面质量和用户体验 。
渐进复杂度分析可以用于比较不同算 法的性能,为实际应用中选择合适的 算法提供依据。
促进学科发展
渐进复杂度分析是计算科学领域的重 要研究方向之一,对算法设计和分析 理论的发展具有重要意义。
未来研究方向与挑战
探索更复杂的算法模型
随着计算科学的发展,越来越多的复杂算法涌现出来,需 要发展更精确、更复杂的渐进复杂度分析方法来评估这些 算法的性能。
THANKS.
渐进复杂度通常用大O表示法来表示 ,例如O(n)、O(n^2)、O(log n)等, 其中n表示输入规模。
为什么关心算法的渐进复杂度
01
算法的效率是衡量算法好坏的重 要标准之一,而渐进复杂度是评 估算法效率的重要指标。
02
通过分析算法的渐进复杂度,可 以了解算法在不同规模输入下的 性能表现,从而在实际应用中选 择合适的算法。
算法设计与分析-第2章-算法分析基础PPT课件

2k
1 5(
n 2k 1
)2
L 2×5´( 2n)2
5n2
T (n)
7n
k 1 5
i0
n 2i
2
7n
5n2 (2
2
1
k 1
)
10 n2 3n 10 n2 O (n2 )
• 例: Merge-sort排序算法的复杂性递归方程为
T(n)=(1)
if n=1
T(n)=2T(n/2)+(n) if n>1
T(n) = ?
.
27
2.5 递归算法的分析
三、递推关系式的求解-- 扩展递归技术
步骤: 循环地展开递推关系式, 把递推关系式转化为求和表达式, 然后可使用求和技术解之。
能解决输入规模为多大的问题?
设在新机器上用 t 秒时间能解决输入规模为 N 的问题,则
由于此时
f (N)
N,2 新机器的运行速度/每语句为: t新
t0 , 64
代入关系式
f (N ) *t新 t ,得
N2
*
t0 64
t
n2
* t0
解,得
N 8n
思考:以上说明了什么问题?
.
14
2.2 算法的渐进分析
.
28
2.5 递归算法的分析
求以下递推式的时间复杂性
7
T (n)
2T (n
2)
5n2
解:设 n=2k
T (n) 2T (n 2) 5n2
n1 n>1
2(2T (n 4)( n 4)2 ) 5(n 2)2 ) 5n2
2k T (1)
间就一个常因子范围内而言是相同的。
算法分析——算法的渐进效率分析
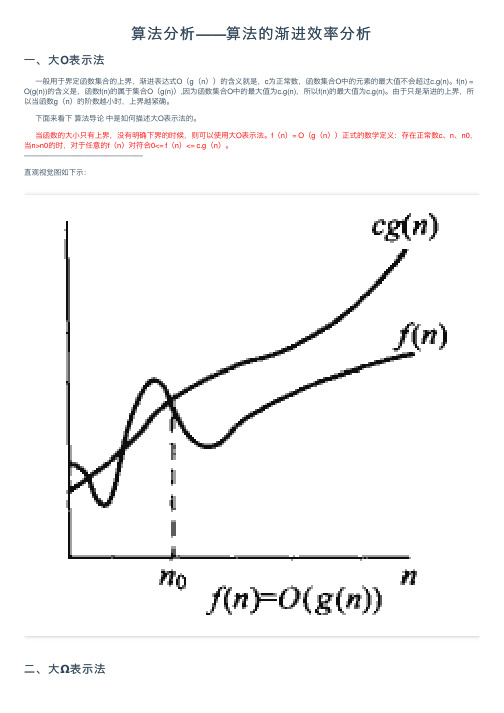
算法分析——算法的渐进效率分析⼀、⼤O表⽰法⼀般⽤于界定函数集合的上界,渐进表达式O(g(n))的含义就是,c为正常数,函数集合O中的元素的最⼤值不会超过c.g(n)。
f(n) = O(g(n))的含义是,函数f(n)的属于集合O(g(n)),因为函数集合O中的最⼤值为c.g(n),所以f(n)的最⼤值为c.g(n)。
由于只是渐进的上界,所以当函数g(n)的阶数越⼩时,上界越紧确。
下⾯来看下算法导论中是如何描述⼤O表⽰法的。
当函数的⼤⼩只有上界,没有明确下界的时候,则可以使⽤⼤O表⽰法。
f(n)= O(g(n))正式的数学定义:存在正常数c、n、n0,当n>n0的时,对于任意的f(n)对符合0<= f(n)<= c.g(n)。
————————————————直观视觉图如下⽰:⼆、⼤Ω表⽰法⼀般⽤于界定函数集合的下界,渐进表达式Ω(g(n))的含义就是,函数集合Ω中的元素的最⼩值不会低于c.g(n)。
f(n) = Ω(g(n))的含义是,函数f(n)的属于集合Ω(g(n)),因为函数集合Ω中的最⼩值为c.g(n),所以f(n)的最⼩值为c.g(n)。
算法导论中是如何描述⼤Ω表⽰法的。
当函数的⼤⼩只有下界,没有明确的上界的时候,可以使⽤⼤Ω表⽰法。
f(n)= Ω(g(n))正式的数学定义:存在正常数c、n、n0,当n>n0的时,对于任意的f(n)对符合0<= c.g(n)<= f(n)。
直观视觉图如下所⽰:三、⼤θ表⽰法⽤于界定函数的渐进上界和渐进下界。
当f(n)= θ(g(n))的时候,代表着g(n)为f(n)的渐进紧确界。
⽽θ渐进描述符在所有的渐进描述符中是最严格的⼀个,因为它既描述了函数的上界,有描述了函数的下界。
算法导论中是如何描述⼤θ表⽰法的。
f(n)= θ(c.g(n))正式的数学定义:存在正常数c1、c2、n、n0,当n>n0的时,对于任意的f(n)对符合c1.g(n)<= f(n)<= c2.g(n),c1.g(n)、c2.g(n)都是渐进正函数(当n趋于⽆穷⼤的时候,f(n)为正)。
智慧树知道网课《算法分析与设计(山东联盟)》课后章节测试满分答案1

第一章测试1【判断题】(10分)一个问题的同一实例可以有不同的表示形式A.错B.对2【判断题】(10分)同一数学模型使用不同的数据结构会有不同的算法,有效性有很大差别。
A.错B.对3【判断题】(10分)问题的两个要素是输入和实例。
A.对B.错4【单选题】(10分)算法与程序的区别是()A.有穷性B.确定性C.输出D.输入5【单选题】(10分)解决问题的基本步骤是()。
(1)算法设计(2)算法实现(3)数学建模(4)算法分析(5)正确性证明A.(3)(1)(5)(4)(2)B.(3)(4)(1)(5)(2)C.(1)(2)(3)(4)(5)D.(3)(1)(4)(5)(2)6【单选题】(10分)下面说法关于算法与问题的说法的是()。
A.算法是一种计算方法,对问题的每个实例计算都能得到正确答案。
B.证明算法不正确,需要证明对任意实例算法都不能正确处理。
C.如果一个算法能应用于问题的任意实例,并保证得到正确解答,称这个算法解答了该问题。
D.同一问题可能有几种不同的算法,解题思路和解题速度也会显著不同。
7【多选题】(10分)下面关于程序和算法的说法正确的是()。
A.算法的每一步骤必须要有确切的含义,必须是清楚的、无二义的。
B.程序总是在有穷步的运算后终止。
C.程序是算法用某种程序设计语言的具体实现。
D.算法是一个过程,计算机每次求解是针对问题的一个实例求解。
8【多选题】(10分)最大独立集问题和()问题等价。
A.最大团B.稳定匹配问题C.区间调度问题D.最小顶点覆盖9【多选题】(10分)给定两张喜欢列表,稳定匹配问题的输出是()。
A.完美匹配B.最大匹配C.稳定匹配D.没有不稳定配对10【单选题】(10分)问题变换的目的有()。
(1)复杂变简单(2)未知变已知(3)隐式变显式(4)难解变易解(5)以上都是。
A.(5)B.(1)C.(2)D.(3)E.(4)11【单选题】(10分)按照霍纳法则,计算p(x)=a n x n+a n-1x n-1+…+a1x1+a0的数量级为____。
算法设计与分析(精品课件)

xn个
n=4, m=7 可行解 <1, 2, 3, 1>
序列 1 0 1 1 0 1 1 1 0 1
13
蛮力算法的效率
序列个数是输入规模的指数函数
C(m n 1, m) (m n 1)!
m!(n 1)!
((1 )mn1 )
有没有更好的算法?
14
小结
问题求解的关键 • 建模:对输入参数和解给出形式化
本周教学内容
算法课程主要内容及有关概念 .
算法研究内容
算法的有关概念
计算复杂性理论: 货郎问题 背包问题
双机调度问题
问题复杂度概念: 排序问题
算法设计与分析: 调度问题 投资问题
算 几类重要函数的性质
法
的
有关函数渐近的界
伪
的定理
码
表 示
时间复杂度函数的表 示:函数渐近的界
算法及其时间复杂度的定义
2
• NP-hard问题的计算现状 • 计算复杂性理论的核心——NP完全
理论 • 算法研究的主要内容及重要意义
12
算法及其 时间复杂度
1
问题及实例
• 问题
需要回答的一般性提问,通常含若干参数
• 问题描述
定义问题参数(集合,变量,函数,序列等) 说明每个参数的取值范围及参数间的关系 定义问题的解 说明解满足的条件(优化目标或约束条件)
或半形式化的描述
• 设计算法: 采用什么算法设计技术 正确性——是否对所有的实例都得 到正确的解
• 分析算法——效率
15
问题计算复杂度 的界定:排序问题
例3 排序算法的效率
以元素比较作基本运算
算法
最坏情况下
第2章 算法分析基础(《算法设计与分析(第3版)》C++版 王红梅 清华大学出版社)

3
Page 11
2.1.2 算法的渐近分析
常见的时间复杂度:
Ο(1)<(log2n)<(n)<(nlog2n)<(n2)<(n3)<…<(2n)<(n!)
多项式时间,易解问题
算
法
指数时间,难解问题
设 计 与
分
析
(
第
时间复杂度是在不同数量级的层面上比较算法
版 )
清
华
大
学
时间复杂度是一种估算技术(信封背面的技术)
Page 7
2.1.2 算法的渐近分析
3
每条语句执行次数之和 = 算法的执行时间 = 每条语句执行时间之和
基本语句的执行次数 for (i = 1; i <= n; i++)
单位时间
算
法
设
计
与
执行次数 × 执行一次的时间
分 析 (
第
for (j = 1; j <= n; j++)
版 )
x++;
指令系统、编译的代码质量
算法设计:面对一个问题,如何设计一个有效的算法
算
法
设
检
指
验
导
评
计 与 分 析 ( 第 版
改
估
) 清
进
华 大
学
出
版
算法分析:对已设计的算法,如何评价或判断其优劣
社
3
Page 3
2.1.1 输入规模与基本语句
如何度量算法的效率呢?
事后统计:将算法实现,测算其时间和空间开销
缺点:(1)编写程序实现算法将花费较多的时间和精力 (2)所得实验结果依赖于计算机的软硬件等环境因素
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.2
递归函数的渐进分析
T(n)=4 T(n/2) + n, T(1)=θ(1) 先放大点,猜测T(n)=O(n3) 归纳验证: 1 T(1)是满足的; 2 假设对小于n的规模,T(k)<=Ck3 3 T(n)= 4 T(n/2) + n <=4 Cn3/8+n =Cn3-(Cn3/2-n) 因此,只要开始满足C>2,归纳是成立的。 另外,T(1)= θ(1)<C, 故C>max(2, θ(1))
θ(1)
θ(1) θ(1)共有aH=nlogba个 T(n)=f(n)+af(n/b)+a2f(n/b2)+…+aHθ(1)
f(n)~nlogba, akf(n/bk)~ak(n/bk) logba= nlogba Case1:f(n)=O(nlogba-), T(n)=O(Hnlogba-)+nlogba θ(1) Case3:af(n/b)<(1- ε)f(n),akf(n/bk)=(1- ε)kf(n), T(n)=θ(f(n)) Case2:f(n)=θ (nlogbalgkn), T(n)=nlogba (1+logkn+logkn/b+logkn/b2+…)+nlogbaθ(1)=θ(nlogbalogkn)
• T(n)=θ(nlgb )
a
Case 2:
lgba lgkn)对某个k>=0 f(n)=O(n
a
• T(n)=θ(nlgb lgk+1n)
Case 3: f(n)=
lgba+ε)& Ω(n
af(n/b)<=(1-ε’)f(n)
14
• T(n)=θ(f(n))
2.2
递归函数的渐进分析
主方法的例子 1) T(n)=4T(n/2) + n,
4
下界符号
Ω符号
f(n)= Ω (g(n)) 存在常数c及n0, 当n>n0时,满足f(n)>=cg(n)>=0
g(n)是f(n)的一个渐进下界 例 n1/2 =Ω( lgn )
5
同阶符号
Θ符号
f(n)= Θ (g(n)) 当 f(n)= O (g(n))
并且 f(n)= Ω(g(n))时
10
2.2
递归函数的渐进分析
T(n)=4 T(n/2) + n, T(1)=θ(1) 猜测T(n)=O(n2) 归纳验证: 1 T(1)是满足的; 2假设对小于n的规模,T(k)<=C1k2-C2k 3 T(n)= 4 T(n/2) + n <=C1n2-2C2n+n = C1n2-C2n-(C2-1)n 因此当C2>1时,归纳成立。同时还需满足 T(1)= θ(1)< C1-C2
7
常用的阶
多项式 n, n2,…nk 对数 lg n 指数 an
Lg(n) < nk &l的渐进分析
1) 代换法 分为3步: 1 猜渐进形式 g(x) 2 进行归纳验证 3 得到c T(n)=4 T(n/2) + n, T(1)=θ(1) 规模2倍时,时间是4倍?猜测T(n)=θ(n2)
11
2.2
递归函数的渐进分析
T(n)=4 T(n/2) + n, T(1)=θ(1) 猜测T(n)=O(n2) 归纳验证: 1 T(1)是满足的; 2 假设对小于n的规模,T(k)<=Ck2 3 T(n)= 4 T(n/2) + n <=Cn2+n 无法得到 T(n)<=Cn2
16
O(g(n))代表以g(n)为上界的函数集合,f(n)是其 中之一,因此“=”此处是“∈”,
• 错误的表示---O(g(n)) = f(n)
3
渐进符号的运算
f(n) = n3+O(n2) : 存在一个h(n), h(n) =O(n2), 满足f(x)= n3+h(n) n2+O(n)=O(n2) : 对任意的f(n)=O(n), n2+f(n) = O(n2) 因为 n2+f(n) < n2+c1.n < c2.n2
lgba=n2, n
属于case 1, T(n)= θ(n2)
2) T(n)=4T(n/2) + n2
属于case 2, T(n)=θ(n2 lgn)
3) T(n)=4T(n/2) + n3
属于case3 T(n)=θ(n3)
15
主方法的证明思路
递归树
f(n/b) f(n/b2) f(n/b2) f(n) f(n/b)… f(n/b) H=logbn f(n/b2)
12
2.2
递归函数的渐进分析
2)递归树方法 T(n)=T(n/2) + T(n/4) +n2, T(1)=θ(1)
n2 n2 T(n)= T(n/2) T(n/4) n2/4 n2/16 T(n/8)T(n/16) n2 n2/4 n2/16 n2/16
2 n2/64 n2/64 n /256
算法设计与分析
2. 渐进性分析数学基础
徐义春 /chinaxuyichun
目录
渐进符号及其意义 递归函数的渐进性分析
2
2.1 函数渐进符号与意义
O符号
f(n)=O(g(n)) 存在常数c及n0, 当n>n0时,满足0<=f(n)<=cg(n)
g(n)是f(n)的一个渐进上界 例 2n2 =O(n3)
例子:n2+2n+10= Θ(n2)
n2<=n2+2n+10<=2n2
6
另外两个符号
o符号
f(n)= o(g(n)) f(n)<g(n), (O是<=) 例 lgn= ω(n1/2)
ω符号
f(n)= ω(g(n)) f(n)>g(n), (Ω是>=) 例 n1/2 = ω( lgn )
T(n/4) T(n/8)
T(1)
T(1)
T(n)<=(n2+5/16n2+25/256n2+…)+ θ(n)= O(n2)
13
2.2
递归函数的渐进分析
3)主方法 T(n)=a T(n/b) + f(n),其中a,b>1,f(n)>0 lgba 比较f(n)与n lgba-ε)对某个ε>0 Case 1: f(n)=O(n
