电场能量与能量密度
-静电场的能量和能量密度

l
-+ - + R1 - + R2 -+
_
_ _ _
++ + _ + + _ + ++ _
_
R2 Eb R2 U max Eb R1 ln 9.10103 V R1 2 e
9 – 5 静电场的能量 能量密度
C, U, q, E 的变化。 ( 1 ) 充电后切断电源 (2)充电后不切断电源
9 – 静电场的能量 5 静电场的能量 能量密度 第九章静电场中的导体和电介质 例9-9 求半径为R 带电量为Q 的均匀带电球的静电能。 解一:计算定域在电场中的能量 球内 r 处电场
Qr E , 3 4 0 R (r R)
1 2 0 R Qr 2 4r dr W 0 E dV 0 3 2 2 4 0 R
第九章静电场中的导体和电介质
例 1.平行板电容器,其间充满介质 r , 求下列情况充入介质前后的
A
K 300V
E0
d
B
r
U Ed U0
(1)q不变 解 : 提示: (1)q不变
(2)U不变
C r C0 E
r
U (2)U不变 C r C0 E 不变 q CU r CU d S U 基本公式: C E d d q C C r C0 U
Q2 We 8π R1
(孤立导体球贮存的能量)
9 – 5 静电场的能量 能量密度
第九章静电场中的导体和电介质
例2 如图圆柱形电容器,中间是空气,空气的击 2 6 -1 穿场强是 Eb 310 V m,电容器外半径 R2 10 m. 在空气不被击穿的情况下,内半径 R1 ? 可使电容器 存储能量最多. ( 空气 r 1 )43; ++ _
能量密度计算公式

能量密度计算公式
能量密度是指单位体积内所含有的能量,通常用J/m³表示。
能量密度计算公式可以根据不同情况而有所不同,下面以几种常见情况为例进行介绍。
1. 电场能量密度
电场能量密度是指电场中单位体积内所含有的能量。
对于电场能量密度的计算公式,可以使用以下公式:
能量密度= 0.5 * ε * E²
其中,ε代表电场介质的介电常数,E代表电场强度。
2. 磁场能量密度
磁场能量密度是指磁场中单位体积内所含有的能量。
对于磁场能量密度的计算公式,可以使用以下公式:
能量密度= 0.5 * μ * H²
其中,μ代表磁场介质的磁导率,H代表磁场强度。
3. 光能量密度
光能量密度是指光波中单位体积内所含有的能量。
对于光能量密度的计算公式,可以使用以下公式:
能量密度= 0.5 * ε₀ * c * E²
其中,ε₀代表真空中的介电常数,c代表光速,E代表电场强度。
4. 动能密度
动能密度是指物体运动所具有的能量。
对于动能密度的计算公式,可以使用以下公式:
能量密度= 0.5 * ρ * v²
其中,ρ代表物体的密度,v代表物体的速度。
以上是几种常见情况下能量密度的计算公式。
通过这些公式,我们可以计算出不同场景下单位体积内所含有的能量。
能量密度的计算对于各个领域的研究和实践都具有重要意义,同时也有助于我们更好地理解和应用能量这一重要概念。
电场能量密度公式

电场能量密度公式
电场能量密度是指一个电场中每单位体积所存在的电能量的大小。
电场能量密度的表达式为:U = 1/2 ρE2,它的单位是电子伏特的平方,其中ρ是电荷密度,E是电场强度。
电场能量密度可以用来计算在一定体积中有多少电能量。
例如,如果电场强度为5伏/厘米,电荷密度为5伏/厘米,则电场能量密度为25电子伏特的平方。
这意味着,在1立方厘米的体积中存在25电子伏特的电能量。
电场能量密度的另一个用途是计算电容器的工作能量。
电容器的电容量C可以用电容器的电场能量密度U来计算:U = 1/2Cv2,其中v是电压。
如果电容器的电压为5伏,那么电容器的工作能量就是25伏特的平方,也就是1/2Cv2。
电场能量密度不仅可以用来计算电能量和电容器的工作能量,还可以用来计算电磁场的能量。
如果电磁场的电场强度为E,磁场强度为H,则电磁场的能量密度可以表示为U = 1/2(E2 + H2)。
电场能量密度的量纲是电子伏特的平方,它可以用来计算一定体积中的电能量、电容器的工作能量和电磁场的能量。
因此,电场能量密度是电力学中非常重要的概念,在电子设备和电力系统的设计中都被广泛使用。
4 静电场的能量和能量密度
1 1 2 电场能量密度 w e = ε E = ED 2 2
电场空间所存储的能量
We =
∫
V
we d V =
∫
V
1 2 εE dV 2
静电场的能量 能量密度
静电场中的导体和电介质
如图所示,球形电容器的内、 例1 如图所示,球形电容器的内、外半径分别为 R1 和 R2,所带电荷为 ± Q .若在两球壳间充以电容率为 的电介质,问此电容器贮存的电场能量为多少? 的电介质,问此电容器贮存的电场能量为多少?
静电场中的导体和电介质
Q C= U
Q 2C
2
1 1 2 W = QU = CU 2 2
Q2 1 1 电容器贮存的电能 We = = QU = CU 2 2C 2 2
静电场的能量 能量密度 二 静电场的能量 能量密度
静电场中的导体和电介质
1 2 1 εS 1 2 2 ( Ed ) = ε E Sd We = CU = 2 2 d 2
静电场的能量 能量密度 一
静电场中的导体和电介质
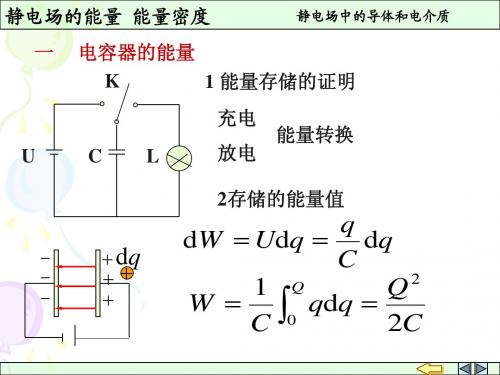
电容器的能量 K 1 能量存储的证明 充电 能量转换
U
C
L
放电
2存储的能量值 存储的能量值
− − −
+ dq ++ +
q dW = U dq = dq C 2 Q 1 Q W = ∫0 q d q = 2 C C
静电场的能量 能量密度 电容器存储能量为
ε
v 1 Qv 解 E= e 2 r 4π ε r 2 1 Q 2 we = εE = 2 4 2 32 π ε r
2
R 1drຫໍສະໝຸດ Q d W e = we d V = dr 2 R 2 8π εr 2 2 R 2 dr Q Q 1 1 We = ∫ dWe = ∫R 1 r 2 = 8 π ε ( R1 − R 2 ) 8π ε
平均磁场能量密度()平均电场能量密度。

平均磁场能量密度()平均电场能量密度。
平均磁场能量密度(H)平均电场能量密度(E)在电磁学中,磁场能量密度和电场能量密度是描述电磁场能量分布的重要参数。
平均磁场能量密度(H)和平均电场能量密度(E)是两个关键概念,用于解释电磁场的能量特性。
首先,我们来讨论平均磁场能量密度(H)。
磁场能量密度指的是磁场中单位体积的能量。
磁场能量密度与磁场强度(H)的平方成正比。
在一个恒定的磁场中,磁场能量密度可以通过求解磁场强度的平方并乘以一个常数来计算。
平均磁场能量密度表示一个时间段内磁场能量密度的平均值。
接下来,我们来探讨平均电场能量密度(E)。
电场能量密度指的是电场中单位体积的能量。
电场能量密度与电场强度(E)的平方成正比。
在一个恒定的电场中,电场能量密度可以通过求解电场强度的平方并乘以一个常数来计算。
平均电场能量密度表示一个时间段内电场能量密度的平均值。
平均磁场能量密度(H)和平均电场能量密度(E)在电磁学中扮演着重要的角色。
它们的计算可以帮助我们了解电磁场的能量分布情况,并为电磁场的应用提供理论基础。
同时,在电磁波的传播中,平均磁场能量密度(H)和平均电场能量密度(E)的比值也决定了电磁波的传播速度和传播性质。
总结而言,平均磁场能量密度(H)和平均电场能量密度(E)是描述电磁场能量分布的重要参数。
它们的计算可以帮助我们了解电磁场的能量特性,并为电磁场的应用提供理论基础。
在编写文章时,我们需要确保标题与内容相符,避免涉及广告信息和侵权争议,并注意排除不适宜展示的敏感词或其他不良信息。
同时,文章的结构应当清晰,段落完整,使得读者能够流畅地理解和阅读。
物理电场公式大全

物理电场公式大全电场是物理学中的一个重要概念,它描述了电荷之间相互作用的力场。
在现代科学和工程中,电场理论被广泛应用于各种领域,包括电子学、电力系统、通讯工程等。
本文将为您详细介绍物理电场的相关公式,帮助您更好地理解和应用电场理论。
1. 电场强度公式。
电场强度描述了单位正电荷在电场中所受到的力。
在真空中,电场强度E与电荷Q之间的关系可以用以下公式表示:E = k Q / r^2。
其中,E为电场强度,k为电场常数(8.9910^9 N·m^2/C^2),Q为电荷量,r 为距离。
2. 电场能量密度公式。
电场能量密度表示单位体积内的电场能量。
在电场强度为E的情况下,电场能量密度u可以用以下公式表示:u = 0.5 ε E^2。
其中,ε为介质的介电常数。
3. 静电势能公式。
静电势能表示电荷在电场中由于位置而具有的能量。
当电荷Q在电场中移动时,它的静电势能U可以用以下公式表示:U = k (Q1 Q2) / r。
其中,U为静电势能,Q1和Q2分别为两个电荷的大小,r为它们之间的距离。
4. 电场中的电势公式。
电势描述了单位正电荷在电场中所具有的势能。
在电场强度为E的情况下,电势V可以用以下公式表示:V = k Q / r。
其中,V为电势,其他符号的含义同上。
5. 电场中的电势能公式。
电场中的电势能可以用电势和电荷量来表示。
在电势为V的情况下,电场中的电势能可以用以下公式表示:U = Q V。
以上是物理电场中常见的几个重要公式,它们描述了电场强度、能量密度、势能、电势等重要物理量之间的关系。
通过这些公式,我们可以更好地理解电场的特性,并在实际应用中进行计算和分析。
在工程技术领域,电场理论被广泛应用于电力系统的设计与分析、电子电路的研究与开发、电磁场的模拟与优化等方面。
掌握电场公式,对于工程技术人员来说是非常重要的,它可以帮助他们更好地理解和应用电场理论,提高工作效率和解决问题的能力。
总之,物理电场公式是电场理论的重要组成部分,它们描述了电荷之间相互作用的规律,是现代科学和工程技术中不可或缺的重要知识。
6-5 静电场的能量和能量密度

R r
Q
12
物理学
第五版
6-5 静电场的能量和能量密度
1 1 1 2 2 We = ∫ ( DE )dV = ∫ ε0 E1 dV + ∫ ε0 E2 dV V 2 V1 2 V2 2 2 2 R1 ∞1 Qr Q 2 4πr dr + ∫ ε0 4πr 2 dr = ∫ ε0 3 R 2 4 πε r 2 0 2 0 4πε0 R
B
17
物理学
第五版
总结:电容器 电容 总结:
电容器的电容
6-5 静电场的能量和能量密度
C = q −U
U
A
B
三种常见的电容器 平行板电容器 圆柱形电容器的电容 球形电容器的电容 电容器的能量
C =
C
q U AB
=
=
ε0S
d
0
2 πε ln R R
l
2 1
4πε 0 R B R A C = (R B − R A )
dr
r
R2
R1
Q
-Q
4
物理学
第五版
6-5 静电场的能量和能量密度
2 2
1 1 1 Q Q ( − )= 讨 论 We = 8 π ε R1 R 2 2 4πε R1 R 2 R 2 − R1 (1) C = 4 π ε R2 R1 ) R2 − R1 dr 球形电容器) (球形电容器) r R1 Q2 We = R2 2 2 C Q (2) R2 → ∞ W e = ) 8 π εR 1
_
6
物理学
第五版
6-5 静电场的能量和能量密度
解 E=
Eb =
U =
电场能量密度等于磁场能量密度,是均匀平面波在()中的传播特点。

电场能量密度等于磁场能量密度,是均匀平面波在( )中的传播特点
电场能量密度等于磁场能量密度,是均匀平面波在理想介质中的传播特点。
电场能量密度和磁场能量密度是两个不同的物理量,它们分别描述电场和磁场中能量的分布情况。
在某些特定的情况下,例如均匀介质中,电场能量密度可以等于磁场能量密度。
但是,这种情况并不是普遍适用的,因为电场和磁场的能量分布受到多种因素的影响,如介质的性质、波的传播方向、波的振幅等。
在均匀平面波中,电场和磁场的方向是固定的,且与波的传播方向垂直。
在这种情况下,如果介质的性质和波的参数(如振幅、频率等)保持不变,那么电场能量密度和磁场能量密度也可以保持相等。
但是,如果介质的性质或波的参数发生变化,那么电场能量密度和磁场能量密度也会随之改变。
总的来说,电场能量密度等于磁场能量密度并不是均匀平面波在理想介质中的传播特点。
在实际应用中,需要根据具体情况考虑多种因素,如介质的性质、波的传播方向、波的振幅等,才能得出准确的结论。
对于不同类型的波(如电磁波、声波等),其传播特点也会有所不同,因此需要具体问
题具体分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 1 We E DdV D ndS 2 V 2 S'
第二章 静 电 场 式中V已经扩展到无穷大,故S′在无穷远处。对于分布在有限区域 的电荷,φ∝1/R,D∝1/R2, S′∝R2, 因此当R→∞时,上式中的面积 分为零,于是
1 We E DdV 2 V
第二章 静 电 场
2.8.2 能量密度
图 2 -15 能量密度
第二章 静 电 场
1 1 We dV SdS 2 V 2 S
将▽· D=ρ和D· n=ρS代入上式,有
1 1 We DdV D ndS 2 V 2 S
利用矢量恒等式
D (D) D (D) E D
第二章 静 电 场
2.8 电场能量与能量密度
2.8.1 电场能量
设每个带电体的最终电位为φ1、φ2、…、φn,最终电荷为q1、
q2 、… 、 qn 。带电系统的能量与建立系统的过程无关,仅仅与系
统的最终状态有关。假设在建立系统过程中的任一时刻,各个带 电体的电量均是各自终值的 α 倍 (α<1) ,即带电量为 αqi ,电位为 αφi,经过一段时间,带电体i的电量增量为d(αqi),外源对它所作 的功为αφid (αqi)。外源对n个带电体作功为
b
2
第二章 静 电 场
1 We S ( r ) ( r )dS S 2 1 We l ( r ) ( r )dl l2
We
i 1 n n
1 pij qi q j j 1 2 1 ij i j j 1 2
n
n
We
i 1
2 1 1 q We qU CU 2 2 2 2C
1 We 0 E 2dV 2 V 1 q 0 2 4 0 3q 2 20 0a
2
a r 2 1 2 2 0 3 4r dr a 4 4r dr r a
第二章 静 Hale Waihona Puke 场第二章 静 电 场 则
1 1 1 DdV (D )dV E DdV 2 V 2 V 2 V 1 1 D dS E DdV 2 S S ' 2 V 1 1 1 D ndS D n ' dS E DdV 2 S' 2 S 2 V
dA qi i ada
i 1
n
第二章 静 电 场 因而,电场能量的增量为
dWe qi i ada
i 1
n
在整个过程中,电场的储能为
We dWe qii
i 1
n
1
0
1 n ada qii 2 i 1
We
V
1 ( r ) ( r )dV 2
例2-14 若一同轴线内导体的半径为a,外导体的内半径为b,
之间填充介电常数为 ε的介质,当内、外导体间的电压为U(外导 体的单位为零)时,求单位长度的电场能量。 解:设内、外导体间电压为U时,内导体单位长度带电量为 ρl, 则导体间的电场强度为
l E er ( a r b) 2r
we E D
对于各向同性介质:
1 2 we E 2
第二章 静 电 场 例2-13 若真空中电荷q均匀分布在半径为a的球体内,计算电 场能量。
解: 用高斯定理可以得到电场为
qr E er 3 4 0a E er q 4 0 r
3
(r<a)
(r<a)
第二章 静 电 场 所以
两导体间的电压为
l b U 1n 2 a
第二章 静 电 场 即
2U l b 1n a l b E er 1n 2 a
2
( a r b)
单位长度的电场能量为
1 U U 2 We E dV 2rdr a b 2 2 2 b 2r 1n 1n a a
