第十一章 波动光学 练习题
大学物理第十一章波动光学作业ppt课件
平面处的屏幕上的中央明条纹宽度为2.0mm，则入射
光波长约为
(A) 100 nm
(B) 400 nm
(C) 500 nm
(D) 600 nm
［ C］
解：对单缝衍射，中央明条纹的宽度为正、负一级暗
条纹间的距离
一级暗条纹到中央明条纹的距离为 x1
则中央明条纹的宽度为
x0
2x1
2 b
f
f
b
f
入射光波长为
解：条纹间距即条纹的宽度为 b
2 n
逆时针转动，增加，则b变小，即间隔变小
由的条2纹d 被2高 级k次可的知占，据d，增因加此，向干棱涉边级方次向k增平加移，原来处
.
选A
2.在夫琅禾费单缝衍射实验中，对于给定的入射单色 光，当缝宽度变小时，除中央亮纹的中心位置不变外， 各级衍射条纹 (A) 对应的衍射角变小． (B) 对应的衍射角变大． (C) 对应的衍射角也不变．(D) 光强也不变． ［ B ］
3.在用钠光(=589.3nm)做光源进行的单缝夫琅禾费
衍射实验中，单缝宽度b=0.5mm，透镜焦距f=700mm． 求透镜焦平面上中央明条纹的宽度．
解：对一级暗条纹有
则中央明条纹的宽度为 x1 b f
5 8 9 .3 1 0 6
x 0 2 x 1 2 bf 2 . 0 .5 7 0 0 1 .6 5 m m
透射光加强，为明条纹，则有 2ndk
d k
2n
当k=1时，膜有最小厚度，即
d m 2 n 2 6 1 0 .0 5 4 1 9 4 n m 1 .9 4 1 0 4 m m
或透射光加强时，反射光相消，即对反射光，有
2nd(2k1) 2ndk
11光学习题
Δ 2n2 d k k
h
明纹
r
O
d
dk k
2n2
(k 0,1,2,)
油膜边缘 k
R
0, d0 0 明纹
k 1, d1 250nm k 2, d2 500nm
波动光学习题课选讲例题
k 3, d3 750 nm
h
O
r
R
d
k 4, d 4 1000nm
Δr 2n2e
e 0,
Δr 0
波动光学习题课选讲例题
例 在折射率 射率
n2 为 2.5 的透明介质膜可增强反射.
n1 为 1.5 的玻璃板上表面镀一层折
设在镀膜过
程中用一束波长为 600 nm 的单色光从上方垂直照射
到介质膜上, 并用照度表测量透射光的强度.当介质膜 的厚度逐步增大时，透射光的强度发生时强时弱的变 化，求当观察到透射光的强度第三次出现最弱时，介 质膜镀了多少nm厚度的透明介质膜 （A）300 （B）600 （C）250 （D）420
间距大的是 （A）空气中的玻璃劈尖 （B）玻璃夹层中的空气劈尖 （C）两个劈尖干涉条纹间距相等
（D）观察不到玻璃劈尖的干涉条纹
波动光学习题课选讲例题 例 如图所示两个直径有微小差别的彼此平行的
滚柱之间的距离为 L，夹在两块平晶的中间，形成空
气劈尖，当单色光垂直入射时，产生等厚干涉条纹，
如果滚柱之间的距离变小，则在 L 范围内干涉条纹的 （A）数目减少，间距变大 （B）数目不变，间距变小 （C）数目增加，间距变小 （D）数目减少，间距不变 L
波动光学习题课选讲例题
例 用波长为 的单色光垂直照射到空气劈尖 上，从反射光中观察干涉条纹，距顶点为 L 处是暗 纹，使劈尖角
大学物理复习总结题(第11章)
第11章 波动光学一、填空题易：1、光学仪器的分辨率R= 。
(R= a 1.22λ) 易：2、若波长为625nm 的单色光垂直入射到一个每毫米有800条刻线的光栅上时，则第一级谱线的衍射角为 。
(6π) 易：3、在单缝的夫琅和费衍射实验中，屏上第三级暗纹对应的单缝处波面可划分为 个半波带。
(6)易：4、在单缝夫琅和费衍射实验中波长为λ的单色光垂直入射在宽度为a=2λ的单缝上，对应于衍射角为30°方向，单缝处的波面可分成的半波带数目为 个。
(2)易：5、干涉相长的条件是两列波的相位差为π的 （填奇数或偶数）倍。
(偶数)易：6、如图（6题）所示，1S 和2S ，是初相和振幅均相同的相干波源，相距4.5λ，设两波沿1S 2S 连线传播的强度不随距离变化，则在连线上1S 左侧各点和2S 右侧各点是 （填相长或相消）。
(相消)易：7、在麦克耳逊干涉仪的一条光路中，插入一块折射率为n ，厚度为d 的透明薄片，插入薄片使这条光路的光程改变了 ；[ 2(n-1)d ]易：8、波长为λ的单色光垂直照射在由两块平玻璃板构成的空气劈尖上，测得相邻明条纹间距为L 若将劈尖角增大至原来的2倍，则相邻条纹的间距变为 。
(2L ) 易：9、单缝衍射中狭缝愈窄，条纹间距愈 。
(宽)易：10、在单缝夫琅和费衍射实验中，第一级暗纹发生在衍射角300的方向上，所用单色光波长为500nm λ=，则缝宽为： 。
（1000nm ）易：11、用波长为λ的单色光垂直照射置于空气中的厚度为e 的折射率为1.5的透明薄膜，两束反射光的光程差为 ；(23λ+e )易：12、光学仪器的分辨率与 和 有关，且 越小，仪器的分辨率越高。
(入射波长λ，透光孔经a ，λ)易：13、由马吕斯定律，当一束自然光通过两片偏振化方向成30o 的偏振片后，其出射光与入射光的光强之比为 。
（3：8）易：14、当光由光疏介质进入光密介质时，在交界面处的反射光与入射光有相位相反的现象，这种现象我们称之为 。
大学物理题库通用版-第11章-波动光学--光的干涉(含答案解析)
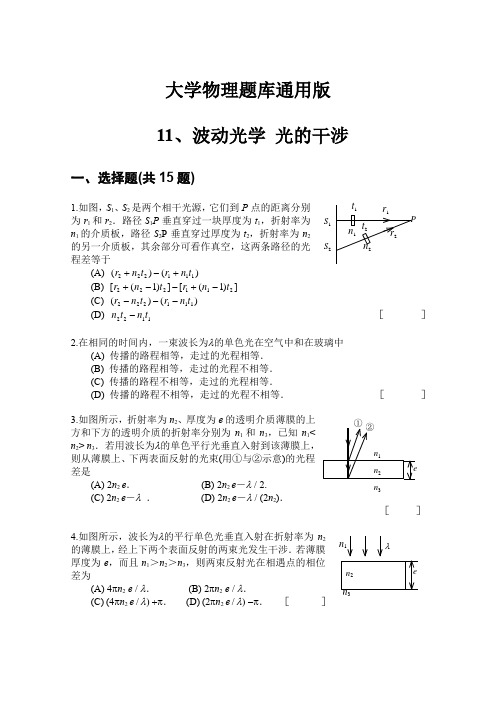
大学物理题库通用版11、波动光学 光的干涉一、选择题(共15题)1.如图，S 1、S 2是两个相干光源，它们到P 点的距离分别为r 1和r 2．路径S 1P 垂直穿过一块厚度为t 1，折射率为n 1的介质板，路径S 2P 垂直穿过厚度为t 2，折射率为n 2的另一介质板，其余部分可看作真空，这两条路径的光程差等于 (A) )()(111222t n r t n r +-+(B) ])1([])1([211222t n r t n r -+--+(C) )()(111222t n r t n r ---(D) 1122t n t n - ［ ］2.在相同的时间内，一束波长为λ的单色光在空气中和在玻璃中(A) 传播的路程相等，走过的光程相等．(B) 传播的路程相等，走过的光程不相等．(C) 传播的路程不相等，走过的光程相等．(D) 传播的路程不相等，走过的光程不相等． ［ ］3.如图所示，折射率为n 2、厚度为e 的透明介质薄膜的上方和下方的透明介质的折射率分别为n 1和n 3，已知n 1<n 2> n 3．若用波长为λ的单色平行光垂直入射到该薄膜上，则从薄膜上、下两表面反射的光束(用①与②示意)的光程差是(A) 2n 2 e ． (B) 2n 2 e －λ / 2. (C) 2n 2 e －λ ． (D) 2n 2 e －λ / (2n 2)．［ ］4.如图所示，波长为λ的平行单色光垂直入射在折射率为n 2的薄膜上，经上下两个表面反射的两束光发生干涉．若薄膜厚度为e ，而且n 1＞n 2＞n 3，则两束反射光在相遇点的相位差为(A) 4πn 2 e / λ． (B) 2πn 2 e / λ． (C) (4πn 2 e / λ) +π． (D) (2πn 2 e / λ) -π． ［ ］P S 1S 2 r 1 n 1 n 2 t 2 r 2 t 1n 3n 1 λ5.如图所示，平行单色光垂直照射到薄膜上，经上下两表面反射的两束光发生干涉，若薄膜的厚度为e ，并且n 1＜n 2＞n 3，λ1为入射光在折射率为n 1的媒质中的波长，则两束反射光在相遇点的相位差为 (A) 2πn 2e / ( n 1 λ1)． (B)[4πn 1e / ( n 2 λ1)] + π． (C) [4πn 2e / (n 1 λ1) ]+ π． (D) 4πn 2e / ( n 1 λ1)． ［ ］6.一束波长为λ的单色光由空气垂直入射到折射率为n 的透明薄膜上，透明薄膜放在空气中，要使反射光得到干涉加强，则薄膜最小的厚度为(A) λ / 4 ． (B) λ / (4n )．(C) λ / 2 ． (D) λ / (2n )． ［ ］7. 两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的(A) 间隔变小，并向棱边方向平移．(B) 间隔变大，并向远离棱边方向平移．(C) 间隔不变，向棱边方向平移．(D) 间隔变小，并向远离棱边方向平移． ［ ］8.用白光光源进行双缝实验，若用一个纯红色的滤光片遮盖一条缝，用一个纯蓝色的滤光片遮盖另一条缝，则(A) 干涉条纹的宽度将发生改变．(B) 产生红光和蓝光的两套彩色干涉条纹．(C) 干涉条纹的亮度将发生改变．(D) 不产生干涉条纹． ［ ］9.把双缝干涉实验装置放在折射率为n 的水中，两缝间距离为d ，双缝到屏的距离为D (D >>d )，所用单色光在真空中的波长为λ，则屏上干涉条纹中相邻的明纹之间的距离是(A) λD / (nd ) (B) n λD /d ．(C) λd / (nD )． (D) λD / (2nd )． ［ ］10.在双缝干涉实验中，若单色光源S 到两缝S 1、S 2距离相等，则观察屏上中央明条纹位于图中O 处．现将光源S 向下移动到示意图中的S '位置，则 (A) 中央明条纹也向下移动，且条纹间距不变．(B) 中央明条纹向上移动，且条纹间距不变． (C) 中央明条纹向下移动，且条纹间距增大． (D) 中央明条纹向上移动，且条纹间距增大． ［ ］11.在双缝干涉实验中，入射光的波长为λ，用玻璃纸遮住双缝中的一个缝，若玻璃n 1λ1 S S '纸中光程比相同厚度的空气的光程大2.5 λ，则屏上原来的明纹处(A) 仍为明条纹；(B) 变为暗条纹；(C) 既非明纹也非暗纹；(D) 无法确定是明纹，还是暗纹．［］12.在牛顿环实验装置中，曲率半径为R的平凸透镜与平玻璃扳在中心恰好接触，它们之间充满折射率为n的透明介质，垂直入射到牛顿环装置上的平行单色光在真空中的波长为λ，则反射光形成的干涉条纹中暗环半径r k的表达式为(A) r k =Rkλ．(B) r k =nRk/λ．(C) r k =Rknλ．(D) r k =()nRk/λ．［］13.把一平凸透镜放在平玻璃上，构成牛顿环装置．当平凸透镜慢慢地向上平移时，由反射光形成的牛顿环(A)向中心收缩，条纹间隔变小．(B)向中心收缩，环心呈明暗交替变化．(C)向外扩张，环心呈明暗交替变化．(D)向外扩张，条纹间隔变大．［］14.如图a所示，一光学平板玻璃A与待测工件B之间形成空气劈尖，用波长λ＝500 nm (1 nm=10-9 m)的单色光垂直照射．看到的反射光的干涉条纹如图b所示．有些条纹弯曲部分的顶点恰好与其右边条纹的直线部分的连线相切．则工件的上表面缺陷是(A) 不平处为凸起纹，最大高度为500 nm．(B) 不平处为凸起纹，最大高度为250 nm．(C) 不平处为凹槽，最大深度为500 nm．(D) 不平处为凹槽，最大深度为250 nm．［］15.在迈克耳孙干涉仪的一条光路中，放入一折射率为n，厚度为d的透明薄片，放入后，这条光路的光程改变了(A) 2 ( n-1 ) d．(B) 2nd．(C) 2 ( n-1 ) d+λ / 2．(D) nd．(E) ( n-1 ) d．［］二、填空题(共15题)1. 在双缝干涉实验中，两缝分别被折射率为n1和n2的透明薄膜遮盖，二者的厚度均为e．波长为λ的平行单色光垂直照射到双缝上，在屏中央处，两束相干光的相位差∆φ＝________．图b2. 如图所示，假设有两个同相的相干点光源S 1和S 2，发出波长为λ的光．A 是它们连线的中垂线上的一点．若在S 1与A 之间插入厚度为e 、折射率为n 的薄玻璃片，则两光源发出的光在A 点的相位差∆φ＝_2π (n -1) e / λ_．若已知λ＝500 nm ，n ＝1.5，A 点恰为第四级明纹中心，则e ＝_____nm ．(1 nm =10-9 m)3. 如图所示，两缝S 1和S 2之间的距离为d ，媒质的折射率为n ＝1，平行单色光斜入射到双缝上，入射角为θ，则屏幕上P 处，两相干光的光程差为___ ______．4.在双缝干涉实验中，所用光波波长λ＝5.461×10–4 mm ，双缝与屏间的距离D ＝300 mm ，双缝间距为d ＝0.134 mm ，则中央明条纹两侧的两个第三级明条纹之间的距离为________ _______．5.用波长为λ的单色光垂直照射折射率为n 的劈形膜形成等厚干涉条纹，若测得相邻明条纹的间距为l ，则劈尖角θ＝________．6.把双缝干涉实验装置放在折射率为n 的媒质中，双缝到观察屏的距离为D ，两缝之间的距离为d (d <<D )，入射光在真空中的波长为λ，则屏上干涉条纹中相 邻明纹的间距是_____________．7.用λ＝600 nm 的单色光垂直照射牛顿环装置时，从中央向外数第４个(不计中 央暗斑)暗环对应的空气膜厚度为____________．(1 nm=10-9 m)8.用波长为λ的单色光垂直照射折射率为n 2的劈形膜(如图)图中各部分折射率的关系是n 1＜n 2＜n 3．观察反射光的干涉条纹，从劈形膜顶开始向右数第5条暗条纹中心所对应的厚度e ＝____________．9.波长为λ的平行单色光，垂直照射到劈形膜上，劈尖角为θ，劈形膜的折射率为n ，第三条暗纹与第六条暗之间的距离是______．10. 一束波长为λ＝600 nm (1 nm=10-9 m)的平行单色光垂直入射到折射率为n ＝1.33的透明薄膜上，该薄膜是放在空气中的．要使反射光得到最大限度的加强，薄膜最小厚度应为________________nm ．11.波长为λ的平行单色光垂直照射到劈形膜上，劈尖角为θ，劈形膜的折射率为n ，第k 级明条纹与第k ＋5级明纹的间距是__________．12.波长λ＝600 nm 的单色光垂直照射到牛顿环装置上，第二个明环与第五个明环所对应的空气膜厚度之差为____nm ．(1 nm=10-9 m)n 1n 2n 313.折射率分别为n 1和n 2的两块平板玻璃构成空气劈尖，用波长为λ的单色光垂直照射．如果将该劈尖装置浸入折射率为n 的透明液体中，且n 2＞n ＞n 1，则劈尖厚度为e 的地方两反射光的光程差的改变量是_______．14.如图所示，在双缝干涉实验中SS 1＝SS 2，用波长为λ的光照射双缝S 1和S 2，通过空气后在屏幕E 上形成干涉条纹．已知P 点处为第三级明条纹，则S 1和S 2到P 点的光程差为___3λ ____．若将整个装置放于某种透明液体中，P 点为第四级明条纹，则该液体的折射率n ＝________．15.已知在迈克耳孙干涉仪中使用波长为λ的单色光．在干涉仪的可动反射镜移动距离d 的过程中，干涉条纹将移动__________条． 三、计算题(共5题)1.白色平行光垂直入射到间距为a ＝0.25 mm 的双缝上，距D =50 cm 处放置屏幕，分别求第一级和第五级明纹彩色带的宽度．(设白光的波长范围是从400nm 到760nm ．这里说的“彩色带宽度” 指两个极端波长的同级明纹中心之间的距离．) (1 nm=10-9 m)2.在双缝干涉实验中，波长λ＝550 nm 的单色平行光垂直入射到缝间距a ＝2×10-4 m 的双缝上，屏到双缝的距离D ＝2 m ．求：(1) 中央明纹两侧的两条第10级明纹中心的间距；(2) 用一厚度为e ＝6.6×10-5 m 、折射率为n ＝1.58的玻璃片覆盖一缝后，零级明纹将移到原来的第几级明纹处？(1 nm = 10-9 m)3.用波长为500 nm (1 nm=10-9 m)的单色光垂直照射到由两块光学平玻璃构成的空气劈形膜上．在观察反射光的干涉现象中，距劈形膜棱边l = 1.56 cm 的A 处是从棱边算起的第四条暗条纹中心．(1) 求此空气劈形膜的劈尖角θ；(2) 改用600 nm 的单色光垂直照射到此劈尖上仍观察反射光的干涉条纹，A 处是明条纹还是暗条纹？(3) 在第(2)问的情形从棱边到A 处的范围内共有几条明纹？几条暗纹？2分4.图示一牛顿环装置，设平凸透镜中心恰好和平玻璃接触，透镜凸表面的曲率半径是R ＝400 cm ．用某单色平行光垂直入射，观察反射光形成的牛顿环，测得第5个明环的半径是0.30 cm ． (1) 求入射光的波长． (2) 设图中OA ＝1.00 cm ，求在半径为OA 的范围内可观察到的明环数目．5.用波长λ＝500 nm 的平行光垂直照射折射率n ＝1.33的劈形膜，观察反射光的等厚干涉条纹．从劈形膜的棱算起，第5条明纹中心对应的膜厚度是多少？ P E光的干涉习题答案一、选择题1、B ；2、C ；3、B ；4、A ；5、C ；6、B ；7、A ；8、D ；9、A ；10、B ；11、B ；12、B ；13、B ；14、B ；15、A二、填空题1、 2π(n 1 – n 2) e / λ2、4×103 nm3、d sin θ ＋(r 1－r 2)4、7.33 mm5、nl 2λ6、D λ / (dn )7、1.2=2λ μm8、249n λ9、3λ / (2n θ)10、113nm11、5λ / (2n θ)12、900 nm13、2 ( n – 1) e – λ /214、1.3315、2d /λ三、计算题1解：由公式x ＝kD λ / a 可知波长范围为∆λ时,明纹彩色宽度为∆x k ＝kD ∆λ / a2分 由 k ＝1可得，第一级明纹彩色带宽度为∆x 1＝500×(760－400)×10-6 / 0.25＝0.72 mm2分 k ＝5可得，第五级明纹彩色带的宽度为∆x 5＝5·∆x 1＝3.6 mm1分2解：(1) ∆x ＝20 D λ / a2分 ＝0.11 m2分 (2) 覆盖云玻璃后，零级明纹应满足(n －1)e ＋r 1＝r 22分 设不盖玻璃片时，此点为第k 级明纹，则应有r 2－r 1＝k λ 2分所以 (n －1)e = k λ k ＝(n －1) e / λ＝6.96≈7 零级明纹移到原第7级明纹处 2分3解：(1) 棱边处是第一条暗纹中心，在膜厚度为e 2＝21λ处是第二条暗纹中心，依此可知第四条暗纹中心处，即A 处膜厚度 e 4=λ23 ∴ ()l l e 2/3/4λθ==＝4.8×10-5 rad 5分(2) 由上问可知A 处膜厚为 e 4＝3×500 / 2 nm ＝750 nm对于λ＇＝600 nm 的光，连同附加光程差，在A 处两反射光的光程差为λ'+2124e ，它与波长λ'之比为0.321/24=+'λe ．所以A 处是明纹 3分 (3) 棱边处仍是暗纹，A 处是第三条明纹，所以共有三条明纹，三条暗纹．4解：(1) 明环半径 ()2/12λ⋅-=R k r 2分()Rk r 1222-=λ＝5×10-5 cm (或500 nm) 2分 (2) (2k －1)＝2 r 2 / (R λ) 对于r ＝1.00 cm ， k ＝r 2 / (R λ)＋0.5＝50.5 3分 故在OA 范围内可观察到的明环数目为50个． 1分5解： 明纹， 2ne ＋λ21＝k λ (k ＝1，2，…) 3分 第五条，k ＝5，ne 2215λ⎪⎭⎫ ⎝⎛-=＝8.46×10-4 mm 2分。
波动光学习题
解：1.判断零级条纹( 0)的移动方向，
相折射率大的n2方向移动
S
S1 n1, d
P
O
2. (n2 1)d (n1 1)d
(n2 n1)d N
S2 n2 , d
d 8106 m
3.间距不变
例3 白光垂直照射在空气中厚度为 0.40mm旳玻璃片 上，玻璃旳折射率为1.50，试问在可见光范围内 (
3
因为 2 级缺级，实际呈现条纹旳全部级数为
0, 1, 3
例9、要测定硅片上二氧化硅薄膜旳厚度，
将薄膜旳一端做成劈尖形，用波长为
0
5461 A
旳绿光从空气照射硅片，观察反射光第7条暗
纹在与平行膜旳交线M处，二氧化硅旳折射率
为n2=1.5, 硅旳折射率为n3=3.4
求:二氧化硅薄膜旳厚度 n1 1
向平行于入射面；
（D）是部分偏振光。
例15 自然光以60°旳入射角照射到某一透明介质表面 时,反射光为线偏振光,则由此可拟定：
(A)折射光为线偏振光，折射角为30° (B)折射光为线偏振光，折射角为60°
（C）
(C)折射光为部分偏振光，折射角为30°
(D)折射光为部分偏振光，折射角为60°
分析： 此时入射角为布儒斯特角，ib 60
因为反射光较弱，不可能某一
振动方向旳光被完全反射，所以折
600
射光仍为部分偏振光。
又因为在入射角为布儒斯特角旳情
况下，反射光与折射光相互垂直，所以 折射角为300。
例16 在双缝干涉试验中，用单色自然光，在屏 上形成干涉条纹．若在两缝后放一种偏振片，则 (A) 干涉条纹旳间距不变，但明纹旳亮度加强． (B) 干涉条纹旳间距不变，但明纹旳亮度减弱． (C) 干涉条纹旳间距变窄，且明纹旳亮度减弱． (D) 无干涉条纹．
大学物理A第十一章 波动光学
第十一章 波动光学一、填空题（每空3分）11-1 相干光的条件是________________.(频率相同,振动方向相同,相位差恒定.)11-2 ______ 和 _______是波动的重要特征，光的偏振现象证明光是_____波.( 干涉,衍射, 横.)11-3当一束自然光在两种介质分界面处发生反射和折射时，若反射光为线偏振光，则折射光为_____________偏振光,且反射线和折射线之间的夹角为_______.(部分, 2π.) 11-4 当光从折射率n______ 的介质射向折射率n___________的介质,并在分界面上反射时,将产生半波损失.(填:大;小.)( 答案：大, 小.)11-5 在双缝实验中，若把一厚度为e ，折射率为n 的薄云母片覆盖在S 1缝上,中央明纹将向__________移动,覆盖云母片后两束相干光至原中央明纹O 处的光程差为_______________.(向上,(n-1)e )11-6光的干涉和衍射现象反映了光的__________________性质;光的偏振现象说明光波是_____________波.( 波动 , 横)11-7使一束自然光和线偏振光混合而成的光束垂直通过一偏振片，以入射光束为轴旋转偏振片，测得透射光的最大值为最小值的4倍，则入射光中自然光与线偏振光的强度之比为 。
（23）11-8杨氏双缝干涉实验、薄膜干涉实验、劈尖干涉实验、牛顿环干涉实验，其中属于分波面干涉的实验为 。
（杨氏双缝干涉实验）11-9 用不同波长的红光（10.7m λμ=）和紫光（20.42m λμ=）进行双缝实验，发现红光照射时第k 级明纹正好与用紫光照射时的第k+2级明纹重合，则k = 。
( 3) 11-10用两块平玻璃构成劈尖观察等厚干涉条纹。
若将劈尖上表面向上缓慢地平移，则干涉条纹向 方向移动；若将劈尖角e S 2 S 1 Oθ逐渐增大，则干涉条纹向 方向移动。
(左；左)11-11光强均为0I 的两束相干光相遇而发生干涉时，在相遇区域内有可能出现的最大光强是 。
大学物理第十一章波动光学习题答案
第十一章 波动光学习题11-1 在杨氏双缝实验中，双缝间距d ＝0.20 mm ，缝屏间距D ＝1.0 m ，若第2级明条纹离屏中心的距离为6.0 mm ，试求：（1）入射光的波长；（2）相邻两明条纹间的距离。
解：（1）由λk d D x =明知， λ22.01010.63⨯⨯= 30.610m m 600n m λ-=⨯= （2）3106.02.010133=⨯⨯⨯==∆-λd D x mm 11-2 在双缝装置中，用一很薄的云母片（n ＝1.58）覆盖其中的一条缝，结果使屏幕上的第7级明条纹恰好移到屏幕中央原零级明纹的位置。
若入射光的波长为550 nm ，求此云母片的厚度。
解：设云母片厚度为e ，则由云母片引起的光程差为e n e ne )1(-=-=δ 按题意 λδ7= ∴610106.6158.1105500717--⨯=-⨯⨯=-=n e λm 6.6=m μ 11-3 在折射率n 1＝1.52的镜头表面涂有一层折射率n 2＝1.38的MgF 2增透膜，如果此膜适用于波长λ＝550 nm 的光，问膜的最小厚度应取何值？解：设光垂直入射增透膜，欲透射增强，则膜上、下两表面反射光应满足干涉相消条件，即λ)21(22+=k e n ),2,1,0(⋅⋅⋅=k 222422)21(n n k n k e λλλ+=+=)9961993(38.14550038.125500+=⨯+⨯=k k o A令0=k ，得膜的最薄厚度为996o A 。
11-4 白光垂直照射在空气中厚度为0.4μm 的玻璃片上，玻璃的折射率为1.50。
试问在可见光范围内（λ= 400~700nm ），哪些波长的光在反射中增强？哪些波长的光在透射中增强？解：（1）222n d j λδλ=+= 24 3,480n m 21n d j j λλ===- （2）22(21) 22n d j λλδ=+=+ 22n d j λ= 2,600n m j λ==；3,400nm j λ== 11-5 白光垂直照射到空气中一厚度为380 nm 的肥皂膜上，设肥皂膜的折射率为1.33，试问该膜的正面呈现什么颜色？背面呈现什么颜色？ 解：由反射干涉相长公式有42221ne ne k k λδλλ=+==-， ),2,1(⋅⋅⋅=k 得4 1.3338002674nm 2214 1.3338003404nm 231k k λλ⨯⨯===⨯-⨯⨯===⨯-，红色，紫色所以肥皂膜正面呈现紫红色。
第11章 波动光学(习题与答案)
第11章 波动光学一. 基本要求1. 解获得相干光的方法。
掌握光程的概念以及光程差与相位差的关系。
2. 能分析、确定杨氏双缝干涉条纹及等厚、等倾干涉条纹的特点（干涉加强、干涉减弱的条件及明、暗条纹的分布规律；了解迈克耳逊干涉仪的原理。
3. 了解惠更斯——菲涅耳原理；掌握分析单缝夫琅禾费衍射暗纹分布规律的方法。
4. 理解光栅衍射公式，会确定光栅衍射谱线的位置，会分析光栅常数及波长对光栅衍射谱线分布的影响。
5. 理解自然光和偏振光及偏振光的获得方法和检验方法。
6. 理解马吕斯定律和布儒斯特定律。
二. 内容提要1. 相干光及其获得方法 能产生干涉的光称为相干光。
产生光干涉的必要条件是：频率相同；振动方向相同；有恒定的相位差。
获得相干光的基本方法有两种：一种是分波阵面法（如杨氏双缝干涉、洛埃镜干涉、菲涅耳双面镜和菲涅耳双棱镜等）；另一种是分振幅法（如平行波膜干涉、劈尖干涉、牛顿环和迈克耳逊干涉仪等）。
2. 光程、光程差与相位差的关系 光波在某一介质中所经历的几何路程l 与介质对该光波的折射率n 的乘积n l 称为光波的光学路程，简称光程。
若光波先后通过几种介质，其总光程为各分段光程之和。
若在界面反射时有半波损失，则反射光的光程应加上或减去2λ。
来自同一点光源的两束相干光，经历不同的光程在某一点相遇，其相位差Δφ与光程差δ的关系为δλπϕ2=∆ 其中λ为光在真空中的波长。
3. 杨氏双缝干涉 经杨氏双缝的两束相干光在某点产生干涉时有两种极端情况：一种是相位差为零或2π的整数倍，合成振幅最大—干涉加强；另一种是相位差为π的奇数倍，合成振动最弱或振幅为零——称干涉减弱或相消。
其对应的光程差为⎪⎩⎪⎨⎧=-±=±= 21k 212 210 干涉减弱），，（）（干涉加强），，（ λλδk k k 杨氏双缝干涉的光程差还可写成Dx d=δ ，式中d 为两缝间距离，x 为观察屏上纵轴坐标，D 为缝屏间距。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
11-1 钠黄光波长为589.3mm ，试以一次延续时间810-计，计算一个波列中的完整波的个数。
解 178631010510589.3c N τλ-⨯⨯==≈⨯ 11-2 在杨氏双缝实验中，当做如下调节时，屏幕上的干涉条纹将如何变化？（要说明理由）（1） 使两缝之间的距离逐渐减小；（2） 保持双缝的间距不变，使双缝与屏幕的距离逐渐减小；（3）如图11.3所示，把双缝中的一条狭缝遮住，并在两缝的垂直平分线上放置一块平面反射镜。
解 （1）由条纹间距公式Dx dλ∆=，在D 和λ不变的情况下，减小d 可使x ∆增大，条纹间距变宽。
（2）同理，若d 和λ保持不变，减小D ，x ∆变小，条纹变密，到一定程度时条纹将难以分辨。
（3）此装置同洛埃镜实验，由于反射光有半波损失，所以()212D x k d D x k dλλ=-=明暗与杨氏双缝的干涉条纹相比，其明暗条纹分布的状况恰好相反，且相干的区域仅在中心轴线上方的一部分。
11-3 洛埃镜干涉装置如图11.4所示，光源波长77.210m λ-=⨯，试求镜的右边缘到第一条明纹的距离。
解 因为镜右边缘是暗纹中心，它到第一明条纹的距离h 应为半个条纹间隔，()531120307.210 4.510220.4D h cm d λ--+==⨯⨯⨯=⨯ 11-4 由汞弧灯发出的光，通过一绿光滤光片后，照射到相距为0.60mm 的双缝上，在距双缝2.5m 远处的屏幕上出现干涉条纹。
现测得相邻两明条纹中心的距离为2.27mm ，求入射光的波长 解 有公式Dx dλ∆=得()()3372.27100.0610 5.5105502.5d x m nm D λ---⨯⨯⨯=∆∙==⨯=11-5 在双缝装置中，用一很薄的云母片（n=1.58）覆盖其中的一条狭缝，这时屏幕上的第七级明条纹恰好移到屏幕中央原零级明条纹的位置。
如果入射光的波长为550mm ，则这云母片的厚度应为多少？解 设云母片的厚度为()17ne e n e σλ=-=-=，根据题意，插入云母片而引起的光程差为()967755010 6.6101 1.581e m n λ--⨯⨯===⨯--11-6 在杨氏干涉装置中，光源宽度为0.25b mm =，光源至双孔的距离为20R cm =，所用光波波长为546nm λ=。
（1）试求双孔处的横向相干宽度d ；（2）试求当双孔间距为0.50d mm '=时，在观察屏幕上能否看到干涉条纹？（3）为能观察到干涉条纹，光源至少应再移动多少距离？ 解 （1） 由公式Rb dλ<得()62010546100.440.25R b mm d λ-⨯⨯⨯<=≈（2）不能，因为，0.50d mm '=()170.25100.50102354610bd R cm λ-'⨯⨯⨯'>=≈⨯（3）()23203R R R cm '∆=-=-=11-7 在杨氏实验装置中，采用加有蓝绿色滤光片的白色光源，其波长范围为100nm λ∆=，平均波长为490nm λ=。
试估计从第几级开始，条纹将变得无法分辨？ 解 设蓝绿光的波长范围为12λλ-，则按题意有()()()212110014902nm nm λλλλλλ-=∆=+== 相应于1λ和2λ，杨氏干涉条纹中k 级极大的位置分别为1122,D D x kx k d dλλ== 因此，k 级干涉条纹所占据的宽度为2121D D Dx x kk k d d dλλλ-=-= 显然，当此宽度大于或等于相应与平均波长λ的条纹间距时，干涉条纹变得模糊不清，这个条件可以表达为D D kd dλλ∆≥ 即4.9k λλ≥=∆ 所以，从第五级开始，干涉条纹变得无法分辨。
11-8 （1）在白色的照射下，我们通常可看到呈彩色花纹的肥皂膜和肥皂泡，并且当发现有黑色斑纹出现时，就预示着泡沫即将破裂，试解释这一现象。
（2）在单色照射下观察牛顿环的装置中，如果在垂直于平板的方向上移动平凸透镜，那么，当透镜离开或接近平板时，牛顿环将发生什么变化？为什么？解 （1）肥皂泡沫是由肥皂水形成的厚度一般并不均匀的薄膜，在单色光照射下便可产生等厚干涉花纹。
用白光照射可产生彩色的干涉花纹。
设泡沫上的黑斑这一局部区域可近似看作是厚度e 均匀的薄膜，由于它的两表面均与空气相接触，因此在薄膜干涉的反射光相消条件中须计入半波损失，其为()222sin 21,0,1,2,3,22e n i k k λλ-+=+=…… 式中，为入射光的波长，i 为光线的入射角。
挡在白光照射下观察到黑斑这一现象，说明对于任何波长的可见光在该处均产生干涉相消，于是由上面的公式可见，此时惟有k=0,厚度0e →时，才能成立。
因而黑斑的出现即使肥皂沫先破裂的先兆。
（2）在牛顿环装置中，若平凸透镜球面与平板玻璃相接触，空气膜上下表面反射光之间的光程差22e λδ=+式中e 是空气薄膜厚度，离中心不同的地方，e 的大小不同。
将平凸透镜垂直于平板方向向上移动一距离h ，则各处的空气层厚度均增加同一量值2h ，为()22e h λδ=++因此，各处的干涉条纹的级数。
每当h 增加4λ时，干涉条纹向内收缩，明与暗之间交替变化一次。
而每当h 增加2λ，干涉条纹有变得与原来相同（仅是干涉条纹的级数k 增加1）。
所以，当透镜离开（或接近）平板时，牛顿环发生收缩（或扩张），各处将整体同步地发生明、暗的交替变化，而在指定的圆环范围内，包含的条纹数目则是始终不变的。
11-9 波长范围为400nm-700nm 的白光垂直入射在肥皂膜上，膜的厚度为550nm ，折射率为1.35。
试问在反射光中哪些波长的光干涉增强？那些波长的光干涉相消？ 解 垂直入射是，考虑到半波损失，反射干涉光的光程差为22ne λδ=+当2,1,2,3,2ne k k λλ+==… 时，干涉相长，()322 1.350.55101122ne nm k k λ⨯⨯⨯=--=当3k =时594nm λ=，当4k =时424nm λ= 当2(21),0,1,2,3,22ne k k λλ+=+=…时，干涉相消，2ne kλ=取3,495k nm λ== 。
11-10 在棱镜()1 1.52n =表面涂一层增透膜，为使此增透膜()2 1.30n =适用于550m 波长的光，膜的厚度应取何值？解 设垂直入射于增透膜上，根据题意：212,0,1,2,,2n e k k λ⎛⎫=+= ⎪⎝⎭…膜厚2122e k n λ⎛⎫=+ ⎪⎝⎭ 令0k = ，可得增透膜的最薄厚度为()min 105.8e nm =11-11 有一楔形薄膜，折射率 1.4n =，楔角410rad θ-=，在某一单色光的垂直照射下，可测得两相邻明条纹之间的距离为0.25cm ，试求：（1）此单色光在真空中的波长;（2）如果薄膜长为3.5cm ，总共可出现多少条明条纹？ 解 （1） 由楔形薄膜的干涉条件得两相邻明条纹间距：2sin 2n x n λλθθ∆=≈2n x λθ=∙∆以421,10,0.2510n rad x m θ--==∆=⨯代入上式得60.710700m nm λ-=⨯=（2）在长为23.510m -⨯的楔形膜上，明条纹总数为()14lm x==∆条 11-12 图11.5为一干涉膨胀仪的示意图，AB 与A B ''二平面玻璃板之间放一热膨胀系数极小的熔石英环柱CC '，被测样品W 置于该环柱内，样品的上表面与AB 板的下表面形成一楔形空气层，若以波长为λ 的单色光垂直射于此空气层，就产生等厚干涉条纹。
设在温度为0t C ︒时，测得样品的长度为0L ；温度升高到时0t C ︒，测得样品的长度为L.并且在这过程中，数得通过视场中某一刻线的干涉条纹数目为N,设环柱CC '的长度变化可以忽略不计，求证：被测样品材料的热膨胀系数β为()002N L t t λβ=-解 该装置中AB 平板玻璃与样品W 表面中间所夹的是一楔形空气薄膜，在等厚干涉条纹中，设在温度0t 时，某一刻线所在位置对应于第k 级暗条纹，此处楔形空气层的厚度为k e 满足2k e kλ=温度升高到时，由于样品W 的长度发生膨胀，有N 条干涉条纹通过此刻线，则对应该刻线处干涉条纹级数变为k-N,于是楔形空气层厚度变为()2k N e k N λ-=-依照题意，忽略石英环的膨胀，则该处空气层厚度的减少为02k k N L L L e e Nλ-∆=-=-=由膨胀系数的定义得()0000012L L N L t t L t t λβ-=∙=-- 11-13 利用楔形空气薄膜的等厚干涉条纹，可以测量经精密加工后工件表面上极小纹路的深度。
如图11.6，在工件表面上放一平板玻璃，使期间形成楔形空气薄膜，以单色光垂直照射玻璃表面，用显微镜观察干涉条纹，由于工件表面不平，观察到的条纹如图所示，试根据条纹弯曲的方向，说明工件表面上纹路是凹的还是凸的？并证明纹路深度可用下式表示：2a Hb λ=∙ 其中a,b 如图所示。
解 纹路是凹的，因工件表面有凹纹，故各级等厚线的相应部分向楔形膜顶端移动。
两相邻暗纹间距离为b,对应高度差为2λ，则有sin 2b λθ=当条纹移动距离为a 是，对应高度差H(即纹路深度）为sin 2a H ab λθ==∙ 11-14 （1）若用波长不同的观察牛顿环，12600,450nm nm λλ==，观察到用1λ时的第k 个暗环与用2λ时的第k+1个暗环重合，已知透镜的曲率半径是190cm ，求用时第k 个暗环的半径.(2)若在牛顿环中波长为500nm 的光的第5个明环与波长为的光的第6个明环重合，求波长λ。
解 （1）牛顿环中k 级暗条纹半径k r kR λ=依照题意，当1λ光的k 级暗条纹与2λ光的第1k +级暗条纹在r 处重合是满足()121r kR r k R λλ==+由(1）、（2）式解得212k λλλ=-（3）式代入(1)式得()312121.8510R r m λλλλ-==⨯-（2）用波长1500nm λ=的光照射，15k =级的明环与用波长的光照射时，26k =级的明环重合，则有关系式()()112212122k R k R r λλ--==所以，()11221251500409.121261k nm k λλ-⨯-==⨯=-⨯-11-15 在图11.7所示的装置中，平面玻璃板是由两部分组成的（冕牌玻璃和火石玻璃），透镜是用冕牌玻璃制成，而透镜与玻璃板之间的空间充满着二硫华碳，试问 由此而成的牛顿环的花样如何？为什么？解 由于火石玻璃的折射率大于二硫化碳的折射率，而二硫化碳的折射率大于冕牌玻璃，当光波由冕牌玻璃射向二硫化碳，以及由二硫化碳射向火石玻璃时，都有“半波损失”，上、下表面反射没有额外程差2λ，而光波由二硫化碳射向冕牌玻璃时没有半波损失，因此在右半边上下表面反射有额外程差，所以此扭动环的花样有以下特点：（1）在牛顿环中心，火石玻璃一侧外为亮斑，冕牌玻璃一侧处为暗斑，（2）火石玻璃处，由中心向外为亮斑、暗斑、亮环交替变化；冕牌玻璃处由中心向外为暗斑、亮环、暗环交替变化。