Excel,wps中熵值法、熵权法、指标赋权、权重计算。
熵权法

基于熵权法评价指标权值的确定熵权法原理是把评价中各个待评价单元的信息进行量化与综合后的方法;采用熵权法对各因子赋权,可以简化评价过程。
因此,本文采用熵值法对指标的权值进行确定。
首先,由以上四个评价指标,可以得到一个449⨯的原始数据矩阵为:m n nm n n n n x x x x x x x x x X ⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=212222111211 其中,n 为日期,其取值为49天,m 为评价指标,其取值为4,n x x 111~表示排队长,n x x 221~表示逗留时间,n x x 331~表示周转次数,n x x 441~表示病床使用率。
由此,X 矩阵可知。
其次,对指标进行同趋势性变换,建立同正向矩阵;因为以上四个指标在评价时有高优指标和低优指标,其中,高优指标为周转次数和病床使用率,低优指标为排队长和逗留时间;评价时不同指标之间应该具有同趋势性,所以将低优指标化为高优指标即采用倒数法,转化后的矩阵为:m n nm n n n n y y y y y y y y y Y ⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=212222111211 将该矩阵进行归一化处理,即取Y 矩阵中列向量ij y 与该矩阵中所有元素之和的比值作为归一化结果,其计算公式如下:),,2,1(,1m j Yy z ni ijijij ==∑=其中,ij z 为归一化后矩阵中的元素;归一化后的矩阵见附录1。
在确定评价指标的熵权值时,本文规定其运算公式如下:m j z z k x H ni ij ij j ,,2,1,ln )(1=-=∑=其中,k 为调节系数,n k ln 1=,因此2569.0=k ;ij z 为第i 个评价单元第j 个指标标准化值。
通过计算可得0569.0)(1=x H ;0155.0)(2=x H ;1549.38)(3-=x H ;8242.4)(4-=x H 。
将评价指标的熵值转化为权重值:m j x H m x H d mj j j j ,,2,1,)()(11 =--=∑=其中,10≤≤j d ,∑==mj j d 11;至此,得到权重值,计算得出其权值如表5所示。
熵权法和熵值法

熵权法和熵值法嘿,你问熵权法和熵值法啊?这俩玩意儿听着挺高深,其实也不难理解啦。
咱先说说啥是熵权法哈。
有一次啊,我和几个朋友一起玩游戏,就是那种猜数字的游戏。
每个人都给出一个数字,然后我们要根据一些规则来猜出正确的数字。
这时候呢,我们就用到了类似熵权法的思路。
比如说,有的人猜的数字特别离谱,那我们就会觉得他的猜测不靠谱,给他的权重就低一些。
而有的人猜的数字比较接近正确答案,那我们就会给他的猜测更高的权重。
这就跟熵权法一样,根据不同的数据的重要性来分配权重。
熵权法呢,就是通过计算数据的熵值来确定权重。
熵值越大,说明数据的不确定性越大,权重就越低。
反之,熵值越小,数据的确定性越大,权重就越高。
就像我们玩游戏的时候,如果一个人总是乱猜,那他的熵值就大,权重就低。
如果一个人很有逻辑地猜测,那他的熵值就小,权重就高。
再说说熵值法。
有一回我去菜市场买菜,我发现不同的摊位上卖的同一种菜价格都不一样。
这时候我就想啊,怎么才能知道哪个摊位的菜最划算呢?我就想到了熵值法。
我把每个摊位的菜价都看成一个数据,然后计算它们的熵值。
熵值越大,说明价格的波动越大,不确定性越高。
熵值越小,说明价格比较稳定,确定性越高。
最后我根据熵值的大小来选择了一个价格比较稳定的摊位买菜。
熵值法呢,就是通过计算数据的熵值来衡量数据的离散程度。
熵值越大,数据越分散;熵值越小,数据越集中。
就像菜市场的菜价一样,如果各个摊位的价格相差很大,熵值就大;如果价格比较接近,熵值就小。
总之啊,熵权法和熵值法虽然听起来很复杂,但其实在我们的生活中也有很多应用。
就像玩游戏和买菜的时候,我们都可以用到类似的思路。
它们可以帮助我们更好地分析数据,做出更明智的决策。
嘿嘿,你觉得我说得对不?。
熵值法的综合指数计算公式

熵值法的综合指数计算公式熵值法是一种多指标综合评价方法,它通过计算各指标的熵值来确定各指标的权重,从而得到综合评价结果。
在实际应用中,熵值法被广泛应用于环境评价、经济评价、企业绩效评价等领域。
本文将介绍熵值法的综合指数计算公式及其应用。
首先,我们来看看熵值法的基本原理。
熵值法是基于信息论的一种多指标综合评价方法,它利用信息熵的概念来衡量各指标的不确定性程度,从而确定各指标的权重。
在熵值法中,各指标的信息熵越大,说明其不确定性程度越高,对综合评价结果的影响也越大。
因此,信息熵越大的指标在综合评价中所占的权重也越大。
熵值法的综合指数计算公式如下:\[E_j = -\frac{1}{\ln(n)}\sum_{i=1}^{n}p_{ij}\ln(p_{ij})\]其中,\(E_j\)表示指标j的熵值,n表示评价对象的指标数,\(p_{ij}\)表示评价对象在指标j下的占比。
在实际应用中,我们通常将各指标的熵值标准化处理,得到各指标的权重,然后利用权重对各指标进行加权求和,得到综合评价结果。
具体步骤如下:1. 计算各指标的熵值,根据上述公式,计算各指标的熵值。
2. 熵值标准化,将各指标的熵值除以其最大可能熵值,得到各指标的权重。
3. 加权求和,利用各指标的权重对各指标进行加权求和,得到综合评价结果。
熵值法的综合指数计算公式能够很好地反映各指标的重要性,因此在实际应用中得到了广泛的应用。
下面我们将以环境评价为例,介绍熵值法的应用。
环境评价是指对某一区域或项目对环境的影响进行全面评价,以确定其对环境的适应性和可持续性。
在环境评价中,往往涉及多个指标,如大气污染、水质污染、土壤污染等。
利用熵值法可以很好地确定各指标的权重,从而得到综合评价结果。
以某个工业项目的环境评价为例,假设涉及大气污染、水质污染和土壤污染三个指标。
首先,我们需要收集各指标的数据,并计算各指标的熵值。
然后,对各指标的熵值进行标准化处理,得到各指标的权重。
excel权重计算公式

excel权重计算公式
Excel 权重计算是一种常用的数据分析工具,它可以将多个变量的数值结合在一起,计算出一个总体的计算结果。
它主要用于求解复杂问题,比如市场营销,新产品开发,财务预测等。
Excel 权重计算的基本思想是:根据每个变量的重要性,将变量的数值进行加权,然后再求和。
这种权重的计算方法可以精确的衡量变量的重要性,并且可以得出一个总体的计算结果。
使用 Excel 权重计算的步骤如下:
1. 首先,确定要计算的变量,并输入变量的数值。
2. 然后,为每一个变量定义一个权重,衡量变量的重要性。
3.接下来,将变量的数值与权重相乘,得出权重计算结果。
4. 最后,对所有变量的权重计算结果求和,得出最终的总体计算结果。
使用Excel 权重计算可以帮助企业在复杂的环境中,快速的确定各个变量的重要性,从而能够更加有效的决策。
此外,它也可以用来评估资产配置,投资决策,产品定价等等。
总之,Excel 权重计算是一项强大而有效的数据分析工具,可以帮助企业做出更加准确的决策。
Excel-wps中熵值法、熵权法、指标赋权、权重计算。说课讲解

Excel 、wps 实现熵权法计算过程:1.熵权法下指标权重的计算熵权法下首先计算第i 年份的第j 项指标值的权重:i=1,2,3…n; j=1,2,3…m (2)令k=1/ln(n)>0,为调节系数,计算指标信息熵: i=1,2,3…n; j=1,2,3…m (3)最后确定计算指标权重:(0<w j <1,,j=1,2,3…m ) (4)1. 用标准化后的数据计算,若为时间序列下: ∑==ni ijij ij yy p 1'')ln (1ij ni ij jp p k e ∑=-=∑=--=mj jj j e m e w 1111=∑=mj j wB CA1 1998 0.1028 0.10022 1999 0.2178 0.14573 2000 0.3063 0.14254 2001 0.1000 0.16915 2002 0.2455 0.16386 2003 0.1710 0.12617 2004 0.2852 0.14658 2005 0.3170 0.12919 2006 0.6475 0.212110 2007 0.6475 0.280311 2008 0.562183898 0.40375096412 2009 0.585203446 0.58858552113 2010 0.694865622 0.46510671514 2011 0.500221291 0.47224960715 2012 1 0.60299302616 2013 0.863566837 0.55895494417 2014 0.835655753 0.523401776 18 2015 0.193615668 0.586089558 19 2016 0.521055261.00034725520 =SUM(B1:B19) =SUM(C1:C19) 21pij=B1/B$20 =C1/C$20下拉后得到19行新数据最后一步就是这个式子的计算,下拉就好了,$会让你下拉的时候总是除以20行这个数字保持不变。
权重确定方法之熵权法
权重确定方法之熵权法引言在构建指标评价体系时候,如何确定各指标权重是经常会遇到的问题,这方面的理论已经十分成熟,通常我们可以分为三大类:主观赋权法、客观赋权法以及组合赋权法。
而我们这里要讲的熵权法是客观赋权法中的经常用到的方法,它直接通过样本数据计算得出,不受人为主观因素的影响,比较符合数据分析的路子。
下面直接进入正题,介绍熵权法。
熵权法熵权法,首先得从熵说起,熵的概念最早起源于物理学,用于度量热力学系统中的无序程度。
后来在在信息论中发展起来,用来度量系统的不确定性。
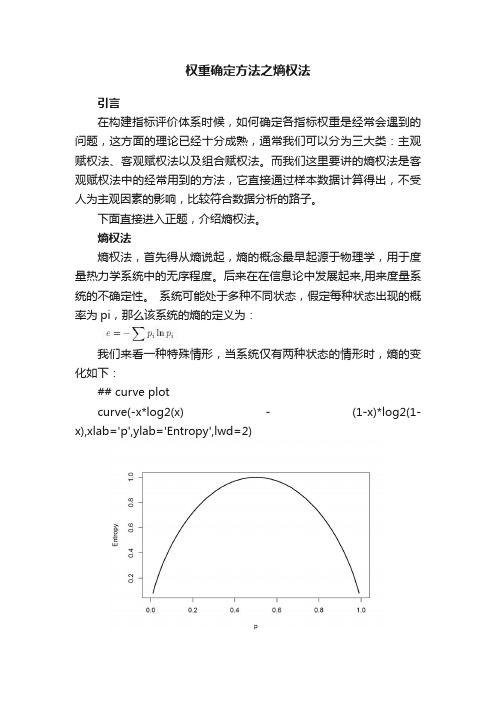
系统可能处于多种不同状态,假定每种状态出现的概率为pi,那么该系统的熵的定义为:我们来看一种特殊情形,当系统仅有两种状态的情形时,熵的变化如下:## curve plotcurve(-x*log2(x) - (1-x)*log2(1-x),xlab='p',ylab='Entropy',lwd=2)可以看到,当两种状态的概率相等时,熵的取值最大,反之,当其中一种状态的概率接近于1时,熵最小。
正是由于熵的这种性质,它在很多方面都有应用,比如在决策树中它用来度量不纯度,生成新的分支。
而在这里,用它来确定指标的权重。
一般步骤熵权法确定指标权重的一般步骤:•1 获取样本数据,该数据包含p个指标,m个样本,数据矩阵•2 计算第j个指标下第i个样本的比重矩阵•3 计算第j个指标的熵值•4 计算第j个指标的熵权权重确定后,通过加权便可计算综合指标了。
示例数据采用案例数据中的asdat数据集,尝试使用熵权法来计算各位球员的综合得分。
直接上代码:library(dplyr)# 计算综合得分#1st.数据归一化,各项指标按1-10分打分myfun <- function(x) (x-min(x))/(max(x)-min(x))*9 + 1datM <- select(asdat,pts:wr) %>% mutate_all(myfun) %>% as.matrix# 行为项目(即样本数),列为指标m <- nrow(datM)n <- ncol(datM)#2nd.计算第j个指标下第i个样本的比重矩阵P_ij <- apply(X = datM,MARGIN = 2,FUN = function(x) x/sum(x))#3rd.计算第j个指标的熵值k <- 1/log(m)e_j <- apply(X = P_ij,MARGIN = 2,FUN = function(x) -k*sum(x*log(x)))#4rd.计算第j个指标的熵权w_j <- (1-e_j)/sum(1-e_j)cat('权重:',w_j,'\t')## 权重: 0.3919 0.3966 0.2113## 综合得分library(knitr)asdat$score <- datM %*% w_j %>% round(2) %>% droparrange(asdat,desc(score)) %>% head(10)作者比较懒,直接拿以前的案例数据来做分析,套得太生硬。
熵值法 excel 计算过程

熵值法 excel 计算过程1.打开Excel软件,新建一个表格。
Open Excel software and create a new spreadsheet.2.在第一列依次输入各个选项的名称。
Enter the names of the options in the first column.3.在接下来的列中,依次输入各个选项的相关数据。
Enter the relevant data for each option in the following columns.4.在Excel中选择一个空白单元格,输入以下函数:=ENTROPY (A2:A52)Select a blank cell in Excel and enter the following function: =ENTROPY(A2:A52)5.按下回车键,Excel会自动计算出这些选项的熵值。
Press Enter, and Excel will automatically calculate the entropy of the options.6.熵值法是一种用来度量不确定性的方法。
The entropy method is a way to measure uncertainty.7.它可以帮助我们对各个选项之间的差异进行量化评估。
It can help us quantitatively evaluate the differences between the options.8.在excel中使用熵值法可以方便快捷地进行大量数据的计算。
Using the entropy method in Excel can quickly and easily calculate large amounts of data.9.通过比较不同选项的熵值,我们可以找出最优的选择。
By comparing the entropy of different options, we can find the optimal choice.10.熵值法在决策分析和风险评估中有着广泛的应用。
SPSS权重分析(熵权法)怎么做?附案例讲解一文搞懂

权重分析(熵权法)1、作用权重分析是通过熵权法对问卷调查的指标的重要性进行权重输出,根据信息熵的定义,对于某项指标,可以用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大,该指标对综合评价的影响(即权重)就越大,如果某项指标的值全部相等,则该指标在综合评价中不起作用。
因此,可利用信息熵这个工具,计算出各个指标的权重,为多指标综合评价提供依据。
2、输入输出描述输入:至少两项或以上的定量变量(正向指标与负向指标),一般要求数据为量表量数据。
输出:输入定量变量对应的权重值。
3、案例示例案例:数据是 100 个客户的各方面(能力,品格,担保,资本,环境)评分,利用熵权法来计算各个变量(能力,品格,担保,资本,环境)的重要性,即所占的权重。
4、案例数据权重分析(熵权法)案例数据模型要求为至少两项或以上的定量变量(正向指标与负向指标),一般要求数据为量表量数据,可以均为正向指标或负向指标。
其中能力,品格,担保,资本,环境均为正向指标。
5、案例操作Step1:新建分析;Step2:上传数据;Step3:选择对应数据打开后进行预览,确认无误后点击开始分析;Step4:选择【权重分析(熵权法)】;Step5:查看对应的数据数据格式,【权重分析(熵权法)】要求特征序列为类变量,且至少有两项;Step6:点击【开始分析】,完成全部操作。
6、输出结果分析输出结果1:权重分析计算结果图表说明:上表展示了熵权法的权重计算结果,根据结果对各个指标的权重进行分析。
结果分析:熵权法的权重计算结果显示能力的权重为10.484%、品格的权重为19.313%、担保的权重为28.014%、资本的权重为18.062%、环境的权重为24.128%,其中指标权重最大值为担保(28.014%),最小值为指标能力(10.484%)输出结果 2:指标重要度直方图图表说明:可选择直方图、折线图、条形图、饼图四种方式对权值比重进行可视化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel 、wps 实现熵权法计算过程:
1.熵权法下指标权重的计算
熵权法下首先计算第i 年份的第j 项指标值的权重:
i=1,2,3…n; j=1,2,3…m (2)
令k=1/ln(n)>0,为调节系数,计算指标信息熵:
i=1,2,3…n; j=1,2,3…m (3)
最后确定计算指标权重:
(0<w j <1,,j=1,2,3…m ) (4)
1. 用标准化后的数据计算,若为时间序列下:
A B C 1 1998 0.1028 0.1002 2 1999 0.2178 0.1457 3 2000 0.3063 0.1425 4 2001 0.1000 0.1691 5 2002 0.2455 0.1638 6 2003 0.1710 0.1261 7 2004 0.2852 0.1465 8 2005 0.3170 0.1291 9 2006 0.6475 0.2121 10 2007 0.6475
0.2803
11
2008
0.562183898 0.403750964
∑==
n
i ij
ij ij y
y p 1
'
'
)ln (1
ij n
i ij j p p k e ∑=-=∑=--=
m
j j
j j e m e w 1111
=∑=m
j j w
12 2009 0.585203446 0.588585521 13 2010 0.694865622 0.465106715 14 2011 0.500221291 0.472249607 15 2012 1
0.602993026
16 2013 0.863566837 0.558954944 17 2014 0.835655753 0.523401776 18 2015 0.193615668 0.586089558 19 2016 0.52105526
1.000347255
20 =SUM(B1:B19) =SUM(C1:C19) 21 pij =B1/B$20 =C1/C$20
下拉后得到19
行新数据
最后一步就是这个式子的计算,下拉就好了,$会让你下
拉的时候总是除以20行这个数字保持不变。
66 =B21*ln(B21) =C21*LN(C21)
67
下拉后得到19
行新数据
68
(方便起见这里就以这个表格位置输
入了,实际操作中肯定不是,因为
=C$68*B66
=C$*C66
-k=-ln(1/19)(表格中位置为
(C68)
∑==
n
i ij
ij ij y
y p 1
'
'
每次计算都会多19行数据,不会是68,也不会是66,)
下拉后得到19
行新数据
=sum (上面19个数据)
=sum (上面19个
数据) 得到的就是ej
计算出-k=-ln(1/19),因为标准化后的初始数据有19个年份的数据
的计算过程如上
102
e1
e2
102) 103
=(1-b102)/d$103
小十字横拉
过来
=2-D102(为只有两指标赋权)
)ln (1
ij n
i ij j p p k e ∑=-=
计算过程如上。
Wj 的和肯定为1.否则则是计算出错。
∑=--=
m
j j
j j e m e w 11。
