6自由度控制算法
六自由度机械臂轨迹规划算法设计及仿真分析
准 化 算法 ，将 时 间进 行 处理 ，经 过 处 理 后 的 时 间
０ 引言
随 着 相 关 科 学 技 术 和 计 算 机 技 术 的 高 速 发
展 ， 传 统 的 机 械 系统 已 不 能 满 足 社 会 进 步 的 需 求 ， 机 械 系 统 正 朝 着 智 能 化 和 信 息 化 的 方 向发
法 可 以实 现对 （ ｎ 一 １ ） 段３ 次 多项 式 每一 段 的 系数 进 行 求 解 ，其 中 采用 了时 间 归 一化 算 法 ，从 而 简化 了 求解 的过 程 ，大大提 高 了计算 的效率 。 算法 具体 实现过 程 ： １ ）时 间标 准化 算法 根 据 三 次 多 项式 轨 迹 规 划 的流 程 可 知 ，对每
ａｎｄ ｓｉ ｍ ｕｌ ａｔ ｉ ｏｎ ａｎ ａｌ ｙ ｓｉ ｓ
李进 生
Ｌ Ｉ Ｊ ｉ ｎ － ｓ ｈ ｅ ｎ ｇ
（ 武汉软件工程职业学院 ，武汉 ４ ３ ０ ２ ０ ５ ）
摘 要 ： 六 自由度机械臂轨迹规划关键技术是要设计一套机器臂轨迹规划算法 ，本文设计的轨迹规划算 法可以根据使 用者的作业任 务要求 ，计算 出六自由度机械 臂末端执行器 预期的轨迹 。因为对 六 自由度机械 臂的轨迹控制 最终是通过六 个关节的轨迹 来具体实现 的 ，所以算法将轨 迹换算 成六个关 节的预期轨迹 ， 将 其作为位置 信息 ，实 时发 送给相应 的关 节控制器 ，借 此实现六自 由度机械臂的运 动控制 。
基于遗传算法的六自由度平台参数优化设计
量 Ｘ＝【 Ｒ ｔ Ｏ ｒ Ｏ ／ ｌ ２
】 。
Ｆ
Ｆ６
Ｆ２ Ｆｓ 、
Ｆ
Ｆ
｜
１２ 约 束条件 确定 ． 该平台主要用于 室 内演示 ，要 求 占用 空 间有 限 ， 便于移动 ，因此确定各参数尺寸 范围如下 ：
０． ≤ ｒ ０ ６ Ｉ ２ｍ ≤ ． １ Ｔ
图 ２ 平 台驱 动 杆 受 力 示 意 图
若 已知上 平 台 的位姿 （ ，Ｙ ， ，Ｏ ｔ ，卢，ｙ ， ）
则可得到各驱动杆 的长度 、受力 以及运动速度 ，即驱
图中 ，坐标 系 ０ｘｚ 一ｙ 为定坐标 系 （ 坐标原点 ０位
于下平台铰接点外接 圆 中心 ，方 向如 图示 ） ，坐标 系
收 稿 日期 ：２ １ — ４—１ ０１ ０ ８ 基 金 项 目 ： 国家 ８ ３项 目 （ ０ ８ Ａ ４ ８ ２ ６ ２０Ａ ０２０ ）
２１ ０２年 ５月 第４ Ｏ卷 第 １ ０期
机床与液压
Ｍ ＡＣＨＩ ＮＥ ＴＯＯＬ ＆ ＨＹＤＲＡＵＬ ＣＳ Ｉ
Ｍａ ０ ２ ｖ２ １
Ｖｏ． ０ Ｎｏ １ １４ ． ０
Ｄ ：１ ．９ ９ ｊｉｓ． ０ １—３ ８ ． ０ ２ １ ． ０ ＯＩ ０ ３ ６ ／．ｓｎ １ ０ ８ １２ １．０ ０ １
Ｗ ＡＮＧ ｕ Ｊ ｎ， Ｗ Ｕ Ｈａ ｑ ， Ｗ ＡＮＧ Ｗ ｅ ， Ｃ Ｎ ｕｉｎ ｎｉ ｉ ＨＥ Ｚ ｌ ｇ ａ
（ ａｙＩｔｌｇｎ ｏ ｔ ｌ ｑ ｉｍｅｔ ｏ ，Ｌｄ ｈ ｎ ｓａＨ ｎｎ４ ０ ０ ，Ｃ ｉａ Ｓ ｎ ｅｌ ｅｔ ｎｒ ｕｐ ｎ ． ｔ ，Ｃ ａｇｈ ｕ ａ １ １０ ｈｎ ） ｎ ｉ Ｃ ｏＥ Ｃ
Ａ Ｘ） （ 为在 结构参数 下 ，分 别实 现 ６个单 由 度运动规律过程 中，各驱动杆所受最大 力的函数 ； 曰 ） （ 为在结构参数 下 ，分 别实 现 ６个 自由 度运动规律过程 中，各驱动杆最大速度的函数 ； Ｃ ） （ 为在结构参 数 下 ，分别实 现 ６个单 自
基于NI实时控制器的六自由度平台测控系统设计与实现
基于NI实时控制器的六自由度平台测控系统设计与实现王效亮;张芳;曾宪科;栾婷;陈成峰【摘要】六自由度平台测控系统是六自由度平台的电气控制部分,它通过对六路液压缸的实时闭环控制,实现对平台位姿的控制;该测控系统采用NI的计算机,配置多种类型的PXI板卡,实现了对平台的电压、电流、数字IO、CAN总线等多种接口类型的测量和控制,满足了可靠性需求;采用了典型的上下位机控制,分别进行实时计算与任务管理,解决了实时性的控制需求;采用NI的虚拟仪器Labview开发测控软件,完成实时计算平台的正解与反解模块,作动器闭环控制等功能,增强系统的功能和灵活性;目前六自由度平台测控系统的硬件部分和软件部分都已经通过了调试,对系统进行了正弦运动和暂态特性测试,实验结果表明,运行速度快,满足了平台的控制要求.【期刊名称】《计算机测量与控制》【年(卷),期】2019(027)002【总页数】6页(P24-28,33)【关键词】六自由度平台;软件;SIT仿真模型【作者】王效亮;张芳;曾宪科;栾婷;陈成峰【作者单位】北京精密机电控制设备研究所,北京 100081;北京精密机电控制设备研究所,北京 100081;北京精密机电控制设备研究所,北京 100081;北京精密机电控制设备研究所,北京 100081;北京精密机电控制设备研究所,北京 100081【正文语种】中文【中图分类】TP273+.50 引言六自由度平台是一种模拟航天器空间运动姿态的模拟器，在其行程范围内可以模拟任意空间运动。
六自由度是平台具有六个自由运动的维度，即纵向、升降、横向、俯仰、横滚、偏航[1]。
通过对6个液压作动器的精确控制和解藕算法，实现对平台的6个自由度的位姿控制。
其系统示意图如图1所示。
图1 六自由度平台示意图六自由度运动平台可以实现对既定的轨迹的跟踪，作为运动仿真平台有着广泛的应用：1)可以作为航空飞行模拟器；2)可以作为机器人的模拟运动机构；3)在娱乐界可以作为体感模拟娱乐机；4)用作飞机、船舶、潜艇、航天器等运动载体中相关仪器设备的试验。
六自由度电磁跟踪系统位置参数求解算法的改进
六自由度电磁跟踪系统位置参数求解算法的改进殷勤;陈彬;汪莹;杨波【摘要】为了获得精度较高、稳定性较好的六自由度电磁跟踪系统目标参数求解算法,在分析原参数求解算法误差产生原理的基础上,引入特征值和特征向量的概念,提出了一种结合特征向量法和单位指向矢最大分量跟踪法的改进算法来求解目标的位置参数,并对改进算法的稳定性进行了分析.通过数值模拟和实验验证,算法很好地解决了原跟踪算法在位置参数α、β角度较小区域将误差放大的问题,提高了算法的稳定性和系统定位计算的精度.【期刊名称】《解放军理工大学学报（自然科学版）》【年(卷),期】2010(011)006【总页数】4页(P613-616)【关键词】电磁跟踪系统;跟踪算法;特征向量【作者】殷勤;陈彬;汪莹;杨波【作者单位】解放军理工大学,工程兵工程学院,江苏,南京,210007;解放军理工大学,工程兵工程学院,江苏,南京,210007;解放军理工大学,理学院,江苏,南京211101;解放军理工大学,工程兵工程学院,江苏,南京,210007【正文语种】中文【中图分类】TN961六自由度电磁跟踪系统是一种新型的跟踪定位装置,可实时地确定目标的 6个参数(位置参数 R、T、U,姿态参数j、θ、O),在机载火控系统、精密医疗器械、虚拟现实系统、作战模拟训练和管道缺陷无损检测等[1～4]方面获得了广泛的应用。
文献[7]以跟踪算法为基础提出了一种目标参数求解的算法。
在数值模拟中,对于理想接收信号,该算法能够快速准确地求解出目标的位置参数,而在系统实验调试时,当接收信号存在误差时,特别是位置参数T、U值较小,计算结果误差较大,说明该算法对误差比较敏感,稳定性较差。
文献[8]利用特征向量法求解电磁式头盔瞄准具位置参数,稳定性较好,但是参数求解范围有限,不能满足系统全方位定位计算的要求。
本文结合特征向量法和跟踪算法,对原系统最大分量的跟踪算法进行改进,解决了原算法局部误差放大的问题,提高目标参数的求解精度和算法的稳定性。
六自由度机械臂逆运动学算法
六自由度机械臂逆运动学算法六自由度机械臂逆运动学算法六自由度机械臂逆运动学算法朱齐丹王欣璐（哈尔滨工程大学，哈尔滨，150001）摘要：根据D-H参数法确定六自由度机械臂的运动学方程，结合平面几何法和欧拉角变换法将机械臂的逆运动学求解问题分为两部分，一通过平面几何法确定机械臂腕部点的坐标与前三个关节角的关系，二通过欧拉角变换法确定机械臂末端姿态与后三个关节角的关系，根据逆运动解的选取原则从八组解中选取最优解；利用MATLAB中的Robotics Toolbox建立机械臂的正运动学模型，通过多组位姿下的正逆运动解对比验证逆运动学求解算法的准确性；利用VC++中的QueryPerformanceCounter函数和MATLAB中tic-toc 语句得到不同算法所消耗的平均时间，通过消耗时间的对比说明该算法的快速性；利用VC++编程实现机械臂写字的过程，通过对比输入字的形状与机械臂末端的实际运动轨迹，进一步验证该算法是一种快速而准确的逆运动学求解算法。
关键词：机器人，六自由度，机械臂，逆运动解，平面几何法，欧拉角变换法0 引言机械臂被广泛应用于机械制造、航空航天、医疗和原子能等领域，机械臂的逆运动学问题是其轨迹规划与控制的重要基础，逆运动学求解是否快速准确将直接影响到机械臂轨迹规划与控制的精度，因此针对工业中常用的六自由度机械臂，设计一种快速准确的逆运动学求解方法是十分重要的。
目前，机械臂逆运动学的求解方法主要有：迭代法、解析法和几何法。
迭代法虽然在大多数情况下是可行的，但却无法得到全部解；解析法计算较为复杂，但可以得到全部根；几何法针对机械臂的某些特殊结构进行简化，再进行求解，虽然对于一般机械臂不通用，但是其形式简单，求解所需的计算量远远小于迭代法和解析法。
Paul 等[1]于1981年提出的解析算法对后来的机械臂逆运动学问题研究有着指导性意义。
Regnier[2]于1997年提出一种基于迭代法和分布式的算法，能够求出多种结构的六自由度机械臂的位置逆解，但相应的计算时间也会变长。
六自由度运动平台设计方案
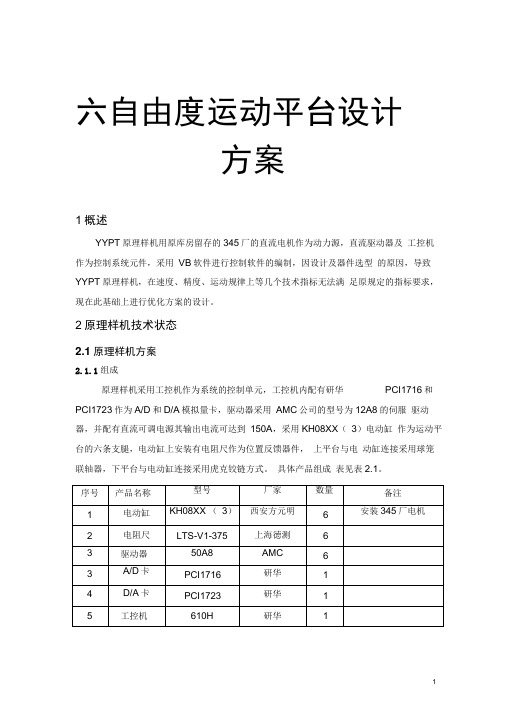
六自由度运动平台设计方案1概述YYPT原理样机用原库房留存的345厂的直流电机作为动力源，直流驱动器及工控机作为控制系统元件，采用VB软件进行控制软件的编制，因设计及器件选型的原因，导致YYPT原理样机，在速度、精度、运动规律上等几个技术指标无法满足原规定的指标要求，现在此基础上进行优化方案的设计。
2原理样机技术状态2.1原理样机方案2.1.1组成原理样机采用工控机作为系统的控制单元，工控机内配有研华PCI1716和PCI1723作为A/D和D/A模拟量卡，驱动器采用AMC公司的型号为12A8的伺服驱动器，并配有直流可调电源其输出电流可达到150A，采用KH08XX（3）电动缸作为运动平台的六条支腿，电动缸上安装有电阻尺作为位置反馈器件，上平台与电动缸连接采用球笼联轴器，下平台与电动缸连接采用虎克铰链方式。
具体产品组成表见表2.1。
2.1.2结构方案六自由度运动平台是由六条电动缸通过虎克铰链和球笼万向节联轴器将上、下两个平台连接而成，下平台固定在基础上，借助六条电动缸的伸缩运动，完成上平台在三维空间六个自由度（X，丫，Z，a，B, 丫）的运动，从而可以模拟出各种空间运动姿态。
图1六自由度平台外形图a）球笼联轴器（如图2所示）采用球笼铰链与上平面连接。
球笼铰链结构简单、体积小、运转灵活、易于维护。
初选球笼铰链型号BJB （JB/T6139-1992）,公称转矩Tn=2000N/m，工作角度40度，外径D=68mm,轴孔选用圆柱孔d=24mm,总长度L1=148mm ,转动惯量为0.00008kg.m2，重量5kg。
图2球笼联轴器b）虎克铰链（如图3所示）采用虎克铰链与下平面连接。
万向节铰链传动效率高，允许两轴间的角位移大，适用于有大角位移的两轴之间的连接，一般两轴的轴间角最大可达35o~45o,噪音小，对润滑要求不高，传递转矩大，而且使用可靠，因此获得广泛的应用。
图3虎克铰链F固定板的连接（如图4所示）F 固定板与电动缸用法兰连接初选深沟球轴承型号61808 (GB/T276-1994),额定载荷 Cr=5.1kN ，外径D=52mm ，轴承孔选用 d=40mm ，宽 B=7mm ，重量 0.26kg 。
6自由度控制算法
6自由度控制算法在机器人控制与运动规划中，6自由度（6DoF）控制算法是一种常用的方法。
这种算法可以实现对机械臂或机器人的六个自由度进行精确控制，使其在三维空间内能够实现各种复杂的运动轨迹和任务。
6自由度控制算法的核心思想是：通过对机械臂的关节角度进行精确控制，从而实现末端执行器的运动。
一般来说，典型的6自由度机械臂由6个关节组成，每个关节可以控制一个自由度。
常见的机械臂有工业机械臂、服务机器人臂等。
实现6自由度控制的算法可以分为两个主要步骤：逆运动学求解和控制器设计。
逆运动学求解是根据机械臂的末端位姿（位置和姿态），确定关节角度以实现期望运动。
控制器设计是针对不同的任务需求，设计合适的控制策略以保证机械臂的精确控制和稳定性。
在逆运动学求解方面，一种常用的方法是使用解析解法。
对于六自由度的机械臂，可以通过对正运动学方程求逆，从而得到关节角度与末端位姿之间的映射关系。
一般来说，这种方法可以快速计算出关节角度，但对于一些特殊情况（例如奇异构型）可能无法求解解析解，需要使用数值解法来求解逆运动学问题。
在控制器设计方面，常见的方法包括PID控制、基于模型的控制（如轨迹跟踪控制、力/力矩控制）和基于反馈线性化的控制等。
PID控制是一种经典的控制策略，通过调节比例、积分和微分参数，实现机械臂位置和速度的精确控制。
基于模型的控制方法利用机械臂的动力学模型，通过预测机械臂的运动轨迹或实施力/力矩控制来实现精确控制。
而基于反馈线性化的控制方法，则通过设计非线性转换器和线性控制器，将非线性动力学系统转化为线性系统，从而实现控制目标。
除了逆运动学求解和控制器设计，6自由度控制算法还需要考虑如传感器选取与数据融合、路径规划、碰撞检测和碰撞回避等问题。
传感器可以提供机械臂的姿态和位姿信息，用于控制系统的反馈；数据融合则将多个传感器的信息进行整合，提高机械臂的感知能力。
路径规划是将机械臂的运动轨迹优化为最佳路径，以提高运动效率和精确度。
6自由度算法
6自由度算法
6自由度算法是一个在机器人学中常用的概念，它指的是描述机器人在三维空间中的运动的六个自由度。
这六个自由度分别是：平移自由度（x、y、z轴方向上的移动）和旋转自由度（绕x、y、z轴的旋转）。
在机器人的运动控制中，六自由度算法被广泛应用于路径规划、逆运动学求解以及姿态控制等方面。
路径规划是机器人在给定起点和终点的情况下，通过计算合适的路径来实现从起点到终点的移动。
在使用六自由度算法进行路径规划时，机器人需要考虑到其在三维空间中的运动限制，例如避免碰撞障碍物或者避免出现关节超过其可行动范围的情况。
通过合理地选择路径规划算法和使用六自由度算法，机器人可以更加高效地完成路径规划任务。
逆运动学求解是指根据给定的机器人末端执行器的位置和姿态，计算机器人各关节的角度以实现末端执行器的准确位置控制。
在实际应用中，通过使用六自由度算法，机器人可以根据末端执行器的位置和姿态，逆向计算出各关节的角度，并将其应用于机器人的控制系统中，实现精确的位置控制。
姿态控制是指机器人在执行任务过程中，保持特定的末端执行器姿态。
通过使用六自由度算法，机器人可以根据任务要求，计算出合适的关节角度，使得末端执行器保持所需的姿态。
这对于需要精确控制姿态的应用场景，如装配、焊接等任务非常重要。
总的来说，六自由度算法在机器人的运动控制中起到了至关重要的作用。
它能够帮助机器人实现路径规划、逆运动学求解和姿态控制等任务，提高机器人的运动精度和效率。
未来随着机器人技术的不断发展，六自由度算法也将进一步完善和应用于更多的机器人应用场景中，为人们的生产和生活带来更多的便利和效益。
6自由度水下机器人动力学分析与运动控制
Ａｂ“聃ｃｔ：功ｍ锄ｉｃ柚ａｌｙｓｉｓ姐ｄ ｍｏ曲ｎ ｃ∞ｔｍｌ ｏｆ廿ｌｅ ６一ＤＯＦ
硼１ｄ豇ｗａｔｃｒ ｒｏｂｏｔ ａｒｃ ｒ髓ｅ缸ｃｈｅ文Ｆｉｒｓｔｌ弘ｃｏｎｓｉｄｅｆｉｎｇ ｍｅ∞ｍ－
ｆａｃｔｏ坪ｓｕｃｈ∞ｔｈｅ刚坝 ｐ碍ｈｅｎｓｉＶｅ ｊｎｆｌｕ％ｃｅ ｃａｕｓｅｄ ｂｙ
ｂ∞ｙ锄ｃｙ’ｍ如ｉｎｇ ｆｏｒｃ髑，ｈｙｄｒｏ由ｍ锄ｉｃ ｆ．ｏｒｃ髓。ｅｔｃ．，由ｍａｍｉｃ
瑚ｄｅ聊ａｔｅｒ ｒｏｂｏｔｓ【Ｊ】．１１１ｔｅｌ瑚ｔｉ∞ａｌ
ｏｆ Ｏ由妯。坞锄ｄ
Ｐｏｌ盯Ｅｎ咖ｅｃｒｉｎｇ’２００３，１３（２）：１２０－１２７．
【４】陈伟．水下无人潜器回收导引和控制技术的研究【Ｄ】． 哈尔滨：哈尔滨工程大学，２００１．
万方数据
机械工程学报
第４３卷第７期
【５】蒋新松，封锡盛，王棣棠．水下机器人【Ｍ】．沈阳：
作者： 作者单位： 刊名：
英文刊名： 年，卷(期)： 被引用次数：
边宇枢， 高志慧， 贠超， BIAN Yushu， GAO Zhihui， YUN Chao 北京航空航天大学机械工程及自动化学院,北京,100083
机械工程学报 CHINESE JOURNAL OF MECHANICAL ENGINEERING 2007,43(7) 3次
墨为对角阵，对角阵元素分别为ｌＯ和１００，仿真步 长为０．０１ ｓ。图６～８分别为飘ｙ和ｚ方向的偏差变 化曲线。从图中可以看出，水下机器人的实际轨迹 与理论轨迹在ｘ轴、ｙ轴和ｚ轴三个方向上的偏差 趋近于零，从而验证了水下机器人的动力学模型是 正确的，控制方法是可行的。
７结论
从运动控制的角度出发，综合考虑重力、浮力、 推力和水动力的影响，建立了比较完整的６自由度 水下机器人的动力学模型，在此基础上利用解出加 速度法设计了非线性控制器对水下机器人的路径跟 踪进行控制。从控制的仿真结果可以看出：用文中 方法对水下机器人的运动实施控制，可以使机器人 具有较强的抗干扰能力，准确实现对时变理论轨迹 的跟踪。
六自由度机器人的圆弧轨迹规划算法研究
１ ２ ：起 点到 第 －Ａ实 际 的运动 时 间 ； ２ ３ ：第 － ＇ Ａ 到终 点 实际 的运动 时 间 。
轨迹规划 分为关节空间和笛卡尔空 间的轨迹 规 划 ， 大 部 分 科 学 文 献 对 关 节 空 间 基 于 时 间 最 优 、 能 量 最 优 和 加 速 度 最 优 进 行 了 轨 迹 规 划 研 究 。 在 笛 卡 尔 空 间 ，文 献 ［ ２ ］ 只 对 其 位 置 进 行 规 划 ， 文献 【 ３ 】 先对 位 置 规 划 得 出总 运 动 时 问 ，再 对
Ｄ ｏ ｉ ：１ ０ ． ３ ９ ６ ９ ／ Ｊ ． （ ｓ ｓ ｎ ． １ ０ ０ ９ － ０ １ ３ ４ ． ２ ０ １ ３ ． １ １ （ 下） ． ０ ２
文章编号 ：１ ０ ０ ９ － ０ １ ３ ４ （ ２ ０ １ ３ ） １ １ （ 下） －０ ０ ０ ５ － ０ ３
迹规划算法的输入量都是 ：几何路径 ，运动和动
力 方 面 的 约 束 。 各 关 节 或 机 器 臂 末 端 的 规 划 输 出 量是 ：各 插 补点 的位 姿 ，速度 和加 速 度 Ⅲ。
、 是 、
磊、 、
：各姿态角起点到第二点的时间；
：各 姿态角第二 点到终 点的时 间；
赁。
２ ）对 圆弧 的位 置 进 行规 划 ：起 点到 终点 间采 用 速度 梯形 曲线 进行 规划
。
Ｐ ３ （ ３ 、 Ｙ ３ 、 ｚ ｓ 、 ３ 、 、 ３ ） ：圆弧上 的终 点； ｖ ｏ： 已知 的速 度 ； ａ ｏ ： 已知 的加 减 速 度 ； ｉ ： 速 度
六自由度机械臂控制系统设计与运动学仿真
六自由度机械臂控制系统设计与运动学仿真一、本文概述随着机器人技术的快速发展，六自由度机械臂作为一种重要的机器人执行机构，在工业自动化、航空航天、医疗手术等领域得到了广泛应用。
六自由度机械臂控制系统设计与运动学仿真研究对于提高机械臂的运动性能、优化控制策略以及实现高精度操作具有重要意义。
本文旨在深入探讨六自由度机械臂控制系统的设计原理与实现方法，并通过运动学仿真验证控制系统的有效性和可靠性。
本文将首先介绍六自由度机械臂的基本结构和运动学原理，包括机械臂的正运动学和逆运动学分析。
在此基础上，详细阐述六自由度机械臂控制系统的总体设计方案，包括硬件平台的选择、控制算法的设计以及传感器的配置等。
接着，本文将重点介绍控制系统的核心算法，如路径规划、轨迹跟踪、力控制等，并分析这些算法在六自由度机械臂运动控制中的应用。
为了验证控制系统的性能，本文将进行运动学仿真实验。
通过构建六自由度机械臂的运动学模型，模拟机械臂在不同工作环境下的运动过程，并分析控制系统的实时响应、运动精度以及稳定性等指标。
本文将总结六自由度机械臂控制系统设计与运动学仿真的研究成果，并展望未来的研究方向和应用前景。
通过本文的研究，旨在为六自由度机械臂控制系统的设计与优化提供理论支持和实践指导，推动机器人技术在各领域的广泛应用和发展。
二、六自由度机械臂基本理论六自由度机械臂，又称6DOF机械臂，是现代机器人技术中的重要组成部分。
其理论基础涉及机构学、运动学、动力学以及控制理论等多个领域。
六自由度机械臂之所以得名，是因为其末端执行器（如手爪、工具等）可以在三维空间中实现六个方向上的独立运动，包括三个平移运动（沿、Y、Z轴的移动）和三个旋转运动（绕、Y、Z轴的转动）。
机构学基础：六自由度机械臂的机构设计是其功能实现的前提。
通常，它由多个连杆和关节组成，每个关节都有一个或多个自由度。
通过合理设计连杆的长度和关节的配置，可以实现末端执行器在所需空间内的灵活运动。
六自由度机械臂轨迹规划及优化研究
六自由度机械臂轨迹规划及优化研究一、本文概述理论基础与问题阐述：本文将系统梳理六自由度机械臂的数学模型，包括其笛卡尔坐标系下的运动学逆解与正解、动力学建模，以及关节空间与操作空间之间的转换关系。
在此基础上，明确阐述轨迹规划与优化所面临的关键问题，如奇异位形规避、关节速度与加速度限制、路径平滑性要求、动态负载变化等因素对规划算法设计的影响。
轨迹规划方法：针对上述问题，我们将探讨和比较多种有效的轨迹规划策略。
这包括基于插值的连续路径生成方法（如样条曲线、Bzier曲线），基于优化的全局路径规划算法（如RRT、PRM等），以及考虑机械臂动力学特性的模型预测控制（MPC）方法。
对于每种方法，将详细分析其原理、优势、适用场景及可能存在的局限性，并通过实例演示其在典型任务中的应用效果。
轨迹优化技术：在基本轨迹规划的基础上，本文将进一步探究如何运用先进的优化算法对初始规划结果进行精细化调整，以达到性能最优。
这包括使用二次规划、非线性优化、遗传算法等手段对轨迹的关节角序列、时间参数化、能量消耗等指标进行优化。
还将讨论如何引入避障约束、柔顺控制策略以及自适应调整机制，以增强机械臂在复杂环境和不确定条件下的适应性和鲁棒性。
实验验证与性能评估：本文将通过仿真研究与实际硬件平台上的试验，对所提出的轨迹规划与优化方案进行详细的验证与性能评估。
实验设计将涵盖多种典型应用场景，考察规划算法的计算效率、轨迹跟踪精度、能耗表现以及对意外扰动的响应能力。
实验结果将以定量数据与可视化方式呈现，以便于对比分析和理论验证。
本文致力于构建一套全面且实用的六自由度机械臂轨迹规划与优化框架，为相关领域的研究者和工程技术人员提供理论指导与实践参考，推动六自由度机械臂技术在实际应用中的效能提升与技术创新。
二、六自由度机械臂系统建模在六自由度机械臂的研究与应用中，系统建模是一个关键环节。
本节将重点讨论六自由度机械臂的数学建模，包括其运动学模型和动力学模型。
基于6自由度机械臂系统的路径规划算法
、 、 、 、
、
（ １ ２ ）
由 式 （１ ２）可 解 得 ｍ值 的取 值 空 间 ，联 立 式
，
， ， ，
（ １ １），可 解得 ｎ 值 ， 由此 可 得 出
范 围。 由此可得
坐 标 的取 值
／
～ 一 ， ，
图５ 平 面 三 连 杆 坐 标 系示 意 图
， ｚ ≥０
（１ ０）
将 （ ｍ，， ｚ ）点 代 人 到 网 Ｏ 方 程 ，联 立 式
（ ２）和 （ １ ０）可得
， ｚ＝
√ 一 ｍ
（ １ １ ）
联立式 （ ７）和 （ １ １ ）可得
√ （ 一 ） ＋ （ ６ 一 √ － ｍ ２ ） ≥ √ ＋
由ｌ ｌ ≤ 可知
负 值 ；若Ｐ 点在 直线 Ｎ 下半 部 ， ０ 取 正值 。
ｌ Ｍ Ｐ １ ＞ ４ ｌ ＃ ＋
也即 √ （ 一 ， ） ＋ （ ６ 一 ） ， 、 『 ２ ＋
由机械 臂臂 长参 数ｆ 。 、ｆ 、ｆ 。 值可 知
（ ６ ）
Ｉ
方程 为 （
Ｉ ≤ｆ １ ＋ ｆ ３
（ ３ ）
６ ｌ ａ Ｉ ｒ ｃ ｓ ｌ ｎ ■
（ １ ３）
以 （ ， ）为 圆心 ，１ ２ 为半 径 作 圆 ，该 圆
） ＋（ ｙ － ｎ） ＝ ｆ ２
（ ４）
以Ｐ （ ａ ，ｂ）为 圆心 ，１ ３ 为 半径 作 圆Ｐ ，该 圆
（ ７ ）
由机 械臂 参数 规定 ， ０ 、 ０， 、０ 取 值均 在 空
间 ｌ 一 三 ， Ｉ 内 。
３ ＿ ３ 路径 规 划算 法 的优 化
基于Leap Motion的六自由度机械臂控制系统
Ｂ
ｍ（ Ｊ ）
２ ． ２ 整体 软 件设 计 本 项 目在软 件 设计 与实 现 中 ，Ｐ Ｃ端 采用 Ｗｉ ｎ ｄ ｏ ｗｓ 系 统 、ｃ ＋ ＋ 语 言 。 主 程 序 启动 后 ，进 行 Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ ｏ ｎ 操 作 和 按键 操 作 的选 择 界 面 ，当 操作 者 执 行 个 手 势 后 ，Ｐ Ｃ端 会 有 相 应 的 函 数 对 操 作 进 行 解 析 ， 再 通 过 串 口发 送 给 Ａ ｒ ｄ ｕ ｉ ｎ ｏ 开 发板 控 制机 械 臂 的舵 机 ，从 而 控 制机 械 臂 的旋 转 和抓 取 运动 。
等 的非 接 触式 人 机 交互 本 文设 计 了一种 新 型的 移动 机械 臂 控 制 系统 ，即利 用Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ ｏ ｎ 体 感设 备 控 制 器代替 传 统的 人机 交互 方式 ，进 行
人体 手 部 动作 的数 据 采集 ，将 其 识 别 的手 势 动作 经 过计 算机 分析 处 理后 ，控 制 六 自由度 的 机械 臂 进行 旋 转 、抓 取 等任 务 。 文章 分析 了Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ Ｏ Ｈ 的 原理 和技 术基 础 ，然后 给 出了整个 系统 中六 自由度机 械臂 的控 制 模 型 实验 测试 结 果表 明 系统 可 实 时控 制机 械 臂并 较 为准确 地模 拟
０ ｔ ＝ ａ ｍ￣ ｔ （ 苎 二 土 ） ＋ 一 ０
一
２
图 １系统 结 构框 图 １ ． １ Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ ｏ ｎ 手 势 传 感设 备 Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ ｏ ｎ 是Ｌ ｅ ａ ｐ 公１ 卅生 产 的 一 种 专 门采 集手 部 运 动 信 息 的 传 感 器 ， 内 部 主 要 由 颗 红 外 Ｌ Ｅ Ｄ和 两 个 摄 像 头 构 成 。 利 用 视 差 对 进 入 视 野 以 别 区 内 的 目标 立 二 维 影 像 模 型 ， 并 实 时 获 取手 势 的 空 间 信 息 。基 于 计 算机 视 觉 的 Ｆ势 识 别 算 法 仃 琏 于模 板 匹配 的 算法 、 基 于 神 经 网 络 的 算 法 和 基 于 隐 尔 町 夫模 ’ 的 算法 等 ， 由此 得 小 Ｌ ｅ ａ ｐ Ｍｏ ｔ ｉ ｏ ｎ 检 测 到 的 手 对象属性表如 捉１ 所示 。 表１手对 象属性表
六自由度喷涂机器人结构设计及控制共3篇
六自由度喷涂机器人结构设计及控制共3篇六自由度喷涂机器人结构设计及控制1六自由度喷涂机器人结构设计及控制随着制造业的发展，机器人已经被广泛应用于生产线的自动化生产中。
其中，喷涂机器人是其中的一种典型应用。
而当涉及到六自由度喷涂机器人的结构设计及控制时，更需要考虑其复杂性和高精度的要求。
一、六自由度喷涂机器人结构设计1、机械结构六自由度喷涂机器人的机械结构主要包括：（1）底座、支架：底座承载整个机器人，用来支持其机械运动系统的移动；而支架则承载喷涂枪，完成喷涂操作。
（2）关节连接处：分别为底座转轴、肩部转轴、肘部转轴、腕部转轴、手部旋转轴和手部前后移动轴，用来实现机器人的六个自由度。
（3）运动机构：用来实现机械手运动的机构，其中包括减速机、电动机、蜗轮蜗杆等。
2、喷涂系统喷涂系统主要由喷涂枪、贮液桶、涂料管路和涂布机构等组成。
其核心部分是喷涂枪，通常使用喷雾型或高压喷涂型枪头，可以通过电磁阀控制气液流量来完成涂布操作。
3、控制系统机器人控制系统是机器人运作的核心，主要包括控制器、编码器、传感器、处理器等组件。
它可以实现自主控制、运动规划、轨迹控制及误差修正等功能。
二、六自由度喷涂机器人控制1、运动规划机器人的自由度有六个，因此机器人的控制需要先进行轨迹规划，确定机器人的运动轨迹。
轨迹规划通常采用树形规划、势场规划、自适应控制等算法。
2、轨迹控制机器人运动轨迹的控制是机器人完成喷涂任务的基础。
通过轨迹控制，可以根据预先设定的速度、加速度和运动方向等参数来控制机器人的运动。
轨迹控制常常采用PID控制算法、滑动模式控制算法等。
3、误差修正机器人运动过程中难免会出现机械臂的摆动、移动误差等问题。
因此，需要对机器人的运动轨迹进行精细调整，使用传感器对机器人运动误差进行实时监测，通过机器人控制器对机器人运动轨迹进行误差修正。
三、结论六自由度喷涂机器人的设计和控制都需要实现高精度和高效率。
因此，机器人控制系统的优化和控制算法的改进是机器人技术进一步发展的关键。
6自由度控制算法
由于六自由度位置姿态调整平台动力学特性和串联机器人是相通的, 所以可以借鉴。
增强型PD控制器,这种控制器是在一个线性PD控制的基础上加上沿期望轨迹计算的名义动力学前馈部分以及一个非线性补偿部分, 它的最大优点是可以根据规划好的期望轨迹离线计算前馈补偿部分, 从而降低实时计算的计算量。
计算力矩控制方法, 它通过计算力矩的方式控制非线性系统沿期望轨迹运动, 如果机器人动力学模型是准确的, 计算力矩控制器可以实现动态解耦, 并得到一个指数稳定的闭环动力方程,从而实现跟踪误差的指数收敛。
在并联机器人的控制策略中，除了常用的PID控制之外，还有自适应控制，滑模变结构控制，鲁棒控制以及智能控制等控制方法。
基于滑模控制的方法在具有不确定性的系统的研究和应用中，滑模控制一直是一个非常有效的控制方法。
滑模控制也叫变结构控制，其本质是一类特殊的非线性控制，且非线性表现为控制的不连续性。
这种控制策略与其他控制的不同之处在于系统的“结构”不是一成不变的，而是可根据系统当前的状态有目的地不断变化。
对于具有信号传输时延的交互控制遥操作系统，也可以应用滑模控制来实现。
只要知道时延大小，滑模控制就可以实现变时延情况下的遥操作系统的稳定控制。
由于滑动模态与系统对象参数及扰动无关，因此滑模控制具有响应快、对应参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。
鲁棒控制由于遥操作系统中操作对象的不确定性，以及操作任务的实时变化，导致遥操作系统的特性和参数随工作状态和工作环境的变化而变化，这样就无法得到精确的描述遥操作系统特性的数学模型，给控制系统的设计带来困难。
鲁棒控制设计的目标就是在模型不精确和存在其他变化因素的条件下，使系统仍能保持预期的性能。
因此鲁棒控制在遥操作系统中发挥了巨大作用，它较大程度地消除了主观上认识的模型和真实的被控对象之间的误差和不确定性。
基于干扰观测器（DOB）的鲁棒运动控制方法由Ohnishi提出,目前广泛应用于各类电动高精度机械伺服系统" 干扰观测器设计基于被控对象的开环数学模型, 其基本思想是将外部力矩干扰及模型参数变化造成的实际对象与名义模型输出的差异, 统统等效到控制输入端, 即观测出等效干扰, 在控制中引入等量的补偿, 实现对各种干扰的完全抑制, 同时还可以减弱非线性环节对伺服系统性能的影响, 具有很强的鲁棒性。
基于单片机的六自由度机械手臂控制系统设计
《如及乡悅乡報》2021年第2期工程科技基于单片机的六自由度机械手臂控制系统设计陈心怡学张春雨2朱丽华1(1.池州职业技术学院，安徽池州247000; 2•安徽科技学院，安徽滁州239000)摘要:机械手臂在工业生产中的自主识别、精准判断和快速响应能力，体现了加工过程的自动化程度和智能化水平，文章提出了基于TK-A66自由度机械手臂和LD1501-MG 数字舵机,STC89C52单片机为核心 的工业机械臂控制系统的设计。
运用运动学模型和TM 算法，对机械臂手臂的运动速度和轨迹进行控 制设计，在控制程序设计中利用微分插补法生成多路舵机PWM 速度控制信号，通过在Protues 软件中 仿真调试,完成了对机械臂的控制功能遥关键词:单片机;机械臂;6自由度机械臂;舵机中图分类号:TP241 文献标识码:A 文章编号：1672-0547(2021)02-0106-004一、弓I 言机械臂也称工业机器人，是以运动作为控制对象 的智能控制装备，主要由手臂、舵机、抓手等组成叫机 器人手臂的张开、夹紧等系列动作由电动机驱动，并 准确地反馈到可编程逻辑控制器。
在工业生产中控 制机械臂完成我们所需要的夹取和分拣动作，本项 目便是围绕六自由度机械臂控制系统展开的。
通常 一个52系列的单片机包含有FLASH R0M 、RAM 、3 个16位的定时器/计数器和1个UART 等，它具有性 能可靠、性价比高等特点。
在工业生产中，往往需要 机械手臂完成一些相对复杂的控制运动，机械手臂 系统中一个单片机远远不够，仍需要TK-A66自由 度机械手臂、1501 数字舵机等控制机械臂的运动。
本文就是用单片机作为核心控制器,LD1501- MG 数字舵机作为TK-A66自由度机械手臂的运动控 制单元，结合制成的6自由度机械臂的控制系统。
系 统采用单片机芯片STC89C52作为主控制器，A/D 转 换采用以双积分方式运行的ICL7135,利用定时计数 器的计数功能，测量外部电压,省去很多处部电路罠 单片机通过产生PWM 信号控制机械臂的舵机，从而图1机械臂模型控制6自由度的机械手臂。
六自由度电磁探测的快速数值算法
基 金 项 目 ：四川 省 教 育 厅 科技 研 究 （ １ ２ Ｚ Ｂ １ ９ ４ ） 及 四川 省 乐 山 市科 技 厅 科 研 项 目（ ２ ０ １ ３ Ｇ Ｚ Ｄ ０ ４ ２ ） 资助项 目
中 图 分 类 号 ：Ｔ Ｎ ９ ８ 文 献 标 识 码 ：Ａ
０ 引 言
医疗 手术 导航是 指在 手术过 程 中跟 踪控 制手术 刀 的运动并 将 手术 刀 的位置 和方 向实 时显示 在病人 的影
像 资料上 ， 通过 电磁探 测技 术使 医生 明确手 术刀相 对 于病人解 剖结构 的位 置 ， 使 外科 手术更 快 、 更 精确 、 更安 全 Ｉ ２ ． 其 中电磁探 测技 术作 为一种 较为 先 进 的空 间定 位 技术 ， 以其 利用 磁 场对 非 磁 屏 蔽 物体 （ 人体 ） 的 穿
的高 速 定位 探 测 ．
１ 电磁 探 测 基 本 原 理
如图 １ 所示 ， 圆环线 圈 电流 的中心在 直角 坐标 系的原 点 处 ， 坐标 系 中任 意点 Ｐ（ ， Ｙ ， ） 处 的磁 感 应 强度 矢量 ， 根据 毕奥 一萨伐 尔定 律 （ Ｂ ｉ ｏ ｔ ． Ｓ ａ ｖ ａ ｒ ｔ ｌ ａ ｗ） 可得
第３ Ｏ卷 第 ５期
２ ０ １ ３年 ９月
计
算
物
理
Ｖｏ １ ． ３ ０． ＮＯ ． ５ Ｓ ｅ ｐ ．，２ ０ １ ３
Ｃ ＨＩ Ｎ Ｅ Ｓ Ｅ Ｊ Ｏ ＵＲＮ ＡＬ Ｏ Ｆ Ｃ ＯＭＰ ＵＴ ＡＴ Ｉ ＯＮ ＡＬ Ｐ ＨＹＳ Ｉ Ｃ Ｓ
文章编号 ： １ ０ ０ １ — ２ ４ ６ Ｘ （ ２ ０ １ ３ ） ０ ５ － ０ ７ ２ ０ － ０ ７
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
由于六自由度位置姿态调整平台动力学特性和串联机器人是相通的,所以可以借鉴。
增强型PD控制器,这种控制器是在一个线性PD控制的基础上加上沿期望轨迹计算的名义动力学前馈部分以及一个非线性补偿部分,它的最大优点是可以根据规划好的期望轨迹离线计算前馈补偿部分,从而降低实时计算的计算量。
计算力矩控制方法,它通过计算力矩的方式控制非线性系统沿期望轨迹运动,如果机器人动力学模型是准确的,计算力矩控制器可以实现动态解耦,并得到一个指数稳定的闭环动力方程,从而实现跟踪误差的指数收敛。
在并联机器人的控制策略中,除了常用的PID控制之外,还有自适应控制，滑模变结构控制，鲁棒控制以及智能控制等控制方法。
基于滑模控制的方法
在具有不确定性的系统的研究和应用中，滑模控制一直是一个非常有效的控制方法。
滑模控制也叫变结构控制，其本质是一类特殊的非线性控制，且非线性表现为控制的不连续性。
这种控制策略与其他控制的不同之处在于系统的“结构”不是一成不变的，而是可根据系统当前的状态有目的地不断变化。
对于具有信号传输时延的交互控制遥操作系统，也可以应用滑模控制来实现。
只要知道时延大小，滑模控制就可以实现变时延情况下的遥操作系统的稳定控制。
由于滑动模态与系统对象参数及扰动无关，因此滑模控制具有响应快、对应参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。
鲁棒控制
由于遥操作系统中操作对象的不确定性，以及操作任务的实时变化，导致遥操作系统的特性和参数随工作状态和工作环境的变化而变化，这样就无法得到精确的描述遥操作系统特性的数学模型，给控制系统的设计带来困难。
鲁棒控制设计的目标就是在模型不精确和存在其他变化因素的条件下，使系统仍能保持预期的性能。
因此鲁棒控制在遥操作系统中发挥了巨大作用，它较大程度地消除了主观上认识的模型和真实的被控对象之间的误差和不确定性。
基于干扰观测器(DOB)的鲁棒运动控制方法由Ohnishi提出,目前广泛应用于各类电动高精度机械伺服系统"干扰观测器设计基于被控对象的开环数学模型,其基本思想是将外部力矩干扰及模型参数变化造成的实际对象与名义模型输出的差异,统统等效到控制输入端,即观测出等效干扰,在控制中引入等量的补偿,实现对各种干扰的完全抑制,同时还可以减弱非线性环节对伺服系统性能的影响,具有很强的鲁棒性。
六自由度并联平台运动控制器的设计可以分为基于铰接空间控制和基于工作空间控制两大类。
基于铰接空间的控制器设计主要依靠平台机构的运动学关系和驱动装置的动态模型,而不考虑六自由度平台的动力学模型,它假设六个液压缸是独立、无耦合的关系,对每个液压伺服系统分别设计控制器而不用考虑其它关节的影响,这就使得并联平台的控制器设计任务转化为一系列单轴伺服系统的控制器设计。
基于工作空间的控制器设计则需要进行平台动力学分析,建立整个并联平台系统的动力学模型,在给定了平台期望的运动轨迹后,求出按照期望轨迹运动所需的力或力矩,然后控制各个液压伺服系统的驱动装置输出所求出的力或力矩,从而使平台按照期望轨迹运动。
常规PID控制
常规PID目前是最常用的工业控制方法，PID控制器各校正环节的作用
如下:
比例环节:比例控制是用常数乘以误差信号,偏差一旦产生,控制器立即产生作用,以减少偏差。
比例控制器实质是一个具有可调增益的放大器,在信号变换过程中,比例控制器只是改变信号的增益而不影响其相位。
积分环节:积分控制的作用是产生一个与误差信号对时间的积分成正比的信号,主要用于消除静差,积分作用的强弱取决于积分常数界,界越大,积分作用越弱,反之则越强。
微分环节:能反应输入信号的变化趋势,产生有效的早期修正信号,从而加快系统的动作速度,减少调节时间,有助于系统动态性能的改善。
铰点空间 PID 控制
基本原理
并联机构最常用的控制策略是基于铰点空间的 PID 控制，这种控制方法对并联机构的各个单通道分别设计 PID 控制器，即分别控制各驱动器完成各自的动作，驱动并联机构动平台实现各种位姿。
对于电动驱动的并联机构来说，铰点空间PID 控制策略的控制结构如图 4-1 所示。
各个通道均具有独立的 PID 控制器，每一个控制器只负责该通道的闭环控制。
在并联机构不同的运动状态下，各驱动器的负载特性是时变和相互耦合的，而此控制策略的控制器参数一般不能精确反映不断变化的负载特性，带有一定的近似性。
然而在很多场合下，相对电动系统驱动能力来说负载特性变化不大，铰点空间 PID 控制还是能够充分发挥其结构简单、调试方便的特点，因此在工程上铰点空间 PID 控制应用是最广泛的。
铰点空间控制器设计时一个基本的出发点是：通过提高各单通道系统的性能，以便提高并联机构的位姿响应性能。
由该控制结构可见，各个通道之间具有相对独立性，并在动平台处形成相互作用。
图 4-1 中还凸显了铰点空间控制策略的另一个特点，即虽然各驱动器是闭环控制的，但从位姿输入 qi到位姿输出 qo实际是一种开环控制。
开环意味着无法将实际的位姿误差重新引入控制系统进行修正。
这样，在系统的运动过程中动平台的位姿精度取决于驱动器系统的跟踪精度以及系统机械结构的加工精度，因此要想进一步提高平台的性能，必须在PID 控制器的基础上想方设法改善各路电动控制系统的响应特性。
工作空间计算力矩控制
基本原理
基于铰点空间的 PID 控制是一种基于运动学的控制方法，它不需要并联机构的动力学模型，因此实现起来比较容易。
但是，并联机构的动力学模型表明，各路电动缸驱动器之间是相互耦合的。
若想进一步提高系统动态特性，并减小各个自由度之间的耦合作用，有必要采用基于动力学模型的控制策略。
基于并联机构动力学模型的控制方法有很多种，但是绝大多数都是以计算力矩控制结构为基础。
计算力矩控制是一种基于模型的控制方法，利用并联机构动力学模型实现线性化和解耦。
Turbo PMAC可编程多轴运动控制器,是世界上功能最强的运动控制器之一,具有响应速度快,精度高,开发周期短,编程和操作简单的特点,发达国家广泛运用于机器人和数控机床等多轴控制的高精度伺服装置上。
GDS系列直流伺服驱动器是针对雷达天线，火控系统，精密测试转台等军用自动化设备开发的新一代伺服驱动器,它功率部分采用最新IGBT或IMP模块,在高速电流伺服单元和速度伺服单元的控制下,实现更高精度,更快响应的伺服控制。
为适应现代军用装备的发展要求,GDS系列进行了更加严格的电磁兼容性设计及可靠性研究,实现了全方位的自我保护,如欠压、过压、缓上电、过流、超载、超温、电机漏电、控制超差、上下限位、系统泵能泄放等保护。
检修机器人的基本控制结构如图3.1所示,Turbo PMAC自动闭合所有活动的电机的数字伺服环,实现位置环控制,产生一个反馈,使得电机的实际位置逼近所要求的位置的输出。
它的效果依靠伺服滤波器的调节、参数的设置、和被控物理对象系统的动力学性能。
电机速度闭环由驱动器完成。
速度环调节是通过驱动器自身的数字面板调整其参数实现的。
本系统选择美国DelatTua公司的Turbo PMAC CPI多轴运动控制卡作为关节伺服控制的主控制器
Turbo PMAC是美国DelatTau公司在PMAC的基础上推出的基于工业CP和WindowS 操作系统的开放式多轴运动控制器,采用了更高速度的DSP563OO系列数字信号处理器,提供全新的高性能技术和WindwoS平台,满足用户在运动控制各个领域的需要。
Turbo PMAC可同时控制1一32个轴,实现多轴联动控制,Turbo PMAC既可单独执行存储于控制器内部的程序,也可执行运动程序和PLC程序。
它可以自动对任务优先级进行判别,从而进行实时多任务处理。
同PMAC系列多轴运动控制器相比,Turbo PMAC除运算速度和内存增加外,还增加了新控制特性,主要有:先进的加速超前预测,内建的正向运动学和逆向运动学计算能力,三维刀具半径补偿功能,在线改变运动目标,多端口连续通讯,为每个电动机制定正弦转换表,可单独选择电动机的PID伺服控制算法或使用外部定义的算法,大大增加了同步M 变量缓冲区,为每个坐标系设置两个伺服速率定时器,运动轨迹反求能力。
其中,正向/逆向运动学计算功能和伺服控制算法定义功能,体现了Turbo PMAC运动平台在面向用户的开放性方面向前跨了一大步,使用户能灵活地在该平台上配置自己的运动算法,快速开发复杂数控系统的应用产品。
伺服系统的检测元件
轴角传感器种类很多,如光电编码器,旋转变压器,感应同步器,电位计,接触式编码器等"旋转变压器是一种高可靠性!高精度且具有绝对位置输出的角度传感器,其特点是结构简单,稳定性好,抗干扰能力强,易于数字化,因此广泛应用于工业自动化和国防军事领域。
六自由度一体式坦克模拟器控制系统设计。