2018AMC8考题及答案
2018年美国数学竞赛 AMC 试题

2018 AIME I ProblemsProblem 1Let be the number of ordered pairs ofintegers with and such that thepolynomial can be factored into the product of two (not necessarily distinct) linear factors with integer coefficients. Find the remainder when is divided by .Problem 2The number can be written in base as , can be written inbase as , and can be written in base as , where . Find the base- representation of .Problem 3Kathy has red cards and green cards. She shuffles the cards and laysout of the cards in a row in a random order. She will be happy if and only if all the red cards laid out are adjacent and all the green cards laid out are adjacent. For example, card orders RRGGG, GGGGR, or RRRRR will make Kathy happy,but RRRGR will not. The probability that Kathy will be happy is ,where and are relatively prime positive integers. Find . Problem 4In and . Point lies strictlybetween and on and point lies strictly between and on sothat . Then can be expressed in the form ,where and are relatively prime positive integers. Find .Problem 5For each ordered pair of real numbers satisfyingthere is a real number such thatFind the product of all possible values of .Problem 6Let be the number of complex numbers with the propertiesthat and is a real number. Find the remainder when is divided by .Problem 7A right hexagonal prism has height . The bases are regular hexagons with side length . Any of the vertices determine a triangle. Find the number of these triangles that are isosceles (including equilateral triangles).Problem 8Let be an equiangular hexagon suchthat , and . Denote the diameter of the largest circle that fits inside the hexagon. Find .Problem 9Find the number of four-element subsets of with the propertythat two distinct elements of a subset have a sum of , and two distinct elements of a subset have a sum of . Forexample, and are two such subsets.Problem 10The wheel shown below consists of two circles and five spokes, with a label at each point where a spoke meets a circle. A bug walks along the wheel, starting at point . At every step of the process, the bug walks from one labeled point to an adjacent labeled point. Along the inner circle the bug only walks in a counterclockwise direction, and along the outer circle the bug only walks in a clockwise direction. For example, the bug could travel along thepath , which has steps. Let be the number of paths with steps that begin and end at point . Find the remainder when is divided by .Problem 11Find the least positive integer such that when is written in base , its two right-most digits in base are .Problem 12For every subset of , let be the sum of the elements of , with defined to be . If is chosen at random among allsubsets of , the probability that is divisible by is , where and are relatively prime positive integers. Find .Problem 13Let have side lengths , , and .Point lies in the interior of , and points and are the incentersof and , respectively. Find the minimum possible areaof as varies along .Problem 14Let be a heptagon. A frog starts jumping at vertex . From any vertex of the heptagon except , the frog may jump to either of the two adjacentvertices. When it reaches vertex , the frog stops and stays there. Find the number of distinct sequences of jumps of no more than jumps that end at .Problem 15David found four sticks of different lengths that can be used to form three non-congruent convex cyclic quadrilaterals, , which can each be inscribed in a circle with radius . Let denote the measure of the acute angle made by the diagonals of quadrilateral , and define and similarly. Supposethat , , and . All three quadrilaterals have thesame area , which can be written in the form , where and are relatively prime positive integers. Find .2018 AMC 8 ProblemsProblem 1An amusement park has a collection of scale models, with ratio , of buildings and other sights from around the country. The height of the United States Capitol is 289 feet. What is the height in feet of its replica to the nearest whole number?Problem 2What is the value of the productProblem 3Students Arn, Bob, Cyd, Dan, Eve, and Fon are arranged in that order in a circle. They start counting: Arn first, then Bob, and so forth. When the number contains a 7 as a digit (such as 47) or is a multiple of 7 that person leaves the circle and the counting continues. Who is the last one present in the circle?Problem 4The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in ?Problem 5What is the valueof ?Problem 6On a trip to the beach, Anh traveled 50 miles on the highway and 10 miles on a coastal access road. He drove three times as fast on the highway as on the coastal road. If Anh spent 30 minutes driving on the coastal road, how many minutes did his entire trip take?Problem 7The -digit number is divisible by . What is the remainder when this number is divided by ?Problem 8Mr. Garcia asked the members of his health class how many days last week they exercised for at least 30 minutes. The results are summarized in the following bar graph, where the heights of the bars represent the number of students.What was the mean number of days of exercise last week, rounded to the nearest hundredth, reported by the students in Mr. Garcia's class?Problem 9Tyler is tiling the floor of his 12 foot by 16 foot living room. He plans to place one-foot by one-foot square tiles to form a border along the edges of the room and to fill in the rest of the floor with two-foot by two-foot square tiles. How many tiles will he use?Problem 10The of a set of non-zero numbers is the reciprocal of the average of the reciprocals of the numbers. What is the harmonic mean of 1, 2, and 4?Problem 11Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?Problem 12The clock in Sri's car, which is not accurate, gains time at a constant rate. One day as he begins shopping he notes that his car clock and his watch (which is accurate) both say 12:00 noon. When he is done shopping, his watch says 12:30 and his car clock says 12:35. Later that day, Sri loses his watch. He looks at his car clock and it says 7:00. What is the actual time?Problem 13Laila took five math tests, each worth a maximum of 100 points. Laila's score on each test was an integer between 0 and 100, inclusive. Laila received the same score on the first four tests, and she received a higher score on the last test. Her average score on the five tests was 82. How many values are possible for Laila's score on the last test?Problem 14Let be the greatest five-digit number whose digits have a product of . What is the sum of the digits of ?Problem 15In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?Problem 16Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?Problem 17Bella begins to walk from her house toward her friend Ella's house. At the same time, Ella begins to ride her bicycle toward Bella's house. They each maintain a constant speed, and Ella rides 5 times as fast as Bella walks. The distancebetween their houses is miles, which is feet, and Bella covers feet with each step. How many steps will Bella take by the time she meets Ella?Problem 18How many positive factors does have?Problem 19In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?Problem 20In a point is on with and Point ison so that and point is on so that What is the ratio of the area of to the area ofProblem 21How many positive three-digit integers have a remainder of 2 when divided by 6, a remainder of 5 when divided by 9, and a remainder of 7 when divided by 11?Problem 22Point is the midpoint of side in square and meets diagonal at The area of quadrilateral is What is the areaofProblem 23From a regular octagon, a triangle is formed by connecting three randomly chosen vertices of the octagon. What is the probability that at least one of the sides of the triangle is also a side of the octagon?Problem 24In the cube with opposite vertices and and are the midpoints of edges and respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What isProblem 25How many perfect cubes lie between and , inclusive?2018 AMC 10A ProblemsProblem 1What is the value ofProblem 2Liliane has more soda than Jacqueline, and Alice has more soda than Jacqueline. What is the relationship between the amounts of soda that Liliane and Alice have?Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Liliane has more soda than Alice.Problem 3A unit of blood expires after seconds. Yasin donates a unit of blood at noon of January 1. On what day does his unit of blood expire?Problem 4How many ways can a student schedule 3 mathematics courses -- algebra, geometry, and number theory -- in a 6-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)Problem 5Alice, Bob, and Charlie were on a hike and were wondering how far away the nearest town was. When Alice said, "We are at least 6 miles away," Bob replied, "We are at most 5 miles away." Charlie then remarked, "Actually the nearest town is at most 4 miles away." It turned out that none of the three statements were true. Let be the distance in miles to the nearest town. Which of the following intervals is the set of all possible values of ?Problem 6Sangho uploaded a video to a website where viewers can vote that they like or dislike a video. Each video begins with a score of 0, and the score increases by 1 for each like vote and decreases by 1 for each dislike vote. At one point Sangho saw that his video had a score of 90, and that of the votes cast on his video were like votes. How many votes had been cast on Sangho's video at that point?Problem 7For how many (not necessarily positive) integer values of is the value of an integer?Problem 8Joe has a collection of 23 coins, consisting of 5-cent coins, 10-cent coins, and 25-cent coins. He has 3 more 10-cent coins than 5-cent coins, and the total value of his collection is 320 cents. How many more 25-cent coins does Joe have than 5-cent coins?Problem 9All of the triangles in the diagram below are similar to iscoceles triangle , inwhich . Each of the 7 smallest triangles has area 1, and has area 40. What is the area of trapezoid ?Problem 10Suppose that real number satisfies. What is the valueof ?Problem 11When fair standard -sided die are thrown, the probability that the sum of the numbers on the top faces is can be written as, where is a positive integer. What is ?Problem 12How many ordered pairs of real numbers satisfy the following system ofequations?Problem 13A paper triangle with sides of lengths 3, 4, and 5 inches, as shown, is folded so that point falls on point . What is the length in inches of the crease?Problem 14What is the greatest integer less than or equal toProblem 15Two circles of radius 5 are externally tangent to each other and are internally tangent to a circle of radius 13 at points and , as shown in the diagram. The distance can be written in the form , where and are relatively prime positive integers. What is ?Problem 16Right triangle has leg lengths and . Including and , how many line segments with integer length can be drawn from vertex to a point on hypotenuse ?Problem 17Let be a set of 6 integers taken from with the property that if and are elements of with , then is not a multiple of . What is the least possible values of an element inProblem 18How many nonnegative integers can be written in theformwhere for ?Problem 19A number is randomly selected from the set , and a number is randomly selected from . What is the probabilitythat has a units digit of ?Problem 20A scanning code consists of a grid of squares, with some of its squares colored black and the rest colored white. There must be at least one square of each color in this grid of squares. A scanning code is called if its look does not change when the entire square is rotated by a multiple of counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?Problem 21Which of the following describes the set of values of for which thecurves and in the real -plane intersect at exactly points?Problem 22Let and be positive integers suchthat , , ,and . Which of the following must be a divisor of ?Problem 23Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplantedsquare so that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from to the hypotenuse is 2 units. What fraction of the field is planted?Problem 24Triangle with and has area . Let be the midpointof , and let be the midpoint of . The angle bisectorof intersects and at and , respectively. What is the area of quadrilateral ?Problem 25For a positive integer and nonzero digits , , and , let be the -digit integer each of whose digits is equal to ; let be the -digit integer each of whose digits is equal to , and let be the -digit (not -digit) integer each of whose digits is equal to . What is the greatest possiblevalue of for which there are at least two values of such that ?2018 AMC 10B ProblemsProblem 1Kate bakes a 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?Problem 2Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?Problem 3In the expression each blank is to be filled in with one of the digits or with each digit being used once. How many different values can be obtained?Problem 4A three-dimensional rectangular box with dimensions , , and has faces whose surface areas are 24, 24, 48, 48, 72, and 72 square units. What is ?Problem 5How many subsets of contain at least one prime number?Problem 6A box contains 5 chips, numbered 1, 2, 3, 4, and 5. Chips are drawn randomly one at a time without replacement until the sum of the values drawn exceeds 4. What is the probability that 3 draws are required?Problem 7In the figure below, congruent semicircles are drawn along a diameter of a large semicircle, with their diameters covering the diameter of the large semicircle with no overlap. Let be the combined area of the small semicircles and be the area of the region inside the large semicircle but outside the small semicircles. The ratio is 1:18. What is ?Problem 8Sara makes a staircase out of toothpicks as shown:This is a 3-step staircase and uses 18 toothpicks. How many steps would be in a staircase that used 180 toothpicks?Problem 9The faces of each of 7 standard dice are labeled with the integers from 1 to 6. Let be the probability that when all 7 dice are rolled, the sum of the numbers on the top faces is 10. What other sum occurs with the same probability ?Problem 10In the rectangular parallelepiped shown, , , and . Point is the midpoint of . What is the volume of the rectangular pyramid with base and apex ?Problem 11Which of the following expressions is never a prime number when is a prime number?Problem 12Line segment is a diameter of a circle with . Point , not equal to or , lies on the circle. As point moves around the circle, the centroid (center of mass) of traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?Problem 13How many of the first numbers in the sequence are divisible by ?Problem 14A list of positive integers has a unique mode, which occurs exactly times. What is the least number of distinct values that can occur in the list?Problem 15A closed box with a square base is to be wrapped with a square sheet of wrapping paper. The box is centered on the wrapping paper with the vertices of the base lying on the midlines of the square sheet of paper, as shown in the figure on the left. The four corners of the wrapping paper are to be folded up over the sides and brought together to meet at the center of the top of the box, point in the figure on the right. The box has base length and height . What is the area of the sheet of wrapping paper?Problem 16Let be a strictly increasing sequence of positive integers suchthat What is the remainderwhen is divided by ?Problem 17In rectangle , and . Points and lie on ,points and lie on , points and lie on , and points and lie on so that and the convex octagon is equilateral. The length of a side of this octagon can be expressed in the form , where , , and are integers and is not divisible by the square of any prime. What is ?Problem 18Three young brother-sister pairs from different families need to take a trip in a van. These six children will occupy the second and third rows in the van, each of which has three seats. To avoid disruptions, siblings may not sit right next to each other in the same row, and no child may sit directly in front of his or her sibling. How many seating arrangements are possible for this trip?Problem 19Joey and Chloe and their daughter Zoe all have the same birthday. Joey is 1 year older than Chloe, and Zoe is exactly 1 year old today. Today is the first of the 9 birthdays on which Chloe's age will be an integral multiple of Zoe's age. What will be the sum of the two digits of Joey's age the next time his age is a multiple of Zoe's age?Problem 20A function is defined recursivelyby and for allintegers . What is ?Problem 21Mary chose an even -digit number . She wrote down all the divisors of in increasing order fromleft to right: . At some moment Mary wrote as a divisor of . What is the smallest possible value of the next divisor written to the right of ?Problem 22Real numbers and are chosen independently and uniformly at random from the interval . Which of the following numbers is closest to the probability that and are the side lengths of an obtuse triangle?Problem 23How many ordered pairs of positive integers satisfy theequation where denotes the greatest common divisor of and , and denotes their least common multiple?Problem 24Let be a regular hexagon with side length . Denote by , , and the midpoints of sides , , and , respectively. What is the area of the convex hexagon whose interior is the intersection of the interiors of and ?Problem 25Let denote the greatest integer less than or equal to . How many real numbers satisfy the equation ?2018 AMC 12A ProblemsProblem 1A large urn contains balls, of which are red and the rest are blue. How many of the blue balls must be removed so that the percentage of red balls in the urn will be ? (No red balls are to be removed.)Problem 2While exploring a cave, Carl comes across a collection of -pound rocks worth each, -poundrocks worth each, and -pound rocks worth each. There are at least of each size. He can carry at most pounds. What is the maximum value, in dollars, of the rocks he can carry out of the cave?Problem 3How many ways can a student schedule 3 mathematics courses -- algebra, geometry, and number theory -- in a 6-period day if no two mathematics courses can be taken in consecutive periods? (What courses the student takes during the other 3 periods is of no concern here.)Problem 4Alice, Bob, and Charlie were on a hike and were wondering how far away the nearest town was. When Alice said, "We are at least 6 miles away," Bob replied, "We are at most 5 miles away." Charlie then remarked, "Actually the nearest town is at most 4 miles away." It turned out that none of the three statements were true. Let be the distance in miles to the nearest town. Which of the following intervals is the set of all possible values of ?Problem 5What is the sum of all possible values of for which the polynomials andhave a root in common?Problem 6For positive integers and such that , both the mean and the median ofthe set are equal to . What is ?Problem 7For how many (not necessarily positive) integer values of is the value of an integer?Problem 8All of the triangles in the diagram below are similar to iscoceles triangle , in which. Each of the 7 smallest triangles has area 1, and has area 40. What is the area of trapezoid ?Problem 9Which of the following describes the largest subset of values of within the closed interval forwhich for every between and , inclusive?How many ordered pairs of real numbers satisfy the following system of equations?Problem 11A paper triangle with sides of lengths 3,4, and 5 inches, as shown, is folded so that point falls on point . What is the length in inches of the crease?Problem 12Let be a set of 6 integers taken from with the property that if and are elements of with , then is not a multiple of . What is the least possible value of an element inProblem 13How many nonnegative integers can be written in the formwherefor ?Problem 14The solutions to the equation , where is a positive real number other thanor , can be written as where and are relatively prime positive integers. What is ?A scanning code consists of a grid of squares, with some of its squares colored black and therest colored white. There must be at least one square of each color in this grid of squares. A scanning code is called if its look does not change when the entire square is rotated by a multiple of counterclockwise around its center, nor when it is reflected across a line joining opposite corners or a line joining midpoints of opposite sides. What is the total number of possible symmetric scanning codes?Problem 16Which of the following describes the set of values of for which the curves andin the real -plane intersect at exactly points?Problem 17Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths 3 and 4 units. In the corner where those sides meet at a right angle, he leaves a small unplanted squareso that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from to the hypotenuse is 2 units. What fraction of the field is planted?Triangle with and has area . Let be the midpoint of, and let be the midpoint of . The angle bisector of intersects and atand , respectively. What is the area of quadrilateral ?Problem 19Let be the set of positive integers that have no prime factors other than , , or . The infinite sumof the reciprocals of the elements of can be expressed as , where and are relatively primepositive integers. What is ?Problem 20Triangle is an isosceles right triangle with . Let be the midpoint ofhypotenuse . Points and lie on sides and , respectively, so thatand is a cyclic quadrilateral. Given that triangle has area , the length canbe written as , where , , and are positive integers and is not divisible by the square of any prime. What is the value of ?Problem 21Which of the following polynomials has the greatest real root?Problem 22The solutions to the equations and whereform the vertices of a parallelogram in the complex plane. The area of thisparallelogram can be written in the form where and are positive integersand neither nor is divisible by the square of any prime number. What isProblem 23In and Points and lie on sidesand respectively, so that Let and be the midpoints of segmentsand respectively. What is the degree measure of the acute angle formed by linesandProblem 24Alice, Bob, and Carol play a game in which each of them chooses a real number between 0 and 1. The winner of the game is the one whose number is between the numbers chosen by the other two players. Alice announces that she will choose her number uniformly at random from all the numbers between 0 and 1, and Bob announces that he will choose his number uniformly at random from all thenumbers between and Armed with this information, what number should Carol choose to maximize her chance of winning?Problem 25For a positive integer and nonzero digits , , and , let be the -digit integer each of whosedigits is equal to ; let be the -digit integer each of whose digits is equal to , and let bethe -digit (not -digit) integer each of whose digits is equal to . What is the greatest possible value of for which there are at least two values of such that ?2018 AMC 12B ProblemsProblem 1Kate bakes 20-inch by 18-inch pan of cornbread. The cornbread is cut into pieces that measure 2 inches by 2 inches. How many pieces of cornbread does the pan contain?Problem 2Sam drove 96 miles in 90 minutes. His average speed during the first 30 minutes was 60 mph (miles per hour), and his average speed during the second 30 minutes was 65 mph. What was his average speed, in mph, during the last 30 minutes?Problem 3A line with slope 2 intersects a line with slope 6 at the point . What is the distance between the -intercepts of these two lines?Problem 4A circle has a chord of length , and the distance from the center of the circle to the chord is . What is the area of the circle?Problem 5How many subsets of contain at least one prime number?Suppose cans of soda can be purchased from a vending machine for quarters. Which of the following expressions describes the number of cans of soda that can be purchased for dollars, where 1 dollar is worth 4 quarters?Problem 7What is the value ofProblem 8Line segment is a diameter of a circle with . Point , not equal to or , lies on the circle. As point moves around the circle, the centroid (center of mass) of traces out a closed curve missing two points. To the nearest positive integer, what is the area of the region bounded by this curve?Problem 9What isProblem 10A list of positive integers has a unique mode, which occurs exactly times. What is the least number of distinct values that can occur in the list?Problem 11。
中国amc8数学竞赛试卷

中国AMC8数学竞赛试卷一、选择题(每题1分,共5分)1.下列哪个数是素数?A.21B.23C.25D.272.一个等差数列的前三项分别是2、5、8,那么第10项是多少?A.29B.30C.31D.323.一个正方体的表面积是54平方厘米,那么它的体积是多少立方厘米?A.27B.36C.45D.544.下列哪个图形不是轴对称图形?A.矩形B.菱形C.梯形D.正五边形5.下列哪个数是偶数?A.-3B.0C.1D.3二、判断题(每题1分,共5分)1.任何一个整数都可以表示为3的倍数和5的倍数的和。
()2.一个等边三角形的三个角都是60度。
()3.1的倒数是1。
()4.任何一个正整数都可以分解为几个质数的乘积。
()5.两条平行线之间的距离是相等的。
()三、填空题(每题1分,共5分)1.2的平方根是______。
2.一个等差数列的前三项分别是2、5、8,那么它的公差是______。
3.一个正方体的体积是64立方厘米,那么它的表面积是______平方厘米。
4.下列哪个数既是偶数又是素数?______5.一个等腰三角形的底角是40度,那么它的顶角是______度。
四、简答题(每题2分,共10分)1.解释什么是质数。
2.什么是等差数列?给出一个等差数列的例子。
3.什么是等边三角形?它的特点是什么?4.解释什么是平行线。
5.什么是等腰三角形?它的特点是什么?五、应用题(每题2分,共10分)1.一个等差数列的前三项分别是2、5、8,求第10项。
2.一个正方体的表面积是54平方厘米,求它的体积。
3.下列哪个数既是偶数又是素数?为什么?4.一个等腰三角形的底角是40度,求它的顶角。
5.一个等边三角形的周长是18厘米,求它的边长。
六、分析题(每题5分,共10分)1.证明:如果一个整数既是3的倍数又是5的倍数,那么它一定是15的倍数。
2.证明:如果一个整数既是4的倍数又是6的倍数,那么它一定是12的倍数。
七、实践操作题(每题5分,共10分)1.画出一个等边三角形,并标出它的三个角。
2018年AMC8考题和问题详解解析汇报
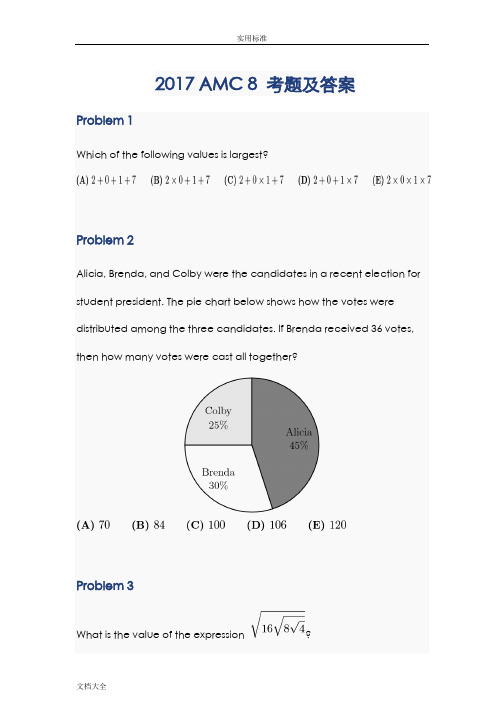
2017 AMC 8 考题及答案Problem 1Which of the following values is largest?Problem 2Alicia, Brenda, and Colby were the candidates in a recent election for student president. The pie chart below shows how the votes were distributed among the three candidates. If Brenda received 36 votes, then how many votes were cast all together?Problem 3What is the value of the expression ?Problem 4When 0.000315 is multiplied by 7,928,564 the product is closest to which of the following?Problem 5What is the value of the expression ?Problem 6If the degree measures of the angles of a triangle are in the ratio , what is the degree measure of the largest angle of the triangle?Problem 7Let be a 6-digit positive integer, such as 247247, whose first three digits are the same as its last three digits taken in the same order. Which of the following numbers must also be a factor of ?Problem 8Malcolm wants to visit Isabella after school today and knows the street where she lives but doesn't know her house number. She tells him, "My house number has two digits, and exactly three of the following four statements about it are true."(1) It is prime.(2) It is even.(3) It is divisible by 7.(4) One of its digits is 9.This information allows Malcolm to determine Isabella's house number. What is its units digit?Problem 9All of Marcy's marbles are blue, red, green, or yellow. One third of her marbles are blue, one fourth of them are red, and six of them are green. What is the smallest number of yellow marbles that Marcy could have?Problem 10A box contains five cards, numbered 1, 2, 3, 4, and 5. Three cards are selected randomly without replacement from the box. What is the probability that 4 is the largest value selected?Problem 11A square-shaped floor is covered with congruent square tiles. If the total number of tiles that lie on the two diagonals is 37, how many tiles cover the floor?Problem 12The smallest positive integer greater than 1 that leaves a remainder of 1 when divided by 4, 5, and 6 lies between which of the following pairs of numbers?Problem 13Peter, Emma, and Kyler played chess with each other. Peter won 4 games and lost 2 games. Emma won 3 games and lost 3 games. If Kyler lost 3 games, how many games did he win?Problem 14Chloe and Zoe are both students in Ms. Demeanor's math class. Last night they each solved half of the problems in their homework assignment alone and then solved the other half together. Chloe had correct answers to only of the problems she solved alone, but overall of her answers were correct. Zoe had correct answers to of the problems she solved alone. What was Zoe's overall percentage of correct answers?Problem 15In the arrangement of letters and numerals below, by how many different paths can one spell AMC8? Beginning at the A in the middle, a path allows only moves from one letter to an adjacent (above, below, left, or right, but not diagonal) letter. One example of such a path is traced in the picture.Problem 16In the figure below, choose point on so that and have equal perimeters. What is the area of ?Problem 17Starting with some gold coins and some empty treasure chests, I tried to put 9 gold coins in each treasure chest, but that left 2 treasure chests empty. So instead I put 6 gold coins in each treasure chest, but then I had 3 gold coins left over. How many gold coins did I have?Problem 18In the non-convex quadrilateral shown below, is a right angle, , , , and .What is the area of quadrilateral ?Problem 19For any positive integer , the notation denotes the product of the integers through . What is the largest integer for which is a factor of the sum ?Problem 20An integer between and , inclusive, is chosen at random. What is the probability that it is an odd integer whose digits are all distinct?Problem 21Suppose , , and are nonzero real numbers, and . What are the possible value(s) for ?Problem 22In the right triangle , , , and angle is a right angle. A semicircle is inscribed in the triangle as shown. What is the radius of the semicircle?Problem 23Each day for four days, Linda traveled for one hour at a speed that resulted in her traveling one mile in an integer number of minutes. Each day after the first, her speed decreased so that the number of minutes to travel one mile increased by 5 minutes over the preceding day. Each of the four days, her distance traveled was also an integer number of miles. What was the total number of miles for the four trips?Problem 24Mrs. Sanders has three grandchildren, who call her regularly. One calls her every three days, one calls her every four days, and one calls her every five days. All three called her on December 31, 2016. On how many days during the next year did she not receive a phone call from any of her grandchildren?Problem 25In the figure shown, and are line segments each of length 2, and . Arcs and are each one-sixth of a circle with radius 2. What is the area of the region shown?2017 AMC 8 Answer Key1. A2. E3. C4. D5. B6. D7. A8. D9. D10.C11.C12.D13.B14.C15.D16.D17.C18.B19.D20.B21.A22.D23.C24.D25.B。
AMC8-2018

2018 AMC 8 ProblemsProblem 1An amusement park has a collection of scale models, with ratio , of buildings and other sights from around the country. The height of the United States Capitol is 289 feet. What is the height in feet of its replica to the nearest whole number?Problem 2What is the value of the productProblem 3Students Arn, Bob, Cyd, Dan, Eve, and Fon are arranged in that order in a circle. They start counting: Arn first, then Bob, and so forth. When the number contains a 7 as a digit (such as 47) or is a multiple of 7 that person leaves the circle and the counting continues. Who is the last one present in the circle?Problem 4The twelve-sided figure shown has been drawn on graph paper. What is the area of the figure in ?Problem 5What is the valueof ?Problem 6On a trip to the beach, Anh traveled 50 miles on the highway and 10 miles on a coastal access road. He drove three times as fast on the highway as on the coastal road. If Anh spent 30 minutes driving on the coastal road, how many minutes did his entire trip take?Problem 7The -digit number is divisible by . What is the remainder when this number is divided by ?Problem 8Mr. Garcia asked the members of his health class how many days last week they exercised for at least 30 minutes. The results are summarized in the following bar graph, where the heights of the bars represent the number of students.What was the mean number of days of exercise last week, rounded to the nearest hundredth, reported by the students in Mr. Garcia's class?Problem 9Tyler is tiling the floor of his 12 foot by 16 foot living room. He plans to place one-foot by one-foot square tiles to form a border along the edges of the room and to fill in the rest of the floor with two-foot by two-foot square tiles. How many tiles will he use?Problem 10The of a set of non-zero numbers is the reciprocal of the average of the reciprocals of the numbers. What is the harmonic mean of 1, 2, and 4?Problem 11Abby, Bridget, and four of their classmates will be seated in two rows of three for a group picture, as shown.If the seating positions are assigned randomly, what is the probability that Abby and Bridget are adjacent to each other in the same row or the same column?Problem 12The clock in Sri's car, which is not accurate, gains time at a constant rate. One day as he begins shopping he notes that his car clock and his watch (which is accurate) both say 12:00 noon. When he is done shopping, his watch says 12:30 and his car clock says 12:35. Later that day, Sri loses his watch. He looks at his car clock and it says 7:00. What is the actual time?Problem 13Laila took five math tests, each worth a maximum of 100 points. Laila's score on each test was an integer between 0 and 100, inclusive. Laila received the same score on the first four tests, and she received a higher score on the last test. Her average score on the five tests was 82. How many values are possible for Laila's score on the last test?Problem 14Let be the greatest five-digit number whose digits have a product of . What is the sum of the digits of ?Problem 15In the diagram below, a diameter of each of the two smaller circles is a radius of the larger circle. If the two smaller circles have a combined area of square unit, then what is the area of the shaded region, in square units?Problem 16Professor Chang has nine different language books lined up on a bookshelf: two Arabic, three German, and four Spanish. How many ways are there to arrange the nine books on the shelf keeping the Arabic books together and keeping the Spanish books together?Problem 17Bella begins to walk from her house toward her friend Ella's house. At the same time, Ella begins to ride her bicycle toward Bella's house. They each maintain a constant speed, and Ella rides 5 times as fast as Bella walks. The distancebetween their houses is miles, which is feet, and Bella covers feet with each step. How many steps will Bella take by the time she meets Ella?Problem 18How many positive factors does have?Problem 19In a sign pyramid a cell gets a "+" if the two cells below it have the same sign, and it gets a "-" if the two cells below it have different signs. The diagram below illustrates a sign pyramid with four levels. How many possible ways are there to fill the four cells in the bottom row to produce a "+" at the top of the pyramid?Problem 20In a point is on with and Point ison so that and point is on so that What is the ratio of the area of to the area ofProblem 21How many positive three-digit integers have a remainder of 2 when divided by 6, a remainder of 5 when divided by 9, and a remainder of 7 when divided by 11?Problem 22Point is the midpoint of side in square and meets diagonal at The area of quadrilateral is What is the areaofProblem 23From a regular octagon, a triangle is formed by connecting three randomly chosen vertices of the octagon. What is the probability that at least one of the sides of the triangle is also a side of the octagon?Problem 24In the cube with opposite vertices and and are the midpoints of edges and respectively. Let be the ratio of the area of the cross-section to the area of one of the faces of the cube. What isHow many perfect cubes lie between and , inclusive?。
2018澳洲AMC中学高级组中文试题答案

: (D)
2. (A) 15 km
250 km (B) 20 km
8 × 30 = 240
(C) 30 km 30 km
8 (D) 40 km
(E) 80 km : (C)
5 Senior paper — draft for traditional chinese translation
3. (A) 16
11. 小
11-20
4
80
(
)
(A) 14
(B) 20
(C) 25
1 1 30 = 14 + 1 + 14 + 1
14 1
14
28
14
14
2 10 × 3 = 30
n
3n − 2(n − 1) = n + 2 n + 2 = 30
3n n−1
28
(D) 28 30 1
2
(E) 30 : (D) : (D)
218 = 29 × 29 < 1000 × 1000 = 106 : (A)
2018 = 262 144 000 000 000 000 000 000
23/8/2018
5 Senior paper — draft for traditional chinese translation
87
19.
88
20. 1◦
(A) 30
中 (B) 40
小 (C) 45
5 (D) 50
(E) 60
1 小
n
n 2
小
θ>0
n
n+5
(n − 2) × 180◦
180(n − 2) ◦ n
美国数学竞赛AMC8 -- 2008年真题解析(英文解析+中文解析)

美国数学竞赛AMC8 – 2008年真题解析(英文解析+中文解析)Problem 1Answer: BSolution:50-12-24=14中文解析:总共花的钱是:12+12*2=36元。
剩余50-36=14元。
答案是BProblem 2Answer: ASolution:We can derive that c=8,L=6, U=7,and E=1. Therefore, the answer is 8671.中文解析:这10个字母的对应关系是: B -0;E-1; S-2; ......K -9. 按照这个对应关系:C-8,L-6,U-7,E-1. 即8671. 答案是A。
Problem 3Answer: ASolution:We can go backwards by days, but we can also backwards by weeks. If we go backwards by weeks, we see that February 6 is a Friday. If we now go backwards by days, February 1 is a Sunday.中文解析:13日是周五,则13-7=6,即6日也是周五,则倒推2月1日是周日。
答案是A。
Problem 4Answer: CSolution:The area outside the small triangle but inside the large triangle is 16-1=15. This is equally distributed between the three trapezoids. Each trapezoid has an area of 15/3=5.中文解析:大三角形的面积等于小的等边三角形的面积加上3个梯形的面积。
据此,三个梯形的面积是16-1=15. 每个梯形的面积是15/3=5. 答案是C。
AMC8(美国数学竞赛)历年真题、答案及中英文解析
AMC8(美国数学竞赛)历年真题、答案及中英文解析艾蕾特教育的AMC8 美国数学竞赛考试历年真题、答案及中英文解析:AMC8-2020年:真题 --- 答案---解析(英文解析+中文解析)AMC8 - 2019年:真题----答案----解析(英文解析+中文解析)AMC8 - 2018年:真题----答案----解析(英文解析+中文解析)AMC8 - 2017年:真题----答案----解析(英文解析+中文解析)AMC8 - 2016年:真题----答案----解析(英文解析+中文解析)AMC8 - 2015年:真题----答案----解析(英文解析+中文解析)AMC8 - 2014年:真题----答案----解析(英文解析+中文解析)AMC8 - 2013年:真题----答案----解析(英文解析+中文解析)AMC8 - 2012年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 2010年:真题----答案----解析(英文解析+中文解析)AMC8 - 2009年:真题----答案----解析(英文解析+中文解析)AMC8 - 2008年:真题----答案----解析(英文解析+中文解析)AMC8 - 2007年:真题----答案----解析(英文解析+中文解析)AMC8 - 2006年:真题----答案----解析(英文解析+中文解析)AMC8 - 2005年:真题----答案----解析(英文解析+中文解析)AMC8 - 2004年:真题----答案----解析(英文解析+中文解析)AMC8 - 2003年:真题----答案----解析(英文解析+中文解析)AMC8 - 2002年:真题----答案----解析(英文解析+中文解析)AMC8 - 2001年:真题----答案----解析(英文解析+中文解析)AMC8 - 2000年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1998年:真题----答案----解析(英文解析+中文解析)AMC8 - 1997年:真题----答案----解析(英文解析+中文解析)AMC8 - 1996年:真题----答案----解析(英文解析+中文解析)AMC8 - 1995年:真题----答案----解析(英文解析+中文解析)AMC8 - 1994年:真题----答案----解析(英文解析+中文解析)AMC8 - 1993年:真题----答案----解析(英文解析+中文解析)AMC8 - 1992年:真题----答案----解析(英文解析+中文解析)AMC8 - 1991年:真题----答案----解析(英文解析+中文解析)AMC8 - 1990年:真题----答案----解析(英文解析+中文解析)AMC8 - 1989年:真题----答案----解析(英文解析+中文解析)AMC8 - 1988年:真题----答案----解析(英文解析+中文解析)析)AMC8 - 1986年:真题----答案----解析(英文解析+中文解析)AMC8 - 1985年:真题----答案----解析(英文解析+中文解析)◆AMC介绍◆AMC(American Mathematics Competitions) 由美国数学协会(MAA)组织的数学竞赛,分为 AMC8 、 AMC10、 AMC12 。
2018年全国高中数学联合竞赛一试B卷参考答案(含加试)
三)叶
(9a+b+I) — ( 6矗+ b) 分 [1, 9], 均有 11cx)I<2, 则 ………………10 分 切 @ @
由句,@得, 2a-6 = /(2)-/(1); 又由@,@得, 6a-2 = /(3)-/(2). 由上述两式消去 a, 可知 但 /(3)-4/(2)+3/(1)<2+4 . 2+3. 2=16, 矛盾!从而命题得证.
2018年全国高中数学联合竞赛一试(B卷) 参考答案及评分标准
为
是0+1+ 2+ 4+8+16=31. 2. 已知 圆锥的 顶点为P, 底面半径长为2'高为1.在圆锥 底面 上取 一 点Q , ° 使得 直线PQ与底面所成角不大千45 , 则满足条件的点Q所构成的区域 的面积 解:圆锥顶点 P在底面上的投影即为底面中心, 记之为o. 由条件知, OP = tan乙OQP三1'即OQ之1'故所求 的区域面积为7r·22 -Jr-12 =31r. OQ 3. 将1,2,3,4,5,6随机排成 一 行,记为a,b,c,d,e ,f, 则abc+def是奇数的概 答案: 1 — 答案: 31r.
说明: 1. 评阅试卷时,请依据本评分标准.填空题只设8分和0分两档;其他各题的 评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次. 2. 如果考生的解答方法和本解答不同, 只要思路合理、步骤正确,在评卷时可 一 个档次 ,第10、 参考本评分标准适当划分档次评分,解答题中第9小题4分为 一 个档次 ,不得增加其他中间档次. 11小题5分为 一、填空题:本大题共8小题,每小题8分,满分64分. {2, 0,1,8}, B= {2a I a E A}, 则AUB的所有元素之和是 1. 设集合A= .
2018年全国高中数学联赛试题及答案详解(B卷)
说明: 1. 评阅试卷时,请严格按照本评分标准的评分档次给分. 2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可 参考本评分标准适当划分档次评分,10 分为一个档次,不得增加其他中间档次.
一、(本题满分 40 分)设 a, b 是实数,函数 f (x) = ax + b + 9 . x
知,满足条件的情况数为 36 × 2 =72 种.从而所求概率为= 72 7= 2 1 . 6! 720 10
4. 在平面直角坐标系 xOy 中,直线 l 通过原点, n (3, 1) 是 l 的一个法向
量.已知数列{an}满足:对任意正整数 n ,点 (an1, an ) 均在 l 上.若 a2 6 ,则
11.(本题满分 20 分)如图所示,在平面直角 坐 标 系 xOy 中 , A 、 B 与 C 、 D 分 别 是 椭 圆
x2 y2 : a2 b2 1 (a b 0) 的左、右顶点与上、下顶 A 点.设 P, Q 是 上且位于第一象限的两点,满足
y
R
P
C
M
Q
O
Bx
OQ ∥ AP , M 是线段 AP 的中点,射线 OM 与椭
是 0 1 2 4 8 16 31 .
2. 已知圆锥的顶点为 P ,底面半径长为 2 ,高为1.在圆锥底面上取一点 Q ,
使得直线 PQ 与底面所成角不大于 45 ,则满足条件的点 Q 所构成的区域的面积
为
.
答案: 3 .
解:圆锥顶点 P 在底面上的投影即为底面中心,记之为 O .由条件知, OP tan OQP 1 ,即 OQ 1 ,故所求的区域面积为 22 12 3 . OQ
2018年世界少年奥林匹克数学竞赛八年级海选赛试题含答案
绝密★启用前世界少年奥林匹克数学竞赛(中国区)选拔赛地方海选赛选手须知:1、本卷共三部分,第一部分:填空题,共计50分;第二部分:计算题,共计12分;第三部分:解答题,共计58分。
2、答题前请将自己的姓名、学校、赛场、参赛证号码写在规定的位置。
3、比赛时不能使用计算工具。
4、比赛完毕时试卷和草稿纸将被收回。
八年级试题(A卷)(本试卷满分120分 ,考试时间90分钟 )一、填空题。
(每题5分,共计50分)1、36的平方根是 。
2、若方程mx+ny=6的两个解是⎩⎨⎧==11y x 及⎩⎨⎧-==12y x ,则m= ,n = 。
3、已知1=-b a ,=+=+b a b a ,2522。
4、已知x=y+z=2,则=+++xyz z y x 333223。
5、如果实数a ,b 满足条件,12|21|,12222a b a b a b a -=+++-=+则a+b= 。
6、某班级春游时48人到杭州西湖划船。
已知每只小船坐3个人,租金16元;每只大船坐5个人,租金24元,则这个班级租金至少花 元。
7、在△ABC 中,∠B=60°,∠C >∠A ,且222B A )C ()()(∠+∠=∠,则△ABC 的形状是 。
8、观察下列式子:181092+⨯=;198100992+⨯=;199810009992+⨯=,……,按规律写出=2999999 。
(填写具体数字)9、如图,韩梅梅从A 点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,照这样子走下去,他第一次回到起点A 时走了 米。
10、如图直线L 与∠A 的两边相交于点B 、C ,则图中以A 、B 、C 为端点的射线有 条。
二、计算题。
(每题6分,共计12分)11、 1+3+5+7+9+…+2017+201912、 1+5+52+53+…+5100省 市 学校 姓名 赛场 参赛证号∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕∕〇∕∕∕∕∕∕ 密 〇 封 〇 装 〇 订 〇 线 ∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕〇∕∕∕∕∕∕密 封 线 内 不 要 答 题三、解答题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017AMC8 考题及答案ProblemlWhichofthefollowi ngvaluesislargest?(A)2 + 8 + 1+7 (B)2x0+l + 7 (C)2 + 0xl + 7 (D) 2 + 0+1 x 7 (E) 2 x 0 x 1 x 7 Problem2Alicia,Bre nda,a ndColbyweretheca ndidatesi narece ntelectio nforstude ntpr eside nt.Thepiechartbelowshowshowthevotesweredistributedam on gthethreeca ndidates.lfBre ndareceived36votes,the nhowma nyv oteswerecastallt ogether?(A) 70 (B) 84 (C) 100 (D) 10G (E) 120Problem3WhatisthevalueoftheeGpressio n(A) 4 (B) 4“(C) 8 (D) (E) 16Problem4Whe n0.000315ismultipliedby7,928,564theproductisclosesttowhichofthef ollowi ng?(A) 210' (B) 240 (C) 2100 (D) 2400 (E) 24000Problem5WhatisthevalueoftheeGpression 1 + 2 + 3 4 4 + 5 + 6 + 7(A) 1020 (T3) 1120 (C) 1220 (D) 2240 (E) 3360Problem6Ifthedegreemeasuresofthea nglesofatria ngleare in theratio3:3: 4,whatisthedegreemeasureofthelargestangleofthetriangle?(A) 18 (B) 36 (C) 60 (D) 72 (E) 90Problem7Let Zbea6-digitpositivei nteger,suchas247247,whosefirstthreedigitsarethesam easitslastthreedigitstake nin thesameorder.Whichofthefollowi ngnu mbers mustalsobeafactorof Z?(A) 11 (B) 19 (C) 101 (D) 111 (E) 1111Problem8Malcolmwa ntstovisitlsabellaafterschooltodaya ndkno wsthestreetwheres helivesbutdoes n'tk no wherhouse nu mber.Shetellshim,"Myhouse nu mberh astwodigits,a ndeGactlythreeofthefollowi ngfourstateme ntsaboutitaretru e."(1) ltisprime.(2) ltiseve n.(3) Itisdivisibleby7.(4) O neofitsdigitsis9.Thisi nformatio nallowsMalcolmtodetermi nelsabella'shouse nu mber.Whati sits un itsdigit?(A) 4 (B) 6 (C) 7 (D) 8 (E) 9Problem9AllofMarcy'smarblesareblue,red,gree n,o ryellow. On ethirdofhermarblesar eblue, on efourthofthemarered,a ndsiGofthemaregree n. Whatisthesmallest nu mberofyellowmarblesthatMarcycouldhave?(A) 1 (B) 2 (C) 3 (D) 4 (E) 5Problem10AboGco ntai nsfivecards, nu mbered1,2,3,4,a nd5.Threecardsareselectedra n domlywithoutreplaceme ntfromtheboG.Whatistheprobabilitythat4isthela rgestvalueselected?(A)二(B) : (C)二(D) - (E)-v 7 10 、' 5 x 7 10 1 7 5 v f2Problem11Asquare-shapedflooriscoveredwithc on grue ntsquaretiles .I fthetota Inumb eroftilesthatlie on thetwodiago nalsis37,howma nytilescoverthefloor?(A) 148 (B) 324 (C) 361 (D) 1296 (E) 1369Problem12Thesmallestpositivei ntegergreatertha n1thatleavesaremai nderof1whe ndi videdby4,5,a nd6liesbetwee nwhichofthefollowi ngpairsofnumbers?(A) 2 and 19 (B) 20 and 39 (C) 40 and 59 (D) 60 and79 (E) 80 and 124Problem13Peter,Emma,a ndKylerplayedchesswitheachother.Peterw on 4gamesa ndlost2games.Emmaw on 3gamesa ndlost3games .1 fKylerlost3games,howma ny gamesdidhew in?(A) 0 (B) 1 (C) 2 (D) 3 (E) 4Problem14Chloea ndZoearebothstude ntsi nMs.Demea no r'st ni ghttheye achsolvedhalfoftheproblemsi ntheirhomeworkassig nmen talo nean dthe ns olvedtheotherhalftogether.Chloehadcorrecta nswerstoo nly 80% oftheproblemsshesolvedal on e,butoverall 88%ofhera nswerswerecorrect.Zoehadcorrecta nswersto 90 % oftheproblemsshesolvedal on e.WhatwasZoe'soverallperce ntageofcorrect an swers?(A) 89 (B) 92 (C) 93 (D) 96 (E) 98Problem15In thearra ngeme ntoflettersa ndnu meralsbelow,byhowma ny differe ntpaths canon espellAMC8?Begi nnin gattheAi nthemiddle,apathallows on lymovesf romon elettertoa nadjace nt(above,below,left,orright,but no tdiag on al)lette r.On eeGampleofsuchapathistracedi nthepicture.8 C 8(A) 8 (B) 9 (C) 12 (D) 24(E) 30 Problem16Inthefigurebelow,choosepoint D o n 打Csothat △-4CD and 氐ADDhaveequalperimeters.Whatistheareaof △/!!?£)?I _____________________________ x=A X BM M 丄盃!M(A) - (B) - (C) 2 (D) —(E)-Problem17Starti ngwithsomegoldcoi nsan dsomeemptytreasurechests,ltriedtoput9goldcoi nsin eachtreasurechest,butthatleft2treasurechestsempty.Soi nsteadl put6goldcoi nsi neachtreasurechest,butthe nlhad3goldcoi nsleftover.How many goldco in sdidIhave?(A) 9 (B) 27 (C) 15 (D) 63 (E) 81Problem18In the non-conv eGquadrilateral 貝£?C"D show nbelow, /EC? D isarighta ngle, AB= 12, BC = 4,CD = 3,and AD = 13.Whatistheareaofquadrilatera^ A D C U?(A) 12 (B) 24 (C) 26 (D) 30 (E) 36Problem19Foranypositiveinteger Tl/,thenotation A°denotestheproductoftheintegers through A/.Whatisthelargestinteger nforwhich 5"isafactorofthesum98!+99!+ 100!?(A) 23 (B) 24 (C) 25 (D) 26 (E) 27Problem20Anin tegerbetwee n 10 00a nd9999,i nclusive,ischose natra ndom.Whatistheprobabilitythatitisa no ddi nte gerwhosedigitsarealldist inct?JLP J UU * & 丄 I * 心—— (B)—— (C)—— (D) — (E)—— 75 v } 225 k 7 40U v y 25 “25Problem21Suppose a ,b ,a nd care non zeroreal nu mbers,a nd a+ b + c = O.Whatarethepossiblevalue(s)for (A) 0(B) 1 and - 1 (C) 2 aixl 一 2 (D) 0,2, and 一 2 Problem22 Intherighttriangle ABC/C =丄2QC = 5,andangle Cisarighta ngle.Asemicircleis in scribedi nthetria ngleasshow n. Whatistheradi usofthesemicircle?A --------- ----------- c(—何扌(C )豈(D )寸—(E)豈Problem23Eachdayforfourdays,Li ndatraveledforo nehourataspeedthatresultedi nhert raveli ngon emilei nanin tegernumberofmi nu tes.Eachdayafterthefirst,hersp a b c abc ---- 1 1 --- 1 G | - |&| ---- |c| ---- \abc\(E) 0T1, and 一eeddecreasedsothatthe nu mberofm inu testotravel on emile in creasedby5m inu tesoverthepreced in gday.Eachofthefourdays,herdista ncetraveledwasal soa nin tegernumberofmiles.Whatwasthetotal nu mberofmilesforthefourtri ps?(A) 10 (B) 15 (C) 25 (D) 50 (E) 82Problem24Mrs.Sa ndershasthreegra ndchildre n,whocallherregularly.O necallsherever ythreedays, on ecallshereveryfourdays,a ndon ecallshereveryfivedays.Allthr eecalledhero nDecember31,2O16.O nhowma nydaysduri ngthe neGtyeardid she notreceiveaph on ecallfroma ny ofhergra ndchildre n?(A) 78 (B) 80 (C) 144 (D) 11G (E) 152Problem25Inthefigureshown, 〔'S and /T arelinesegmentseachoflength2,andm-ZTUS= G0°Arcs 云 a nd SRareeach on e-siGthofacirclewithradius2.Whatistheareaoftheregio nshow n?iR(A) 3^3 一7T (B) 4/3 —宁(C) 273 (D) 4\/3 一子(E) 4 + 2017AMC8A nswerKey1. A2. E3. C4. D5. B6. D8. D10. C11. C12. D13. B14. C15. D16. D17. C18. B19. D20. B21. A22. D23. C24. D25. B。
