基本初等函数知识点总结
初等基本函数知识点总结

初等基本函数知识点总结函数是数学中最基本的概念之一,它在数学的各个分支中都有着重要的应用。
初等基本函数是指在初等数学范围内常见的基本函数,包括常数函数、一次函数、二次函数、指数函数、对数函数、幂函数、三角函数等。
本文将对这些初等基本函数的概念、性质等进行总结和介绍。
一、常数函数常数函数的定义是f(x) = c (c为常数)。
这里的c就是常数函数的函数值,它是一个常数,和x的取值无关。
在坐标系中,常数函数的图象是一条水平的直线,它的斜率为0。
常数函数的性质有:1. 常数函数的图象是一条水平的直线。
2. 常数函数的定义域是全体实数集R,值域为{c}。
3. 常数函数的导数为0,即f'(x) = 0。
4. 常数函数是一个一一对应的函数。
5. 常数函数是奇函数,偶函数,周期函数,增函数,减函数等的特殊情况。
二、一次函数一次函数的定义是f(x) = kx + b (k和b为常数,k≠0)。
在坐标系中,一次函数的图象是一条通过点P(k,b)的直线,它的斜率为k,截距为b。
一次函数的性质有:1. 一次函数的图象是一条直线,斜率k决定了直线的倾斜程度,截距b决定了直线与y轴的交点位置。
2. 一次函数的定义域是全体实数集R,值域是一切实数集R。
3. 一次函数的导数为k,即f'(x) = k。
4. 当k>0时,一次函数是增函数;当k<0时,一次函数是减函数;当k=0时,一次函数是常数函数。
5. 一次函数是一个奇函数,因为f(-x) = -kx + b = -f(x)。
三、二次函数二次函数的定义是f(x) = ax^2 + bx + c (a、b和c为常数,a≠0)。
二次函数的图象是一个开口向上或者向下的抛物线,它的开口方向由a的正负决定。
当a>0时,抛物线开口向上;当a<0时,抛物线开口向下。
二次函数的性质有:1. 二次函数的图象是一个抛物线,它关于y轴对称,对称轴方程为x = -b/2a。
基本初等函数知识总结

1
0
x
y loga x
y log2 x
y log3 x y log1 x x
3
y log1 x
2
性 质
底数互为倒数的两个指数
一 函数的图象关于y轴对称。
底数互为倒数的两个对数 函数的图象关于x轴对称。
性
质 在 y轴的右边看图象,图象 二 越高底数越大.即底大图高
在 x=1的右边看图象,图象 越高底数越小.即底小图高
幂函数
函数y=xα叫做幂函数, 其中x是自变量, α是常 数.
对于幂函数,我们只
讨论 1, 2, 3, 1 , 1
2
时的情形
y y x3
y x2
1 -1
O1
-1
yx
1
y x2
y1 x
x
幂函数的性质
函数 性质
定义域 值域
奇偶性
单调性
公共点
y=x y=x2
R
R
R [0,+∞) 奇偶
增
[0,+∞)增
n am
同时: 0的正分数指数幂等于0; 0的负分数指数幂
没有意义
2.有理数指数幂的运算性质
a a a r s
r s(a 0,r, s Q) 同底数幂相乘,底数不变指数相加
r
a a r -s (a 0,r, s Q) 同底数幂相除, 底数不变指数相减 as
(a ) a r s
rs (a 0,r, s Q) 幂的乘方底数不变,指数相乘
o
x
①x∈ (0,+∞) ; ② y∈ R;
③过定点(1, 0)
性 ④当x> 1时,y> 0, 质 0< x< 1时, y< 0
基本初等函数知识点归纳

基本初等函数知识点归纳1.常值函数:常值函数是指在定义域上的值始终相同的函数。
常见的常值函数有恒等于0的零函数和恒等于1的单位函数。
常值函数的图像是一条与x轴平行的直线。
2.幂函数:幂函数是指形如y=x^n的函数,其中n是一个实数。
当n 为正偶数时,函数的图像在原点右侧递增;当n为正奇数时,图像在全定义域递增;当n为负数时,图像在全定义域递减。
特殊地,当n为0时,函数为常值函数13.指数函数:指数函数是形如y=a^x的函数,其中a为正实数且a≠1、指数函数的图像可以是递增或递减的曲线,具体取决于底数a的大小关系。
当a>1时,函数递增;当0<a<1时,函数递减。
指数函数特点是它们的图像都经过点(0,1)。
4. 对数函数:对数函数是指形如y = log_a(x)的函数,其中a为正实数且a ≠ 1、对数函数是指数函数的反函数,因此它们的图像是关于y = x对称的。
对数函数的图像在定义域上递增,对数函数的唯一一个特殊点是(1,0)。
5. 三角函数:三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。
这些函数在三角学中起着重要的作用,并且它们的图像都是周期性的。
正弦函数和余弦函数的图像是一条在[-1,1]之间往复的波浪线,而正切函数和余切函数的图像是一条通过原点的无数个波浪线。
6. 反三角函数:反三角函数是三角函数的反函数。
反三角函数包括反正弦函数asin(x)、反余弦函数acos(x)、反正切函数atan(x)等。
它们的定义域和值域与所对应的三角函数的范围正好相反。
反三角函数的图像和所对应的三角函数的图像关于y = x对称。
以上是基本初等函数的主要内容,它们是数学中最常见的函数,不仅在实际问题中有着广泛的应用,而且还在高中数学的教学中起到了重要的作用。
通过对这些函数的学习与理解,可以更好地掌握数学知识,提高数学解题的能力。
基本初等函数定义及性质知识点归纳
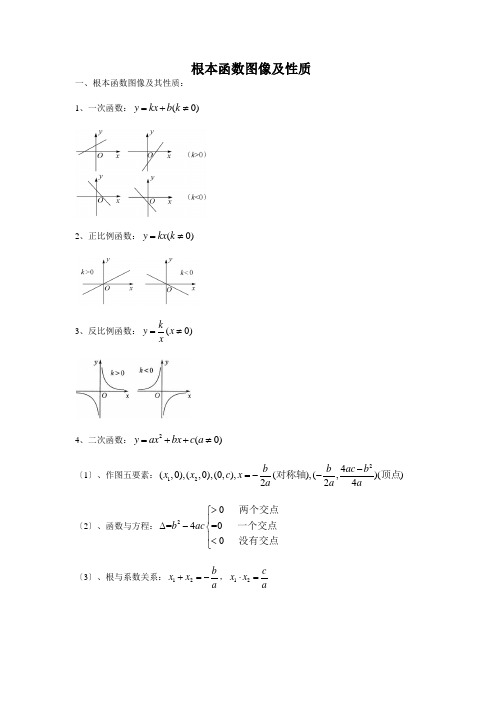
根本函数图像及性质一、根本函数图像及其性质: 1、一次函数:(0)y kx b k =+≠2、正比例函数:(0)y kx k =≠3、反比例函数:(0)ky x x=≠4、二次函数:2(0)y ax bx c a =++≠〔1〕、作图五要素:2124(,0),(,0),(0,),(),(,)()224b b ac b x x c x a a a -=--对称轴顶点 〔2〕、函数与方程:2=4=00b ac >⎧⎪∆-⎨⎪<⎩两个交点一个交点没有交点〔3〕、根与系数关系:12b x x a +=-,12c x x a⋅=5、指数函数:(0,1)x y a a a =>≠且 〔1〕、图像与性质:〔i 〕1()(0,1)x xy a y a a a==>≠与且关于y 轴对称。
〔ii 〕1a >时,a 越大,图像越陡。
(2)、应用:〔i 〕比拟大小: 〔ii 〕解不等式: 1、回忆:〔1〕()mmmab a b =⋅ 〔2〕()mm m a a b b=2、根本公式:〔1〕m n m na a a+⋅= 〔2〕m m n n a a a-= 〔3〕()m n m na a ⨯=3、特殊:〔1〕01(0)a a =≠ 〔2〕11(0)aa a-=≠ 〔3〕1;0)na n a R n a =∈≥为奇数,为偶数,(4;0;0||a n aa aa a n ≥⎧⎧==⎨⎨-<⎩⎩为奇其中,为偶例题1:〔1〕22232[()()]3x x y xy y x x y x y ---÷;32235()()(5)x xy xy ÷(2)112032170.027()(2)1)79----+-;20.520371037(2)0.1(2)392748π--++-+(3例题2:〔1〕化简:212212)9124()144(+-+++a a a a(2)方程016217162=+⨯-xx 的解是 。
基本初等函数知识点

基本初等函数知识点1.函数的定义:函数是一种特殊的关系,它将一个或多个输入数值映射到唯一的输出数值。
函数通常用f(x)来表示,其中x是输入变量,f(x)是输出变量。
函数可以用图形、符号或表格来表示。
2.定义域和值域:函数的定义域是所有可输入的数值的集合,而函数的值域是所有可能的输出数值的集合。
定义域可写作D(f),值域可写作R(f)。
3.线性函数:线性函数是一种具有常数斜率的函数。
它的形式为f(x) = mx + b,其中m是斜率,b是截距。
线性函数的图形是一条直线。
4.幂函数:幂函数是一种形如f(x) = ax^b的函数,其中a和b是常数。
幂函数的图形通常是一条平滑的曲线。
当b为正偶数时,曲线在x轴的正半轴都是上升的;当b为负偶数时,曲线在x轴的正半轴是下降的。
5.指数函数:指数函数是以常数e为底的函数,它的形式为f(x)=a^x,其中a是指数底数。
指数函数的图形为一条逐渐增长(或逐渐减小)的曲线。
6.对数函数:对数函数是指以常数a为底的对数函数,它的形式为f(x) =log_a(x),其中a为底数,x为函数的输入值。
对数函数是指数函数的反函数,即f(x) = a^x的反函数。
7.三角函数:三角函数是有关三角形角度与边长之间的关系的函数。
常见的三角函数包括正弦函数、余弦函数和正切函数。
三角函数的图形是周期性的曲线,周期为2π。
8.反函数:反函数是指满足f(f^(-1)(x))=x和f^(-1)(f(x))=x的函数对。
反函数可以通过交换函数的输入和输出得到。
9.复合函数:复合函数是指将一个函数的输出作为另一个函数的输入的函数关系。
复合函数可以表示为f(g(x)),其中g(x)是一个函数,f(x)是另一个函数。
10.奇偶函数:奇函数是满足f(-x)=-f(x)的函数,而偶函数是满足f(-x)=f(x)的函数。
奇函数的图形关于原点对称,偶函数的图形关于y轴对称。
这些是基本初等函数的一些常见知识点,掌握了这些知识点可以帮助你理解函数的基本概念、性质和图像,为进一步学习更高级的数学知识打下坚实的基础。
基本初等函数知识总结

基本初等函数知识总结含义:常数函数、幂函数、指数函数、对数函数、三角函数和反三角函数统称为基本初等函数1.常数函数(y=C)(1)定义域: D(f)=(-∞,+∞)(2)值域: Z(f)=C(3) 性质: 它的图像是一条平行于x轴并通过点(0,C)在y轴上截距为C的直线(4 )图像:(5)周期性:常值函数是一个周期函数. 因对于任何x∈(-∞,+∞)和实数T,f(x+T)=f(x)=T,但并无最小正周期【注】常值函数不含自变量且不存在反函数2.幂函数(1)定义:形如y=x^a(a为常数)的函数,即以底数为自变量,幂为因变量,指数为常量的函数称为幂函数.(2)性质:在(0,+∞)内总有意义①当α>0时函数图像过点(0,0)和(1,1),在(0,+∞)内单调增加且无界②当α<0时函数图像过点(1,1),在(0,+∞)内单调减少且无界(3)图像:3.指数函数y=a^x(a>0且a≠1)(1)定义域:x∈R(2)值域:(0,+∞)(3)性质:①单调性:1.当0<a<1时,在(-∞,+∞)内单调减少 2.当a >1时,在(-∞,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(4)图像:①由指数函数y=a^x与直线x=1相交于点(1,a)可知:在y轴右侧,图像从下到上相应的底数由小变大。
②由指数函数y=a^x与直线x=-1相交于点(-1,1/a)可知:在y轴左侧,图像从下到上相应的底数由大变小。
③指数函数的底数与图像间的关系可概括的记忆为:在y轴右边“底大图高”;在y轴左边“底大图低” 如图:(5)运算法则:①②③④4.对数函数y=logax(a>0 且a≠1)(1)定义:如果a^x=N(a>0,且a ≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数一般地,函数y=logax(a>0,且a ≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数(2)定义域:(0,+∞),即x>0(3)值域:R(4)性质:①单调性:1.当0<a<1时,在(0,+∞)内单调减少 2.当a >1时,在(0,+∞)内单调增加②奇偶性:非奇非偶函数③周期性:非周期函数④有界性:无界函数(5)图像:【注】①负数和零没有对数②1的对数是零③底数的对数等于1(6)常用法则/公式:5.三角函数⑴正弦函数y=sin x(1)定义:对边与斜边的比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ(K∈Z)时,Y 取最大值1 2.当X=2Kπ+3π/2(K∈Z时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:奇函数③对称性:对称中心是(Kπ,0),K ∈Z;对称轴是直线x=Kπ+π/2,K ∈Z④单调性:在[2Kπ-π/2,2Kπ+π/2],K∈Z上单调递增;在[2Kπ+π/2,2Kπ+3π/2],K∈Z上单调递减⑤有界性:有界函数(6)图像:(2)余弦函数y=cos x(1)定义:邻边与斜边之比(2)定义域:R(3)值域:【-1,1】(4)最值:1.当X=2Kπ +π /2(K∈Z)时,Y取最大值1 2.当X=2Kπ +π (K∈Z)时,Y取最小值-1(5)性质:①周期性:最小正周期都是2πT=2π②奇偶性:偶函数③对称性:对称中心是(Kπ+π/2,0),K∈Z;对称轴是直线x=Kπ,K∈Z④单调性:在[2Kπ,2Kπ+π],K∈Z上单调递减;在[2Kπ+π,2Kπ+2π],K∈Z上单调递增⑤有界性:有界函数(6)图像:(3)正切函数y=tan x(1)定义:对边与邻边之比(2)定义域:{x∣x≠Kπ+π/2,K∈Z}(3)值域:R(4)最值:无最大值和最小值(5)性质:①周期性:最小正周期都是πT=π②奇偶性:奇函数③对称性:对称中心是(Kπ/2,0),K∈Z④单调性:在[Kπ-π/2,Kπ+π/2],K∈Z上单调递增⑤有界性:无界函数(6)图像:(4)余切函数y=cot x(1)定义:在直角三角形中,某锐角的相邻直角边和相对直角边的比,叫做该锐角的余切。
基本初等函数知识点总结

基本初等函数知识点总结1.常数函数:常数函数是指函数的值在定义域内都保持不变的函数。
表示为f(x)=c,其中c是常数。
常数函数的图像是一条平行于x轴的直线。
常数函数的性质是恒等性,即f(x)=f(x'),对于任意x和x'都成立。
2.平方函数:平方函数是指函数的值与自变量的平方成正比的函数。
表示为f(x)=x²。
平方函数的图像是一条开口向上的抛物线。
平方函数的性质是奇偶性,即f(-x)=f(x),对于任意实数x都成立。
3.立方函数:立方函数是指函数的值与自变量的立方成正比的函数。
表示为f(x)=x³。
立方函数的图像是一条通过原点且存在于所有象限的曲线。
立方函数的性质是单调性,即在定义域内,当x₁<x₂时,有f(x₁)<f(x₂)或f(x₁)>f(x₂)成立。
4.绝对值函数:绝对值函数是指函数的值与自变量的绝对值成正比的函数。
表示为f(x)=,x。
绝对值函数的图像是一条以原点为顶点且对称于y轴的V字形曲线。
绝对值函数的性质是非负性,即对于任意实数x,有f(x)≥0成立。
5.指数函数:指数函数是指函数的值与自变量的指数幂成正比的函数。
表示为f(x)=aˣ,其中a是一个正实数且a≠1、指数函数的图像是一条通过点(0,1)且与x轴和y轴都无交点的曲线。
指数函数的性质是增长性,即在定义域内,当x₁<x₂时,有f(x₁)<f(x₂)成立。
6. 对数函数:对数函数是指函数的值与自变量的对数成正比的函数。
表示为f(x)=logₐ(x),其中a是一个正实数且a≠1、对数函数的图像是一条通过点(1, 0)且与x轴和y轴都无交点的曲线。
对数函数的性质是单调性,即在定义域内,当x₁<x₂时,有f(x₁)<f(x₂)成立。
7. 三角函数:三角函数包括正弦函数、余弦函数、正切函数等。
正弦函数表示为f(x)=sin(x),余弦函数表示为f(x)=cos(x),正切函数表示为f(x)=tan(x)。
基本初等函数知识点

4.对数的运算性质 如果 ,那么①ห้องสมุดไป่ตู้法:
②减法:
③数乘:
④
⑤
⑥换底公式:
知识点四:对数函数及其性质
2
1.对数函数定义 一般地,函数 2.对数函数性质: 函数名称 定义 函数 对数函数 且 叫做对数函数 叫做对数函数,其中 是自变量,函数的定义域 .
图象
定义域 值域 过定点 奇偶性 单调性 在 上是增函数 图象过定点 ,即当 非奇非偶 在 上是减函数 时, .
4
4.函数值域: ①y
3 2x
②y
x3 5 x
5、函数图像变换知识 ①平移变换: 形如:y=f(x+a):把函数 y=f(x)的图象沿x轴方向向左或向右平移|a|个单位,就得到 y=f(x+a)的图象。 形如:y=f(x)+a:把函数 y=f(x)的图象沿y轴方向向上或向下平移|a|个单位,就得到 y=f(x)+a 的图象 ②.对称变换 y=f(x)→ y=f(-x),关于y轴对称 y=f(x)→ y=-f(x) ,关于x轴对称 ③.翻折变换 y=f(x)→y=f|x|, (左折变换) 把y轴右边的图象保留,然后将y轴右边部分关于y轴对称 y=f(x)→y=|f(x)|(上折变换) 把x轴上方的图象保留,x轴下方的图象关于x轴对称 在第一象限内,底数越大,图像(逆时针方向)越靠近 y 轴。 6 函数的表示方法 ①列表法:通过列出自变量与对应的函数值的表来表达函数关系的方法叫列表法 ②图像法:如果图形 F 是函数 y f ( x) 的图像,则图像上的任意点的坐标满足函数的关系式,反之满足函数关系的点 都在图像上.这种由图形表示函数的方法叫做图像法. ③如果在函数 y f ( x) ( x A) 中, f ( x) 是用代数式来表达的,这种方法叫做解析法 7.分段函数 在函数的定义域内,对于自变量 x 的不同取值区间,有着不同的对应法则,这样的函数通常叫做分段函数。 8 函数单调性及证明方法: ①增函数:一般地 , 设函数 f(x) 的定义域为 D, 如果对于定义域 D 内的某个区间上的任意两个自变量的值 x1,x2 , 当 x1<x2 时 , 都有 f(x1)< f(x2), 那么就说 f(x) 在这个区间上是增函数。 此区间就叫做函数 f(x) 的单调增区间。 ②减函数: 一般地 , 设函数 f(x) 的定义域为 D, 如果对于定义域 D 内的某个区间上的任意两个自变量的值 x1,x2 , 当 x1<x2 时 , 都有 f(x1)> f(x2), 那么就说 f(x) 在这个区间上是减函数。此区间叫做函数 f(x) 的单调减区间。 ③证明方法 第一步:设 x1、x2 是给定区间内的两个任意的值,且 x1<x2; 第二步:作差 f(x2)-f(x1),并对“差式”变形,主要采用的方法是“因式分解”或“配方法”; 第三步:判断差式 f(x2)-f(x1)的正负号,从而证得其增减性 9.函数的奇偶性 ⑴奇函数 ①设函数 y=f(x)的定义域为 D,如果对 D 内的任意一个 x,都有-x∈D,且 f(-x)=-f(x),则这个函数叫做奇函数。 ②奇函数图象关于原点(0,0)中心对称。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本初等函数
一、指数函数
一指数与指数幂的运算
1.根式的概念:一般地,如果a x n =,那么x 叫做a 的n 次方根,其中n >1,且n ∈N .
◆ 负数没有偶次方根;0的任何次方根都是0,记作00=n ;
当n 是奇数时,a a n n =,当n 是偶数时,⎩
⎨
⎧<≥-==)0()
0(||a a a a a a n n
2.分数指数幂
正数的分数指数幂的意义,规定:
)
1,,,0(*>∈>=n N n m a a a
n m n
m ,
)1,,,0(1
1*>∈>=
=
-
n N n m a a a
a
n
m
n
m n
m
◆ 0的正分数指数幂等于0,0的负分数指数幂没有意义
3.实数指数幂的运算性质 1r a ·s
r r a a += ),,0(R s r a ∈>;
2rs s r a a =)(
),,0(R s r a ∈>;
3
s r r a a ab =)( ),,0(R s r a ∈>.
二指数函数及其性质
1、指数函数的概念:一般地,函数)1,0(≠>=a a a y x 且叫做指数函数,其中x 是自变量,函数的定义域为R . 注意:指数函数的底数的取值范围,底数不能是负数、零和1.
2、指数函数的图象和性质
注意:利用函数的单调性,结合图象还可以看出: 1在a,b 上,)1a 0a (a )x (f x ≠>=且值域是)]b (f ),a (f [或)]a (f ),b (f [;
2对于指数函数)1a 0a (a )x (f x ≠>=且,总有a )1(f =; 二、对数函数 一对数
1.对数的概念:一般地,如果N a x =)1,0(≠>a a ,
那么数x 叫做以.a 为底..N 的对数,记作:N x a log =a — 底数,N — 真数,N a log — 对数式
说明:错误! 注意底数的限制0>a ,且1≠a ;
错误! x N N a a x
=⇔=log ;
错误! 两个重要对数:
错误! 常用对数:以10为底的对数N lg ; 错误! 自然对数:以无理数 71828.2=e 为底的对数的对数N ln .
指数式与对数式的互化
幂值 真数
b = N b
对数 二对数的运算性质
如果0>a ,且1≠a ,0>M ,0>N ,那么: 错误! M a (log ·=)N M a log +N a log ;
错误! =N M
a
log M a log -N a log ; 错误! n
a M log n =M a log )(R n ∈.
注意:换底公式
a
b
b c c a log log log =
0>a ,且1≠a ;0>c ,且1≠c ;0>b . 利用换底公式推导下面的结论 1b m
n b a n a m
log log =;2a
b b a log 1
log =
. 二对数函数 1、对数函数的概念:函数0(log >=a x y a ,且)1≠a 叫做对数函数,其中x 是自变量,函数的定义域是0,+∞.
注意:错误! 对数函数的定义与指数函数类似,都是形式定义,注意辨别;如:x y 2log 2=,5
log 5
x y = 都
不是对数函数,而只能称其为对数型函数. 错误! 对数函数对底数的限制:0(>a ,且)1≠a .
>0
值域为R 值域为R 在R 上递
增
在R 上递减
函数图象
都过定点
1,0 函数图象都过
定点1,0
三幂函数
1、幂函数定义:一般地,形如αx y =)(R a ∈的函数称为幂函数,其中α为常数.
2、幂函数性质归纳.
1所有的幂函数在0,+∞都有定义并且图象都过点1,1;
20>α时,幂函数的图象通过原点,并且在区间
),0[+∞上是增函数.
特别地,当1>α时,幂函数的图象下凸;当10<<α时,幂函数的图象上凸; 30<α时,幂函数的图象在区间),0(+∞上是减函数.在第一象限内,当x 从右边趋向原点时,图象在y 轴右方无限地逼近y 轴正半轴,当x 趋于∞+时,图象在x 轴上方无限地逼近x 轴正半轴. 例题:
1. 已知a>0,a 0,函数y=a x 与y=log a -x 的图象只能是
2.计算: 1 2
log 227log 553
125
+= ;
221343
101.016])2[()8
7(064
.075
.030++-+----- =
3.函数y=log 2
12x 2-3x+1的递减区间为
4.若函数)10(log )(<<=a x x f a
在区间]2,[a a 上的最大值是最小值的
3倍,
则a= 5.已知1()log (01)1a
x
f x a a x
+=>≠-且,1求()f x 的定义域2求使()0f x >的x 的取
值范围 6.
7. .。
