基本初等函数复习
基本初等函数知识总结
1
0
x
y loga x
y log2 x
y log3 x y log1 x x
3
y log1 x
2
性 质
底数互为倒数的两个指数
一 函数的图象关于y轴对称。
底数互为倒数的两个对数 函数的图象关于x轴对称。
性
质 在 y轴的右边看图象,图象 二 越高底数越大.即底大图高
在 x=1的右边看图象,图象 越高底数越小.即底小图高
幂函数
函数y=xα叫做幂函数, 其中x是自变量, α是常 数.
对于幂函数，我们只
讨论 1, 2, 3, 1 , 1
2
时的情形
y y x3
y x2
1 -1
O1
-1
yx
1
y x2
y1 x
x
幂函数的性质
函数 性质
定义域 值域
奇偶性
单调性
公共点
y=x y=x2
R
R
R [0,+∞) 奇偶
增
[0,+∞)增
n am
同时: 0的正分数指数幂等于0； 0的负分数指数幂
没有意义
2.有理数指数幂的运算性质
a a a r s
r s(a 0,r, s Q) 同底数幂相乘,底数不变指数相加
r
a a r -s (a 0,r, s Q) 同底数幂相除, 底数不变指数相减 as
(a ) a r s
rs (a 0,r, s Q) 幂的乘方底数不变,指数相乘
o
x
①x∈ (0,+∞) ； ② y∈ R;
③过定点(1, 0)
性 ④当x＞ 1时,y＞ 0, 质 0＜ x＜ 1时, y＜ 0
基本初等函数知识点归纳
基本初等函数知识点归纳1.常值函数：常值函数是指在定义域上的值始终相同的函数。
常见的常值函数有恒等于0的零函数和恒等于1的单位函数。
常值函数的图像是一条与x轴平行的直线。
2.幂函数：幂函数是指形如y=x^n的函数，其中n是一个实数。
当n 为正偶数时，函数的图像在原点右侧递增；当n为正奇数时，图像在全定义域递增；当n为负数时，图像在全定义域递减。
特殊地，当n为0时，函数为常值函数13.指数函数：指数函数是形如y=a^x的函数，其中a为正实数且a≠1、指数函数的图像可以是递增或递减的曲线，具体取决于底数a的大小关系。
当a>1时，函数递增；当0<a<1时，函数递减。
指数函数特点是它们的图像都经过点(0,1)。
4. 对数函数：对数函数是指形如y = log_a(x)的函数，其中a为正实数且a ≠ 1、对数函数是指数函数的反函数，因此它们的图像是关于y = x对称的。
对数函数的图像在定义域上递增，对数函数的唯一一个特殊点是(1,0)。
5. 三角函数：三角函数包括正弦函数sin(x)、余弦函数cos(x)、正切函数tan(x)、余切函数cot(x)、正割函数sec(x)和余割函数csc(x)。
这些函数在三角学中起着重要的作用，并且它们的图像都是周期性的。
正弦函数和余弦函数的图像是一条在[-1,1]之间往复的波浪线，而正切函数和余切函数的图像是一条通过原点的无数个波浪线。
6. 反三角函数：反三角函数是三角函数的反函数。
反三角函数包括反正弦函数asin(x)、反余弦函数acos(x)、反正切函数atan(x)等。
它们的定义域和值域与所对应的三角函数的范围正好相反。
反三角函数的图像和所对应的三角函数的图像关于y = x对称。
以上是基本初等函数的主要内容，它们是数学中最常见的函数，不仅在实际问题中有着广泛的应用，而且还在高中数学的教学中起到了重要的作用。
通过对这些函数的学习与理解，可以更好地掌握数学知识，提高数学解题的能力。
基本初等函数复习课
基本初等函数一、知识点回顾1．设]1,(,2),1(,log 81{)(-∞∈+∞∈-=x x x x x f ，则满足41)(=x f 的x 的值为2．下列函数中，既是奇函数，又在定义域内为减函数的是 （ ）x y A )21(.= 2x y .B -= 3x y .C -= x log y .D 32=3．不论a 为何正实数,函数12x y a+=-的图象一定通过一定点,则该定点的坐标是_________4．如果,10<<a 那么下列不等式中准确的是（ ）2131)1()1.(a a A ->- 0)1(log .1>+-a B a 23)1()1.(a a C +>- 1)1.(1>-+a a D5．已知函数()()()f x x a x b =--（其中a b >）的图象如下面右图所示，则函数()xg x a b =+的图象是( )三、典型例题：例1．已知函数）1a ,0a (,1])21[(log )x (f x 3≠>-= （1）求函数的定义域；（2）求使0)x (f >的x 的取值范围。
例2．已知函数).1(log )1(log )x (f x x a a +--=（1）求)x (f 的定义域; （2）求使0)(>x f 的x 的取值范围。
(3) 并判断其奇偶性；例3．已知m x f x +-=132)(是奇函数， (1)求函数的定义域 (2)求常数m 的值；例4．已知定义在R 上的奇函数f(x)，且当x ∈),0(+∞时，1)(2log )x (f x2-=. （1）求f （x)在R 上的解析式；（2）判断f(x)在),0(+∞的单调性并用定义证明.四、当堂检测：1.幂函数53m x )x (f -=( N m ∈)在)(0,+∞是减函数,且x)(f )x (f =-,则m=2．函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(21x x x x f x ，满足1)(>x f 的x 的取值范围 （ ） A ．)1,1(- B ． ),1(+∞-C ．}20|{-<>x x x 或D ．}11|{-<>x x x 或3．已知2)(x x e e x f --=，则下列准确的是（ ）A ．奇函数，在R 上为增函数B ．偶函数，在R 上为增函数C ．奇函数，在R 上为减函数D ．偶函数，在R 上为减函数 4．函数210)2()5(--+-=x x y 的定义域（ ）A ．}2,5|{≠≠x x xB ．}2|{>x xC ．}5|{>x xD ．}552|{><<x x x 或 5．设指数函数)1,0()(≠>=a a a x f x，则下列等式中不准确的是（ ）A ．f (x +y )=f(x )·f (y )B ．)()(y f x f y x f =-）（ C ．)()]([)(Q n x f nx f n∈= D ．)()]([·)]([)(+∈=N n y f x f xy f nnn6．下列关系式中，成立的是（ ）A ．10log 514log 3103>⎪⎭⎫⎝⎛>B ． 4log 5110log 3031>⎪⎭⎫⎝⎛>C ． 03135110log 4log ⎪⎭⎫⎝⎛>>D ．0331514log 10log ⎪⎭⎫⎝⎛>>7．当a ≠0时，函数y ax b =+和y b ax=的图象只可能是 （ ）8.函数2lg 11y x ⎛⎫=-⎪+⎝⎭的图像关于（ ） A 、x 轴对称 B 、y 轴对称 C 、原点对称 D 、直线y x =对称基本初等函数复习卷一、选择题 1. ·等于( )A.-B.-C.D.2.函数y=(m 2+2m-2)是幂函数,则m=( ) A.1B.-3C.-3或1D.23.设y 1=40.9,y 2=lo4.3,y 3=()1.5,则( ) A.y 3>y 1>y 2B.y 2>y 1>y 3C.y 1>y 2>y 3D.y 1>y 3>y 24.已知log 2m=2.013,log 2n=1.013,则等于( ) A.2B.C.10D.5.函数f(x)=+lg(2x +1)的定义域为( ) A.(-5,+∞)B.[-5,+∞)C.(-5,0)D.(-2,0)6.已知f(x)是函数y=log 2x 的反函数,则y=f(1-x)的图象是( )7.下列函数中,图象关于y 轴对称的是( ) A.y=log 2xB.y=C.y=x|x|D.y=8.下列各函数中,值域为(0,+∞)的是( ) A.y=B.y=C.y=x 2+x+1D.y=9. x=+的值属于区间( ) A.(-3,-2)B.(-2,-1)C.(-1,0)D.(2,3)10.设函数f(x)=已知f(a)>1,则实数a 的取值范围是( )A.(-2,1)B.(-∞,-2)∪(1,+∞)C.(1,+∞)D.(-∞,-1)∪(0,+∞) 二、填空题11.已知=(a>0),则lo a= .12.若函数f(x)=(3-a)x 与g(x)=log a x 的增减性相同,则实数a 的取值范围是 . 13．函数f (x )＝a x －2＋1的图象一定过定点P ，则P 点的坐标是________．14．已知函数f (x )＝⎩⎨⎧log 2x ，x >03x ，x ≤0则f ⎣⎢⎡⎦⎥⎤f ⎝ ⎛⎭⎪⎫14的值是________．三、解答题15.计算下列各题：(1)0.008+()2+(-16-0.75.(2)(lg5)2+lg2·lg50+.16.已知函数f(x)=log3(ax+b)的图象经过点A(2,1),B(5,2),(1)求函数f(x)的解析式及定义域.(2)求f(14)÷f()的值.17．已知函数f(x)＝log a(x2＋1)(a>1)．(1)判断f(x)的奇偶性；(2)求函数f(x)的值域．18. 函数f(x)＝log a(1－x)＋log a(x＋3)，(0<a<1)．(1)求函数f(x)的定义域；(2)若函数f(x)的最小值为－2，求a的值．答案预习自测 3 C (－1,-- 1) A A 例1解：（1）由题意得(12)x －1>0(12)x >1=(12)0 解得x<0，即f(x)的定义域为(－∞，0) （2）由题意得log 3((12)x －1)> log 3 1所以1()1021()112x x ⎧->⎪⎪⎨⎪->⎪⎩,即0111()()2211()()22xx -⎧>⎪⎪⎨⎪>⎪⎩ 解得x<－1，所以x 的取值范围是(－∞,－1)例2 解：(1)由题意得1010x x ->⎧⎨+>⎩解得－1<x<1，所以f(x)的定义域为(－1,1)(2) f(x)>0即log a (1－x)>log a (1+x)当a>1时，101011x x x x ->⎧⎪+>⎨⎪->+⎩，解得x ∈(－1,0)当0<a<1时，101011x x x x ->⎧⎪+>⎨⎪-<+⎩，解得x ∈(0,1)综上所述，当a>1时，x 的取值范围是(－1,0)；当0<a<1时，x 的取值范围是(0,1) (3)∵f(x)的定义域 (－1,1)关于原点对称，以及f(－x)= log a (1+x)－log a (1－x)= －(log a (1－x) －log a (1+x)) = －f(x) 所以f(x)是奇函数。
基本初等函数总复习
指数函数总复习【知识点回顾】一、指数与指数幂的运算 （1）根式的概念①如果,,,1n x a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n 次方根用符号n 是偶数时，正数a 的正的n n 次方根用符号0的n 次方根是0；负数a 没有n 次方根．n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．n a =；当n a =；当n 为偶数时， (0)|| (0) a a a a a ≥⎧==⎨-<⎩． （2）分数指数幂的概念①正数的正分数指数幂的意义是：0,,,m na a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 1()0,,,m m nn aa m n N a -+==>∈且1)n >．0的负分数指数幂没有意义． 注意口诀：底数取倒数，指数取相反数． （3）分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈ 二、指数函数及其性质 （4）指数函数定义域R值域（0,+∞）过定点图象过定点（0,1），即当x=0时，y=1．奇偶性非奇非偶单调性在R上是增函数在R上是减函数函数值的变化情况y＞1(x＞0), y=1(x=0), 0＜y＜1(x＜0)y＞1(x＜0), y=1(x=0), 0＜y＜1(x＞0)a变化对图象的影响在第一象限内，a越大图象越高，越靠近y轴；在第二象限内，a越大图象越低，越靠近x轴．在第一象限内，a越小图象越高，越靠近y轴；在第二象限内，a越小图象越低，越靠近x轴．【考点链接】考点一、指数的运算xay=xy(0,1)O1y=xay=xy(0,1)O1y=例1．化简：1114424111244()a b b a a b --=- ．例2. 根据下列条件求值：已知32121=+-xx ，求23222323-+-+--x x x x 的值；练习1：计算：（1）1020.5231(2)2(2)(0.01)54--+⋅-（2）120.750311(0.064)()16()2322----÷+-．(3) 2433221)(---⋅÷⋅a b b a（4）211511336622263a b a b a b ⎛⎫⎛⎫⎛⎫-÷- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭考点二、定义域例3． 求下列函数的定义域：21(1).2-=x y 31(2).3-⎛⎫= ⎪⎝⎭xy练习2．求下列函数的定义域:（1）1x 21y ()2-= （2）2x 3y 5-=考点三、值域例4． 函数11x x e y e -=+的值域练习3、(1)求函数2(0)21xxy x =>+的值域．(2)求下列函数的定义域、值域： （1）1218x y -= （2）11()2x y =-（3）3x y -=考点四、指数型函数例5. 已知函数3234+⋅-=x x y 的定义域为[0，1]，则值域为 。
基本初等函数经典复习题+答案
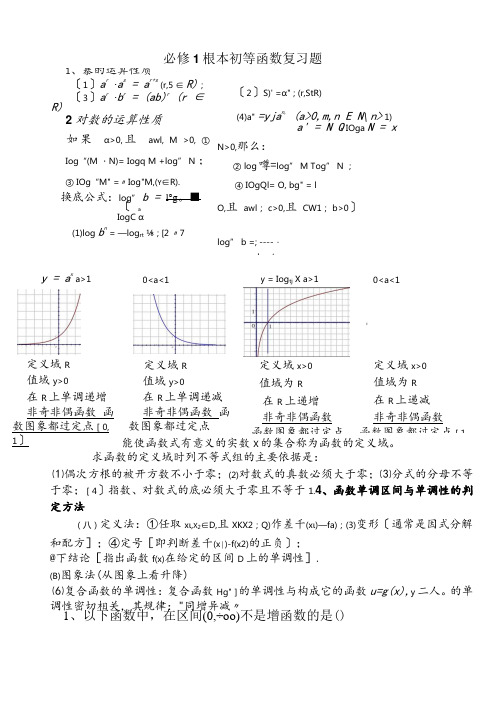
必修1根本初等函数复习题求函数的定义域时列不等式组的主要依据是：⑴偶次方根的被开方数不小于零；(2)对数式的真数必须大于零；⑶分式的分母不等于零；［4〕指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法（八）定义法：①任取xι,X 2∈D,且XKX2；Q)作差千(xι)—fa)；(3)变形〔通常是因式分解和配方］；④定号［即判断差千(x∣)-f(x2)的正负〕；@下结论［指出函数f(x)在给定的区间D 上的单调性］.(B)图象法(从图象上看升降)⑹复合函数的单调性：复合函数Hg"］的单调性与构成它的函数u=g(x),y 二人。
的单调性密切相关，其规律："同增异减〃 1、以下函数中，在区间(0,÷oo)不是增函数的是()1、暴的运算性质 〔1〕a r ∙a s = a r+s (r,5 ∈ R)； 〔3〕a r ∙b r = (ab)r (r ∈ R) 2对数的运算性质 如果 α>0,且 awl, M >0, ① Iog“(M ・N)= Iogq M +log” N ； ③ IOg“M" =〃Iog"M,(Y ∈R). 换底公式：log” b = l°g 。
■ 〔 a IogC α(1)log b n= —log rt ⅛ ; [2 〃7 〔2〕S)' =α" ; (r,StR)(4)a" =yja n, (a>0,m,n E N ∖n> 1) a' = N Q IOga N = x N>0,那么：② log 噂=log” M Tog” N ；④ IOgQl= O, bg" = lO,且 awl ； c>0,且 CW1； b>0〕 log” b =; ---- ∙log/y = a x a>1 0<a<1 y = Iog tj X a>1 II0<a<1定义域R 值域y>0 在R 上单调递增 非奇非偶函数 函数图象都过定点［0, 1〕 3、定义域： 定义域R 值域y>0 在R 上单调递减 非奇非偶函数 函数图象都过定点〔〕 定义域x>0 值域为R在R 上递增 非奇非偶函数 函数图象都过定点定义域x>0值域为R 在R 上递减 非奇非偶函数 函数图象都过定点［1, 能使函数式有意义的实数X 的集合称为函数的定义域。
第三章基本初等函数I复习
【例2】求定义域
（1）f (x)=1 2x-1来自（2）f(x)=
log1
1 (x-1）+3
（3）f (x)= log2x+1 3x-2
【练习4】求定义域P82
（1）f
(x)=
log3
1 (3x-2）
（2）f (x)= loga (2-x)
（3）f (x)= loga (1-x)2
解：
（1）
1 2
指数函数
定义 图象和性质
基本初等函数
定义 对数 运算性质
对数与对数函数
对数换底公式
对数函数
定义 图象和性质
三、重点内容
（一）基本概念：
m
1.根式与分数指数幂：a n n am ,(a 0,m, n N * ,且n 1)
2.对数式与指数式的转化：
a x N x logaN(a 0,a 1). 两种特殊情况：
a0 1,a1 a loga 1 0,logaa 1(a 0,a 1).
3.反函数的概念
y a x x logay(a 0,a 1), y loga x与y a x互为反函数.
三、重点内容
（二）基本运算：
1.指数运算
aras ars (a r )s ars (ab)r aras
y=ax和y=loga x互为反函数
y ax
y =a x
底数ɑ:ɑ0且
定ɑ义1 域:R y=x
值域:（y0=l，og+a x∞）
y log a x
底数ɑ: ɑ0且 ɑ定义1 域: （0，+∞）
值域:R
二.知识结构
n次方根及其性质
指数与指数函数
指数
高考基本初等函数知识点总结
基本初等函数综合复习一、知识点总结 1. 对数函数的概念一般地，把函数y ＝log a x (a >0，且a ≠1)叫做对数函数，其中x 是自变量，函数的定义域是 . 2. 对数函数y ＝log a x (a >0，且a ≠1)的图象与性质定义 y ＝log a x (a >0，且a ≠1)底数a >10<a <1图象定义域 值域 R单调性 在(0，＋∞)上是增函数在(0，＋∞)上是减函数共点性 图象过定点 ，即x ＝1时，y ＝0函数值特点x ∈(0,1)时，y ∈ ；x ∈[1，＋∞)时，y ∈ x ∈(0,1)时，y ∈ ；x ∈[1，＋∞)时，y ∈ 对称性函数y ＝log a x 与y ＝1log ax 的图象关于 对称【易错题1】 如图，已知正方形ABCD 的边长为2，BC 平行于x 轴，顶点A ，B 和C 分别在 函数y 1＝3log a x ，y 2＝2log a x 和y 3＝log a x （a ＞1）的图象上，则实数a 的值为________。
【题模1】 函数图象（1）底数与图像位置关系：1、指数函数图象恒过（0，1）在第一象限是“底大图高”，2、对数函数图象恒过（1，0）：在直线1x =的右侧，当1a >时，底数越大，图象越靠近x 轴；当01a <<时，底数越小，图象越靠近x 轴，即“底大图低”．3、幂函数图象恒过（1，1），在（1，1）右侧：是“指大图高”.2）函数图象变换①y ＝f (x )―――――→关于x 轴对称y ＝－f (x )． ②y ＝f (x )―――――→关于y 轴对称y ＝f (－x )． ③y ＝f (x )―――――→关于原点对称y ＝－f (－x )．④y ＝a x (a >0且a ≠1)―――――→关于y ＝x 对称y ＝log a x (a >0且a ≠1)． (3)伸缩变换①y ＝f (x )――――――――――――――――――――→a >1，横坐标缩短为原来的倍，纵坐标不变0<a <1，横坐标伸长为原来的倍，纵坐标不变 y ＝f (ax )．②y ＝f (x )―――――――――――――――――――→a >1，纵坐标伸长为原来的a 倍，横坐标不变0<a <1，纵坐标缩短为原来的a 倍，横坐标不变 y ＝af (x )． (4)翻折变换①y ＝f (x )――――――――――→保留x 轴上方图象将x 轴下方图象翻折上去 y ＝|f (x )|. ②y ＝f (x )―――――――――――→保留y 轴右边图象，并作其关于y 轴对称的图象 y ＝f (|x |)． 【讲透例题】1．设0,1a a >≠且，函数2log (2)a y x =++的图象恒过定点P ，则P 点的坐标是A ．(1,2)-B ．(2,1)-C ．(3,2)-D ．(3,2)2、不论a 为何值时,函数图象恒过一定点,这个定点坐标是 .3． 函数()2e e x xf x x--=的图像大致为 ( ) A ． B ． C ． D ．5、设函数f (x )＝2x ，则如图所示的函数图象对应的函数解析式是( ) A ．y ＝f (|x |) B ．y ＝－|f (x )| C ．y ＝－f (－|x |) D ．y ＝f (－|x |)6．(多选)若函数y ＝a x ＋b －1(a >0，且a ≠1)的图象经过第一、三、四象限，则下列选项中正确的有( )A ．a >1B ．0<a <1C ．b >0D ．b <07、已知指数函数()x f x a =，将函数()f x 的图象上的每个点的横坐标不变，纵坐标扩大为原来的3倍，得到函数()g x 的图象，再将()g x 的图象向右平移2个单位长度，所得图象恰好与函数()f x 的图象重合，则a 的值是（ ） A ．32B ．23C ．33D ．3【相似题练习】1． 已知函数2(log )y x a b =++的图象不经过第四象限，则实数a b 、满足( ) A ．1,0a b ≥≥ B ．0,1a b >≥ C ． 2log 0b a +≥ D ．20b a +≥ 2．函数f (x )＝ln(x 2＋1)的图象大致是( )3、 已知()g x 图像与x y e =关于y 轴对称，将函数()g x 的图像向左平移1个单位长度，得到()f x ，则()f x =（ ）A. 1x e +B.1x e -C.1x e -+D. 1x e -- 4、（多选题）为了得到函数ln()y ex =的图象，可将函数ln y x =的图象（ ）A ．纵坐标不变，横坐标伸长为原来的e 倍B ．纵坐标不变，横坐标缩短为原来的1eC ．向上平移一个单位长度D ．向下平移一个单位长度 5、函数y =a x －a (a ＞0，且a ≠1)的图象恒过定点（ ， ） 6、函数(其中且的图象一定不经过第 象限。
基本初等函数(I)复习
定义
指数函数 对数函数
图象与性质
幂函数
三、了解指数函数、对数函数的作用
1、在生物学上的应用（有n对等位基因的个体自交后代的表现型
种类；与细胞分裂有关的计算； DNA复制的相关计算等等 ）；
2、推测生物死亡的时间，即推算古墓的年代（根据生物体内碳14 含量的变化）； 3、预测人口数量，可以为有效控制人口增长提供依据； 4、溶液酸碱度的测量； 5、在工程、天文、航海、经济学等方面都有重要的作用。
基本初等函数（Ⅰ）复习
第2课时
教师：马福广
一、学习目标
1、理解指数函数、对数函数的定义； 2、结合图像进一步研究它们的性质，从而学会利用指数函
数、对数函数的图像与性质来解决简单的问题，体会指数函数、
对数函数是一类重要的函数模型.
二、知识结构
整数指数幂 有理指数幂 无理指数幂
定义
指数
对数
运算性质
定义
y
1
图象
0
1
x
0
x
定义域 值域
性质
三、重点内容 （二）基本性质： y loga x(a 0,且a 1)
0 a 1y来自a 1y图象 定义 域 值域 性质
O
1
x
O
1
x
四、例题分析
见学案
五、小结
1、指数函数、对数函数的定义； 2、借助图像研究性质； 3、指数函数、对数函数、性质的应用
三、重点内容
（一）定义：
1、指数函数：一般地，函数
叫做指数函数.
y a (a 0, 且a 1)
x
2、对数函数：一般地，函数 y log a x (a 0, 且a 1)
基本初等函数复习
基本初等函数复习1、指数与指数函数【知识梳理】一．根式与分数指数幂1. 若n x a=，则x叫做a的n n>1，且n N*∈.n次方根（*1,n n N>∈且）有如下恒等式：n a=,||,a na n⎧⎨⎩为奇数为偶数；==2. 规定正数的分数指数幂：mna=（0,,,1a m n N n*>∈>且）；1mnmnaa-==二、指数幂的运算律m na a=()m na=m ma b=例1 化简（1）211511336622(2)(6)(3)a b a b a b-÷-=（2例2函数()x bf x a-=的图象如图，其中a、b为常数，则下列结论正确的是（）.A．1,0a b><B．1,0a b>>C．01,0a b<<>D．01,0a b<<<（2）在同一坐标系下，函数,,,x x x xy a y b y c y d====的图，则,,,,1a b c d之间从小到大的顺序是__________．★指数函数图像的排列规律：例3. 比较下列各题中两个值的大小（用“<”或“>”填空）：(1) 2.51.731.7； (2)0.10.8-0.20.8-； (3)0.31.7 3.10.9★比较大小的方法：例4. 求下列函数的值域（1）()f x=(2)193 5 [1,2]x xy x+=++∈（3）2221()2x xy--=2、对数与对数函数【知识梳理】一．对数的概念与运算律1. 定义：如果x a N=(0,1)a a>≠，那么数x叫做以a为底N的对数记作logax N=2. 我们通常将以10为底的对数叫做常用对数，并把常用对数10log N简记为lg N以e为底的对数叫自然对数，并把自然对数logeN简记作ln N（e=2.71828……）3.对数与指数间的互化关系：当0,1a a>≠时，log baN b a N=⇔=.4. 负数与零没有对数；log10a=，log1aa=5.对数的运算法则：log()aM N=，logaMN=，log naM=，练习：用log,log,loga a ax y z表示下列各式：①logaxyz；②log a6. 对数的换底公式logloglogbabNNa=. 如果令N=b，则得到了对数的倒数公式logab=同样，也可以推导出一些对数恒等式，如log lognnaaN N=，log logmnaanN Nm=二、对数函数1.定义：一般地，当a＞0且a≠1时，函数ay=log x叫做对数函数，函数的定义域是（0，+∞）.2.性质【典例分析】例1求下列各式的值：⑴lg100 ⑵2ln e - ⑶ 91log 529-⑷21log 32.51log 6.25lg 2100+++ （5）33(lg 2)(lg5)3lg 2lg5++（6）已知log 2,log 3,a a m n ==求2m na +的值例2．（1）已知0x y z ≠ ，346xyz==，求证1112z x y-=（2）已知18log 9,185b a ==，用,a b 表示36log 5例3．如右图是对数函数①log a y x =，②log b y x =，③log c y x =，④log d y x =的图象，则,,,a b c d 与1的大小关系是★指数函数图像的排列规律： 例4．比较大小（1）2log 3.4 2l o g 8.5 （2）0.3log 1.8 0.3l o g 2.7 （3）6log 7 7l o g 6 （4）3log 2 2l o g 0.9 （5）lg 0.1 l n 0.1 （6）30.40.4log 3 0.4 3 例5．求下列函数的值域（1）2lg(22)y x x =++； （2）()()1122log 1log 3y x x =-++ （3）()22log log 2884x xy x =≤≤例6．（1） 函数22log (2)y x x =++的单调增区间为 ，减区间为 （2） 函数2lg(235)y x x =--的单调增区间为 ，减区间为（3） 函数212log (23)y x x =-++的单调增区间为 ，减区间为（4）已知函数()2log 3y ax =-在[]0,2x ∈上是减函数，则实数a 的取值范围为3、幂函数【知识梳理】一． 幂函数的定义1. 幂函数的基本形式是y x α=，其中x 是自变量，α是常数. 要求掌握y x =，2y x =，3y x =，12y x =，1y x -=这五个常用幂函数的图象. 二、幂函数的图象和性质观察出幂函数的共性，总结如下：（1）当0α>时，图象过定点(0,0),(1,1)；在(0,)+∞上是增函数. （2）当0α<时，图象过定点(1,1)；在(0,)+∞上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近.【典例分析】例：已知幂函数()y f x =的图象过点(27,3)，试讨论其单调性.4、函数的应用【知识梳理】一、方程的根与函数的零点 1．方程的根与函数零点的关系2．零点存在性定理：【典例分析】例1.(1)若函数()2f x x ax b =--的两个零点是2和3，函数()21g x bx ax ==--的零点为_________(2)若函数()1f x ax a =-+在区间()1,2-内存在零点，则实数a 的取值范围是_________ 例2.(1)函数()333f x x x =--有零点的区间是（ ）A.()1,0-B.()0,1C.()1,2D.()2,3 (2)函数()2ln f x x x=-的零点所在的大致区间是（ ） A.()2,3 B.(),e +∞ C.()1,2 D.()1,e 和(),e +∞ （3）求函数()ln 26f x x x =+-的零点的个数．。
必修一基本初等函数复习PPT课件
18
底数互为倒数的两个 对数函数
y = loga x, y = log1 x
的函数图像关于x轴对a称。
19
当a>1时，a值越大， y=logax的图像越靠近x轴；
当0<a<1时，a值越大， y=logax的图像越远离x轴。
20
4.若loga2＜logb2＜0，则( B )
(A)0＜a＜b＜1
(B)0＜b＜a＜1
y
叫做幂函数，
其中x是自变
量，α是常数.
O
x
23
幂函数的性质
函数
性质 y=x
y=x2
1
y=x3 y = x 2
y=x-1
定义域 R
R
R [0,+∞) {x|x≠0}
值域 R [0,+∞) R [0,+∞) {y|y≠0}
奇偶性 奇
偶
奇
单调性
增
[0,+∞)增 (-∞，0]减
增
非奇非偶 奇
(0,+∞)减
常用对数：通常将log10N的对数叫做常用对数，为了简便， N的常用对数记作lgN。
自然对数：通常将使用以无理数e=2.71828…为底的对数
叫
做自然对数，为了简便，
N的自然对数logeN简记作lnN.
12
2024/10/27
13
9.对数恒等式
( ) aloga N = N a 0且a 1，N 0 叫做对数恒等式
10.对数的性质 (1)负数和零没有对数； (2)1的对数是零，即loga1=0； (3)底数的对数等于1，即logaa=1 11.对数的运算法则 如果a＞0，a≠1，M＞0，N＞0，那么
§4.基本初等函数复习专题
§4.基本初等函数1.指数与指数运算（1(0)|| (0) a a a a a ≥⎧=⎨-<⎩.（2）分数指数幂：),,0(1,+-∈>==N n m a a a a a n m n mn m n m .（3）分数指数幂的运算性质：当a>0时，有：①n m n m a a a +=⋅,n m n m n ma a a a a --=⋅=; ②mn n m a a =)(; ③nn n b a ab =)(.例1：化简121121333225(3)(4)6a b a b a b ----⎛⎫- ⎪⎝⎭÷= .2.对数与对数运算(1)定义：a x ＝N ⇔x ＝log a N (a>0，且a≠1).(2)对数的运算性质：①01log =a ；1log =a a ；②对数恒等式:N a Na =log ；b a b a =log .③运算法则：N M N M a a a log log )(log +=⋅；N M N Ma a a log log log -=；M n M a n a log log =；④换底公式：a bb c c a log log log =；b m nb a n a m log log =；1log log =⋅a b b a例2：化简()()481293log 3log 3log 2o 2l g log ++-=练习：解方程：（1）3log 2=x (2) 32=x(3).012242=--+x x)24.指数型函数与对数型函数练习：函数22+=x y 过定点 ，函数1)3(log 3--=x y 过定点 .(1)求定义域：（1）y （2）x x x x f ---=4lg 32)((2)求值域：（1）)2(log 22+-=x y (2)]100,1001[,lg 2lg 2∈+=x x x y(3)求单调区间：(1) x x y 222-= (2))32(log 23++-=x x y练习：比较大小(1)7.27.1 37.1 (2)37.0 36.0 (3) 3.07.1 3.29.0(4)2.4log 2 4.3l o g 2 (5)5.1log 2，2log 5.0，5.15.1例5：若ln 2ln 3ln 5,,235a b c ===，则 （ ）A ．a <b<cB ．c<b<aC ．c<a <bD ．b<a <c6.反函数(1)反函数的定义域是原函数的值域，值域是原函数的定义域；(2)反函数与原函数单调性相同，只有单调函数才具有反函数；(3)互为反函数的两个函数的图像关于直线y=x 对称；(4)若点(a,b)在原函数的图像上，则点(b,a)在其反函数的图像上；练习：(1)若函数f x ()的图像过点(1,2)，且1211f x ()-+=， 则x = . (2)函数)1(log )(4+=x x f 的反函数)(1x f -=__________．7.自我补充：过关检测一、选择题：本大题共10小题，每小题5分.1.函数1()x y e x R +=∈的反函数是（ ）A ．y=1+lnxB ．y=1-lnx C.y=-1-lnx D ．y=-1+lnx2.已知⎩⎨⎧≥<+-=1,log 1,4)13()(x x x a x a x f a 是(,)-∞+∞上的减函数，那么a 的取值范围是 ( ) A.(0,1) B.1(0,)3 C.11[,)73 D.1[,1)7 3.函数y ( )A.(3,+∞)B.[3, +∞)C.(4, +∞)D.[4, +∞)4.设f (x )= 1232,2,log (1),2,x e x x x -⎧<⎪⎨-≥⎪⎩ 则不等式f (x )>2的解集为 A （1，2）⋃（3，+∞） B （10，+∞） (C)（1，2）⋃ （10 ，+∞） (D)（1，2）5.设2log 3P =，3log 2Q =，23log (log 2)R =，则（ ）Ａ．R<Q<P Ｂ．P<R<Q Ｃ．Q<R<P Ｄ．R<P<Q6.设函数2211()21x x f x x x x ⎧-⎪=⎨+->⎪⎩，，，，≤则1(2)f f ⎛⎫ ⎪⎝⎭的值为（ ） A ．1516 B ．2716- C ．89D ．18 7.函数lg ||x y x =的图象大致是 ( )A B C D8.若)2(log ax y a -=在]1,0[上是减函数,则a 的取值范围是 ( )A.)1,0(B.)2,0(C.)2,1(D.),2(+∞9.若函数f(x)＝是奇函数，则m 的值是（ ） A ．0 B ． C ．1 D ．2 10.定义在R 的偶函数f (x )在[0,＋∞)上单调递减，且f (21)＝0，则f (log 41x )＜0的解集为( ) A.(－∞，12)∪(2，＋∞) B.(12，1)∪(1,2) C.(12，1)∪(2，＋∞) D.(0，12)∪(2，＋∞) 二、填空题（每小题5分共25分）11.方程1)12(log 3=-x 的解=x .12.设0,1a a >≠，函数2()log (23)a f x x x =-+有最小值，则不等式log (1)0a x ->的解集为 . 13.方程0224=-+x x 的解是__________.14.函数y =的单调递减区间是 ．15.函数()22231m m y m m x --=--是幂函数且在(0,)+∞上单调递减，则实数m 的值为 .三、解答题.（共75分）16.记函数f(x)=132++-x x 的定义域为A, g(x)=lg[(x －a －1)(2a －x)](a<1)的定义域为B.(1) 求A ； (2) 若B ⊆A, 求实数a 的取值范围.17.已知函数2lg )2lg()(2-++=x x x f . (1)判断函数)(x f 的奇偶性。
高中基本初等函数复习(1)
高中基本初等函数复习一、指数函数00,1(0),0n a a a a a a a =⋅⋅⋅⋅⋅=≠无意义 1(0)n na a a -=≠ ;()m n m n m n mn a a a a a +⋅== (),()n m m n nn na a ab a b ==在下列的关系式中，哪些不是指数函数，为什么？ （1）22x y += （2）(2)x y =- （3）2xy =-（4）x y π= （5）2y x = （6）24y x = （7）xy x = （8）(1)xy a =- （a ＞1，且2a ≠）二、对数函数复习：对数的定义及对数恒等式log b a N b a N =⇔= （a ＞0，且a ≠1，N ＞0），如果a ＞0且a ≠1，M ＞0，N ＞0，那么： （1）log log log a a a MN M N =+ （2）log log log a a a MM N N=- （3）log log ()na a M n Mn R =∈（4）换底公式、a ＞0，且a ≠1，c ＞0，且e ≠1，b ＞0log log log c a c bb a=3．幂函数的定义一般地，形如y x α=（x ∈R ）的函数称为幂孙函数，其中x 是自变量，α是常数. 如11234,,y x y x y x-===等都是幂函数，1、已知0.70.90.80.8,0.8, 1.2,a b c ===按大小顺序排列,,a b c . 2．研究函数的图像（1）y x = （2）12y x = （3）2y x = （4）1y x -= （5）3y x = 填写下表：习题、1．下列幂函数为偶函数的是( ) A ．y ＝x 12 B ．y ＝3xC ．y ＝x 2D ．y ＝x －12．函数y ＝1－x ＋x 的定义域是( ) A ．{x |x ≤1} B ．{x |x ≥0} C ．{x |x ≥1或x ≤0} D ．{x |0≤x ≤1} 3、若,则的元素个数为( )0 1234．已知p >q >1,0<a <1,则下列各式中正确的是（ ）A ．q p a a >B ．a a q p >C ．q p a a -->D ．a a q p --> 5、已知(10)x f x =，则(5)f =（ ）A 、510B 、105C 、lg10D 、lg5 6．函数x y a log =当x >2 时恒有y >1，则a 的取值范围是A ．1221≠≤≤a a 且B ．02121≤<≤<a a 或C ．21≤<aD ．2101≤<≥a a 或7、设 1.50.90.4812314,8,2y y y -⎛⎫=== ⎪⎝⎭，则 （ ）A 、312y y y >>B 、213y y y >>C 、132y y y >>D 、123y y y >>8．设f ：x →x 2是集合A 到集合B 的函数，如果B ＝{1,2}，则A ∩B 一定是( )A ．∅B ．∅或{1}C ．{1}D ．∅或{2}9．下列函数完全相同的是( )A ．f (x )＝|x |，g (x )＝(x )2B ．f (x )＝|x |，g (x )＝x 2C ．f (x )＝|x |，g (x )＝x 2xD ．f (x )＝x 2－9x －3，g (x )＝x ＋310．下列函数中哪个与函数x y =相等？ （1）2)(x y = （2）33x y =（3）2x y = （4）xx y 2=11、设f （x ）是定义在R 上奇函数，且当x ＞0时，等于（ ）A．－1 B． C．1 D．－12、已知则等于A B C D14、已知，则、、的大小关系是（）A． B． C． D．15、设函数是定义在R上周期为3的奇函数，若，则有A .且 B. 或 C. D.16．设α∈{－1,1，12，3}，则使函数y＝xα的定义域为R，且为奇函数的所有α值为( )A．1,3 B．－1,1 C．－1,3 D．－1,1,317．幂函数的图象过点(2，14)，则它的单调递增区间是( )A．(0，＋∞) B．[0，＋∞) C．(－∞，0) D．(－∞，＋∞)18．给出四个说法：①当n＝0时，y＝x n的图象是一个点；②幂函数的图象都经过点(0,0)，(1,1)；③幂函数的图象不可能出现在第四象限；④幂函数y＝x n在第一象限为减函数，则n＜0.其中正确的说法个数是( )A．1 B．2 C．3 D．419．若[a,3a－1]为一确定区间，则a的取值范围是________．20．函数y＝x＋103－2x的定义域是________．21．函数y＝x2－2的定义域是{－1,0,1,2}，则其值域是________．22．已知f(x)＝11＋x(x∈R且x≠－1)，g(x)＝x2＋2(x∈R)．求f(g(2))的值．23 已知2(21)2f x x x +=-，则(3)f =____________ 24. 函数]3,0[,322∈--=x x x y 的值域是_____________ 25. 设1,(0)(), (0)0, (0)x x f x x x π⎧⎪⎨⎪⎩+>==<，则{[(1)]}f f f -=________________26 若函数2()2(1)2f x x a x =+-+在(,4)-∞上是减函数，则实数a 的取值范围是__________27．已知函数 f (x )的定义域是（1，2），则函数)2(x f 的定义域是 .28．函数y=)124(log 221-+x x 的单调递增区间是 .29、函数是定义在上的奇函数，且，对于任意，都有恒成立，则的值为 。
完整版)基本初等函数经典复习题+答案
完整版)基本初等函数经典复习题+答案1、幂的运算性质1) $a^r\cdot a^s=a^{r+s}$，其中$r,s\in R$；2) $(a^r)^s=a^{rs}$，其中$r,s\in R$；3) $a^r\cdot b^r=(ab)^r$，其中$r\in R$；4) $a^{-n}=\dfrac{1}{a^n}$，其中$a>0,n\in N^*,n>1$。
2、对数的运算性质若$a>0$且$a\neq 1$，$M>0,N>0$，则有：1) $a^x=N\iff \log_a N=x$；2) $\log_a(MN)=\log_a M+\log_a N$；3) $\log_a\dfrac{M}{N}=\log_a M-\log_a N$；4) $\log_a M^n=n\log_a M$，其中$n\in R$；5) $\log_a 1=0$；6) 换底公式：$\log_a b=\dfrac{\log_c b}{\log_c a}$，其中$a>0,a\neq 1,c>0,c\neq 1,b>0$。
3、函数的定义域能使函数式有意义的实数$x$的集合称为函数的定义域。
求函数的定义域时，需要注意以下几点：1) 偶次方根的被开方数不小于零；2) 对数式的真数必须大于零；3) 分式的分母不等于零；4) 指数、对数式的底必须大于零且不等于1.4、函数单调区间与单调性的判定方法A) 定义法：1.任取$x_1,x_2\in D$，且$x_1<x_2$；2.作差$f(x_1)-f(x_2)$；3.变形（通常是因式分解和配方）；4.定号（即判断差$f(x_1)-f(x_2)$的正负）；5.下结论（指出函数$f(x)$在给定的区间$D$上的单调性）。
B) 图象法（从图象上看升降）。
C) 复合函数的单调性：复合函数$f[g(x)]$的单调性与构成它的函数$u=g(x),y=f(u)$的单调性密切相关，其规律为“同增异减”。
基本初等函数知识点归纳
函数及其基本初等函数〖1.1〗函数及其表示 【1.1.1】函数的概念 （1）函数的概念①设A 、B 是两个非空的数集，如果按照某种对应法则f ，对于集合A 中任何一个数x ，在集合B 中都有唯一确定的数()f x 和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的一个函数，记作:f A B →．②函数的三要素:定义域、值域和对应法则．（所以进行已知对应关系()f x 的函数，一定先求出函数的定义域）③只有定义域相同，且对应法则也相同的两个函数才是同一函数． （2）区间的概念及表示法①设,a b 是两个实数，且a b <，满足a x b ≤≤的实数x 的集合叫做闭区间，记做[,]a b ；满足a x b <<的实数x 的集合叫做开区间，记做(,)a b ；满足a x b ≤<，或a x b <≤的实数x 的集合叫做半开半闭区间，分别记做[,)a b ，(,]a b ；满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞．注意：对于集合{|}x a x b <<与区间(,)a b ，前者a 可以大于或等于b ，而后者必须a b <，（前者可以不成立，为空集；而后者必须成立）．而且无论闭区间或者开区间，,a b 均称为端点。
（3）求函数的定义域时，一般遵循以下原则：①()f x 是整式时，定义域是全体实数．②()f x 是分式函数时，定义域是使分母不为零的一切实数．③()f x 是偶次根式时，定义域是使被开方式为非负值时的实数的集合．④对数函数的真数大于零，当对数或指数函数的底数中含变量时，底数须大于零且不等于1．⑤tan y x =中，()2x k k Z ππ≠+∈．⑥零（负）指数幂的底数不能为零．⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时，则其定义域一般是各基本初等函数的定义域的交集．⑧对于求复合函数定义域问题，一般步骤是：若已知()f x 的定义域为[,]a b ，其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出．⑨对于含字母参数的函数，求其定义域，根据问题具体情况需对字母参数进行分类讨论． ⑩由实际问题确定的函数，其定义域除使函数有意义外，还要符合问题的实际意义． （4）求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，只是提问的角度不同．求函数值域与最值的常用方法： ①观察法：对于比较简单的函数，我们可以通过观察直接得到值域或最值．②配方法：将函数解析式化成含有自变量的平方式与常数的和，然后根据变量的取值范围确定函数的值域或最值．③判别式法：若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=，则在()0a y ≠时，由于,x y 为实数，故必须有2()4()()0b y a y c y ∆=-⋅≥，从而确定函数的值域或最值．④不等式法：利用基本不等式确定函数的值域或最值．⑤换元法：通过变量代换达到化繁为简、化难为易的目的，三角代换可将代数函数的最值问题转化为三角函数的最值问题． ⑥反函数法：利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值． ⑦数形结合法：利用函数图象或几何方法确定函数的值域或最值． ⑧函数的单调性法．例1 已知函数32()f x x ax bx c =+++，下列结论中错误的是（ ）A 00,()0x R f x ∃∈=B 函数()y f x =的图像是中心对称图形C 若0x 是()f x 的极小值点，则()f x 在区间（-∞，0x ）上单调递减D 若0x 是()f x 的极值点，则'()0f x =例2 已知偶函数()f x 在[0,)+∞上单调递减，(2)f =0，若(1)0f x ->，则x 的取值范围是（ ）例 3 设函数()xf x mπ=，若存在()f x 的极值点0x 满足22200[(()]x f x m +<，则m 的取值范围是（ ）A （-∞，-6）∪（6，+∞）B （-∞，-4）∪（4，+∞）C （-∞，-2）∪（2，+∞）D （-∞，-1）∪（1，+∞） 例4 下列函数与y=x 有相同图像的一个函数是（ ）A y =B 2x y x=C log (01)xy aa a =>≠且 D log xa a y =【1.2.2】函数的表示法（5）函数的表示方法表示函数的方法，常用的有解析法、列表法、图象法三种． 解析法：就是用数学表达式表示两个变量之间的对应关系．列表法：就是列出表格来表示两个变量之间的对应关系． 图象法：就是用图象表示两个变量之间的对应关系． （6）映射的概念①设A 、B 是两个集合，如果按照某种对应法则f ，对于集合A 中任何一个元素，在集合B 中都有唯一的元素和它对应，那么这样的对应（包括集合A ，B 以及A 到B 的对应法则f ）叫做集合A 到B 的映射，记作:f A B →．②给定一个集合A 到集合B 的映射，且,a A b B ∈∈．如果元素a 和元素b 对应，那么我们把元素b 叫做元素a 的象，元素a 叫做元素b 的原象． 〖1.3〗函数的基本性质【1.3.1】单调性与最大（小）值 （1）函数的单调性①定义及判定方法②在公共定义域内，两个增函数的和是增函数，两个减函数的和是减函数，增函数减去一个减函数为增函数，减函数减去一个增函数为减函数．③对于复合函数[()]y f g x =，令()u g x =，若()y f u =为增，()u g x =为增，则[()]y f g x =为增；若()y f u =为减，()u g x =为减，则[()]y f g x =为增；若()y f u =为增，()u g x =为减，则[()]y f g x =为减；若()y f u =为减，()u g x =为增，则[()]y f g x =为减．（2）打“√”函数()(0)af x x a x=+>的图象与性质 ()f x 分别在(,]a -∞-、[,)a +∞上为增函数，分别在[,0)a -、(0,]a 上为减函数（判定方法2）． （3）最大（小）值定义①一般地，设函数()y f x =的定义域为I ，如果存在实数M满足：（1）对于任意的x I ∈，都有()f x M ≤； （2）存在0x I ∈，使得0()f x M =．那么，我们称M 是函数()f x 的最大值，记作max ()f x M =．②一般地，设函数()y f x =的定义域为I ，如果存在实数m 满足：（1）对于任意的x I ∈，都有()f x m ≥；（2）存在0x I ∈，使得0()f x m =．那么，我们称m 是函数()f x 的最小值，记作max ()f x m =． 【1.3.2】奇偶性（4）函数的奇偶性①定义及判定方法函数的 性 质定义图象判定方法 函数的 奇偶性如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．－．f(x)．．．．,那么函数f(x)叫做奇函数．．．．（1）利用定义（要先判断定义域是否关于原点对称） （2）利用图象（图象关于原点对称）yxo如果对于函数f(x)定义域内任意一个x ，都有f(．．－．x)=．．．f(x)．．．．,那么函数f(x)叫做偶函数．．．．（1）利用定义（要先判断定义域是否关于原点对称） （2）利用图象（图象关于y 轴对称）②若函数()f x 为奇函数，且在0x =处有定义，则(0)0f =．③奇函数在y 轴两侧相对称的区间增减性相同，偶函数在y 轴两侧相对称的区间增减性相反．④在公共定义域内，两个偶函数（或奇函数）的和（或差）仍是偶函数（或奇函数），两个偶函数（或奇函数）的积（或商）是偶函数，一个偶函数与一个奇函数的积（或商）是奇函数．〖补充知识〗函数的图象（1）作图利用描点法作图：①确定函数的定义域； ②化解函数解析式； ③讨论函数的性质（奇偶性、单调性）； ④画出函数的图象． 利用基本函数图象的变换作图：要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象．①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩 01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象，并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去（2）识图对于给定函数的图象，要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性，注意图象与函数解析式中参数的关系． （3）用图函数图象形象地显示了函数的性质，为研究数量关系问题提供了“形”的直观性，它是探求解题途径，获得问题结果的重要工具．要重视数形结合解题的思想方法．第二章 基本初等函数(Ⅰ)〖2.1〗指数函数【2.1.1】指数与指数幂的运算 （1）根式的概念①如果,,,1nx a a R x R n =∈∈>，且n N +∈，那么x 叫做a 的n 次方根．当n 是奇数时，a 的n 次方根用符号n a 表示；当n 是偶数时，正数a 的正的n 次方根用符号n a 表示，负的n 次方根用符号n a -表示；0的n 次方根是0；负数a 没有n 次方根．②式子n a 叫做根式，这里n 叫做根指数，a 叫做被开方数．当n 为奇数时，a 为任意实数；当n 为偶数时，0a ≥．③根式的性质：()n n a a =；当n 为奇数时，nn a a =；当n 为偶数时，(0)|| (0) nn a a a a a a ≥⎧==⎨-<⎩． （2）分数指数幂的概念①正数的正分数指数幂的意义是：(0,,,mn m na a a m n N +=>∈且1)n >．0的正分数指数幂等于0．②正数的负分数指数幂的意义是： 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >．0的负分数指数幂没有意义． 注意口诀：底数取倒数，指数取相反数．（3）分数指数幂的运算性质①(0,,)rsr sa a aa r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈③()(0,0,)r r rab a b a b r R =>>∈ 【2.1.2】指数函数及其性质（4）指数函数 函数名称指数函数定义 函数(0xy a a =>且1)a ≠叫做指数函数图象1a > 01a <<xa y =xy(0,1)O1y =xa y =xy(0,1)O1y =〖2.2〗对数函数【2.2.1】对数与对数运算 （1）对数的定义①若(0,1)xa N a a =>≠且，则x 叫做以a 为底N 的对数，记作log a x N =，其中a 叫做底数，N 叫做真数．②负数和零没有对数．③对数式与指数式的互化：log (0,1,0)xa x N a N a a N =⇔=>≠>．（2）几个重要的对数恒等式log 10a =，log 1a a =，log b a a b =．（3）常用对数与自然对数常用对数：lg N ，即10log N ；自然对数：ln N ，即log e N （其中 2.71828e =…）． （4）对数的运算性质 如果0,1,0,0a a M N >≠>>，那么①加法：log log log ()a a a M N MN += ②减法：log log log a a aM M N N-= ③数乘：log log ()na a n M M n R =∈ ④log a N a N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式：log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质 （5）对数函数函数 名称 对数函数定义函数log (0a y x a =>且1)a ≠叫做对数函数图象1a > 01a <<定义域 (0,)+∞值域 R过定点 图象过定点(1,0)，即当1x =时，0y =．奇偶性 非奇非偶单调性在(0,)+∞上是增函数在(0,)+∞上是减函数函数值的 变化情况log 0(1)log 0(1)log 0(01)a a a x x x x x x >>==<<<log 0(1)log 0(1)log 0(01)a a a x x x x x x <>==><<a 变化对图象的影响 在第一象限内，a 越大图象越靠低；在第四象限内，a 越大图象越靠高．(6)反函数的概念设函数()y f x =的定义域为A ，值域为C ，从式子()y f x =中解出x ，得式子()x y ϕ=．如果对于y 在C 中的任何一个值，通过式子()x y ϕ=，x 在A 中都有唯一确定的值和它对应，那么式子()x y ϕ=表示x是y 的函数，函数()x y ϕ=叫做函数()y f x =的反函数，记作1()x f y -=，习惯上改写成1()y f x -=．x yO(1,0)1x =log a y x=xyO (1,0)1x =log a y x=（7）反函数的求法①确定反函数的定义域，即原函数的值域；②从原函数式()y f x =中反解出1()x f y -=；③将1()x f y -=改写成1()y f x -=，并注明反函数的定义域（即原函数的值域）．（8）反函数的性质①原函数()y f x =与反函数1()y f x -=的图象关于直线y x =对称．②函数()y f x =的定义域、值域分别是其反函数1()y f x -=的值域、定义域．③若(,)P a b 在原函数()y f x =的图象上，则'(,)P b a 在反函数1()y f x -=的图象上．④一般地，函数()y f x =要有反函数则它必须为单调函数．〖2.3〗幂函数（1）幂函数的定义一般地，函数y x α=叫做幂函数，其中x 为自变量，α是常数．（2）幂函数的图象（3）幂函数的性质①图象分布：幂函数图象分布在第一、二、三象限，第四象限无图象．幂函数是偶函数时，图象分布在第一、二象限(图象关于y 轴对称)；是奇函数时，图象分布在第一、三象限(图象关于原点对称)；是非奇非偶函数时，图象只分布在第一象限． ②过定点：所有的幂函数在(0,)+∞都有定义，并且图象都通过点(1,1)．③单调性：如果0α>，则幂函数的图象过原点，并且在[0,)+∞上为增函数．如果0α<，则幂函数的图象在(0,)+∞上为减函数，在第一象限内，图象无限接近x 轴与y 轴． ④奇偶性：当α为奇数时，幂函数为奇函数，当α为偶数时，幂函数为偶函数．当q pα=（其中,p q 互质，p 和q Z ∈），若p 为奇数q 为奇数时，则qpy x =是奇函数，若p 为奇数q 为偶数时，则q py x =是偶函数，若p 为偶数q 为奇数时，则q py x =是非奇非偶函数．⑤图象特征：幂函数,(0,)y x x α=∈+∞，当1α>时，若01x <<，其图象在直线y x =下方，若1x >，其图象在直线y x =上方，当1α<时，若01x <<，其图象在直线y x =上方，若1x >，其图象在直线y x =下方．〖补充知识〗二次函数（1）二次函数解析式的三种形式①一般式：2()(0)f x ax bx c a =++≠②顶点式：2()()(0)f x a x h k a =-+≠③两根式：12()()()(0)f x a x x x x a =--≠（2）求二次函数解析式的方法①已知三个点坐标时，宜用一般式．②已知抛物线的顶点坐标或与对称轴有关或与最大（小）值有关时，常使用顶点式． ③若已知抛物线与x 轴有两个交点，且横线坐标已知时，选用两根式求()f x 更方便． （3）二次函数图象的性质①二次函数2()(0)f x ax bx c a =++≠的图象是一条抛物线，对称轴方程为,2bx a=-顶点坐标是24(,)24b ac b a a--． ②当0a >时，抛物线开口向上，函数在(,]2b a -∞-上递减，在[,)2ba-+∞上递增，当2b x a =-时，2min 4()4ac b f x a -=；当0a <时，抛物线开口向下，函数在(,]2ba -∞-上递增，在[,)2b a -+∞上递减，当2bx a=-时，2max 4()4ac b f x a -=．③二次函数2()(0)f x ax bx c a =++≠当240b ac ∆=->时，图象与x 轴有两个交点11221212(,0),(,0),||||M x M x M M x x =-． （4）一元二次方程20(0)ax bx c a ++=≠根的分布一元二次方程根的分布是二次函数中的重要内容，这部分知识在初中代数中虽有所涉及，但尚不够系统和完整，且解决的方法偏重于二次方程根的判别式和根与系数关系定理（韦达定理）的运用，下面结合二次函数图象的性质，系统地来分析一元二次方程实根的分布．设一元二次方程20(0)ax bx c a ++=≠的两实根为12,x x ，且12x x ≤．令2()f x ax bx c =++，从以下四个方面来分析此类问题：①开口方向：a ②对称轴位置：2bx a=-③判别式：∆ ④端点函数值符号． ①k ＜x 1≤x 2 ⇔②x 1≤x 2＜k ⇔③x 1＜k ＜x 2 ⇔ af (k )＜0④k 1＜x 1≤x 2＜k 2 ⇔x y1x 2x 0>a O ••1k 2k 0)(1>k f 0)(2>k f ab x 2-=xy1x 2x O•<a 1k •2k 0)(1<k f 0)(2<k f a b x 2-=⑤有且仅有一个根x 1（或x 2）满足k 1＜x 1（或x 2）＜k 2 ⇔ f (k 1)f (k 2)<0，并同时考虑f (k 1)=0或f (k 2)=0这两种情况是否也符合x y1x 2x 0>a O ••1k 2k 0)(1>k f 0)(2<k fxy1x 2x O•<a 1k •2k 0)(1>k f 0)(2<k f⑥k 1＜x 1＜k 2≤p 1＜x 2＜p 2 ⇔ 此结论可直接由⑤推出．（5）二次函数2()(0)f x ax bx c a =++≠在闭区间[,]p q 上的最值 设()f x 在区间[,]p q 上的最大值为M ，最小值为m ，令01()2x p q =+． （Ⅰ）当0a >时（开口向上） ①若2b p a -<，则()m f p = ②若2b p q a ≤-≤，则()2b m f a =- ③若2b q a->，则()m f q =①若02b x a -≤，则()M f q = ②02b x a->，则()M f p =f(p) f (q) ()2b f a-f (p)f(q)()2bf a-f (p)f (q)()2b f a-f(p) f (q)()2b f a-0x f(p) f(q)()2b f a-0x(Ⅱ)当0a <时(开口向下) ①若2b p a -<，则()M f p = ②若2b p q a ≤-≤，则()2b M f a =- ③若2b q a->，则()M f q =①若02b x a -≤，则()m f q = ②02b x a->，则()m f p =．第三章 函数的应用〖3.1〗方程的根与函数的零点 一、方程的根与函数的零点1、函数零点的概念：对于函数))((D x x f y ∈=，把使0)(=x f 成立的实数x 叫做函数))((D x x f y ∈=的零点。
基本初等函数全章复习
二次函数的定义和性质
二次函数是指形如y=ax^2+bx+c的函数，其中a、b和c为常数，且a不等于0。它的图像是一个开口向上或向下的 抛物线。
二次函数的图像及其性质
二次函数的图像是一个开口向上或向下的抛物线。顶点表示函数的最值，对 称轴是x=-b/(2a)。
一元二次方程的解法
一元二次方程是形如ax^2+bx+c=0的方程，其中a、b和c为常数，且a不等于0。可以使用公式或配方法求解。
基本初等函数全章复习
对基本初等函数进行全面复习，包括一次函数、二次函数、指数函数等内容。 整理如下：
一次函数的定义和性质
一次函数是指形如y=ax+b的函数，其中a和b为常数。它的图像是一条直线，斜率为a，截距为b。
一次函数的图像及其性质
一次函数的图像是一条直线，通过两个点即可确定。斜率大于0表示函数增长， 斜率小于0表示函数减小。
函数的极值和最值
函数的极值是指函数在某些特定点上取得的最大值或最小值。最值是函数的 最大值和最小值。
函数的单调性和区间
函数的单调性是指函数在某个区间上的增减性。区间是由函数图像上的点组 成的连续区域。
函数的导数及其意义
函数的导数是函数在某个点上的变化率。导数表示函数的斜率和曲线的曲率。
对数函数的图像及其性质
对数函数的图像是一个递增或递减的曲线。底数a大于1时，曲线递增；底数a 小于1时，曲线递减。过原点(1,0)。
ቤተ መጻሕፍቲ ባይዱ
指数函数和对数函数的关系
指数函数和对数函数是互为反函数的关系。指数函数的反函数是对数函数， 对数函数的反函数是指数函数。
复合函数的定义和性质
复合函数是由一个函数和另一个函数组合而成的新函数。复合函数的性质有 层层嵌套、结果与顺序无关等。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基本初等函数复习一、知识梳理1．知识网络2．要点归纳 (1)分数指数幂①m na ＝na m (a >0、m 、n ∈N *、且n >1)． ②1m n m naa-=(a >0、m 、n ∈N *、且n >1)．(2)根式的性质 ①(na )n ＝a .②当n 为奇数时、na n ＝a ；当n 为偶数时、na n ＝|a |＝⎩⎪⎨⎪⎧a ，a ≥0，－a ，a <0.(3)指数幂的运算性质 ①a r ·a s ＝a r ＋s (a >0、r 、s ∈R )． ②(a r )s ＝a rs (a >0、r 、s ∈R )． ③(ab )r ＝a r b r (a >0、b >0、r ∈R )． (4)指数式与对数式的互化式log a N ＝b ⇔a b ＝N (a >0、且a ≠1、N >0)． (5)对数的换底公式log a N ＝log m Nlog m a(a >0、且a ≠1、m >0、且m ≠1、N >0)．推论：log m na b ＝n m log a b (a >0、且a ≠1、m 、n >0、且m ≠1、n ≠1、b >0)．(6)对数的四则运算法则若a >0、且a ≠1、M >0、N >0、则 ①log a (MN )＝log a M ＋log a N ； ②log a MN ＝log a M －log a N ；③log a M n ＝n log a M (n ∈R )． (7)指数函数①理解指数函数概念及单调性．②会画具体指数函数图象并掌握图象通过的特殊点． (8)对数函数①理解对数函数概念及单调性．②会画具体对数函数图象并掌握图象通过的特殊点． ③了解y ＝a x 、y ＝log a x (a >0、且a ≠1)互为反函数． (9)幂函数①了解幂函数的概念．②结合y ＝x α、α＝－1、12、1、2、3的图象、了解它们的性质．二、专题讲解1、 指数、对数的运算1、化简：(1)2932)-⨯ (2)2log 32－log 3329＋log 38－5log 325.2、已知22(xxa a -+=为常数、)x Z ∈、求88x x -+的值3、计算80.25×42＋(32×3)6＋log 32×log 2(log 327)的值为________．4、22(lg 2)(lg 5)2lg 2lg 5++⋅= 5、设,,a b c 都是正数、且346a b c ==、则下列正确的是（ ）111.A c a b =+ 221.B c a b =+ 122.C c a b =+ 212.D c a b =+ 6、已知1414log 7,log 5,a b ==则用,a b 表示35log 28=2、函数的解析式1、函数()xa a a 33y 2+-=是指数函数、求a 的值。
2、已知函数21()(1)a a f x a x +-=-⋅、①当a ＝______时、()f x 为正比例函数； ②当a ＝______时、()f x 为反比例函数； ③当a ＝______时、()f x 为二次函数； ④当a ＝______时、()f x 为幂函数.3、为了保证信息安全、传输必须使用加密方式、有一种方式其加密、解密原理如下：明文――→加密密文――→发送密文――→解密明文已知加密为2xy a =- (x 为明文、y 为密文)、如果明文“3”通过加密后得到密文为“6”、再发送、接收方通过解密得到明文“3”、若接收方接到密文为“14”、则原发的明文是________．4、通常候鸟每年秋天从北方飞往南方过冬、若某种候鸟的飞行速度y (m/s) 可以表示为函数25log 10xy =、其中x 为这种候鸟在飞行过程中耗氧量的单位数. （1） 该种候鸟的耗氧量是40个单位时、它的飞行速度是多少？ （2） 该种候鸟的飞行速度为15m/s 时、它的耗氧量是多少个单位？3、定义域和值域1、函数()xf x a =（0a >、且1a ≠）在[1,2]上的最大值与最小值的和为6、则a 的值为 .2、函数y = ）1.(,)2A +∞ [).1,B +∞ 1.,12C ⎛⎤⎥⎝⎦.(,1)D -∞3、已知函数22()lg (1)(1)1f x a x a x ⎡⎤=-+++⎣⎦、若()f x 的定义域为R 、求实数a 的取值范围。
4、已知函数2lg(1)y x ax =++的值域是R 、求实数a 的取值范围。
5、设全集{}3xU x y ==、集合{}3log P x y x ==、12{}Q x y x ==、则(P Q)UC⋂等于( )A ．{}0B ．(0,)+∞C ．(,0)-∞D ．(,0]-∞4.过定点问题1、函数log (21)2a y x =+-的图像恒过定点2、已知指数函数y ＝(2b －3)a x 经过点(1、2)、求a 、b 的值．5、比较大小1、比较下列各组数的大小：①27、82； ②log 20.4、log 30.4、log 40.4； ③132,-log 213、121log .32、设x 、y 、z 为正数、且2x ＝3y ＝5z 、则( ) A ．2x <3y <5z B ．5z <2x <3y C ．3y <5z <2xD ．3y <2x <5z3、已知a ＝log 23.6、b ＝log 43.2、c ＝log 43.6、则( )A ．a ＞b ＞cB ．a ＞c ＞bC ．b ＞a ＞cD ．c ＞a ＞b4、已知a ＝log 0.70.8、b ＝log 1.10.9、c ＝1.10.9、则a 、b 、c 的大小关系是( )． A ．a ＜b ＜c B ．a ＜c ＜b C ．b ＜a ＜c D ．c ＜a ＜b 6、单调性问题1、已知函数21xf x a =（）（﹣）、当m n ＞时、()()f m f n ＜、则实数a 的取值范围是 2、已知关于x 的不等式2221122x axx a ++-⎛⎫⎛⎫< ⎪⎪⎝⎭⎝⎭恒成立、则a 的取值范围是 ．3、函数212()log (2)f x x x =-的单调递增区间是（ ）A. (1,)+∞B. (2,)+∞C. (,1)-∞D. (,0)-∞4、函数12()log f xx =的单调递增区间是（ ）A. 1(0,]2B. (0,1]C. (0,)+∞D. [1,)+∞5、如果函数2()log (82)a f x ax x =+-在[1,3]-上是增函数、则a 的取值范围是 .6、函数()f x 的图像与函数1()()3x g x =的图像关于直线y x =对称、求2(2)f x x -的单调递减区间.7、若函数2()(1)mf x m m x =--是幂函数、且在(0,)+∞上为增函数、则实数m = .7、不等式与方程1、方程143280x x +-⋅+=的解集为_____________2、若不等式1240x x a ++⋅>在(,1]x ∈-∞时总成立、求实数a 的取值范围.3、若函数f (x )＝2112log 1xx x x ⎧⎛⎫≤⎪ ⎪⎨⎝⎭⎪>⎩，，，，则f (x )≥2的解集为________ 4、已知函数f (x )＝log a (1－a x )(a ＞0、且a ≠1)、解关于x 的不等式log a (1－a x )＞f (1)8、图像问题1．若函数y ＝log a x (a >0、且a ≠1)的图象如图所示、则下列函数图象正确的是( )2、函数()1xxa y a x=>的图象的大致形状是（ ）A ．B ．C ．D ．3、已知函数1log ()(,4a y xb a b =+为常数）的图象如下图所示、则a b +的值为 .4、函数()y f x =如下图所示、则函数12log ()y f x =的图象大致是（ ）5、幂函数my x =、ny x =、py x =的图象如图所示、以下结论正确的是（ ）A ．m n p >>B ．m p n >>C ．n p m >>D ．p n m >>9、函数性质综合应用1、对于函数212()log (3)f x x ax =-+、解答下列问题：（1）若()f x 的定义域是R 、求a 的取值范围； （2）若()f x 的值域是R 、求a 的取值范围；（3）若()f x 在[1,)-+∞上有意义、求a 的取值范围； （4）若()f x 的值域是(,1]-∞-、求a 的取值范围； （5）若()f x 在 (,1]-∞-内为增函数、求a 的取值范围.2、已知函数f (x )＝a ·2x ＋b ·3x 、其中常数a 、b 满足ab ≠0. (1)若ab >0、判断函数f (x )的单调性；(2)若ab <0、求f (x ＋1)>f (x )时的x 的取值范围．3、已知函数41()log ,[,4]16f x x x =∈的值域为集合A 、关于x 的不等式31()2()2x ax a R +>∈的解集为B 、集合5{|0}1xC x x -=≥+、集合{|121}(0)D x m x m m =+≤<-> （1）若A B B ⋃=、求实数a 的取值范围； （2）若D C ⊆、求实数m 的取值范围．4、已知函数4411)xf x log k x x R =+∈（）（）-（﹣（）为偶函数． （1）求常数k 的值；（2）当x 取何值时函数f x （）的值最小？并求出f x （）的最小值；（3）设44•2)03xg x log a aa =≠（）（﹣（）、试根据实数a 的取值、讨论函数f x （）与()g x 的图象的公共点个数．三、课后练习一、选择题1．函数f (x )＝1ln (x ＋1)＋4－x 2的定义域为( )A ．[－2、0]∪(0、2]B ．(－1、0)∪(0、2]C ．[－2、2]D ．(－1、2]2．已知x 、y 为正实数、则( ) A ．2lg x ＋lg y＝2lg x ＋2lg yB ．2lg(x＋y )＝2lg x ·2lg yC ．2lg x ·lg y ＝2lg x ＋2lg y D ．2lg(xy )＝2lg x ·2lg y3．设函数f (x )＝⎩⎪⎨⎪⎧1＋log 2(2－x )，x ＜1，2x －1，x ≥1，则f (－2)＋f (log 212)等于( )A ．3B ．6C ．9D ．124．下列区间中、函数f (x )＝|ln(2－x )|在其上为增函数的是( ) A ．(－∞、1] B.⎣⎡⎦⎤－1，43 C.⎣⎡⎭⎫0，32 D ．[1、2)5．函数y ＝log 2(|x |＋1)的图象大致是( )6．函数f (x )＝9x ＋13x 的图象( )A ．关于原点对称B ．关于直线y ＝x 对称C ．关于x 轴对称D ．关于y 轴对称7．已知奇函数f (x )在R 上是增函数．若a ＝－f ⎝⎛⎭⎫log 215、b ＝f (log 24.1)、c ＝f (20.8)、则a 、b 、c 的大小关系为( ) A ．a <b <c B ．b <a <c C ．c <b <aD ．c <a <b8．函数y ＝(x ＋2)ln|x |的图象大致为( )二、填空题9．若lg 2＝a 、lg 3＝b 、则log 512＝________.10．若函数y ＝log 12(3x 2－ax ＋5)在[－1、＋∞)上是减函数、则实数a 的取值范围是________．11．若函数f (x )＝2|x －a |(a ∈R )满足f (1＋x )＝f (1－x )、且f (x )在[m 、＋∞)上单调递增、则实数m 的最小值为________． 三、解答题12．若lg a 、lg b 是方程2x 2－4x ＋1＝0的两根、求lg(ab )·⎝⎛⎭⎫lg a b 2的值．13．已知常数a (a >1)和变量x 、y 之间的关系式是log a x ＋3log x a －log x y ＝3、若x ＝a t (t ≠0)、且当t ≥1时、y 的最小值是8、求相应的x 的值．14.如图、矩形ABCD 的三个顶点A 、B 、C 分别在函数y ＝log2x 、y ＝x 12、y ＝⎝⎛⎭⎫22x的图象上、且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2、则点D 的坐标为________．15．已知函数f (x )＝x n －4x 、且f (4)＝3.(1)判断f (x )的奇偶性并说明理由；(2)判断f (x )在区间(0、＋∞)上的单调性、并证明你的结论；(3)若对任意实数x 1、x 2∈[1、3]、有|f (x 1)－f (x 2)|≤t 成立、求t 的最小值．四、反思总结。