SPSS处理多元方差分析报告例子
spss多因素方差分析报告例子

作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
spss 方差分析(多因素方差分析)实验报告

大学经济管理学院学生实验报告实验课程名称:统计软件及应用专业工商管理班级学号姓名成绩实验地点实验性质:演示性 验证性综合性设计性实验项目名称方差分析(多因素方差分析)指导教师一、实验目的掌握利用SPSS 进行单因素方差分析、多因素方差分析的基本方法,并能够解释软件运行结果。
二、实验内容及步骤(包括实验案例及基本操作步骤)实验案例:为研究某商品在不同地区和不同日期的销售差异性,调查收集了以下日平均销售量数据。
销售量日期周一至周三周四至周五周末地区一5000 6000 4000 6000 8000 3000 4000 7000 5000地区二700080008000500050006000500060004000地区三300020004000600060005000800090006000(1)选择恰当的数据组织方式建立关于上述数据的SPSS数据文件。
在SPSS输入数据。
(2)利用多因素方差分析法,分析不同地区和不同日期对该商品的销售是否产生了显著影响。
1. 选择菜单Analyze,General Linear Model,Univariate;2. 指定观测变量销售额到Dependant Variable框中;3. 指定固定效应的控制变量到Fixed Factors框中,4. OK,得到分析结果。
(3)地区和日期是否对该商品的销售产生了交互影响?若没有显著的交互影响,则试建立非饱和模型进行分析,并与饱和模型进行对比。
三、实验结论(包括SPSS输出结果及分析解释)SPSS输出的多因素方差分析的饱和模型分析:表的第一列是对观测变量总变差分解的说明;第二列是观测变量变差分解的结果;第三列是自由度;第四列是方差;第五列是F检验统计量的观测值;第六列是检验统计量的概率P-值。
F日期,,F地区,F日期*地区概率P-值分别为0.254,0.313,0.000。
如果显著性水平α为0.05,由于F日期、,F地区大于显著性水平α,所以不应拒绝原假设,不同地区和不同日期对该商品没有显著性影响。
spss多因素方差分析报告例子
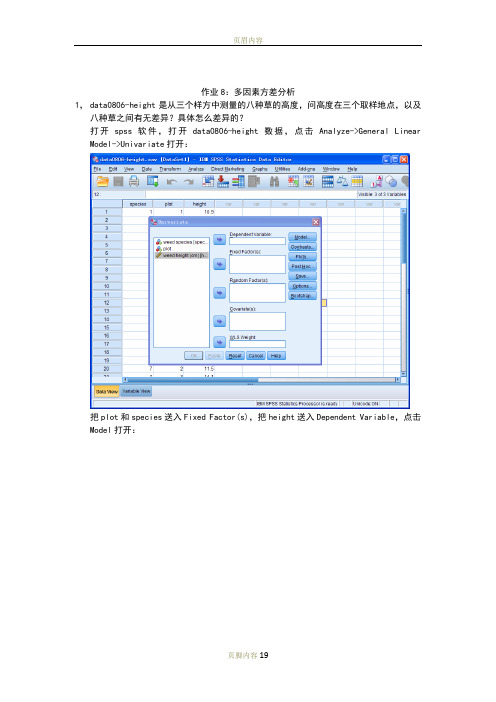
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
多元方差分析spss实例

多元方差分析1992年美国总统选举的三位候选人为布什、佩罗特、克林顿。
从支持三位候选人的选民中分别分析:该题自变量为三位候选人,因变量为年龄段和受教育程度。
从自变量来看要进行方差分析,从因变量来看是二元分析,所以最终确定使用多变量分析具体操作(spss)1、打开spss,录入数据,定义变量和相应的值在此不作详述。
结果如图1图1 被投票人:1、布什2、佩罗特3、克林顿2、在spss窗口中选择分析——一般线性模型——多变量,调出多变量分析主界面,将年龄段和受教育程度移入因变量框中,被投票人移入固定因子框中。
如图2图2 多变量分析主界面3、点击选项按钮在输出框中选择方差齐性分析(既包括协方差矩阵等同性分析也包括误差方差齐性分析),其它使用默认即可,点击继续返回主界面。
如图3图3 选项子对话框4、点击确定,运行多变量分析过程。
结果解释1、协方差矩阵等同性的Box检验结果,如图4图4 协方差矩阵检验结果说明:此Box检验的协方差矩阵为三位候选人每个人的支持者的年龄段和受教育程度的协方差矩阵。
因为sig>0.05,所以差异不显著,即各个因变量的协方差矩阵在所有三个候选人组中是相等的。
可以对其进行多元方差分析。
2、多变量检验结果,如图5图5 多变量检验结果说明:被投票人在四种统计方法中的sig均小于0.05,所以差异显著,即三组的总体均值有显著性差异3、误差方差等同性的Levene检验结果,如图6图6 Levene检验结果说明:只考虑单个变量,年龄段或者受教育程度,每位候选人的20名支持者的随机误差是否有显著性差异。
因为sig>0.05,差异不显著,所以三位候选人的20名支持者的随机误差相等。
可以进行单因素方差分析。
4、主体间效应的检验结果,如图7图7 主体间效应的检验结果说明:被投票人一行中,年龄段的sig<0.05,差异显著,即支持三位候选人的选民中,年龄段之间存在显著差异;而受教育程度的sig>0.05,差异不显著,即支持三位候选人的选民中,受教育程度差异不显著。
spss多因素方差分析报告例子

作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate 打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model 打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算rror,即无法分开intercept和error,无法检测interaction的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate主对话框,点击Plots:Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
SPSS实验多因素方差分析8
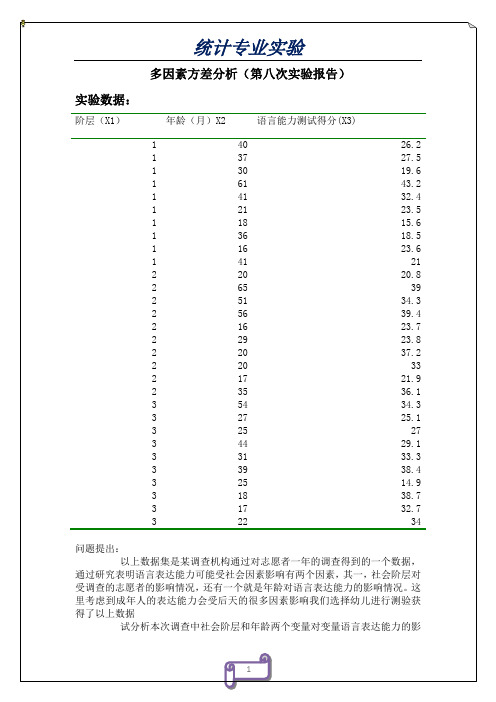
29.211a
1.597
24.778
33.644
a. Based on modified population marginal mean.
Multiple Comparisons
Dependent Variable:语言能力测试得分(X3)
(I)阶层(X1)
2.两个因素即年龄和阶层对语言表达能力的影响都不显著,而且两个变量各自对语言表达能力的影响都是不显著的。
3.由于本数据中的方差齐性检验结果是具有方差齐性的,所以应就LSD的输出结果进行分析,有以上数据分析的结果表中比较相应两组均值的P值与显著性水平为0.05下可知阶层两两之间没有显著性可言,也就进一步说明了阶层对语言能力的影响不是显著性的。
Intercept
23859.980
1
23859.980
336.849
.000
阶层(X1)
300.323
2
150.162
2.120
.236
年龄(月)X2
1226.352
22
55.743
.787
.689
阶层(X1)*年龄(月)X2
24.807
1
24.807
.350
.586
Error
283.332
4
70.833
F
df1
df2
Sig.
1.328
25
4
.434
Tests the null hypothesis that the error variance of the dependent variable is equal across groups.
spss多因素方差分析报告例子
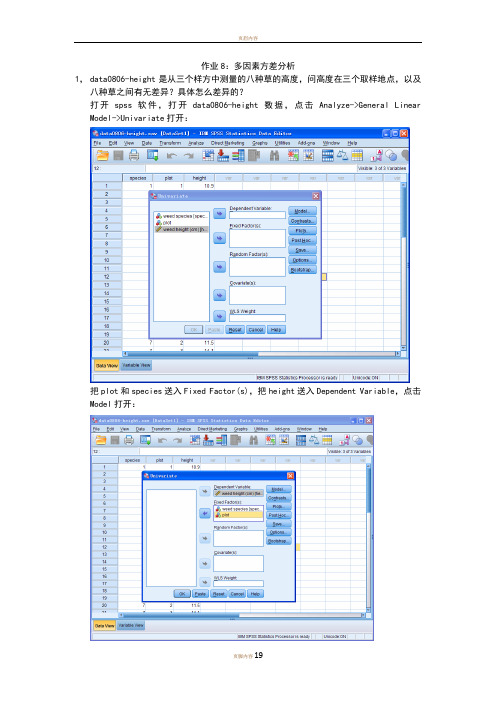
作业8:多因素方差分析1,data0806-height是从三个样方中测量的八种草的高度,问高度在三个取样地点,以及八种草之间有无差异?具体怎么差异的?打开spss软件,打开data0806-height数据,点击Analyze->General Linear Model->Univariate打开:把plot和species送入Fixed Factor(s),把height送入Dependent Variable,点击Model打开:选择Full factorial,Type III Sum of squares,Include intercept in model(即全部默认选项),点击Continue回到Univariate主对话框,对其他选项卡不做任何选择,结果输出:因无法计算MM M rror,即无法分开MM intercept 和MM error,无法检测interaction 的影响,无法进行方差分析,重新Analyze->General Linear Model->Univariate打开:选择好Dependent Variable和Fixed Factor(s),点击Model打开:点击Custom,把主效应变量species和plot送入Model框,点击Continue回到Univariate 主对话框,点击Plots:把date送入Horizontal Axis,把depth送入Separate Lines,点击Add,点击Continue 回到Univariate对话框,点击Options:把OVERALL,species, plot送入Display Means for框,选择Compare main effects,Bonferroni,点击Continue回到Univariate对话框,输出结果:可以看到:SS species=33.165,df species=7,MS species=4.738;SS plot=33.165,df plot=7,MS plot=4.738;SS error=21.472,df error=14,MS error=1.534;Fspecies=3.089,p=0.034<0.05;Fplot=12.130,p=0.005<0.01;所以故认为在5%的置信水平上,不同样地,不同物种之间的草高度是存在差异的。
多元方差分析

多元方差分析在SPSS软件的数据窗口依次定义变量并输入数据,由题可知数据来自三个不同的总体,下面对不同组的贫血患者比较其血红蛋白浓度及红细胞计数是否存在差异。
一、对总体进行多元正态分布检验首先将数据进行分组,然后通过SPSS软件分析—描述统计—探索得到检验结果如下:上述两个表给出了对每一个变量进行正态检验的结果,由表可以看出血红蛋白浓度和红细胞计数的显著性水平均大于0.05,即接受原假设,所以这两个变量均遵从正态分布。
下面判断总体是否满足方差齐性:上表是对协方差阵相等的检验,检验统计量是Box’s M,由Sig.值可以看出,0.670显著的大于0.05,所以在0.05的显著性水平下接受协方差阵相等的原假设。
即可以认为三组的协方差阵是相等的,符合方差齐性。
二、多元方程分析上表为多变量检验表,该表给出了几个统计量,显著性水平均为0.001显著的小于0.05,拒绝原假设,故无论从哪个统计量来看,三组不同患者的血红蛋白浓度和红细胞计数这两个指标间均存在显著差异。
下面分别分析三组患者间x1指标是否有显著差异,x2指标是否有显著差异,结果如下:由上表GROUP行可以看到:血红蛋白浓度和红细胞计数这两个指标的显著性水平分别为0.003和0.002均小于0.05,这说明三个组在血红蛋白浓度和红细胞计数这两个指标上均有显著差异。
三、对各组进行两两比较,给出更具体的分析结果通过软件操作得到比较结果如下表:由表中数据可以看出:①在血红蛋白浓度这个指标上A组和B组、B组和C组的显著性水平均小于0.05,拒绝原假设,故A组和B组、B组和C组在血红蛋白浓度这个指标上有显著差异,且B组的血红蛋白浓度显著高于A组和C组。
②在红细胞计数这个指标上A组和C组的显著性水平为0.014小于0.05,故A组和C组在红细胞计数指标上有显著差异,且C组的红细胞计数远远高于B 组。
四、画出三组患者x1,x2两指标的均值图由软件绘图得到均值图如下:由上图可以看出,A组与B组、C组与B组的红蛋白浓度有显著差异,而A组与C组的血红蛋白浓度没有显著差别,大致在一水平线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三多元方差分析一、实验目的用多元方差分析说明民族和城乡对人均收入和文化程度的影响。
二、实验要求调查24个社区,得到民族与城乡有关数据如下表所示,其中人均收入为年均,单位百元。
文化程度指15岁以上小学毕业文化程度者所占百分比。
试依此数据通过方差分析说明民族和城乡对人均收入和文化程度的影响。
三、实验容1.依次点击“分析”---- “常规线性模型”----“多变量”,将“人均收入”和“文化程度”加到“因变量”中,将“民族”和“居民”加到“固定因子”中,如下图一所示。
【图一】2.点击“选项”,将“输出”中的相关选项选中,如下图二所示:【图二】3.点击“继续”,“确定”得到如下表一的输出:【表一】常规线性模型主体间因子描述性统计量民族居民均值标准差N人均收入1 农村56.0000 9.93311 4城市64.2500 11.02648 4总计60.1250 10.66955 8 2 农村59.7500 8.99537 4城市67.2500 9.10586 4总计63.5000 9.28901 8 3 农村62.0000 7.61577 4城市70.2500 7.84750 4总计66.1250 8.40812 8 总计农村59.2500 8.45442 12 城市67.2500 8.89458 12总计63.2500 9.41899 24文化程度1 农村82.7500 10.68878 4城市90.2500 7.93200 4总计86.5000 9.59166 82 农村80.0000 8.28654 4城市85.7500 8.18026 4总计82.8750 8.21910 83 农村73.2500 7.135594城市80.7500 8.77021 4总计77.0000 8.41767 8 总计农村78.6667 9.00841 12城市85.5833 8.53291 12总计82.1250 9.27977 24 协方差矩阵等同性的Box 检验(a)检验零假设,即观测到的因变量的协方差矩阵在所有组中均相等。
a 设计: Intercept+A+B+A * B多变量检验(d)a 使用 alpha 的计算结果 = .05b 精确统计量c 该统计量是 F 的上限,它产生了一个关于显著性级别的下限。
d 设计: Intercept+A+B+A * B Roy 的最大根215.5611832.265(b)2.00017.000.000.9953664.5301.000APillai 的跟踪 .9017.378 4.000 36.000 .000 .450 29.511 .991Wilks 的Lambda .101 18.305(b)4.000 34.000 .000 .683 73.221 1.000Hotelling的跟踪 8.93035.7204.000 32.000 .000 .817 142.882 1.000Roy 的最大根8.928 80.356(c)2.000 18.000 .000 .899 160.712 1.000BPillai 的跟踪 .2052.198(b) 2.000 17.000 .142 .205 4.397 .386Wilks 的Lambda .7952.198(b) 2.000 17.000 .142 .205 4.397 .386Hotelling的跟踪 .2592.198(b) 2.000 17.000 .142 .205 4.397 .386Roy 的最大根.2592.198(b) 2.000 17.000 .142 .205 4.397 .386A * BPillai 的跟踪 .016.071 4.000 36.000 .991 .008 .282 .063Wilks 的Lambda .984.067(b) 4.000 34.000 .991 .008 .268 .062Hotelling的跟踪 .016.063 4.000 32.000 .992 .008 .253 .061Roy 的最大根.016.142(c) 2.000 18.000 .868 .016 .284 .069误差方差等同性的Levene 检验(a)F df1 df2 Sig.人均收入.643 5 18 .670文化程度.615 5 18 .690检验零假设,即在所有组中因变量的误差方差均相等。
a 设计: Intercept+A+B+A * B4.实验结果分析在“协方差矩阵等同性的Box 检验(a)”中可以看出,p=0.887,大于0.05,故接受原假设,即认为方差是齐性的,可以进行方差分析。
在“多变量检验”中,仅以wilks的Lambda为例进行分析,在效应A中p值接近0,故拒绝原假设,认为民族(A)对文化水平和收入有显著影响,在效应B中p=0.142,故接受原假设,即认为B(居民)对对文化水平和收入没有显著影响。
在A*B中,p=0.991,大于0.05,故接受原假设,即认为AB的交互作用对文化水平和收入的影响不显著。
故应该不考虑交互作用,重新改进该试验。
步骤如下:1.第一、二步和前面一样,只需要点击“模型”,将“全因子”改为“定制”,“建立项”中改为“主效应”接着将“A,B”添加到“模型”中,如下图三所示:【图三】2.点击“继续”“确定”,得到如下表二结果:【表二】常规线性模型主体间因子协方差矩阵等同性的Box 检验(a)检验零假设,即观测到的因变量的协方差矩阵在所有组中均相等。
a 设计: Intercept+A+B多变量检验(d)a 使用 alpha 的计算结果 = .05b 精确统计量c 该统计量是 F 的上限,它产生了一个关于显著性级别的下限。
d 设计: Intercept+A+B主体间效应的检验Hotelling 的跟踪212.7052020.700(b)2.00019.000.000.9954041.4001.000Roy 的最大根212.7052020.700(b)2.00019.000.000.9954041.4001.000A Pillai 的跟踪 .900 8.176 4.000 40.000 .000 .450 32.702 .996 Wilks 的 Lambda .102 20.265(b) 4.000 38.000 .000 .681 81.059 1.000 Hotelling 的跟踪 8.802 39.608 4.000 36.000 .000 .815 158.434 1.000 Roy 的最大根 8.800 88.002(c) 2.000 20.000 .000 .898 176.004 1.000B Pillai 的跟踪 .205 2.457(b) 2.000 19.000 .112 .205 4.914 .433 Wilks 的 Lambda .795 2.457(b) 2.000 19.000 .112 .205 4.914 .433 Hotelling 的跟踪 .259 2.457(b) 2.000 19.000 .112 .205 4.914 .433Roy 的最大根.2592.457(b)2.00019.000.112.2054.914.433a 使用alpha 的计算结果= .05b R 方= .259(调整R 方= .148)c R 方= .331(调整R 方= .230)主体间SSCP 矩阵基于 III 型平方和3.实验结果分析去掉A 与B 的交互作用后,在“协方差矩阵等同性的 Box 检验(a)”表格中,p=0.887,大于0.05,故接受原假设,即认为方差是齐性的,可以进行方差分析。
在“多变量检验”中,仅以Wilks 的Lambda 为例进行分析,在效应A 中p 值接近0,故拒绝原假设,认为民族(A )对文化水平和收入有显著影响,在效应B 中p=0.205,故接受原假设,即认为B (居民)的不同对文化水平和收入没有显著影响。
在“多变量检验”中,“A ”与“人均收入”的p=0.401,大于0.05,故接受原假设,即认为民族的不同对人均收入没有显著影响,“A ”与“文化程度”的p=0.086,大于0.05,故接受原假设,即认为民族的不同对文化程度没有显著影响,但这个显著性强于对人均收入的显著性。
同样,可以分析出,居民的身份(农村或城市)对人均收入有显著影响,但对文化程度没有显著影响。
四、存在问题与解决情况本次试验主要进行多元方差分析,主要对“协方差矩阵等同性的 Box 检验(a)”,“多变量检验”和“多变量检验”中的数据进行分析,和以往一样,都是通过p 值来判断是否接受原假设。
现将一些实习后的收获总结如下:在此实验中要注意,第一方差分析后发现其交互作用对文化程度和收入水平影响不显著,因此应将其去掉,再此进行方差分析。
由于总是对原假设难以把握,故将其列在此,以提醒自己:1.在“协方差矩阵等同性的 Box 检验(a)”中,原假设是:方差是齐性的,可以进行方差分析。
2.在“多变量检验”和“多变量检验”中,原假设是:两因素间的影响不显著。
附:记H 为总的组间离差阵 E 为组离差阵1.Pillai ’s tracePillai ’s trace = trace 1()H H E -⎡⎤+⎣⎦标准文案大全 2.Hotelling-Lawley ’s traceHotelling-Lawley ’s trace = trace(1HE -)3.Wilk ’s lambdaWilk ’s lambda =E H E+ 4.Roy ’s largest rootRoy ’s largest root = 111ηη+ 。
其中1η为1HE -的最大特征根 其中:Pillai ’s trace 是最为稳定的,值恒为正数,值越大表示该效应对模型的贡献越大。
Hotelling-Lawley ’s trace 检验矩阵的特征根之和,值越大贡献越大。
Wilk ’s lambda 值在0-1之间,值越小贡献越大。
Roy 最大根统计量,为检验矩阵特征根中最大值,值越大贡献越大。
