第七章非线性系统分析分析
合集下载
第7章 非线性系统的分析
x(t)
x0
无 论 x0 取 何 值 ， 该 系 统 的 运动均以指数规律收敛 到 0， 平衡 t 系统稳定。且只有一个 点 状 态 x 0。
x0
'
5
2 例 : 讨 论 非 线 性 ：x x x
x(t)
1 t
解
分析：
x 0e x t 1 x 0 x 0e
t
(3)当 x0 01时 (2)当 1时 0 x
1 G ( j )与 交点的坐标是 1.66。 N(X ) 1 交点处G ( j )的频率＝ 2， 的 N(X ) 幅值X 2.1
x
G ( j )
-1.66
0
Re
结论：该非线性系统存在自持振荡，振荡频率为 幅为2.1。
2 ，振
y
r 0
1
0
x
1
Gp(s)
c(t )
Ⅲ区 Ⅱ区 2 1 A -1 -1 -2 1 2 3
平面，根据继电器的 在 ee 非线性特性，可分为三个区域，
(0) 0 ， 设初始状态 e(0) 3， e
绘制相轨迹如图所示，(设r=3)
根据系统的相轨迹，可对 系统的性能分析如下：
e
Ⅰ区
e
1、系统的相轨迹收敛于A 点，是稳定的，奇点为稳定 焦点。e是单调衰减的。
B
1
kx[1
(arcsin
1
0
0 X a N(X) 2 a a (arcsin k[1 x x
2 a 1 )] x
X a
2、理想继电器非线性的描述函数
y 1 0 -1 x
自动控制原理第七章非线性控制系统的分析
X X
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e
这里，M=3，h=1
负倒描述函数为
N 1 X
X
12 1 1 2
X
X 1
X 1, N 1 X , N 1
必有极值
d N 1X 令
0 dX
得 X 2
N 1 2
2
0.523
12
1
1 2
2
6
X： 1 2
-N-1(X)： 0.523
2.自振的稳定性分析
在A点，振幅XA，频率A。
扰动：
X : A点 C点 C点被G(j)轨迹包围，不稳定，
振幅 ，工作点由C点向B点运动；
A点一个不稳 定的极限环。
X : A点 D点 D点不被G(j)轨迹包围，稳定，
振幅 ，工作点由D点左移。
在B点，振幅XB，频率B 。 扰动：
X : B点 E点 E点不被G(j) 轨迹包围，稳定，
振幅 ，工作点由E点到B点；
X : B点 F点 F点被G(j)轨迹包围，不稳定，
振幅 ，工作点由F回到B点。
B点呈现稳定的自激振荡:振幅XB ,频率B。
3.闭环系统稳定性判别步骤
1）绘制非线性部分的负倒描述函数曲线和线 性部分的频率特性曲线。
2）若G(j)曲线不包围“-N-1(X)”曲线，则系统稳定。 若G(j)曲线包围“-N-1(X) ”曲线，系统不稳定。 若G(j)曲线与“-N-1(X)”曲线相交，系统出现自振。
3）若G(j )曲线与“-N-1(X)”曲线有交点，做以 下性能分析：
（1）不稳定的极限环
（2）稳定的极限环 计算自振频率和幅值。
例1：非线性系统如图所示,其中非线性特性为 具有死区的继电器,分析系统的稳定性。
0e
非线性系统分析方法
解：1. 死去继电特性的描述函数
4M N(X)
1 ( )2
X
X
2. 绘制描述函数的负倒数特性
1
X
N(X ) 4M 1 ( )2
X
3. 绘制线性部分的极坐标图
4. 判断稳定性，分析两曲线相交点的性质
1 N(X)
X
-1.56 300 400 B -1 -0.5
X 130 A 140
120 G(j)
趋于奇点 远离奇点 包围奇点
例：二阶线性定常系统
••
•
x 2n x n2 x 0
试分析其奇点运动性质。
dx/dt x
稳定节点
••
•
x 2n x n2 x 0
dx/dt x
1
稳定节点
相轨迹趋于原点，该奇点称为 稳定节点
••
•
x 2n xn2 x 0
dx/dt x
1
不稳定节点
相轨迹远离原点，该奇点为 不稳定节点
者是自持振荡的
自持振荡点 a 振荡幅值=Xa
振荡频率=a
Im Re
X a
0
1 G(j) N ( X )
例：已知死区继电非线性系统如图
R(s)
+M
460
C(s)
+-
- -M
( j)(0.01 j 1)(0.005 j 1)
继电参数： M 1.7 死区参数：Δ 0.7 应用描述函数法作系统分析。
•
x
-1 -5/4
-3/2
-5/3
=
-2
-3/7
-3
-5 - x
3
1 1/3
0 -3/4 -1/2 -1/3
非线性系统的分析 (3)
第七章 非线性系统的分析
2、饱和特性
输出
k x( t ) y( t ) ka sgn x( t )
输入
x( t ) a x( t ) a
特征：当输入信号超出其线性范 围后，输出信号不再随输入信号 变化而保持恒定。
放大器的饱和输出特性、磁饱和、元件的行程限制、 功率限制等等。 饱和特性对系统性能的影响： 使系统在大信号作用下开环增益下降，因而降低了 稳态精度。
继电器特性对系统性能的影响
带死区的继电特性，将会增加系统的定位误差，对 其他动态性能的影响，类似于死区、饱和非线性特 性的综合效果
第七章 非线性系统的分析
三、非线性系统的特点
１、系统的稳定性
非线性系统的稳定性不仅与系统的结构参数有关， 而且与初始状态有关。 ２、系统的自持振荡 非线性系统即使无外界作用，也可能会发生某一 固定振幅和频率的振荡，称为自持振荡。
第七章 非线性系统的分析
7-2 相平面分析法
相平面法是Poincare在1885年首先提出来 的，它是一种求解一、二阶微分方程的图解法。 这种方法的实质是将系统的运动过程形象 地转化为相平面上一个点的移动，通过研究这 个点移动的轨迹，就能获得系统运动规律的全 部信息。 由于它能比较直观、准确、全面地表征系 统的运动状态，因而获得广泛应用。
第七章 非线性系统的分析
用x1、x2描述 二阶系统常微分方程方程的解，也就是 用质点的状态来表示该质点的运动。在物理学中，状态又称 为相。
把由x1—x2所组成的平面坐标系称为相平面，系统的一 个状态则对应于相平面上的一个点。
当t变化时，系统状态在相平面上移动的轨迹称为相轨 迹。
而与不同初始状态对应的一簇相轨迹所组成的图叫做 相平面图。 利用相平面图分析系统性能的方法称为相平面法。
第7章非线性系统分析
描述函数的定义是：输入为正弦函数时，输 出的基波分量与输入正弦量的复数比。
其数学表达式为
N
X
R
X
Y1
sin(t X sint
1)
Y1 X
1
A12 B12 arctan A1
A1
1
2
y(t) costdt
0
X
B1
1
B1
2
y(t ) sin tdt
0
7.3 非线性特性的描述函数法
（2）举例说明描述函数
(1) 降低了定位精度，增大了系统的静差。 (2) 使系统动态响应的振荡加剧，稳定性变坏。
7.2 非线性环节及其对系统结构的影响
4.摩擦特性
Mf
M1 •
M2
•
M f 摩擦力矩
转速
M1 静摩擦力矩
M 2 动摩擦力矩
7.2 非线性环节及其对系统结构的影响
摩擦特性的影响
(1)对随动系统而言，摩擦会增加静差，降低精 度。
7.2 非线性环节及其对系统结构的影响
2.饱和特性
x1 a ，等效增益 为常值，即线性段 斜率；
而 x1 a ，输出饱
和，等效增益随输 入信号的加大逐渐 减小。
7.2 非线性环节及其对系统结构的影响
饱和特性的影响
(1) 饱和特性使系统开环增益下降， 对动态响应的 平稳性有利。
(2) 如果饱和点过低，则在提高系统平稳性的同时， 将使系统的快速性和稳态跟踪精度有所下降。
7.3 非线性特性的描述函数法
KX sint
y(t) Ka
0 t 1 1 t / 2
∵ y(t) 单值奇对称， A0 0 A1 0
B1
4
第7章 非线性系统的分析
某一初始条件出发在相平面上按照式(7-13)或式(7-14)绘出的
曲线称为相平面轨迹,简称相轨迹。不同初始条件下构成的
相轨迹,称为相轨迹簇。由相轨迹簇构成的图称为相平面图。
利用相平面图分析系统性能的方法,称为相平面分析法。
图7-6为某个非线性系统的相平面图。图中,相轨迹上的
箭头表示相变量随着时间的增加沿相轨迹运动的方向。
第7章 非线性系统的分析 7.2 相平面分析法
7.2.1 相平面的基本概念 设二阶非线性系统的微分方程为
第7章 非线性系统的分析
第7章 非线性系统的分析
1.相平面和相轨迹
前面已经设定
我们称以x1(或x)为横坐
标、以x2(或 )为纵坐标构成的平面为相平面(注意,纵坐标x2
是横坐标x1的一阶导数),如图7-6所示。x1、x2为相变量。由
7.2.2 线性系统的相轨迹 在学习非线性系统的相平面分析法之前,我们先对非常
熟悉的线性系统做相平面分析。设二阶线性系统的微分方程 为
第7章 非线性系统的分析
也就是说,无论系统特征参数ωn和ξ是何值,系统的奇点是 不变的。此外,式(7-21)的特征方程为
系统的特征根为
对于不同的阻尼比ξ,二阶系统特征根的形式是不同的,而 线性系统的时域响应是由特征根决定的。下面介绍系统特征 根与系统的奇点(0,0)以及相轨迹的关系。
行线性化。我们只研究系统平衡点附近的特性时,就可以采 用平衡点附近的线性化方法,将非线性系统在平衡点附近小 范围线性化。当然,也可以将非线性系统分为几个区域,对每 个区域进行分段线性化。
第7章 非线性系统的分析
2.相平面分析法 相平面分析法简称相平面法,是非线性系统的图解分析 法。其基本思路是:建立一个相平面,在相平面上根据非线性 系统的结构和特性,绘制非线性系统的相轨迹。相轨迹就是 非线性系统中的变量在不同初始条件下的运动轨迹,根据相 轨迹就可以对非线性系统进行分析。该方法只适用于一阶和 二阶非线性微分方程。
第七章 非线性系统的分析
一次近似，则得到奇点附近关于 微分方程：
x 增量 x 的线性二阶
x 0
线上相轨迹任一点的切线斜率
dx dx ax bx x ax bx 0 dx dx x b x Kx 等倾线方程： x a
相等，所以当相轨迹
运动至特殊等倾线上时，将沿特殊等倾线收敛或发散。
①
b 0时
a2 4 b 2 a2 4 b 2 0 0
解： x dx 2x 0 dx xdx 2 xdx
2 2
(1, 0)
( x) ( x) c x 2 ( ) x 2 a 2 相轨迹是椭圆。
0
x
例7-1：二阶系统微分方程为 m 0，其中 m为常数， x 绘制相平面图。 dx 解： x m0
4) 0
s1,2 jn
这时二阶系统为:
bx 0 x
中心点
0 时线性二阶系统的相平面图
5) 1 0
s1,2 n jn 1 2
两个具有正实
部共轭复根。
不稳定焦点
0.5，n 1 时线性二阶系统的相轨迹
6) 1
Te e Ke T r，Tc c Kc Kr r
K 1 n ， 2n T T 1 T 1 K 2 KT 2 T 1 1 设 0 2 KT
c e
10AcE NhomakorabeaB
C
单位阶跃响应
D F
e
t
1. 相平面
若以 e 为横坐标，以 称这一平面为相平面。 2. 相轨迹 设输入为单位阶跃函数，即
第七章 非线性控制系统的分析
2 2
6
(7.3)
式中：
N 为非线性环节的描述函数； 描述函数 A 为正弦输入信号的幅值； y1 为输出信号基波分量的幅值；
ϕ1 为输出信号基波分量的相移角。
7.1.1 描述函数
若非线性环节中不含储能元件 N = N( A ) 若非线性环节中含有储能元件 N = N( A,ω )
7
7.1.2 典型非线性特性的描述函数
14
为与输入振幅A有关的复函数，输出的基波分量的相角 滞后于输入信号的相角。
7.1.2 典型非线性特性的描述函数
(7.5)式中, b=0, 为理想继电型特性的描述函数： 理想继电型特性
N ( A) = 4M πA
15
(7.6)
7.1.2 典型非线性特性的描述函数
(7.5)式中, m = 1, 为具有死区的三位置继电型特性
−1 N (A -− N -1(A )) 稳定区域
24
G ( jω )
d
G ( jω )
7.2 非线性控制系统的描述函数分析
(若非线性系统的线性部分G(s) 是非最小相位系 统，则系统闭环稳定的条件为N = -P. ) 自持振荡可用一个正弦振荡来近似，振荡的 频率和振幅，分别由交点处的 G(jω) 曲线上的 ω 值和 “-N-1(A)” 曲线上的 A 值来确定。 正弦振荡存在表明非线性系统存在周期解， 可用Nyquist判据分析其稳定性。只有稳定的正弦 振荡才能近似表示非线性系统实际存在的自持振 荡：稳定的自持振荡(极限环)可通过试验观察到， 而不稳定的自持振荡却观察不到。
22
7.2 非线性控制系统的描述函数分析
推广的Nyquist判据： 判据
23
设非线性系统的线性部分 G(s) 是最小相位的，于是，闭 环系统稳定的条件为 N = 0。 当 s 在 s平面上顺时针方向沿D型围线变化一周时: 2) 若 G(jω) 曲线包围 “-N-1(A)” 曲线 (图b所示) 则非线性系统是不稳定的 不稳定
6
(7.3)
式中：
N 为非线性环节的描述函数； 描述函数 A 为正弦输入信号的幅值； y1 为输出信号基波分量的幅值；
ϕ1 为输出信号基波分量的相移角。
7.1.1 描述函数
若非线性环节中不含储能元件 N = N( A ) 若非线性环节中含有储能元件 N = N( A,ω )
7
7.1.2 典型非线性特性的描述函数
14
为与输入振幅A有关的复函数，输出的基波分量的相角 滞后于输入信号的相角。
7.1.2 典型非线性特性的描述函数
(7.5)式中, b=0, 为理想继电型特性的描述函数： 理想继电型特性
N ( A) = 4M πA
15
(7.6)
7.1.2 典型非线性特性的描述函数
(7.5)式中, m = 1, 为具有死区的三位置继电型特性
−1 N (A -− N -1(A )) 稳定区域
24
G ( jω )
d
G ( jω )
7.2 非线性控制系统的描述函数分析
(若非线性系统的线性部分G(s) 是非最小相位系 统，则系统闭环稳定的条件为N = -P. ) 自持振荡可用一个正弦振荡来近似，振荡的 频率和振幅，分别由交点处的 G(jω) 曲线上的 ω 值和 “-N-1(A)” 曲线上的 A 值来确定。 正弦振荡存在表明非线性系统存在周期解， 可用Nyquist判据分析其稳定性。只有稳定的正弦 振荡才能近似表示非线性系统实际存在的自持振 荡：稳定的自持振荡(极限环)可通过试验观察到， 而不稳定的自持振荡却观察不到。
22
7.2 非线性控制系统的描述函数分析
推广的Nyquist判据： 判据
23
设非线性系统的线性部分 G(s) 是最小相位的，于是，闭 环系统稳定的条件为 N = 0。 当 s 在 s平面上顺时针方向沿D型围线变化一周时: 2) 若 G(jω) 曲线包围 “-N-1(A)” 曲线 (图b所示) 则非线性系统是不稳定的 不稳定
第7章 非线性系统分析
1 2 1 2 1 2 2
x 0
1
x 0
4. 间隙特性
齿轮传动中的齿隙
a
输出
b
液压传动中的油隙
b
a
输入
元件开始运动 输入信号<2 a 时，输出信号不变； 当输入信号>2 a 以后，输出随输入线性变化。 元件反向运动 保持在运动方向发生变化瞬间的输出值； 输入反向变化>2 a ，输出随输入线性变化。
理想饱和特性的数学描述为：
ka y kx ka
x a | x | a xa
饱和特性的存在，将使系统的开环增益有所 降低，对系统的稳定性有利。 出于对系统安全性的考虑，常常加入各种限 幅装置，其特性也属饱和特性。
3．继电特性
继电特性顾名思义就是继电器所具有的特性 , 继
一种近似分析法。也可采用基于
Simulink的非线性系统分析方法。
§7-2
常见非线性特性
一个单输入单输出静态非线性特性的数 学描述为：
y f ( x)
静态非线性特性中，死区特性、饱和特性、继
电特性、间隙特性是最常见的，也是最简单。
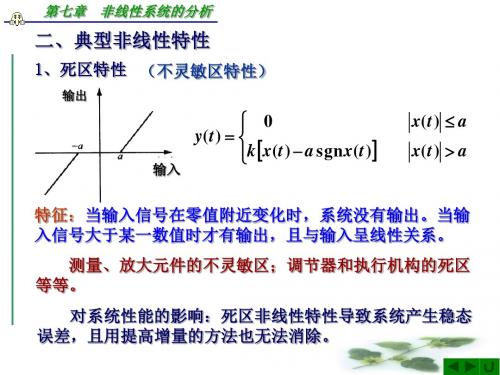
1. 死区特性
输出
（不灵敏区特性）
各类液压阀的正重叠量； 系统的库伦摩擦； 测量变送装置的不灵敏区； 调节器和执行机构的死区； 弹簧预紧力；等等。
2.稳定性
线性系统的稳定性仅和系统的结构和参数有关，
而和系统的输入信号大小，初始状态无关。
而非线性系统的稳定性，除了和系统的结构，
参数有关外，还与系统的初始状态及输入信号大
小有密切关系，这一点非常重要。即可能在某个
初始条件下稳定，而在另一个初始条件下系统可
能不稳定。
x 0
1
x 0
4. 间隙特性
齿轮传动中的齿隙
a
输出
b
液压传动中的油隙
b
a
输入
元件开始运动 输入信号<2 a 时，输出信号不变； 当输入信号>2 a 以后，输出随输入线性变化。 元件反向运动 保持在运动方向发生变化瞬间的输出值； 输入反向变化>2 a ，输出随输入线性变化。
理想饱和特性的数学描述为：
ka y kx ka
x a | x | a xa
饱和特性的存在，将使系统的开环增益有所 降低，对系统的稳定性有利。 出于对系统安全性的考虑，常常加入各种限 幅装置，其特性也属饱和特性。
3．继电特性
继电特性顾名思义就是继电器所具有的特性 , 继
一种近似分析法。也可采用基于
Simulink的非线性系统分析方法。
§7-2
常见非线性特性
一个单输入单输出静态非线性特性的数 学描述为：
y f ( x)
静态非线性特性中，死区特性、饱和特性、继
电特性、间隙特性是最常见的，也是最简单。
1. 死区特性
输出
（不灵敏区特性）
各类液压阀的正重叠量； 系统的库伦摩擦； 测量变送装置的不灵敏区； 调节器和执行机构的死区； 弹簧预紧力；等等。
2.稳定性
线性系统的稳定性仅和系统的结构和参数有关，
而和系统的输入信号大小，初始状态无关。
而非线性系统的稳定性，除了和系统的结构，
参数有关外，还与系统的初始状态及输入信号大
小有密切关系，这一点非常重要。即可能在某个
初始条件下稳定，而在另一个初始条件下系统可
能不稳定。
7第七章非线性系统的分析
第七章 非线性系统的分析
5、 ( 1)
jω
××
λ1 λ2
x
x
系统的运动是非周期发散运动。相轨迹是由原点出发的发散 型抛物线。原点处的奇点称为不稳定节点。
第七章 非线性系统的分析
6、
, 为一正一负两实根
12
jω
×
λ1
0
×
λ2
x
x
系统的自由运动是发散运动，原点处的奇点称为鞍点。 以上6种奇点，类似的奇点在非线性系统中也常见到。
复平面中，根据二者的相对位置可分析非线性系统的稳定
性。
一、非线性系统稳定
Im
1 不被G(j)包围
N(X)
x a
1 N(X)
0
Re
G( j)
第七章 非线性系统的分析
二、非线性系统不稳定 1 被G( j)包围
N(X)
三、非线性系统产生自持振荡
1 与G(j)相交
N(X)
图示系统在a点产生稳定的自 持振荡。由交点可确定自持 振荡的频率和幅值。
Im
0
Re
x a
G( j) 1
N(X)
Im
1 N(X)
a0
Re
x b a
G( j)
非线性系统即使无外界作用，也可能会发生某一 固定振幅和频率的振荡，称为自持振荡。
３、频率响应畸变 非线性系统在输入为正弦函数时，输出为包含一定数
量的高次谐波的非正弦周期函数。
第七章 非线性系统的分析
线性系统分析可用叠加原理，在典型输入信号下系 统分析的结果也适用于其它情况。
非线性系统不能应用叠加原理，没有一种通用的方 法来处理各种非线性问题。
第七章 非线性系统的分析 7
系统的频率特性中相移不是一回事。
退出
典型非线性特性的描述函数 下面介绍几种典型非线性特性的描述函数。 这些特性都是对称奇函数。包括： （1）饱和特性的描述函数； （2）不灵敏区特性的描述函数； （3）间隙特性的描述函数； （4）继电器特性的描述函数；
退出
（1）饱和特性的描述函数
输出 y (t)
y (t)
A
A
1
2 A
(A )
退出
N( A) K
1.0 0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 A
退出
问题：请大家绘出
1 N( A)
退出
（3）间隙特性的描述函数；
输出 y (t)
退出
一般概念 1 非线性系统的基本概念 （1）实际控制系统在某种程度上都具有非线 性，所谓线性系统是在实际系统中，忽略了非线 性因素后的理想模型。 （2）若系统的非线性特性y=f(x) 在工作点附近能 展开台劳级数，忽略变量增量的高次项，仅取变 量增量的一次项，则函数增量与变量增量之间是 线性关系。此时，系统可近似成线性系统。若 y=f(x) 在工作点附近不能展开成台劳级数，则称 y=f(x) 为本质非线性，这样的系统只能按非线性 系统理论来进行分析。
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 S A
退出
问题：请大家绘出
1 N( A)
S A
退出
（2）不灵敏区特性的描述函数
输出 y (t)
y (t)
K
0
x (t)
0
t
输入
第七章 非线性系统的分析
自激振荡或自振荡,如图所示。 自振荡是人们特别感兴趣的一个 问题,对它的研究有很大的实际意义。
Nanjing University of Technology
四、非线性系统的正弦输入响应 正弦信号作用下，线性系统的输出是与输入信 号同频率的正弦信号。 而非线性系统在正弦信号作用下的响应则很复 杂，一般不是正弦信号，但仍是周期信号；有 时输出信号频率为输入频率的倍频、分频等现 象。 非线性系统响应还有其他与线性系统不同的现 象,无法用线性系统的理论来解释。在一些情况 下,引入某些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智能控制都 属于非线性控制范畴。
Nanjing University of Technology
图7-6-3非线性控制系统的稳定性分析
二、自振荡分析
Nanjing University of Technology
• 若复平面中-1／N (X)曲线与G (j)曲线有交点,则该交 点对应着可能的等幅振荡,问题是这个等幅振荡能否稳 定地存在？也就是说,如果系统受到某个扰动使振荡的 振幅发生变化,系统是否具有恢复到扰动前的等幅振荡 状态的能力？如果系统具备这种能力,则该等幅振荡能 够稳定地存在,并能被观察到,称这个稳定的等幅振荡为 自持振荡。反之,振荡不能稳定地存在,必然转移到其它 运动状态(收敛到零或发散)。 • 以图7-6-3(c) 为例进行分析。图中-1／N (X)曲线与G (j)曲线有两个交点a和b, 对应于不同的振荡频率和振 幅。对a点,振幅及频率为Xa及 (j),若由于扰动使振 荡的振幅略有增大,这时工作点将沿-1／N (X)曲线由a 点移动到c点。由于c点不被G (j)所包围,故系统进入稳 定区,周期振荡的振幅要衰减,并逐步恢复到Xa,即自动返 回原状态；若由于扰动使振荡的振幅略有减小,这时工 作点将沿-1／N (X)曲线由a 点转移到d点，由
Nanjing University of Technology
四、非线性系统的正弦输入响应 正弦信号作用下，线性系统的输出是与输入信 号同频率的正弦信号。 而非线性系统在正弦信号作用下的响应则很复 杂，一般不是正弦信号，但仍是周期信号；有 时输出信号频率为输入频率的倍频、分频等现 象。 非线性系统响应还有其他与线性系统不同的现 象,无法用线性系统的理论来解释。在一些情况 下,引入某些非线性环节,使系统获得比线性系 统更为优异的性能。实际上大多数智能控制都 属于非线性控制范畴。
Nanjing University of Technology
图7-6-3非线性控制系统的稳定性分析
二、自振荡分析
Nanjing University of Technology
• 若复平面中-1／N (X)曲线与G (j)曲线有交点,则该交 点对应着可能的等幅振荡,问题是这个等幅振荡能否稳 定地存在？也就是说,如果系统受到某个扰动使振荡的 振幅发生变化,系统是否具有恢复到扰动前的等幅振荡 状态的能力？如果系统具备这种能力,则该等幅振荡能 够稳定地存在,并能被观察到,称这个稳定的等幅振荡为 自持振荡。反之,振荡不能稳定地存在,必然转移到其它 运动状态(收敛到零或发散)。 • 以图7-6-3(c) 为例进行分析。图中-1／N (X)曲线与G (j)曲线有两个交点a和b, 对应于不同的振荡频率和振 幅。对a点,振幅及频率为Xa及 (j),若由于扰动使振 荡的振幅略有增大,这时工作点将沿-1／N (X)曲线由a 点移动到c点。由于c点不被G (j)所包围,故系统进入稳 定区,周期振荡的振幅要衰减,并逐步恢复到Xa,即自动返 回原状态；若由于扰动使振荡的振幅略有减小,这时工 作点将沿-1／N (X)曲线由a 点转移到d点，由
自动控制原理-第七章 非线性系统分析
p p p ( x1 , x 2 ) ( x1 x 10 ) ( x 2 x 20 ) x1 x 2 Q ( x , x ) Q ( x x ) Q ( x x ) 1 2 1 10 2 20 x1 x 2
p ( x1 , x 2 ) a ( x1 x10 ) b( x 2 x 20 ) Q( x1 , x 2 ) c( x1 x10 ) d ( x 2 x 20 )
c 区域： a Tc c k m
c k m c 1 （k m c) T T ct 0 由奇点定义： k m c 0 c 常数 c k m 1 k m c dc T dc c 区域： c 常数 奇线： c k m
§7-4
奇点及极限环
dx 0 奇点概念：相轨迹上满足 dx 0 不定式的特殊点，称为奇点。
在奇点处有多条相轨迹穿过或趋于该奇点，相当于系统处于 平衡状态 一 奇点分类：(线性系统)
2 2 n x n x 0 x 2 2 n x n x x dx 2 x dx 2 n x n x dt (*) 相轨迹方程 dx x dx x dt
介绍：典型非线性特性、相平面法、描述 函数法
§7-1引言
稳定性 1．线性系统与非线性系统区别： 输出曲线 等幅振荡 稳态输出
2．非线性特性（典型） 1）死区
0 x a y k ( x a ) x a k ( x a ) x a
0 = k ( x aSignx)
x1 a ( x1 x 10 ) b( x 2 x 20 ) x 2 c( x1 x10 ) d ( x 2 x 20 )
自动控制原理第七章非线性系统分析
或者非线性不严重的准线性系统，常常采用线性化的方 法进行处理，然后在线性分析的基础上加以修正。而对 于包括像继电特性那样根本不存在线性区的非线性特性， 工程上常用相平面方法和描述函数方法进行研究。
7-2 常见非线性因素对系统 运动特性的影响
一.不灵敏区
不灵敏区又叫 死区，系统中
的死区是由测量元件的死区、 放大器的死区以及执行机构的 死区所造成的。
x
（7-14）
（1）无阻尼运动 ( 0)
由方程（7-14），相轨迹方程为：
x2
(t)
x2 (t)
n2
A2
其中
A
x02
x02
2 n
（7-16）
相轨迹如图7－24所示，在相平面上是为一族同心 的椭圆。 每个椭圆相当于一个简谐振动。
图7-24 系统无阻尼运动时的相轨迹
相轨迹的方向如 图7-24中箭头所示。 相轨迹垂直穿过 横轴。 坐标原点处相轨 迹的斜率不能由该 点的坐标唯一地确 定，这种点叫做奇 点。
第7章 非线性系统分析
基本要求 7-1 非线性问题概述 7-2 常见非线性因素对系统运动特性的影响 7-3 相平面法基础 7-4 非线性系统相轨迹分析 7-5 描述函数 7-6 用描述函数分析非线性系统
返回主目录
基本要求
① 明确非线性系统动态过程的本质特征。掌握系 统中非线性部分、线性部分结构归化的方法。
若继电系统的方框图如图7—41 所示
图7-41
• 研究图中继电特性为图7-40(b) 的情况
e c时
KM c h
Tc(t)
c(t)
0
| c | h
KM c h
• 很明显，相平面以直线c h为界被分成
三个不同的区域，在每个区域里，系统的 相轨迹完全由一个线性微分方程所确定
7-2 常见非线性因素对系统 运动特性的影响
一.不灵敏区
不灵敏区又叫 死区，系统中
的死区是由测量元件的死区、 放大器的死区以及执行机构的 死区所造成的。
x
（7-14）
（1）无阻尼运动 ( 0)
由方程（7-14），相轨迹方程为：
x2
(t)
x2 (t)
n2
A2
其中
A
x02
x02
2 n
（7-16）
相轨迹如图7－24所示，在相平面上是为一族同心 的椭圆。 每个椭圆相当于一个简谐振动。
图7-24 系统无阻尼运动时的相轨迹
相轨迹的方向如 图7-24中箭头所示。 相轨迹垂直穿过 横轴。 坐标原点处相轨 迹的斜率不能由该 点的坐标唯一地确 定，这种点叫做奇 点。
第7章 非线性系统分析
基本要求 7-1 非线性问题概述 7-2 常见非线性因素对系统运动特性的影响 7-3 相平面法基础 7-4 非线性系统相轨迹分析 7-5 描述函数 7-6 用描述函数分析非线性系统
返回主目录
基本要求
① 明确非线性系统动态过程的本质特征。掌握系 统中非线性部分、线性部分结构归化的方法。
若继电系统的方框图如图7—41 所示
图7-41
• 研究图中继电特性为图7-40(b) 的情况
e c时
KM c h
Tc(t)
c(t)
0
| c | h
KM c h
• 很明显，相平面以直线c h为界被分成
三个不同的区域，在每个区域里，系统的 相轨迹完全由一个线性微分方程所确定
第七章 非线性系统分析
2.死区非线性（不灵敏区特性）
输出 -a k 0 a 输入
0 y( t ) k x(t ) a sgn x(t ) x( t ) a x( t ) a
死区又叫不灵敏区，系统
中的死区是由测量元件的死 区、放大器的死区以及执行 机构的死区所造成的。
死区特性对系统性能的影响：
1 N ( A)
?
(-1,j0)
设：系统开环的线性部分G(j)稳定
① G(j)不包围负倒描述 函数 闭环系统稳定
② G(j)包围负倒描述函 数 闭环系统不稳定
③ G(j) 与负倒描述函数相交 闭环系统出现自持振荡(极限环振荡) 稳定 ？不稳定？ 振幅（A）？ 频率()？
偏离到1点工作时， 偏离到２点工作时， 不被G（jω）包围， 被G（jω）包围， 系统不稳定，故振 系统稳定，故振幅 收敛衰减． 幅发散．
j
稳定条件： X≤Xa
1 N
a
X 0
X
负倒描述函数由 外向内穿入时， 系统条件稳定。
振幅增大 振幅减小 系统趋向 不稳定 0 稳定
G ( j )
偏离到２点工作时， 偏离到１点工作时， 系统不稳定 不被G（jω）包围， 被G（jω）包围， 系统不稳定，故振 系统稳定，故振幅 有自持振荡 收敛衰减． 幅发散．
0
输入
齿轮传动中的齿隙 液压传动中的油隙
死区特性对系统性能的影响：
间隙输出相位滞后，减小稳定性裕量， 动态特性变坏自持振荡。
齿轮传动中的间隙
间隙非线性特性
传动机构(如齿轮传动、杆系传动)的间隙也 是控制系统中的一种常见的非线性因素。
非线性系统的特点
１、系统的稳定性 系统的稳定性不仅与系统的结构参数有关， 而且与初始状态有关。 ２、系统的自持振荡 产生某一固定振幅和频率的振荡。 ３、频率法不适用于非线性系统 非线性系统中，系统对正弦输入的响应并 非正弦。 ４、叠加原理不能应用与非线性系统
第七章 非线性系统分析
k
-e
e
f (e)
+M
-e
e
f (e) +M +e0 -e k e
0 +e
0 +e -M
0 +e
-e0
-M
a）线性 + 死区 b）继电 + 死区 c）饱和 + 死区
0, f (e) ke,
M ,
e e e e
f
(e)
0,
M ,
e e e e e e
M ,
f
(e)
0, ke,
M ,
1、解析法作图 •
方程不显含 x时，采用一次积分法得相轨迹方程作图
方程为
••
x f (x) 0
因为 代入方程
•
•
•
•• d 2 x d x dx d x dt • d x
x dt 2
dt
dt
dt
x dx dx
••
x d x f (x)dx
两边一次积分，得相轨迹方程
• •
xd x
f (x)dx
•
•
代入方程得 x x x 0源自等倾线方程为•1
x x
1
等倾线的斜率为
1
k 1
给定不同斜率值 ，作等倾线如图
等倾线 与 相轨迹
线性定常系统的等倾线方程为 过原点的一次曲线族。
•
x
-1 -5/4
-3/2
-5/3
=
-2
-3/7
-3
-5 - x
3
1 1/3
0 -3/4 -1/2 -1/3
三、相轨迹的运动特性
=0
•
e
第七章非线性系统的分析
2、死区非线性
x1 ≤ ∆ 0, x2 = k ( x1 − ∆signx1 ), x1 > ∆
1 signx1 = −1
x1 > 0 x1 < 0
在实际系统中死区可由众多原因引起，它对系统可产生不同的 影响：一方面它使系统不稳定或者产生自振荡；另一方面有时 人们又人为的引入死区特性，使系统具有抗干扰能力。
第七章 非线性控制系统
7-2
1、饱和非线性
kx1 = x2 = ka x2 m −ka = − x 2m
典型非线性环节
x1 < a x1 ≥ a x1 ≤ −a
x2m
x2
−a
0
k
a
x1
此处：输入 x1 − − − − x2 − − − −输出 k − − − −比例系数
− x2m
第七章 非线性控制系统
第七章 非线性控制系统
4）混沌(Chaos)
蝴蝶效应（ The Butterfly Effect） 是指在一个动力系统中，初始条 件下微小的变化能带动整个系统 的长期的巨大的连锁反应。这是 一种混沌现象。 核心理念：看似微不足道的细小 变化，却能以某种方式对社会产 生微妙的影响，甚至影响整个社 会系统的正常运行。
第七章 非线性控制系统
r(t)
e(t)
N(A,ω) NLS
x(t)
G(s)
c(t)
非线性系统的闭环“传递函数”：
G ( jω ) N ( A, ω ) Φ ( jω ) = 1 + G ( jω ) N ( A, ω )
0 闭环“特征方程”： 1 + G ( jω ) N ( A, ω ) =
即
1 G ( jω ) = − N ( A, ω )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x
(*)
dt
相轨迹方程
有奇点： （0，0） （原点为奇点）
1． 0 （一对虚根）
s2
2 n s
2 n
0
x
s1.2
4n
2
j n
dx
2 n
x
dx x
得：x 2
x 2
2 n
A2
为一簇封闭曲线包围奇点（0，0）称奇点为中心点。
2．0 1（一对负实部共轭根）
S1.2 n n 1 2 j
介绍：典型非线性特性、相平面法、描述 函数法
§7-1引言
稳定性
1．线性系统与非线性系统区别：
输出曲线 等幅振荡
稳态输出
2．非线性特性（典型）
1）死区
0 y k(x a) k(x a)
x a xa x a
0
x a
=
k(x aSignx) x a
2)饱和
y
k x
x a
kaSignx x a
3）滞环
y
k x +a
y
4）继电
M
x -M
k(x aSignx) y 0
y Cost 常数 y 0
y=M·Signx
y
M
Signx
M M
x a 且 x 0 x a 且 x 0
y
a x
ma
M
y
0
M
x ma 且 x 0 0 x a 且 x 0 或 a x 0 且 x 0 ma x, x 0
X
如奇点构成曲线称为奇线，极限环就是常见奇线。
二 极限环 非线性系统的相轨迹有时出现一种特别情况，即相轨迹 上出现孤立的封闭曲线，称这种特殊相轨迹为极限环。
极限环的几种情况：
x
x
x
x
无论初值落在环内外相轨迹 的运动朝环逼近，称为稳定 极限环
不稳定极限环
x
x
x
x
称为半稳定极限环
稳定极限环为 非线性系统的一种特殊现象称为自激振荡
第七章 非线性系统分析
内容提要
控制系统在不同程度上都存在着非线性。有 些系统可通过在工作点附近线性化来处理，但当 系统包含有本质非线性特性时，就不能用线性化 的方法处理。非线性系统与线性系统有本质的差 别，非线性系统不满足叠加原理，它的稳定性不 仅取决于控制系统的固有结构和参数，而且与系 统的初始条件与输入信号有关。
§7-2
相平面及相平面的概念
m m
将m 人为 移到某位置x0 松手后m的运动过程：
时刻t t0 t1 t2 t3
位移x x0 0
x2 0
速度 x 0 负最大 0 正最大
考查位置x和速度构成的平面（x－平面） 初始点一定时：形成曲线称为相轨迹 可得： 不同初始点，相轨迹将布满平面
利用x- x 平面分析系统的方称为相平面法，
dx dx
2
n x x
2 n
x
S1.2
(x
n x)2
x ce 2 2
n
2n d
tg
1
xn x d x
相轨迹为一簇螺线，包围奇点（0，0）称为稳定焦点
3． 1 （一对负实根）
S1.2 n n 2 1
S2 S1
(x q1x)q1
(q1
q2
) q1
A q1 1
(q2
q1 ) q2
–0.4 …… -1.67 ……
例2：如图示系统（继电系统）
考查 e e平面上的相迹（c c平面上）
解：
e(t) r(t) c(t) e(t) c(t) 且 e(t) c(t)
y
1 0
e 1 e 1
1 e 1
c(t) c(t) y(e)
得： e(t) e(t) y(e)
几种典型的继电特性
间隙特性
介绍两个方法：相平面法、描述函数法
相平面法是庞加莱（Poincare）1885年首先提出的， 本来它是一种求解二元一阶非线性微分方程组的图解 法,两个变量构成的直角坐标系称为相平面，方程组的 解在相平面上的图象称为相轨迹。
这里是将相平面法用于分析一阶尤其是二阶非线性 控制系统，并形成了一种特定的相平面法，它对弄清 非线性系统的稳定性、稳定域等基本属性,解释极限环 等特殊现象，起到了直观形象的作用。
则
f
(x, x
x)
。称为等倾线方程
具体绘制步骤：
令 dx
则
f
(x, x
x)
dx
为
x, x 方程，对一定的 ，可在x－ x 平
面上画出相应的曲线此为等倾线。
此曲线的特点是：当相轨迹通过该曲线时，其斜率相同。
2 1． 取 不同值，可在相平面上绘出不同曲线（等倾线）。
2． 3 由初值可得到相轨迹上的一个初始点。
三 一般奇点确定
对一般系统
x f (x, x)
可取：x1 x, x2 x1
xx12
x2 f (x1
p , x2
)
Q
dx dx
x2 x1
dx2 dx1
Q p
取：Qp
0 0
有 : e 1
1
区域：有：e 1
1
§7-4 奇点及极限环
奇点概念：相轨迹上满足
dx dx
0 0
不定式的特殊点，称为奇点。
在奇点处有多条相轨迹穿过或趋于该奇点，相当于系统处于 平衡状态
一 奇点分类：(线性系统)
x
2
n
x
2 n
x
0
x
2
n
x
2 n
x
dx
x x
dt dx
dx dx一.二阶系统。
§7-3 相轨迹的绘制
解析法
工程上有二种方法：图解法 只介绍图解法中等倾线法
等倾线法：设二阶系统 x f (x, x)
可得：
x dx dx f (x, x) dx dt
dx dx
f
(
x, x
x)
()
以x－
x
dx
为平面，dx
为相平面上的斜率，可令
dx
dx
e(t) e(t) e(t) y(e) 1 e(t）
1 e(t)
区域 区域
区域
区域由 e 1分界，称为开关线。
利用
de de
f (e, e) e
区域： e e(t)
de e 1 de e
I 中相轨迹为斜- 1率 的直线簇
区域：e 1 e(t)
de de
1 e(t) e
A q2 2
(x q2 x)q2
为一簇抛物线包围奇点（0，0）称为稳定节点
4．1 0 (具正实部共轭根）
对应奇点（0，0）为不稳定焦点
X
5． 1 (有一对正实根）
S1
奇点（0，0）为不稳定节点
S2
6． 有异号实根，称奇点（0，0）为鞍点。
S2
x S1
可见：方程特征根位置决定奇点的类型。
4 从该点出发，按该点所在等倾线斜率所指方向划一小 线数，直到与其相邻另外等倾线相交。 ． 5 其与第二条等倾线交于一点，再从该点出发重复步骤4 ，得到曲线为相轨迹
x x x 0
例： 可得：x x x
由 dx dx
f (x, x) x
X
则 x 1 x
1
α
9
2
1
0
-1/1+α -0.1 -0.33 -0.5 -1