GB31029—1993原子物理学和核物理学的量和单位节录

合集下载

有关量、单位和符号的一般原则

==有关量、单位和符号的一般原则==Quantities and units-General principles国家技术监督局1993-12-27 批准1994-07-01 实施引言本标准等效采用国际标准ISO31 - 0 ：1992 《量和单位第零部分：一般原则》。

本标准是目前已经制定的有关量和单位的一系列国家标准之一，这一系列国家标准是：GB 3100 国际单位制及其应用；GB 3101 有关量、单位和符号的一般原则；GB 3102 ．1 空间和时间的量和单位；GB 3102 ．2 周期及其有关现象的量和单位；GB 3102 ．3 力学的量和单位；GB 3102 ．4 热学的量和单位；GB 3102 ．5 电学和磁学的量和单位；GB 3102 ．6 光及有关电磁辐射的量和单位；GB 3102 ．7 声学的量和单位；GB 3102 ．8 物理化学和分子物理学的量和单位；GB 3102 ．9 原子物理学和核物理学的量和单位；GB 3102 ．10 核反应和电离辐射的量和单位；GB 3102 ．11 物理科学和技术中使用的数学符号；GB 3102 ．12 特征数；GB 3102 ．13 固体物理学的量和单位。

上述国家标准贯彻了《中华人民共和国计量法》、《中华人民共和国标准化法》、国务院于1984 年2 月27 日公布的《关于在我国统一实行法定计量单位的命令》和《中华人民共和国法定计量单位》。

主题内容与适用范围本标准规定了各科学技术领域使用的量、单位和符号的一般原则。

其中包括物理量、方程式、量和单位、一贯单位制，特别是国际单位制的原则说明。

1 本标准适用于各科学技术领域。

2 量和单位2 ．1 物理量、单位和数值在GB 3101 和GB 3102 ．1~3102 ．13 中只处理用于定量地描述物理现象的物理量。

物理量可分为很多类，凡可以相互比较的量都称为同一类量，例如：长度、直径、距离、高度和波长等就是同一类量。

GB31028—1993物理化学和分子物理学的量和单位节录

Ｂ λ
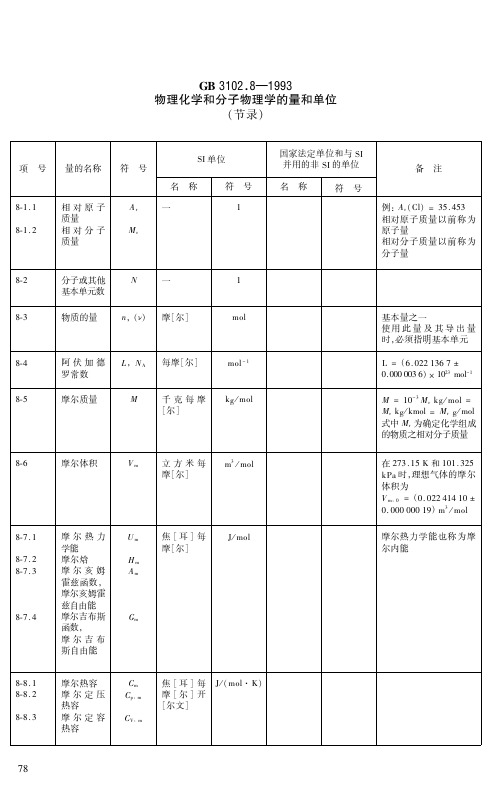
表国家法定单位和与ＳＩ并用的非Ｓ的单位Ｉ号名称符号此量只是温度的函数
备
注
称
符
一
１
８２２．１
ｆＢ
一
１
此量也称为Ｂ的活度系数
８２２．２
Ｂ λ
一
１
此量只是温度的函数
８２３
ａＢ一Ｂ，ａｍ，
１
８２４．１
摩尔热容摩尔定压热容摩尔定容热容
ＣｍＣ，ｍｐＣ，ｍＶ
焦［耳］每摩［尔］开［尔文］
（ ·Ｋ）Ｊ／ｍｏｌ
７８
物理化学和分子物量学的量和单位
续单位ＳＩ项号量的名称符号名８９摩尔熵Ｓｍ称符号表国家法定单位和与ＳＩ并用的非Ｓ的单位Ｉ名称符号
备
注
８２
分子或其他基本单元数物质的量
Ｎ
一
１
８３
，（）ｎ ν
摩［尔］
ｍｏｌ
基本量之一使用此量及其导出量时，必须指明基本单元Ｌ＝（６．０２２１３６７ʃ ２３１－）ˑ１０ｍｏｌ０．０００００３６
３－Ｍ＝１０Ｍｒｋ／ｍｏｌ＝ｇ／ｋｍｏｌ／ｍｏｌＭ＝Ｍｇｒｋｒｇ式中Ｍｒ为确定化学组成的物质之相对分子质量
备
注
Π
Ｂ ν
帕［斯卡］一
８２８
Ａ
焦［耳］每摩［尔］摩［尔］
Ｊ／ｍｏｌ

磁学单位制及相关问题(免费资料,共同学习)

仍以 SI 单位制为例，即使采用一贯单位制单位，用 SI 单位制的 7 个基本单位表示一些导出量的单位时，书写仍然非常繁琐，例如电压的单位符号将为：m2·kg·s−3·A−1。因此，为了使用方便，在国际单位制中规定了 21 个（包括原来的 2 个辅助单位）具有专门名称用以代替由基本单位及辅助单位表示时书写比较繁琐的导出单位，与基本单位和辅助单位并行使用。实践证明，SI 单位制是一种简洁、科学、完善而且实用的一贯单位制。所以，《中华人民共和国计量法》（中华人民共和国主席令第 28 号，1985 年 09 月 06 日第六届全国人民代表大会常务委员会第十二次会议通过）第一章第三条中以法律形式规定“国家采用国际单位制” 。 “国际单位制计量单位和国家选定的其它计量单位，为国家法定计量单位。国家法定计量单位的名称、符号由国务院公布。 ” 我们在实际工作中应该使用磁学量的国家法定计量单位。关于 SI 单位制的详细内容可以查阅下列相关国家标准。 GB 3100－93 GB 3101－93 GB 3102.1－93 GB 3102.2－93 GB 3102.3－93 GB 3102.4－93 GB 3102.5－93 GB 3102.6－93 GB 3102.7－93 GB 3102.8－93 GB 3102.9－93 GB 3102.10－93 GB 3102.11－93 GB 3102.12－93 GB 3102.13－93 国际单位制及其应用；有关量、单位和符号的一般原则；空间和时间的量和单位；周期及其有关现象的量和单位；力学的量和单位；热学的量和单位；电学和磁学的量和单位；光及有关电磁辐射的量和单位；声学的量和单位；物理化学和分子物理学的量和单位；原子物理学和核物理学的量和单位；核反应和电离辐射的量和单位；物理科学和技术中使用的数学符号；特征数；固体物理学的量和单位。

GB31021—1993空间和时间的量和单位节录

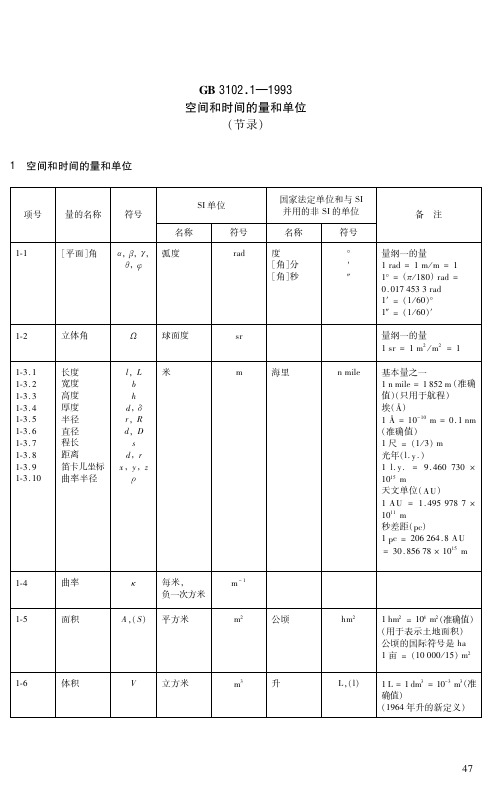
备
注
１８１９
角速度角加速度
ω α
弧度每秒弧度每二次方秒米每秒
ｒａｄ／ｓ
２ｒａｄ／ｓ
１１０
速度
ｖｃ，ｖ，ｗｕ
ｍ／ｓ
千米每［小］时节
ｋｍ／ｈｋｎ
１（准确ｍ／ｓ３．６值）＝０．２７７７７８ｍ／ｓ１ｋｎ＝１ｎｍｉｌｅ／ｈ＝０．５１４４４４ｍ／ｓ（只用于航行）１ｋｍ／ｈ＝标准自由落体加速度：２（准．８０６６５ｍ／ｓｇｎ＝９确值）伽（）Ｇａｌ２１Ｇａｌ．０１ｍ／ｓ＝０毫伽常用于大地测量学中
４８
空间和时间的量和单位
续量的项号１５量的名称面积单位名称与符号平方英寸２ｉｎ表换算因数和备注
２２（准确值）１ｉｎ４５．１６ｍｍ＝６有时用“ 圆密耳” 表示面积：６２２ π ˑ１－０ｉｎ０６．７０７５＝５ μｍ４２２（准确值）．０９２９０３０４ｍ１ｆｔ＝０
gb310211993空间和时间的量和单位节录量的名称符号si单位名称符号国家法定单位和与si并用的非si的单位名称符号弧度rad180rad017453球面度sr量纲一的量10长度宽度高度厚度半径直径距离笛卡儿坐标曲率半径mile基本量之一852m准确值只用于航程1010nm准确值4607301015495978101120626430856781015每米负一次方米公顷hm准确值用于表示土地面积公顷的国际符号是ha100001031964年升的新定义量的名称符号si单位名称符号国家法定单位和与si并用的非si的单位名称符号时间时间间隔持续时间60min86400星期月年a是通常使用的单位弧度每秒rad弧度每二次方秒rad110速度277778514444只用于航行111

有关量、单位和符号的一般原则.答案

例：
但不能写成
然而
，但不能写成
在分子和分母包含相加或相减的情况下，如果已经用圆括号(或方括号、或花括号)，则也可以用斜线。
例：意为；括号是必需的。
；意为但为了避免发生误解，可写成。
括号也可以用于消除由于在数学运算中使用某些标志和符号而造成的混淆。3．2单位的名称和符号3．2．1单位的符号本标准只推荐使用GB 3100中所规定的符号。在某些必须使用中文符号的情况下，可按GB 3100的规定构成中文符号。单位的中文名称构成原则见GB 3100。在印刷中，无论其他部分的字体如何，单位符号都应当用正体印刷。在复数时，单位符号的字体不变。除正常语法句子结尾的标点符号外，单位符号后不得附加圆点。单位符号应当置于量的整个数值之后，并在其间留一空隙。
例2：半径为r的球体在电容率为ε的介质中的电容C为：
C＝4πεr
2．2．5量制和量的方程式；基本量和导出量物理量是通过描述自然规律的方程式或定义新量的方程式而相互联系的。为制定单位制和引入量纲的概念，通常把某些量作为互相独立的，即把它们当作基本量，而其他量则根据这些基本量来定义，或用方程式来表示。后者称为导出量。
1 kA／m＝(103A)／m＝103A／m
注：由于历史原因，质量的基本单位名称千克中含有词头“千”。质量的十进倍数和分数单位由词头加在“克”字之前构成，例如毫克(mg)，而非微千克(μkg)。
SI词头的使用规则以及中文词头符号的使用规则见GB 3100。
3．3数
3．3．1数的印刷
数一般应当用正体印刷。
用多少或用哪些量作为基本量，只是一个选择问题。
在GB 3101和GB 3102．1~3102．13中所包括的全部物理量，都是以七个基本量即长度、质量、时间、电流、热力学温度、物质的量和发光强度为基础的。

(技术规范标准)JS技术标准执行表

1、综合基础部分…………………………………………………………………………2
2、工艺安装部分…………………………………………………………………………5
3、自控部分………………………………………………………………………………26
4、设备部分………………………………………………………………………………28
63
石油化工装置工艺设计包（成套技术工艺包）内容规定
SHSG-052-2003
64
石油化工装置详细工程设计内容规定
SHSG-053-2011
65
石油化工厂工厂基础工程设计内容规定
SHSG-054-2012
2012.9.5实施
66
化工建设项目安全设计管理导则
AQ/T3033-2010
67
危险化学品重大危险源安全监督通用技术规范
5、建筑部分………………………………………………………………………………33
6、结构部分………………………………………………………………………………38
7、总图部分………………………………………………………………………………44
8、电气部分………………………………………………………………………………50
62
六角头螺栓全螺纹
GB/T 5783-2000
63
六角头螺栓细牙
GB/T 5785-2000
64
粉尘作业场所危害程度分级
GB/T5817-2009
65
石油储罐阻火器
GB5908-2005
66
1型六角螺母
GB/T6170-2000
67
1型六角螺母细牙
GB/T6171-2000
68
2型六角螺母

国际单位制-量及其单位符号标准清单

国际单位制—量及其单位符号标准链接清单序号标准编号标准名称相应国际标准编号备注1. GB 2586-1991热量单位、符号与换算2. GB 3100-1993国际单位制及其应用ISO 1000:1992,EQV3. GB 3101-1993有关量、单位和符号的一般原则ISO 31-0:1992EQV4. GB 3102.1-1993空间和时间的量和单位ISO 31-1:1992EQV5. GB 3102.2-1993周期及其有关现象的量和单位ISO 31-2:1992EQV6. GB 3102.3-1993力学的量和单位ISO 31-3:1992EQV7. GB 3102.4-1993热学的量和单位ISO 31-4:1992EQV8. GB 3102.5-1993电学和磁学的量和单位ISO 31-5:1992EQV9. GB 3102.6 光及有关电磁辐射的量和单位ISO 31-6:1992-1993EQV10. GB 3102.7-1993声学的量和单位ISO 31-7:1992EQV11. GB 3102.8-1993物理化学和分子物理学的量和单位ISO 31-8:1992EQV12. GB 3102.9-1993原子物理学和核物理学的量和单位ISO 31-9:1992EQV13. GB 3102.10-1993核反应和电离辐射的量和单位ISO 31-10:1992，EQV14. GB 3102.11-1993物理科学和技术中使用的数学符号ISO 31-11:1992，EQV15. GB 3102.12-1993特征数ISO 31-12:1992，EQV16. GB 3102.13-1993固体物理学的量和单位ISO 31-13:1992，EQV17. GB/T 14559-1993变化量的符号和单位18. B S_ISO80000-1-2009Quantities and units Part 1:General19. B S ISO 80000-2:2009Quantities and units-Mathematical signs and symbols to be used in the natural sciences and technology20. B S ISO 80000-3-2007Quantities and units Part 3 :Space and time21. B S ISO 80000-5-2007Quantities and units Part5: Thermodynamics22. B S EN 80000-6-2008Quantities and units — Part 6 Electromagnetism23. B S ISO 80000-7-2008Quantities and units Part:7 Light24. B S EN ISO80000-8-2007Quantities and units Part 8: Acoustics25. B S ISO 80000-9-2009Quantities and units. Physical chemistry and molecular physics26. B S ISO 80000-10-2009量和单位原子和核物理学27. B S ISO 80000-11-2008Quantities and units Part 11 Characteristic numbers28. B S ISO 80000-12-2009Quantities and units Part 12 Solid state physics29. B S EN 80000-13-2008Quantities and units –– Part 13 Information science and technology30. B S EN 80000-14-2009Quantities and units — Part 14 Telebiometrics related to human physiology31. I EEE ASTMSI 10-2002Use of the International System of Units(SI32. I EEE Std260.1-2004(Revision1993IEEE Standard Letter Symbols for Units of Measurement (SI Units, Customary Inch-Pound Units, and Certain Other Units33. I EEE Std 270-2006Standard Definitions for Selected Quantities, Units and Related Terms with Special Attention to the International System of Units。

GB31025—1993电学和磁学的量和单位节录

５２０５２１
Φ
Ａ
韦［伯］韦［伯］每米亨［利］
ＷｂＷｂ／ｍ
·ｓ１Ｗｂ＝１Ｖ
５２２．１５２２．２
ＬＭ，Ｌ１２
Ｈ
１Ｈ＝１Ｗｂ／Ａ＝ ·ｓ１Ｖ／Ａ电感：自感和互感的统称
５２３．１５２３．２
Ｃ
法［拉］法［拉］每米
ＦＦ／ｍ
ε
０ ε
５１１
ｒ ε
一
１
６３
电学和磁学的量和单位
续单位ＳＩ项号量的名称符号名５１２５１３电极化率电极化强度称符号１
２Ｃ／ｍ
表国家法定单位和与ＳＩ并用的非Ｓ的单位Ｉ名称符号
２Ｃ／ｍ
５５５６．１５６．２
Ｅ，Ｖ φ ，（）ＵＶ
Ｖ／ｍＶ
１Ｖ／ｍ＝１Ｎ／Ｃ１Ｖ＝１Ｗ／Ａ
５６．３５７
ＥＤ库［仑］每平方米库［仑］
２Ｃ／ｍ
量的名称也使用名称 “ 电位移” 量的名称也使用名称 “ 电位移通量” １Ｆ＝１Ｃ／Ｖ
备
注
μｒ
一
，（ κ χｍ， χ）一ｍ安［培］平方米
电ＩＳＯ还给出量的名称“ 磁矩” ＩＥＣ还定义了磁偶极矩，ｊ＝μ ０ｍ磁偶极矩的单位为Ｗｂ ·ｍ
５２８
磁化强度
）安［培］Ｍ，（Ｈｉ每米，（）特［斯拉］ＪＢｉ

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

千克
ｋｇ
９５．１９５．２９５．３
千克
ｋｇ
原子质量单位
ｕ
９６
ｅ
库仑
Ｃ
一个电子的电荷等于－ｅ１．６０２１７７３３ʃ ｅ＝（１９－）ˑ１００．００００００４９Ｃｈ＝（６．６２６０７５５ʃ ３４－） ·ｓ０．０００００４００Ｊ ˑ１ａ０．５２９１７７２４９ ʃ ０＝（１０－）ˑ１０．０００００００２４０ｍ埃（）， ? １０－１ ? ＝１０ｍ１０ ? ＝１ｎｍＲ１．０９７３７３１５３４ ʃ ɕ ＝（７）ˑ １０．００００００００１３０１－ｍＥ４．３５９７４８２ʃ ｈ＝（１８－）ˑ１０．０００００２６０Ｊ
９７
普朗克常量
ｈ
焦［耳］秒
·ｓＪ
９８
玻尔半径
ａ０
米
ｍ
９９
里德伯常量
Ｒ ɕ
每米，负一次方米
ｍ－１
９１０
哈特里能［量］
Ｅｈ
焦［耳］
Ｊ
８３
原子物理学和核物理学的量和单位
续单位ＳＩ项号量的名称符号名９１１．１９１１．２９１１．３粒子或原子核的磁矩玻尔磁子核磁子称符号表国家法定单位和与ＳＩ并用的非Ｓ的单位Ｉ名称符号磁矩通常是磁偶极矩的简称９．２７４０１５４ ʃ μＢ＝（２４－）ˑ１ · ０．０００００３１０Ａ２ｍ５．０５０７８６６ʃ μＮ＝（２７－）ˑ１ · ０．０００００１７０Ａ２ｍ质子的磁旋系数２．６７５２２１２８ʃ γｐ＝（８）ˑ１ · ０．００００００８１０Ａ２（） ·ｓｍ／Ｊ２（）＝１ ·ｍ ·ｓ · Ａ１Ａ／Ｊ１１－－ ·ｓｓ／ｋｇ＝１Ｔ这些量也称为ｇ值或朗德因数
单位ＳＩ项号量的名称符号名９１质子数，原子序数中子数Ｚ一称符
备
注
９２
Ｎ
一
１
９３
核子数，质量数
Ａ
一
１
９４．１
９４．２
［核素Ｘ的］，ｍａ原子质量，（），ｍＸ核素质量（，）ｍＺＡ原子质量ｍｕ常量电子［静］质量质子［静］质量中子［静］质量元电荷ｍｅｍｐｍｎ
９１８
轨道角动量量子数自旋角动量量子数总角动量量子数核自旋量子数核的宇称
，ｌＬｉ
一
１
９１９
，ｓＳｉ
一
１
９２０
，Ｊｊｉ
一
１
９２１
Ｉ
一
１

９２２
π
一
１
在粒子物理中常用Ｐ表示粒子的宇称
８４
原子物理学和核物理学的量和单位
续单位ＳＩ项号量的名称符号名９２３超精细结构量子数主量子数磁量子数Ｆ一称符号１表国家法定单位和与ＳＩ并用的非Ｓ的单位Ｉ名称符号
ｇｇ
一
１
９１４．１９１４．２
ωＬ ωＮ
每秒，负一次方秒弧度每秒
－１ｓ
ｒａｄ／ｓ
９１５
ωｃ
每秒，负一次方秒弧度每秒二次方米米
－１ｓｒａｄ／ｓ
９１６９１７
核四极矩核半径
ＱＲ
２ｍ
ｍ
常使用飞米（）表示Ｒｆｍ１５－１ｆｍ＝１０ｍ通常ｌ的，指Ｌｉ指粒子ｉ整个系统的通常ｓ的，指Ｓｉ指粒子ｉ整个系统的通常ｊ的，指Ｊｉ指粒子ｉ整个系统的也常用Ｊ表示
备
注
９２４９２５
ｎ，ｍＭｉ
一一
１１通常ｍ的，Ｍｉ指粒子ｉ指整个系统的，加下标，，等则指相应角动ＬＳＪ量的磁量子数７．２９７３５３０８ʃ α ＝（３－０．００００００３３ˑ１０１－３７．０３５９８９５ʃ α ＝１０．０００００６１ｒ２．８１７９４０９２ʃ ｅ＝（１５－）ˑ１０．００００００３８０ｍ对于质子，１．３２１４１００２ʃ ，ｐ＝（ λＣ１５－）ˑ１０．００００００１２０ｍ对于中子，１．３１９５９１１０ʃ ，ｎ＝（ λＣ１５－）ˑ１０．００００００１２０ｍ原子质量单位ｕ１ｕ＝（１．６６０５４０２ʃ ２７－）ˑ１０．０００００１００ｋｇ通常用单位ｕ或相应的质量能电子伏表示通常用电子伏表示１ｅＶ＝（１．６０２１７７３３ʃ １９－）ˑ１００．００００００４９Ｊ每个核子的］ ε也称为［平均结合能Ｓｎ也称为最后一个中子结合能Ｓｐ也称为最后一个质子结合能也可用年（）ａ
备
注
μ μＢ μＮ
安［培］平方米
２ ·ｍＡ
９１２
磁旋系数，（磁旋比）
γ
安［培］平方米每焦［耳］秒
２ ·ｍＡ／（ ·ｓ）Ｊ
９１３．１９１３．２
原子或电子因数的ｇ原子核或核子的ｇ因数原子进动角频率核进动角频率回旋角频率
—１ＧＢ３１０２．９９９３原子物理学和核物理学的量和单位（节录）
国家法定单位和与Ｓ并Ｉ用的非Ｓ的单位Ｉ号１名称符号具有相同Ｚ值不同Ａ值的核素称为同位素具有相同Ｎ值不同Ｚ值的核素称为同中子素具有相同Ａ值不同Ｚ值的核素称为同量异位素原子质量单位ｕ１ｕ＝（１．６６０５４０２ʃ ２７－）ˑ１０ｋ０．０００００１０ｇｍ１．６６０５４０２ʃ ｕ＝（２７－）ˑ１００．０００００１０ｋｇ＝１ｕ１ｕ＝（１．６６０５４０２ʃ ２７－）ˑ１０．０００００１００ｋｇ