正方体平面展开图
正方体11种平面展开图(精心整理)
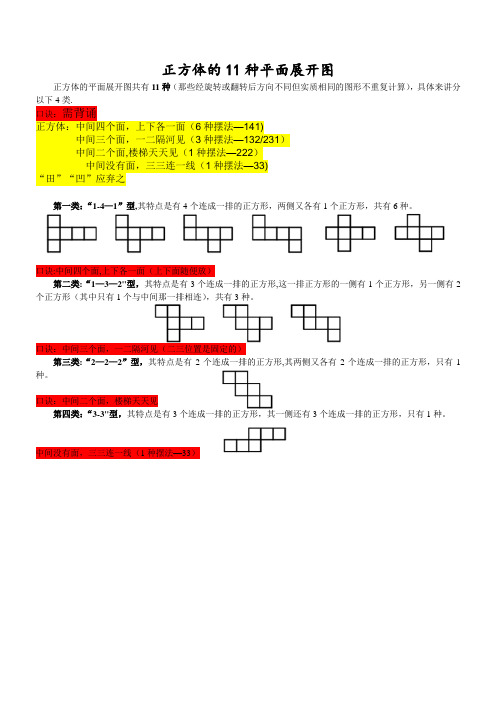
正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类.
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法—141)
中间三个面,一二隔河见(3种摆法—132/231)
中间二个面,楼梯天天见(1种摆法—222)
中间没有面,三三连一线(1种摆法—33)
“田”“凹”应弃之
第一类:“1-4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2"型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3-3"型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法—33)。
正方体的11种展开图规律大全-正方体展开264种

正方体的11种展开图之五兆芳芳创作
判断技能
我们知道,同一个立方体图形,按不合的方法展开得到的平面展开图形一般是不一样的.罕有的正方体平面展开图究竟有几种不合的形状呢?
同学们一定熟悉这样一种操纵:把一个正方形纸片平均分红9个小正方形,剪去角上四个小正方形,可以拼成一个无盖的正方体纸盒,其中五个面按习惯无妨记为下、左、右、前、后,如图一.
好啦!现在只要把方才剪去的一个小正方形作为“上”面,就可拼成一个正方体.作为正方体平面展开图,这个“上”应该和图1(1)中哪个面拼接在一起呢?不雅察图1(2),知“上”和前、后、左、右任一个面拼接都行(这四种拼接看作同一种情形),无妨和“后”拼接在一起,如图2.按照上和下、左和右、前和后相距离这一纪律,现在我们把图2中的“左”或“右”平移,可得图3~图7五种情形.
平移图2中的“前”,可得图8;再平移图8中的“左”,可得图9、图10;把图10中的“上”向左平移,得图11;若移动图8(或图9、图10)中的“左”,又可得图1 2.
同学们,当你和我一样,把图2~图12这11个图剪下来,动手折一折,得到11个漂亮的小正方体时,你一定为我们的收获感应欢天喜地吧!
对正方体概略展开图的11种情况,为加深记忆,可编成如下口诀:一四一呈6种,一三二有3种,二二二与三三各1种,展开图共有11种.“动手实践,自主探索和协作交换”是新课程尺度建议学习数学的三种重要办法,而实践勾当是培养我们进行主动探索与协作交换的重要途径.只要通过自己主动不雅察、实验、猜测、验证等数学勾当,就能使我们“成立空间不雅念,成长几何直觉”,提高思维能力.。
4.1.1正方体的展开图

B
D
E
F
G
下列平面图形能折叠成正方体吗?
×
√
×
×
√
√
活动五 看看谁学得更好
判断下列图形能不能折成正方体?
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
正方体展开图的对面
1
2
3
4
观察,黑板上的立方体平面展开,
有何特点?
Z端是对面
相隔是对面
考考你 下面图形中,哪些是正方体的平面展 开图 ? 若是,找出相对面。
我思故我进步!
反思:几种常见的不能折叠成正方体 的图形。
一、由五个正方形组连成的 “五子连” 形 如
二、由五个正方形组成的“7字”形 如
SKIP
我思故我进步!
三、由五个正方形组成的“凹字” 形
如
四、由四个正方形组成的“田字” 形
SKIP
试一试
下面六个正方形连在一起的图形,经折 叠后能围成正方体的图形有哪几个?(动手试 试)
KEY: 棒
2、“坚”在下,“就”在后,胜利在哪里?
坚
持
就
胜 利
是
下图是一个正方体的展开图,标注了字母 A的面是正方体的正面,如果正方体的左面与 右面所标注代数式的值相等,求 x 的值.
-2
3
-4
1
A 3x-2
再 见
正方体展开图能得到下例图形吗?
①
②
③
④
⑤
⑥
⑦
⑧
⑨
⑩
11
第一类: 一四一,共六种。
结构特点
一 四 一
第二类: 二三一,共三种
(完整word版)正方体的11种展开图

正方体的11种展开图
判断技巧
我们知道,同一个立方体图形,按不同的方式展开得到的平面展开图形一般是不一样的。
常见的正方体平
面展开图究竟有几种不同的形状呢?
同学们一定熟悉这样一种操作:把一个正方形纸片平均分成9个小正方形,剪去角上四个小正方形,可以拼成一个无盖的正方体纸盒,其中五个面按习惯不妨记为下、左、右、前、后,如图一。
好啦!现在只要把刚才剪去的一个小正方形作为“上"面,就可拼成一个正方体。
作为正方体平面展开图,这个“上”应该和图1(1)中哪个面拼接在一起呢?观察图1(2),知“上”和前、后、左、右任一个面拼接都行(这四种拼接看作同一种情形),不妨和“后”拼接在一起,如图2.
根据上和下、左和右、前和后相间隔这一规律,现在我们把图2中的“左”或“右”平移,可得图3~图7五种情形.
平移图2中的“前”,可得图8;再平移图8中的“左”,可得图9、图10;把图10中的“上"向左平移,得图11;若移动图8(或图9、图10)中的“左",又可得图12。
同学们,当你和我一样,把图2~图12这11个图剪下来,动手折一折,得到11个漂亮的小正方体时,你一定为我们的收获感到欢欣鼓舞吧!
对正方体表面展开图的11种情况,为加深记忆,可编成如下口诀:一四一呈6种,一三二有3种,二二二与三三各1种,展开图共有11种。
“动手实践,自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法,而实践活动是培养我们进行主动探索与合作交流的重要途径。
只要通过自己主动观察、实验、猜想、验证等数学活动,就能使我们“建立空间观念,发展几何直觉”,提高思维能力.。
正方体11种展开图

图1
图2
图3
图4
图5
图6
第二类(3种):中间三连方,两侧各有二、一个。 “二三一”
型
图7
图8
图9
第三类(1种):中间二连方,两侧各有二个。
图 10 “二二二”型
第四类 (1种):两排各有三个。
“三三”型
图 11
展开1 第一类(6种):中间四连方,两侧各有一个。
展开第一类(6种):中间四连方,两侧各有一个。 2
(16)
(17)
(18)
在展开的过程中注意你剪开了几条棱?
将正方体展开成平面图形 需要剪开7条棱
(无论用哪种方案展开)
开始时我们已经在正方体的 相对的面上标上相同的数字,现在观察一下这些数字在展
开图中有什么规律?
“一四一” 型
“二三一”型
“三三”型
“二二二”型
考考你 下图是正方体的表面展开图。
1、如果“你”在前面,那么谁在 后面?
了!
太棒
你们
2、“坚”在下,“就”在后, “胜”、“利”在哪里?
坚
持就是
胜
利
圆 柱 圆 锥
三 棱 锥
四棱 锥
五棱锥
展开第3 一类(6种):中间四连方,两侧各有一个。
展开4 第一类(6种):中间四连方,两侧各有一个。
展开5 第一类(6种):中间四连方,两侧各有一个。
展开6 第一类(6种):中间四连方,两侧各有一个。
展开7
第二类(3种):中间三连方,两侧各有一、二个。
展开8
第二类(3种):中间三连方,两侧各有一、二个。
展开9
第二类(3种):中间三连方,两侧各有一、二个
展开10
第三类(1种):中间二连方,两侧各有二个。
正方体的11种展开图经典实用

(17)
正方体的11种展开图
(18)
正方体的11种展开图
2.如图有一正方体房间,在房间内 的一角A 处有一只小虫,它想到房 间的另一角B处去吃食物,它采取怎 样的行走路线最近?
A
B
正方体的11种展开图
变形:如图有一长方体房间,在房间 内一角A 处有一只小虫,它想到房间 的另一角B处去吃食物,它采取怎样 的行走路线最近?
(6)
正方体的11种展开图
(7)
正方体的11种展开图
(8)
正方体的11种展开图
(9)
正方体的11种展开图
(10)
正方体的11种展开图
(11)
正方体的11种展开图
(12)
正方体的11种展开图
(13)
正方体的11种展开图
(14)
正方体的11种展16)
A
B
正方体的11种展开图
这节课我们探索了...... 这节课我体验到了...... 这节课我还想......
正方体的11种展开图
正方体的11种展开图
将正方体剪开展成一个平面图形。
正方体的11种展开图
“一四一”型
正方体的11种展开图
“二三一”型
“三三”型
“二二二”型
正方体的11种展开图
判断下列图形能不能折成正方体?
(1)
正方体的11种展开图
(2)
正方体的11种展开图
(3)
正方体的11种展开图
(4)
正方体的11种展开图
(5)
正方体的11种展开图
正方体11种展开图

第一类,1,4, 1型,共六种。
第二类,2,3,1型,共三种。
第三类,2,2,2型,只有一种。
第四类,3,3型,只有一种。
1.既然都是正方体,为什么剪出的平 面图形会不一样呢? 2. 一个正方体将其展开成一个平面图 形,必须沿几条棱剪开?
A B
C D F E
总结规律:
正方体的表面展开图用“口诀”:
一线不过四,
田凹应弃之;
相间、“Z”端是对面, 间二、拐角是邻面。
一线不过四
×
×
田凹应弃之
×
×
×
×
相间、“Z”端是对面
A
B
A
B
A和B为相对的两个面
间二、拐角邻面知
C D C
D
C和D为相邻的两个面
7
把一个正方体的表面沿某些棱剪开,展成 一个平面图形,能得到下面的平面图形吗?
下列图形都是正方体的展开图吗?
图1
是
图2
图3
是
是
图4
是
图5
图6
不是
不是
下面图形都是正方体的展开图吗?
不是
图(1)
图(2)
图(3)
不是
是
图(4)
不是
不是
图(5)
图(6)
不是
如图是一个正方体的展开图,面 A , 面B,面C的对面各是哪个面?
(完整word版)正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆—132/231)
中间二个面,楼梯天天见(1种摆法—222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种.
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3-2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种.
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2-2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种.
口诀:中间二个面,楼梯天天见
第四类:“3—3"型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法—33)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
日常生活中,我们经常可以看到各种 各样的长(正)方体形状的包装盒, 如粉笔盒、文具盒、牙膏盒等(如某些 棱剪开,再展成平面图形.
思考:在展成平面图形的过程 中,你一共剪了几条棱?
把同一个正方 体的表面沿某些棱剪 开,展开所得到的平面 图形是否一样?
考考你
1、如果“你”在前面,那么什么在后面? 了 太 你 们 棒 !
KEY: 棒
2、“坚”在下,“就”在后,“胜”、“利” 在哪里?
坚 持 就 是
胜
利
动动手
把一个正方体的表面 沿某些棱剪开,展成一 个平面图形,能得到哪 些平面图形?请与同伴 进行交流。
想一想:
下列的图形都是正方体的展开图吗? (2) (1) (3)
(√) (4) (5)
(√) (6)
(√)
(√)
(× )
(× )
将相对的两个面涂上相同的颜色, 正方体的平面展开图共有以下11种:
