应用MATLAB软件建立的收入预测模型
利用Matlab进行数据预测和建模

利用Matlab进行数据预测和建模引言:在当今信息时代,数据的达成速度越来越快,数据的确保来自于不同的途径。
但是对于用户来说,如何将这些数据转变为有价值的信息是一个巨大的挑战。
数据预测和建模是一种有效的方式来解决这个问题。
本文将介绍如何利用Matlab进行数据预测和建模的方法和技巧。
一、数据预处理在进行数据预测和建模之前,首先需要进行数据预处理。
数据预处理是一个重要的步骤,它包括数据清洗、缺失值处理、异常值处理等。
在Matlab中,有许多工具可以帮助我们完成这些任务。
例如,Wiener滤波器可以用来降噪,空值可以使用插值法来填充,异常值可以通过统计方法进行识别和修复。
二、数据可视化在进行数据预测和建模之前,我们需要对数据进行可视化分析,以了解数据的特征和趋势。
Matlab提供了丰富的绘图函数,可以方便地绘制各种图表。
例如,绘制折线图可以显示数据的变化趋势,绘制散点图可以显示数据之间的关系。
此外,Matlab还提供了交互式绘图工具,可以通过交互操作来进一步分析数据。
三、数据预测数据预测是根据已有的数据,来预测未来的走势。
利用Matlab进行数据预测主要有两种方法:基于统计模型的预测和基于机器学习的预测。
1. 基于统计模型的预测在Matlab中,我们可以使用统计工具箱中的函数来构建各种统计模型,如线性回归模型、ARMA模型、时间序列模型等。
这些模型可以通过最小二乘法、极大似然估计等方法来求解,从而得到模型的参数。
利用这些参数,我们可以对未来的走势进行预测。
2. 基于机器学习的预测Matlab提供了强大的机器学习工具箱,可以用来构建各种机器学习模型。
例如,我们可以使用神经网络模型来进行预测,也可以使用支持向量机模型来进行分类。
这些模型可以通过训练数据进行学习,然后利用学习得到的模型对未知数据进行预测。
四、数据建模数据建模是根据已有的数据,来构建一个模型,从而描述数据的特征和规律。
利用Matlab进行数据建模主要有两种方法:基于物理模型的建模和基于统计模型的建模。
matlab预测模型算法

matlab预测模型算法使用Matlab进行预测模型算法在现代数据分析和机器学习领域,预测模型算法是非常重要的工具。
通过预测模型算法,我们可以根据已有的数据来预测未来的结果或者行为。
在这篇文章中,我将介绍如何使用Matlab来构建和应用预测模型算法。
Matlab是一种功能强大的数值计算和数据分析软件,广泛应用于科学和工程领域。
它提供了许多有用的工具和函数,可以帮助我们构建和评估预测模型算法。
在使用Matlab进行预测模型算法之前,我们首先需要准备好数据集。
数据集是进行预测模型算法的基础。
它包含了我们要预测的变量(也称为目标变量)以及用于预测的其他相关变量(也称为特征变量)。
在准备数据集时,我们需要确保数据的完整性和准确性,并进行必要的数据清洗和转换。
Matlab提供了许多数据处理和清洗的函数,可以帮助我们处理数据集。
一旦我们准备好数据集,我们就可以开始构建预测模型算法了。
在Matlab中,有许多常用的预测模型算法可以选择,如线性回归、决策树、支持向量机等。
我们可以使用Matlab内置的函数来构建这些模型,并根据数据集来训练和优化模型。
在训练模型之后,我们可以使用测试数据集来评估模型的性能。
在Matlab中,我们可以使用交叉验证和其他评估指标来评估模型的准确性和鲁棒性。
通过评估模型的性能,我们可以选择最合适的模型来进行预测。
一旦我们选择了最合适的模型,我们就可以将其应用于新的数据集来进行预测。
在Matlab中,我们可以使用训练好的模型来对新的数据进行预测,并生成相应的结果。
通过预测模型算法,我们可以得到有关未来行为或结果的预测,并作出相应的决策。
除了构建和应用预测模型算法外,Matlab还提供了许多其他功能来增强预测模型的性能。
例如,我们可以使用特征选择和特征工程来选择最相关的特征变量,并对特征进行转换和组合。
此外,我们还可以使用模型集成和深度学习等技术来进一步提高预测模型的准确性和鲁棒性。
总结起来,使用Matlab进行预测模型算法是一种非常有效和方便的方法。
使用MATLAB进行数据预测和预测

使用MATLAB进行数据预测和预测引言:数据预测和预测在许多领域中都具有重要的应用价值。
它们可以帮助我们预测未来的发展趋势,做出合理的决策,并在经营和决策中提供有力的支持。
在这一过程中,MATLAB作为一种功能强大的编程语言和数据分析工具,为我们提供了一个强大的工具箱,可以进行数据预测和预测。
数据预处理:在开始数据预测和预测之前,我们首先需要对数据进行预处理。
预处理包括数据清洗、数据归一化、特征选择等步骤。
通过这些步骤,我们可以提高数据的质量,减少噪声的影响,并使数据更适合于预测模型的建立。
数据清洗是指删除或修复数据中的错误值、缺失值和异常值。
在MATLAB中,我们可以使用一些函数和工具箱来处理这些问题。
例如,我们可以使用`isnan`函数来检测缺失值,并使用`fillmissing`函数来填充缺失值。
对于异常值,我们可以使用一些统计方法,如3σ原则或箱线图来识别和处理。
数据归一化是将不同尺度的数据映射到统一的尺度上。
这是因为不同尺度的数据可能对预测模型的训练和预测产生不利影响。
在MATLAB中,有许多方法可以实现数据归一化,如MinMax归一化、Z-score归一化等。
我们可以使用`mapminmax`函数来实现MinMax归一化,并使用`zscore`函数来实现Z-score归一化。
特征选择是从原始数据中选择最相关的特征,以降低数据维度并提高预测模型的准确性。
在MATLAB中,我们可以使用一些算法和函数来实现特征选择。
例如,我们可以使用`fsrnca`函数(基于相关系数的特征选择)或`sequentialfs`函数(基于逐步搜索的特征选择)来选择最佳特征子集。
在完成数据预处理后,我们可以使用各种算法和方法进行数据预测。
在MATLAB中,有许多经典的预测算法和函数可供选择。
以下是几个常用的预测方法。
1. 线性回归:线性回归是一种基本的预测方法,它使用线性模型来建立输入变量和输出变量之间的关系。
如何使用Matlab进行时间序列分析和预测模型构建

如何使用Matlab进行时间序列分析和预测模型构建引言时间序列分析和预测在许多领域都具有重要的应用价值,如金融、经济、气象等。
而Matlab作为一种功能强大的数学软件,提供了丰富的工具和函数用于时间序列分析和预测模型的构建。
本文将介绍如何使用Matlab进行时间序列分析和预测模型构建,帮助读者快速掌握这一有用的技能。
一、数据预处理在进行时间序列分析和预测之前,首先需要对数据进行预处理。
常见的预处理方法包括数据清洗、缺失值处理、异常值检测等。
1. 数据清洗数据清洗是指对数据进行筛选和剔除,以保证数据的质量和准确性。
在Matlab 中,可以使用各种函数进行数据清洗,如isnan、isinf等。
例如,可以通过isnan函数判断数据是否含有缺失值,并使用isnan函数将缺失值替换为NaN。
2. 缺失值处理缺失值是指数据中的某些观测值缺失或无法获取。
在时间序列分析中,缺失值会对模型的预测产生较大影响。
因此,对于缺失值的处理是非常重要的。
在Matlab中,可以使用一些统计函数,如mean、median等,来对缺失值进行插补或填充。
例如,可以使用mean函数将缺失值替换为数据的均值。
3. 异常值检测异常值是指与其他观测值相比,具有异常数值的观测值。
异常值可能由于测量误差、数据录入错误或其他原因造成。
在时间序列分析中,异常值会对模型的精度和可靠性产生较大影响。
因此,需要对异常值进行检测并进行相应的处理。
在Matlab中,可以使用箱线图、离群点检测等方法来检测异常值,并使用插补或删除等方法进行处理。
二、时间序列分析时间序列分析是指对一系列时间上连续观测值的统计分析与建模。
时间序列分析常用于探索数据的内在规律和结构,并建立相应的数学模型。
1. 数据可视化数据可视化是进行时间序列分析的重要步骤,可以帮助我们直观地了解数据的特征和趋势。
在Matlab中,可以使用plot、scatter等函数进行数据可视化。
例如,可以使用plot函数绘制时间序列的折线图,以展示数据的趋势和变化。
基于Matlab的金融数据分析与预测系统设计

基于Matlab的金融数据分析与预测系统设计金融数据分析与预测在当今社会中扮演着至关重要的角色,它不仅可以帮助投资者做出明智的决策,还可以为企业提供战略指导。
而Matlab作为一种强大的数学计算软件,在金融领域也有着广泛的应用。
本文将介绍基于Matlab的金融数据分析与预测系统设计,包括系统架构、功能模块以及实现方法等内容。
1. 系统架构设计基于Matlab的金融数据分析与预测系统主要包括数据获取模块、数据处理模块、数据分析模块和预测模块。
其中,数据获取模块负责从各个金融市场获取实时或历史数据,数据处理模块用于清洗和整理原始数据,数据分析模块则通过各种统计方法和算法对数据进行深入分析,最后预测模块基于历史数据和分析结果进行未来走势的预测。
2. 功能模块设计2.1 数据获取模块数据获取模块是整个系统的基础,它可以通过网络接口获取股票、期货、外汇等金融市场的实时行情数据,也可以通过数据库查询获取历史数据。
在Matlab中,可以利用相关工具包如Datafeed Toolbox或者直接编写网络爬虫程序来实现数据的自动获取。
2.2 数据处理模块数据处理模块主要负责对原始数据进行清洗和整理,包括去除异常值、填充缺失值、标准化等操作。
在Matlab中,可以利用内置函数和工具箱来实现这些操作,也可以编写自定义函数来处理特定需求。
2.3 数据分析模块数据分析模块是整个系统的核心部分,它可以通过统计分析、时间序列分析、机器学习等方法对金融数据进行深入挖掘。
在Matlab中,可以利用Statistics and Machine Learning Toolbox等工具箱来实现各种复杂的分析算法。
2.4 预测模块预测模块基于历史数据和分析结果,利用时间序列预测、回归分析、神经网络等方法对未来走势进行预测。
在Matlab中,可以通过编写预测算法函数来实现不同类型的预测模型,并结合可视化工具展示预测结果。
3. 实现方法3.1 Matlab环境搭建首先需要在计算机上安装Matlab软件,并配置相应的工具箱和支持包。
matlab酒店收益模型

matlab酒店收益模型酒店收益管理是酒店业的重要部分,它涉及预测和优化酒店客房和其它资源的销售,以提高酒店的收入和利润。
为了有效地进行收益管理,我们需要建立一个数学模型。
在本文中,我们将建立一个简单的MATLAB酒店收益模型。
模型假设:1. 酒店的可用客房数量是固定的。
2. 需求受到季节性、价格、市场状况等多种因素的影响。
3. 客房的需求量符合泊松分布。
4. 客房的预订符合指数分布。
变量定义:* K:酒店的可用客房数量* D:每日客房需求量* P:每日房价* R:每日收入* B:每日预订数量* T:预订周期(天)模型建立1. 需求预测我们假设客房需求量D符合泊松分布,其概率密度函数为:\(f(D) = \frac{e^{-λD}}{D!}\)其中λ是每日客房需求的平均发生率。
根据历史数据,我们可以估计λ的值。
2. 预订模型我们假设预订数量B符合指数分布,其概率密度函数为:\(f(B) = \frac{μe^{-μB}}{B!}\)其中μ是每日预订取消率。
同样,我们可以根据历史数据估计μ的值。
3. 收入模型每日收入R可以表示为:\(R = P × D\)如果D超过了K(可用客房数量),则只接受K个预订。
未被接受的预订将转移到下一个预订周期。
4. 总收益模型总收益可以表示为:\(Total_Income = Σ(R)\)在预订周期T内,我们对每个预订周期的收入进行求和,得到总收益。
模型求解:1. 使用泊松分布和指数分布的概率密度函数,我们可以计算每个预订周期的预期需求和预期预订数量。
2. 根据预期需求和可用客房数量,我们可以确定哪些预订被接受,哪些被拒绝。
3. 根据接受的预订,我们可以计算每个预订周期的预期收入。
4. 最后,我们将每个预订周期的预期收入相加,得到总预期收入。
模型验证:为了验证模型的准确性,我们可以使用历史数据来模拟预订过程,并计算实际收入与预期收入的差异。
如果差异很小,那么我们可以认为模型是准确的。
[毕业设计论文]财政收入预测与分析MATLAB
![[毕业设计论文]财政收入预测与分析MATLAB](https://img.taocdn.com/s3/m/6467b52d0b4c2e3f57276396.png)
一、根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。
表1 美国人口统计数据提示:指数增长模型:r te x t x 0)(=解:设)(t x 为第t 年美国人口数,记时刻(t=0)的人口为0x 。
假设人口增长率为常数r,则有t t rx t x t t x ∆=-∆+)()()( 令0→∆t ,有关于)(t x 的微分方程0)0(,x x rx dtdx==,故可解出得到热口指数增长模型:rt e x t x 0)(=,(1)将(1)式去对数,可得0ln ,ln ,x a x y a rt y ==+=用MATLAB 软件计算可得r=0.214/10年,0x =-36.6198,预测估计美国2010年的人口数为x(2010)= 598.4,拟合图17801800182018401860188019001920194019601980050100150200250300350用MA TLAB 解题具体步骤如下: 程序:t=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76 92 106.5 123.2 131.7 150.7 179.3 204 226.5]v=log(y);p=polyfit(t,v,1) %得到指数模型参数值r 和a 结果:y =Columns 1 through 93.9000 5.3000 7.2000 9.6000 12.9000 17.1000 23.2000 31.4000 38.6000Columns 10 through 1850.2000 62.9000 76.0000 92.0000 106.5000 123.2000 131.7000 150.7000 179.3000Columns 19 through 20204.0000 226.5000 p =0.0214 -36.6198 程序:ti=1790:2:1980; vi=polyval(p,ti); yi=exp(vi)plot(t,y,'*',ti,yi,'r')legend('数据点(x,y)','拟合曲线y=f(x)'))x(2010)=exp(0.0214*2010-36.6198) %估计2010年美国人口 Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭首先我们可用微积分将连续的微分方程离散化,不妨设x(t)表示第t 次所得人口数,r 为人口固有增长率,根据logistic 模型()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭,m x ,为人口容量,以下用k 代替m x ,可得:())())(1()()1(t x kt x r t x t x -=-+))(1()()()1(kt x r t x t x t x -=-+这里可以假设)()()1(t x t x t x y -+=,)(t x x =,则krs sx r y =-=,现在我们可以用线性拟合,借助matlab 来进行运算得到r,ky=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5]; t=1:20; for k=1:19x(k)=(y(k+1)-y(k))/y(k); endA=polyfit(y(1:19),x,1) %求出参数r 与s A =-0.0014 0.3368这里求出r=0.3368,k=0.3368/0.0014=240.57143(下面的b0就是这里求出) function y=lin(b,t);f(x)=b(1)./[1+(b(1)./3.9-1).*exp(-b(2).*t)];t=1:20;y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5]; b0=[240.57143,0.3368]; b=nlinfit(t,y,'lin',b0) b0 =240.5714 0.3368 b =312.6056 0.2615这里就求出了函数的值r=0.2615,m x =312.6065,0x =3.9(最初的值,1790年的) 则可求出()te t x 2615.0155282.8016065.312-+=t=1790:10:1980;y=[3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5];x1=1:20;F=312.6056./[1+80.155282.*exp(-0.2615.*x1)]; plot(t,y,'r*');hold on plot(x1,F,'b-');hold off ,legend('数据点(xi,yi)','拟合曲线y=f(x)') xlabel('t'),ylabel('x(t)') 下面是图形预测2010年,当t=23时,求出美国2010年的人口为261.4142结论:从以上两个图形可以看出,logistic 拟合的更好,误差更少,预测用logistic 模型更加准确。
财政收入预测matlab
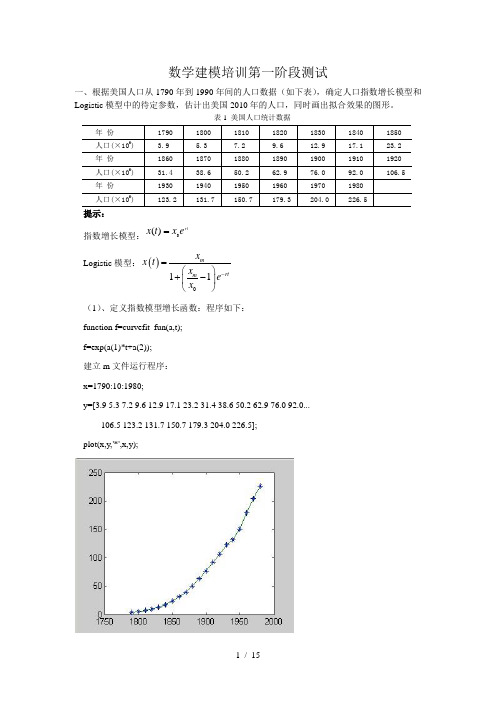
数学建模培训第一阶段测试一、根据美国人口从1790年到1990年间的人口数据(如下表),确定人口指数增长模型和Logistic 模型中的待定参数,估计出美国2010年的人口,同时画出拟合效果的图形。
表1 美国人口统计数据年 份 1790 1800 1810 1820 1830 1840 1850 人口(×106) 3.9 5.3 7.2 9.6 12.9 17.1 23.2 年 份 1860 1870 1880 1890 1900 1910 1920 人口(×106) 31.4 38.6 50.2 62.9 76.0 92.0 106.5 年 份 1930 1940 1950 1960 1970 1980 人口(×106)123.2131.7150.7179.3204.0226.5提示:指数增长模型:rte x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭(1)、定义指数模型增长函数:程序如下: function f=curvefit_fun(a,t); f=exp(a(1)*t+a(2)); 建立m 文件运行程序: x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5]; plot(x,y,'*',x,y);x=1790:10:1980;y=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0... 106.5 123.2 131.7 150.7 179.3 204.0 226.5];plot(x,y,'*',x,y);a0=[0.001,1];a=lsqcurvefit('curvefit_fun',a0,x,y);a1=num2str(a)disp(a1);xi=1790:2:2020;yi=curvefit_fun(a,xi);hold on;plot(xi,yi,'r')x1=2010;y1=curvefit_fun(a,x1)hold off(2)、二、f(x)的定义如下:2226,04()56,010,231,x x x x f x x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且其它1、写一个函数文件f(x)实现该函数,要求参数x 可以是向量; (1)建立函数文件: function y=f(x); x=-10:0.1:10 y1=zeros(size(x)); y2=zeros(size(x)); y3=zeros(size(x)); n=length(x); for k=1:nif x(k)<0&x(k)~=-4; y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6; else y3(k)=x(k).^2-x(k)-1; end end y=y1+y2+y32、作出该函数的图形;(2)、先建立函数文件,再运行程序 function y=f(x); x=-10:0.1:10 y1=zeros(size(x));y2=zeros(size(x));y3=zeros(size(x));n=length(x);for k=1:nif x(k)<0&x(k)~=-4;y1(k)=x(k).^2+x(k)-6;elseif x(k)>=0&x(k)<10&x(k)~2&x(k)~=3; y2(k)= x(k).^2-5*x(k)+6;else y3(k)=x(k).^2-x(k)-1;endendy=y1+y2+y3plot(x,y)3、求出f(x)的零点与最值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
标题:应用MATLAB软件对中国电信运营收入的发展趋势分析及预测
摘要:在对中国电信产业发展进程进行分析研究的基础上,本文在应用MATLAB软件基础上建立了电信收入发展趋势分析的经济模型。
根据此模型,可预测以下结果:未来几年我国电信收入持续增长的同时,发展速度会逐渐放缓,但增速仍明显高于经济的增速。
电信产业将从高速增长期进入稳健的发展期。
关键词:电信产业;发展模型;收入预测
China Telecom's Operating Income Trend Analysis And Forecasting Model
Abstract: In the development process of China's telecom industry on the basis of analytical studies, this paper based on the application of MATLAB software, telecommunications revenue trends analysis of economic models. According to this model, can predict the following results: the next few years, China's telecommunications revenue growth, while growth rate will gradually slow down, but growth was still significantly higher than the economic growth. Period of rapid growth in the telecommunications industry will enter a stable development period. Keywords:telecommunications industry; the development of model; revenue forecasts
应用MATLAB 软件对中国电信运营收入的发展趋势分析及预测
前言
据调查显示,近几年中国电信产业发展迅速,年收入从1999年的2787.9亿元增加到2006年的6483.8亿元,年平均增速达到12.83%,7年间收入增长了2.3倍。
(资料来源:中国电信07~08年度总结报告)从0国
3+01家经济形势的大环境分析,未来几年的中国电信的年收入仍然会以较高的速度增长。
下面建立的中国电信的年收入经济模型,用定量的方法研究其发展趋势,以便了解中国电信的长期收益情况。
一、根据历史数据做定性分析:
表1:1999~2006年中国电信各年收入
年份
1999
2000
2001
2002
2003
2004
2005
2006 年收入(亿) 2787.9 3074.0 3571.9 4116.0 4610.0 5187.6 5799.0
6483.8
从表1可以看出,中国电信年收入数值随时间的变化呈上升趋势且无明显的周期变化。
取变量t 作为时间变量,并且取正整数,设t y 为中国电信t 时间的年收入值,令1999年对应的t 值为1,2000年对相应的t 值为2,以后以此类推,则1y 至8y 依次表示1999至2006年中国电信各年收入值,即:
9.27871=y , 0.30742=y , 9.35713=y , 0.41164=y , 0.46105=y , 6.51876=y , 0.57997=y , 8.64838=y
运行MATLAB 过程如下:(截图)
图1:MATLAB散点图
经MATLAB 散点图(图1)检验表明,年收入数值具有长期随时间上升趋势,因此可以通过用时间序列预测的趋势方程,建立中国电信年收入的预测模型。
二、利用趋势方程定量分析预测:
方法:用n 次多项式拟合趋势方程
运行数量经济学的MATLAB 软件,取n =2,建立中国电信的年收入随时间变化的二次拟合趋势方程如下:
2237.3262397t t y
t
++= (1)
以该方程为预测模型,对1999~2006年中国电信各年收入t y 的历史数据进行了模拟。
运行MATLAB 过程如下:(截图)
图2:1999~2006年中国电信各年收入模拟与实际对比从图2可以直观地看出,预测值(蓝色带“+”曲线)与实际值(红色带“*”曲线)吻合的很好,两者误差值(图2内下方绿色曲线)趋于零,说明利用该二次拟合趋势方程的预测模型的预测效果不错。
进一步分析见表2,从表2中可以看出,预测值与实际值相对误差的最大值2.22%,远远低于预测允许精度10%的标准,表明模型达到了很高的预测精度。
表2:预测的与实际的年收入对比
年份实际年收入(亿)预测年收入(亿)两者相对误差1999 2787.9 2746.6 0.0148
2000 3074.0 3142.3 0.0222
2001 3571.9 3584.1 0.0034
2002 4116.0 4071.8 0.0107
2003 4610.0 4605.6 0.0009
2004 5187.6 5185.4 0.0004
2005 5799.0 5811.2 0.0021
2006 6483.8 6483.1 0.0001
三、结论
为便于观察和得出结论,下面对预测收入趋势单独作图。
t取值1~12,用预测模型对2007~2010年未来4年中国电信年收入进行了预测。
MATLAB运行过程的截图如下:
图3:中国电信年收入预测
如图3所示,通过预测可以看出,未来几年的电信运营收入将呈平稳增长态势。
2007~2010年平均增长率将达10.25%,较十五期间平均增长率12.83%将有所放缓。
2010年,预计电信运营收入将达到9630亿元。
通过对电信收入的定量分析表明,未来几年我国电信收入持续增长的同时,发展速度会逐渐放缓,电信产业将从高速增长期进入稳健的发展期。
参考文献:
苏金明,王永利.MATLAB7.0实用指南[M].北京:电子工业出版社,2004。
