第四章 滑移线理论
合集下载
第4章 滑移线场理论
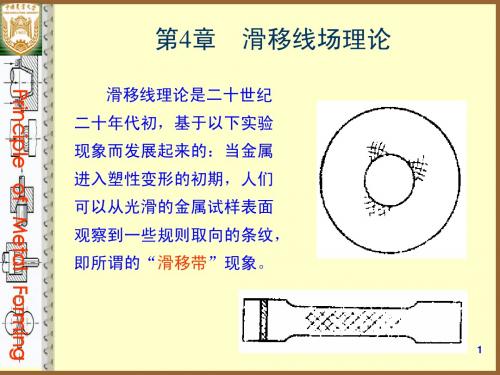
点起、始位置的另一族两条滑移线的曲率变化量 (如dRβ)等于该点所移动的路程(如dSα)。
11
4.3 塑性区应力边界条件:
自由表面
Principle of Metal Forming
12ቤተ መጻሕፍቲ ባይዱ
接触表面之:
摩擦切应力为零
摩擦切应力为某中间值
Principle of Metal Forming
13
摩擦切应力为最大值
7
由称Saint-Venant塑性流动方程
Principle of Metal Forming
8
4.2 滑移线的性质
4.2.1 H.Hencky方程 也称沿线特性,描述滑移线上各点的平均应力变化规律。
Principle of Metal Forming
由上式知,任一族中任一条滑移线上 两点的平均应力符合下列关系式:
一条滑移线(如β1或β2 )相交两点的倾角差和静水压力变化量均保
Principle of Metal Forming
持不变。
若单元三个节点角ω、σm知,则第四点知。 推论: 异族截区内,一直皆直。
10
4.2.3 H.Hencky第二定理
一动点沿某族任意一条滑移线移动时,过该动
Principle of Metal Forming
Principle of Metal Forming
14
4.2 常见的滑移线场类型
正交直线 1 ) 直 线 型
Principle of Metal Forming
2 ) 简 单 型
奇点
有心扇形:直线+圆弧 无心扇形:包络+渐开
15
3 ) 直 简 组 合 型
Principle of Metal Forming
7-2 滑移线速度场理论及应用

ω+dω
P2
vα ω
x
滑移线上邻近两点的速率分解
金属塑性成形原理
盖林格尔速度方程:
dv v d 0 (沿α线) dv vd 0 (沿β线)
(7-12)
此方程式给出了沿滑移线上速度分量的变化特性,它可确定塑性变形 区内的速度分布。
若 α 滑移线为直线,则
d 0, v 常数
直线滑移线场,
v 常数,v 常数
金属塑性成形原理
对于由两族 α与β 连续正交的曲线网络所 构成的滑移线场,则在速度平面上相应有一 由两族连续正交的速度矢端曲线网络所构成 的速度矢端图(速端图),即为速度场。
滑移线和速度矢端曲线之间的关系
金属塑性成形原理
2.几种速度间断线的速端图
(1)滑移线ab为速度间断直线 其一侧为刚性区(“-”) ,另一侧为塑性区(”+‘)。由于ab两侧分别具有同一
(7-10)
金属塑性成形原理
过P点取滑移线为坐标系,以滑移线α、β的切线代替x、y轴,则有:
x , y
x ,y
由于σα,σβ 是最大切应力所在平面上的正应力
m
代入(7-10)得:
0, 0
(7-11a)
d
dt
0 d
0
d
dt
0 d
0
(7-11b)
取滑移线为坐标系
速度,故在速度平面的速度矢端曲线分别归缩为一个点,其速端图如图所示。
a)速度间断直线
b)速端图
图7-22 速度间断直线及其速端图
金属塑性成形原理
(2)滑移线ab为速度间断曲线,两侧分别为刚性区与塑性区 刚性区一侧在速度平面上的速度矢端曲线归缩为一点,而塑性区一侧
(塑性成形力学)4滑移线场理论及应用

(滑移线为速度不连续线) 4. 切向速度不连续量沿速度不连续线是一常数。
存在速度不连续线的速端图:
两条速度不连续线相交于一点附近的速度不连续量的矢量和为零。
4.6滑移线场的绘制
建立变形区内滑移线场通常是一个相当复杂的问题。
在给定的应力边界条件下,作滑移线场的方法: 1. 积分滑移线的微分方程; 2. 图解法; 3. 数值积分法。
相关规定:
1. 使单元体产生顺时针转效果的剪应力方向为α线,反之为β线;(例题)
2. 分别以α线和β线构成一右手坐标系时的横轴和纵轴,则代数值最大的主应力
σ1的作用线在穿过原点条件下是在第Ⅰ和第Ⅲ象限内;(例题)
3. α线各点的切线与所取的x轴的夹角为φ,逆时针转为正,顺时针转为负。
y
右手坐标系: 姆指指向α线正方向 食指指向β线正方向 中指指向自己
不少的塑性加工过程,由于变形区域 沿某一方向(z轴方向)的尺寸较大, 沿该方向的相对变形量很小,可近似 认为是平面变形问题。 如:薄板轧制 矩形件压缩
莫尔圆 (应力圆)
单辉祖,“材料力学教程”, 国防工业出版社,1982
-p
k
4.1.2 基本假设
各向同性的理想刚-塑性材料 变形抗力为常数 忽略热应力和惯性力等
(①+②)/2 (①-②)/4
① ②
式(4.25) 式(4.26)
式(4.27) 式(4.28)
4.5 滑移线场求解的应力边界条件和步骤
4.5.1 应力边界条件 4.5.2 滑移线求解的一般步骤
4.5.1 应力边界条件
常见边界: 工件与工具接触表面:σ、τ 自由表面
单辉祖,“材料力学教程”,国防工 业出版社,1982,P208
图1.28 理想刚-塑性材料
存在速度不连续线的速端图:
两条速度不连续线相交于一点附近的速度不连续量的矢量和为零。
4.6滑移线场的绘制
建立变形区内滑移线场通常是一个相当复杂的问题。
在给定的应力边界条件下,作滑移线场的方法: 1. 积分滑移线的微分方程; 2. 图解法; 3. 数值积分法。
相关规定:
1. 使单元体产生顺时针转效果的剪应力方向为α线,反之为β线;(例题)
2. 分别以α线和β线构成一右手坐标系时的横轴和纵轴,则代数值最大的主应力
σ1的作用线在穿过原点条件下是在第Ⅰ和第Ⅲ象限内;(例题)
3. α线各点的切线与所取的x轴的夹角为φ,逆时针转为正,顺时针转为负。
y
右手坐标系: 姆指指向α线正方向 食指指向β线正方向 中指指向自己
不少的塑性加工过程,由于变形区域 沿某一方向(z轴方向)的尺寸较大, 沿该方向的相对变形量很小,可近似 认为是平面变形问题。 如:薄板轧制 矩形件压缩
莫尔圆 (应力圆)
单辉祖,“材料力学教程”, 国防工业出版社,1982
-p
k
4.1.2 基本假设
各向同性的理想刚-塑性材料 变形抗力为常数 忽略热应力和惯性力等
(①+②)/2 (①-②)/4
① ②
式(4.25) 式(4.26)
式(4.27) 式(4.28)
4.5 滑移线场求解的应力边界条件和步骤
4.5.1 应力边界条件 4.5.2 滑移线求解的一般步骤
4.5.1 应力边界条件
常见边界: 工件与工具接触表面:σ、τ 自由表面
单辉祖,“材料力学教程”,国防工 业出版社,1982,P208
图1.28 理想刚-塑性材料
弹塑性力学讲义9
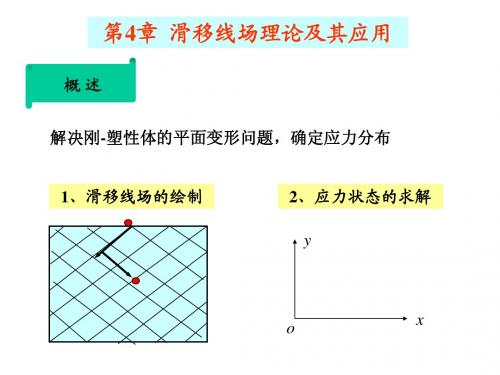
y
k P
k
o x
规 定
1) 使变形体素顺时针转的 y 切应力方向为α线方向; 反之为β线方向。
2) 线各点的切线与所取 的x 轴的正向夹角为 , 逆时针转为正,顺时针 转为负 。
3), 构成右手坐标系,
1 在一、三象限。
o
k P
k
x
(2)平面变形时的应力和莫尔圆
3
汉基应力方程
x yx 0 x y
xy x y y 0
y p k sin 2 p k sin 2
x p k sin 2 p k sin 2
xy k cos2
(1) (2)
n = p =k 1 3 3
+k +
p /4
-
3
2
2 = p /2
1
0
-k
n = p
-
0.5 arccos
k 0 k
p n k sin 2 n 2
由莫尔圆
1 n k
3 n k
面的问题
(4)库仑摩擦的接触面
0
3 =-2 k
-
0.5 arccos
0 p k 4
舍去负的
p n k sin 2 0 k sin
p
2
k 2
由莫尔圆
1 0
3 2k
面的问题
(2)无摩擦的接触面
3 = 0
3
+k
+
p /4
-
1 = 0
p/4 p /4
k P
k
o x
规 定
1) 使变形体素顺时针转的 y 切应力方向为α线方向; 反之为β线方向。
2) 线各点的切线与所取 的x 轴的正向夹角为 , 逆时针转为正,顺时针 转为负 。
3), 构成右手坐标系,
1 在一、三象限。
o
k P
k
x
(2)平面变形时的应力和莫尔圆
3
汉基应力方程
x yx 0 x y
xy x y y 0
y p k sin 2 p k sin 2
x p k sin 2 p k sin 2
xy k cos2
(1) (2)
n = p =k 1 3 3
+k +
p /4
-
3
2
2 = p /2
1
0
-k
n = p
-
0.5 arccos
k 0 k
p n k sin 2 n 2
由莫尔圆
1 n k
3 n k
面的问题
(4)库仑摩擦的接触面
0
3 =-2 k
-
0.5 arccos
0 p k 4
舍去负的
p n k sin 2 0 k sin
p
2
k 2
由莫尔圆
1 0
3 2k
面的问题
(2)无摩擦的接触面
3 = 0
3
+k
+
p /4
-
1 = 0
p/4 p /4
滑移线理论_弹塑性力学讲稿

R ` R R
R
"
S R S
B B`
S `
`
S
`
`
R `
A S
A`
R
`
证明:由于
1 R S 1 R S
(定义)
又可写为
R ` S R ` S
o
★ 屈服条件:(Mises)
(4-37)
化简后为
(4-38)
于是,在塑性区内主应力为
(4-39)
(4-40)
(4-41)
这就是说,在塑性区内任一点 的应力状态,可用静水压力 o 与
o
纯剪应力 两个分量来表示,
如图示。
o o
o o
o
★ 在不计体力的情况下,平衡方程为:
可解出
xm,m1 , ym,m1
(d) 重复计算可得出ABP范围内的塑性应力场。
(3) 第二边值问题(黎曼问题)
已知边界上某一点的两条正交的滑移线,其各点的、 已知,如图示: 求:区域AoBC内的塑性应力场。 步骤: (a) 分网,如图示 (b)求、,由汉基第 y B
(0,n) (o,2) (0,1) (m,0) (1,1) (m-1,n)
沿这两组滑移线分别有一一相
等的值和一一相等的值。而所有
也必相等,应力是均匀分布的,即称为均匀应力场。
例:图示直线边界上 n const, n 0 则
n k sin 2( ) 常数 p n k cos 2( ) 0
n
即
将上式代入(4-51(a)式得:
n k sin 2( ) n k cos 2( )
极限分析与滑移线理论

A
Ti
u
* i
dA
V Fiui*dv
v
0
ij
* ij
dv
如果物体内部存在速度间断时, 其虚功率方程可表示为:
ATiui*dA
v Fiui*dv
v
0 ij
* ij
dv
s ( ntg )[vt ]ds
以上几个定理的证明可参考土力学有关 书本,这里从略。根据虚功率方程可以 证明极限分析中两个重要的定理,即上 下限定理。
下限定理证明
上述两式相减得
s (Ti Ti0 )uids
v
( ij
0 ij
)ji
dv
sL
[C
(s
tg (Ti Ti0)u&ids n
)][vt
]dsL
由Drucker公式得到
( ij
0 ij
)ij
≥0
由于C≥ ntg 同时 [C ( ntg )][vt ] ≥0,
θ+μ θ θ-μ
μμ β族曲线
σ τ
σ1 σΧ σ3
τ
τ σΧ σ
σ3 σ τ
1
图6.2
滑移线与滑移线方程
线和 线的微分方程为
dz tg( )
dx
dz tg( )
dx
α族曲线
θ+μ θ θ-μ
μμ β族曲线
σ τ
σ1
σΧ
σ3
τ
τ σ3 σ
σΧ σ τ
1
图6.2
上、下限定理
塑性加工理论滑移线法

3
m k
O
1
k
m 3
m
图 9-19 无摩擦的接触表面
n=m 摩 擦 切 应 力
=k
为k 的接触面
O
xy k cos 2 0,
1 k m 3
n=m 摩 擦 切 应 力
=k
为k 的接触面
O
4
3 k m 1
k m
O
m
k
k
O
m
m
k
3
k m
1
(a)
1 m k 3 (b)
图 9-20 摩擦切应力达最大值 k 的接触表面
β β
β
O
α
O′
α
α
a) 中心扇形场 b) 无中心扇形场 图 9-23 简单滑移线场
(3)滑移线场由两族互相正交的光滑曲 线构成
属于这一类的滑移线场有以下几种
(a)当圆形界面为自由表面或作用有均 匀载荷时,其滑移线场为两族正交的对数 螺线所构成(如图9-24a所示);
β α
(a)对数螺旋线场
(b)在粗糙平行刚性模板间压缩 时, 相应于接触面上摩擦切应力达 到最大值的那一段滑移线场为正 交的圆摆线(如图9-24b所示)
1 arccos xy 1 arccos f
2
k2
k
y
=xy
0
y
m
xy k
m k
x
O xy
xy
x
k
k m
m
xy
y
(a)
y
r
y
3
1 O
xy
2 x
x
m
(b)
图 9-21 当 0 f k 时的接触表面
c4-5

晶粒越细,强度硬度逾高 原因:晶粒越小,单位面积上晶粒的数量越多,晶界的总面积 越大,因晶界变形的抗力较大,所以整个金属的强度水平较高。 晶粒越细,塑性韧性逾好 原因: 晶粒数愈多,金属的总变形量可分布在更多的晶粒内,晶粒间 的变形不均匀性减小,使塑性较好; 晶界的影响较大,晶粒内部和晶界附近的变形量差减小,晶粒 变形也较均匀,所以减小了应力集中,推迟了裂纹的形成和发 展,使金属在断裂之前可发生较大的塑性变形。 由于细晶粒金属的强度较高,塑性较好,所以断裂时需要消耗 较大的功,所以韧性较好。 细晶强化
8
二、 实际晶体的塑性变形
1、晶界在变形 中的作用 1) 多晶体晶界上原子排列不很规则,为相 邻晶粒原子排列的过渡排列; 2)晶界是缺陷和杂质集中的地方,因而是 滑移的主要障碍,使变形抗力增大。 3)晶界发生塑性变形,使晶粒间的应力集 中松弛; 4)晶界对相邻晶粒的塑性变形起协调作用。
9
2、晶粒对变形的影响
12
二、金属组织和结构的变化
纤维组织--在外力的作用下,晶粒被压扁 或拉长,变形很大时,晶粒变成细条状,金属中的 夹杂物也被拉长而形成的组织。性能产生各向异性。 亚结构 织构现象--金属塑性变形到很大程度 (70%以上)时,由于晶粒发生转动,使各晶粒位 向趋近于一致,形成特殊的择优取向,这种有序化 的结构叫做变形织构。包括: 丝织构 平行于拉拨方向 板织构 平行于轧制方向16源自二、再结晶的温度及其影响因素:
金属的变形程度 金属的纯度 加热速度和时间
三、 影响再结晶晶粒大小的因素: 预变形度: 预变形度愈大,金属的晶格缺陷愈多,组织
愈不稳定,开始再结晶温度也就越低;
金属的溶点:金属的溶点越高,它的最低再结晶温度越高; 金属中的微量杂质和合金元素特别是高溶点元素, 因阻碍原子扩散和晶界迁移,可显著提高再结晶温度; 加热速度 保温时间
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3
sin (θ + µ ) ∂ −sin (θ − µ ) ∂
∂=
∂Sα
∂S β
∂x
sin 2µ
− cos (θ + µ ) ∂ + cos (θ − µ ) ∂
∂=
∂Sα
∂Sβ
∂y
sin 2µ
代入一阶拟线性偏 微分方程:
− sin 2µ
∂p ∂Sα
+ 2R
∂θ ∂Sα
+γ
⎡ ⎢sin ⎣
(α
+2µ
y
β
2
α
1 θ
β
1
α
2 x
y
β
2
α 1β
θ
1 α
2 x
(a) Tresca材料
(b) Coulomb 材料
Tresca材料两族滑移线是正交的,与主应力迹线的夹角为π /4。而Coulomb材料的两族滑移线相互夹角为2μ= π/2-φ,与主 应力迹线的夹解为μ,在本章,我们约定:以第一主应力σ1为基 线,顺时针方向与基线成锐角的称为α线,逆时针与基线成锐解 的称为β线。 α线和β线的微分方程式为:
σx −σy τ xy
2
( ( ) ) ( ) 于是有: sin 2α1 =
± σx
σx −σy 2
−σ y
2
2
+τ
2 xy
;cos 2α1
=
±τ xy
σ x −σ y
2
4
+τ
2 xy
( ( ) ) τα
=
σ
x
−σ 2
y
sin
2α
+τ
xy
cos
2α
⇒
⎧⎪τ α max ⎨ ⎪⎩τ α min
= =
−
τ
C O
(σx,τxy)
α 2μ
2θ β
ccotφ p=(σx+σy)/2
β (σy,τxy)
σ
μα σ3
σ1
第一主应力与x轴的夹角为θ: tan 2θ = − 2τ xy σy −σx
剪切破坏面(α面和β面)与第一主应力方向的夹角为:
2µ = π −ϕ ⇒ µ = π − ϕ
2
42
应力分量 σ x,σ y ,τxy 可表示为:
4.1 基本假设和应力基本方程
在本章分析中,假设土体是理想刚塑性体,屈服 条件为Mohr-Coulomb屈服条件,或Tresca屈服条件。 在荷载作用下,土体中的塑性区域在某些方向可以自 由流动,土体塑性变形较大,弹性变形可以忽略的情 况下,上述刚塑性体假设可以推导出较可靠的近似 解,否则可能引起较大的误差。在岩土工程的稳定性 问题──地基承载力问题、挡土墙压力问题和土坡稳定 性问题中,滑移线场理论得到广泛的应用。
y
σx
γ
σ
x
+
∂σ x ∂x
d
x
σ
y
+
∂σ y ∂y
d
y
τ xy
+
∂τ xy ∂y
d
y
τ yx
+
∂τ yx ∂x
d
x
上述三个式子是滑移线场理论的应力基本方程。方程中只包 含三个未知量,即应力分量 σ x,σ y ,τxy ,如果已知应力边界条件, 就可以求解三个未知量。但是直接求解这些方程在数学上仍有困难 需要应用滑移线法求解。
4.3 应力方程的特征线解法
∂σ x + ∂τ xy = γ cosα ∂x ∂y
∂τ yx + ∂σ y = −γ sinα ∂x ∂y
将
⎧σ ⎪
x
=
p
+
R cos 2θ
⎨σ y = p − R cos 2θ
R = p sin ϕ + c cos ϕ
⎪⎩τ xy = R sin 2θ
代入上式得:
∂σ x + ∂τ xy = ∂p + ∂R cos 2θ − 2Rsin 2θ ∂θ + ∂R sin 2θ +2 Rcos 2θ ∂θ
γ cos
α
∂τ yx + ∂σ y = ∂R sin 2θ + 2Rcos 2θ ∂θ + ∂p − ∂R cos 2θ +2 Rsin 2θ ∂θ
∂x ∂y ∂x
∂x ∂y ∂y
∂y
= ∂p sinϕ sin 2θ + 2 Rcos 2θ ∂θ + ∂p − ∂psin ϕcos 2θ +2 Rsin 2 θ ∂θ
⎧σ ⎪
x
=
p
+
R
cos 2θ
⎨σ y = p − R cos 2θ
⎪⎩τ xy = R sin 2θ
( ) p ─平均应力, p = σ x +σ y 2 = (σ1 + σ 3 ) 2
R ─应力圆半径, R = (σ1 − σ3 ) 2 = p sin ϕ + c cos ϕ
2
在平面应变问题中,平面上任一点都存在着两个相互垂直的 主应力。把表示各点主应力方向的线段连续地联接起来,就得到 二族相互正交的曲线,称为主应力迹线,如下图的1-1和2-2。当 材料处于塑性状态时,每一点都存在两个剪切破坏面,把各点的 剪切破坏面(或称滑移面)连续地联接起来,又可以得到二族曲 线,称为滑移线,如α-α和β-β。滑移线上一点的切线方向就 是相应点的滑移面方向。
) ∂x
∂Sα
+ cos
(α
+2µ
) ∂y
∂Sα
⎤ ⎥=0 ⎦
sin 2µ ∂p ∂Sβ
+2 R ∂θ ∂Sβ
应力分量 σ x,σ y ,τxy 可表示为:
⎧σ ⎪xຫໍສະໝຸດ =p+
R
cos 2θ
⎨σ y = p − R cos 2θ
⎪⎩τ xy = R sin 2θ
( ) p ─平均应力, p = σ x +σ y 2 = (σ 1 + σ 3 ) 2
R ─应力圆半径, R = (σ1 − σ3 ) 2
(2) Coulomb材料
σα
=
σx
+σ y 2
+σx
−σ y 2
cos 2α
−τ xy sin 2α
τα = σ x sinα cos α −σ y sin α cos α +τ xycos 2α −τ yxsin 2α
τα
=
σx
−σ y 2
sin 2α
+τ xy
cos 2α
1
( ) 令: dσα ( ) dα
α =α0
=−
σx
−σ y
sin 2α 0 − 2τ xy cos 2α 0 = 0 ⇒ tan 2α 0 =
−τ xy σ x −σ y
2
( ) ( ( ) ) 于是有: sin 2α0 =
±τ xy
2
σx −σ y
;cos 2α0 =
4
+τ
2 xy
∓ σx −σy 2
σx −σ y
2
4
+τ
2 xy
σ x cos2 α +σ y sin 2 α −τ xy sinα cos α −τ yx sin α cos α
∂Sα
∂x
∂y
∂ = cos (θ + µ ) ∂ + sin (θ + µ ) ∂
∂Sβ
∂x
∂y
2
α 1β
θ
1 dSa α dx dy
2 x
于是:
∂ sin (θ − µ )
∂Sα
∂=
∂ sin (θ + µ )
∂Sβ
sin (θ + µ ) ∂ −sin (θ − µ ) ∂
=
∂Sα
∂Sβ
∂x cos (θ − µ ) sin (θ − µ )
α
∂σ x + ∂τ xy = γ cosα ∂x ∂y
τ xy
∂τ yx + ∂σ y = −γ sinα ∂x ∂y
σy
γ 为土体的容重。
Mohr-Coulomb屈服条件的表达式为: x
⎛σx ⎜ ⎝
−σ 2
y
2
⎞ ⎟ ⎠
+
τ
2 xy
=
⎛σx ⎜ ⎝
+σ 2
y
+
C
2
⎞ cot ϕ ⎟
⎠
sin2
ϕ
dx
β线: d y = tan (θ + µ )
dx
µ =π −ϕ 42
也就是说:一阶拟线性偏微分方程的特征线方程与滑移线方程
是一致的。拟线性偏微分方程数学上的特征线,其物理意义就
是滑移线。双曲线型方程组的解与特征线密切相差。取与滑移
线α、β相重合的曲线坐标系(Sα,Sβ),根据方向的公式:
y
β
∂ = cos (θ − µ ) ∂ + sin (θ − µ ) ∂
∂τ yx + ∂σ y = 0 ∂x ∂y
( ) σ x −σ y
2
+
4τ
2 xy
= 4C2
上述三式就是传统塑性力学(或称金属塑性力学)滑移线场理 论中的应力基本方程。
在以后的分析中,为了区分屈服条件不同的材料,将满足 Mohr-Coulomb屈服条件的材料简称为Coulomb材料。将满足 Tresca屈服条件的材料简称为Tresca材料。不排水条件下饱和土体 的内摩擦角 ϕ = 0 ,属于Tresca材料。而 ϕ ≠ 0 的土体属于 coulomb材料,或称为 c −ϕ 材料。
