选 择 排 序 算 法 原 理
完整版)☆排列组合解题技巧归纳总结

完整版)☆排列组合解题技巧归纳总结分类计数原理(加法原理)指完成一件事,有n类办法,在第1类办法中有m1种不同的方法,在第2类办法中有m2种不同的方法。
在第n类办法中有mn种不同的方法,那么完成这件事共有N=m1+m2+。
+mn种不同的方法。
分步计数原理(乘法原理)指完成一件事,需要分成n个步骤,做第1步有m1种不同的方法,做第2步有m2种不同的方法。
做第n步有mn种不同的方法,那么完成这件事共有N=m1×m2×。
×mn种不同的方法。
分类计数原理和分步计数原理的区别在于,分类计数原理方法相互独立,任何一种方法都可以独立地完成这件事;分步计数原理各步相互依存,每步中的方法完成事件的一个阶段,不能完成整个事件。
解决排列组合综合性问题的一般过程如下:1.认真审题弄清要做什么事。
2.确定采取分步还是分类,或是分步与分类同时进行,确定分多少步及多少类。
3.确定每一步或每一类是排列问题(有序)还是组合(无序)问题,元素总数是多少及取出多少个元素。
4.解决排列组合综合性问题,往往类与步交叉,因此必须掌握一些常用的解题策略。
一种常用的解题策略是特殊元素和特殊位置优先策略。
例如,由0,1,2,3,4,5可以组成多少个没有重复数字五位奇数,可以先排末位共有C3^1种方法,然后排首位共有C4^3种方法,最后排其它位置共有A4^1 * 3!种方法,根据分步计数原理得到共有C4^1 * 3^1 * A4^1 * 3.= 288种不同的方法。
另一种常用的解题策略是相邻元素捆绑策略。
例如,7人站成一排,其中甲乙相邻且丙丁相邻,共有多少种不同的排法,可以先将甲乙两元素捆绑成整体并看成一个复合元素,同时丙丁也看成一个复合元素,再与其它元素进行排列,同时对相邻元素内部进行自排。
由分步计数原理可得共有A5^2 * A2^2 = 480种不同的方法。
还有一种常用的解题策略是不相邻问题插空策略。
例如,一个晚会的节目有4个舞蹈、2个相声、3个独唱,舞蹈节目不能连续出场,则节目的出场顺序有多少种,可以先将三种不同的节目分别排列,然后在舞蹈节目之间插入一个相声节目,再在相声节目之间插入一个独唱节目,根据分步计数原理可得共有A4^4 * A2^1 * A3^1 = 种不同的方法。
第十章排序(可编辑修改word版)

作业布置
10-4(2),(4),(5),10-6,
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
重点难点
希尔的思想,实现,算法分析
要求掌握知识点和
分析方法
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2。插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段,板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
难点:堆的调整辅助手段:多媒体
作业布置
10-7,10-8
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.5归并排序10.6基数排序
讲授主要内容
归并排序 ,基数排序
重点难点
归并排序 ,基数排序的基本思想与算法实现
本章思考题和习题
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.1概念10.2插入排序
讲授主要内容
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2.
插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段, 板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
教学思路:
算法实例选择排序法ppt课件

总共比较数据1次,交换数据1次。
显然,通过上述3遍处理,数组d中最小、第2 小、第3小的数据已经分别存储在数组元素d(1)、 d(2)、d(3)中,即数组元素d(1)到d(3)变为有序, 而剩下的d(4)中的数据自然是数组中的最大数据 。因此,通过3遍这样的处理,整个数组内的数据 将是有序的。
第3遍
第4遍
60 58 55 48 43 46
第5遍
60 58 55 48 46 43
A.60、58、48、46、43、55 C.60、58、55、46、43、48
B.60、43、48、46、58、55 D.60、58、55、48、46、43
5. 已知算法1与算法2都是排序算法,可能是冒泡排序或者选择排
1
7
2
9
3
13
4
18
5
55
6
43
7
43
第五趟:从3个元素中选出最小者,将其换入位置5,过程 为:令min_elem表示最小元素(初值为位置5的元素),k 为最小元素的位置序号(初值为5),逐一比较,找出最 小元素及其位置
1
7
2
9
3
13
4
18
5
55
6
43
7
43
位置6的元素最小 交换
1
7
2
9
3
13
4
4个元素共需进行3遍加工处理,总的比较次 数为3+2+1=6次,而总计交换次数每一遍一次 ,共计只有3次。
对于n个元素的数组,用选择算法进行排序时 ,比较次数与冒泡算法相同,但交换的次数比冒 泡排序要少,因此它具有较高的效率。
排列组合的基本原理

排列组合的基本原理尊敬的读者:在数学中,排列组合是一种重要的概念,它用于计算可能性和确定事件发生的方式。
本文将介绍排列组合的基本原理,包括排列和组合的定义、计算方法以及应用。
希望通过本文的阐述,您能够更好地理解和运用排列组合的基本原理。
1. 排列的定义和计算方法在数学中,排列指的是从一个集合中选取若干个元素,按照一定顺序排列的方式。
排列通常用P(n,m)表示,其中n为集合的元素个数,m 为选取的元素个数。
排列的计算方法可分为两种情况:1.1 当选取的元素个数m小于或等于集合的元素个数n时,排列的计算公式为:P(n,m) = n! / (n-m)!1.2 当选取的元素个数m大于集合的元素个数n时,排列的计算公式为0,即不存在这种情况。
2. 组合的定义和计算方法组合指的是从一个集合中选取若干个元素,不考虑顺序的方式。
组合通常用C(n,m)表示,其计算方法可分为两种情况:2.1 当选取的元素个数m小于或等于集合的元素个数n时,组合的计算公式为:C(n,m) = n! / (m! * (n-m)!)2.2 当选取的元素个数m大于集合的元素个数n时,组合的计算公式为0,即不存在这种情况。
3. 排列组合的应用排列组合在实际问题中的应用非常广泛,下面举几个例子来说明:3.1 生日排列问题:假设有5个人,每个人的生日在一年中任意选择。
我们可以用排列来计算不考虑年份的情况下,5个人生日的所有可能排列数量。
根据排列的计算公式,可知P(365,5)即为所求。
3.2 钥匙排列问题:某人有5把钥匙,但只有其中一把能打开家门。
每次进门都尝试一把钥匙,直到能够打开为止。
这个过程中,我们可以用排列来计算需要尝试的所有可能方式的数量。
根据排列的计算公式,可知P(5,5)即为所求。
3.3 选课组合问题:某学校的学生需要选择4门选修课,而学校提供了8门选修课供选择。
我们可以用组合来计算学生选择的所有可能组合的数量。
根据组合的计算公式,可知C(8,4)即为所求。
有序和无序排列组合公式

有序和无序排列组合公式好的,以下是为您生成的关于“有序和无序排列组合公式”的文章:咱先来说说啥是有序和无序排列组合公式哈。
打个比方,你去超市买水果,苹果、香蕉、橙子摆在那,你要是规定了先拿苹果再拿香蕉最后拿橙子,这就是有序;要是不管顺序,随便拿,这就是无序。
咱先瞅瞅有序排列,也就是排列公式。
比如说从 5 个不同的东西里选 3 个,按照一定顺序排好,这就可以用排列公式 A(5, 3) 来算。
就像学校组织活动,选 3 个同学分别当主持人、表演节目和后勤服务,这就得考虑顺序,谁先谁后作用可不一样。
再讲讲无序组合,也就是组合公式。
还是那 5 个东西,这次不考虑顺序,只要选出 3 个就行,那就用组合公式 C(5, 3) 。
比如说选 3 个人参加知识竞赛,不管谁在前谁在后,只要选出来就行。
我记得之前给学生讲这个的时候,有个小同学特别可爱。
他瞪着大眼睛问我:“老师,这和我搭积木有啥关系?”我笑着跟他说:“你搭积木的时候,要是规定了先放红色的再放蓝色的,这就是有序;要是随便拿随便放,不讲究顺序,那就是无序呀。
”这小家伙一听,好像恍然大悟了。
在生活中,有序和无序排列组合公式的应用可多了去了。
比如你安排假期出去玩,有 5 个景点,你计划 3 天逛完,每天去一个,这就得用有序排列来算算有多少种安排方法。
要是你只是想挑 3 个景点去,不管先后顺序,那就是无序组合的问题啦。
还有啊,咱过年包饺子,准备了 3 种馅,韭菜鸡蛋、猪肉大葱和虾仁三鲜。
要是规定了第一顿吃韭菜鸡蛋的,第二顿吃猪肉大葱的,第三顿吃虾仁三鲜的,这就是有序;要是不管顺序,反正这三顿就吃这三种馅,这就是无序组合。
再比如说抽奖,从 10 个号码里抽 3 个中奖号码,这就不管顺序,是无序组合。
但要是颁奖,先颁三等奖,再颁二等奖,最后颁一等奖,这就得考虑顺序,是有序排列。
所以说,这有序和无序排列组合公式啊,就藏在咱们生活的角角落落里,等着咱们去发现,去用它们解决问题。
选择排序法的基本思路

选择排序法的基本思路
选择排序法是一种简单直观的排序算法,基本思路如下:
1. 首先,在序列中找到最小(或最大)的元素,将其放在序列的起始位置。
2. 然后,从剩余的未排序序列中继续寻找最小(或最大)的元素,将其放在已排序序列的末尾。
3. 重复上述步骤,直到所有元素都排好序。
具体步骤如下:
1. 设定一个初始索引为0的位置,表示已排序序列的末尾。
2. 从剩余的未排序序列中,遍历查找最小元素的索引。
将该最小元素与已排序序列的末尾元素交换位置,并更新已排序序列的末尾索引。
3. 重复上述步骤,直到遍历完整个序列。
选择排序的特点是每次只需要找到剩余序列中的最小元素,并进行交换,因此时间复杂度为O(n^2)。
虽然效率较低,但对于小规模的序列来说,它的实现简单且不占用额外的内存空间。
排序算法实验报告
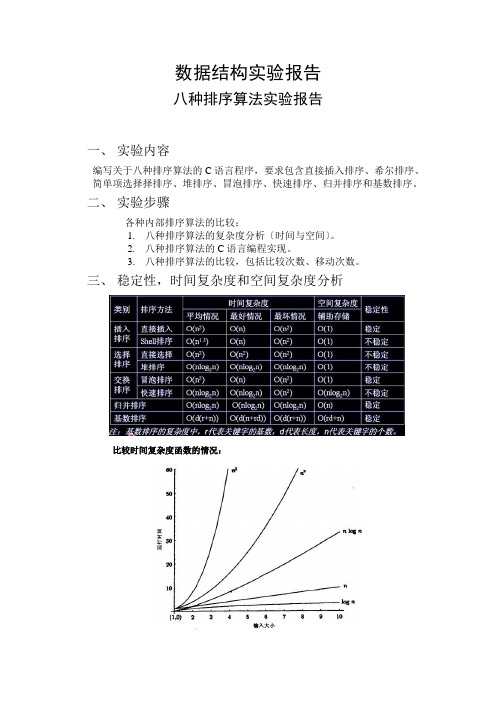
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序,要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。
二、实验步骤各种内部排序算法的比较:1.八种排序算法的复杂度分析〔时间与空间〕。
2.八种排序算法的C语言编程实现。
3.八种排序算法的比较,包括比较次数、移动次数。
三、稳定性,时间复杂度和空间复杂度分析比较时间复杂度函数的情况:时间复杂度函数O(n)的增长情况所以对n较大的排序记录。
一般的选择都是时间复杂度为O(nlog2n)的排序方法。
时间复杂度来说:(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序;(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序;(3)O(n1+§))排序,§是介于0和1之间的常数。
希尔排序(4)线性阶(O(n))排序基数排序,此外还有桶、箱排序。
说明:当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O〔n〕;而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O〔n2〕;原表是否有序,对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
稳定性:排序算法的稳定性:假设待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的;假设经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。
另外,如果排序算法稳定,可以防止多余的比较;稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
选择法排序

a[0]
9 6 17 2 12
9
9
9 6 17
9 6
k
a[1]
2
k
a[2]
j k
6 17 2 12
k 6
j k
17 2 12
第一轮,i=0; k=i; for(j=i+1;j<5;j++) if(a[k]>a[j]) k=j; if(k!=j) {t=a[k];a[k]=a[i];a[i]=t;}
17 9 12
ቤተ መጻሕፍቲ ባይዱ
17 9
17 9 12
a[3]
{t=a[k];a[k]=a[i];a[i]=t;} 第四轮 I=3;k=I;
j
12 12
for(j=i+1;j<5;j++) if(a[k]>a[j])k=j;
a[4]
j
if(k!=i)
{t=a[k];a[k]=a[i];a[i]=t;}
i从0变到3 for(i=0;i<4;i++) 第i轮 k=I;认为第I个数最小, 从下一个数到最后一个数与 a[k]比较, If(a[k]>a[j]) k=j;k就赋值小数 的下标 If(k!=i) {t=a[k];a[k]=a[i];a[i]=t;}既a[k] 与第I个位置上的数交换位 置。
选择法排序(以5个数为例) 基本思路:
第一轮i=0:认为第一个数a[0]最小,把它的下标赋值给k,k=i;(k=0;) 从下一个数(a[1])到最后一个数a[4]与a[k]比较,如果a[k]大于哪个 数,k就赋值哪个数的下标,一轮结束后,k放最小数的下标,则a[k]与 a[0]交换位置。 第二轮i=1;k=i;认为a[1]最小,下标赋给k,将a[k]从下一个数(a[2]) 开始到最后一个数(a[4])比较,找到最小数,把它的下标赋给k,然后 a[k]与a[1]交换位置。 ……5个数比4轮,第i轮认为第i个位置上的数最小(k=i),将a[k]从 下一个数a[i+1]开始到最后一个数一一比较。找出最小数,把下标赋给 k,将a[k]与第i个位置上的数a[i]交换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
各种排序算法的原理、Java实现与比较分析(二)三、交换排序3.1 冒泡排序(1)基本思想在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。
即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
(2)特点冒泡排序是一种稳定的排序方法冒泡排序是最慢的排序算法。
在实际运用中它是效率最低的算法起泡排序平均时间复杂度为O(n2)(3)Java实现package com.sort;public class bubble {public static void main(String[] args) {int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};System.out.println("排序之前:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");--冒泡排序for (int i = 0; i a.length; i++) {for(int j = 0; ja.length-i-1; j++){--这里-i主要是每遍历一次都把最大的i个数沉到最底下去了,没有必要再替换了if(a[j]a[j+1]){int temp = a[j];a[j] = a[j+1];a[j+1] = temp;System.out.println();System.out.println("排序之后:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");3.2 快速排序(1)基本思想选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
(2)特点快速排序是不稳定的排序。
快速排序的时间复杂度为O(nlogn)。
当n较大时使用快排比较好,当序列基本有序时用快排反而不好。
快速排序比大部分排序算法都要快。
尽管我们可以在某些特殊的情况下写出比快速排序快的算法,但是就通常情况而言,没有比它更快的了。
快速排序是递归的,对于内存非常有限的机器来说,它不是一个好的选择。
(3)Java实现package com.sort;public class quick {public static void main(String[] args) {int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};System.out.println("排序之前:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");--快速排序quick(a);System.out.println();System.out.println("排序之后:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");private static void quick(int[] a) {if(a.length0){quickSort(a,0,a.length-1);private static void quickSort(int[] a, int low, int high) { if(lowhigh){ --如果不加这个判断递归会无法退出导致堆栈溢出异常int middle = getMiddle(a,low,high);quickSort(a, 0, middle-1);quickSort(a, middle+1, high);private static int getMiddle(int[] a, int low, int high) { int temp = a[low];--基准元素while(lowhigh){--找到比基准元素小的元素位置while(lowhigh a[high]=temp){a[low] = a[high];while(lowhigh a[low]=temp){a[high] = a[low];a[low] = temp;return low;四、归并排序(1)基本思想归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。
然后再把有序子序列合并为整体有序序列。
(2)特点归并排序是稳定的排序方法。
归并排序的时间复杂度为O(nlogn)。
速度仅次于快速排序,一般用于对总体无序,但是各子项相对有序的数列。
合并排序比堆排序稍微快一点,但是需要比堆排序多一倍的内存空间,因为它需要一个额外的数组。
(3)Java实现package com.sort;public class merge {public static void main(String[] args) {int[] a={49,38,65,97,76,13,27,49,78,34,12,64,1,8};System.out.println("排序之前:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");--归并排序mergeSort(a,0,a.length-1);System.out.println();System.out.println("排序之后:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");private static void mergeSort(int[] a, int left, int right) { if(leftright){int middle = (left+right)-2;--对左边进行递归mergeSort(a, left, middle);--对右边进行递归mergeSort(a, middle+1, right);merge(a,left,middle,right);private static void merge(int[] a, int left, int middle, int right) {int[] tmpArr = new int[a.length];int mid = middle+1; --右边的起始位置int tmp = left;int third = left;while(left=middle mid=right){--从两个数组中选取较小的数放入中间数组if(a[left]=a[mid]){tmpArr[third++] = a[left++];tmpArr[third++] = a[mid++];--将剩余的部分放入中间数组while(left=middle){tmpArr[third++] = a[left++];while(mid=right){tmpArr[third++] = a[mid++];--将中间数组复制回原数组while(tmp=right){a[tmp] = tmpArr[tmp++];五、基数排序(1)基本思想将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。
然后,从最低位开始,依次进行一次排序。
这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
(2)特点基数排序是稳定的排序算法。
基数排序的时间复杂度为O(d(n+r)),d为位数,r为基数。
只能用于整数的排序,如果我们要把同样的办法运用到浮点数上,我们必须了解浮点数的存储格式,并通过特殊的方式将浮点数映射到整数上,然后再映射回去,这是非常麻烦的事情(3)Java实现package com.sort;import java.util.ArrayList;import java.util.List;public class radix {public static void main(String[] args) {int[] a={49,38,65,97,176,213,227,49,78,34,12,164,11,18,1};System.out.println("排序之前:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");--基数排序sort(a);System.out.println();System.out.println("排序之后:");for (int i = 0; i a.length; i++) {System.out.print(a[i]+" ");private static void sort(int[] array) {--找到最大数,确定要排序几趟int max = 0;for (int i = 0; i array.length; i++) {if(maxarray[i]){max = array[i];--判断位数int times = 0;while(max0){max = max-10;times++;--建立十个队列ListArrayList queue = new ArrayListArrayList(); for (int i = 0; i 10; i++) {ArrayList queue1 = new ArrayList();queue.add(queue1);--进行times次分配和收集for (int i = 0; i times; i++) {for (int j = 0; j array.length; j++) {int x = array[j]%(int)Math.pow(10, i+1)-(int)Math.pow(10, i);ArrayList queue2 = queue.get(x);queue2.add(array[j]);queue.set(x,queue2);int count = 0;for (int j = 0; j 10; j++) {while(queue.get(j).size()0){ArrayListInteger queue3 = queue.get(j);array[count] = queue3.get(0);queue3.remove(0);count++;for (; 2 * i + 1 len; i = child)place data[i] in its proper position;public static void mergeSortRecur(int[] arr, int left, int right)minValue=min(a(1,i:end)); %找到剩余序列的最大值tree[(i-1)-2] = ((Comparable)tree[i-1]).compareTo(tree[i]) 0 ? tree[i-1]:tree[i];System.out.print( a[i] + “t” );public static void selectSort(int[] a)public static void sort(int a[],int min,int max) { void insertSort(int *arr,int n){void Sort::TreeMidRetrival(T *array, T* temp, int pos, T* lChild, T* rChild)?。
