条件平差习题
条件平差习题

条件平差习题一、重点内容及难点1. 水准网条件平差● 条件方程列法 ● 权的确定方法2. 边角网条件平差● 条件方程个数确定方法● 条件方程类型:图形条件 极条件 边条件 方位角条件 基线条件3. 条件方程线性化11112ˆ()()()()()()()ˆˆˆˆnn i i ni f f f f f Lf L V V V f L V L L L L =∂∂∂∂=++++=+∂∂∂∂∑● 极条件方程及线性化● 符合三角网条件方程4. 理解条件平差的函数模型和随机模型● 明确必要起算数据、必要观测数据、多余起算数据和多余观测数据的概念; ● 条件平差的出发点:观测值的平差值之间应该存在的函数关系式; ● 随机模型的含义和作用二、公式汇编及条件平差计算步骤1. 根据实际问题,确定出总观测值的个数n 、必要观测值的个数t及多余观测个数r = n – t ,2. 列出条件平差值方程,对其线性化进一步列出改正数条件方程平差值条件方程 ˆ()0F L=改正数条件方程 0=+W AV3. 据具体情况确定观测值的权阵;)(21n p p p diag P =4. 组成法方程式,求出联系数;W NK =1K N W -=-5. 算出观测值改正数和观测值的平差值Lˆ; 1T V P A K -= V L L+=ˆ 6. 检查平差计算的正确性,将平差值L ˆ代入平差值条件方程式,检验平差值是否满足应有的条件关系式;0)ˆ(=LF 7. 计算单位权方差和单位权中误差;rPV V T =20ˆσ8. 列出平差值函数关系式,计算平差值函数及其精度。
对平差值函数全微分,应用广义传播律计算平差值函数的协因数,进一步计算出平差值函数的方差、协方差。
12ˆˆˆˆ(,,,)nf L L L ϕ= ˆˆˆˆTLL Q fQ f ϕϕ= 2ˆˆˆˆ0ˆD Q ϕϕϕϕσ=三、思考题:1.发现误差的必要条件是什么?2. 几何模型的必要元素与什么有关?为什么?3. 测量平差的函数模型和随机模型分别表示哪些量之间的什么关系?4. 什么叫必要起算数据?各类控制网的必要起算数据是如何确定的?5. 条件平差中求解的未知量是什么?能否由条件方程直接求得改正数?6.设某一平差问题的观测个数为n ,必要观测数为t ,若按条件平差法进行平差,其条件方程,法方程及改正数方程的个数各为多少?7. 通常用什么公式将非线性函数模型转化为线性函数模型? 8. 在条件平差中,能否根据已列出的法方程计算单位权方差? 9. 条件平差中的精度评定主要是解决哪些方面的问题?四、计算题5.1 有水准网如下图P1点位已知点Hp1=50.002米,P2、P3、P4,为待定点,观测六条线路的线路长度和高差为:S1= 1.0km h1=1.576m,S2=1.5 km h2=2.215m,S3=1.5 km h3=-3.800m,S4=1.0 km h4=0.871m,S5=2.0 km h5=-2.438m,S6= 2.0 km h6=-1.350m。
测量平差期末试题汇总

一、填空。
(每空1分,共22分)1.与的比值称为相对中误差。
2.误差椭圆的三个参数是________、________、_________。
3.闭合导线按条件平差时条件方程式的个数等于___个,分别是____个____________________条件和____对_______________________条件。
4 .设某平差问题中,观测值个数为n个,必要观测数为t个,若按条件平差,条件方程的个数等于______个,法方程的个数等于_______个。
若按间接平差,误差方程式的个数等于______个,未知数的个数等于______个,法方程的个数等于____个。
5.根据误差传播定律,若某一站观测高差的中误差为2mm,在A、B两点间共观测了4站,则A、B两点间高差的中误差为mm。
6.导线网按条件平差,所列条件方程中的未知数,既有___________的改正数,也有___________的改正数。
7.在水准测量中若已知每公里观测高差的中误差均相等,且又知各水准路线的长度为Si(I=1,2,……n),则观测高差的权可用公式_________求出。
8.偶然误差的特性为:绝对值较小的误差出现的可能性;绝对值相等的正负误差出现的可能性;偶然误差的理论平均值。
1.__________、_________和_________合称为观测条件。
2.水准路线的定权方法有两种:根据_________定权和根据_________定权。
3.由三角形闭合差来计算测角中误差的公式为,称其为菲列罗公式。
4.由不等精度的双观测值之差计算单位权中误差的公式为σ0= ,由等精度的双观测值之差计算观测值中误差的公式为。
5 .单导线按条件平差时条件方程的个数永远等于个,附合导线中个坐标方位角条件和一对条件,闭合导线中一个条件和对闭合条件。
6.常用的衡量精度的指标有、、、1.独立边角同测网条件方程式的种类,除了具有测角网和测边网的条件式外,还具有反映边角关系的二种条件,它们是和。
平差试卷——精选推荐

平差试卷试卷⼀⼀、简答题(每题5分,共15分)1、何谓系统误差?测量中是如何处理的?2、误差椭圆与误差曲线是否⼀致?如何根据误差椭圆来求任意⽅向位差?3、⾃由⽹平差⽅法有哪些?秩亏⾃由⽹平差中,秩亏数如何确定的?秩亏⾃由⽹平差准则是什么?⼆、填空题(每空3分,共15分)1、常⽤衡量向量的绝对精度指标是();常⽤()作为衡量向量的相对精度指标。
2、设有同精度独⽴观测值12,L L 两个⾓值,且构成函数12sin sin ABL y S L =。
式中AB S 为已知边长,认为⽆误差。
测⾓中误差 1.2σ''=。
则该函数的中误差为()。
3、已知某待定点观测的测⾓中误差2βσ''=,测边中误差2s mm σ=。
已知点⾄待定点距离为185⽶。
则该点的点位中误差为()。
4、观测向量[]12TL L L =的权阵为4223LL P ??=,则1L P =( )。
三、下图所⽰测量控制⽹,试按要求完成如下⼯作:1、下图条件平差时,条件式个数?条件式类型?每种类型各建⽴其中⼀个,⾮线性需要线性化。
(10分)2、下图间接平差时,参数个数?误差⽅程个数?类型?每种类型各建⽴⼀个,⾮线性需要线性化。
(10分)四、已知某⼀个待定点的控制⽹中,设该点坐标为参数,采⽤间接平差得到法⽅程为:6.01 3.02 6.00xy --= ??3.02 1.58 3.40xy -++= 已计算得到单位权中误差估值0? 1.2σ''=。
求:(1)该点的误差椭圆参数;(2)该点的点位误差。
(共15分)五、下图所⽰的⽔准⽹中,已知⾼程为135.000A H m =。
⾼差观测数据列于下表中。
试任选⼀种平差法:(1)求待定点⾼程的平差值;(2)求第⼆段⾼差平差值的协因数;(3)求待定点⾼程平差值的中误差。
(共20分)名称 1 2 3 ⾼差观测值(m ) 6.885 6.890 -6.892 ⽔准路线长(km ) 428六、证明:测量平差中根据最⼩⼆乘准则可以求得参数以及观测值的平差值的唯⼀解。
11第十一讲 条件平差习题课
6.指出图示导线网按条件平差时条件方程的总数及 各类条件式的个数。
0
v3
(2)法方程及其解 Naa
K (3)求改正数V
V=
(4)求各观测值的平差值 Lˆ1 Lˆ2 Lˆ3
2.如图所示,设A点的 高程为100.000m,各测段的 观测高差及路线长度分别为:
h1 1.335m h2 1.055m h3 2.396m
S1 2km S2 2km S3 3km
试用条件平差法求 P1 、P2 点的高程平差值(观 测值改正数及条件式闭合差以mm为单位)。
(1)列条件方程
v1
v2
0
v3
(2)观测高差的权(以2km观测值的权为单位权)
P1
P2
P3
(3)组成并解算法方程
Naa K
(4)求各观测值的平差值及待定点的高程平差值
Lˆ2
Lˆ3
xˆ2
3.指出图示自由 测角网按条件平差时 条件方程的总数及各 类条件式的个数。
4.指出图示非自由 测角网按条件平差时条 件方程的总数及各类条 件式的个数。
5.指出图示非自由 测角网按条件平差时条件 方程的总数及各类条件式 的个数。
条件平差习题课
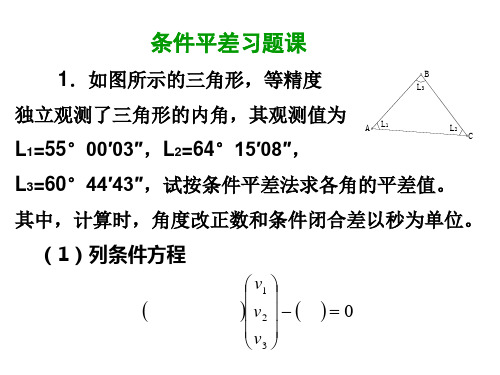
1.如图所示的三角形,等精度
独立观测了三角形的内角,其观测值为 A L1
L1=55°00′03″,L2=64°15′08″,
B L3
L2 C
L3=60°44′43″,试按条件平差法求各角的平差值。
其中,计算时,角度改正数和条件闭合差以秒为单位。
(1)列条件方程
vHale Waihona Puke v2
(完整word版)测量平差经典试卷含答案

一、填空题(每空2分,共20分)1、最优估计量应具有的性质为 、 和 最优估计量主要针对观测值中仅含 误差而言。
2、间接平差中,未知参数的选取要求满足 、 。
3已知条件平差的法方程为024322421=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡k k ,则PV V T = ,μ= , 1k p = ,2k p = 。
4、已知某平差问题,观测值个数为79,必要观测量个数为35,则按间接平差进行求解时,误差方程式个数为 ,法方程式个数为 。
5、已知某平差问题观测值个数为50,必要观测量个数为22,若选6个独立参数按具有参数的条件平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 ;若在22个独立参数的基础上,又选了4个非独立参数按具有条件的参数平差进行求解,则函数模型个数为 ,联系数法方程式的个数为 。
6、条件平差中条件方程的个数等于________________,所选参数的个数等于_______________。
7、已知真误差向量1⨯∆n 及其权阵P ,则单位权中误差公式为 ,当权阵P 为 此公式变为中误差公式。
二、计算题(每题2分,共20分)1、条件平差的法方程等价于:A 、0=+W K Q KB 、0=+W Q K WC 、0=+W P K WD 、0=+W P K K答:______2、水准测量中,10km 观测高差值权为8,则5km 高差之权为:A 、2B 、4C 、8D 、16答:______3、已知⎥⎦⎤⎢⎣⎡=∆3112P ,则2L p 为:A 、2B 、3C 、25D 、35答:______4、间接平差中,L Q ˆ为:A 、TA AN 1- B 、A N A T1-C 、T A AN P11--- D 、A N A P T 11---答:______5、观测条件是指:A)产生观测误差的几个主要因素:仪器,观测者,外界条件等的综合B)测量时的几个基本操作:仪器的对中,整平,照准,度盘配置,读数等要素的综合 C)测量时的外界环境:温度,湿度,气压,大气折光……等因素的综合. D)观测时的天气状况与观测点地理状况诸因素的综合答:______ 6、已知观测向量()L L L T=12的协方差阵为D L =--⎛⎝ ⎫⎭⎪3112,若有观测值函数Y 1=2L 1,Y 2=L 1+L 2,则σy y 12等于?(A)1/4 (B)2 (C)1/2 (D)4 答:_____ 7、已知观测向量()L L L T=12的权阵P L =--⎛⎝ ⎫⎭⎪2113,单位权方差σ025=,则观测值L 1的方差σL 12等于:(A)0.4 (B)2.5 (C)3 (D)253答:____ 8、已知测角网如下图,观测了各三角形的内角,判断下列结果,选出正确答案。
第五章条件平差
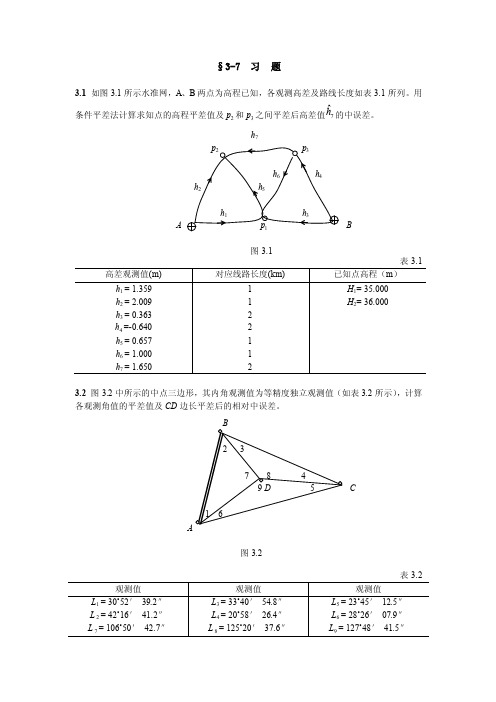
§3-7 习 题3.1 如图3.1所示水准网,A 、B 两点为高程已知,各观测高差及路线长度如表3.1所列。
用条件平差法计算求知点的高程平差值及p 2和p 3之间平差后高差值7ˆh 的中误差。
表3.13.2 图3.2中所示的中点三边形,其内角观测值为等精度独立观测值(如表3.2所示),计算各观测角值的平差值及CD 边长平差后的相对中误差。
表3.23.3 如图3.3所示单一附合导线,起算数据和观测值如表3.3所示,测角中误差为±3″,测边标称精度为±(5+5D )mm ,按条件平差法计算各导线点的坐标平差值,并评定3点平差后的点位精度。
表3.33.4 设某平差问题是按条件平差法进行的,其法方程式为:⎥⎦⎤⎢⎣⎡--42210⎥⎦⎤⎢⎣⎡21k k +⎥⎦⎤⎢⎣⎡66=0试求:(1)单位权中误差0m ;(2)若已知某一平差函数式L f F t ˆ=,并计算得[]p ff /=44,[]p af /=16,[]p bf /=4,试求该平差值函数的权倒数F p /1及其中误差F m 。
3.5 有三角网(如图3.5),其中B 、C 为已知点,A 、D 、E 为待定点,观测角i L (i =1,2,…,10),(1)试写出AD 边的权函数式; (2)设观测值同精度,且E Q LL =,已知方位角BC a 无误差,试求平差后BE a 的权倒数。
3.6 试按条件平差法求证在单一水准路线(如图3.6)中,平差后高程最弱点在水准路线中央。
3.7 已知条件式为0=+W AV ,其中AL W =,观测值协因数阵为1-=P Q LL ,现有函数式)(V L f F T +=,(1) (1) 试求:FF Q ;(2) (2) 试证: V 和F 是互不相关的。
3.8 有独立测边网(如图3.8),边长观测值列于下表。
试按条件平差法求出改正数i S V 以及边长平差值。
(已知E Q S =)。
表3.8。
条件平差习题

作业
h1 h5 A h2
P1 h3 B h6 h4 h7 P2
h5
h6 h7
4.651
5.856 10.500
1.0
1.0 2.0
HA=50.000m HB=40.000m
P3
试用条件平差法求:各高差的平差值。
华北科技学院
保留四位小数 条件平差习题
4/在图一所示测角网中,A、B、C为已知点,P为待定点,
T ˆ h h V 1.001 1.000 1.063 0.500 0.503 0.060 0.562 0.001
华北科技学院
条件平差习题
习题3
2:图中, A, B为已知水准点,其高成为:H A 12.013m, H B 10.013m, 为了确定C , D点的高程,观测了四段高差 高差观测值与水准路线的距离如下:
A L4 P L3 L2 L1 B
华北科技学院
C
条件平差习题
解:n=4,t=3,r=1,因为同精度观测,
1 1 p 1 1
列出平差值条件方程:
ˆ L ˆ L2 1 1 1 1 ˆ 360 0 L3 L ˆ 4 57 3216 73 0308 W ( AL A0 ) ([1 1 1 1] 360 ) 12 126 51 28 104 3320
S1 = 1 km S1 = 2 km
S1 = 2 km S1 = 1 km
h5 = + 0.504 m h6 = + 0.060 m
h7 = + 0.560 m h8 = + 1.000 m
S1 = 2 km S1 = 2 km
误差理论和测量平差习题5(含答案)
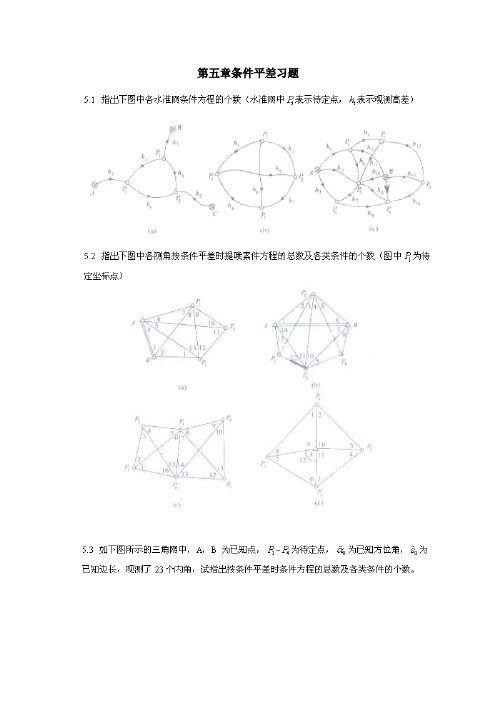
第五章条件平差习题第五章思考题参考答案5.1(a)n=6,t=3,r=3(b)n=6,t=3,r=3(c)n=14,t=5,r=95.2(a)n=13,t=6,r=7共有7个条件方程,其中有5个图形条件,2个极条件。
(b)n=14,t=8,r=6共有6个条件方程,其中有3个图形条件,3个极条件。
(c)n=16,t=8,r=8共有8个条件方程,其中有6个图形条件,2个极条件。
(d)n=12,t=6,r=6共有6个条件方程,其中有4个图形条件,1个圆周条件,1个极条件。
5.3n=23,t=6,r=17共有17个条件方程,其中有9个图形条件,1个圆周条件,1个固定角条件,1个固定边条件,5个极条件。
5.4 (1)n=22,t=9,r=13:7个图形条件,1个圆周条件,2个极条件,2个边长条件,一个基线条件。
(2)12837941314121520111718195610166101119910111213510ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆ1800ˆˆˆˆˆ1800ˆˆˆsin sin sin L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L L ++-=++-=++-=++-=+++-=+++-=+++-=++++-=171961116203614184715192211151217121318124ˆsin 1()ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin 1()ˆˆˆˆsin sin sin sin ˆˆ()ˆˆˆˆsin sin sin sin ˆˆ(ˆˆˆˆsin sin sin sin FG FG L L L L L L L L L L L L L S S S S L L L L S S L L L L ===→=以大地四边形中心为极以中点四边形D 点为极的边长条件1213611891719ˆˆ)ˆˆˆˆsin sin sin sin ˆˆˆˆsin sin sin sin FG AB S S L L L L S S L L L L →=的边长条件(基线条件)5.5 n=8,t=4,r=4;有多种条件方程的列法,其中之一为:1001000100110000120001001104000011014V ⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥-=⎢⎥⎢⎥--⎢⎥⎢⎥---⎣⎦⎣⎦(注意常数项单位为mm ) 5.6 (1)P=3/2,(2)P=15.7 (1)P B =1.6,P C =2.1,P D =2.1,P E =1.6(2)P hCD =1.85.8 []ˆ 2.4998 1.9998 1.3518 1.8515h=2P σ=0.32(mm)5.9 1234561110009100110900101016V V V V V V ⎡⎤⎢⎥⎢⎥-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦ []045452TV mm =---[]ˆ 1.576 2.219 3.7950.867 2.443 1.352T h m =--- 5.10 (1)1ˆ10.3556h m = 2ˆ15.0028h m = 3ˆ20.3556h m = 4ˆ14.5008h m =5ˆ 4.6472h m = 6ˆ 5.8548h m = 7ˆ10.5020h m =(2)±2.2mm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
写出改正数条件方程: 写出改正数条件方程:
法方程: 法方程:
AP −1 AT K − W = 0
华北科技学院
[4][ k a ] – [ - 12″] = 0
条件平差习题
计算联系数: 计算联系数:
K = − N aa −1W
[ k a ] = [0.25][ 12″] = - 3″ ″] ″
计算改正数: 计算改正数:
1 −3′′ 1 −3′′ [1 1 1 1][ −3] = V = P −1 AT K = −3′′ 1 1 −3′′
计算观测值平差值: 计算观测值平差值:
华北科技学院
ˆ L1 L1 + v1 57 32′33′′ ˆ L2 + v2 73 03′05′′ L2 = = ⋮ ⋮ 126 51′ 25′′ ˆ Ln Ln + vn 104 33′17′′
条件平差习题
条件平差
精度评定
AV −W = 0
N aa K − W = 0
V T PV ˆ σ0 = ± r
K = N aa W
V = P −1 A T K
−1
ˆ ˆ ˆ ˆ F = f ( L1 , L2 , ⋯ , Ln )
ˆ ˆ ˆ ˆ dF = f1 dL1 + f 2 dL2 + ⋯⋯ + f n dLn
或
α AB + ∠2+ ∠4− 360° − α CP = 0
∧
∧
华北科技学院
条件平差习题
华北科技学院
条件平差习题
序号 h1 h2 h3 h4 h5 h6 h7
观测高差 /m 10.356 15.000 20.360 14.501 4.651 5.856 10.500
路线长 /km 1.0 1.0 2.0 2.0 1.0 1.0 2.0
华北科技学院
条件平差习题
习题4 习题
如图所示,A和P点为等级三角点,PA方向的方位角已知, 如图所示, 和 点为等级三角点, 方向的方位角已知, 点为等级三角点 方向的方位角已知 在测站P上等精度测得的各方向的夹角观测值如下 上等精度测得的各方向的夹角观测值如下: 在测站 上等精度测得的各方向的夹角观测值如下: TPA=48 24 36,L1=57 32 16 , L2=73 03 08 L3=126 51 28 L4=104 33 20 按照条件平差方法计算各角的平差值并计算T 按照条件平差方法计算各角的平差值并计算 PC的方位角及 其精度。 其精度。 D
条件平差习题
计算单位权中误差: 计算单位权中误差:
σ0 = ±
1 −3 1 −3 = 36 V T PV = [ −3 −3 −3 −3] 1 −3 T 1 −3 V PV 36
r PC边的方位角: 边的方位角:
=
1
华北科技学院
T ˆ h = h + V = (1.001 1.000 1.063 0.500 0.503 0.060 0.562 0.001)
条件平差习题
习题3 习题
2:图中 A, B为已知水准点,其高成为:HA =12.013m, , HB =10.013m,为了确定C, D 点的高程,观测了四段高差 高差观测值与水准路线的距离如下:
Q FF = f T Qf − f T QAT N −1 AQf
2 D FF = m0 Q FF
ˆ L = L +V
华北科技学院
条件平差习题
习题1 习题 N=7,t=4.r=3
∠2+ ∠3+ ∠4+ ∠5− 180° = 0 ∠1+ ∠7 + ∠6− 180° = 0 sin(∠1+ ∠2) sin ∠4sin ∠6 sin ∠1sin ∠3sin(∠5+ ∠6)
华北科技学院
=1
条件平差习题
作业
A
A,B为已知点,CP为已 , 为已知点 为已知点, 为已 知方位角, 知方位角,列出全部 条件方程。 条件方程。
∠1+ ∠2+ ∠3− 180° = 0 ∠3+ ∠5− ∠4 = 0
∧ ∧
P 1
∧
∧
∧
4 2 5 C
∧
∧
∧
B
3
α AB − ∠1+ ∠5− 180° − α CP = 0
误差理论与测量平差
条件平差习题集
总结
1. 计算最或是值
确定n、 确定 、t 、 r = n – t 列出最或是值条件方程或改正数条件方程 组成法方程式,计算联系数K 组成法方程式,计算联系数 计算观测值改正数和计算观测值的平差值
2. 精度评定
计算单位权方差和单位权中误差 确定平差值函数关系式 进行全微分,求出线性函数的系数阵f 进行全微分,求出线性函数的系数阵 计算平差值函数的协因数QFF 计算平差值函数的协因数 计算平差值函数的协方差D 计算平差值函数的协方差 FF 华北科技学院
E
条件平差习题
N=10,t=6,r=4
L1 + L5 + L8 − 180° = 0 L1 + L6 + L7 − 180 = 0 L7 + L8 − L2 − L5 − 180 = 0
∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ∧ ° ∧ ∧ ∧ °
∧
∧
∧
sin L 1 sin L 3 sin L 5 sin L 2 sin L 4 sin L 6
5 −1 T 2 N = AP A = 1 0
2 6 −2 −2
0 −2 −2 5.5 2 2 5.5 1
0.6426 −0.1061 K = N −1W = −1.0010 −0.3254
T
V = P −1 AT K = ( −0.3 −1.1 −1.1 0.4 −1.3 −0.2 2.5 −0.8 )
华北科技学院
条件平差习题
解:n = 8,t = 4,r = n – t = 4 , ,
平差值条件方程式为: 平差值条件方程式为:
ˆ Ah + A0 = 0
ˆ ˆ ˆ h2 − h4 − h5 = 0 ˆ ˆ ˆ h2 − h3 + h6 = 0 ˆ − h − h = 0 ˆ ˆ h3 4 7 ˆ + h + h + H − H = 0 h1 ˆ3 ˆ8 A B
= ±6′′
ˆ ˆ TPC = TPA + L1 + L2 = 178°59 '54 ''
华北科技学院
条件平差习题
其中系数阵为: 其中系数阵为:
f = [1 1 0 0]
T
边的协因数: 计算PC边的协因数: QPC = f TQ − f TQAT N−1AQf f T
1 1 1 1 1 1 1 1 1 1 1 1 −[1 1 0 0] [0.25][1 1 1 1] =[1 1 0 0] 1 0 1 1 1 0 10 11 10 =0.5 边方位角的中误差为: 则PC边方位角的中误差为:
改正数条件方程式为: 改正数条件方程式为
AV − W = 0
华北科技学院
v2 − v4 − v5 − w1 = 0 v2 − v3 + v6 − w2 = 0 v3 − v4 − v7 − w3 = 0 v1 + v3 + v8 − w4 = 0
条件平差习题
取:
1 −1 −1 1 −1 1 A= 1 −1 −1 1 1 1
组成法方程
-1.5000
2.5000
1.0000
0 4 2.0000 0 5.5000 -1.5000 0 -1.5000 2.5000 K + −4 = 0 0 0 0 1.5000
华北科技学院
条件平差习题
K=
v=Q*A'*K -0.6957 1.3913 -0.6957 T -2.6087
作业
h1 h5 A h2
P1 h3 B
h6 h4 h7 P3
HA=50.000m HB=40.000m
∧
∧
-0.3478
hi = hi1.3913 + vi
∧
∧
h = [ −1, 0047 1.5174 −2.5127 1.5174]
V T PV σ0 = ± r
∧
H C = H A + L 1 = 11.0083m H D = H A + L1 + L4 = 12.5257m
∧
∧
H D = H A + h1 + h4 f = [1 0 0 1] QTPC = f T Qf − f T QAT N −1 AQf
h1 h4 C
D
h3 h2
h2 − h4 = 0 华北科技学院
∧
∧
B 条件平差习题
改正数方程: 改正数方程:
v1 + v3 + v4 + 4 = 0 v2 − v4 − 4 = 0
Naa =AQAT
A=
w=
1 0 0 0
4 -4
5.5000 -1.5000
2.0000 0
1 2 2 1 P −1 = 2 2 2.5 2.5
令C=1,观测值的权倒数: C=1,观测值的权倒数:
华北科技学院
条件平差习题
