第5章 轮系(基础) (2)
合集下载
杨可桢《机械设计基础》(第5版)笔记和课后习题(轮系)

图 5-3 解:这是一个定轴轮系,由题意可得:
1 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
反转原理:给周转轮系施以附加的公共角速度 H 后,不改变轮系中各构件之间的相
对运动,原轮系将转化成为一假想的定轴轮系,由此可按定轴轮系的公式计算该新轮系的传
动比。
设周转轮系中两个太阳轮分别为 G、K,行星架为 H,则其转化轮系的传动比:
圣才电子书 十万种考研考证电子书、题库视频学习平台
第5章 轮 系
5.1 复习笔记
一、轮系的类型 轮系是指由一系列齿轮组成的传动系统。 根据轮系运转时各个齿轮轴线相对于机架位置是否固定,分为三类: 1.定轴轮系:轮系中各齿轮轴线相对于机架均为固定,又分为平面定轴轮系和空间定 轴轮系。 2.周转轮系:轮系中至少有一个齿轮轴线位置不固定,而是绕着其他齿轮的固定轴线 回转。周转轮系由太阳轮、行星轮、系杆及机架组成,又可分为差动轮系(自由度为 2)和 行星轮系(自由度为 1)。 3.复合轮系:既包含定轴轮系,又包含周转轮系,或者是由几部分周转轮系组成。 根据轮系中各轮几何轴线在空间的相对位置,分为两类:平面轮系和空间轮系。
图 5-2
5-2 在图 5-3 所示轮系中,已知 z1=15,z2=25, z2' =15,z3=30, z3' =15z4=30, z4' =2(右 旋),z5=60, z5' =20(m=4 mm),若 n1=500 r/min,求齿条 6 线速度 v 的大小和方向。
3 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
(5)空间周转轮系中,由于角速度矢量与系杆的角速度矢量不平行,所以不能用代数 法相加减。但是不影响基本构件之间传动比的计算。
机械设计基础第5章 轮系习题解答1
45 30 34 15 15 17
12
例2:在下图所示的轮系中,已知z1=20,z2=40,
z2'=20,z3=30,z4=80,试求传动比i1H。
解: i12
n1 n2
z2 z1
40 20
2
i2H4
n2 n4
nH nH
z4 z2
80 4 20
n2 n2
n4 0
联立求解得:
i1H
解: 将轮系分解
4 13
1-2为定轴轮系 2-2’共轴
2
H
H-4-3-2’为周转轮系
2’
定轴轮系: i12=ω1/ω2 =-z2/ z1
周转轮系: iH2’4=(1- i2’H) =-z4 /z2’
连接条件: ω2=ω2’
i12 • i2’HBiblioteka 联立解得 i1H1 H
z2 (1 z4 ) 40 (1 20) 10 z1 z2 20
n1 1 991909100
nH
1010000000
n1 19091909011 1100 1 nH 1100000 1010000000 100
iH 1
1 i1H
10100000
例题5.4:如图所示的轮系中 ,已知若 z1=20, z2=40,
z2’=20, z3=30,z4=80,试求传动比i1H。
z2=25,z2'=20,z3=75,齿轮1的转速为200r/min(箭头朝
上),齿轮3的转速为50r/min,求行星架转速的nH大小和
方向。
解: i13H
n1H n3 H
n1 nH n3 nH
z2z3 z1 z2
25 75 25 30 20 8
机械设计基础 第5章 轮系

z’2 =100,
Z2 H Z1
Z’2
Z3
=99。 z3=99。源自101×99/100× i1H=1-iH13=1-101×99/100×100 =1/10000, iH1=10000 结论:系杆转10000圈时, 结论:系杆转10000圈时,轮1同向转1圈。 10000圈时 同向转1 100, 又若 Z1=100, z2=101, z2’=100, z3=100, =-1/100, i1H=1-iH1H=1-101/100 =-1/100, iH1=-100
所有齿轮几何轴线的位置均固定不 变的轮系,称为定轴轮系。 变的轮系,称为定轴轮系。
§5-1 轮系的类型
二、周转轮系
周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。
方向: 方向:见图 复合轮系
Z5
Z’5
§5-4 复合轮系及其传动比
复合轮系:几个基本周转轮系构成, 复合轮系:几个基本周转轮系构成,或定轴轮系与周转轮系构成 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 1 区分其中的基本周转轮系和定轴轮系 2 分别计算各轮系的传动比 3 各传动比联合求解
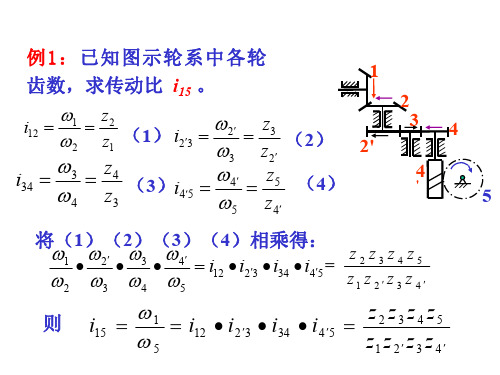
ω1 3 Z2 Z3 Z5 = i12i2′3i34i45 = (− 1) ω5 Z1Z2′ Z3′
§5-2 定轴轮系及其传动比
传动比计算
ω1 (− 1)3 Z2Z3Z4 Z5 i15 = =i i ′ i i = ω5 12 2 3 34 45 Z1Z2′ Z3′ Z4
Z2 H Z1
Z’2
Z3
=99。 z3=99。源自101×99/100× i1H=1-iH13=1-101×99/100×100 =1/10000, iH1=10000 结论:系杆转10000圈时, 结论:系杆转10000圈时,轮1同向转1圈。 10000圈时 同向转1 100, 又若 Z1=100, z2=101, z2’=100, z3=100, =-1/100, i1H=1-iH1H=1-101/100 =-1/100, iH1=-100
所有齿轮几何轴线的位置均固定不 变的轮系,称为定轴轮系。 变的轮系,称为定轴轮系。
§5-1 轮系的类型
二、周转轮系
周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。
方向: 方向:见图 复合轮系
Z5
Z’5
§5-4 复合轮系及其传动比
复合轮系:几个基本周转轮系构成, 复合轮系:几个基本周转轮系构成,或定轴轮系与周转轮系构成 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 1 区分其中的基本周转轮系和定轴轮系 2 分别计算各轮系的传动比 3 各传动比联合求解
ω1 3 Z2 Z3 Z5 = i12i2′3i34i45 = (− 1) ω5 Z1Z2′ Z3′
§5-2 定轴轮系及其传动比
传动比计算
ω1 (− 1)3 Z2Z3Z4 Z5 i15 = =i i ′ i i = ω5 12 2 3 34 45 Z1Z2′ Z3′ Z4
杨可桢《机械设计基础》章节题库(轮系)【圣才出品】

【答案】√
三、计算题 1.在如图 5-1 所示轮系中,已知蜗杆为单头且右旋,转速 n1=1440r/min,转动方 向如图 5-1 所示,其余各轮齿数为:z2=40,z2’=20,z2=30,z3’=18,z4=54, 试: (1)说明轮系属于何种类型; (2)计算齿轮 4 的转速 n4; (3)在图中标出齿轮 4 的转动方向。
来判定。
4.在定轴轮系中,每个齿轮的轴线都是 【答案】固定
的。
5.惰轮对轮系的
并无影响,但却可以改变
【答案】传动比;从动轮
的转动方向。
6.如果在齿轮传动中,一个齿轮的
绕另一个齿轮的
1 / 17
旋转,这个轮系称周
圣才电子书
转轮系。
十万种考研考证电子书、题库视频学习平台
(1)机构自由度 F; (2)搅拌轴的角速度 ωF 及转向。
图 5-8 解:(1)机构自由度:F=3n-2PL-PH=3×2-2×2-1=1 (2)轮 1 为固定轮,即 1=0 ,则得:
有 又 得搅拌轴的角速度:
,方向与ωR 相同。
10.计算行星轮系的传动比时,可把行星轮系转化为一假想的定轴轮系,用定轴轮系 的方法解决行星轮系的问题。( )
3 / 17
圣才电子书
【答案】√
十万种考研考证电子书、题库视频学习平台
11.定轴轮系和行星轮系的主要区别在于系杆是否转动。( ) 【答案】√
12.渐开线标准直齿圆柱齿轮传动,由于安装不准确,产生了中心距误差,但其传动 比的大小仍保持不变。( )
6.在周转轮系中,凡具有固定几何轴线的齿轮就称为行星轮。( ) 【答案】×
7.定轴轮系可以把旋转运动转变成直线运动。( ) 【答案】√
8.轮系的传动比计算,不但要确定其数值,还要确定其转向关系。( ) 【答案】√
三、计算题 1.在如图 5-1 所示轮系中,已知蜗杆为单头且右旋,转速 n1=1440r/min,转动方 向如图 5-1 所示,其余各轮齿数为:z2=40,z2’=20,z2=30,z3’=18,z4=54, 试: (1)说明轮系属于何种类型; (2)计算齿轮 4 的转速 n4; (3)在图中标出齿轮 4 的转动方向。
来判定。
4.在定轴轮系中,每个齿轮的轴线都是 【答案】固定
的。
5.惰轮对轮系的
并无影响,但却可以改变
【答案】传动比;从动轮
的转动方向。
6.如果在齿轮传动中,一个齿轮的
绕另一个齿轮的
1 / 17
旋转,这个轮系称周
圣才电子书
转轮系。
十万种考研考证电子书、题库视频学习平台
(1)机构自由度 F; (2)搅拌轴的角速度 ωF 及转向。
图 5-8 解:(1)机构自由度:F=3n-2PL-PH=3×2-2×2-1=1 (2)轮 1 为固定轮,即 1=0 ,则得:
有 又 得搅拌轴的角速度:
,方向与ωR 相同。
10.计算行星轮系的传动比时,可把行星轮系转化为一假想的定轴轮系,用定轴轮系 的方法解决行星轮系的问题。( )
3 / 17
圣才电子书
【答案】√
十万种考研考证电子书、题库视频学习平台
11.定轴轮系和行星轮系的主要区别在于系杆是否转动。( ) 【答案】√
12.渐开线标准直齿圆柱齿轮传动,由于安装不准确,产生了中心距误差,但其传动 比的大小仍保持不变。( )
6.在周转轮系中,凡具有固定几何轴线的齿轮就称为行星轮。( ) 【答案】×
7.定轴轮系可以把旋转运动转变成直线运动。( ) 【答案】√
8.轮系的传动比计算,不但要确定其数值,还要确定其转向关系。( ) 【答案】√
机械设计基础第五章轮系

2. 根据周转轮系的组合方式,利用周转轮系传动比计算公式求
03
出周转轮系的传动比。
实例分析与计算
1
3. 将定轴轮系和周转轮系的传动比相乘,得到复 合轮系的传动比。
2
4. 根据输入转速和复合轮系的传动比,求出输出 转速。
3
计算结果:通过实例分析和计算,得到了复合轮 系的输出转速。
05 轮系应用与实例分析
仿真结果输出
将仿真结果以图形、数据等形式输出,以便 进行后续的分析和处理。
实验与仿真结果对比分析
01
数据对比
将实验数据和仿真数据进行对比 ,分析两者之间的差异和一致性 。
结果分析
02
03
优化设计
根据对比结果,分析轮系设计的 合理性和可行性,找出可能存在 的问题和改进方向。
针对分析结果,对轮系设计进行 优化和改进,提高轮系的性能和 稳定性。
04 复合轮系传动比计算
复合轮系构成及特点
构成
由定轴轮系和周转轮系(或几个周转轮系)组合而成,称为复合轮系。
特点
复合轮系的传动比较复杂,其传动比的计算需结合定轴轮系和周转轮系的传动比计算公式进行。
复合轮系传动比计算公式
对于由定轴轮系和周转轮系组成的复合轮系,其传动比计算 公式为:i=n1/nK=(Z2×Z4×…×Zk)/(Z1×Z3×…×Zk-1)×(1)m,其中n1为输入转速,nK为输出转速,Z为各齿轮齿数 ,m为从输入轴到输出轴外啮合齿轮的对数。
火车车轮与轨道
通过轮系保证火车在铁轨 上的平稳运行和导向作用 。
船舶推进器
利用轮系将主机的动力传 递给螺旋桨,推动船舶前 进。
军事装备中轮系应用举例
坦克传动系统
采用轮系实现坦克发动机的动力 输出与行走机构的连接,确保坦 克在各种地形条件下的机动性。
【机械设计基础】第五章 轮系

轮
系
三个运动件中,有两个构件为主动件 一个为从动 三个运动件中 有两个构件为主动件,一个为从动, 运动复合的差动轮系 有两个构件为主动件 一个为从动, 三个运动件中,有一件主动,两件从动, 三个运动件中,有一件主动,两件从动,运动分解的差动轮系 三个运动件中,两个中心轮之一固定, 三个运动件中,两个中心轮之一固定, 行星轮系 系杆H固定 演变为定轴轮系。 固定, 系杆 固定,演变为定轴轮系。
第五章
轮
系
重点学习内容
1.定轴轮系和周转轮系的传动比计算 2.轮系中从动轮转动方向的判定
机 械 设 计 基 础
第五章
轮
系
第一节 定轴轮系及其传动比计算 第二节 周转轮系及其传动比计算 第三节 轮系的功用
机 械 设 计 基 础
第五章
轮
系
现代机械中, 现代机械中,为了满足不同的工作要求只用一对齿轮传 动往往是不够的,通常用一系列齿轮共同传动。 动往往是不够的,通常用一系列齿轮共同传动。这种由一系列 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮系
机 械 设 计 基 础
周转轮系的分类: 周转轮系的分类:
第五章
轮
系
1、行星轮系:自由度为1的周转轮系,需要两个原动 、行星轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。 2、差动轮系:自由度为2的周转轮系,需要一个原动 、差动轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。
第五章
转化后的定轴轮系 的传动比为: 的传动比为:
H 13
n1 n1 − nH i = H = n3 n3 − nH
大连理工大学 机械设计基础 作业解答:第5章-轮系

齿轮1、2组成定轴轮系,齿轮3、4、 4’、5和行星架组成周转轮系
定轴轮系
i12
n1 n2
Z2 Z1
Z2 17
周转轮系
i3H5
n3H n5H
n3 nH n5 nH
Z5Z4 Z4'Z3
2419 114 20 23 115
nH
n2 , n3
0,所以 n2 n5 n2
114 115
n1 n3
Z3 Z1
85 17
5,所以n3
n1 5
周转轮系中,i4H7
n4H n7H
n4 nH n7 nH
Z7Z5 Z6Z4
63 24 4 2118
nH
n3, n7
nP
,
所以
n4 nP
n1 / 5 n1 / 5
4, nP
n1
n4 4
(1)当n1
10001r
/ min 、n4
5-2 Z1=15, Z2=25 ,Z2'=15 ,Z3=30,Z3'=15, Z4=30, Z4'=2(右旋),Z5=60,Z5'=20(m=4mm), 若
n1=500(r/min),求齿条6的线速度。
传动4 .Z 3 .Z 2 Z 4' .Z 3' .Z 2' .Z1
的传动比 iSM 和分针与时针的传动比 iMH 。
秒针S到分针M的传动路线为齿轮 6—5—4—3,所以
i SM
Z3.Z5 Z 4 .Z 6
64 60 88
60
分针M到时针H的传动路线为 齿轮9—10—11—12,所以
iMH
Z12 .Z10 Z11.Z9
24 24 68
12
5-4 Z1 = Z2 =17, Z3 =51。当手柄转过90°时,转盘 H 转过 多少角度?
机械设计基础完美第五章轮系PPT课件

三、偕波齿轮传动
36
第六节 几种特殊的行星传动简介
37
第六节 几种特殊的行星传动简介
• 四、活齿传动
• 随着原动机和工作机向着多样化方向的发展,对 传动装置的性能要求也日益苛刻。为了适应这一 要求,除对齿轮、蜗杆蜗轮等传统的传动装置作 大量的研究和改进外,近20多年来人们还研究出 了多种新型传动装置如谐波传动、摆线针轮传动 等。这些传动都成功地应用于许多行业的各种机 械装置中。
须相等。
20
• 3、邻接条件 • 确定齿轮齿数时,必须保证相邻两行星齿轮的齿
顶圆之间有一定间隙,如图所示,即满足以下不 等式
• 4、装配条件 • 为了保证各行星齿轮能能均匀的分布在两中心轮
之间,并且与两中心轮啮合良好而没有错位现象, 即在行星轮数目确定后齿数的选择应满足装配条 件。
21
22
第四节 混合轮系及其传动比
9
第二节 定轴轮系及其传动比 当主动轮1和最末从动轮K的轴线平行时,两轮 转向的同异可用传动比的正负表达。两轮转向相同 时,传动比为“+”;两轮转向相反时,传动比为“-”。 因此,平行二轴间的定轴轮系传动比计算公式 为:
10
第二节 定轴轮系及其传动比
11பைடு நூலகம்
第三节 周转轮系及其传动比
周转轮系中行星轮的运动不是绕固定轴线的 简单转动(包括自转和公转),所以周转轮系各 构件间的传动比就不能直接用定轴轮系的方法来 计算了。
16
第三节 周转轮系及其传动比
17
第三节 周转轮系及其传动比
18
第三节 周转轮系及其传动比
19
第三节 周转轮系及其传动比
• 齿数的确定 • 确定齿数的条件 • 在选择行星齿轮传动的齿数时应满足以下条件: • 1、传动比条件 • 齿数的选择首先应保证实现给定传动比的要求。 • 2、同心条件 • 为了保证正确的啮合,各对啮合齿轮的中心距必
36
第六节 几种特殊的行星传动简介
37
第六节 几种特殊的行星传动简介
• 四、活齿传动
• 随着原动机和工作机向着多样化方向的发展,对 传动装置的性能要求也日益苛刻。为了适应这一 要求,除对齿轮、蜗杆蜗轮等传统的传动装置作 大量的研究和改进外,近20多年来人们还研究出 了多种新型传动装置如谐波传动、摆线针轮传动 等。这些传动都成功地应用于许多行业的各种机 械装置中。
须相等。
20
• 3、邻接条件 • 确定齿轮齿数时,必须保证相邻两行星齿轮的齿
顶圆之间有一定间隙,如图所示,即满足以下不 等式
• 4、装配条件 • 为了保证各行星齿轮能能均匀的分布在两中心轮
之间,并且与两中心轮啮合良好而没有错位现象, 即在行星轮数目确定后齿数的选择应满足装配条 件。
21
22
第四节 混合轮系及其传动比
9
第二节 定轴轮系及其传动比 当主动轮1和最末从动轮K的轴线平行时,两轮 转向的同异可用传动比的正负表达。两轮转向相同 时,传动比为“+”;两轮转向相反时,传动比为“-”。 因此,平行二轴间的定轴轮系传动比计算公式 为:
10
第二节 定轴轮系及其传动比
11பைடு நூலகம்
第三节 周转轮系及其传动比
周转轮系中行星轮的运动不是绕固定轴线的 简单转动(包括自转和公转),所以周转轮系各 构件间的传动比就不能直接用定轴轮系的方法来 计算了。
16
第三节 周转轮系及其传动比
17
第三节 周转轮系及其传动比
18
第三节 周转轮系及其传动比
19
第三节 周转轮系及其传动比
• 齿数的确定 • 确定齿数的条件 • 在选择行星齿轮传动的齿数时应满足以下条件: • 1、传动比条件 • 齿数的选择首先应保证实现给定传动比的要求。 • 2、同心条件 • 为了保证正确的啮合,各对啮合齿轮的中心距必
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§5-4 复合轮系及其传动比
在差动轮系中:
H i13
Z2Z3 n1H n1 n H 52 78 H ( ) ( ) (a) n3 n H 24 21 n3 ZZ
1 2
在定轴轮系中
n3 Z5 78 13 i35 ( ) n5 18 3 Z
§5-3
周转轮系及其传动比
一、周转轮系的组成
1.行星轮:轴线位置变动的齿轮,即既作自转又作公转的齿轮; 2.行星架(转臂或系杆):支持行星轮作自转和公转的构件; 3.中心轮(或太阳轮):轴线位置固定并与行星轮啮合的齿轮。 上图: 行星轮-- 齿轮2; 行星架– H杆; 中心轮-- 齿轮1、3 。
§5-3
图中1、3二轮虚线箭头反向,故取“-”,由 此得
n1 n H 61 () 0 nH 27
解得:
i1H
n1 61 1 3.26 nH 27
n1 6000 nH 1840r / min i1H 3.26
设n1的转向为正,则
nH的转向和n1相同。
§5-3
四、例题
周转轮系及其传动比
例5-3 在图5-6所示圆锥齿轮组成的差动轮系中,已知Z1=60,Z2=40, Z2′=Z3=20,若n1和n3均为120r/min,但转向相反(如图中实线箭头 所示),求nH的大小和方向。 解 将H固定,画出转化轮系各 轮的转向,如虚线箭头所示。 由通式可得:
H i13
Z2Z3 n1H n1 n H H () n3 n H n3 ZZ
在周转轮系中,设ωH为行星架H的角速度。根据相对运动原 理,当给整个周转轮系加上一个绕轴线OH转动的公共转速(-ωH) 后,行星架H便静止不动了,而各构件间的相对运动并不改变。这 样,所有齿轮的几何轴线的位置全部固定,原来的周转轮系便成 了定轴轮系),这一定轴轮系称为原来周转轮系的转化轮系。
§5-3
传动比大小:
n1 z 2 i12 n2 z1
在图上用画箭头方法表示。
传动比方向:
§5-2
定轴轮系及其传动比
1.一对齿轮转向关系的确定 蜗轮的转向不仅与蜗杆的转向有 关,而且与其螺旋线方向有关。
用左右手定则判断:左旋左手,右 旋右手,四指转向,则拇指的相反 方向即是蜗轮在啮合节点的速度方 向。
2.平面定轴轮系传动比计算
上式表明:定轴轮系传动比的数值等于组成该轮系的各对啮合齿 轮传动比的连乘积,也等于各对啮合齿轮中所有从动轮齿数的乘 积与所有主动轮齿数乘积之比。
§5-2
平面定轴轮系:
定轴轮系及其传动比
主从动轮转向关系的确定:
§5-2
空间定轴轮系:
定轴轮系及其传动比
主从动轮转向关系的确定:
也可以计算出行星齿轮2的转速n2
n i n
H 12
H 1 H 2
n1 nH Z2 () n2 n H Z1
代人已知数值
6000 1840 17 () n2 1840 27
解得
n2 4767r / min
负号表示n2的转向与nl相反。
§5-3
四、例题
周转轮系及其传动比
n1 z2 i12 n2 z1
“-”号表示两轮转向相反。
§5-2
定轴轮系及其传动比
1.一对齿轮转向关系的确定 一对平行轴内啮合齿轮: 两轮转向相同,故用方向相同 的箭头表示。
n1 z2 i12 n2 z1
“+”号表示两轮转向相同。
§5-2
定轴轮系及其传动比
1.一对齿轮转向关系的确定 一对圆锥齿轮传动:在节点具有 相同速度,故表示转向的箭头或 同时指向节点,或同时背离节点。
§5-4 复合轮系及其传动比
在机械中,经常用到由几个基本周转轮系或定轴轮系和周转 轮系组合而成的复合轮系。由于整个复合轮系不可能转化成一个 定轴轮系,所以不能只用一个公式来求解。 计算复合轮系时 , 首先必须将各个基本周转轮系和定轴轮系 区分开来,然后分别列出计算这些轮系的方程式,最后联立解出 所要求的传动比. 正确区分各个轮系的关键在于找出各个基本周转轮系。找基 本周转轮系的一般方法是:先找出行星轮,即找出那些几何轴线 绕另一齿轮的几何轴线转动的齿轮;支持行星轮运动的那个构件 就是行星架;几何轴线与行星架的回转轴线相重合,且直接与行 星轮相啮合的定轴齿轮就是中心轮,这组行星轮、行星架、中心 轮构成一个基本周转轮系。区分出各个基本周转轮系以后,剩下 的就是定轴轮系。
转化机构的传动比 i13H 可按定轴轮系传动比的方法求得:
H i13
z2 z3 z3 1H 1 H H 3 H z1 z 2 z1 3
§5-3
H iGK
周转轮系及其传动比
周转轮系传动比计算的一般公式:
H nG nG nH 转化轮系从G至K所有从动轮齿数乘积 H ( ) nK nH 转化轮系从G至K所有主动轮齿数乘积 nK
§5-5 轮系的应用
四、合成运动和分解运动
§5-5 轮系的应用
END
轮系的型
2.周转轮系:至少有一个齿轮的几何轴线绕另一齿轮的几何轴 线转动的轮系。
3.复合轮系:由几个周转轮系或定轴轮系和周转轮系组合而成的 轮系
§5-2
定轴轮系及其传动比
传动比:在轮系中,输入轴与输出轴的角速度(或转速)之比称为轮 系的传动比。 1.一对齿轮转向关系的确定
一对平行轴外啮合齿轮: 两轮转向相反,故用方向相 反的箭头表示。
二、分类
周转轮系及其传动比
1.差动轮系: 在周转轮系中,若两个中心轮都能转动,机构自由度=2,需要 两个原动件,这种周转轮系称为差动轮系。
F=3*4-2*4-2=2
§5-3
二、分类
周转轮系及其传动比
2.行星轮系: 在周转轮系中,若只有一个中心轮能转动,机构自由度=1,只 需一个原动件,这种周转轮系称为行星轮系。
第五章 轮 系
§5-1 轮系的类型
§5-2 定轴轮系及其传动比
§5-3 §5-4 §5-5 周转轮系及其传动比 复合轮系及其传动比 轮系的应用
§5-1
一、轮系
轮系的类型
由一系列互相啮合的齿轮组成的传动系统称为轮系。 二、类型 1.定轴轮系:传动时每个齿轮的几何轴线都是固定的轮系。
§5-1
二、类型
传动比大小:
n1 z 2 i12 n2 z1
传动比方向:在图上用画箭头方法表示。
§5-2
定轴轮系及其传动比
2.平面定轴轮系传动比计算 例:已知轮系各轮齿数。 求:总传动比i15 解:一对互相啮合的定 轴齿轮的转速比等于其 齿数反比,故各对啮合 齿轮的传动比数值为 :
§5-2
定轴轮系及其传动比
§5-4 复合轮系及其传动比
例5-4 在图5-7所示的电动卷扬机减速器中,各轮齿数为Z1=24, Z2=52,Z2` =21,Z3=78,Z3′=18,Z4=30,Z5=78。 求i1H
解:在该轮系中
行星轮:双联齿轮2-2′;
行星架:构件(卷筒H) 中心轮:齿轮1和3。 因两个中心轮都能转动,齿轮1、2-2′、 3和行星架H组成一个差动轮系。 剩下的齿轮3、4、5是一个定轴轮系。 二者合在一起便构成一个复合轮系。
解: 将行星架视为固定,画出转化轮系中各 轮的转向,如图5-5中虚线箭头所示(虚线箭头 不是齿轮真实转向,只表示假想的转化轮系中 的齿轮转向,二者不可混淆)。
H Z2 Z3 n n1 nH H 1 i13 H () n3 nH Z1 Z 2 n3
§5-3
四、例题
周转轮系及其传动比
3
由上式得 n 13 n 13 n 3 5 H
3
3
代入式(a)
n1 n H 169 13 21 nH nH 3
得
i1H=43.9
§5-5 轮系的应用
轮系广泛应用于各种机械中,它的主要功用如下:
一、相距较远的两轴之间的传动
二、实现变速传动
§5-5 轮系的应用
三、获得大的传动比
周转轮系及其传动比
周转轮系传动比计算的基本思路 设法使系杆H 固定不动,将周转轮系转化为定轴轮系。
周转轮系的转化机构(转化轮系): 指给整个周转轮系加上一个“-ωH”的公共角速度,使系杆H变为 相对固定后,所得到的假想的定轴轮系。
原轮系
转化轮系
§5-3
周转轮系及其传动比
周转轮系加上一公共角速度“-ωH”后,各构件的角速度:
注意事项:
1.上式只适用于转化轮系首末两轮轴线平 行的情况。
2.齿数比之前要加“+”号或“–”号来表示各 对齿轮之间的转向关系。 3.将nG、nK、nH 的数值代入上式时,必须 同时带“±”号。
§5-3
四、例题
周转轮系及其传动比
例 5-2 在图 5-5 所示的行星轮系中,各轮的齿数为: Z1=27 , Z2=17,Z3=61,已知n1=6000r/min。 求传动比i1H和行星架H的转速nH。
1 2
上式中的“+”号是由轮1和轮3虚线箭头同向而确定的,与实线箭 头无关。
§5-3
四、例题
周转轮系及其传动比
设实线箭头朝上为正,则nl= 120r/min,n3=-120r/min,代入上式 得
120 nH 40 ( ) 120 nH 60
解得: nH=600r/min
nH的转向与n1相同,箭头朝上。 注意,本例中行星齿轮 2-2’ 的轴线和齿轮 1( 或齿轮 3) 及行星架 H 的轴线不平行,所以不能用通式来计算n2
F=3*3-2*3-2=1
§5-3
周转轮系及其传动比
三、周转轮系传动比的计算
周转轮系中行星轮的运动不是绕固定轴线的简单转动,其传动 比不能直接用求解定轴轮系传动比的方法来计算。但,如果能使行 星架变为固定不动,并保持周转轮系中各个构件之间的相对运动不 变,则周转轮系就转化成为一个假想的定轴轮系,便可利用定轴轮 系传动比计算式,求出周转轮系的传动比。
