第五章 轮系(机械设计基础)
杨可桢《机械设计基础》(第5版)笔记和课后习题(轮系)

图 5-3 解:这是一个定轴轮系,由题意可得:
1 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
反转原理:给周转轮系施以附加的公共角速度 H 后,不改变轮系中各构件之间的相
对运动,原轮系将转化成为一假想的定轴轮系,由此可按定轴轮系的公式计算该新轮系的传
动比。
设周转轮系中两个太阳轮分别为 G、K,行星架为 H,则其转化轮系的传动比:
圣才电子书 十万种考研考证电子书、题库视频学习平台
第5章 轮 系
5.1 复习笔记
一、轮系的类型 轮系是指由一系列齿轮组成的传动系统。 根据轮系运转时各个齿轮轴线相对于机架位置是否固定,分为三类: 1.定轴轮系:轮系中各齿轮轴线相对于机架均为固定,又分为平面定轴轮系和空间定 轴轮系。 2.周转轮系:轮系中至少有一个齿轮轴线位置不固定,而是绕着其他齿轮的固定轴线 回转。周转轮系由太阳轮、行星轮、系杆及机架组成,又可分为差动轮系(自由度为 2)和 行星轮系(自由度为 1)。 3.复合轮系:既包含定轴轮系,又包含周转轮系,或者是由几部分周转轮系组成。 根据轮系中各轮几何轴线在空间的相对位置,分为两类:平面轮系和空间轮系。
图 5-2
5-2 在图 5-3 所示轮系中,已知 z1=15,z2=25, z2' =15,z3=30, z3' =15z4=30, z4' =2(右 旋),z5=60, z5' =20(m=4 mm),若 n1=500 r/min,求齿条 6 线速度 v 的大小和方向。
3 / 14
圣才电子书 十万种考研考证电子书、题库视频学习平台
(5)空间周转轮系中,由于角速度矢量与系杆的角速度矢量不平行,所以不能用代数 法相加减。但是不影响基本构件之间传动比的计算。
机械设计基础第5章 轮系习题解答1
45 30 34 15 15 17
12
例2:在下图所示的轮系中,已知z1=20,z2=40,
z2'=20,z3=30,z4=80,试求传动比i1H。
解: i12
n1 n2
z2 z1
40 20
2
i2H4
n2 n4
nH nH
z4 z2
80 4 20
n2 n2
n4 0
联立求解得:
i1H
解: 将轮系分解
4 13
1-2为定轴轮系 2-2’共轴
2
H
H-4-3-2’为周转轮系
2’
定轴轮系: i12=ω1/ω2 =-z2/ z1
周转轮系: iH2’4=(1- i2’H) =-z4 /z2’
连接条件: ω2=ω2’
i12 • i2’HBiblioteka 联立解得 i1H1 H
z2 (1 z4 ) 40 (1 20) 10 z1 z2 20
n1 1 991909100
nH
1010000000
n1 19091909011 1100 1 nH 1100000 1010000000 100
iH 1
1 i1H
10100000
例题5.4:如图所示的轮系中 ,已知若 z1=20, z2=40,
z2’=20, z3=30,z4=80,试求传动比i1H。
z2=25,z2'=20,z3=75,齿轮1的转速为200r/min(箭头朝
上),齿轮3的转速为50r/min,求行星架转速的nH大小和
方向。
解: i13H
n1H n3 H
n1 nH n3 nH
z2z3 z1 z2
25 75 25 30 20 8
机械设计基础 第5章 轮系

Z2 H Z1
Z’2
Z3
=99。 z3=99。源自101×99/100× i1H=1-iH13=1-101×99/100×100 =1/10000, iH1=10000 结论:系杆转10000圈时, 结论:系杆转10000圈时,轮1同向转1圈。 10000圈时 同向转1 100, 又若 Z1=100, z2=101, z2’=100, z3=100, =-1/100, i1H=1-iH1H=1-101/100 =-1/100, iH1=-100
所有齿轮几何轴线的位置均固定不 变的轮系,称为定轴轮系。 变的轮系,称为定轴轮系。
§5-1 轮系的类型
二、周转轮系
周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 周转轮系:在运转过程中至少有一个齿轮几何轴线的位置并不固定, 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。 而是绕着其它定轴齿轮轴线回转的轮系,称为周转轮系。
方向: 方向:见图 复合轮系
Z5
Z’5
§5-4 复合轮系及其传动比
复合轮系:几个基本周转轮系构成, 复合轮系:几个基本周转轮系构成,或定轴轮系与周转轮系构成 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 整个复合轮系不可能转化为一个定轴轮系,所以正确的做法是: 1 区分其中的基本周转轮系和定轴轮系 2 分别计算各轮系的传动比 3 各传动比联合求解
ω1 3 Z2 Z3 Z5 = i12i2′3i34i45 = (− 1) ω5 Z1Z2′ Z3′
§5-2 定轴轮系及其传动比
传动比计算
ω1 (− 1)3 Z2Z3Z4 Z5 i15 = =i i ′ i i = ω5 12 2 3 34 45 Z1Z2′ Z3′ Z4
机械设计基础第五章轮系

2. 根据周转轮系的组合方式,利用周转轮系传动比计算公式求
03
出周转轮系的传动比。
实例分析与计算
1
3. 将定轴轮系和周转轮系的传动比相乘,得到复 合轮系的传动比。
2
4. 根据输入转速和复合轮系的传动比,求出输出 转速。
3
计算结果:通过实例分析和计算,得到了复合轮 系的输出转速。
05 轮系应用与实例分析
仿真结果输出
将仿真结果以图形、数据等形式输出,以便 进行后续的分析和处理。
实验与仿真结果对比分析
01
数据对比
将实验数据和仿真数据进行对比 ,分析两者之间的差异和一致性 。
结果分析
02
03
优化设计
根据对比结果,分析轮系设计的 合理性和可行性,找出可能存在 的问题和改进方向。
针对分析结果,对轮系设计进行 优化和改进,提高轮系的性能和 稳定性。
04 复合轮系传动比计算
复合轮系构成及特点
构成
由定轴轮系和周转轮系(或几个周转轮系)组合而成,称为复合轮系。
特点
复合轮系的传动比较复杂,其传动比的计算需结合定轴轮系和周转轮系的传动比计算公式进行。
复合轮系传动比计算公式
对于由定轴轮系和周转轮系组成的复合轮系,其传动比计算 公式为:i=n1/nK=(Z2×Z4×…×Zk)/(Z1×Z3×…×Zk-1)×(1)m,其中n1为输入转速,nK为输出转速,Z为各齿轮齿数 ,m为从输入轴到输出轴外啮合齿轮的对数。
火车车轮与轨道
通过轮系保证火车在铁轨 上的平稳运行和导向作用 。
船舶推进器
利用轮系将主机的动力传 递给螺旋桨,推动船舶前 进。
军事装备中轮系应用举例
坦克传动系统
采用轮系实现坦克发动机的动力 输出与行走机构的连接,确保坦 克在各种地形条件下的机动性。
机械设计基础轮系

机械设计基础轮系在机械设计中,轮系的设计和布局是至关重要的。
轮系,或者称为齿轮系,是由一系列齿轮和轴组成的,它们通过精确的配合和排列,将动力从一个轴传递到另一个轴,或者改变轴的转速。
这种设计广泛应用于各种机械设备中,如汽车、飞机、机床等。
一、轮系的基本类型根据轮系中齿轮的排列和组合方式,我们可以将其分为以下几种基本类型:1、定轴轮系:在这种轮系中,齿轮是固定在轴上的,因此轴的旋转速度是恒定的。
这种轮系主要用于改变动力的大小和方向。
2、行星轮系:在这种轮系中,有一个或多个齿轮是浮动的,它们可以随着轴一起旋转,也可以绕着轴旋转。
这种轮系主要用于平衡轴的转速和改变动力的方向。
3、差动轮系:在这种轮系中,有两个或多个齿轮的旋转速度是不一样的,它们之间存在一定的速度差。
这种轮系主要用于实现复杂的运动规律。
在设计轮系时,我们需要遵循以下原则:1、确定传递路径:根据机械设备的需要,确定动力从哪个轴输入,需要传递到哪个轴。
2、选择合适的齿轮类型:根据需要传递的动力大小、转速等因素,选择合适的齿轮类型(直齿、斜齿、锥齿等)。
3、确定齿轮的参数:根据需要传递的动力大小、转速等因素,确定齿轮的模数、齿数、压力角等参数。
4、确定齿轮的排列方式:根据需要实现的传动比、转速等因素,确定齿轮的排列方式(串联、并联等)。
5、确定轴的结构形式:根据需要传递的动力大小、转速等因素,确定轴的结构形式(实心轴、空心轴、悬臂轴等)。
6、确定支承形式:根据需要传递的动力大小、转速等因素,确定支承形式(滚动支承、滑动支承等)。
7、确定润滑方式:根据需要传递的动力大小、转速等因素,确定润滑方式(油润滑、脂润滑等)。
在满足设计要求的前提下,我们还可以通过优化设计来提高轮系的性能。
以下是一些常用的优化方法:1、优化齿轮参数:通过调整齿轮的模数、齿数、压力角等参数,来提高齿轮的承载能力和降低噪声。
2、优化齿轮排列:通过优化齿轮的排列方式,来提高传动效率、降低传动噪声和减少摩擦损失。
机械设计基础_孙立鹏_习题第五章轮系
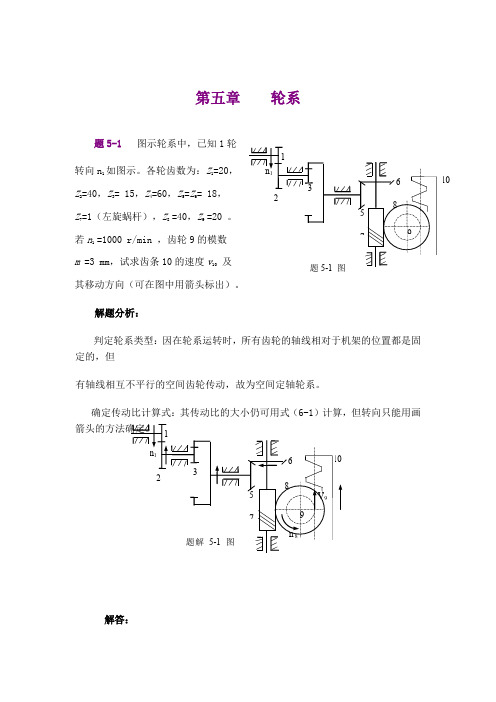
第五章轮系题5-1图示轮系中,已知1轮Array如图示。
各轮齿数为:Z1=20,转向n1Z=40,Z3= 15,Z4=60,Z5=Z6= 18,2Z=1(左旋蜗杆),Z8=40,Z9 =20 。
7若n1 =1000 r/min ,齿轮9的模数m =3 mm,试求齿条10的速度v及10其移动方向(可在图中用箭头标出)。
解题分析:判定轮系类型:因在轮系运转时,所有齿轮的轴线相对于机架的位置都是固定的,但有轴线相互不平行的空间齿轮传动,故为空间定轴轮系。
确定传动比计算式:其传动比的大小仍可用式(6-1)计算,但转向只能用画解答:1.确定齿条10的速度v 10 大小∵ 320118152040186040753186428118=⨯⨯⨯⨯⨯⨯===z z z z z z z z n n i∴min /125.3min /320100018189r r i n n n ====s /mm .s /mm .n mz n d v v 82960125320360609999910=⨯⨯⨯π=π=π==2.确定齿条10移动方向根据圆柱齿轮传动、锥齿轮传动及蜗杆传动的转向关系,可定出蜗轮转向n 8为逆时针方向,齿轮9与蜗轮8同轴,n 9 = n 8,齿条10线速度v 10与9轮线速度v 9方向一致,故齿条10的移动方向应朝上(↑)题5-2 图示轮系中,已知蜗杆1的齿数为Z 2= 50 ;蜗杆2′为单头右旋蜗杆, 蜗轮3的齿数为Z 3=40;其余各轮齿 数为;Z 3′=30,Z 4 = 20 ,Z 4′ = 26 , Z 5 =18,Z 5′=28,Z 6=16,Z 7=18。
要求:(1) 分别确定蜗轮2、蜗轮3的 轮齿螺旋线方向及转向n 2、n 3 ;(2) 计算传动比i 17 ,并确定齿 轮7的转向n 7。
解题分析:判定轮系类型:因在轮系运转时,所有齿轮的轴线相对于机架的 位置都是固定的,但有轴线相互不 平行的空间齿轮传动,故为空间定 轴轮系。
【机械设计基础】第五章 轮系

轮
系
三个运动件中,有两个构件为主动件 一个为从动 三个运动件中 有两个构件为主动件,一个为从动, 运动复合的差动轮系 有两个构件为主动件 一个为从动, 三个运动件中,有一件主动,两件从动, 三个运动件中,有一件主动,两件从动,运动分解的差动轮系 三个运动件中,两个中心轮之一固定, 三个运动件中,两个中心轮之一固定, 行星轮系 系杆H固定 演变为定轴轮系。 固定, 系杆 固定,演变为定轴轮系。
第五章
轮
系
重点学习内容
1.定轴轮系和周转轮系的传动比计算 2.轮系中从动轮转动方向的判定
机 械 设 计 基 础
第五章
轮
系
第一节 定轴轮系及其传动比计算 第二节 周转轮系及其传动比计算 第三节 轮系的功用
机 械 设 计 基 础
第五章
轮
系
现代机械中, 现代机械中,为了满足不同的工作要求只用一对齿轮传 动往往是不够的,通常用一系列齿轮共同传动。 动往往是不够的,通常用一系列齿轮共同传动。这种由一系列 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮系
机 械 设 计 基 础
周转轮系的分类: 周转轮系的分类:
第五章
轮
系
1、行星轮系:自由度为1的周转轮系,需要两个原动 、行星轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。 2、差动轮系:自由度为2的周转轮系,需要一个原动 、差动轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。
第五章
转化后的定轴轮系 的传动比为: 的传动比为:
H 13
n1 n1 − nH i = H = n3 n3 − nH
机械设计基础----第5章轮系

图5-4c
三、周转轮系的传动比计算
一)基本思路
如图5-4 a、b所示。
周转轮系与定轴轮系的
根本区别在于周转轮系
中有一个转动着的行星
架,因此使行星轮既自
转又公转。如果能
图5-4 a、b
够设法使行星架固定不动,那么周转轮系就可转化成一个
假想的定轴轮系,并称其为周转轮系的转化轮系。
在周转轮系转化为转化轮系后,就可以对转化轮系应
2、5的转向相同)
∴
i17=
z2 z1
•
z3 z 2
•
z4 z3
•
z5 z4
•
z6 z5
•
z7 z6
上例中的轮4,其齿数多少不影响传动比的大小,只
起改变转向的作用,在轮系中的这种齿轮称为惰轮(过桥
齿轮)——仅影响 i 的符号,而不影响 i 的大小。
▲自学:P74例5-1。
§5—3 周转轮系及其传动比
构件的轴线可互不平行;
3、正负号——指转化轮系中轮G、K的转向关系,图上画 箭头来确定(同定轴轮系);
4、真实转速nG、nK、nH中的已知量代入公式时要带正负 号(可假定某一转向为正,则相反的转向为负),求
得的未知量的转向也依据计算结果的正负号来确定。
例:在图示的轮系中,已知z1=z2=30,z3=90。试求当构件 1、3的转速分别为 n1=10rpm,n3=10rpm (转向如图) 时,求 nH及i1H的值。
转轮系)。
图a
图b
三、轮系的传动比(Transmission ratio)
一对齿轮的传动比:是指两轮的角速度或转速之比,即 i12=ω1 /ω2= n1 /n2 = z2 /z1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第五章 轮系
1.轮系是由一系列齿轮组成的传动系统,轮系可分为 定轴轮系 、 周转轮系 。
2.在轮系运转过程中至少有一个齿轮几何轴线的位置并不固定,而是绕着其它定轴齿轮轴线回转的轮系,称为 周转轮系 。
3.在轮系运转过程中,所齿轮几何轴线的位置都是固定,这种轮系称为 定轴轮系 。
4.轮系的传动比的定义是,轮系中输入轴与输出轴的角速度(或转速)之比,以iab 表示。
5.计算轮系传动比包括:计算传动比的 大小 、确定输出和输入轴的 转向 关系。
6.计算轮系传动时,其符号规定是:输出轴与输入轴转向相同,取 正 号;反之取 负 号。
7.惰轮既是前一级传动的从动轮,又是后一级传动的主动轮(又称过桥齿轮),在传动比计算中,它不该变传动比的 大小 ,却改变传动的 方向 。
8.一个基本的周转轮系是由 行星轮 、 转臂 和 中心轮 组成。
9.周转轮系的转化轮系是一个假想的 定轴轮系 。
10.复合轮系可由几个基本 周转轮系 构成,或 定轴轮系+周转轮系 构成。
11.在图示行星轮系中,各轮的齿数为: z 1=27, z 2=17, z 3=61 。
已知n 1=6000r/min ,求传动比i 1H 和行星架H的转速n H 。
解:该周转轮系为行星轮系。
27
61
)1(1313113-=-=--=
z z n n n n i H H H
因n 1=6000r/min, n 3=0 , 代入上式,得
26.32761111=+==
H H n n i , 184011==H
H i n n r/min 所以:系杆H 的转速1840r/min ,方向与轮1相同。
12.在图示轮系中,已知1H 3221i 40Z ,80Z ,20
Z Z 求==='=。
解:820
2040
80Z Z Z Z n n n n i 2132H 3H 1H
13-=⨯⨯-='-=--=
81n n H 1-=+-
所以 9n n
i H
11H == n 1与n H 转向相同。
13.图示周转轮系中,已知各齿轮的齿数为z 1=20,z 2=30,z ’
2=15,z 3=65。
轮1的转速
n 1=150r/min,求系杆H 的转速n H 的大小及方向。
解:该周转轮系为行星轮系。
5
.615
2065
30)1('213213113-=⨯⨯-=-=--=
z z z z n n n n i H H H
因n1=150r/min ,n3=0 ,代入上式,得nH=20r/min 所以:系杆H 的转速20r/min ,方向与轮1相同。
14.在图示轮系中,201=z ,152=Z ,102='z ,253=Z ,H n =120r/min ,
min /1003r n -=,求轮1的转速?(10分)
解:该轮系为差动轮系。
则有:120
100120102025
151
21323113----=⨯⨯-='⋅⋅-=--=
n z z z z n n n n i H H H
min /5
.2921r n =⇒
所以轮1的转速为292.5r/min ,方向与轮H 的方向相同。
15.如图所示的轮系中,已知n 1 =-2n 3 =100 r/min ,z 1=2z '=20,z 2 =z 3 =40 。
求:n H 。
解:(1)计算传动比的大小
H 231H 133H 12z z n n 4040
i 4n n 2020
z z -⨯=
===-⨯'
31H 4n n 450100
n 33
300100r /min
3
--⨯-=
=-==-
(2) 确定传动的方向
n 1与n H 方向相反。
16.已知图示轮系中各轮齿数,Z1=1(右旋),Z2=Z2’=20, Z3=30,Z3’=17,Z4=34, Z4’=18,Z5=54,求传动比 i15 解:1.先确定各齿轮的转向 齿轮5的转向如图所示。
2. 计算传动比
180181720154343020,
,,432154325
1
15=⨯⨯⨯⨯⨯⨯=
=
=
Z Z Z Z Z Z Z Z i ωω
17.已知图示轮系中各轮齿数,求传动比 i15 。
解:1.先确定各齿轮的转向
2. 计算传动比
4
,,
315
435
1
15Z Z Z Z Z Z i -==
ωω
1。
