2018--必修5-等差数列(基础)
高中数学必修五-等差数列

等差数列知识集结知识元等差数列的性质知识讲解1.等差数列的性质【等差数列】如果一个数列从第二项起,每一项与它的前一项的差等于同一个常数,这个数列就叫做等差数列.这个常数叫做等差数列的公差,公差常用字母d表示.等差数列的通项公式为:a n=a1+(n﹣1)d;前n项和公式为:S n=na1+n(n﹣1)或S n=(n∈N+),另一重要特征是若p+q=2m,则有2a m=a p+a q(p,q,m都为自然数)例:已知等差数列{a n}中,a1<a2<a3<…<a n且a3,a6为方程x2﹣10x+16=0的两个实根.(1)求此数列{a n}的通项公式;(2)268是不是此数列中的项?若是,是第多少项?若不是,说明理由.解:(1)由已知条件得a3=2,a6=8.又∵{a n}为等差数列,设首项为a1,公差为d,∴a1+2d=2,a1+5d=8,解得a1=﹣2,d=2.∴a n=﹣2+(n﹣1)×2=2n﹣4(n∈N*).∴数列{a n}的通项公式为a n=2n﹣4.(2)令268=2n﹣4(n∈N*),解得n=136.∴268是此数列的第136项.这是一个很典型的等差数列题,第一问告诉你第几项和第几项是多少,然后套用等差数列的通项公式a n=a1+(n﹣1)d,求出首项和公差d,这样等差数列就求出来了.第二问判断某个数是不是等差数列的某一项,其实就是要你检验看符不符合通项公式,带进去检验一下就是的.【等差数列的性质】(1)若公差d>0,则为递增等差数列;若公差d<0,则为递减等差数列;若公差d=0,则为常数列;(2)有穷等差数列中,与首末两端“等距离”的两项和相等,并且等于首末两项之和;(3)m,n∈N+,则a m=a n+(m﹣n)d;(4)若s,t,p,q∈N*,且s+t=p+q,则a s+a t=a p+a q,其中a s,a t,a p,a q是数列中的项,特别地,当s+t=2p时,有a s+a t=2a p;(5)若数列{a n},{b n}均是等差数列,则数列{ma n+kb n}仍为等差数列,其中m,k均为常数.(6)a n,a n﹣1,a n﹣2,…,a2,a1仍为等差数列,公差为﹣d.(7)从第二项开始起,每一项是与它相邻两项的等差中项,也是与它等距离的前后两项的等差中项,即2a n+1=a n+a n+2,2a n=a n﹣m+a n+m,(n≥m+1,n,m∈N+)(8)a m,a m+k,a m+2k,a m+3k,…仍为等差数列,公差为kd(首项不一定选a1).例题精讲等差数列的性质例1.设等差数列{a n}的前n项和为S n,若a2+a8=15-a5,则S9等于()A.18B.36C.45D.60例2.记等差数列{a n}的前n项和为S n.若a5=3,S13=91,则a1+a11=()A.7B.8C.9D.10例3.在等差数列{a n}中,a3+a9=24-a5-a7,则a6=()A.3B.6C.9D.12等差数列的通项公式知识讲解1.等差数列的通项公式【知识点的认识】等差数列是常见数列的一种,数列从第二项起,每一项与它的前一项的差等于同一个常数,已知等差数列的首项a1,公差d,那么第n项为a n=a1+(n﹣1)d,或者已知第m项为a m,则第n项为a n=a m+(n﹣m)d.【例题解析】eg1:已知数列{a n}的前n项和为S n=n2+1,求数列{a n}的通项公式,并判断{a n}是不是等差数列解:当n=1时,a1=S1=12+1=2,当n≥2时,a n=S n﹣S n﹣1=n2+1﹣(n﹣1)2﹣1=2n﹣1,∴a n=,把n=1代入2n﹣1可得1≠2,∴{a n}不是等差数列考察了对概念的理解,除掉第一项这个数列是等差数列,但如果把首项放进去的话就不是等差数列,题中a n的求法是数列当中常用到的方式,大家可以熟记一下.eg2:已知等差数列{a n}的前三项分别为a﹣1,2a+1,a+7则这个数列的通项公式为解:∵等差数列{a n}的前三项分别为a﹣1,2a+1,a+7,∴2(2a+1)=a﹣1+a+7,解得a=2.∴a1=2﹣1=1,a2=2×2+1=5,a3=2+7=9,∴数列a n是以1为首项,4为公差的等差数列,∴a n=1+(n﹣1)×4=4n﹣3.故答案:4n﹣3.这个题很好的考察了的呢公差数列的一个重要性质,即等差中项的特点,通过这个性质然后解方程一样求出首项和公差即可.【考点点评】求等差数列的通项公式是一种很常见的题型,这里面往往用的最多的就是等差中项的性质,这也是学习或者复习时应重点掌握的知识点.例题精讲等差数列的通项公式例1.在等差数列{a n}中,a4,a12是方程x2+3x+1=0的两根,则a8=()A.B.C.D.不能确定例2.在等差数列{a n}中,a2+a10=0,a6+a8=-4,a100=()A.212B.188C.-212D.-188例3.在等差数列{a n}中,若a2=5,a4=3,则a6=()A.-1B.0C.1D.6当堂练习单选题练习1.在等差数列{a n}中,a3+a9=24-a5-a7,则a6=()A.3B.6C.9D.12练习2.等差数列{a n}中,已知a2+a6=4,则a4=()A.1B.2C.3D.4练习3.在等差数列{a n}中,若a3+a9=17,a7=9,则a5=()A.6B.7C.8D.9练习4.《孙子算经》是中国古代重要的数学著作,上面记载了一道有名的“孙子问题”(又称“物不知数题”),后来我国南宋数学家秦九韶在《数书九章∙大衍求一术》中将此问题系统解决.“大衍求一术”是中国古算中最有独创性的成就之一,属现代数论中的一次同余式组问题.后传入西方,被称为“中国剩余定理”.现有一道一次同余式组问题:将正整数中,被3除余2且被5除余1的数,按由小到大的顺序排成一列,则此列数中第10项为()A.116B.131C.146D.161练习5.已知2,b的等差中项为5,则b为()A.B.6C.8D.10练习6.数列{a n}是等差数列,a1=1,公差d∈[1,2],且a4+λa10+a16=15,则实数λ的最大值为()A.B.C.D.练习7.等差数列{a n}中,S n是它的前n项和,a2+a3=10,S6=54,则该数列的公差d为()A.2B.3C.4D.6练习8.等差数列{a n}中,a1+a8=10,a2+a9=18,则数列{a n}的公差为()A.1B.2C.3D.4练习9.在等差数列{a n}中,已知a2+a6=18,则a4=()A.9B.8C.81D.63。
2018秋新版高中数学北师大版必修5:第一章数列 1复习课1

∴S9=9(������12+������9) = 9×22������5=9a5=34π.
∴cos S9=cos34π=- 22.
答案:D
目标导航
Z D 知识梳理 HISHISHULI
典例透析
IANLITOUXI
S随堂演练 UITANGYANLIAN
2.等差数列的性质
已知数列{an}是等差数列,Sn是其前n项和. (1)若m,n,p,q,k是正整数,且m+n=p+q=2k,则am+an=ap+aq=2ak. (2)am,am+k,am+2k,am+3k,…仍是等差数列,公差为kd . (3)数列Sm,S2m-Sm,S3m-S2m,…也是等差数列. (4)若数列{an}的前n项和为Sn,则S2n-1=(2n-
由①式得 1
������������
−
���������1���-1=2(n≥2).
∴
1 ������������
是等差数列,其中首项为���1���1
= ���1���1=2,公差为 2.
(2)
解∵ 1
������������
=
���1���1+2(n-1)=���1���1+2(n-1),∴Sn=21������.
答案:B
目标导航
Z D 知识梳理 HISHISHULI
典例透析
IANLITOUXI
S随堂演练 UITANGYANLIAN
【做一做 1-2】 已知数列{an}为等差数列,其前 n 项和为 Sn,若
a4+a5+a6=π4,则 cos S9 的值为(
)
A.12
B.
高一数学必修5PPT课件:等差数列的性质
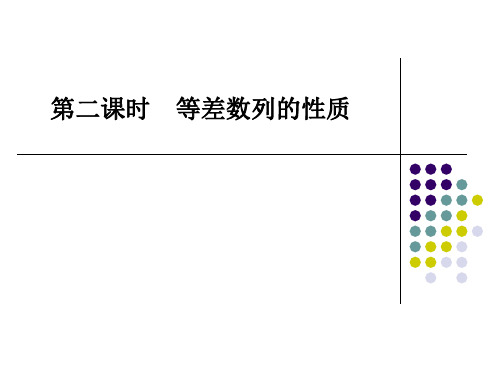
a4= 11 a7= 17
∴d= _2或2, 从而a14= _列的 性质
变 式 1 : 已 知 { a } 为 等 差 数 列 , a a a 高一数学必修5PPT课件:等差数列的性质
n
4
5
6
a7 56,a4a7 187,求a1,d
变式2:已知{an }为等差数列,a2 a5 a8 9, a3a5a7 21,求数列通项公式
解: a3+a11 =a6+a8 =2a7 ,又已知 a3+a11=10, ∴ a6+a7+a8= 23(a3+a11)=15
(解3):已a4+知a5+aa4+6+aa57+=a566+a7=a54+6a,7=a248a7①=187,求a14及公差d.
又 a4a7=187 ② , 解 ①、 ② 得
a4= 17 或 a7= 11
研究性问题
1. 若a12=23,a42=143, an=263,求n. d= 4 n=72
2.已知{an}为等差数列,若a10= 20 ,d= -1 ,求a 3 ?
a 3= a 10 +(3-10)d
a 3=27
3. 三数成等差数列,它们的和为12,首尾二数的
积为12,求此三数. 6,4,2或2,4,6
笔记①: 三个数等差的设法:a-d,a,a+d
练习2、成等差数列的四个数之和为26,第二个 与第三个数之积为40,求这四个数。
笔记:
四个数等差的设法: a-3d,a-d,
a+d,a+3d
公差为2d
性质一、任意两项的关系
在等差数列 an 中,有
an
高中数学必修5等差数列知识点总结和题型归纳

等差数列一.等差数列知识点:知识点1、等差数列的定义:①如果一个数列从第2项起,每一项与它的前一项的差等于同一个常数,那么这个数列就叫做等差数列,这个常数叫做等差数列的公差,公差通常用字母d表示知识点2、等差数列的判定方法:②定义法:对于数列,若(常数),则数列是等差数列③等差中项:对于数列,若,则数列是等差数列知识点3、等差数列的通项公式:④如果等差数列的首项是,公差是,则等差数列的通项为该公式整理后是关于n的一次函数知识点4、等差数列的前n项和:⑤⑥对于公式2整理后是关于n的没有常数项的二次函数知识点5、等差中项:⑥如果,,成等差数列,那么叫做与的等差中项即:或在一个等差数列中,从第2项起,每一项(有穷等差数列的末项除外)都是它的前一项与后一项的等差中项;事实上等差数列中某一项是与其等距离的前后两项的等差中项知识点6、等差数列的性质:⑦等差数列任意两项间的关系:如果是等差数列的第项,是等差数列的第项,且,公差为,则有⑧对于等差数列,若,则也就是:⑨若数列是等差数列,是其前n项的和,,那么,,成等差数列如下图所示:10、等差数列的前项和的性质:①若项数为,则,且,.②若项数为,则,且,(其中,).二、题型选析:题型一、计算求值(等差数列基本概念的应用)1、。
等差数列{a n}的前三项依次为a-6,2a -5, -3a +2,则a 等于()A . -1B . 1C 。
—2 D. 22.在数列{a n}中,a1=2,2a n+1=2a n+1,则a101的值为( )A.49 B.50 C.51 D.523.等差数列1,-1,-3,…,-89的项数是()A.92 B.47 C.46 D.454、已知等差数列中,的值是()()A 15B 30C 31D 645. 首项为-24的等差数列,从第10项起开始为正数,则公差的取值范围是()A.d>B.d<3 C。
≤d<3 D.<d≤36、。
在数列中,,且对任意大于1的正整数,点在直上,则=_____________。
高中数学必修5《等差数列》精品课件第1课时

2o 若an pn q 则an1 an p(n 1) q ( pn q) p(常数) {an }为等差数列
④数列{ a n }的前n项和 S nA2 nB(A n ,B 为常 ,n N 数 *)
1o 若{an }为等差数列, 首项为a1, 公差为d
则Sn
na1
n(n 1) 2
d
d 2
n2
(a1
d )n 2
An2
Bn( A, B为常数)
2o 若Sn An2 Bn( A, B为常数)
当n 1时,a1 S1 A B 当n 2时,an Sn Sn1 An2 Bn [ A(n 1)2 B(n 1)]
等差中项法:2an an1 an1(n 2) {an }为等差数列
通项公式法:an pn q( p,q为常数) {an }为等差数列
前n项和公式法:Sn An2 Bn( A, B为常数) {an }为等差数列
【应用体验】
二、等差数列的通项公式与前n项和公式综合应用
体验2:
设 {an}是 一 个d公 (d差 0)的为 等 差 数 列 ,1它 0项的 和 S10 前 11,且 0a22a1a4, 求 数 {an}列 的 通 项 . 公 式
【应用体验】
三、等差数列前n项和的最值
体验3:
设等差数 {an列 }的前n项和为 Sn,已知 a5 -8, S3 -51,求当 n取何值S时 n 取得最小值,并 它的最小 . 值
【应用体验】
三、等差数列前n项和的最值
变式探究:
在 等 差{a数 n}中列 , 已 a1知 24, 前n项 和Sn且 为S1 0S1 5,求 当 n 时, Sn取得最. 大值
人教版高中数学必修5《等差数列》PPT课件

等差数列的通项公式中包含四个量: an、a1、n、d
这四个量只需知道其中的三个就可以求出第四个.
例2.在等差数列{an}中, a5=10, (1)若a12=31,求a25 ; (2)若d=2,求a10; 解:(1)依题意得
a1+4d=10 a1+11d=31 解得 a1= - 2 , d = 3 ∴ a25=a1+24d = -2+24×3=70
解:a8=a1+7d=-1+7×4=27
(2)已知a1=15,an=3,d= -3,求n; 解:∵3=15-3(n-1) ∴n=5
(3)已知a1=8,a6=23,求d; 解:∵a6=a1+5d,即23=8+5d ∴ d=3
(4)已知d=2,a7=9,求a1; 解:∵a7=a1+6d 即9=a1+6×2 ∴a1=-3
拓展:在等差数列{an}中, 若a5=10,a12=31,求a25 。 解:设等差数列{an}的公差为d,则依题意有
d a12 a5 3110 3 12 5 7
∴ a25=a5+20d = 10+20×3=70
练习:在下列两个数中间再插入两个数,使这四个数组成 一个等差数列,(1)-1,5; (2)-12,0.
观察并发现:下面数列有什么共同特点?
(1)0,5,10,15,20,25,…
(2)鞋的尺寸,按照国家统一规定,有: 22,22.5,23,23.5,24,24.5,25,25.5,26,… (3)21,19,17,15,…… (4)3,3,3,3,……
(1)从第2项起,每一项与前一项的差都等于 5 (2)从第2项起,每一项与前一项的差都等于 0.5 (3)从第2项起,每一项与前一项的差都等于 -2 (4)从第2项起,每一项与前一项的差都等于 0
必修5_2.2等差数列

能用前项减后项来求;
(2)对于数列{an},若an-an-1 =d(d是与n
无关的数或字母),n≥2,则此数列是
等差数列,d 为公差; 为递增数列; d<0,该数列为递减数列。
(3)若d=0,则该数列为常数列.d>0,则该数列
练习:判断下列数列是否等差数列,若是, 则公差是多少? 判断或证明一 ① 1 , 2, 3 ,2,… 个数列是否等 ② 3,3,3,3,… 差数列,应根 据等差数列的 ③1,2,4,7,… 定义进行:即 ④1.1,1.11,1.111,1.1111,… 对于n∈N*, 1 1 1 1 ⑤ , , , ,… an+1-an是否 4 16 32 8 ⑥-2,-1,0,1,2,3,… 等于常数。
以上n-1式联加可得: an a1 (n 1)d
这就是等差数列的通项公式
an ( an an 1 ) ( an 1 an 2 ) ( a3 a2 ) ( a2 a1 ) a1
通项公式 的推广:
a n a m ( n m) d
则 a5 a8 __________
4、 已知等差数列{an }中,a2 a6 a10 1,
则 a3 a9 __________
(2)a k , a k m , a k 2 m 组成公差为 md
的等差数列,
(3)若{an},{bn}为等差,则{pan+qbn}也为等差数列
例 已知两个等差数列5, 8, 11, …和3, 7, 11, … 都有100项,问它们有多少共同项
析:两个等差数列的相同的项按原来的前后次序组成一 个等差数列,且公差为原来两个公差的最小公倍数。 解:设两数列的共同项组成的新数列为{an},则{an} 是首项为11的等差数列。
高中数学人教版必修5课件:2.2.1等差数列的性质(共14张PPT)

ap a1 ( p 1)d , aq a1 (q 1)d ,
am an 2a1 (m n 2)d ,
ap aq 2a1 ( p q 2)d , m n p q,am an ap aq.
2、等差数列的性质二:
பைடு நூலகம்
课后作业
• 1. 在等差数列{an}中 ,已知a5=10 , a12=31 , 公差 d 及a19 。
• 2.已知为等差数列, a1+a5=10,
a2+a4+a6=33,则求a3+a4的值。
懂得如何避开问题的人,胜过知道怎样解决问题的人。在这个世界上,不知道怎么办的时候,就选择学习,也许是最佳选择。胜出者往往不是能力而是观念!在 永远是家,走出去看到的才是世界。把钱放在眼前,看到的永远是钱,把钱放在有用的地方,看到的是金钱的世界。给人金钱是下策,给人能力是中策,给人观 财富买不来好观念,好观念能换来亿万财富。世界上最大的市场,是在人的脑海里!要用行动控制情绪,不要让情绪控制行动;要让心灵启迪智慧,不能让耳朵 人与人之间的差别,主要差在两耳之间的那块地方!人无远虑,必有近忧。人好的时候要找一条备胎,人不好的时候要找一条退路;人得意的时候要找一条退路 时候要找一条出路!孩子贫穷是与父母的有一定的关系,因为他小的时候,父母没给他足够正确的人生观。家长的观念是孩子人生的起跑线!有什么信念,就选 有什么态度,就会有什么行为;有什么行为,就产生什么结果。要想结果变得好,必须选择好的信念。播下一个行动,收获一种习惯;播下一种习惯,收获一种 一种性格,收获一种命运。思想会变成语言,语言会变成行动,行动会变成习惯,习惯会变成性格。性格会影响人生!习惯不加以抑制,会变成生活的必需品, 随时改变人生走向。人往往难以改变习惯,因为造习惯的就是自己,结果人又成为习惯的奴隶!人生重要的不是你从哪里来,而是你到哪里去。当你在埋头工作 定要抬头看看你去的方向。方向不对,努力白费!你来自何处并不重要,重要的是你要去往何方,人生最重要的不是所站的位置,而是所去的方向。人只要不失 永远不会失去自己!这个世界唯一不变的真理就是变化,任何优势都是暂时的。当你在占有这个优势时,必须争取主动,再占据下一个优势,这需要前瞻的决断 是智慧!世上本无移山之术,惟一能移山的方法就是:山不过来,我就过去。人生最聪明的态度就是:改变可以改变的一切,适应不能改变的一切!学一分退让 宜;增一分享受,减一分福泽。念头端正,福星临,念头不正,善人行善,从乐入乐,从明入明;行恶,从苦入苦,骨宜刚,气宜柔,志宜大,胆宜小,心宜虚 慧宜增,福宜惜,虑不远,忧亦近。人之所以痛苦,在于追求错误的东西。你目前拥有的,都将随着你的而成为他人的。那为何不现在就给真正需要的人呢?如 往,凡做事应有余步。我们最值得自豪的不在于从不跌倒,而在于每次跌倒之后都爬得起来。见己不是,万善之门。见人不是,诸恶之根。为了向别人、向世界 努力拼搏,而一旦你真的取得了成绩,才会明白:人无须向别人证明什么,只要你能超越自己。没有哪种教育能及得上逆境。如果你想成功,那么请记住:遗产 第一、学习第二、礼貌第三、刻苦第四、精明第五。任何的限制,都是从自己的内心开始的。失败只是暂时停止成功,假如我不能,我就一定要;假如我要,我 无论你如何为他人着想,烦你的人眼里,你就是居心叵测;不管你怎样据理力争,不懂你的人心里,你就是胡搅蛮缠。最后你会发现,有些事不是你做错了,而 人;有些人不是不理解你,而是根本不想懂你。不管怎样,生活还是要继续向前走去。有的时候伤害和失败不见得是一件坏事,它会让你变得更好,孤单和失落 每件事到最后一定会变成一件好事,只要你能够走到最后。工资是发给日常工作的人,高薪是发给承担责任的人,奖金是发给做出成绩的人,股权是分给能干忠 誉是颁给有理想抱负的人,辞退信将送给没结果还耍个性的人,这里一定有个你。内心想成为什么样的人,就会努力成为这样的人,做你想做的那种人。与其指 谁,不如指望自己能够吸引那样的人;与其指望每次失落的时候会有正能量出现温暖自己,不如指望自己变成一个正能量满满的人;与其担心未来,不如现在好 虹绚烂多姿,是在与狂风暴雨争斗之后;枫叶似火燃烧,是在与秋叶的寒霜争斗之后;雄鹰的展翅高飞,是在与坠崖的危险争斗之后。他们保持着奋斗的姿态, 们的成功。有能力的人影响别人,没能力的人受人影响;不是某人使自己烦恼不安,而是自己拿某人的言行来烦恼自己;树一个目标,一步步前行,做好自己就 不需鼓掌,也在飞翔;小草,没人心疼,也在成长;野花,没人欣赏,也在芬芳;做事不需人人都理解,只需尽心尽力;做人不需人人都喜欢,只需坦坦荡荡。 为力,拼搏到感动自己;吃过的苦,受过的累,会照亮未来的路;没有年少轻狂,只有胜者为王。真正成功的人生,不在于成就的大小,而在于你是否努力地去 喊出自己的声音,走出属于自己的道路。选一个方向,定一个时间;剩下的只管努力与坚持,时间会给我们最后的答案。许多人企求着生活的完美结局,殊不知 结局,而在于追求的过程。慢慢的才知道:坚持未必就是胜利,放弃未必就是认输,。给自己一个迂回的空间,学会思索,学会等待,学会调整。人生没有假设 全部。背不动的,放下了;伤不起的,看淡了;想不通的,不想了;恨不过的,抚平了。在比夜更深的地方,一定有比夜更黑的眼睛。一切伟大的行动和思想, 不足道的开始。从来不跌倒不算光彩,每次跌倒后能再站起来,才是最大的荣耀。这个世界到处充满着不公平,我们能做的不仅仅是接受,还要试着做一些反抗 苦、最卑贱、最为命运所屈辱的人,只要还抱有希望,便无所怨惧。有些人,因为陪你走的时间长了,你便淡然了,其实是他们给你撑起了生命的天空;有些人 就忘了吧,残缺是一种大美。照自己的意思去理解自己,不要小看自己,被别人的意见引入歧途。没人能让我输,除非我不想赢!花开不是为了花落,而是为了 烂。随随便便浪费的时间,再也不能赢回来。不管从什么时候开始,重要的是开始以后不要停止;不管在什么时候结束,重要的是结束以后不要后悔。当你决定 情,全世界都会为你让路。只有在开水里,茶叶才能展开生命浓郁的香气。别想一下造出大海,必须先由小河川开始。不要让未来的你,讨厌现在的自己,困惑 成功只配得上勇敢的行动派。人生最大的喜悦是每个人都说你做不到,你却完成它了!如果你真的愿意为自己的梦想去努力,最差的结果,不过是大器晚成。不 得始终。每个人都有潜在的能量,只是很容易:被习惯所掩盖,被时间所迷离,被惰性所消磨。不论你在什么时候开始,重要的是开始之后就不要轻言放弃。恨 的却是自己。每天醒来,敲醒自己的不是钟声,而是梦想。你不能拼爹的时候,你就只能去拼命!、如果人生的旅程上没有障碍,人还有什么可做的呢。我们无 的出身,可是我们的未来是自己去改变的。励志名言:比别人多一点执着,你就会创造奇迹伟人之所以伟大,是因为他与别人共处逆境时,别人失去了信心,他 现自己的目标。人生就像一道漫长的阶梯,任何人也无法逆向而行,只能在急促而繁忙的进程中,偶尔转过头来,回望自己留下的蹒跚脚印。时间,带不走真正 月,留不住虚幻的拥有。时光转换,体会到缘分善变;平淡无语,感受了人情冷暖。有心的人,不管你在与不在,都会惦念;无心的情,无论你好与不好,只是 一段路,总能有一次领悟;经历一些事,才能看清一些人。我们无法选择自己的出身,可是我们的未来是自己去改变的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、导入①.1,4,7,10,1316,…②.2,0,-2,-4,-6,-8,…它们共同的规律是什么?从第2项起,每一项与前一项的差等于同一个常数,我们把有这一特点的数列叫做等差数列.二、新课1、等差数列的定义一般地,如果一个数列从第2项起,,那么这个数列就叫做等差数列。
这个常数叫做等差数列的公差,公差通常用字母d表示.2、思考:(1)定义中的关键词有哪些?(2)公差d是哪两个数的差?3、等差数列定义的数学表达式:4、试一试:它们是等差数列吗?(1)1,3,5,7,9,2,4,6,8,10,…;(2)5,5,5,5,5,5,…;(3)-1,-3,-5,-7,-9,…;(4)数列{a n},a n+1-a n=3.5、将下列填上适当的数,使它成为等差数列①、___,2,4 ②、1,3,5,__三、.等差数列的通项公式1、等差数列的通项公式(求法一:不完全归纳法) 如果等差数列{a n}的首项是a1,公差是d,那么这个等差数列中的a2,a3,a4如何表示?a n呢?根据等差数列的定义可得:a2-a1=d,a3-a2=d,a4-a3=d,….所以a2=a1+d,a3=a2+d=(a1+d)+d=a1+2d,a4=a3+d=(a1+2d)+d=a1+3d,…由此得a n=.因此等差数列的通项公式就是:a n=a1+(n-1)d,n∈N*.2、通项公式的推导①1,3,5,7,9,11,13,…….我们发现:a2-a1=da3-a2=da4-a3=d……a n-a n-1=d用叠加的方法,推得a n-a1=d+d+d+….+d=(n-1)d,∴a n=a1+(n-1)d.可以推出a n=2n-1 也就是说1,3,5,7,9,11,13,……2n-1将以上n-1个式子相加所得到的等差数列的通项公式为a n=a1+(n-1)d,n∈N*.第n项是2n-1. a n=2n-1,n取1,2,3,…,分别可以得到数列中不同的项;1,3,5,7,….②若a n=2n+1,求前5项。
③若a n=2n,求a200四、运用规律,解决问题1. (1)求等差数列8,5,2,…的第20项.(2)等差数列-5,-9,-13,…的第几项是-401?2.在等差数列中,已知a 5=10,a 12=31,求首项a 1与公差d.3.已知等差数列{a n }中,a 3=9,a 9=3,求公差d.4.在等差数列{a n }中,a 1=13,a 3=12,若a n =2,求n.5.等差数列{a n }中,a 1+a 5=10,a 4=7,求数列{a n }的公差.6、2005是数列7,13,19,25,13中的第( )项. A. 332 B. 333 C. 334 D. 3357、若数列{a n }的通项公式为a n =2n+5,则此数列是( ) A.公差为2的等差数列 B. 公差为5的等差数列 C.首项为5的等差数列 D. 公差为n 的等差数列8.等差数列-3,-7,-11,...的一个通项公式为( ) A.4n-7B.-4n-7C.4n+1D.-4n+19.若数列{a n }满足3a n +1=3a n +1,则数列是( )A .公差为1的等差数列B .公差为13的等差数列C .公差为-13的等差数列D .不是等差数列10.对等差数列概念的理解 (1) 等差数列定义中的关键词是:(2) 定义中“每一项与它的前一项的差”的含义(3) 用数学符号语言叙述等差数列的定义:(4)公差d 对数列单调性的影响:当d =0时,数列为数列; 当d >0时,数列为数列; 当d <0时,数列为数列.12.对等差数列通项公式的理解(1) 等差数列{a n }的通项公式为:其中共含有四个变数,即,如果知道了其中的任意三个数,就可以由通项公式求出第四个数,这一求未知量的过程我们通常称之为“知三求一”.请你写出求解另外三个量的公式吧! 13、首项为-24的等差数列从第10项起开始为正数,则公差d 的取值范围是( )[来源:学_科_网Z_X_X_K] A.d>38B.d<3C.38≤d<3D.38<d ≤314、等差数列{a n }中,a 3=50,a 5=30,,则a 7=.15、如果等差数列{a n }的第5项为5,第10项为-5,则此数列的第1个负数项是第项.16、判断数52,2k+7是否是等差数列{a n }:-5,-3,-1,...中的项,若是,是第几项17、已知f(1)=2,f()n+1)=21)(2 n f ,,求f(1001).18从函数的角度研究等差数列的通项公式及等差数列的图象:19、 由思考1可得d =a n -a 1n -1,d =a n -a mn -m,你能联系直线的斜率解释一下这两个式子的几何意义吗?等差数列通项公式可变形为a n =dn +(a 1-d ),其图象为一条直线上孤立的一系列点,(1,a 1),(n ,a n ),(m ,a m )都是这条直线上的点.d 为直线的斜率,故两点(1,a 1),(n ,a n )连线的斜率d =a n -a 1n -1.当两点为(n ,a n ),(m ,a m )时,有d =a n -a mn -m .梳理 等差数列{a n }中,若公差为d ,则a n =a m +(n -m )d ,当n ≠m 时,d =a n -a mn -m .五 等差数列的性质思考 还记得高斯怎么计算1+2+3+…+100的吗?推广到一般的等差数列,你有什么猜想?答案 利用1+100=2+99=….在有穷等差数列中,与首末两项“等距离”的两项之和等于首项与末项的和.即a 1+a n =a 2+a n -1=a 3+a n -2=….梳理 在等差数列{a n }中,若m +n =p +q (m ,n ,p ,q ∈N *),则a m +a n =a p +a q .特别地,若m +n =2p ,则a n +a m =2a p六 由等差数列衍生的新数列思考 若{a n }是公差为d 的等差数列,那么{a n +a n +2}是等差数列吗?若是,公差是多少? 答案 ∵(a n +1+a n +3)-(a n +a n +2) =(a n +1-a n )+(a n +3-a n +2) =d +d =2d .∴{a n +a n +2}是公差为2d 的等差数列.梳理 若{a n },{b n }分别是公差为d ,d ′的等差数列,则有数列 结论{c +a n } 公差为d 的等差数列(c 为任一常数) {c ·a n } 公差为cd 的等差数列(c 为任一常数) {a n +a n +k } 公差为2d 的等差数列(k 为常数,k ∈N *) {pa n +qb n }公差为pd +qd ′的等差数列(p ,q 为常数)1.下面是关于公差是d >0的等差数列{a n }的四个命题: p 1:数列{a n }是递增数列;p 2:数列{na n }是递增数列; p 3:数列{na n}是递增数列; p 4:数列{a n +3nd }是递增数列. 其中的真命题为( )A .p 1,p 2B .p 3,p 4C .p 2,p 3D .p 1,p 4七--------有关等差数列的设定艺术(1)设{a n }是递增等差数列,前三项的和为12,前三项的积为48,求它的首项(2)成等差数列的四个数之和为26,第二数与第三数之积为40,求这四个数。
八、等差数列基1、等差数列-89,-87,-85,…,1的项数是 ( ) A .92 B .47 C .46 D .452、设等差数列{a n }中,a 4=5,a 9=17,则a 14的值等于 (3、已知等差数列的第10项为23,第25项为−22,则此数列的通项公式为a n =.4、等差数列{a n }中,a 7=4,a 19=2a 9,求{a n }的通项公式.5、在等差数列{a n }中,已知a 1=13,a 2+a 5=4,a n =33,则n 等于 ( )6.等差数列{a n }中,a 3=7,a 5=a 2+6,则a 6=________.7、首项为-12的等差数列,从第10项起开始为正数,则公差d 的取值范围是( )8、已知等差数列{a n }的首项a 1=125,第10项是第一个比1大的项,则公差d 的取值范围是9、数列{a n }的通项公式为a n =2n +C (C 为常数),则此数列 ( )A .是公差为2的等差数列B .是公差为5的等差数列C .是首项为5的等差数列D .是公差为n 的等差数列10、在等差数列{a n }中,已知a m+n =A ,a m-n =B ,,且m>n ,则a m =______.11、已知数列a 1,a 2,...,a 30,其中a 1,a 2,...,a 10是首项为1,公差为1的等差数列;a 10,a 11,...a 20是公差为d 的等差数列;302120,,,a a a 是公差为d 2的等差数列(d ≠0).(1)若4020 a ,求d ;(2)试写出a 30关于d 的关系式,并求a 30的取值范围.八、等差1.已知数列{a n }的通项公式为a n =4n-3,则a 5的值是( ) A .9 B .13 C .17 D .212.在等差数列{a n }中,首项a 1=2 公差d=2,a n =32 ,则项数n 为( )A .13B .14C .15D .163.在等差数列{a n }中,a 3=5,a 10=19,则a 51的值为( )A .99B .49C .101D .1024.已知{a n }为等差数列,且a 7-2a 4=-1,a 3=0则公差d ( ) A .-2 B .1/2 C . -1/2 D .25、由a 1=1,d=3确定的等差数列{a n },当a n =298时,序号n ( )A 99B 100C 96D 1016、下列各命题中,真命题是( ) A.若{a n }是等差数列,则{|a n |}也是等差数列 B.若{|a n |}是等差数列,则{a n }也是等差数列 C.若存在自然数n 使2a n+1=a n +a n+2 则{a n }是等差数列D.若{a n }是等差数列,则对任意正整数n 都有2a n+1=a n +a n+27.在等差数列{a n }中,已知a m =n ,a n =m ,则a m +n 的值为________.。
