高二数学理科选修2-2期末测试题(优选.)
高中新课标数学选修(2-2)综合测试题(4)

高中新课标数学选修(2-2)综合测试题一、选择题1、函数2x y =在区间]2,1[上的平均变化率为( ) (A )2 (B )3 (B )4 (D )52曲线3x y =在点)1,1(处的切线与x 轴、直线2=x 所围成的三角形的面积为( )(A )38 (B )37 (C )35(D )343、已知直线kx y =是x y ln =的切线,则k 的值为( ) (A )e1 (B )e1-(C )e2 (D )e2-4、设ai b bi a ++,,1是一等比数列的连续三项,则b a ,的值分别为( )(A )21,23±=±=b a (B )23,21=-=b a(C )21,23=±=b a (D )23,21-=-=b a5、方程)(04)4(2R a ai x i x ∈=++++有实根b ,且bi a z +=,则=z ( )(A )i 22- (B )i 22+(C )i 22+- (D )i 22--6、已知三角形的三边分别为c b a ,,,内切圆的半径为r ,则三角形的面积为a s (21=rc b )++;四面体的四个面的面积分别为4321,,,s s s s ,内切球的半径为R 。
类比三角形的面积可得四面体的体积为( )(A )R s s s s V )(214321+++= (B )Rs s s s V )(314321+++=(C )Rs s s s V )(414321+++= (D )R s s s s V )(4321+++=7、数列 ,4,4,4,4,3,3,3,2,2,1的第50项是( )(A )8 (B )9 (C )10 (D )118、在证明12)(+=x x f 为增函数的过程中,有下列四个命题:①增函数的定义是大前提;②增函数的定义是小前提;③函数12)(+=x x f 满足增函数的定义是小前提;④函数12)(+=x x f 满足增函数的定义是大前提;其中正确的命题是( )(A )①② (B )②④ (C )①③ (D )②③9、若R b a ∈,,则复数i b b a a )62()54(22-+-++-表示的点在( ) (A )在第一象限 (B )在第二象限(C )在第三象限 (D )在第四象限 10、用数学归纳法证明不等式“)2(2413212111>>+++++n nn n ”时的过程中,由k n =到1+=k n 时,不等式的左边( )(A )增加了一项)1(21+k(B )增加了两项)1(21121+++k k(C )增加了两项)1(21121+++k k ,又减少了11+k ;(D )增加了一项)1(21+k ,又减少了一项11+k ;11、如图是函数d cx bx x x f +++=23)(的大致 图象,则2221x x +等于( ) (A )32 (B )34 (C )38 (D )31212、对于函数233)(x x x f -=,给出下列四个命题:①)(x f 是增函数,无极值;②)(x f 是减函数,有极值;③)(x f 在区间]0,(-∞及),2[+∞上是增函数;④)(x f 有极大值为0,极小值4-;其中正确命题的个数为( )(A )1 (B )2(C )3 (D )4班级: 姓名:题号 1 2 3 4 5 6 7 8 9 10 11 12 答案二、填空题13、函数13)(3+-=x x x f 在闭区间]0,3[-上的最大值与最小值分别为:14、若i z 311-=,i z 862-=,且21111z z z =+,则z 的值为 ;15、用火柴棒按下图的方法搭三角形:按图示的规律搭下去,则所用火柴棒数n a 与所搭三角形的个数n 之间的关系式可以是 .16、物体A 的运动速度v 与时间t 之间的关系为12-=t v (v 的单位是s m /,t 的单位是s ),物体B 的运动速度v 与时间t 之间的关系为t v 81+=,两个物体在相距为405m 的同一直线上同时相向运动。
高中数学选修2-2综合测试题(全册含答案)

高中数学选修2-2综合测试题(全册含答案)1.复数就像平面上的点,有实部和虚部。
2.复数就像向量,有大小和方向。
3.复数就像计算机中的复数类型,有实部和虚部。
4.复数就像两个数字的有序对,有序对的第一个数字是实部,第二个数字是虚部。
改写:关于复数的四种类比推理,可以用不同的比喻来描述复数的实部和虚部。
一种比喻是将复数看作平面上的点,实部和虚部分别对应点的横坐标和纵坐标;另一种比喻是将复数看作向量,实部和虚部分别对应向量的大小和方向;还可以将复数看作计算机中的复数类型,实部和虚部分别对应类型中的两个数;最后一种比喻是将复数看作有序对,实部和虚部分别对应有序对的第一个数字和第二个数字。
①复数的加减法运算可以类比多项式的加减法运算法则。
②由向量a的性质|a|²=a²,可以类比得到复数z的性质:|z|²=z²。
③方程ax²+bx+c=0 (a,b,c∈R,且a≠0)有两个不同的实数根的条件是b²-4ac>0,类比可得方程ax²+bx+c=0 (a,b,c∈C且a≠0)有两个不同的复数根的条件是b²-4ac>0.④由向量加法的几何意义,可以类比得到复数加法的几何意义。
其中类比得到的结论正确的是:A。
①③B。
②④C。
②③D。
①④2.删除明显有问题的段落。
3.填空题:11.若复数z满足z+i=0,则|z|=1.12.直线y=kx+1与曲线y=x³+ax+b相切于点A(1,3),则2a+b的值为4.13.第n个正方形数是n²。
14.++=AA′BB′CC′;+++=AA′BB′CC′DD′。
4.解答题:15.1) F(x)的单调区间为(-∞。
0)和(2.+∞)。
2) F(x)在[1,5]上的最小值为-5,最大值为9.16.因为AD⊥BC,所以AB²=AD²+DB²。
又因为AB⊥AC,所以AC²=AD²+DC²。
高二理科数学选修2-2测试题及答案

高二理科数学选修2-2测试题及答案高二选修2-2理科数学试卷第I卷选择题(共12小题,每小题5分,共60分)1.下列复数中,与5-2i共轭的是()。
A。
5+2i B。
5-2i C。
-5+2i D。
-5-2i2.已知f(x)=3x·sinx,则f'(1)=()。
A。
1/3+cos1 B。
11/3sin1+cos1 C。
3sin1-cos1 D。
sin1+cos13.设a∈R,函数f(x)=ex-ae-x的导函数为f'(x),且f'(x)是奇函数,则a为()。
A。
0 B。
1 C。
2 D。
-14.定积分∫1x(2x-e)dx的值为()。
A。
2-e B。
-e C。
e D。
2+e5.利用数学归纳法证明不等式1+1/2+1/3+…+1/(2n-1)<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了()项。
A。
1项 B。
k项 C。
2k-1项 D。
2k项6.由直线y=x-4,曲线y=2x以及x轴所围成的图形面积为()。
A。
40/3 B。
13 C。
25/2 D。
157.函数f(x)=x^3-ax^2-bx+a^2在x=1处有极值10,则点(a,b)为()。
A。
(3,-3) B。
(-4,11) C。
(3,-3)或(-4,11) D。
不存在8.函数f(x)=x^2-2lnx的单调减区间是()。
A。
(0,1] B。
[1,+∞) C。
(-∞,-1]∪(0,1] D。
[-1,0)∪(0,1]9.已知f(x+1)=2f(x)/(f(x)+2),f(1)=1(x∈N*),猜想f(x)的表达式是()。
A。
f(x)=4/(2x+2) B。
f(x)=2^(12/(x+1)) C。
f(x)=(x+1)/2 D。
f(x)=(2x+1)/210.若f(x)=-1/(2x^2+bln(x+2))在(-1,+∞)上是减函数,则b的取值范围是()。
A。
[-1,+∞) B。
(-1,+∞) C。
高二数学选修2-2练习题.doc.docx

0.3
0.4
⑶P(2
x<4)
P( x
2)
P( x
3)
0.20.3
0.5
B组答案
13—17. BABDD 18.
16
19. 15
21
22、解:(1)由题知,总得分X的概率分布列为:
2
3
21. 0.135
X-300-100100300
P
0.23
C320.220.8 C320.2 0.82
0.83
∴EX=3000.23( 100) C320.220.8100 C320.2 0.82300 0.83
X的数学期望EX
6
X
0
1
2
3
P
a
1
1
b
3
6
则a=_____
___.
9、一个袋中有
10个大小相同的小球,其中
6个红球,4个白球,现从中摸
3个,至少摸到2
个白球的概率是__________________.
三.解答题:本大题共
3小题,共
41分,解答题应写出文字说明、证明过程或演算步骤
.
10、(本题
12分)有品,其中
21、已知Y~N(3,1),P(4<Y<5)=_____________.
六、解答 :本大 共3小 ,共41分,解答 写出文字 明、 明 程或演算步 。
22、某考生参加一种 ,需回答三个 , 定:每 回答正确得
100分,回答不正确得
-100
分。已知 考生每 回答正确的概率都是
0.8,且各 回答正确与否相互之 没有
∴所求概率P(A)=19
36
(2)由 分析知,X的可能取0,1,2,
高二理科数学选修2-2测试题及答案(最新整理)

1
B. sin1+cos1
3
1
C. sin1-cos1
3
D.sin1+cos1
3、设 a R ,函数 f x ex aex 的导函数为 f ' x ,且 f ' x 是奇函数,则 a 为( )
A.0
B.1
C.2
D.-1
4、定积分
1
(2
x
e
x
)dx
的值为(
)
0
A. 2 e
B. e
C. e
2
3
3 27
为极大值,而 f (2) 2 c ,则 f (2) 2 c 为最大值,要使 f (x) c2 , x [1, 2]
恒成立,则只需要 c2 f (2) 2 c ,得 c 1,或c 2 …………12 分
21 解:(1) f (x) 6x2 6x, f (2) 12, f (2) 7, ………………………2 分
x
h x hx
0, x2
—
A
x2
0 极小值
x2,
+
A
1
依题意,
1 8a2 1,即 a2 3 ,
4
∵ a 0 ,∴ a 3 .
(2)解:对任意的 x1, x2 1,e 都有 f x1 ≥ g x2 成立等价于对任意的 x1, x2 1,e 都
有 f xmin ≥ g xmax . 当 x [1, e ]时, g x 1 1 0 .
)
A.f(0)+f(2) 2 f(1)
B.f(0)+f(2) 2 f(1)
C.f(0)+f(2)> 2 f(1)
D.f(0)+f(2) 2 f(12)
0
日照实验高中高二下学期期末复习数学练习十(选修2-2和2-3)
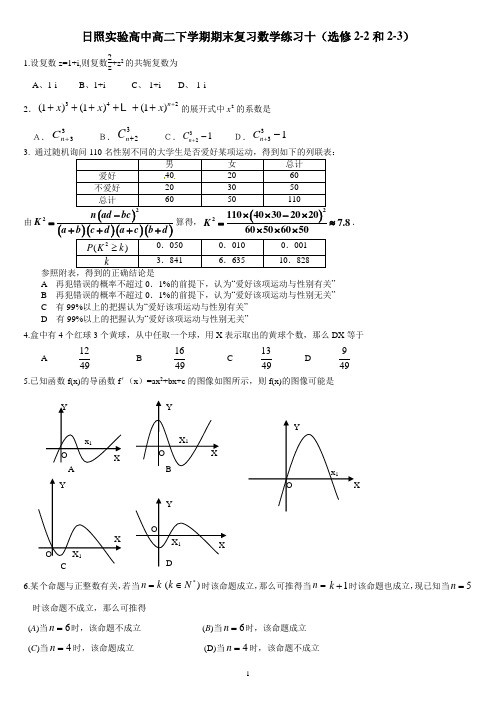
日照实验高中高二下学期期末复习数学练习十(选修2-2和2-3)1.设复数z=1+i,则复数2z +z 2的共轭复数为A 、1-iB 、1+iC 、-1+iD 、-1-i 2.342(1)(1)(1)n x x x +++++++的展开式中2x 的系数是A.33n C +B.32n C + C.321n C +-D.331n C +-3. 40 由()()()()()2n ad bc K a b c d a c b d -=++++算得,()2110403020207.860506050K ⨯⨯-⨯=≈⨯⨯⨯.A 再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B 再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C 有99%以上的把握认为“爱好该项运动与性别有关”D 有99%以上的把握认为“爱好该项运动与性别无关”4.盒中有4个红球3个黄球,从中任取一个球,用X 表示取出的黄球个数,那么DX 等于 A1249 B 1649 C 1349 D 9495.已知函数f(x)的导函数f '(x )=ax2+bx+c 的图像如图所示,则f(x)的图像可能是6.某个命题与正整数有关,若当)(*N k k n∈=时该命题成立,那么可推得当=n 1+k 时该命题也成立,现已知当5=n 时该命题不成立,那么可推得(A )当6=n 时,该命题不成立(B )当6=n 时,该命题成立 (C )当4=n 时,该命题成立 (D)当4=n 时,该命题不成立7.正态总体的概率密度函数为2()8()x x f x -∈=R ,则总体的平均数和标准差分别为 A.0,8B .0,4C.0,2D.0,28.从甲袋中摸出1个红球的概率为13,从乙袋中摸出1个红球的概率为12,从两袋中各摸出一个球,则23等于 (A )2个球都不是红球的概率 (B )2个球都是红球的概率 (C )至少有1个红球的概率 (D )2个球中恰有1个红球的概率 9.若随机变量η的分布列如下:则当()0.8P x η<=时,实数x 的取值范围是( ) A.x ≤2B.1≤x ≤2C.1<x ≤2D.1<x <210. 有6位同学在毕业聚会活动中进行纪念品的交换,任意两位同学之间最多交换一次,进行交换的两位同学互赠一份纪念品,已知6位同学之间共进行了13次交换,则收到4份纪念品的同学人数为 ( )A .1或3B .1或4C .2或3D .2或4 11.若x <y <0且xy -(x 2+y 2)i =2-5i ,则x =_____,y =______. 12.任意地向(0,1)上投掷一个点,用x 表示该点坐标,且1A=0,2x x ⎧⎫<<⎨⎬⎩⎭()1B=1,P B 4x x A ⎧⎫<<=⎨⎬⎩⎭则____ 13. 用五种不同的颜色,给图2中的(1)(2)(3)(4)的各部分涂色,每部分涂一种颜色,相邻部分涂不同颜色,则涂色的方法共有 种。
(必考题)高中数学高中数学选修2-2第五章《数系的扩充与复数的引入》测试题(有答案解析)

一、选择题1.已知,a b ∈R ,且2,ai b i ++(i 是虚数单位)是实系数一元二次方程20x px q ++=的两个根,那么,p q 的值分别是( )A .4,5p q ==B .4,3p q =-=C .4,5p q =-=D .4,3p q ==2.若202031i iz i+=+,则z 在复平面内对应点位于( )A .第一象限B .第二象限C .第三象限D .第四象限3.若复数z 的虚部小于0,|z |=4z z +=,则iz =( ) A .13i +B .2i +C .12i +D .12i -4.若复数34sin cos 55z i θθ⎛⎫=-+- ⎪⎝⎭是纯虚数,则tan()θ-π的值为( ) A .34±B .43C .34-D .43-5.已知i 是虚数单位,复数134z i =-,若在复平面内,复数1z 与2z 所对应的点关于虚轴对称,则12z z ⋅= A .25-B .25C .7-D .76.已知(,)z x yi x y R =+∈且1z =,则x +的最大值( ) A.1B .2C .1D7.已知复数12,z z 在复平面内对应的点分别为()()2,1,0,1--,则122z z z +=( ) A .22i +B .22i -C .2i -+D .2i --8.下列命题中,正确的是( ). A .若z 是复数,则22||z z = B .任意两个复数不能比较大小C .当240b ac ->时,一元二次方程20ax bx c ++=(,,)a b c C ∈有两个不相等的实数根D .在复平面xOy 上,复数2z m mi =+(m R ∈,i 是虚数单位)对应的点的轨迹方程是2y x =9.复数1234ii-+在复平面上对应的点位于第________象限 A .一B .二C .三D .四10.设i为虚数单位,则复数z =的共轭复数是( ) A .1i +B .1i -C .1i -+D .2i +11.已知向量OA =(2,2),OB =(4,1),在x 轴上一点P ,使AP ·BP 有最小值,则点P 的坐标为 ( ) A .(-3,0)B .(2,0)C .(3,0)D .(4,0)12.已知复数z 的模为2,则z i -的最大值为:( ) A .1B .2CD .3二、填空题13.已知复数乘法()()cos sin x yi i θθ++(,x y R ∈,i 为虚数单位)的几何意义是将复数x yi +在复平面内对应的点(),x y 绕原点逆时针方向旋转θ角,则将点()8,4绕原点逆时针方向旋转3π得到的点的坐标为_________. 14.已知复数12,z z 满足122,3z z ==,若它们所对应向量的夹角为60︒,则1212z z z z +=-___ 15.已知i 为虚数单位,计算1i1i-=+__________. 16.411i i +⎛⎫=⎪-⎝⎭__________. 17.已知复数43i z =+(i 为虚数单位),则z =____. 18.已知复数43cos sin 55z i θθ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭是纯虚数,(i 为虚数单位),则tan 4πθ⎛⎫-= ⎪⎝⎭__________.19.复平面内,已知复数13z x i =-所对应的点都在单位圆内,则实数x 的取值范围是__________.20.复平面内有,,A B C 三点,点A 对应的复数为2i +,向量BA 对应的复数为23i +,向量BC 对应的复数为3i -,则点C 对应的复数是___________.三、解答题21.已知复数2(1)(24)33Z i m i m i =+-+-+ (1)当m 为何值时 , Z 为纯虚数 ?(2) 当m 为何值时 , Z 对应的点在y x =上?22.已知关于x 的方程2()40x x m m R ++=∈的两个虚根为α、β,且||2αβ-=,求m 的值. 23.计算:(1))()245i +(2)1-的值.24.设z 是虚数,1=z zω+ 是实数,且-1<2ω< (1) 求z 的实部的取值范围(2)设11zzμ-=+ ,那么μ是否是纯虚数?并说明理由. 25.已知复数2z i =-(i 为虚数单位). (1)求复数z 的模z ; (2)求复数z 的共轭复数;(3)若z 是关于x 的方程250x mx -+=一个虚根,求实数m 的值.26.设m ∈R ,复数z 1=22m mm +++(m -15)i ,z 2=-2+m (m -3)i ,若z 1+z 2是虚数,求m的取值范围.【参考答案】***试卷处理标记,请不要删除一、选择题 1.C 解析:C 【分析】利用根与系数的关系列出方程组,根据复数相等运算即可得出所求结果. 【详解】因为2,ai b i ++(i 是虚数单位)是实系数一元二次方程20x px q ++=的两个根,所以()()22ai b i p ai b i q +++=-⎧⎨++=⎩,所以210220b p a b a q ab +=-⎧⎪+=⎪⎨-=⎪⎪+=⎩,解得1245a b p q =-⎧⎪=⎪⎨=-⎪⎪=⎩. 故选:C 【点睛】本题主要考查复数的有关计算,解题的关键是熟练掌握复数相等的条件和一元二次方程根与系数的关系.2.A解析:A 【分析】化简得到2z i =+,得到答案.【详解】()()()()202013131342211112i i i i i i z i i i i i +-+++=====++++-,对应的点在第一象限.故选:A . 【点睛】本题考查了复数对应象限,意在考查学生的计算能力.3.C解析:C 【分析】根据4z z +=可得()2z mi m =+∈R ,结合模长关系列方程,根据虚部小于0即可得解. 【详解】由4z z +=,得()2z mi m =+∈R ,因为||z ==1m =±. 又z 的虚部小于0,所以2z i =-,12iz i =+. 故选:C 【点睛】此题考查复数的概念辨析和模长计算,根据复数的概念和运算法则求解.4.C解析:C 【分析】根据所给的虚数是一个纯虚数,得到虚数的实部等于0,而虚部不等于0,得到角的正弦和余弦值,根据同角三角函数之间的关系,得到结果. 【详解】 若复数34sin (cos )55z i θθ=-+-是纯虚数, 则3sin 05θ-=且4cos 05θ-≠, 所以3sin 5θ=,4cos 5θ=-,所以3tan 4θ=-,故tan()θ-π=3tan 4θ=-. 故选C . 【点睛】本题主要考查了复数的基本概念,属于基础题.纯虚数是一个易错概念,不能只关注实部为零的要求,而忽略了虚部不能为零的限制,属于易错题.5.A解析:A 【解析】 【分析】根据复数1z 与2z 所对应的点关于虚轴对称,134z i =-,求出2z ,代入计算即可 【详解】复数1z 与2z 所对应的点关于虚轴对称,134z i =-234z i ∴=--()()12343425z z i i ⋅=---=-故选A 【点睛】本题主要考查了复数的运算法则及其几何意义,属于基础题6.B解析:B 【解析】分析:由1z =可得221x y +=,可设cos x θ=,sin y θ=,R θ∈,可得2sin()6x πθ=+,进而利用正弦函数的性质求出答案.详解:∵(),z x yi x y R =+∈且1z = ∴221x y +=设cos x θ=,sin y θ=,R θ∈.∴cos 2sin()6x πθθθ+=+=+∴x +的最大值是2 故选B.点睛:本题主要考查复数的求模公式及三角函数的性质,解答本题的关键是利用三角换元结合三角函数的性质求函数的最值.7.A解析:A 【解析】分析:首先确定复数12,z z ,然后结合题意进行复数的混合运算即可. 详解:由题意可得:122,z i z i =-=-, 则:()1222212i i z i i z i i--===+--,21z =, 据此可得:12222z z i z +=+.本题选择A 选项.点睛:本题主要考查复数的定义及其运算法则等知识,意在考查学生的转化能力和计算求解能力.8.D解析:D 【分析】举例说明A 错误;当两复数为实数时B 错误;由实系数一元二次方程的判别式与根的关系说明C 错误;求出z 的参数方程,消参后得到z 的轨迹方程说明D 正确. 【详解】 解:对于A ,若zi ,则2||1z =,21z =-,22||z z ≠,故A 错误;对于B ,当两个复数均为实数时,可以比较大小,故B 错误;对于C ,只有当a ,b ,c 均为实数时,在满足240b ac ->时,一元二次方程20ax bx c ++=有两个不相等的实数根,故C 错误;对于D ,由2(z m mi m R =+∈,i 是虚数单位),设z 对应的点(,)Z x y ,得2x m y m⎧=⎨=⎩,消去m 得,2y x =,∴在复平面xOy 上,复数2(z m mi m R =+∈,i 是虚数单位)对应的点的轨迹方程是2y x =.故D 正确. 故选:D . 【点睛】本题考查命题的真假判断与应用,考查了复数的有关概念,考查复数的代数表示法及其几何意义,属于基础题.9.C解析:C 【解析】 【分析】将复数化简为a bi +的形式,得到(,)a b ,就可以得到答案. 【详解】 ∵复数12(12)(34)5101234(34)(34)2555i i i i i i i i -----===--++- ∴复数1234ii -+在复平面上对应的点位于第三象限 故选C. 【点睛】复数化简为a bi +的形式,是解题关键,a b 、的符号决定复数在复平面上对应的点位于的象限.基础题目.10.A解析:A 【解析】【分析】利用复数的运算法则和共轭复数即可求得结果 【详解】()22111i z i i-====--,则共轭复数为1i +故选A 【点睛】本题主要考查了复数的运算法则和共轭复数,属于基础题11.C解析:C 【解析】设点P 坐标为(x ,0),则AP =(x-2,-2),BP =(x-4,-1),·AP BP =(x-2)(x-4)+(-2)×(-1)=x 2-6x+10=(x-3)2+1.当x=3时,P?A BP 有最小值1. 故点P 坐标为(3,0).选C.12.D解析:D 【解析】因为z i -213z i ≤+-=+= ,所以最大值为3,选D.二、填空题13.【分析】写出点对应的复数再乘以即得新复数其对应点坐标为所求【详解】点对应复数为对应点坐标为故答案为:【点睛】本题考查复数的新定义考查复数的乘法运算与复数和几何意义正确理解新定义把新定义转化为复数的乘解析:(42-+【分析】写出点()8,4对应的复数,再乘以cos sin33i ππ+即得新复数,其对应点坐标为所求.【详解】点()8,4对应复数为84z i =+,1(cossin )(84)()332z i i ππ+=+(4(2i =-++,对应点坐标为(42-+.故答案为:(42-+. 【点睛】本题考查复数的新定义,考查复数的乘法运算与复数和几何意义.正确理解新定义把新定义转化为复数的乘法解题关键.14.【解析】【分析】由余弦定理可得故【详解】如图在三角形中由余弦定理得同理可得故答案为:【点睛】本题主要考查复数的运算借助于余弦定理是解决问题的关键属中档题 解析:1337【解析】 【分析】由余弦定理可得12||19Z Z +=,12||7Z Z -=,故12121212||133||||7z z z z z z z z ++==-- 【详解】如图在三角形OAC 中由余弦定理得2212||||23223cos12019Z Z OB +==+-⨯⨯⨯︒=, 同理可得2212||||23223cos607Z Z CA -==+-⨯⨯⨯︒=,∴12121212||19133||||77z z z z z z z z ++===--. 故答案为:1337【点睛】本题主要考查复数的运算,借助于余弦定理是解决问题的关键,属中档题.15.【解析】分析:根据复数除法法则求解详解:复数点睛:首先对于复数的四则运算要切实掌握其运算技巧和常规思路如其次要熟悉复数相关基本概念如复数的实部为虚部为模为对应点为共轭为 解析:i -【解析】分析:根据复数除法法则求解.详解:复数1i (1)(1)2ii 1i (1)(1)2i i i i ----===-++-. 点睛:首先对于复数的四则运算,要切实掌握其运算技巧和常规思路,如()()()(),(,,.)++=-++∈a bi c di ac bd ad bc i a b c d R . 其次要熟悉复数相关基本概念,如复数(,)a bi a b R +∈的实部为a 、虚部为b(,)a b 、共轭为.-a bi16.1【解析】分析:先利用复数除法的运算法则化简再利用复数乘方运算法则求解即可详解:故答案为点睛:本题主要考查的是复数的乘法除法运算属于中档题解题时一定要注意和以及运算的准确性否则很容易出现错误解析:1 【解析】分析:先利用复数除法的运算法则化简11ii+-,再利用复数乘方运算法则求解即可. 详解:411i i +⎛⎫ ⎪-⎝⎭()()()4241i 2i =11i 1i 2⎡⎤+⎛⎫==⎢⎥ ⎪-+⎝⎭⎢⎥⎣⎦,故答案为1. 点睛:本题主要考查的是复数的乘法、除法运算,属于中档题.解题时一定要注意21i =-和()()()()a bi c di ac bd ad bc i ++=-++以及()()()()a bi c di a bi c di c di c di +-+=++- 运算的准确性,否则很容易出现错误.17.5【解析】解析:5 【解析】5z ==.18.【分析】利用复数为纯虚数可得实部为零虚部不为零从而可求利用同角的三角函数的基本关系式和两角差的正切可求的值【详解】所以故答案为:【点睛】本题考查复数的概念同角的三角函数的基本关系以及两角差的正确理解 解析:7-【分析】利用复数为纯虚数可得实部为零,虚部不为零,从而可求43cos 0,sin 055θθ-=-≠,利用同角的三角函数的基本关系式和两角差的正切可求tan 4πθ⎛⎫- ⎪⎝⎭的值. 【详解】4333cos 0,sin 0sin tan 5554θθθθ-=-≠⇒=-⇒=-, 所以tan 4πθ⎛⎫-= ⎪⎝⎭3147314--=--, 故答案为:7-.【点睛】本题考查复数的概念、同角的三角函数的基本关系以及两角差的正确,理解纯虚数的概念是关键,本题为中档题.19.【详解】∵z 对应的点z(x -)都在单位圆内∴|z|<1即<1∴x2+<1∴x2<∴- 解析:222233x -<<【详解】 ∵z 对应的点z (x ,-)都在单位圆内, ∴|z|<1,即<1.∴x 2+<1.∴x 2<. ∴-.20.【解析】试题分析:由得同理所以点对应的复数是考点:复数的几何意义 解析:33i -【解析】 试题分析:由得(2,1)(2,3)(0,2)OB OA BA =-=-=-,同理(0,2)(3,1)(3,3)OC OB BC =+=-+-=-,所以点C 对应的复数是33i -.考点:复数的几何意义.三、解答题21.(1) 1m =-(2) 3m =. 【解析】 【分析】化简复数为22(23)(43)Z m m m m i =--+-+,(1)由Z 为纯虚数,列出方程组,即可求解;(2)根据Z 对应的点在y x =上,列出方程,即可求解. 【详解】由题意,复数2(1)(24)33Z i m i m i =+-+-+,则22(23)(43)Z m m m m i =--+-+,(1)若Z 为纯虚数,则有22230430m m m m ⎧--=⎨-+≠⎩,解得:1m =-;(2)根据Z 对应的点在y x =上,则有222343m m m m --=-+,解得:3m =.【点睛】本题主要考查了复数的概念,以及复数的表示的应用,其中解答中熟记复数的表示方法,列出相应的方程(组)是解答的关键,着重考查了推理与运算能力,属于基础题. 22.5【解析】【分析】本题首先可以根据复数根虚根必共轭的性质设,a bi a bi αβ=+=-,然后根据韦达定理可得2a =-以及m ,再通过||2αβ-=计算得1b =±,最后通过运算即可得出结果。
日照实验高中高二下学期期末复习数学练习二十四(选修2-2和2-3)

日照实验高中高二下学期期末复习数学练习二十四(选修2-2和2-3)1.设复数z 满足i 2)i 1(=-z ,则=z A .i 1+- B .i 1-- C .i 1+ D .i 1-2.函数x e x f x ln )(=在点))1(,1(f 处的切线方程是A .)1(2-=x e y B .1-=ex y C .)1(-=x e y D .e x y -=3.观察下列关于两个变量x 和y 的三个散点图,它们从左到右的对应关系依次为A .正相关、负相关、不相关B .负相关、不相关、正相关C .负相关、正相关、不相关D .正相关、不相关、负相关4.曲线12ex y =在点2(4e),处的切线与坐标轴所围三角形的面积为 A 、24eB 、29e 2C 、2eD 、22e5.某班有48名学生,其中男生32人,女生16人. 李老师随机地抽查8名学生的作业,用X 表示抽查到的女生人数, 则E (X )的值为 A .316 B .38 C .3 D .46.若,A x ∈则,1A x ∈就称A 是伙伴关系集合,集合⎭⎬⎫⎩⎨⎧-=4,3,2,1,21,31,0,1M 的所有非空子集中,具有伙伴关系的集合的个数为A.15B.16C.82D. 527.函数2e 1x y x =-的部分图象为BD 8.设2()(,,),f x ax bx c a b c R e =++∈为自然对数的底数,若/()()ln f x f x x x>,则 A 2(2)()ln 2,2()()f f e f e f e <> B 2(2)()ln 2,2()()f f e f e f e << C2(2)()ln 2,2()()f f e f e f e >< D 2(2)()ln 2,2()()f f e f e f e >>9.将5名学生分到A ,B ,C 三个宿舍,每个宿舍至少1人至多2人,其中学生甲不到A 宿舍的不同分法有A .18种B .36种C .48种D .60种10.从1开始的自然数按照如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有9个数在此三角形内,则这9个数的和可以是A 2097B 1553C 1517D 211111.若二项式22nx x ⎛⎫+ ⎪⎝⎭的展开式共7项,则该展开式中的常数项为__________.12.已知函数2()x f x ex ae =+在图像上点(1,(1))f 处的的切线斜率为e ,则1()f x dx ⎰=_________13.对于*n N ∈,定义2()[][][]101010k n nnf n =+++,其中k 是满足10k n ≤的最大整数,[]x 表示不超过x 的最大整数,如[2.5]2,[3]3==,则(1)(2014)f =________;(2)满足()100f m =的最大整数m 为___________ 14.当,1x R x ∈<时,有如下表达式:211.......1n x x x x+++++=- 两边同时积分得:1111122222200011.......1ndx xdx x dx x dx dx x+++++=-⎰⎰⎰⎰⎰从而得到如下等式:23111111111()()...()...ln 2.2223212n n +⨯+⨯+⨯++⨯+=+ 请根据以上材料所蕴含的数学思想方法,计算:122311111111()()...()_____2223212nn n n n nn C C C C +⨯+⨯+⨯++⨯=+ 15.一袋中装有5个白球,3个红球,现从袋中往外取球,每次取出一个,取出后记下球的颜色,然后放回,直到红球出现2次停止,用X 表示取球的次数,则==)3(XP ___________.16.已知箱子中装有标号分别为1,2,3,4,5的五个小球,现从该箱子中取球,每次取一个球(无放回,且每球取到的机会相等)(1)若连续取两次,求取出的两球上的标号都是奇数或都是偶数的概率;(2)若取出的球的标号为奇数即停止取球,否则继续取,求取球次数X 的分布列和期望.17.现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.(Ⅰ)求张同学至少取到1道乙类题的概率;(Ⅱ)已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是35,答对每道乙类题的概率都是45,且各题答对与否相互独立.用X 表示张同学答对题的个数,求X 的分布列和数学期望. 解:(Ⅰ)设事件A =“张同学所取的3道题至少有1道乙类题”,18.第22届索契冬奥会期间,来自俄罗斯国际奥林匹克大学的男、女共9名志愿者被随机地平均分配到速滑、冰壶、自由式滑雪这三个岗位服务,且速滑岗位至少有一名女大学生志愿者的概率是1621. (1)求冰壶岗位至少有男、女大学生志愿者各一人的概率;(2)设随机变量X 为在自由式滑雪岗位服务的男大学生的人数,求X 的分布列及期望. 19.已知曲线()x f x ax e =-(0)a ≠.(Ⅰ)求曲线在点(0,(0)f )处的切线方程;(Ⅱ)若存在0x 使得0()0f x ≥,求a 的取值范围.20.已知函数12e ()44x f x ax x +=++,其中a ∈R .(Ⅰ)若0a =,求函数()f x 的极值;(Ⅱ)当1a >时,试确定函数()f x 的单调区间. 21.已知函数()(2)x f x nx n e =-+,(其中,n R e ∈为自然数的底数).(1)求()f x 在[0,1]的最大值; (2)若函数22*()1330(1,)g x nx nx n n N =-->∈,当0x >时,若/2()()f x g x >恒成立,求最大正整数n .日照实验高中高二下学期期末复习数学练习二十四(选修2-2和2-3)答案ACDCB AABDC11. 60 12. 213e - 13. 223,919 14. 113[()1]12n n +-+15. 25645 16.17.∴X的分布列为19.解:(Ⅰ)因为(0)1f =-,所以切点为(0,-1).()xf x a e '=-,(0)1f a '=-, 所以曲线在点(0,(0)f )处的切线方程为:y =(a -1)x -1(Ⅱ)(1)当a>0时,令()0f x '=,则ln x a =. 因为()xf x a e '=-在(,)-∞+∞上为减函数, 所以在(,ln )a -∞内()0f x '>,在(ln ,)a +∞内()0f x '<,所以在(,ln )a -∞内()f x 是增函数,在(ln ,)a +∞内()f x 是减函数, 所以()f x 的最大值为(ln )ln f a a a a =-因为存在0x 使得0()0f x ≥,所以ln 0a a a -≥,所以a e ≥. (2)当0a <时,()xf x a e '=-<0恒成立,函数()f x 在R 上单调递减,而11()10a f e a=->,即存在0x 使得0()0f x ≥,所以0a <.综上所述,a 的取值范围是(-∞,0)∪[e,+∞)20.(Ⅰ)解:函数1e ()44x f x x +=+的定义域为{|x x ∈R ,且1}x ≠-.11122e (44)4e 4e ()(44)(44)x x x x x f x x x ++++-'==++.令()0f x '=,得0x =, 当x 变化时,()f x 和()f x '的变化情况如下:故()f x 的单调减区间为(,1)-∞-,(1,0)-;单调增区间为(0,)+∞. 所以当0x =时,函数()f x 有极小值e(0)4f =. (Ⅱ)解:因为 1a >,所以 22244(2)(1)0ax x x a x ++=++->,所以函数()f x 的定义域为R ,求导,得12112222e (44)e (24)e (42)()(44)(44)x x x ax x ax x ax a f x ax x ax x +++++-++-'==++++, 令()0f x '=,得10x =,242x a=-, 当 12a <<时,21x x <, 当x 变化时,()f x 和()f x '的变化情况如下:故函数()f x 的单调减区间为(2,0)a -,单调增区间为(,2)a-∞-,(0,)+∞. 当 2a =时,210x x ==,因为12222e ()0(244)x x f x x x +'=++≥,(当且仅当0x =时,()0f x '=)所以函数()f x 在R 单调递增. 当 2a >时,21x x >, 当x 变化时,()f x 和()f x '的变化情况如下:故函数()f x 的单调减区间为4(0,2)a-,单调增区间为(,0)-∞,4(2,)a -+∞. 综上,当 12a <<时,()f x 的单调减区间为4(2,0)a -,单调增区间为4(,2)a-∞-,(0,)+∞;当 2a =时,函数()f x 在R 单调递增;当 2a >时,函数()f x 的单调减区间为4(0,2)a-;单调增区间为(,0)-∞,4(2,)a-+∞.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改
选修2-2巩固练习
1.给出下列四个命题:(1)若z C ∈,则02≥z ;(2)2i 1虚部是2i ; (3)若,i i a b a b >+>+则;(4)若12,z z ,且1
2z z ,则12,z z 为实数;
其中正确命题....
的个数为 ( ) A.1个 B.2个 C.3个 D.4个 2.复数(1i)(2i)b (b 是实数)表示的点在第四象限,则b 的取值范围是( )
A.b <12
-
B.b >1
2
-
C.1
2
-< b < 2 D.b < 2
3.定义运算a b ad bc c d
=- ,则符合条件
1142i i
z z -=+ 的复数z 为( )
A .3i -
B .13i +
C .3i +
D .13i -
4.有一段“三段论”推理是这样的:对于可导函数()f x ,如果0()0f x '=,那么
0x x = 是函数()f x 的极值点;因为函数3()f x x =在0x =处的导数值(0)0f '=,所
以,0x =是函数3()f x x =的极值点.以上推理中( )
A 、大前提错误
B 、小前提错误
C 、推理形式错误
D 、结论正确 5.已知()()3
2213a
f x x a x
=+-
+,若()18f '-=,则()1f -=( ) A .4 B .5 C .2 D .3
6.用数学归纳法证明1+12+13+…+1
2n -1
<n(n ∈N *,n>1)时,第一步应验证不等式
( )
A 、1+12<2
B 、1+12+13<3
C 、1+12+13+14<3
D 、1+12+1
3<2
7.若函数()ln f x x ax =-在点()1,P b 处的切线与320x y +-=垂直,则2a b +=( )
A .2
B .0
C . 1
D .2
8、已知在R 上可导的函数()f x 的图象如图所示,则不等式()()0f x f x ⋅'<的解集为( )。
A 、(2,0)-
B 、(,2)(1,0)-∞-⋃-
C 、(,2)(0,)-∞-⋃+∞
D 、(2,1)(0,)--⋃+∞ 9.a 为实数,若复数(2)
3i z a
是纯虚数,则
i
1i
a a = .
10.函数()ln f x x x x =-,
求函数()f x 的单调减区间为 极小值为
11.32()3f x x x a =++(a 为常数)在[33]-,
上有最小值3,则在[33]-,上()f x 的最大值是
12.曲线y =2y x =所围成的封闭图形的面积s=
13.已知复数12,Z Z 在复平面内对应的点分别为(2,1),(,3)A B a - (1)若
12Z Z a -=的值。
(2)复数12z Z Z =⋅对应的点在二、四象限的角平分线上,求a 的值。
14.观察以下5个等式:
-1=-1 -1+3=2 -1+3-5=-3 -1+3-5+7=4 -1+3-5+7-9=-5
……
(1)写出第6个等式,并猜想第n 个等式(n∈N *)
(2)用数学归纳法证明上述所猜想的第n 个等式(n∈N *)成立。
15.已知三次函数()()32,,f x x bx cx d a b c R =+++∈过点(3,0),且f(x)在点(0,f (0))处的切线恰好是直线y=0 (1)求函数()f x 的解析式;
(2)设g (x )=9x+m-1,若y=f(x)-g(x)在[-2,1]上有两个零点,求实数m 的范围。
16.已知函数()2x f x e ax =+-
(1)若1a =-,求函数f(x)在区间[1,1]-的最小值 (2)求函数f(x)在(0,)+∞的单调区间 (3)若函数x
a
x f x h +=)()(在),0(+∞单调递增,求实数a 的的取值范围。
最新文件---------------- 仅供参考--------------------已改成-----------word 文本 --------------------- 方便更改 赠人玫瑰,手留余香。
