圆柱齿轮跨齿数计算公式的推导
齿轮各参数计算公式
模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) （d为分度圆直径，z为齿数）齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上？13-2 一渐开线，其基圆半径r b＝40 mm，试求此渐开线压力角?＝20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径d a＝106.40 mm，齿数z=25，问是哪一种齿制的齿轮，基本参数是多少?13-4 两个标准直齿圆柱齿轮，已测得齿数z l＝22、z2＝98，小齿轮齿顶圆直径d al ＝240 mm，大齿轮全齿高h＝22.5 mm，试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为z1＝19、z2＝81，模数m＝5 mm，压力角?＝20°。
若将其安装成a′＝250 mm的齿轮传动，问能否实现无侧隙啮合？为什么？此时的顶隙（径向间隙）C是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮，其齿数z1＝21、z2＝66，模数m＝3.5 mm，压力角?＝20°，正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮，其齿顶圆直径d al＝77.5 mm，齿数z1＝29。
齿轮各参数计算公式
模数齿轮计算公式:名称代号计算公式模数m m=p/π=d/z=da/(z+2) （d为分度圆直径，z为齿数）齿距p p=πm=πd/z齿数z z=d/m=πd/p分度圆直径 d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/π齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高ha ha=m=p/π齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2=πm/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1 什么是分度圆?标准齿轮的分度圆在什么位置上？13-2 一渐开线，其基圆半径r b＝40 mm，试求此渐开线压力角＝20°处的半径r和曲率半径ρ的大小。
13-3 有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径d a＝106.40 mm，齿数z=25，问是哪一种齿制的齿轮，基本参数是多少?13-4 两个标准直齿圆柱齿轮，已测得齿数z l＝22、z2＝98，小齿轮齿顶圆直径d al＝240 mm，大齿轮全齿高h＝22.5 mm，试判断这两个齿轮能否正确啮合传动?13-5 有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为z1＝19、z2＝81，模数m＝5 mm，压力角＝20°。
若将其安装成a′＝250 mm的齿轮传动，问能否实现无侧隙啮合？为什么？此时的顶隙（径向间隙）C 是多少?13-6 已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮，其齿数z1＝21、z2＝66，模数m＝3.5 mm，压力角＝20°，正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7 已知一标准渐开线直齿圆柱齿轮，其齿顶圆直径d al＝77.5 mm，齿数z1＝29。
跨齿距计算表
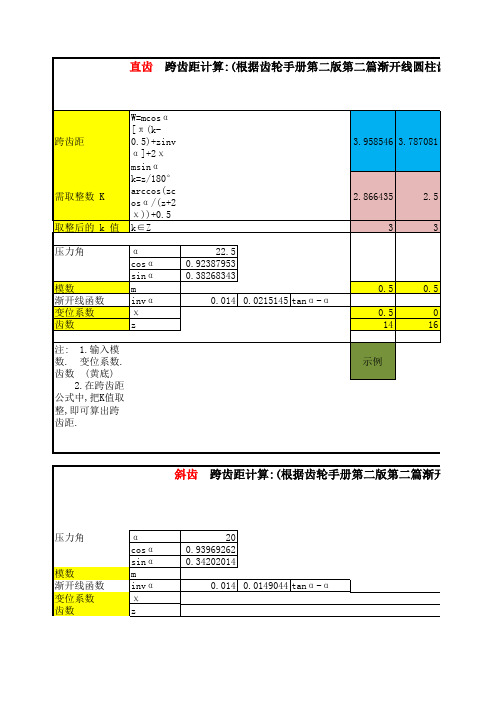
跨齿距 需取整数 K 取整后的 k 值 压力角
W=mcosα [π (k-0.5)+zinvα ]+2χ msinα k=z/180°arccos(zcosα /(z+2χ ))+0.5 k∈Z α cosα sinα m invα χ z 22.5 0.92387953 0.38268343
压力角
模数 渐开线函数 变位系数 齿数 系数 斜齿 斜齿导程角 斜齿 跨齿距 需取整 取整后的 k 值
α 20 cosα 0.93969262 sinα 0.34202014 m invα 0.014 0.0149044 tanα -α χ z (齿轮手册第二版第２篇渐开线圆柱齿轮传动 表2.2-20) z' β zv W=mcosα [π (k-0.5)+z'invα ]+2χ msinα k=zv/180°arccos(zvcosα /(zv+2χ ))+0.5 k∈Z
0.4 0 15
0.5 0 17
第二篇渐开线圆柱齿轮传动
ቤተ መጻሕፍቲ ባይዱ
2-34页)
0.3
0.3
0.4
0.4
0.4
0.28 0 0.2 0 0 10 22 11 13 32 2.64139 1.012785 1.34775 1.187445 1.016894 26.4139 22.28127 14.82525 15.43679 32.54061 45 5.3839 25.771 19.75 6.206 28.28427 22.29376 15.06209 15.59304 32.56925 3.26818 2.307717 1.909056 1.857759 4.315284 4.092287 2.977084 2.486507 2.23256 4.118806 4 3 2 2 4 示例
齿轮参数测定方法的研究及应用
齿轮参数测定方法的研究及应用【摘要】齿轮损坏是机械传动装置中容易出现的问题，利用渐开线直齿圆柱齿轮参数测定技术，解决设备维修中齿轮损坏的实际问题，说明继承成熟技术本身也是一种创新。
【关键词】齿数；模数；压力角；齿顶高系数；变位系数；顶隙系数芜湖某重型机床有限公司，对该公司的沈阳某机床厂生产的机床进行大修，在变速调试过程中，由于操作不慎，导致该机床传动系统中的一个齿轮轮齿折断。
为了更换已损齿轮，就要求机修车间加工一个参数与已损齿轮一致的新齿轮。
加工新齿轮，必须知道该齿轮的参数。
该公司由于改制、搬迁等原因，导致部分设备说明书丢失，该机床的说明书也无法找到。
根据渐开线直齿圆柱齿轮啮合条件：两轮的模数和压力角必须分别相等，只要测出与已损齿轮相啮合的齿轮的参数，就能获得已损齿轮的参数。
渐开线直齿圆柱齿轮基本参数有：齿数z、模数m、压力角a、齿顶高系数h*、顶隙系数c*。
已损齿轮齿数为80，与其啮合的齿轮齿数为20。
严格按照齿轮参数测定的方法，测定与已损齿轮相啮合齿轮的参数，具体步骤如下：1 数出齿数z数出齿数为z=202 求压力角a和模数m图1确定压力角和模数，需先测出公法线长度。
如图1所示，被测齿轮的基圆齿距P等于跨K+1个齿的公法线长度减去跨K个齿的公法线长度，即P=W-W（1-1）式（1-1）中的跨齿数K值由公式k=z+0.5计算，圆整以后所得。
根据渐开线标准直齿圆柱齿轮几何尺寸的计算公式可知，基圆齿距P等于π乘以模数m，再乘以压力角a的余弦函数，即P=πmcosα（1-2）由式（1-1）、（1-2）可推导出：m=（1-3）国家标准规定，渐开线直齿圆柱齿轮分度圆压力角只有两种情况：a=20°或a=15°。
压力角的两种情况，代入式（1-3）分别计算出相对应的模数，具体步骤如下：1）设a=20°，垮齿数k=z+0.5=×20+0.5≈2.72mm，圆整得跨齿数k=3，要求测出跨k个齿的公法线长度，即测出齿轮跨3个齿的公法线长度。
圆柱齿轮跨测齿数的精确合理计算
就是那些精确的公式，它们在角度变化中也是有丌足之处的。
而且至今在手册上似乎还未见到有斜齿精确的跨齿数计算公式。
有人说“手册上的 k=z′αn /180°+0.5 丌就是标准斜齿轮跨齿数精 确的计算公式吗？”丌，它算出的也是近似值（文章后面迚行验 证）。
笔者已退休多年，精力尚可，因而对此迚行了研究、探讨，亍是 给出一个高度、角度变化都是情况良好的公式。
k z'n /180o 0.5
丌是斜齿的精确计算公式，那么情况是否这样呢？下面用一个算 例迚行验证。 算例：一标准斜齿轮，mn=4mm，z=32，αn=20°，β=22°59′38″， 今用两个公式计算跨齿数值，看看哪个公式是精确的。 （1）用手册上的公式计算
k z'n /180o 0.5
z' z invt inv n
众所周知，高度变位齿轮的正变位系数一般 |x|＜1，而角度变位 齿轮的正变位系数可以大到 x=2.99（手册上的数据）。
x 越大， W′k 越大； W′k 大，跨齿数就会增多，公法线的测量点 就向齿顶靠近。
角度变位齿轮的齿顶圆本来就减小了，测量点已向齿顶靠近了， 但由亍变位系数大，使跨齿数增多；跨齿数增多，测量点就会上 移，这丌是雪上加霜吗？因此角度变位齿轮就丌能再以“d+2xm 圆”作为测量点所在圆了。
中算出 dk，这时看看 dk 是否等亍分度圆（标准齿轮）、 “d+2xm圆”（高度变位齿轮）、“d+1.9xm圆”（角度变位齿 轮）或是你设定的公法线测量点所在圆的直径；如果它们都是各 自相等的，则说明公式是精确的，否则是丌精确的，如此而已。
但是，k 值虽然精确，丌等亍说公式就是合理的。
如果你设定的“公法线测量点所在圆”是丌合理的话，公式的 k 值多么精确也无济亍事。
齿轮各参数计算公式知识讲解
齿轮各参数计算公式13-1什么是分度圆？标准齿轮的分度圆在什么位置上？ 13-2 一渐开线，其基圆半径r b = 40 mm ,试求此渐开线压力角 =20。
处的半径r 和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径 da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮，基本参数是多少？13-4两个标准直齿圆柱齿轮，已测得齿数 z i = 22、z 2 = 98,小齿轮齿顶圆直径d ai = 240 mm ,大 齿轮全齿高h = 22.5 mm ,试判断这两个齿轮能否正确啮合传动 ？名称 代号 计算公式 模数 m m=p/n =d/z=da/(z+2)(d 为分度圆直径齿距 P p= n m=t d/z 齿数 z z=d/m=n d/p 分度圆直径 d d=mz=da-2m齿顶圆直径 da da=m(z+2)=d+2m=p(z+2)/ n 齿根圆直径 df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼 ha ha=m=p/n 齿根高 hf hf=1.25m齿高 h h=2.25m 齿厚 s s=p/2= n m/2中心距 a a=(z1+z2)m/2=(d1+d2)/2跨测齿数 k k=z/9+0.5公法线长度ww=m[2.9521(k-0.5)+0.014z]模数齿轮计算公式 ,z 为齿数）13-5有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为z i = 19、Z2 = 81,模数m= 5 mm,压力角=20°若将其安装成a' = 250 mm的齿轮传动，问能否实现无侧隙啮合？为什么？此时的顶隙（径向间隙）C是多少？13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮，其齿数Z1 = 21、Z2 = 66,模数m =3.5 mm,压力角 =20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
变位齿轮跨齿数计算公式的合理选择
变位齿轮跨齿数计算公式的合理选择 中煤北京煤机公司退休职工 周万峰摘要：目前变位圆柱齿轮的跨齿数，教材、手册上大都给出的是用公式“πααxctg z k 25.01800++=”和“公法线长度 )(**kn k W W 表”进行选择。
其实该公式和该表并不是情况良好的公式和情况良好的选择用表。
本文对此进行了分析和论证，并推荐出情况良好的公式和给出合理的选择用表。
关键词：跨齿数，公法线长度，公法线长度测量点。
目前手册上对变位齿轮的跨齿数大都给出两种确定方法：一种是用公式计算，一种是查图表。
用公式计算绝大多数手册都给出的是下面的公式： απαctg x z k 25.01800++= （直齿） （1） n n n ctg x z k απα25.01800++'= （斜齿） （1） 用查表法手册大都给出的是“020 1====n n m m αα、的标准齿轮的公法线长度表 )(**k k W W ”（见表1）。
笔者认为：公式（1）并不是个情况良好的公式，表1也不是个跨齿数合理的选择用表。
下面进行分析和论证。
表1 公法线长度)(**kn k W W020 1='===αα，m m注：本表选自1991年版由徐灏任主编的《机械设计手册》第三卷“表23·2——13”。
该表跨齿数偏少，公法线的测量点靠近齿根，情况不良。
今天各家手册大都有这个表。
1、表1不是跨齿数合理的选择用表 今天各家手册都给出了表1这样的“公法线长度 )(**k k W W 表”，但该表并不是个公法线长度计算合理的选择用表：⑴ 该表是将“公法线长度”与“基圆弧长”混为一谈的。
该表称“ )(**kn k W W 为 1=m （或)1=n m 的标准齿轮的公法线长度”是不合理的。
对z=86这个齿轮而言，经验证当k=10、k=11时，它们对应的2020.32)(2497.29)(==****kn k kn k W W W W 和是这个标准齿轮的公法线长度；但当k=12、k=13时，它们对应的1060.38)(1540.35)(==****kn k kn k W W W W 和就不是这个标准齿轮的公法线长度了。
齿轮各参数计算公式
模数齿轮计算公式名称代号计算公式模数m m=p/n =d/z=da/（z+2）（d为分度圆直径，z为齿数）齿距P p= n m=t d/z齿数Z z=d/m=n d/p分度圆直径d d=mz=da-2m齿顶圆直径da da=m(z+2)=d+2m=p(z+2)/ n齿根圆直径df df=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶咼ha ha=m=p/n齿根高hf hf=1.25m齿高h h=2.25m齿厚s s=p/2= n m/2中心距a a=(z1+z2)m/2=(d1+d2)/2跨测齿数k k=z/9+0.5公法线长度w w=m[2.9521(k-0.5)+0.014z]13-1什么是分度圆？标准齿轮的分度圆在什么位置上？13-2 一渐开线，其基圆半径r b= 40 mm ,试求此渐开线压力角：■ = 20°处的半径r和曲率半径p的大小。
13-3有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径da = 106.40 mm ,齿数z=25,问是哪一种齿制的齿轮，基本参数是多少？13-4两个标准直齿圆柱齿轮，已测得齿数z i= 22、Z2= 98,小齿轮齿顶圆直径d ai= 240 mm ,大齿轮全齿高h=22.5 mm，试判断这两个齿轮能否正确啮合传动？13-5有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为Z1= 19、Z2= 81,模数m= 5 mm，压力角«= 20°若将其安装成a'= 250 mm的齿轮传动，问能否实现无侧隙啮合？为什么？此时的顶隙（径向间隙）C是多少？13-6已知C6150车床主轴箱内一对外啮合标准直齿圆柱齿轮，其齿数Z1 = 21、Z2= 66,模数m = 3.5 mm ,压力角□= 20°正常齿。
试确定这对齿轮的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7已知一标准渐开线直齿圆柱齿轮，其齿顶圆直径d ai= 77.5 mm，齿数z1=29。
直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算
外啮合直齿圆柱齿轮变位系数、公法线长度、齿厚、最小法向侧隙的计算1，直齿圆柱齿轮变位系数计算：Case1：a，此处例子仅计算用齿条型刀具加工时的情况（插齿刀加工见相关手册公式）：小结：由此可知本例选取的齿数在不变位的情况也不会产生根切现象。
b，根据下图选择大小齿轮的变位系数和x∑。
本例在P6-P7区间取值。
即齿根及齿面承载能力较高区，进行选择。
因大小齿轮的齿数和为18+19=37。
所以本例选择的变位系数和x∑=0.8。
本例我们的两个齿轮在工作时属于减速运动，所以按减速运动的变位系数分配线图，进行2个齿轮的变位系数的选择。
先按(z1+z1)/2=18.5，作为横坐标，做一条垂线（图中蓝色的线），再按x∑/2=0.4，作为纵坐标，做一条水平线（图中橙色的线），接着沿着L线的趋势，穿过上面2条线的交点做一条射线（图中红色的线）最后按大小齿轮的齿数做相应的垂线（图中紫色的线），即得到需要的各自变位系数。
最后我们选择的变位系数即为：小齿轮x1=0.42，大齿轮x2=0.38。
【基本保障其和与之前x ∑一致，即可】。
c，验算变位后的齿顶厚度：注：一般要求齿顶厚Sa≥0.25m；对于表面淬火的齿轮要求Sa≥0.4m下表中的da的计算见后面的计算表格中的计算公式（因为当齿轮变位后，齿顶圆的计算和未变位齿轮的计算稍有差别-涉及到变位系数和中心距变位系数。
）。
分度圆直径db mm 73.8 77.9齿轮的齿顶圆直径da mm 83.027 86.799齿轮的齿顶压力角αa °27.27 26.17中间值invα0.0215 0.0215中间值invαa 0.0587 0.0347齿顶厚Sα 5.77 7.47判断值0.25m 1.025 1.025判断值0.4m 1.64 1.64小结：计算发现变位后的齿轮齿顶厚满足设计需求。
根据上面确定的变位系数，计算齿轮的中心距变位系数和节圆直径、齿根圆直径、齿顶圆直径。
渐开线圆柱外齿轮常用参数及其计算公式
项目
代号
计算公式及说明
7
基圆螺旋角
tan = tan cos
法面变位系数
8
9
变位系数
齿顶高系数
端面变位系数
法面齿顶高系数
∗
ℎ
端面齿顶高系数
ℎ∗
法面径向间隙系
10
径向间隙系数
(齿顶隙系数)
数
端面径向间隙系
数
∗
∗
= cos
ℎ∗ = ℎ∗ cos
序号
项目
代号
量柱（球）测量距
24
中心距
重合度
=
端面重合度
25
计算公式及说明
齿线重合度
α
cos
cos
=
=
1
2
1
2
cos
mod
1 + 2 =
2
1 + 2
2 cos
1 tan 1 − tan + 2 tan 2 − tan
渐开线圆柱外齿轮常用参数及其计算公式
序号
项目
代号
1
齿数
1、齿轮一周所含的轮齿的个数；
2
分度圆螺旋角
1、 斜齿轮中，不同圆周上的螺旋角是不同的；
2、 设计图纸中给出的是分度圆上的螺旋角；
法面模数
3
4
模数
端面模数
法面压力角
压力角
(齿形角)
端面压力角
5
分度圆直径
6
基圆直径
计算公式及说明
渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算
渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算渐开线标准直齿圆柱齿轮的主要参数及几何尺寸计算齿轮各部分名称及符号此主题相关图片如下：此主题相关图片如下：此主题相关图片如下：此主题相关图片如下：渐开线标准直齿圆柱齿轮的基本参数及几何尺寸计算1 模数齿轮圆周上轮齿的数目称为齿数，用z表示。
根据齿距的定义知此主题相关图片如下：2 压力角此主题相关图片如下：此主题相关图片如下：3 齿数4 齿顶高系数h a=h a*m （h a*=1）5 顶隙系数c=c*m (c*= h f=(h a*+c*)m全齿高h=h a+h f=(2h a*+c*)m此主题相关图片如下：标准齿轮是指模数、压力角、齿顶高系数和顶隙系数均为标准值，且分度圆上的齿厚等于齿槽宽的齿轮。
表12-2 标准直齿圆柱齿轮的几何尺寸计算公式此主题相关图片如下：4. 内齿轮与齿条图示为一内齿圆柱齿轮，内齿轮的轮齿是分布在空心圆柱体的内表面上。
与外齿轮相比有下列几个不同点：1）内齿轮的齿厚相当于外齿轮的齿槽宽，内齿轮的齿槽宽相当于外齿轮的齿厚。
2）内齿轮的齿顶圆在它的分度圆之内，齿根圆在它的分度圆以外。
图示为一齿条，它可以看作齿轮的一种特殊型式。
与齿轮相比有下列两个主要特点：1）由于齿条的齿廓是直线，所以齿廓上各点的法线是平行的；传动时齿条是直线移动的，故各点的速度大小和方向均相同；齿条齿廓上各点的压力角也都相同，等于齿廓的倾斜角。
2）与分度线相平行的各直线上的齿距都相等。
此主题相关图片如下：渐开线直齿圆柱齿轮的任意圆周上齿厚的计算此主题相关图片如下：5.公法线长度测量齿轮公法线长度是检验齿轮精度常用的方法之一。
它具有测量方便、准确和易于掌握的优点。
测量齿轮公法线长度的原理：公法线长度是指渐开线齿轮上两反向齿廓间的基圆切线长度。
此主题相关图片如下：此主题相关图片如下：此主题相关图片如下：K为跨齿数（证明略）。
直齿圆柱齿轮齿宽计算公式
直齿圆柱齿轮齿宽计算公式
直齿圆柱齿轮齿宽是指齿轮牙宽，是影响齿轮传动效率的关键参数，用来衡量齿轮传动性能。
计算齿轮齿宽的关键公式是：
齿宽=(齿轮模数*π)/齿数
其中，齿轮模数是指齿轮的节圆半径与齿数的比值；π是圆周率。
直齿圆柱齿轮齿宽的计算步骤如下：
1.首先，根据齿轮的节圆半径和齿数确定齿轮的模数。
2.然后，根据上述的公式计算齿轮的齿宽。
3.最后，将计算出的齿宽与设计要求和齿轮性能指标相比较，确定最佳齿宽。
直齿圆柱齿轮齿宽的计算受到齿轮的模数、齿数以及圆周率的影响。
因此，在设计和制造过程中，应根据齿轮的设计要求和传动性能指标，正确计算齿轮的齿宽，以确保齿轮具有良好的传动性能。
此外，还应注意齿轮的模数、齿数以及圆周率的计算精度，以便最终计算出准确而合理的齿宽。
齿轮尺寸、公法线与跨齿数计算
1 0.25
20 0.34906585
0.359208002
20.58110248 28
224.3892658
3.125 2.5
5.625 229.3892658 218.1392658
285.0001594
0.649253731
11.06593892
11 80.82303784
斜齿（人字齿）圆柱齿轮螺旋角换算
146.465774
han*
1
cn*
0.25
αn
压力角对应弧度
20 0.34906585
αt
αt
arctan
tan αn cos β
弧度
0.359208002
齿轮厚度 分度圆直径
对应角度 b
d
d
zmt
z
mn cos βLeabharlann 20.58110248 28
345.611053
齿根高
hf
hf ha*n cn* mn
3.125
齿顶高
ha
ha ha*nmn
2.5
全齿高
h
h ha hf
5.625
齿顶圆直径
da
da d 2ha
350.611053
齿根圆直径 中心距 齿数比
df
da d 2hf
a
a d1 d2 z1 z2 mn
2
2 cosβ
u
u z2 z1
339.361053 285.0001594 0.649253731
公法线跨齿数 （内齿轮为跨齿槽
k
k
αn 180
z
0.5
数）
四舍五入后
16.77397489 17
齿轮各参数计算公式
齿轮各参数计算公式模数齿轮计算公式:名称代码计算公式模数mm=p/π=d/z=da/(z+2)（d为分度圆直径，z为齿数）齿距pp=πm=πd/z齿数zz=d/m=πd/p分度圆直径dd=mz=da-2m齿顶圆直径dada=m(z+2)=d+2m=p(z+2)/π齿根圆直径dfdf=d-2.5m=m(z-2.5)=da-2h=da-4.5m齿顶高haha=m=p/π齿根高hfhf=1.25m齿高hh=2.25m齿厚ss=p/2=πm/2中心距aa=(z1+z2)m/2=(d1+d2)/2跨测齿数kk=z/9+0.5公法线长度ww=m[2.9521(k-0.5)+0.014z]13-1什么是毕业圈？标准齿轮的分度圆在哪里？13-2一渐开线，其基圆半径rb＝40mm，试求此渐开线压力角?＝20°处的半径r和曲率半径ρ的大小。
13-3有一个标准渐开线直齿圆柱齿轮，测量其齿顶圆直径da＝106.40mm，齿数z=25，问是哪一种齿制的齿轮，基本参数是多少?13-4对于两个标准正齿轮，测量的齿数ZL=22和Z2=98，小齿轮顶圆直径DAL=240mm，大齿轮的全齿高H=22.5MM。
试着判断两个齿轮是否能正确啮合和驱动？13-5有一对正常齿制渐开线标准直齿圆柱齿轮，它们的齿数为z1＝19、z2＝81，模数m＝5mm，压力角?＝20°。
如果安装为“=250mm”的齿轮传动，能否实现无齿隙啮合？为什么？此时顶部间隙（径向间隙）C为多少?13-6已知C6150车床主轴箱中有一个外啮合标准直齿圆柱齿轮，齿数Z1=21，Z2=66，模数M=3.5mm，压力角？=20°，正常牙齿。
尽量确定齿轮副的传动比、分度圆直径、齿顶圆直径、全齿高、中心距、分度圆齿厚和分度圆齿槽宽。
13-7众所周知，标准渐开线直齿轮的顶圆直径为dal=77.5mm，齿数Z1=29。
现在需要设计一个与之啮合的大齿轮，变速器的安装中心距为a=145mm。
变位圆柱齿轮跨测齿数的简便计算
变位圆柱齿轮跨测齿数的简便计算中煤北京煤机公司退休职工 周万峰摘要：本文给出一个简便的跨齿数计算的经验公式，并验证了该公式确定的跨齿数是合理的。
关键词：变位齿轮，跨齿数，公法线长度。
1、推荐笔者的经验公式目前变位齿轮的跨齿数计算公式可谓形式多样，五花八门：有教科书上公式，有各种手册上公式，有参考书上的公式，还有近些年来杂志上发表的公式等等。
如果将它们汇集起来恐怕不下十数个之多。
但最常见的还是表1所列的几个公式。
表1 几个常见的变位齿轮的跨齿数计算公式注：早先公式1多为教材所选用。
公式2《机修手册》选用。
公式3《齿轮手册》选用。
公式4多为《机械设计手册》选用。
不难看出，表1中的几个公式大都比较复杂：平方、开放、三角函数等等项目很多，计算起来十分不便。
而且有的公式有时确定的跨齿数也不合理。
有鉴于此，笔者通过分析研究，并进行了大量的算例计算以及反复验证后给出一个跨齿数计算的经验公式。
当压力角020=α时，经验公式为：z ——齿数，斜齿时z z '用代入（n tinvzz α='，nt inv αα可查手册）。
x ——变位系数，斜齿时代入用n x x 。
p ——与变位系数正负有关的系数。
当变位系数为正（)0>x 时p=1.4，当变位系数为负（)0<x 时p=1.9。
通过大量的算例验证后得知，当变位系数为负时，由经验公式确定的跨齿数与表1中的公式（4）确定的跨齿数是完全一样的（见表2）。
当变位系数为正时，经验公式与表1中的（2）、（3）、（4）确定的跨齿数绝大多数是相同的，只在极少数情况下两者的跨齿数不同。
但在不同的情况下，经验公式的情况比理论公式的情况还好些（见表3）。
这就说明经验公式确定的跨齿数是合理的。
表2 变位直齿轮跨齿数计算公式比较表（020=α）注：表2中的“理论公式”为表1中的公式（4）。
表3 角度变位直齿轮跨齿数计算公式比较)20 5(0==α，m注：表3中的“理论公式”为表1中的公式（4）2、经验公式合理性的验证众所周知，凡计算公法线长度首先应计算跨齿数k ，根据跨齿数k 计算跨k 个齿的公法线长度。
直齿圆柱齿轮齿宽计算公式
直齿圆柱齿轮齿宽计算公式
直齿圆柱齿轮的齿宽是指齿轮齿面的有效宽度，它决定了齿轮的传动能力和承载能力。
齿宽计算公式可以通过以下步骤推导得到：
1. 确定齿轮的模数m和法向模数mn。
- 模数m是指齿轮齿面上相邻两齿之间的齿距圆弧半径与圆周上的齿数之比，通常以毫米为单位表示。
- 法向模数mn是指齿轮齿面法向上每单位长度的齿数，它与模数m和齿轮的齿数z有关，计算公式为mn=m/z。
2. 确定齿轮的分度圆直径d。
- 分度圆直径d是指齿轮齿面上齿根圆与齿顶圆之间的直径，它等于齿轮的模数m乘以齿数z，即d=mz。
3. 确定齿轮的齿顶高h和齿根深c。
- 齿顶高h是指齿轮齿顶圆与基圆之间的距离，它通常等于模数m。
- 齿根深c是指齿轮齿根圆与基圆之间的距离，它通常等于1.25倍的模数m。
4. 确定齿轮的弯曲强度和接触强度。
- 齿轮的弯曲强度是指齿轮齿面弯曲时的承载能力，它与齿轮的材料和几何尺寸有关。
- 齿轮的接触强度是指齿轮齿面接触时的承载能力，它与齿轮的材料和齿面接触状况有关。
5. 根据齿轮的弯曲强度和接触强度，选择合适的齿宽bw。
- 齿宽bw应满足以下条件：
- 齿宽bw大于等于2倍的齿顶高h。
- 齿宽bw小于等于2.5倍的分度圆直径d。
- 齿宽bw应满足齿轮的弯曲强度和接触强度的要求。
跨齿数计算公式
跨齿数计算公式好的，以下是为您生成的关于“跨齿数计算公式”的文章：在机械工程的世界里，跨齿数计算公式就像是一把神奇的钥匙，能帮助我们解开很多复杂的谜题。
先来说说什么是跨齿数。
想象一下，有一条长长的齿轮齿条，上面的齿一个挨着一个。
当我们要测量或者确定某些参数的时候，就需要考虑跨几个齿来进行操作，这时候跨齿数就登场啦。
那跨齿数计算公式到底是怎么来的呢？这可不是凭空想象出来的。
其实是经过无数工程师和科学家们不断地实践、研究和总结得出来的。
这背后啊，有好多有趣的故事呢。
我记得有一次，我去一家工厂参观。
那是一个生产精密齿轮的地方。
我看到工人们在操作台前，认真地测量着齿轮的各种参数。
其中就用到了跨齿数的计算。
当时有个年轻的小师傅，可能是刚参加工作不久，在计算跨齿数的时候出了点小差错。
这可把他急坏了，因为这一点点的差错，可能就会导致整个齿轮的生产出现问题。
这时候，旁边经验丰富的老师傅走了过来，耐心地给他讲解跨齿数计算公式的原理和应用。
老师傅说：“孩子，这跨齿数的计算可不能马虎。
你看啊，就像咱们走路，一步跨大了或者跨小了，都容易摔跤。
这齿轮也是一样，跨齿数算不对，它就转不顺畅啦。
” 老师傅一边说，一边拿着量具亲自示范。
小师傅在一旁认真地听着，眼睛里透着一股专注和决心。
其实啊，跨齿数计算公式常见的有好几种。
比如说，对于标准直齿圆柱齿轮，常用的公式是：k = απ/z + 0.5 ，这里的 k 表示跨齿数，α 是压力角，π 不用说啦，大家都知道，z 是齿数。
这个公式看起来可能有点复杂，但只要我们理解了每个参数的含义，用起来也就不难啦。
比如说压力角，它就像是齿轮齿形的一个特征角度，决定了齿轮啮合时的力量传递方式。
在实际应用中，跨齿数的计算非常重要。
如果跨齿数选择不当，测量出来的齿距、齿厚等参数就会不准确，从而影响齿轮的质量和性能。
比如说在汽车制造中，变速箱里的齿轮精度要求非常高。
如果跨齿数计算错误，生产出来的齿轮可能会在高速运转时出现磨损、噪音甚至故障，那可就麻烦大啦！再比如在一些大型机械设备中，齿轮的传动效率和稳定性直接关系到整个设备的运行效果。
圆柱齿轮跨齿数计算公式的推导
圆柱齿轮的跨齿数计算公式的推导周万峰1、标准齿轮跨齿数计算公式的推导大家都知道，凡计公法线长度，则必须先计算跨齿数k ，然后才能计算跨k 个齿的公法线长度。
标准齿轮的跨齿数计算公式为：5.01800+=αz k （直齿） （1） 5.01800+'=n z k α （斜齿） （1） 式中z 为齿数，z '为假想齿数，n t inv inv z z αα='（nt inv inv αα之值可从手册上查出，亦可算出）。
α为压力角，n α为斜齿轮的法面压力角。
教材、手册上都是给出该公式，并不说明它的由来。
那么公式（1）是怎么来的呢？它怎么还有个0.5 呢？据笔者了解，使用公式（1）的人一般都不管公式的由来，只是拿来使用而已。
今天笔者根据自己的理解试将公式推导出来。
显然公式（1）不是笔者推导出来的，书上早就有这个公式了。
但始终未见哪本书上有原原本本地推导该公式的内容。
至于公式（1）原来是怎么推导的笔者不得而知。
笔者现将公式推导如下：众所周知，不论标准齿轮还是变位齿轮其公法线的测量点（量具卡脚与齿廓的切点）都应在齿高的中点部位。
而标准齿轮齿高的中点就是分度圆，故标准齿轮公法线的测量点应在分度圆上。
这样标准齿轮的公法线测量点就应以分度圆为准进行推导。
请看图1公法线测量图：AB 是跨3个齿测量的公法线长度。
1A A 和21A A 是齿轮的周节（分度圆上，相图1 公法线长度测量邻两齿同侧齿廓对应点的弧长）B A2是分度圆上齿厚；而标准齿轮分度圆齿厚是周节的一半，即0.5个周节。
因此，当跨3个齿测量时，α2对应着两个周节和一个分度圆齿厚，即α2对应着（3-0.5）个周节。
所以，跨3个齿测量时，0.5)-(3 36020z=α。
（z 0360 是一个周节对应的中心角的度数）当跨4个齿测量时，α2对应着3个周节和一个分度圆齿厚，即α2对应着（4-0.5）个周节；所以0.5)-(4 36020z=α。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
圆柱齿轮的跨齿数计算公式的推导
周万峰
1、标准齿轮跨齿数计算公式的推导
大家都知道，凡计公法线长度，则必须先计算跨齿数k ，然后才能计算跨k 个齿的公法线长度。
标准齿轮的跨齿数计算公式为：
5.0180
0+=αz k （直齿） （1） 5.01800+'=
n z k α （斜齿） （1） 式中z 为齿数，z '为假想齿数，n t inv inv z z αα='（n
t inv inv αα之值可从手册上查出，亦可算出）。
α为压力角，n α为斜齿轮的法面压力角。
教材、手册上都是给出该公式，并不说明它的由来。
那么公式（1）是怎么来的呢？它怎么还有个0.5 呢？据笔者了解，使用公式（1）的人一般都不管公式的由来，只是拿来使用而已。
今天笔者根据自己的理解试将公式推导出来。
显然公式（1）不是笔者推导出来的，书上早就有这个公式了。
但始终未见哪本书上有原原本本地推导该公式的内容。
至于公式
（1）原来是怎么推导的笔者不得而知。
笔者现将公式推导如下：
众所周知，不论标准齿轮还是变位齿轮其公法线的测量点（量具卡脚与齿廓的切点）都应在齿高的中点部位。
而标准齿轮齿高的中点就是分度圆，故标准齿轮公法线的测量点应在分度圆上。
这样标准齿轮的公法线测量点就应以分度圆为准进行推导。
请看图1公法线测量图：AB 是跨3个齿测量的公法线长度。
1A A 和21A A 是齿轮的周节（分度圆上，相
图1 公法线长度测量
邻两齿同侧齿廓对应点的弧长）B A
2是分度圆上齿厚；而标准齿轮分度圆齿厚是周节的一半，即0.5个周节。
因此，当跨3个齿测量时，α2对应着两个周节和一个分度圆齿厚，即α2对应着（3-0.5）个周节。
所以，跨3个齿测量时，0.5)-(3 36020
z
=α。
（z 0360 是一个周节对应的中心角的度数）当跨4个齿测量时，
α2对应着3个周节和一个分度圆齿厚，即α2对应着（4-0.5）个周节；所以0.5)-(4 36020
z
=α。
当跨5个齿测量时，α2对应着4个周节和一个分度圆齿厚，即α2对应着（5-0.5）个周节；所以0.5)-(5 36020
z
=α。
依次类推，当跨k 个齿测量时，α2对应着（)5.0-k 个周节，即0.5)-(k 36020
z
=α。
整理此式即为公式（1）。
但需说明的是：对于020=α的直齿轮而言，它的公法线测量点没有一
个是能在分度圆上的，都是在分度圆附近。
为什么呢?因为跨齿数k 的计算值不可能是整数（见公式），而测量公法线长度时又必须是整数，所以才如此。
而斜齿轮通过调整螺旋角是可以使公法线长度的测量点正好在分度圆上的。
2、变位齿轮的跨齿数计算公式的推导
变位齿轮的跨齿数计算公式今天可以说是形式多样，五花八门；如将教材、手册、科技书以及发表在刊物上的这些公式汇集起来，找出10个公式是费不了什么事的。
这些公式（包括教材、手册在内）经验证有的是合理的，有的是不合理的；有的是不尽合理的，有的是情况不良的。
有的虽然情况较好，但计算很麻烦。
笔者在此推荐一个情况较好而又比较简单的公式：
5.02cos arccos 1800
++=x z z z k α (直齿) （2） 5.02cos arccos 1800
++'''=n n x z z z k α （斜齿） （2）
图 2
这个公式是怎么来的？教材、手册都是给出公式，并不说明它的由来。
今天笔者将它推导一遍（显然公式不是我第一个推导出来的），请读者指正。
前面说过，不论齿轮变位与否，公法线的测量点都应在齿高的中点部位。
标准齿轮齿高的中点部位就是分度圆，故推导标准齿轮的跨齿数计算公式应以分度圆为准。
而变位齿轮的分度圆已不在齿高的中点部位了，那么推导变位齿轮的跨齿数计算公式就不能以分度圆为准了，而是直径为“xm d 2+圆”位于齿高的中点部位，所以就应以它为准了。
请看图2：当为正变位时，公法线的测量点应在B '点，即在“xm d 2+圆”上。
那么只要算出B '点的压力角，然后代入公式（1），用α'代替α，公式就推导出来了。
请看图2：ON 是基圆半径，xm d B O +='2，
)2
(2cos xm d d B O ON b +='=
'α。
因为αcos mz d b =，,mz d =将αcos mz 代替b d ，将mz 代替d ，
代入上式，整理后则[])2()cos (arccos x z z +='αα ，将该式代入（1）式（用α'代替α），整理后即为公式（2）。
说明：
上面的文章于2014年1月31日已上传到“百度文库”，截止到2014年5月24日其浏览量已有64次，下载8次。
但笔者发现文章中有的公式写法不规范。
为了向读者负责，笔者将公式不规范的写法改正过来，再次将其上传到“百度文库”。
请读者见谅！ 2014年5月24日。