大学物理C1第七章振动
大物知识点总结振动

大物知识点总结振动振动是物体周围环境引起的周期性的运动。
它是自然界中普遍存在的物理现象,了解振动现象对于理解物质的性质和物理规律具有重要意义。
振动现象广泛存在于自然界和人类生活中,如大地的地震、声波的传播、机械振动、弹性体的振动等等。
本文将介绍大物知识点中与振动相关的内容,并做相应总结。
一、简谐振动简谐振动是指体系对于某个平衡位置附近作微幅振动,其回复力正比于位移的现象。
它是最基本的振动形式,也是在自然界中广泛存在的振动。
简谐振动的重要特征包括振幅、周期、频率、角频率、相位等。
简谐振动的数学描述是通过简谐振动的运动方程来完成的,对于弹簧振子来说,它的运动方程是x = Acos(ωt + φ),其中x为位移,A为振幅,ω为角频率,t为时间,φ为相位。
利用这个方程,我们可以得到简谐振动的各种运动参数,如速度、加速度、动能、势能以及总机械能。
对于简谐振动系统,我们可以利用牛顿第二定律与胡克定律来进行分析。
牛顿第二定律可以得出振动体的加速度与回复力的关系,而胡克定律则是描述了挠性介质的回复力与位移的关系。
利用这两个定律,我们可以得到简谐振动的运动参数和系统的动力学性质。
二、受迫振动和共振在实际中,许多振动都是在外力的驱动下进行的,这种振动被称为受迫振动。
受迫振动是振动中的另一个重要现象,它包括了临界阻尼和过阻尼等多种振动状态。
受迫振动系统的特点是具有固有振动频率以及外力频率,当外力频率与系统的固有振动频率相近时,就会出现共振现象。
共振是指系统受到外力作用后,振幅或能量急剧增大的现象。
共振现象在实际工程中有着重要应用,如建筑结构的抗震设计、桥梁的结构设计等。
三、波的传播波是另一种重要的振动形式,它在自然界和人类生活中都有着广泛的应用。
波的传播包括机械波、电磁波、物质波等多种形式,它的传播速度和传播方式与特定介质的性质密切相关。
波的传播是通过介质中的微小振动来实现的,振动的传递使得能量和信息得以传播。
在波的传播中,我们可以通过波动方程来描述波的传播规律,如弦上的横波传播可以通过波动方程来描述,光波的传播也可以通过麦克斯韦方程来描述。
大学物理《弦振动》实验报告

大学物理《弦振动》实验报告大学物理《弦振动》实验报告(报告内容:目的、仪器装置、简单原理、数据记录及结果分析等)一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动,这时弦上的张力将使这小段恢复到平衡位置,但是弦上每一小段由于都具有惯性,所以到达平衡位置时并不立即停止运动,而是继续向相反方向运动,然后由于弦的张力和惯性使这一小段又向原来的方向移动,这样循环下去,此小段便作横向振动,这振动又以一定的速度沿整条弦传播而形成横波。
理论和实验证明,波在弦上传播的速度可由下式表示:=ρ1------------------------------------------------------- ①另外一方面,波的传播速度v和波长λ及频率γ之间的关系是:v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内,另一端固定在张力杠杆水平调节旋钮的螺钉上。
②设置两个弦码间的距离为60.00cm,置驱动线圈距离一个弦码大约5.00cm的位置上,将接受线圈放在两弦码中间。
将弦音计信号发生器和驱动线圈及示波器相连接,将接受线圈和示波器相连接。
③将1kg砝码悬挂于张力杠杆第一个槽内,调节张力杠杆水平调节旋钮是张力杠杆水平(张力杠杆水平是根据悬挂物的质量精确确定,弦的张力的必要条件,如果在张力杠杆的第一个槽内挂质量为m的砝码,则弦的张力T=mg,这里g是重力加速度;若砝码挂在第二个槽,则T=2mg;若砝码挂在第三个槽,则T=3mg…….)④置示波器各个开关及旋钮于适当位置,由信号发生器的信号出发示波器,在示波器上同时显示接收器接受的'信号及驱动信号两个波形,缓慢的增加驱动频率,边听弦音计的声音边观察示波器上探测信号幅度的增大,当接近共振时信号波形振幅突然增大,达到共振时示波器现实的波形是清晰稳定的振幅最大的正弦波,这时应看到弦的震动并听到弦振动引发的声音最大,若看不到弦的振动或者听不到声音,可以稍增大驱动的振幅(调节“输出调节”按钮)或改变接受线圈的位置再试,若波形失真,可稍减少驱动信号的振幅,测定记录n=1时的共振频率,继续增大驱动信号频率,测定并记录n=2,3,4,5时的共振频率,做γn图线,导出γ和n的关系。
《大学物理》-第二版-课后习题答案--第七章

习题精解7-1一条无限长直导线在一处弯折成半径为R 的圆弧,如图7.6所示,若已知导线中电流强度为I,试利用比奥—萨伐尔定律求:(1)当圆弧为半圆周时,圆心O 处的磁感应强度;(2)当圆弧为1/4圆周时,圆心O 处的磁感应强度。
解(1)如图7.6所示,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于直线电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据比奥—萨伐尔定律,半圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB Rμπ=方向垂直纸面向内。
半圆弧在O 点产生的磁感应强度为 000220444RIIdl I B R R R Rπμμμπππ===⎰方向垂直纸面向里。
(2)如图7.6(b )所示,同理,圆心O 处的磁感应强度可看作由3段载流导线的磁场叠加而成。
因为圆心O 位于电流AB 和DE 的延长线上,直线电流上的任一电流元在O 点产生的磁感应强度均为零,所以直线电流AB 和DE 段在O 点不产生磁场。
根据毕奥—萨伐尔定理,1/4圆弧上任一电流元在O 点产生的磁感应强度为 024IdldB R μπ=方向垂直纸面向内,1/4圆弧电流在O 点产生的磁感应强度为00022204428RIIdl I R B R R Rπμμμπππ===⎰方向垂直纸面向里。
7.2 如图7.7所示,有一被折成直角的无限长直导线有20A 电流,P 点在折线的延长线上,设a 为,试求P 点磁感应强度。
解 P 点的磁感应强度可看作由两段载流直导线AB 和BC 所产生的磁场叠加而成。
AB 段在P 点所产生的磁感应强度为零,BC 段在P 点所产生的磁感应强度为 0120(cos cos )4IB r μθθπ=- 式中120,,2r a πθθπ=== 。
所以500(cos cos ) 4.010()42I B T a μπππ=-=⨯ 方向垂直纸面向里。
大学物理C1、C2(University Physics C1、C2

(三)环境土木类大学物理C1、C2(University Physics C1、C2)一、课程说明:课程编号:080J33Y、080J34Y学分数:3、3 总学时:51、51 学时分配:讲课51(讲课34+自主学习17)、讲课51(讲课34+自主学习17)适用专业:教育技术、化学、信息与计算科学等专业先修课程:高等数学二、课程教学目的和任务:掌握物理学的基本知识和基本规律,并学会用物理学的基本原理来分析自然现象和有关的工程技术问题,为专业课的学习打好物理基础。
并初步学习科学的思维方法和研究问题的方法。
三、课程教学基本内容:内容简介:牛顿力学、热学、电磁学、振动和波、波动光学。
基本内容:绪论(1学时)第一册力学(20学时)1、质点运动学(3学时)理解:质点运动学的几个基本概念掌握:匀加速运动、抛体运动、圆周运动理解:相对运动、伽利略变换2、质点动力学(10学时)理解:牛顿运动定律、技术中常见的几种力和基本自然力掌握:应用牛顿定律解题理解:惯性系和非惯性系、惯性力掌握:冲量和动量定理、动量守恒定律掌握:质点的角动量、角动量守恒定律掌握:功、动能定理、保守力、势能、功能原理、机械能守恒定律理解:守恒定律的意义3、刚体的转动(7学时)理解:刚体的定轴转动掌握:刚体定轴转动定律、转动惯量计算、转动中的功和能、刚体的角动量和角动量守恒定律习题课:三大定律、运动定理、牛顿定律、运动学、刚体的转动(2学时)第二册热学(15学时)1、气体分子运动论(6学时)掌握:平衡状态、理想气体状态方程掌握:理想气体的压强和温度掌握:能量均分定理理解:麦克斯韦速率分布律、波耳兹曼分布定律了解:实际气体等温线、范得瓦耳斯方程掌握:气体分子的平均自由程2、热力学的物理基础(9学时)理解:准静态过程掌握:功、热量、热力学第一定律、热容量、理想气体的绝热过程掌握:循环过程、卡诺循环、致冷循环理解:自然过程的方向、不可逆性的相互沟通、热力学第二定律及其微观意义、玻耳兹曼熵公式及熵增加原理了解:克劳修斯熵公式习题课:气体分子运动论、热力学定律(2学时)第三册电磁学(38学时)1、静电场(10学时)掌握:库仑定律、电场、电场强度、高斯定理、电势差和电势理解:电势梯度掌握:静电势能2、静电场中的导体和电介质(6学时)理解:静电场中的导体、电介质对电场的影响、电介质的极化掌握:D的高斯定理、电容器、电容、电容器的能量和电场的能量3、稳恒电流(4学时)理解:电流密度、稳恒电流掌握:欧姆定律和电阻、电动势、有电动势的电路了解:电路的一种经典微观图象4、稳恒磁场(8学时)掌握:磁力和磁场、磁感应强度、毕奥—萨伐尔定律、磁场高斯定理和安培环路定理、带电粒子在磁场中的运动、载流导线在磁场中受力理解:霍耳效应5、物质的磁性(4学时)理解:磁介质对磁场的影响、磁介质的磁化掌握:H的环路定理了解:铁磁质6、电磁感应(6学时)理解:法拉第电磁感应定律掌握:动生电动势、感生电动势和感应电场、互感、自感、磁场能量习题课:静电场、及导体和电介质、稳性磁场、电磁感应(2学时)第四册波动与光学(28学时)1、振动(6学时)理解:简谐振动的描述掌握:旋转矢量和振动的相位、简谐振动的动力学方程、简谐振动的能量理解:阻尼振动、受迫振动、共振、同一直线上振动合成、相互垂直的振动合成了解:谐振分析2、波动(6学时)理解:机械波的形成掌握:波的周期性和波速、简谐波的波函数、波的能量、能流密度理解:波动方程、惠更斯原理、波的干涉、驻波了解:多普勒效应、声波2、光的干涉(6学时)理解:普通光源发光微观机制的特点、获得相干光的方法掌握:光程和光程差、薄膜干涉(一)、(二)理解:迈克耳逊干涉仪了解:光的空间相干性和时间相干性3、光的衍射(4学时)理解:光的衍射图样和惠更斯——菲理耳原理掌握:单缝的夫琅和费衍射、光栅衍射、光栅光谱理解:光学仪器的分辨本领了解:X射线的衍射4、光的偏振(6学时)理解:自然光和偏振光掌握:起偏和检偏、马吕斯定律、反射和折射对光的偏振理解:双折射现象、偏振光的干涉了解:椭圆偏振光和圆偏振光、人工双折射、旋光现象习题课:光的干涉、衍射、偏振(2学时)四、教学方法本课程主要内容以教师主讲为主。
大学物理受迫振动

A
[(
2 0
ห้องสมุดไป่ตู้
f0 2 )2
4
2
2 ]1/ 2
稳态时受迫振动物体的速度为:
d x A cos( t )
dt
2
速度的振幅为:
m A
f0
1
2
(
2 0
2
)2
(2
)2
由上式可知
=0
时,速度的振幅最大:
m
f0
2
当策动力的频率等于系统的固有频率时,受迫振动速度的振
幅 A 达到极大值的现象称为速度共振。
共振时: = 0 m = f0 /2
d x A cos( t )
dt
2
周期性策动力 f =F0cost
tg
2
2 0
2
dx
Acos t
dt
比较
速度共振时,速度与策动力同相, 一周期内策动力总作正功,此时向 系统输入的能量最大。
d2 x dt 2
2
dx dt
2 0
x
f0 cos t
受迫振动微分方程
其中 0
k, m
,
2m
f0
F0 m
d2 x dt 2
2
dx dt
2 0
x
f0 cos t
受迫振动微分方程
方程的解 = 阻尼振动的通解+受迫振动的特解
设特解为: x Acos( t )
《大学物理C1(上、下)》练习册及答案

大学物理C(上、下)练习册✧质点动力学✧刚体定轴转动✧静电场电场强度✧电势静电场中的导体✧稳恒磁场✧电磁感应✧波动、振动✧光的干涉✧光的衍射注:本习题详细答案,结课后由老师发放一、质点动力学一、选择题1. 以下几种运动形式中,加速度a保持不变的运动是:(A )单摆的运动; (B )匀速率圆周运动;(C )行星的椭圆轨道运动; (D )抛体运动 。
[ ] 2. 质点沿半径为R 的圆周作匀速率运动,每T 秒转一圈.在2T 时间间隔中,其平均速度大小与平均速率大小分别为(A) 2 R /T , 2 R/T . (B) 0 , 2 R /T(C) 0 , 0. (D) 2 R /T , 0. [ ]3. 质点作曲线运动,r表示位置矢量,v 表示速度,a 表示加速度,S 表示路程,a 表示切向加速度,下列表达式中, (1) a t = d /d v , (2) v =t r d /d ,(3) v =t S d /d , (4) t a t =d /d v.(A) 只有(1)、(4)是对的. (B) 只有(2)、(4)是对的. (C) 只有(2)是对的. (D) 只有(3)是对的. [ ]4. 一运动质点在某瞬时位于矢径r的端点处,其速度大小的表达式为(A )t d dr ; (B )dt r d ; (C )dt r d || ; (D )222dt dz dt dy dt dx ⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛[ ] 5. 质点作半径为R 的变速圆周运动时的加速度大小为(v 表示任一时刻质点的速率)(A) t d d v . (B)2V R.(C) R t 2d d v v +. (D) 2/1242d d ⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛R t v v . [ ]6. 质量为m的质点,以不变速率v沿图中正三角形ABC的水平光滑轨道运动.质点越过A角时,轨道作用于质点的冲量的大小为(A) mv. (B).(C) . (D) 2mv.[]7. 在水平冰面上以一定速度向东行驶的炮车,向东南(斜向上)方向发射一炮弹,对于炮车和炮弹这一系统,在此过程中(忽略冰面摩擦力及空气阻力)(A) 总动量守恒.(B) 总动量在炮身前进的方向上的分量守恒,其它方向动量不守恒.(C) 总动量在水平面上任意方向的分量守恒,竖直方向分量不守恒.(D) 总动量在任何方向的分量均不守恒.[]8. 一炮弹由于特殊原因在水平飞行过程中,突然炸裂成两块,其中一块作自由下落,则另一块着地点(飞行过程中阻力不计)(A) 比原来更远. (B) 比原来更近.(C) 仍和原来一样远. (D) 条件不足,不能判定.[]9. 如图,在光滑水平地面上放着一辆小车,车上左端放着一只箱子,今用同样的水平恒力F拉箱子,使它由小车的左端达到右端,一次小车被固定在水平地面上,另一次小车没有固定.试以水平地面为参照系,判断下列结论中正确的是(A)在两种情况下,F做的功相等.(B)在两种情况下,摩擦力对箱子做的功相等.(C)在两种情况下,箱子获得的动能相等.(D)在两种情况下,由于摩擦而产生的热相等.[]10. 质量为m的一艘宇宙飞船关闭发动机返回地球时,可认为该飞船只在地球的引力场中运动.已知地球质量为M,万有引力恒量为G,则当它从距地球中心R 1处下降到R 2处时,飞船增加的动能应等于(A)2R GMm(B)22R GMm(C) 2121R R R R GMm - (D) 2121R R R GMm - (E) 222121R R R R GMm -[ ]二 填空11. 灯距地面高度为h 1,一个人身高为h 2,在灯下以匀速率v 沿水平直线行走,如图所示.他的头顶在地上的影子M 点沿地面移动的速度为v M = .12. 质量分别为m 1、m 2、m 3的三个物体A 、B 、C ,用一根细绳和两根轻弹簧连接并悬于固定点O ,如图.取向下为x 轴正向,开始时系统处于平衡状态,后将细绳剪断,则在刚剪断瞬时,物体B 的加速度B a=_______;物体A 的加速度A a=______.13. 两个相互作用的物体A 和B ,无摩擦地在一条水平直线上运动.物体A 的动量是时间的函数,表达式为 P A = P 0 – b t ,式中P 0 、b 分别为正值常量,t是时间.在下列两种情况下,写出物体B 的动量作为时间函数的表达式:(1) 开始时,若B 静止,则 P B 1=__________________; (2) 开始时,若B的动量为 – P 0,则P B 2 = _____________.三、计算题14. 有一质点沿x 轴作直线运动,t 时刻的坐标为x = 4.5 t 2 – 2 t 3 (SI) .试求:(1) 第2秒内的平均速度;(2)第2秒末的瞬时速度;(3) 第2秒内的路程.15. 质量为m的子弹以速度v 0水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为K,忽略子弹的重力,求:(1) 子弹射入沙土后,速度随时间变化的函数式;(2) 子弹进入沙土的最大深度.16. 一人从10 m深的井中提水.起始时桶中装有10 kg的水,桶的质量为1 kg,由于水桶漏水,每升高1 m要漏去0.2 kg的水.求水桶匀速地从井中提到井口,人所作的功.二、刚体定轴转动一、选择题1. 人造地球卫星,绕地球作椭圆轨道运动,地球在椭圆的一个焦点上,则卫星的 (A)动量不守恒,动能守恒. (B)动量守恒,动能不守恒.(C)对地心的角动量守恒,动能不守恒.(D)对地心的角动量不守恒,动能守恒. [ ] 2. 一质点作匀速率圆周运动时,(A) 它的动量不变,对圆心的角动量也不变. (B) 它的动量不变,对圆心的角动量不断改变. (C) 它的动量不断改变,对圆心的角动量不变.(D) 它的动量不断改变,对圆心的角动量也不断改变. [ ] 3. 如图所示,A 、B 为两个相同的绕着轻绳的定滑轮.A 滑轮挂一质量为M 的物体,B 滑轮受拉力F ,而且F =Mg .设A 、B 两滑轮的角加速度分别为 A 和 B ,不计滑轮轴的摩擦,则有(A) A = B . (B) A > B .(C) A < B . (D) 开始时 A = B ,以后 A < B .[ ] 4. 一圆盘绕过盘心且与盘面垂直的光滑固定轴O 以角速度 按图示方向转动.若如图所示的情况那样,将两个大小相等方向相反但不在同一条直线的力F 沿盘面同时作用到圆盘上,则圆盘的角速度(A) 必然增大. (B) 必然减少. (C) 不会改变. (D) 如何变化,不能确定. [ ] 5. 花样滑冰运动员绕通过自身的竖直轴转动,开始时两臂伸开,转动惯量为J 0,角速度为 0.然后她将两臂收回,使转动惯量减少为31J 0.这时她转动的角速度变为(A) 310. (B) ()3/1 0.(C) 3 0. (D) 3 0. [ ] 6. 如图所示,一匀质细杆可绕通过上端与杆垂直的水平光滑固定轴O 旋转,初始状态为静止悬挂.现有一个小球自左方水平打击细杆.设小球与细杆之间为非弹性碰撞,则在碰撞过程中对细杆与小球这一系统(A) 只有机械能守恒. (B) 只有动量守恒. (C) 只有对转轴O 的角动量守恒.(D) 机械能、动量和角动量均守恒. [ ]二、填空题7. 在光滑的水平面上,一根长L =2 m 的绳子,一端固定于O 点,另一端系一质量m =0.5 kg 的物体.开始时,物体位于位置A ,OA 间距离d =0.5 m ,绳子处于松弛状态.现在使物体以初速度v A =4 m ·s 1垂直于OA 向右滑动,如图所示.设以后的运动中物体到达位置B ,此时物体速度的方向与绳垂直.则此时刻物体对O点的角动量的大小L B =____________,物体速 度的大小v =__________________.8. 如图所示,一匀质木球固结在一细棒下端,且可绕水平光滑固定轴O 转动.今有一子弹沿着与水平面成一角度的方向击中木球而嵌于其中,则在此击中过程中,木球、子弹、细棒系统的____________________守恒,原因是______________________.木球被击中后棒和球升高的过程中,木球、子弹、细棒、地球系统的__________守恒.三、计算题9. 如图所示,一个质量为m 的物体与绕在定滑轮上的绳子相联,绳子质量可以忽略,它与定滑轮之间无滑动.假设定滑轮质量为M 、半径为R ,其转动惯量为221MR ,滑轮轴光滑.试求该物体由静止开始下落的过程中,下落速度与时间的关系.10. 一长为1 m 的均匀直棒可绕过其一端且与棒垂直的水平光滑固定轴转动.抬起另一端使棒向上与水平面成60°,然后无初转速地将棒释放.已知棒对轴的转动惯量为231ml ,其中m 和l 分别为棒的质量和长度.求:(1) 放手时棒的角加速度; (2) 棒转到水平位置时的角加速度.11. 如图所示,A和B两飞轮的轴杆在同一中心线kg·m2.开始时,A轮转速为600 rev/min,B轮静止.C为摩擦啮合器,其转动惯量可忽略不计.A、B分别与C的左、右两个组件相连,当C的左右组件啮合时,B轮得到加速而A轮减速,直到两轮的转速相等为止.设轴光滑,求:(1) 两轮啮合后的转速n;(2) 两轮各自所受的冲量矩.三、静电场 电场强度一、选择题1. 高斯定理 ⎰⎰⋅=VSV S E 0/d d ερ(A) 适用于任何静电场. (B) 只适用于真空中的静电场. (C) 只适用于具有球对称性、轴对称性和平面对称性的静电场.(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场. []2.如图所示,一个电荷为q 的点电荷位于立方体的A角上,则通过侧面abcd 的电场强度通量等于:(A) 06εq . (B) 012εq .(C) 024εq . (D) 048εq . [ ]3. 电荷面密度均为+ 的两块“无限大”均匀带电的平行平板如图放置,其周围空间各点电场强度E随位置坐标x 变化的关系曲线为:(设场强方向向右为正、向左为负) [ ]02εx4. 将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处(如图),测得它所受的力为F .若考虑到电荷q 0不是足够小,则(A) F / q 0比P 点处原先的场强数值大. (B) F / q 0比P 点处原先的场强数值小. (C) F / q 0等于P 点处原先场强的数值.(D) F / q 0与P 点处原先场强的数值哪个大无法确定. [ ] 5. 如图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,沿轴线方向单位长度上所带电荷分别为1和 2,则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E 为:(A) r0212ελλπ+. (B) 20210122R R ελελπ+π(C) 1012R ελπ. (D) 0. []6. 点电荷Q 被曲面S 所包围 , 从无穷远处引入另一点电荷q 至曲面外一点,如图所示,则引入前后:(A) 曲面S 的电场强度通量不变,曲面上各点场强不变. (B) 曲面S 的电场强度通量变化,曲面上各点场强不变. (C) 曲面S 的电场强度通量变化,曲面上各点场强变化. (D) 曲面S 的电场强度通量不变,曲面上各点场强变化. [ ]7. 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε可知下述各种说法中,正确的是:(A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零. (B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零.(C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.P+q 0(D) 闭合面上各点场强均为零时,闭合面内一定处处无电 [ ] 二、填空题7. 三个平行的“无限大”均匀带电平面,其电荷面密度都是+ ,如图所示,则A 、B 、C 、D 三个区域的电场强度分别为:E A =_________________,E B =_____________,E C =_________,E D =___________ (设方向向右为正).8. 一半径为R 的带有一缺口的细圆环,缺口长度为d (d<<R)环上均匀带有正电,电荷为q ,如图所示.则圆心O 处的场强大小E =__________________ __________,场强方向为______________________.9. 如图所示,真空中两个正点电荷Q ,相距2R .若以其中一点电荷所在处O 点为中心,以R 为半径作高斯球面S ,则通过该球面的电场强度通量=______________;若以 0r表示高斯面外法线方向的单位矢量,则高斯面上a 、b 两点的电场强度分别为________________________. 三、计算题10. 带电细线弯成半径为R 的半圆形,电荷线密度为 = 0sin ,式中 0为一常数, 为半径R 与x 轴所成的夹角,如图所示.试求环心O 处的电场强度.11.图中虚线所示为一立方形的高斯面,已知空间的场强分布为:E x =bx , E y+σ+σ+σABCD=0,E z=0.求立方体六个面的电场强度通量。
中国矿业大学(北京)《大学物理》课件-第七章 机械波

y
Acos
t1
2
x
0
以y为纵坐标、x 为 横坐标,
y
u
波形方程
x
给出 t1 时刻空间各
点的位移分布。
给出:t1时刻 波线上各个质点偏离各自平衡位置 的位移所构成的波形曲线(波形图)。
y
u
y
Acos
t1
2
x
0
x
A,波形曲线为余弦曲线,其 “周期” 为 。
B,沿波线(x轴)方向,两个距离相隔的质点的 振动的相位差为:2。
Physics
第7章 机械波
Physics
§7-1 机械波的产生和 传播
§7-1 机械波的产生和传播
波动是振动的传播过程。
机械波:机械振动在介质中的传播过程。
eg,声波、水波、地震波
1、机械波产生的条件
波源 弹性介质
产生机械振动的振源 传播机械振动的介质
注:波动是波源的振动状态或振动能量在介质中 的传播,介质的质点并不随波前进。eg,裙摆
求:1)振幅,2)波长,3)波的周期,4)弦上任一质点的 最大速率,5)图中a、b两点的相位差,6) 3T/4时的波 形曲线。
y / cm
0.5 0.4 0.2 0 0.2 0.4 0.5
中国矿业大学(北京)
M1
a
10 20
M2
b
30 40
50 60
70 x / cm t =0
18/23
补充例题2
波前:在任何时刻,波面有无数多个,最前方的波 面即是波前。波前只有一个。
平面波:波阵面为平面的波动
球面波:波阵面为球面的波动
柱面波:波阵面为柱面的波动
中国矿业大学(北京)
大学物理(第四版)课后习题及答案-机械振动
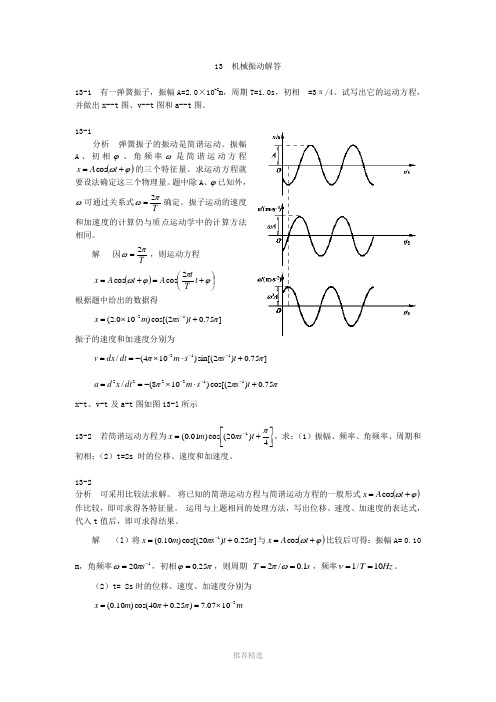
13 机械振动解答13-1 有一弹簧振子,振幅A=2.0×10-2m ,周期T=1.0s ,初相=3π/4。
试写出它的运动方程,并做出x--t 图、v--t 图和a--t 图。
13-1分析 弹簧振子的振动是简谐运动。
振幅A 、初相ϕ、角频率ω是简谐运动方程()ϕω+=t A x cos 的三个特征量。
求运动方程就要设法确定这三个物理量。
题中除A 、ϕ已知外,ω可通过关系式Tπω2=确定。
振子运动的速度和加速度的计算仍与质点运动学中的计算方法相同。
解 因Tπω2=,则运动方程()⎪⎭⎫⎝⎛+=+=ϕπϕωt T t A t A x 2cos cos根据题中给出的数据得]75.0)2cos[()100.2(12ππ+⨯=--t s m x振子的速度和加速度分别为 ]75.0)2sin[()104(/112πππ+⋅⨯-==---t s s m dt dx vπππ75.0)2cos[()108(/112222+⋅⨯-==---t s s m dt x d ax-t 、v-t 及a-t 图如图13-l 所示13-2 若简谐运动方程为⎥⎦⎤⎢⎣⎡+=-4)20(cos )01.0(1ππt s m x ,求:(1)振幅、频率、角频率、周期和初相;(2)t=2s 时的位移、速度和加速度。
13-2分析 可采用比较法求解。
将已知的简谐运动方程与简谐运动方程的一般形式()ϕω+=t A x cos 作比较,即可求得各特征量。
运用与上题相同的处理方法,写出位移、速度、加速度的表达式,代入t 值后,即可求得结果。
解 (l )将]25.0)20cos[()10.0(1ππ+=-t s m x 与()ϕω+=t A x cos 比较后可得:振幅A= 0.10 m ,角频率120-=s πω,初相πϕ25.0=,则周期 s T 1.0/2==ωπ,频率Hz T 10/1==ν。
(2)t= 2s 时的位移、速度、加速度分别为mm x 21007.7)25.040cos()10.0(-⨯=+=ππ)25.040sin()2(/1πππ+⋅-==-s m dt dx v )25.040cos()40(/2222πππ+⋅-==-s m dt x d a13-3 设地球是一个半径为R 的均匀球体,密度ρ5.5×103kg •m -3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ϕ = arctg(− v0 ) ωx0
或
} cosϕ = x0 A sinϕ = − v0
由cosϕ大小和sinϕ的符号决定ϕ
Aω
7.3 简谐振动的描述
(3)相位差
⎧ ⎨ ⎩
x1 x2
= =
Acos(ω t Acos(ω t
+ ϕ1) + ϕ2 )
Δϕ = (ω t + ϕ2 ) − (ω t + ϕ1 ) = ϕ2 −ϕ1
同频率简谐振动的相位差等于其初相差
7.3 简谐振动的描述
注意 同相、反相;超前、落后。
同相和反相
当Δϕ = ±2kπ (k =0,1,2,…), 两振动步调相同,称同相
x
A1 A2
x2 x1
同相 T
o
t
- A2
-A1
x
当Δϕ = ±(2k+1)π (k =0,1,2,…), A1
两振动步调相反,称反相
7.2 简谐振动的定义 简谐振动的定义
代表式
文字表述
适用范围
判 据 Fx = −kx
1
凡物体所受回复力与位移成 正比且反向时,物体的运动 是简谐振动。
只适用于机 械运动
判 据
d2 x dt 2
+
ω
2
x
=
0
任何一个物理量对时间的二 阶导数与其本身成正比且反 号时,该物理量按简谐振动
2
规律变化。
任何运动, 任何物理量
− ϕ0 ω
x-t 图象为振动曲线
7.3 简谐振动的描述
二.简谐振动的特征量
初相
x = Acos(ωt + ϕ )
振幅
角频率
1. 振幅A
振幅A:物理量离开平衡位置的最大距离| xmax | 。
表示振动的范围(强弱),由初始条件决定。
x = Acos(ω t + ϕ ) t = 0 由 v = − Aω sin(ω t + ϕ )
7.1 简谐振动的模型 回顾中学内容:简谐振动模型
弹簧振子
集中弹性
k
M
集中质量
μ=0
m弹 <<M, m弹略去不计
弹簧振子的回复力:
弹性力 F = −kx 弹簧的形变量
弹簧的劲度系数
7.1 简谐振动的模型
单摆 无伸长的轻线下悬挂质点作无阻尼摆动
单摆的回复力:
F = −mg sinθ
mg = k
当θ 很小时 sinθ ≈ θ
x
x
r A
(0
)
A
ωϕ ω t+ϕ 相位
1
t
r A
(t
)
x(t)
0
振幅矢量
1
0
t
2
绕O点以角速度 ω 逆时针旋转的矢量 Ar(t ),在x
轴上的投影正好描述了一个简谐振动。
7.3 简谐振动的描述
3. 比较同频率简谐振动的步调
ω
N
A2ϕ2 Aϕ1 1 M OQ P
x
点Q的振动比点P的振动超前 相位: Δϕ = ϕ 2-ϕ 1 时间: Δt = ϕ2 − ϕ1
ϕ =π 2
ω
x<0
x>0
v<0
v<0
ϕ =π
ϕ=0 x
x<0
x>0
v>0
v>0
ϕ = 3π 2
7.3 简谐振动的描述
利用旋转矢量
1. 画出振动曲线图
x
x
2 1 t=0s
3
11
4
5 67
10 O
9
8
36 9
12 t
理解振动曲线与旋转矢量之间的关系
7.3 简谐振动的描述
2. 求初相和相位 x = Acos(ωt + ϕ )
x0 = Acosϕ v0 = − Aω sinϕ
解得
A=
x02
+
v02 ω2
=
x2
+
v2 ω2
7.3 简谐振动的描述 2.角频率ω 、周期T、频率ν 角频率ω:由系统本身决定的常数,与初始条件无关。
周期T:物体作简谐振动周而复始完全振动一次所需 的时间。 频率ν:表示单位时间内物体完成全振动的次数。
ω 4. 分析振动的合成(下面讲)
7.3 简谐振动的描述
例2 一质点在x轴上作简谐振动,振幅A=4cm,周期T
=2s,其平衡位置取坐标原点。若t=0时刻质点第一次 通过x=-2cm处,且向x轴负方向运动,再过多久质点 第二次通过x=-2cm处?
解:由旋转矢量法作图
v
由图可知质点振动的初相为 2π ,
x(t ) = x1(t) + x2(t )
的仍
= ( A1 cosϕ1 + A2 cosϕ2 )cosωt
简然 谐是
− ( A1 sinϕ1 + A2 sinϕ2 ) sinωt
振同
合振幅 = Acosϕ ⋅ cosωt − Asinϕ ⋅ sinωt
动频 率
= Acos(ωt + ϕ )
式中:A = A12 + A22 + 2 A1 A2 cos(ϕ2 − ϕ1 ) ϕ = arctan A1 sinϕ1 + A2 sinϕ2 A1 cosϕ1 + A2 cosϕ2
基本要求
1. 掌握简谐振动的定义(回复力、动力学方程和 运动学方程) 2. 掌握简谐振动的特征量,振动曲线 3. 掌握并熟练应用旋转矢量法分析解决有关简谐振 动的问题 4. 理解简谐振动的能量 5. 掌握同方向同频率简谐振动的合成 6. 了解拍现象,互相垂直简谐振动的合成 7. 了解阻尼振动和受迫振动
r A t=t
ω t+ϕ0 o
· ϕ0 x
ω ω
r A t = 0x
x = A cos(ω t + ϕ0)
x = A cos(ωt + ϕ )
v = dx
dt
vx = −v sin(ωt + ϕ )= −ωR sin(ωt + ϕ )
a
=
d2 x dt 2
ax = −an cos(ωt + ϕ )= −ω 2 R cos(ωt + φ )
离系统平衡 位置的位移
系统本身决定的常数
7.2 简谐振动的定义
二.简谐振动的微分方程
由回复力: F = −kx
由牛顿第二定律:F
=
ma
=
m
d2x dt 2
令 k = ω 2得 m
d2 x dt2
+
k m
x
=
0
d2 dt
x
2
+
ω
2
x
=
0
7.2 简谐振动的定义
三.简谐振动的运动方程
d2 x dt 2
+
3
那么两次通过x=-2cm处,即时
间由0到t矢量间夹角为 2π ,所以
3 2π
t = 3 ×T = T = 2 (s)
2π
33
t=0
2π 3 -2
t
x (cm)
小结:熟练运用旋转矢量法解决问题
7.4 简谐振动的能量 无阻尼弹簧振子系统
o
μ=0 x
x
以平衡位置为坐标原点
{x = Acos(ω t + ϕ0 ) v = − Aω sin(ω t + ϕ0 )
振动系统动能:
Ek
=
1 2
mv 2
=
1 2
mA2ω 2
sin 2 (ω
t
+ϕ)
=
1 2
kA2
sin 2 (ω
t
+ϕ)
7.4 简谐振动的能量
o
μ=0 x
x
以弹簧振子所在水平面为重力势能零点
振动系统势能:
EP
=
1 2
kx 2
=
1 2
kA2
cos2 (ω
t
+ϕ)
振动系统机械能:
E
=
Ep
+
Ek
=
1 2
kA 2
7.5 简谐振动的合成
几何方法
ω y
v A
=
v A1
+
v A2
ω
v
平行四边形整体旋
A v
A2 sinϕ2 转,其对角线为简谐振
Ao2
- A2
-A1
x1 反相
T
x2
t
7.3 简谐振动的描述 超前和落后
若Δϕ = ϕ 2-ϕ 1>0, 则 x2比x1较早达到正最大, 称 x2 比 x1 超前 (或 x1 比 x2 落后)。 超前、落后以<π 的相位角来判断
x
A1
x1
A2
T
o
- A2
x2
t
-A1
2 超前于1
7.3 简谐振动的描述 三.旋转矢量法
ω
2
x
=
0
求解得运动方程: x = Acos(ωt + ϕ )
积分常数
思考 运动方程可否用正弦函数描述?二者均可
利用函数关系 cos(ωt + ϕ ) = sin(ωt + ϕ + π )
并令 ϕ′ = ϕ + π
2
2
运动方程变形为:x = Asin(ωt + ϕ ′)
一般采用余弦函数描述简谐振动的运动方程
θl
T
Fm
重力的切 向分力
