第七章平面图形的认识(二)单元测试卷(C)及答案

合集下载

(word完整版)苏科版七年级下《第7章平面图形的认识(二)》单元测试题含答案,推荐文档

第7 章平面图形的认识(二)一、选择题(本大题共 6 小题，每小题 4 分，共 24 分；在每个小题列出的四个选项中，只有一项符合题意)1.如图7－Z－1 所示的四个图形中，∠1和∠2是同位角的是( )图 7－Z－1A．②③B．①②③C．①②④D．①④2.下列图形中，不能通过其中一个四边形平移得到的是( ),A) ,B),C) ,D)图 7－Z－23.如图 7－Z－3，AC⊥BC，CD⊥AB，DE⊥BC，垂足分别为C，D，E，则下列说法不正确的是( )图 7－Z－3A．AC 是△ABC 的高 B．DE 是△BCD 的高C．DE 是△ABE 的高 D．AD 是△ACD 的高4. 如图7－Z－4，BE∥AF，D 是AB 上一点，且DC⊥BE 于点C，若∠A＝35°，则∠ADC 的度数为( )图7－Z－4A．105°B．115°C．125°D．135°5.若一个多边形的每一个外角都是24°，则此多边形的内角和为( )A．2160°B．2340°C．2700°D．2880°6.将一张长方形纸片沿一条直线剪成两个多边形，那么这两个多边形的内角和之和不可能是()A．360°B．540°C．720°D．900°二、填空题(本大题共 6 小题，每小题 5 分，共 30 分)7.如图 7－Z－5，直线AB，CD 被直线EF 所截，若要AB∥CD，需增加条件：．(填一个即可)图 7－Z－58.若一个三角形的三边长分别为2，3，x，则x 的值可以为．(只需填一个整数)9.如图7－Z－6，点D，E 分别在AB，BC 上，DE∥AC，AF∥BC，∠1＝70°，则∠2＝°.图 7－Z－610.如图7－Z－7，已知AB∥CD，直线EF 与AB，CD 分别交于点E，F，EG 平分∠BEF.若∠1＝50°，则∠2的度数为．图 7－Z－711．如图7－Z－8 所示，∠A＋∠B＋∠C＋∠D＋∠E＋∠F＝．图 7－Z－812．某中学校园内有一块长30 m，宽22 m 的草坪，中间有两条宽2 m 的小路，把草坪分成了4 块，如图7－Z－9 所示，则草坪的面积为．图 7－Z－9三、解答题(共 46 分)13．(8 分)如图 7－Z－10，在方格纸内将△ABC 水平向右平移 4 个单位长度得到△A′B′C′(每个小方格的边长为 1 个单位长度)．(1)画出△A′B′C′；(2)画出AB 边上的中线CD 和高线CE(利用网格和直尺画图)；(3)△BCD 的面积为．图 7－Z－1014．(8 分)如图 7－Z－11，已知∠1＝∠2，∠B＝100°，求∠D 的度数．图 7－Z－1115．(8 分)已知一个多边形的所有内角的和与它的外角之和为1620°，求这个多边形的边数n..(10 分)如图 7－Z－12，四边形ABCD 中，∠BAD＝100°，∠BCD＝70°，点M，N 分别在AB，BC 上，将△BMN 沿MN 翻折，得到△FMN.若MF∥AD，FN∥DC，求∠B 的度数．图 7－Z－1217．(12 分)如图 7－Z－13，在△ABC 中，AD⊥BC 于点D，AE 平分∠BAC，∠B＝70°，∠C＝30°.求：(1)∠BAE 的度数； (2)∠DAE 的度数．图 7－Z－13教师详解详析1．C [解析] 根据同位角的定义进行判断．2．D 3.C 4.C 5. B6．D [解析] ①将长方形沿对角线剪开，得到两个三角形，两个多边形的内角和为180°＋180°＝360°；②将长方形从一顶点剪向对边，得到一个三角形和一个四边形，两个多边形的内角和为180°＋360°＝540°；③将长方形沿一组对边剪开，得到两个四边形，两个多边形的内角和为360°＋360°＝720°.故选D.7.答案不唯一，如∠EGB＝∠EHD 等8.答案不唯一，如 2 或3 或4，只要填其中一个即可[解析] 根据三角形的三边关系“三角形两边之和大于第三边；三角形两边之差小于第三边”得 3－2＜x＜3＋2，即 1＜x＜5.因为x 为整数，所以x＝2 或 3 或 4.9．70 [解析] 因为DE∥AC，所以∠C＝∠1＝70°.又因为AF∥BC，所以∠2＝∠C＝70°.故答案为 70.10．65° [解析] 因为AB∥CD(已知)，所以∠1＋∠BEF＝180°(两直线平行，同旁内角互补)．又因为∠1＝50°(已知)，所以∠BEF＝130°(等式的性质)．又因为EG 平分∠BEF(已知)，所以∠FEG＝∠BEG＝65°(角平分线的定义)．因为AB∥CD(已知)，所以∠2＝∠BEG＝65°(两直线平行，内错角相等)．11．360°12．560 m2 [解析] (30－2)×(22－2)＝560(m2)．13．解：(1)如图所示，△A′B′C′即为所求．(2)如图所示，CD，CE 即为所求．(3)414．解：由∠1＝∠AEF，∠1＝∠2，得∠AEF＝∠2，所以AB∥CD(同位角相等，两直线平行)，所以∠B＋∠D＝180°(两直线平行，同旁内角互补)．因为∠B＝100°，所以∠D＝80°.15．解：根据题意，得(n－2)·180°＋360°＝1620°，解得n＝9.16．解：因为MF∥AD，FN∥DC，所以∠BMF＝∠A＝100°，∠BNF＝∠C＝70°(两直线平行，同位角相等)．因为△BMN 沿MN 翻折，得到△FMN，1所以∠BMN＝2∠BMF＝50°，1∠BNM＝2∠BNF＝35°.在△BMN 中，∠B＝180°－(∠BMN＋∠BNM)＝180°－(50°＋35°)＝180°－85°＝95°.17．解：(1)因为∠B＋∠C＋∠BAC＝180°，所以∠BAC＝180°－∠B－∠C＝180°－70°－30°＝80°.因为AE 平分∠BAC，1所以∠BAE＝2∠BAC＝40°.(2)因为AD⊥BC，所以∠ADB＝90°.而∠ADB＋∠B＋∠BAD＝180°，所以∠BAD＝180°－∠ADB－∠B＝20°，所以∠DAE＝∠BAE－∠BAD＝40°－20°＝20°.“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

苏科版七年级下数学第七章平面图形的认识(二)单元检测卷含答案.docx

第七章平面图形的认识（二）单元检测卷姓名：_________ 班级：___________题号- 总分评分一、选择题（共12小题；每小题3分，共36分）1•下列长度的三根小木棒能构成三角形的是（）A. 2cm, 3cm, 5cmB. 7cm, 4cm, 2cm C・ 3cm, 4cm, 8cm D. 3cm, 3cm, 4cm2•如图为一张椅子的侧面视图，图中Z1和Z2是一对（）5•如图，由已知条件推出的结论，正确的是（）A.同旁内角B.内错角3.下列说法正确的是（）A. a, b, c 是直线，且a〃b, b〃c,贝!Ja〃cC. a, b, c 是直线，且a/7b, b丄c,贝ija〃cC.同位角D.对顶角B. a, b, c是直线，且a丄b, b丄c,贝!j a_LcD. a, b, c是直线，且a〃b, b〃c,则a丄c 4•如图，对于图中标记的各角, 卜•列条件能够推理得到a//b的是（B. Z2=Z4C. Z3+Z2=Z4D. Z2+Z3+Z4=180°C. rt|Z2=Z6,可以推出 AD 〃BC 6.如图，和Z2是同位角的是（）A. Z1=Z3 C.如果Z2=30°,则有 BC 〃AD 9.如图，下列结论中不正确的是（）10•如图,a//b, c 与 a , b 都相交,Zl=50°,则Z2=(B ・ Z1=Z2+Z4C ・ Z1=Z3+Z4+Z5D ・ Z2=Z4+Z5 A. 40° B. 50° C. 100° D. 130°D.由Z3=Z7,可以推出AB//DC7•若三角形的三边长分别为3, 4, X,则x 的值可能是（A. 1B. 6C. 7D. 10 8 •若将一副三角板按如图所示的方式放置, 则下列结论不正确的是（B.如果Z2=30°,则有 AC 〃DED.如果Z2=30°,必有Z4=ZC口.把一块直尺与一块三角板如图放置，若Zl=40°，则Z2的度数为（）12.如图1,两个等边AABD, ACBD 的边长均为2,将AABD 沿AC 方向向右平移k 个单位到厶A8D 7的位C. 140°D. 130°置，得到图2,则下列说法：①阴彫部分的周长为4；②当k<l 吋，图屮阴影部分为正六边形；③若阴彫部分和空白部分的面积相等，则k 巫.其中正确的说法是（）A.① D.①②③二、填空题（共10题；共13分）GF 交ZDEB 的平分线EF 于点F, ZAGF=130°,则ZF 二14.两个角的两边分别平行，其屮一个角是60。

七上《平面图形的认识(二)》单元综合测试卷(含答案)

第七章《平面图形的认识(二)》单元综合测试卷考试时间:90分钟满分:100分一、选择题(每小题3分，共24分) 1. 下列图形可由平移得到的是( )2. 下列长度的3条线段，能构成三角形的是( )A. 1 cm ，4 cm ，3 cmB. 2 cm ，3 cm ，4 cmC. 4 cm ，4 cm ，8 cmD. 5 cm ，6 cm ，12 cm 3. 如果一个三角形有两个外角的和等于270°，则此三角形一定是( ) A.锐角三角形 B.直角三角形 C.钝角三角形 D.等边三角形 4. 如图，已知ABC 中，//DE BC ，将△ADE 沿DE 翻折，点A 落在平面内的'A 处，若50B ∠=︒，则'BDA ∠的度数是( )A. 90︒B. 100︒C. 80︒D. 70︒5. 如图，由已知条件推出的结论，正确的是( )A.由15∠=∠，可以推出//AD CBB.由48∠=∠，可以推出//AD BCC.由26∠=∠，可以推出//AD BCD.由37∠=∠，可以推出//AB DC 6. 下列说法:①满足a b c +>的a ，b ，c 三条线段一定能组成三角形;②三角形的三条高交于三角形内一点;③三角形的一个外角大于它的任何一个内角;④两条直线被第三条直线所截，同位角相等.其中错误的有( )A. 1个B. 2个C. 3个D. 4个7. 将一个直角三角板和一把直尺如图放置，如果47α∠=︒，则β∠的度数是( ) A. 43︒ B. 47︒ C. 30︒ D. 60︒8. 如图，ABC 的两条中线AM ，BN 相交于点O ，已知ABO 的面积为4，BOM 的面积为2，则四边形MCNO 的面积为( )A. 4B. 3C. 4. 5D. 3. 5 二、填空题(每小题2分，共20分) 9. 在ABC 中，如果40B ∠=︒，70C ∠=︒，那么与A ∠相邻的一个外角等于 ︒.10. 如图，AD 、AE 分别是ABC 的高和角平分线，若36B ∠=︒，66C ∠=︒则EAD ∠= ︒.11. 如图，ABC 中，O 是ABC ∠和ACB ∠的角平分线的交点，若50A ∠=︒，则BOC ∠= ︒.12. 如图，直线//a b ，AC BC ⊥，90C ∠=︒，，则α∠= ︒.13. 如图，四边形ABCD 中，若去掉一个60︒的角得到一个五边形，则12∠+∠= ︒.14. 从一个多边形的一个顶点出发一共可作5条对角线，则这个多边形的内角和为 ︒. 15. 如图，A B C D E F ∠+∠+∠+∠+∠+∠= ︒. 16. 如图，ABC 中，30A ∠=︒，70B ∠=︒，CE 平分艺ACB ，CD AB ⊥于D ，DF CE ⊥，则CDF ∠= ︒.17. 如图，把ABC 纸片沿DE 折叠，当点A 落在四边形BCED 的外部时，则A ∠与1∠和2∠之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是 .18. 如图，若//AB CD ，BF 平分ABE ∠，DF 平分CDE ∠，90BED ∠=︒，则BFD ∠= ︒.三、解答题(共56分)19. (3分)如果一个n 边形的内角都相等，且它的每一个外角与内角的比为2:3，求这个多边形的内角和.20. ( 5分)如图是34⨯的正方形网格(每个小正方形的边长为1)，点A ，B ，C ，D ，E ，F ，G 在格点上.请解答下列各题:(1)在图①中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择)，并将你所画的三角形向左平移2个单位.向上平移1个单位(用阴影表示);(2)在图②中画一个面积为0. 5的钝角三角形(三角形的顶点从以上七个点中选择); (3)在以上七点中选择三点作为三角形的顶点，其中面积为3的三角形有个. 21. (6分)根据题意结合图形填空:如图，点E 在DF 上，点B 在AC 上，12∠=∠，C D ∠=∠.试说明://AC DF .将过程补充完整.证明:因为12∠=∠(已知)且13∠=∠( ) 所以23∠=∠(等量代换).所以 // ( ) 所以C ABD ∠=∠( )又C D ∠=∠ (已知)所以 = (等量代换). 所以//AC DF ()22. ( 6分)如图，四边形ABCD 中，//AD BC ，DE 平分ADB ∠，BDC BCD ∠=∠. 求证:1290∠+∠=︒.23. ( 6分)如图，BD 是ABC ∠的平分线，//DE CB ，交AB 于点E ，150BED ∠=︒，60BDC ∠=︒，求A ∠的度数.24. (6分)如图，在ABC 中，AD 平分BAC ∠，P 为线段AD 上的一个动点，PE AD ⊥交直线BC 于点E .(1)若35B ∠=︒，85ACB ∠=︒，求E ∠的度数;(2)当P 点在线段AD 上运动时，猜想E ∠与B ∠、ACB ∠的数量关系写出结论，无需证明.25. ( 8分)如图，已知//CB OA ，100C OAB ∠=∠=︒，且满足FOB AOB ∠=∠，OE 平分COF ∠.(1)求EOB ∠的度数;(2)若平行移动AB ,那么:OBC OFC ∠∠的值是否随之变化?若变化，找出变化规律;若不变，求这个比值;(3)在平行移动过程中，是否存在某种情况，使OEC OBA ∠==∠若存在，求其度数，若不存在，请说明理由.26. ( 8分)(1)如图①的图形我们把它称为“8字形”，请说明A B C D ∠+∠=∠+∠. (2)阅读下面的内容，并解决后面的问题:如图②，AP ，CP 分别平分BAD ∠，BCD ∠，若36ABC ∠=︒，16ADC ∠=︒，求P ∠的度数.解：∵AP ，CP 分别平分BAD ∠，BCD ∠12∴∠=∠，34∠=∠由(1)的结论得:3124P BP B ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩①+②，得223142P B ∠+∠+∠=∠+∠+∠ ∴1()262P B D ∠=∠+∠=︒ ①如图③，直线AP 平分BAD ∠的外角FAD ∠，CP 平分BCD ∠的外角BCE ∠，若36ABC ∠=︒，16ADC ∠=︒，请猜想P ∠的度数，并说明理由.②在图④中，直线AP 平分BAD ∠的外角FAD ∠，CP 平分BCD ∠的外角BCE ∠，猜想艺P ∠与B ∠，D ∠的关系，直接写出结论，无需说明理由.③在图⑤中，AP 平分BAD ∠，CP 平分BCD ∠的外角BCE ∠，猜想P ∠与B ∠，D ∠ 的关系，直接写出结论，无需说明理由.参考答案1. A2. B3. B4. C5. C6. D7. A8. A9. 110 10. 15 11. 115 12. 25 13. 240 14. 1 080 15. 360 16. 70∠-∠=∠17.122A18. 45°19. 设每个外角为2x，每个内角为3x，则x=︒，272x=︒.+=︒，36x x23180︒÷︒=，则360725故该多边形为五边形.︒⨯-=︒.故多边形的内角和为180(52)54020. (1)答案不唯一，如(2)答案不唯一，如(3) 5∠=∠(已知)，21. 因为12∠=∠(对顶角相等)，且13∠=∠(等量代换).所以23CE DB(同位角相等，两直线平行).所以//∠=∠(两直线平行，同位角相等).所以C ABD又C D ∠=∠ (已知)，所以ABD D ∠=∠ (等量代换).所以//AC DF (内错角相等，两直线平行). 22. 证明:因为//AD BC ,所以180ADC BCD ∠+∠=︒. 因为DE 平分ADB ∠, 所以ADE BDE ∠=∠且因为BDC BCD ∠=∠, 所以90BDE BDC ∠+∠=︒.所以90EDC BDE BDC ∠=∠+∠=︒.所以121801809090EDC ∠+∠=︒-∠=︒-︒=︒. 23. 因为//DE CB .所以180DEB EBC ∠+∠=︒. 因为150BED ∠=︒, 所以30EBC ∠=︒. 因为BD 平分ABC ∠, 所以1152EBD DBC EBC ∠=∠=∠=︒. 因为60BDC ∠=︒,所以601545A BDC EBD ∠=∠-∠=︒-︒=︒ 24. (1)因为35B ∠=︒,85ACB ∠=︒，所以180180358560BAC B ACB ∠=︒-∠-∠=︒-︒-︒=︒ 因为AD 平分BAC ∠,所以11603022DAC BAC ∠=∠=⨯︒=︒. 所以180308565ADE ∠=︒-︒-︒=︒.因为PE AD ⊥D ，所以90EPD ∠=︒. 所以906525E ∠=︒-︒=︒.(2) 1()2E ACB B ∠=∠-∠ 25. (1)因为//CB OA .所以180********AOC C ∠=︒-∠=︒-︒=︒, 因为OE 平分COF ∠, 所以COE EOF ∠=∠. 因为FOB AOB ∠=∠ ,所以11804022EOB EOF FOB AOC ∠=∠+∠=∠=⨯︒=︒.(2)因为//CB OA , 所以AOB OBC ∠=∠. 因为FOB AOB ∠=∠, 所以FOB OBC ∠=∠.所以2OFC FOB OBC OBC ∠=∠+∠=∠. 所以:1:2OBC OFC ∠∠=，是定值.(3)假设存在某种情况，使OEC OBA ∠=∠.在COE 和AOB 中，因为OEC OBA ∠=∠,C OAB ∠=∠ , 所以COE AOB ∠=∠.所以COE EOF FOB AOB ∠=∠=∠=∠.所以11802044COE AOC ∠=∠=⨯︒=︒ 所以1801801002060OEC C COE ∠=︒-∠-∠=︒-︒-︒=︒.故存在某种情况，使OEC OBA ∠=∠,此时60OEC OBA ∠=∠=︒.26. (1)因为180A B AOB ∠+∠+∠=︒,180C D COD ∠+∠+∠=︒. 所以A B AOB C D COD ∠+∠+∠=∠+∠+∠. 因为AOB COD ∠=∠, 所以A B C D ∠+∠=∠+∠. (2) 26P ∠=︒.如图，因为AP 平分BAD ∠的外角FAD ∠,CP 平分BCD ∠的外角BCE ∠, 所以12∠=∠,34∠=∠.由(1)的结论得:PAD P PCD D PAB P PCB B ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩因为1PAB ∠=∠,12∠=∠, 所以2PAB ∠=∠.所以23P B ∠+∠=∠+∠.③①+③，得23P PAD P B PCD P ∠+∠+∠+∠=∠+∠+∠+∠. 即2180180P B D ∠+︒=∠+∠+︒.所以1()262P B D ∠=∠+∠=︒. (其他方法的情给分)(3)1180()2P B D ∠=︒-∠+∠(4)190()2P B D ∠=︒+∠+∠。

(完整word版)第七章平面图形的认识(二)单元提优训练(含答案),推荐文档

第七章平面图形的认识（二）单元提优训练（时间：90分钟总分：100分）一、填空题（每题2分，共30分）1.如图，11 // |2.若/ 2= 2/ 1,则/ 1 = ___________ ，/ 2= _________-f//// r一711. ----------- h/ 1L L—/ ---------------- \C匚D僚1题）｛第2題）（第3駆）(»4«)2.小明不小心将形状是梯形的玻璃打碎成两部分（如图）•若量得上半部分的/ A = 123 ° , / D = 104°,则原梯形玻璃下半部分的/ B= ________ ，/ C= ________ .3•如图，用吸管吮吸易拉罐内的饮料时，吸管与易拉罐上部夹角/ 1 = 74°,那么吸管与易拉罐下部夹角/ 2= __________ .4. ______________________________________________________ 如图，AB // CD，/ A = 35。

，/ C= 78°，则/ M = ____________________________________________ .5. ______________________________________________________________ 如图，CD 平分/ ACB , DE // BC，/ AED = 80°,则/ EDC =________________________________ .6. 如图，AB // CD，/ BAE = 40 °，/ ECD = 62°, EF 平分/ AEC ,则/ AEF = ____________7. 若一个多边形的每个外角都是 ___ 72°,则这个多边形是边形，它的内角和为&如图，已知△ ABC的/ ABC和/ ACB的外角平分线交于点D，/ A = 40°，则/ D =9. 三角形两边的长分别为1和&若该三角形第三边长为偶数，则该三角形的周长为10. ______________ 如图，AB // CD，直线MN 与AB、CD 分别交于E、F, GE丄MN，/ 1= 130 °，则 /2的度数为.11. _________________________________________________________________________如图，等边三角形ABC沿边AB的方向平移到△ BDE的位置，则图中/ CBE = _______________ 连接CE后，线段CE与AD的关系是__________ .12. 如图，AB // CD，/ D = 80°,/ CAD :/ BAC = 3: 2,则/ CAD = _______________ .A .对顶角的平分线B .两条平行线被第三条直线所截，内错角的平分线C .两条平行线被第三条直线所截，D .两条平行线被第三条直线所截， 20.已知等腰三角形的一个底角是 A . 150°B . 120°21 .下列说法：①钝角三角形有两条高在三角形内部；②三角形的三条高最多有两条不在三角形内部；③三角形的三条高的交点不在三角形内部，就在三角形外部；④钝角三角形三个内角的平分线的交点一定不在三角形内部.其中正确的个数为（）〔第 1413. 65° 14. 如图，把△ ABC 平移到△ DEF 的位置，若 AB = 5 cm ，则，/ B = 30 °，那么/ F = _________ .如图，把厶ABC 沿RS 的方向平移到△ DEF 的位置， DE = 贝U AB //,BC =如果/ A = 80°,那么/ D = ____________ . 15. 如图，已知 DE // AB , / ACD = 75°,/ B = 25°, 二、选择题（每题 2分，共22分）16. 经过平移，图形上的每个点都沿同一方向移动了一定距离，下列说法中正确的是（）A .不同的点移动的距离不同B .不同的点移动的距离相同C .不同的点移动的距离可能相同，也可能不同D .无法确定17. 已知在厶ABC 中有两个角的大小分别为A .直角三角形C 钝角三角形则/ ACB 的度数为18 . 如图,AB // CD , 则 a 、3、 A .a+ 3= 180° — Y B .a+ 3= 180 ° + Y C .a+ 3+ Y =360 ° D.a+ 3+ Y= 270 °19 . 下列角平分线中互相垂直的是40° 和 70° B .等边三角形D .等腰三角形丫三角之间的关系是，则这个三角形是同位角的平分线同旁内角的平分线30°，则这个三角形的顶角等于（）C . 75 °D . 30 °【第13题）(第 123)R S D / ---------FA . 1个B . 2个C. 3个 D . 4个22 .下列给出的三条线段长度的相关条件能组成一个三角形的是（）A . 4, 11, 71 1 C . 1 1 , 2, 3丄 2223. 下列叙述错误的是A . △ ABC 中，Z A +Z B<Z C ,此三角形不一定为钝角三角形B .三角形可分为锐角三角形、直角三角形和钝角三角形C .若三角形的一个外角小于与它相邻的一个内角，则这个三角形为钝角三角形D .直角三角形只有一条高在三角形内 24.等腰三角形的一边长等于 5,另一边长等于 9,它的周长是 A . 19 B . 14C . 2325. 如图，Z 1=Z 2, Z DAB =Z BCD .给出下列结论：① B = Z D :④/ D = Z DAC .其中，正确的结论有（ A . 1个B . 2个C . 3个D . 4个29. （5 分）如图，AD // BC ,Z A = 96°,Z D = 104°, BE 、CE 分别是Z ABC 和Z BCD 的角平分线，求Z BEC 的度数.1 : 4: 611—? — ?（）D . 19 或 23AB // DC :② AD // BC :③/（第閒题）Z 2-Z 3= 90°,Z 4 = 115 B . 65°（共48分）如图，Z A + Z B = 180° 26 .如图，Z 1 + 23= 90°, A . 45三、解答题 27 . （ 5 分）C . 60°/ D -Z C = 25° .如图，Z A = 70°,Z 1 = 写出推理过程.28. （5 分）那么23的度数是（）求/ C 、/ D 的度数.70°,Z 2 = 110°,你能判定图中哪些直线平行?30. （6 分）如图，AB // CD，/ 1:Z 2:/ 3 = 1 : 2: 3.（1）求/ 3的度数；⑵/ EBA与/ 2相等吗？为什么?31. （6分）如图，把一张长方形纸片ABCD沿EF折叠,ED'交BC于点G .已知/ EFG = 50°,试求/ DEG与/ BGD'的度数.32. （6分）如图，AD丄BC, EG丄BC ,垂足分别为D、G,/ E = / AFE .试说明AD是△ ABC的角平分线.33. （7分）如图，CE平分/ ACD , F为CA延长线上一点，FG // CE交AB于点G,/ ACD = 100°,/AGF = 20°,你能求出/ B的度数吗？若能，请写出求解过程；若不能，请说明理由.34. （8分）如图，O是厶ABC的3条角平分线的交点，OG丄BC,垂足为G .1⑴猜想/ BOC与90°+ - / BAC之间的数量关系，并说明理由;2⑵/ DOB与/ GOC相等吗？为什么？DG C参考答案、1. 60° 120° 2 .57° 76°3 .74° 4. 43° 5. 40° 6. 51°7 .五 540 ° 8. 70° 9. 17 10. 40°11. 60° CE / AD 且 CE =1 AD212. 60° 135c m 85° 14.DE EF 80 ° 1.80° 、16. B 17. D18.B 19 .D 20 . B 21. A 22. D 23 . A 24 . D 25 .C 26 . B、27./ C = 77.5O/ D = 102.5°28 . AC // DE ,AB // EF ,推理略29./ BEC = 100° 30.⑴/ 3 = 108° (2) / EBA = 180° -Z 1 -Z 2= 180° - 36° —72°= 72°,故/ EBA = / 2. 31 . / DEG = 100 °, / BGD' = 80° 32.因为 AD 丄 BC , EG 丄 BC ，所以 AD // EG ,从而/ E =/ CAD , / AFE =/ BAD .由/ E = / AFE 知，/ CAD = / BAD ，即AD 平分/ BAC ，所以AD 是厶ABC 的角平分线. 33 ./ B = 30° 34. (1)相等，理由略 (2)相等，理由略。

2020-2021学年七年级数学苏科版下册《第7章平面图形的认识(二)》单元测试卷(有答案)

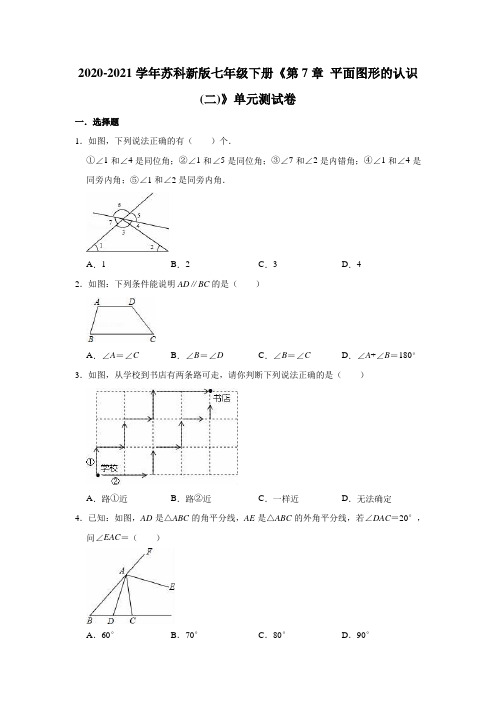
2020-2021学年苏科新版七年级下册《第7章平面图形的认识(二)》单元测试卷一．选择题1．如图，下列说法正确的有（）个．①∠1和∠4是同位角；②∠1和∠5是同位角；③∠7和∠2是内错角；④∠1和∠4是同旁内角；⑤∠1和∠2是同旁内角．A．1B．2C．3D．42．如图：下列条件能说明AD∥BC的是（）A．∠A＝∠C B．∠B＝∠D C．∠B＝∠C D．∠A+∠B＝180°3．如图，从学校到书店有两条路可走，请你判断下列说法正确的是（）A．路①近B．路②近C．一样近D．无法确定4．已知：如图，AD是△ABC的角平分线，AE是△ABC的外角平分线，若∠DAC＝20°，问∠EAC＝（）A．60°B．70°C．80°D．90°5．有长度为9cm、12cm、15cm、36cm，39cm的五根木棒，从中任取三根，则可搭成（首尾连接）直角三角形的取法有（）A．1种B．2种C．3种D．4种6．如图，AB∥CD∥EF，BC∥DE，则∠B与∠E的关系是（）A．相等B．互余C．互补D．不能确定7．两条平行线被第三条直线所截，形成的角平分线互相平行的是（）A．对顶角的角平分线B．同位角的角平分线C．同旁内角的角平分线D．以上都不对8．共有5个正三角形，从位置来看，下图中（）是由如图平移得到的．A．B．C．D．9．从多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2013个三角形，则这个多边形的边数为（）A．2011B．2015C．2014D．201610．图中，可以视为是图形平移的不同组合对数（一个梅花对另一个梅花不计方向）有（）A．9对B．10对C．5对D．8对二．填空题11．将△ABC沿BC方向平移3cm得到△DEF，则CF＝；若∠A＝80°，∠B＝60°，则∠F＝．12．某校初一（3）班共有42名同学，若每两名同学互相握手一次．则每个同学需要握次，全班同学共握手次．13．如图所示，∠ACD＝115°，∠B＝55°，则∠A＝，∠ACB＝．14．伸拉铁门能自由伸拉主要是应用了四边形的．15．△ABC的周长为24cm，a+b＝2c，a：b＝1：2，则a＝，b＝，c＝．16．如图，在△ABC中，BD＝CD，∠ABE＝∠CBE，则（1）是△ABC的中线，ED是△的中线；（2）△ABC的角平分线是，BF是△的角平分线．17．如图，DAE是一条直线，DE∥BC，则x＝．18．小明家买回一批地面砖，规格均为60cm×45cm，现欲在地面上铺成一个正方形的图案，至少要用块地砖．19．如图，求∠A+∠B+∠C+∠D+∠E+∠F＝．20．如图，在△ABC中，点D、E、F分别是三条边上的点，EF∥AC，DF∥AB，∠B＝45°，∠C＝60°．则∠EFD的大小为．三．解答题21．已知AD、AE分别是△ABC的中线和高，△ABD的周长比△ACD大3cm，且AB＝7cm．（1）求AC的长；（2）求△ABD与△ACD的面积关系．22．若把一个多边形剪去一个角，剩余的部分内角和为1440°，那么原多边形有几条边？23．在四边形ABCD中，∠A＝∠C＝90°，BE平分∠ABC，DF平分∠CDA．（1）作出符合本题的几何图形；（2）求证：BE∥DF．24．如图，AD∥BC，BD平分∠ABC，∠A＝120°，∠C＝60°，AB＝CD＝4cm，求：（1）AD的长；（2）四边形ABCD的周长．25．如图（1），MN∥PQ，点A，B在MN上，点C，D在PQ上，点A在点B的左侧，点C在点D的左侧，∠CDE＝∠ADE，∠ABE＝∠CBE，DE，BE交于点E，∠CBN＝100°．（1）若∠ADQ＝130°，求∠BED的度数；（2）将线段AD向左平移，使点D在点C的左侧，其他条件不变，如图（2）．若∠ADQ ＝n°，求∠BED的度数（用含n的代数式表示）．参考答案与试题解析一．选择题1．解：①∠1和∠4找不到被截线，不是同位角，故错误；②∠1和∠5在截线的同一方，被截线的同一侧是同位角，故正确；③∠7和∠2找不到被截线，不是内错角，故错误；④∠1和∠4找不到被截线，不是同旁内角，故错误；⑤∠1和∠2在截线的内部，被截线的同侧是同旁内角，故正确．根据同位角、内错角、同旁内角的定义，正确的是②⑤两个，故选：B．2．解：∵∠A+∠B＝180°，∴AD∥BC．故选：D．3．解：根据平移的性质得出：从学校到书店有两条路一样近．故选：C．4．解：∵AD是△ABC的角平分线，∠DAC＝20°，∴∠BAC＝2∠DAC＝40°，∴∠B+∠ACD＝140°，∴∠EAC＝∠FAC＝（∠B+∠ACD）＝70°．故选：B．5．解：∵92＝81，122＝144，152＝225，362＝1296，392＝1521，又∵81+144＝225，225+1296＝1521，∴92+122＝152，152+362＝392，故选：B．6．解：∵AB∥CD，∴∠B＝∠C，∵BC∥DE，∴∠C+∠D＝180°，∴∠B+∠D＝180°，∵CD∥EF，∴∠D＝∠E，∴∠B+∠E＝180°，即∠B和∠E互补．故选：C．7．解：A、对顶角的角平分线AC、AD共线，故错误；B、同位角的角平分线AC、BF互相平行，∵AM∥BN，∴∠PAM＝∠PBN；∵AC、BF是∠PAM和∠PBN的角平分线，∴∠1＝∠PAM＝∠PBN＝∠2；∴AC∥BF．故正确．C、同旁内角的角平分线AE、BF互相垂直，∵AM∥BN，∴∠MAB+∠PBN＝180°；∵AE、BF是∠MAB和∠PBN的角平分线，∴∠3+∠2＝∠MAB+∠PBN＝90°；∴AE⊥BF．故错误．D、因为B正确，所以错误．故选：B．8．解：A、可以由对称得到；B、可以由平移得到；C、可以由旋转变换得到；D、可以由旋转变换得到；故选：B．9．解：多边形一条边上的一点（不是顶点）出发，连接各个顶点得到2003个三角形，则这个多边形的边数为2013+1＝2014．故选：C．10．解：1和2、3、4、5有四种组合；2和3、4、5有三种组合；3和4、5有两种组合；4和5有一种组合，共有4+3+2+1＝10中组合．故选：B．二．填空题11．解：观察图形可知，对应点连接的线段是AD、BE和CF．∵△ABC沿BC方向平移3cm得到△DEF，∴BE＝CF＝3cm，∴∠F＝∠ACB＝180°﹣∠A﹣∠B＝40°，故答案为：3cm，40°．12．解：∵共有42名同学，若每两名同学互相握手一次，∴每个同学需要握41次，全班同学共握手41×42÷2＝861（次），故答案为：41；861．13．解：∵∠ACD为△ABC的外角，∴∠ACD＝∠A+∠B，则∠B＝115°﹣55°＝60°，又∠ACB和∠ACD互为邻补角，∴∠ACB＝180°﹣∠ACD＝180°﹣115°＝65°．故答案为：60°，65°．14．解：伸拉铁门能自由伸拉主要是应用了四边形的不稳定性．故空中填：不稳定性．15．解：根据题意，得，解得．故答案分别是：，，8．16．解：（1）∵BD＝CD，∴AD是△ABC的中线，ED是△BEC的中线；（2）∵∠ABE＝∠CBE，∴△ABC的角平分线是BE，BF是△ABD的角平分线．故答案为：（1）AD；BEC；（2）BE；ABD．17．解：∵DE∥BC，∴∠DAC＝∠ACF，即70°+x＝134°，解得x＝64°．故答案为：64°．18．解：∵60和45的最大公约数是15，∴60÷15×（45÷15）＝12块，故答案为：12．19．解：∵∠1＝∠A+∠B，∠2＝∠D+∠E，又∵∠1+∠F＝115°，∠2+∠C＝115°，∴∠A+∠B+∠C+∠D+∠E+∠F＝115°+115°＝230°．故答案为：230°．20．解：∵在△ABC中，∠B＝45°，∠C＝60°，∴∠A＝180°﹣∠B﹣∠C＝180°﹣45°﹣60°＝75°．∵EF∥AC，DF∥AB，∴四边形AEFD是平行四边形，∴∠EFD＝∠A＝75°．故答案为：75°．三．解答题21．解：（1）∵AD 是△ABC 的中线，∴BD ＝CD ，∵△ABD 的周长比△ACD 大3cm ，∴AB +BD +AD ﹣（AD +AC +DC ）＝3cm ，AB ﹣AC ＝3cm ，∵AB ＝7cm ，∴AC ＝4cm ；（2）△ABD 与△ACD 的面积相等；∵S △ADB ＝DB •AE ，S △ADC ＝DC •AE ，∴S △ADB ＝S △ADC ．22．解：设新多边形是n 边形，由多边形内角和公式得（n ﹣2）×180°＝1440°，解得n ＝10，原多边形是10﹣1＝9，10+1＝11，故答案为：9、10或11．23．（1）解：如图所示：（2）证明：∵四边形ABCD 中，∠A ＝∠C ＝90°，∴∠ADC +∠ABC ＝180°，∵BE 平分∠ABC ，DF 平分∠CDA ，∴∠ADF ＝∠FDE ＝ADC ，∠EBF ＝∠EBC ＝ABC ，∴∠FBE +∠FDE ＝90°，∵∠A ＝90°，∴∠AFD +∠ADF ＝90°，∴∠AFD +∠EDF ＝90°，∴∠DFA ＝∠EBF ，∴DF∥EB．24．（1）解：∵AD∥BC，∴∠ADB＝∠DBC，∵BD平分∠ABC∴∠ABD＝∠DBC，∴∠ABD＝∠ADB，∴AD＝AB＝4cm；（2）解：∵AD∥BC，∠A＝120°，∠C＝60°，∴∠ADC＝120°，∠ABC＝60°，∠ADB＝∠DBC；∵BD平分∠ABC，∴∠ABD＝∠ADB＝30°，∠BDC＝90°；∴AB＝AD，BC＝2CD；又AB＝CD＝4cm，∴AD＝4，BC＝8，∴AB+BC+CD+AD＝4+8+4+4＝20（cm），∴四边形ABCD的周长为20cm．25．解：（1）如图（1），过点E作EF∥PQ．∵∠CBN＝100°，∠ADQ＝130°，∴∠CBM＝80°，∠ADP＝50°．∵∠CDE＝∠ADE，∠ABE＝∠CBE，∴∠EBM＝40°，∠EDP＝25°．∵EF∥PQ，∴∠DEF＝∠EDP＝25°．∵EF∥PQ，MN∥PQ，∴EF∥MN，∴∠FEB＝∠EBM＝40°，∴∠BED＝∠DEF+∠FEB＝25°+40°＝65°；（2）如图（2），过点E作EF∥PQ．∵∠CBN＝100°，∴∠CBM＝80°．∵∠CDE＝∠ADE，∠ABE＝∠CBE，∴∠EBM＝40°，∠EDQ＝n°．∵EF∥PQ，∴∠DEF＝180°﹣∠EDQ＝180°﹣n°．∵EF∥PQ，MN∥PQ，∴EF∥MN，∴∠FEB＝∠EBM＝40°，∴∠BED＝∠DEF+∠FEB＝180°﹣n°+40°＝220°﹣n°．。

2014苏科版七年级数学下第七章平面图形的认识(二)单元练习试卷含答案(word版)

2014苏科版七年级数学下第七章平面图形的认识(二)单元练习试卷含答案(word版)2014年苏科版七年级下册数学第七章：平面图形的认识（二）考试范围：xxx；考试时间：100分钟；命题人：xxx注意事项：1.在答题前，填写好自己的姓名、班级、考号等信息。

2.请将答案正确填写在答题卡上。

分卷I一、单选题1.若一个多边形除了一个内角外，其余各内角之和为2570°，则这个内角的度数为（）A.90°B.105°C.130°D.120°2.若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是（）A.十三边形B.十二边形C.十一边形D.十边形3.锐角三角形的三个内角是∠A、∠B、∠C。

如果∠α＝∠A+∠B，∠β＝∠B+∠C，则这三个角中（）A.没有锐角B.有1个锐角C.有2个锐角D.有3个锐角4.若一个多边形的内角和等于1080°，则这个多边形的边数是（）A.9B.8C.7D.65.已知一个多边形的外角和等于它的内角和，则这多边形是（）A.三角形B.四边形C.五边形D.六边形6.一个三角形的三个内角中，至少有（）A.一个锐角B.两个锐角C.一个钝角D.一个直角7.如图，DE∥BC，EF∥AB，图中与∠___互补的角共有（）A.3个B.2个C.5个D.4个8.___已知∠１＝∠２，∠ＢＡＤ＝∠ＢＣＤ，则下列结论⑴ＡＢ∥ＣＤ，⑵ＡＤ∥ＢＣ，⑶∠Ｂ＝∠Ｄ，⑷∠Ｄ=∠ＡＣＢ，正确的有（）A.1个B.2个C.3个D.4个9.如果两条直线被第三条直线所截，那么一组内错角的平分线（）A.互相垂直B.互相平行C.互相重合D.以上均不正确10.用A、B、C分别表示学校、___家、___家，已知学校在___家的南偏东25，___家在___家正东，___家在学校北偏东35，则∠BAC=（）A.35B.55C.60D.6511.一架飞机向北飞行，两次改变方向后，前进的方向与原来的航行方向平行，已知第一次向左拐50°，那么第二次向右拐（）A.40°B.50°C.130°D.150°12.如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=125°，则∠DBC的度数为（）A.55°B.65°C.75°D.125°13、一条公路两次转弯后又回到原来的方向，如图所示，如果第一次转弯时的角度为140°，那么第二次转弯时的角度应为180°-140°=40°。

第7章平面图形的认识(二) 单元综合测试题2021-2022学年苏科版七年级数学下册( 含答案)

2021-2022学年苏科版七年级数学下册《第7章平面图形的认识（二）》单元综合测试题（附答案）一．选择题（共8小题，满分40分）1．在同一平面内，将两个完全相同的三角板如图所示摆放（直角边重合），可以画出两条互相平行的直线a，b．这样操作的依据是（）A．内错角相等，两直线平行B．同位角相等，两直线平行C．两直线平行，内错角相等D．两直线平行，同位角相等2．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则平移的距离为（）A．3B．4C．5D．63．如图，下列条件：①∠1＝∠2；②∠4＝∠5；③∠2+∠5＝180°；④∠1＝∠3；⑤∠6+∠4＝180°；⑥∠5+∠1＝180°，其中能判断直线l1∥l2的有（）A．②③④B．②③⑤C．②④⑤D．②④4．如图，AD∥CE，∠ABC＝110°，则∠2﹣∠1的度数是（）A．50°B．60°C．70°D．110°5．如图，把△ABC纸片沿DE折叠，当点A落在四边形BCDE的外面时，此时测得∠1＝112°，∠A＝40°，则∠2的度数为（）A．32°B．33°C．34°D．38°6．如图，若AB∥DE，∠B＝130°，∠D＝35°，则∠C的度数为（）A．80°B．85°C．90°D．95°7．如图，将一条对边互相平行的纸带进行两次折叠，折痕分别为AB，CD．若CD∥BE，∠1＝30°，则∠2的度数是（）A．50°B．60°C．65°D．70°8．如图，∠A+∠B+∠C+∠D+∠E+∠F的值是（）A．240°B．360°C．540°D．720°二．填空题（共8小题，满分40分）9．如图，AB∥CD，AD⊥AC，∠BAD＝40°，则∠ACD等于°．10．如图所示，要在竖直高AC为3米，水平宽BC为12米的楼梯表面铺地毯，地毯的长度至少需要米．11．如图，线段AF⊥AE，垂足为点A，线段GD分别交AF、AE于点C，B，连结GF，ED．则∠D+∠G+∠AFG+∠AED的度数为．12．如图，试求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数为．13．如图，已知∠ABD＝∠PCE，AB∥CD，∠AEC的角平分线交直线CD于点H，∠AFD ＝86°，∠H＝22°，∠PCE＝°．14．如图，∠ABC+∠C+∠CDE＝360°，直线FG分别交AB、DE于点F、G．若∠1＝110°，则∠2＝．15．如图，AB∥CD，∠CDE＝119°，GF交∠AEH的平分线EF于点F，∠DGF＝130°，则∠F＝°．16．如图，已知直线l1∥l2，∠A＝125°，∠B＝85°，且∠1比∠2大4°，那么∠1＝．三．解答题（共5小题，满分40分）17．如图，已知点D，E分别在△ABC的边AB，AC上，DE∥BC．（1）若∠ABC＝80°，∠AED＝40°，求∠A的度数；（2）若∠BFD+∠CEF＝180°，求证：∠EDF＝∠C．18．如图：已知，∠A＝120°，∠ABC＝60°，BD⊥DC于点D，EF⊥DC于点F，求证：（1）AD∥BC；（2）∠1＝∠2．19．如图，CE平分∠ACD，F为CA延长线上一点，FG∥CE交AB于点G，∠ACD＝140°，∠B＝45°，求∠AGF的度数．20．平面内的两条直线有相交和平行两种位置关系．（1）如图1，若AB∥CD，点P在AB、CD内部，∠B＝50°，∠D＝30°，求∠BPD 的度数；（2）如图2，在AB∥CD的前提下，将点P移到AB、CD外部，则∠BPD、∠B、∠D 之间有何数量关系？请证明你的结论；（3）如图3，写出∠BPD、∠B、∠D、∠BQD之间的数量关系？（不需证明）；（4）如图4，计算∠A+∠B+∠C+∠D+∠E+∠F的度数是．21．已知直线AB∥CD，点P为直线AB、CD所确定的平面内的一点．（1）如图1，直接写出∠APC、∠A、∠C之间的数量关系；（2）如图2，写出∠APC、∠A、∠C之间的数量关系，并证明；（3）如图3，点E在射线BA上，过点E作EF∥PC，作∠PEG＝∠PEF，点G在直线CD上，作∠BEG的平分线EH交PC于点H，若∠APC＝30°，∠P AB＝140°，求∠PEH 的度数．参考答案一．选择题（共8小题，满分40分）1．解：如图：∵两个完全相同的三角板，∴∠1＝∠2，而∠1、∠2是一对内错角，∴a∥b，故选：A．2．解：由平移的性质可知，BE＝CF，∵BF＝8，EC＝2，∴BE+CF＝8﹣2＝6，∴BE＝CF＝3，∴平移的距离为3，故选：A．3．解：①∠1＝∠2，不能判定l1∥l2；②∠4＝∠5，能判定l1∥l2；③∠2+∠5＝180°，不能判定l1∥l2；④∠1＝∠3，能判定l1∥l2；⑤∠6+∠4＝180°，不能判定l1∥l2；⑥∠5+∠1＝180°，不能判定l1∥l2；故选：D．4．解：如图，作BF∥AD，∵AD∥CE，∴AD∥BF∥EC，∴∠1＝∠3，∠4+∠2＝180°，∠3+∠4＝110°，∴∠1+∠4＝110°，∴∠2﹣∠1＝70°．故选：C．5．解：如图，设A′D与AD交于点O，∵∠A＝40°，∴∠A′＝∠A＝40°，∵∠1＝∠DOA+∠A，∠1＝112°，∴∠DOA＝∠1﹣∠A＝112°﹣40°＝72°，∵∠DOA＝∠2+∠A′，∴∠2＝∠DOA﹣∠A′＝72°﹣40°＝32°．故选：A．6．解：过C作CM∥AB，∵AB∥DE，∴AB∥CM∥DE，∴∠1+∠B＝180°，∠2＝∠D＝35°，∵∠B＝130°，∴∠1＝50°，∴∠BCD＝∠1+∠2＝85°，故选：B．7．解：如图，延长F A，由折叠的性质，可得∠3＝∠1＝30°，∴∠4＝180°﹣30°﹣30°＝120°，∵CD∥BE，BE∥AF，∴∠ACD＝∠4＝120°，又∵AC∥BD，∴∠2＝180°﹣∠ACD＝180°﹣120°＝60°．故选：B．8．解：如图，AC、DF与BE分别相交于点M、N，在四边形NMCD中，∠MND+∠CMN+∠C+∠D＝360°，∵∠CMN＝∠A+∠E，∠MND＝∠B+∠F，∴∠A+∠B+∠C+∠D+∠E+∠F＝360°，故选：B．二．填空题（共8小题，满分40分）9．解：∵AD⊥AC，∴∠CAD＝90°，∵∠BAD＝40°，∴∠BAC＝∠CAD+∠BAD＝130°，∵AB∥CD，∴∠ACD+∠BAC＝180°，∴∠ACD＝180°﹣∠BAC＝50°．故答案为：50．10．解：由题意可得：地毯的水平长度＝BC＝12米，地毯的垂直长度＝AC＝3米，∴地毯的长度至少需要：12+3＝15米，故答案为：15．11．解：∵∠A+∠ACB+∠ABC＝180°，∠A＝90°，∴∠ACB+∠ABC＝90°，∵∠GCF＝∠ACB，∠DBE＝∠ABC，∴∠GCF+∠DBE＝90°，∵∠G+∠F+∠GCF＝∠D+∠B+∠DBE＝180°，∴∠G+∠F+∠GCF+∠D+∠B+∠DBE＝360°，∴∠D+∠G+∠AFG+∠AED＝270°，故答案为：270°．12．解：如图，根据四边形的内角和可得，∠1+∠2+∠3+∠8＝360°，∠4+∠5+∠9+∠10＝360°，∵∠9＝∠6+∠7，∠8+∠10＝180°，∴∠1+∠2+∠3+∠8+∠4+∠5+∠10+∠6+∠7＝720°，∴∠1+∠2+∠3+∠4+∠5+∠6+∠7＝540°．故答案为：540°．13．解：∵AB∥CD，∴∠ABD＝∠PDB，∵∠ABD＝∠PCE，∴∠PDB＝∠PCE，∴BD∥CE，∴∠CEG＝∠DGH，∵EH平分∠AEC，∴∠CEH＝∠AEH，∵∠DGH＝∠EGF，∴∠EGF＝∠GEF，∵∠AFD＝∠AEG+∠EGF＝2∠EGF＝86°，∴∠EGF＝43°，∴∠DGH＝43°，∴∠PCE＝∠PDG＝∠H+∠DGH＝65°，故答案为：65．14．解：如图，过点C作CH∥AB，则∠ABC+∠BCH＝180°，∵∠ABC+∠C+∠CDE＝360°，即∠ABC+∠BCH+∠DCH+∠CDE＝360°，∴∠DCH+∠CDE＝180°，∴CH∥DE，∴AB∥DE，∴∠DGF＝∠1＝110°，∴∠2＝180°﹣110°＝70°，故答案为：70°．15．解：∵AB∥CD，∠CDE＝119°，∴∠AEH＝∠CDE＝119°，∵EF平分∠AEH，∴∠FEH＝∠AEH＝59.5°，∵∠DGF＝130°，∴∠FGE＝180°﹣∠DGF＝50°，∵∠FEH是△EFG的外角，∴∠F＝∠FEH﹣∠FGE＝9.5°．故答案为：9.5．16．解：如图，过点A作l1的平行线AC，过点B作l2的平行线BD，则∠3＝∠1，∠4＝∠2，∵l1∥l2，∴AC∥BD，∴∠CAB+∠ABD＝180°，∴∠3+∠4＝125°+85°﹣180°＝30°，∴∠1+∠2＝30°，∵∠1＝∠2+4°，∴∠1＝17°，故答案为：17°．三．解答题（共5小题，满分40分）17．（1）解：∵DE∥BC（已知），∴∠C＝∠AED（两直线平行，同位角相等）．∵∠A+∠ABC+∠C＝180°（三角形内角和定理），∴∠A＝180°﹣∠ABC﹣∠C＝180°﹣∠ABC﹣∠AED（等式的性质）．∵∠AED＝40°，∠ABC＝80°（已知），∴∠A＝180°﹣40°﹣80°＝60°（等式的性质）；（2）证明：∵∠BFD+∠DFE＝180°（平角定义），∠BFD+∠CEF＝180°（已知），∴∠DFE＝∠CEF（同角的补角相等）．∴DF∥AC（内错角相等，两直线平行）．∴∠EDF＝∠AED（两直线平行，内错角相等）．∵DE∥BC（已知），∴∠AED＝∠C（两直线平行，同位角相等）．∴∠EDF＝∠C（等量代换）．18．证明：（1）∵∠A＝120°，∠ABC＝60°，∴∠A+∠ABC＝180°．（2）∵AD∥BC，∴∠1＝∠DBC．∵BD⊥DC，EF⊥DC，∴∠BDF＝90°，∠EFC＝90°．∴∠BDF＝∠EFC＝90°．∴BD∥EF．∴∠2＝∠DBC．∴∠1＝∠2．19．解：∵CE平分∠ACD，∠ACD＝140°，∴∠ACE＝×∠ACD＝×140°＝70°，∠ACB＝180°﹣∠ACD＝40°，∵FG∥CE，∴∠AFG＝∠ACE＝70°，∵∠F AG＝∠B+∠ACB＝85°，∴∠ADF＝180°﹣∠AFG﹣∠F AG＝25°．故∠AGF的度数是25°．20．解：（1）如图1，过P点作PO∥AB，∵AB∥CD，∴CD∥PO∥AB，∴∠BPO＝∠B，∠OPD＝∠D，∵∠BPD＝∠BPO+∠OPD，∴∠BPD＝∠B+∠D．∵∠B＝50°，∠D＝30°，∴∠BPD＝∠B+∠D＝50°+30°＝80°；（2）∠B＝∠D+∠BPD，∴∠B＝∠BOD，∵∠BOD＝∠D+∠BPD，∴∠B＝∠D+∠BPD；（3）∠BPD＝∠B+∠D+∠BQD．证明：如图3，连接QP并延长，∵∠BPE＝∠B+∠BQE，∠DPE＝∠D+∠DQE，∴∠BPE+DPE＝∠B+∠BQE+∠D+∠DQE，即∠BPD＝∠B+∠D+∠BQD．（4）∵∠CMN＝∠A+∠E，∠DNB＝∠B+∠F，又∵∠C+∠D+∠CMN+∠DNM＝360°，∴∠A+∠B+∠C+∠D+∠E+∠F＝360°．故答案为：360°．21．解：（1）∠A+∠C+∠APC＝360°如图1所示，过点P作PQ∥AB，∴∠A+∠APQ＝180°，∵AB∥CD，∴PQ∥CD，∴∠C+∠CPQ＝180°，∴∠A+∠APQ+∠C+∠CPQ＝360°，即∠A+∠C+∠APC＝360°；（2）∠APC＝∠A+∠C，如图2，作PQ∥AB，∴∠A＝∠APQ，∵AB∥CD，∴PQ∥CD，∴∠C＝∠CPQ，∵∠APC＝∠APQ﹣∠CPQ，∴∠APC＝∠A﹣∠C；（3）由（2）知，∠APC＝∠P AB﹣∠PCD，∵∠APC＝30°，∠P AB＝140°，∴∠PCD＝110°，∵AB∥CD，∴∠PQB＝∠PCD＝110°，∵EF∥BC，∴∠BEF＝∠PQB＝110°，∵EF∥BC，∴∠BEF＝∠PQB＝110°，∵∠PEG＝∠PEF，∴∠PEG＝∠FEG，∵EH平分∠BEG，∴∠GEH＝∠BEG，∴∠PEH＝∠PEG﹣∠GEH＝∠FEG﹣∠BEG＝∠BEF＝55°．。

苏教版平面图形的认识二测试题含答案

苏教版平面图形的认识二测试题含答案TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】第七章《平面图形的认识（二）》测试题B 1一、选择题。

(每题3分，共21分)1．下列生活现象中，属于平移的是( )A ．足球在草地上滚动B ．拉开抽屉C ．投影片的文字经投影转换到屏幕上D ．钟摆的摆动2．若一个三角形三个内角度数的比为2:7:1，那么这个三角形是( )A ．直角三角形B ．钝角三角形C ．锐角三角形D ．等边三角形3．下面有3个命题：①同旁内角互补；②两直线平行，内错角相等；③在同一平面内，垂直于同一条直线的两直线互相平行．其中真命题为( )A ．① B．② C．③ D．②③4．若一个多边形的内角和等于它的外角和的两倍，则这个多边形的边数为( )A ．6B ．7 C. 8 D ．95．如图，AD 平分∠BAC，DE∥AC 交AB 于点E ，∠1=25，则∠BED 等于( )A ．40B ．50C ．60D ．256．如图，面积为6 2cm 的△ABC 纸片沿BC 方向平移至△DEF 的位置，平移的距离是BC 长的2倍，则△ABC 纸片扫过的面积为( )A ．18 2cmB ．212cmC ．272cmD ．302cm7．如图，∠ABC=∠ACB，AD 、BD 、CD 分别平分△ABC 的外角∠EAC、内角∠ABC、外角∠ACF．以下结论：①AD∥BC；②∠ACB=2∠ADB；③∠ADC =90一∠ABD；④BD 平分∠ADC；⑤∠BDC=12∠BAC 其中正确的结论有( )A ．2个B ．3个C ．4个D ．5个二、填空题。

(每空3分，共21分)8．直角三角形的两条直角边分别为6、8，斜边长为10，则斜边上的高是．9．如图，直线a ∥b ，把三角板的直角顶点放在直线b 上，若、∠1=60。

则∠2的度数为．10．如图，在△ABC 中，∠A=60，若剪去∠A 得到四边形BCDE ，则∠1+∠2= ．11．如图，在直角△ABC 中，∠C=90，AD 、AE 把∠CAB 三等分，AD 交BC 于D ，AE 交BC 于E ，且EF⊥AB，AF=FB ，则∠B 的度数为．12．如图，将边长为4个单位的等边△ABC 沿边BC 向右平移2个单位得到△DEF，则四边形ABFD的周长为．13．如图，将正方形纸片ABCD 沿BE 翻折，使点C 落在点F 处，若∠DEF=40，则∠ABF= ．14．如图，△ABC的两条中线AM、BN相交于点O，已知△ABC的面积为12，△BOM的面积为2，则四边形MCNO的面积为．三、解答题。

第七章平面图形的认识二单元测试卷含答案

第七章平面图形的认识(二)单元测试卷(含答案)第七章平面图形的认识单元检测卷A（时间：90分钟，满分：120分）一、选择题（每题3分，共30分）1.下列语句中不是命题的是（）.A.锐角小于钝角B.作AC的垂直平分线C.对顶角不相等D.狗不是猫科动物2.下列命题中正确的是（）.A.任何数的平方都是正数B.相等的角是对顶角C.内错角相等D.直角都相等3.如图1，能使BF∥DG的条件是（）.A.∠1＝∠3B.∠2＝∠4C.∠2＝∠3D.∠1＝∠44.如图2，AE平分∠ＢＡＣ，CE平分∠ACD，不能判定AB∥CD的条件是（）.A.∠1＝∠2B.∠1+∠2＝90°C.∠3+∠4＝90°D.∠2+∠3＝90°5.三角形的某一角的补角是120°，则此三角形的另两个角的和为（）.A.60°B.120°C.90°D.30°6.满足下列条件的△ABC中，不是直角三角形的是（）.A.∠A+∠B＝∠CB.∠A:∠B:∠C=2:3:1C.∠A=2∠B=3∠CD.一个外角等于和它相邻的内角7.如图3，AB∥EF∥DC，EG∥BD，则图中与∠1相等的角（∠1除外）共有（）.A.6个B.5个C.4个D.2个8.一天，爸爸带小明到建筑工地玩，看见一个如图4所示的人字架，爸爸说：“小明，我考考你，这个人字架的夹角∠1等于130°，你知道∠3比∠2大多少吗？”小明马上得到了正确的答案，他的答案是（）.A.50°B.65°C.90°D.130°9.如果三角形的一个外角等于与它相邻的内角的2倍，且等于与它不相邻的一个内角的2倍，那么这个三角形一定是（）.A.锐角三角形B.直角三角形C.钝角三角形D.等边三角形10.已知α＝80°，β的两边与α的两边分别垂直，则β等于（）.A.80°B.10°C.100°D.80°或100°二、填空题（每题3分，共27分）11.“同旁内角互补，两直线平行”的条件是____________，结论是_________________.12.在△ABC中，∠A+∠B＝150°，∠C＝2∠A，则∠A＝_______，∠B＝_______.13.如图5所示，AB∥CD，BC∥ＤＥ，则∠B+∠D＝_如图6所示，在△ABC中，∠A＝40°，BP、CP是△ABC的外角平分线，则∠P＝________.15.如图7所示，直线a∥b，则∠A＝_______.16.如图8所示，∠A+∠B+∠C+∠D+∠E＝______.17.如果两条直线被第三条直线所截，一组同旁内角的度数比为3：2，差为36°，那么这两条直线的位置关系是___________，这是因为_____________.18.如图9，BC⊥ED于O，∠A＝27°，∠D＝20°，则∠B ＝________，∠ACB＝_____如图10，给出下列论断：①AB∥CD；②AD∥BC；③∠A＝∠C，以其中两个作为条件，另一个作为结论，用“如果…，那么…”的形式，写出一个你认为正确的命题是_____________________________________.三、解答题（共43分）20.（6分）指出下列命题的条件和结论.（1）一个锐角的补角大于这个角的余角；（2）不相等的两个角不是对顶角；（3）异号两数相加得零.21.（7分）已知实数a、b、c满足a＝6-b，c2＝ab-9，你能肯定a等于b吗？22.（7分）如图，∠1＝∠B，∠A＝35°，求∠2的度数.23.（7分）如图，∠BAP+∠APD＝180°，∠1＝∠2.求证：∠E＝∠F.24.（8分）如图，已知AB∥CD，∠B＝∠DCE，求证：CD 平分∠分）如图，△ABC中，∠C＝∠ABC＝2∠A，BD是AC边上的高，求∠DBC的度数.26.（10分）如图，D、E分别在BC、AC上，AD、BE交于F.求证：（1）∠AFB＞∠C；（2）∠AFB＝∠1+∠2+∠C. 27.（10分）如图，∠1＝∠2，∠3＝∠B，FG⊥AB于G，猜想CD与AB的关系，并证明你的猜想.参考答案一、1.B；提示：“作AC的垂直平分线”不失命题2.D；提示：“直角都相等”正确3.A；提示：∠1＝∠2是同位角相等两直线平行4.A；提示：由∠1＝∠2可推出大角相等，同旁内角相等两直线不一定平行5.B；提示：三角形的一个外角等于和它不相邻的两个内角和6.Ｃ；提示：由∠A=2∠B=3∠C不能推出直角三角形7.B；提示：根据同位角、内错角共5个8.A；提示：三角形的一个外角等于和它不相邻的两个内角和9.D；提示：等边三角形10.D；提示：相等或互补二、11.同旁内角互补；两直线平行12.15°，135°13.180°；提示：根据内错角和同位角相等14.70°；提示：根据外角及角平分线15.22°；提示：根据平行线及其三角形外角和16.180°；提示连结AC，转化为三角形的内角和17.平行；同旁内角互补，两直线平行18.43°，110°19.如果在四边形ABCD中，AB∥CD，AD∥BC，那么∠A＝∠C.三、20.解：（1）条件：一个角是锐角；结论：这个角的补角大于这个角的余角.（2）条件：两个角不相等；结论：这两个角不是对顶角. （3）条件：两个数异号；结论：这两个数相加得零. 21.解：能肯定a＝b.理由如下：将a＝6-b代入c2＝ab-9中得，c2＝ab-9＝（6-b）b-9＝6b-b2－9＝－（b－3）2.∵c2≥0，而－（b－3）2≤0，∴c＝0，b－3＝0，即c＝0，b＝3.∴a＝6-b＝6-3＝3.∴a＝b.22.解：∵∠1＝∠B，∴AB∥CD（内错角相等，两直线平行）.∴∠A+∠2＝180°（两直线平行，同旁内角互补）.∴∠2＝180°－∠A＝180°－35°＝145°.23.证明：∵∠BAP+∠APD＝180°（已知），∴AB∥CD（同旁内角互补，两直线平行）.∴∠BAP＝∠APC（两直线平行，内错角相等）.又∵∠1＝∠2（已知），∴∠FPA＝∠内错角相等，两直线平行）.∴∠E＝∠F（两直线平行，内错角相等）.24.证明：∵AB∥CD（已知），∴∠B＝∠BCD（两直线平行，内错角相等）.又∵∠B＝∠DCE（已知），∴∠BCD＝∠DCE（等量代换），即CD平分∠BCE.25.解：∵∠C+∠ABC+∠A＝180°（三角形三个内角的和等于180°），而∠C＝∠ABC＝2∠A，∴2∠A+2∠A+∠A＝180°.∴∠A＝36°.∴∠C＝72°.又∵BD⊥AC，∴∠DBC＝90°－72°＝18°.26.证明：（1）∵∠AFB是△AEF的一个外角，∴∠AFB＞∠AEF（三角形的一个外角大于任何一个与它不相邻的内角）.∵∠AEF是△BCE的一个外角，∴∠AEF＞∠C（三角形的一个外角大于任何一个与它不相邻的内角）.∴∠AFB＞∠C（不等式的性质）.（2）∵∠AFB＝∠AEB+∠1，∠AEB＝∠C+∠2（三角形的一个外角等于和它不相邻的两个内角的和），∴∠AFB＝∠1+∠C+∠2（等量代换）.27.解：猜想CD⊥AB.理由如下：∵∠3＝∠B（已知），∴ED∥BC（同位角相等，两直线平行）.∵FG⊥AB（已知），∴∠AGF＝90°（垂直定义）.∵∠AGF是△BFG的一个外角，∴∠AGF＝∠B+∠2（三角形的一个外角等于和它不相邻的两个内角的和）.∵∠ADC＝∠1+∠3，而∠1＝∠2，∠3＝∠B，∴∠ADC＝∠AGF＝90°（等量代换）.∴CD⊥AB（垂直定义）.。

苏科新版七年级下册《第7章平面图形的认识(二)》2024年单元测试卷+答案解析

苏科新版七年级下册《第7章平面图形的认识（二）》2024年单元测试卷一、选择题：本题共8小题，每小题3分，共24分。

在每小题给出的选项中，只有一项是符合题目要求的。

1.如图，直线a，b被直线c所截，下列条件不能判定直线a与b平行的是()A.B.C.D.2.如图，，，，则()A.B.C.D.3.如图，，，DA平分，则的度数为()A.B.C.D.4.下列图形中，可以由其中一个图形通过平移得到的是()A. B. C. D.5.如图，点A，B，C，D，E在同一平面内，连接AB，BC，CD，DE，EA，若，则()A.B.C.D.6.某多边形的内角和与外角和的总和为，此多边形的边数是()A.4B.5C.6D.77.若与同旁内角，且时，则的度数为()A. B. C.或 D.无法确定8.如图，直线，直线交于点A，交于点B，过点B的直线交于点若，，则等于()A.B.C.D.二、填空题：本题共13小题，每小题3分，共39分。

9.将一副直角三角尺按如图所示的方式摆放，若，则的度数为______.10.如图，一块直角三角板的角的顶点A与直角顶点C分别在两平行线FD，GH上，斜边AB平分，交直线GH于点E，则的度数为__________. 11.如图，，，若，则的度数为______.12.如图，，，则__________度．13.如图，是一块从边长为50cm的正方形中裁出的垫片，现测得，则这块垫片的周长为______14.已知a，b，c是的三边长，a，b满足，c为奇数，则______.15.已知等腰三角形一边等于4，另一边等于9，它的周长是______.16.如图，中，，P是BC上任意一点，于点E，于点F，若，则______.17.如图，AD为的中线，BE为的中线.若的面积为30，，则中BD边上的高为______.18.一个多边形的每一个外角都是，则这个多边形的内角和的度数是______.19.如图，求的度数为______.20.将一块含角的三角尺和一把直尺按如图所示的方式放置.如果，那么的度数是______21.如图摆放的一副学生用直角三角板，，，AB与DE相交于点G，当时，的度数是______.三、解答题：本题共6小题，共48分。

完整版苏科版七年级下册数学第7章平面图形的认识(二) 含答案

苏科版七年级下册数学第7章平面图形的认识（二）含答案一、单选题(共15题，共计45分)1、如图，直线l1∥l2,且分别与直线l交于C,D两点，把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°，则∠2的度数为（）A.92°B.98°C.102°D.108°2、等腰三角形底边长为，一腰上的中线把其分为周长之差为的两部分，则腰长为（）A. B. C. 或 D.不确定3、如图，已知直线AB∥CD，∠C=115°，∠A=25°，则∠E=（）A.70°B.80°C.90°D.100°4、已知等腰三角形一个外角等于120°，则它的顶角是（）A.60°B.20°C.60°或20°D.不能确定5、如图，已知AB∥CO，那么∠1，∠2，∠3之间的关系是（）A.∠1+∠2=∠3B.∠1+∠3=∠2C.∠1+∠2+∠3=180°D.∠1+∠2﹣∠3=180°6、三角形的两边长为2和4，第三边长是方程x2﹣6x+8=0的根，则这个三角形的周长是（）A.8B.10C.8或10D.不能确定7、九边形的内角和为（）A.1260°B.1440°C.1620°D.1800°8、如右图，在△ABC中，∠C=90°，AB的垂直平分线MN分别交AC，AB于点D，E．若∠CBD : ∠DBA =3:1，则∠A为（）．A.18°B.20°C.22.5°D.30°9、已知三角形的两边长分别为5和7，则第三边长不可能是（）A.1B.3C.5D.710、正十二边形的一个内角的度数为（）A.30°B.150°C.360°D.1800°11、下列四个图案是小明家在瓷砖厂选购的四种地砖图案，其中既可用旋转来分析整个图案的形成过程，又可用平移来分析整个图案的形成过程的是（）A. B. C. D.12、701班小明同学想利用木条为七年级数学组制作一个三角形的工具，那么下列哪组数据的三根木条的长度能符合他的要求（）A. 4，2，2B.3，6，6C.2，3，6D.7，13，613、已知非等腰三角形的两边长分别是2 cm和9 cm,如果第三边的长为整数,那么第三边的长为（）A.8 cm或10 cmB.8 cm或9 cmC.8 cmD.10 cm14、下列各组长度的线段，能构成三角形的一组是( )A.1cm，3cm，2cmB.3.5cm，7.1cm，3.6cmC.6cm，1cm，6cm D.4cm，10cm，4cm15、如图，AB∥DE，∠E=65°，则∠B+∠C=( )A.135°B.115°C.36°D.65°二、填空题(共10题，共计30分)16、如图，AB∥CD ，以点A为圆心，小于AC长为半径作圆弧，分别交AB ，AC于E ， F两点，再分别以E ， F为圆心，大于EF长为半径作圆弧，两条圆弧交于点P ，作射线AP ，交CD于点M ．若∠ACD=114°，则∠MAB的度数为________°.17、如图，在△ABC中，AD是BC边上的高，AE平分∠BAC，∠B=30°，∠BCA=100°，则∠DAE的度数为________.18、如图，在△ABC 中，∠A=60°，D 是 AB 上一点，E 是 AC 上一点，BE、CD 相交于 O，且∠BOD=55°，∠ACD=30°，则∠ABE 的度数是________.19、如图，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C 是y轴上的一个动点，当∣BC-AC∣最大时，点C的坐标是________.20、已知如图，BC=3，∠ABC和∠ACB的平分线相交于点O，OE∥AB，OF∥AC，则三角形OEF的周长为________．21、完成以下证明，并在括号内填写理由．已知：如图所示，∠1=∠2，∠A=∠3．求证：∠ABC+∠4+∠D=180°．证明：∵∠1=∠2∴________∥________（________）∴∠A=∠4（________）∠ABC+∠BCE=180°（________）即∠ABC+∠ACB+∠4=180°∵∠A=∠3∴∠3=________∴________∥________∴∠ACB=∠D（________）∴∠ABC+∠4+∠D=180°．22、已知：如图，在△ABC 中，AB=AC，DE垂直平分AB ，交边AB于点 D ，交边AC于点 E，BF垂直平分 CE ，交 AC于点F ，则∠A ________度．23、如图所示，如果把图中任一条线段沿方格线平移1格称为“1步”，那么要通过平移使图中的四条线段首尾相接组成一个四边形，最少需要________ 步．24、已知：△ABC中，∠A+∠B= ∠C，则∠C =________.25、如图1，MA1∥NA2，则∠A1+∠A2=________ 度．如图2，MA1∥NA3，则∠A1+∠A2+∠A3=________ 度．如图3，MA1∥NA4，则∠A1+∠A2+∠A3+∠A4=________ 度．如图4，MA1∥NA5，则∠A1+∠A2+∠A3+∠A4+∠A5=________ 度．从上述结论中你发现了什么规律？如图5，MA1∥NAn，则∠A1+∠A2+∠A3+…+∠An=________ 度．三、解答题(共5题，共计25分)26、化简，并求值，其中a与2，3构成△ABC的三边，且a为整数．27、已知命题：“如图，点B、F、C、E在同一条直线上，则AB∥DE．”判断这个命题是真命题还是假命题，如果是真命题，请给出证明；如果是假命题，在不添加其他辅助线的情况下，请添加一个适当的条件使它成为真命题，并加以证明．28、小明在学习三角形内角和定理时，由于病假缺课，只知道三角形内角和为180度，却不知道原理。

苏科版七年级下册第7章平面图形的认识(二)单元基础练习题(含答案)

七年级下册第7章平面图形的认识（二）单元基础练习题1.已知等腰三角形的两边长分别为4、9，则它的周长为（）A.22B.17C.17或22D.132.如图，在所标识的角中，同位角是( )A.∠1和∠2B.∠1和∠3C.∠1和∠4D.∠2和∠33.一个多边形的内角和与外角和相等，则这个多边形是（）A.四边形B.五边形C.六边形D.八边形4.如图，直线c截二平行直线a、b，则下列式子中一定成立的是（）A.∠1=∠2B.∠1=∠3C.∠1=∠4D.∠1=∠55.如图，AD∥BC，点E在BD的延长线上，若∠ADE＝155°，则∠DBC的度数为（）A.155°B.50°C.45°D.25°6.下列长度的三条线段，能组成三角形的是（）A.1，1，2B.2，3，7C.1，4，6D.3，4，57.如图所示是“福娃欢欢”的五幅图案，②，③，④，⑤哪一个图案可以通过平移图案①得到（）A.②B.③C.④D.⑤8.两条平行直线被第三条直线所截，下列命题中正确的是（）A.同位角相等，但内错角不相等B.同位角不相等，但同旁内角互补C.内错角相等，且同旁内角不互补D.同位角相等，且同旁内角互补9.如果一个正多边形的一个内角等于相邻外角的3倍，则这个正多边形是（）A.正八边形B.正九边形C.正七边形D.正十边形10.如图，CM，ON被AO所截，那么（）A.∠1和∠3是同位角B.∠2和∠4是同位角C.∠ACD和∠AOB是内错角D.∠1和∠4是同旁内角11.如图．∠1与∠C是一对内错角，∠1与∠3是一对________ 角．12.如图，自行车的三角形支架，这是利用三角形具有________性．13.如图所示，添上一个你认为适当的条件________时，a∥b．14.一个多边形每个外角都是60°，这个多边形是________边形，它的内角和是________度，外角和是________度．15.十边形的外角和等于________ 度．16.一个正多边形的内角是外角的2倍，则这个正多边形是________ 边形．17.若多边形所有内角与它的一个外角的和为600°，求这个多边形的边数及内角和．18.（1）如图，已知△ABC，试画出AB边上的中线和AC边上的高；（2）有没有这样的多边形，它的内角和是它的外角和的3倍？如果有，请求出它的边数，并写出过这个多边形的一个顶点的对角线的条数．19.已知：如图，∠1和∠2是直线a，b被直线c截出的同旁内角，且∠1与∠2互补．求证：a∥b．20.若一个多边形的外角和是内角和的，则这个多边形是几边形？21.在△ABC中，AB=9，AC=2，并且BC的长为偶数，求△ABC的周长．22.已知三角形的三条边为互不相等的整数，且有两边长分别为7和9，另一条边长为偶数．（1）请写出一个三角形，符合上述条件的第三边长．（2）若符合上述条件的三角形共有a个，求a的值．参考答案部分第 1 题:【答案】A【解析】【分析】根据腰为4或9分类求解，注意根据三角形的三边关系进行判断．【解答】当等腰三角形的腰为4时，三边为4，4，9，4+4＜9，三边关系不成立，当等腰三角形的腰为9时，三边为4，9，9，三边关系成立，周长为4+9+9=22．故选：A．【点评】本题考查了等腰三角形的性质，三角形三边关系定理．关键是根据已知边那个为腰，分类讨论第 2 题:【答案】C【解析】【分析】同位角就是：两个角都在截线的同旁，又分别处在被截的两条直线同侧的位置的角．【解答】根据同位角、邻补角、对顶角的定义进行判断，A、∠1和∠2是邻补角，故A错误；B、∠1和∠3是邻补角，故B错误；C、∠1和∠4是同位角，故C正确；D、∠2和∠3是对顶角，故D错误．故选：C．【点评】解答此类题确定三线八角是关键，可直接从截线入手．对平面几何中概念的理解，一定要紧扣概念中的关键词语，要做到对它们正确理解，对不同的几何语言的表达要注意理解它们所包含的意义．第 3 题:【答案】A【解析】【分析】首先设此多边形是n边形，由多边形的外角和为360°，即可得方程180（n-2)=360，解此方程即可求得答案．【解答】设此多边形是n边形，∵多边形的外角和为360°，∴180（n-2)=360，解得：n=4．∴这个多边形是四边形．故选A．【点评】此题考查了多边形的内角和与外角和的知识．此题难度不大，注意多边形的外角和为360°，n边形的内角和等于180°（n-2)．第 4 题:【解析】【分析】两直线平行，同位角相等，据此可进行判断．【解答】由图可知，A、∠1和∠2是邻补角，两直线平行不能推出邻补角相等，故错误；B、∵a∥b，∴∠1=∠3（两直线平行，同位角相等)，故正确．C、由B知，∠1=∠3，又∠3+∠4=180°，∴∠1+∠4=180°，故错误；D、由C知，∠1+∠4=180°，又∠4=∠5，∴∠1+∠5=180°，故错误；故选B．【点评】本题重点考查了平行线的性质，是一道较为简单的题目第 5 题:【答案】 D【解析】【分析】先根据邻补角的性质求得∠ADB的度数，再根据平行线的性质求解即可。

七年级下册数学第七章平面图形的认识2单元试卷

七年级下册数学第七章平面图形的认识2单元试卷一、选择题(每题3分，共24分)1.如图，由六个大小一样的等边三角形拼成了六边形，其中可以由△OBC平移得到的是 ( )A.△OCDB.△OABC.△OAFD.△OEF2.一学员在广场上练习驾驶汽车，两次拐弯后，行驶的方向与原来的方向一样，这两次拐弯角度可能是 ( )A.第一次向左拐40，第二次向右拐40B.第一次向右拐40，第二次向左拐140C.第一次向右拐40，第二次向右拐140D.第一次向左拐40，第二次向左拐1403.如图，直线a、b被直线c所截，以下说法正确的选项是A.当时，一定有 // bB.当a // b时，一定有C.当a // b时，一定有D.当a // b时，一定有第3题第4题4.如图，假设AE是△ABC边上的高，EAC的角平分线AD交BC于D，ACB=40，那么DAE等于 ( )A.50B.40C.35D.255.如下图，AB∥CD，CD∥EF且1=30，2=70，那么BCE等于 ( )A.40B.100C.140D.1306.将以下图剪成假设干小块，再分别平移后可以得到①、②、③中的 ( )A.0个B.1个C.2个D.3个7.假如三角形有一条高与三角形的一条边重合，那么这个三角形的形状是 ( )A.锐角三角形B.直角三角形C.钝角三角形D.不能确定8.小明同学在计算某n边形的内角和时，不小心少输入一个内角，得到和为2022.那么n等于 ( )A.11B.12C.13D.14二、填空题(每题4分，共24分)9.如下图，直线AB、CD被直线EF所截，交点分别为M、N，那么 EMB的同位角是____________.第9题第10题第11题10.如图，直线1∥ 2，AB 1，垂足为O，BC与 2相交于点E，假设1=43，那么2=____________.11.在△ABC中，假设A= B= C，那么该三角形的形状是__________.12.如图，将一张长方形纸片沿EF折叠后，点D、C分别落在D、C的位置，ED的延长线与BC交于点G.假设EFG=55，那么1=__________.13.三角形的两边长为3、7，周长为奇数，那么该三角形的周长为_________.14.假假设将n(n3)边形切去一角，那么切去后的多边形的内角和与n边形的内角和之间的关系为______________.三、解答题(15～18题每题7分，19～21题每题8分，共52分)15.如图，EP∥AB，PF∥CD，B=100，C=120，求EPF的度数.16.画图题：(1)如图，△ABC，请你画出△ABC的高AD，中线BE，角平分线CF.并根据画图填空：AD_______BC AE_______CE ACF_______BCF.(2)将以下图所示的四边形按箭头所指方向平移2 cm.17.如图，AB∥CD，1==F，E，求EOF的度数.18.等腰三角形ABC中，一腰AC上的中线把三角形的周长分为12 cm和15 cm两局部，求此三角形各边的长.19.如图，点E在直线DF上，点B在直线AC上，AGB=EHF，D.试问：F吗?假如成立，请你说明理由;假如不成立，说明理由.20.连结多边形不相邻的两个顶点的线段，叫做多边形的对角线.观察以下图形，并阅读图形下面的相关文字，考虑以下问题：(1)三角形的对角线有________条;(2)四边形的对角线有________条;(3)五边形的对角线有________条;(4)六边形的对角线有________条;(5)在此根底上，你能归纳出船边形的对角线有_________条.21.小明有长为20 cm、90 cm、100 cm的三根木条，但是不小心将100 cm的一根折断了.(1)最长的木条被折的情况如何时，小明将不能与另两根木条钉成三角形架?(2)假如最长的木条折去了40 cm，小明可以通过怎样再折木条的方法钉成一个三角形架?参考答案一、1.C 2.A 3.C 4.D 5.C 6.C 7.B 8.D二、9. END 10.133 11.直角三角形 12.110 13.15或17或1914.大180或小180或相等三、15.4016.略17.9018.腰长10 cm，底边长7 cm或腰长8 cm，底边长11cm19.成立，理由，略20.(1)0;(2)2;(3)5;(4)9;(5)21.(1)当被折成的两段都大于30cm，而小于70 cm时，不能与另外两根木条钉成三角形架; (2)将90 cm的木条截去一段，截去局部的长大于10cm，并且小于50 cm，就能钉成三角形架.。