水力学第五章 第五节
合集下载
流体力学 水力学 第五章

7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算(Q、d、H) 有压流:水沿管道满管流动的水力现象。 特点:水流充满管道过水断面,管道内不存在自 由水面,管壁上各点承受的压强一般不等于大 气压强。
短管:局部水头损失和 速度水头在总水头损失 中占有相当的比重,计 算时不能忽略的管道. (一般局部损失和速度 水头大于沿程损失 的5% ~ 10%)。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数: c 0 1 0
1 1 流速系数: c 0 1 0
实验得: 0.97 ~ 0.98 1 推求: 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3:如图所示圆形有压涵管,管长50m, 上下游水位差3m 沿程阻力系数为0.03,局部阻力系数:进口 1=0.5。 第一个转弯 2=0.71,第二个转弯 3=0.65,出口
4=1.0,要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g
v
v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g
v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g
水力学第五章 有旋流动和有势流动

定义
数。
M(x,y,z)
( x, y, z ) = + u x d x + u y d y + u z d z
M 0 ( x0 , y0 , z 0 )
u x =
x
u y =
y
u z =
z
无旋流动
ij ×u=
xy
xy
无旋流动
k
=0 z
z
等价
有势流动
u=
有势流动
u(t)
u(t+dt)
L是由确定流体质点组成的封闭线,是 一个系统,在流动中会改变位置和形状。
简要的证明
dΓ
du
dt
+ d t d l
L
d dt
+
L
u
δ
l
d
+ d t (u δ l)
L
+
L
d
t
δ
d
lL++
δu
2
du
dl
du
+ d t δ l + + u δ d t + d t δ l + + u δ u
=
( uz
u y) + ( ux
uz ) +
uy (
xy z yz x zx
ux ) = 0 y
由于涡管侧壁没有涡 通量,所以根据涡量场是 无源场可得如下结论:
结论 在同一时刻,穿 过同一涡管的各断面的涡 通量都是相同的。即同一 时刻,一根涡管对应一个 涡管强度。
回答了前面的问题
水力学-第5章 明渠恒定均匀流1113

工程中采用最多的是梯形断面, 工程中采用最多的是梯形断面,其边坡系数 m 由 边坡稳定要求确定。 边坡稳定要求确定。在 m 已定的情况下,同样的过水 要求确定 已定的情况下, 面积 A ,湿周的大小因底宽与水深的比值 b / h 而异 。根据水力最佳断面的条件: 根据水力最佳断面的条件: 即
χ = 最小值 A = 常数
解:将已知条件代入基本公式,并用曼宁公 将已知条件代入基本公式, 式计算谢才系数, 式计算谢才系数,整理后可得
nQ( β + 2 1 + m 2 ) 2 / 3 h= 5 / 3 1/ 2 ( β + m) i
3/8
当为水力最佳断面时: 当为水力最佳断面时
β = 2( 1 + m 2 − m) = 2( 1 + 1.252 − 1.25) = 0.702
2
15
用 β m 代替上式中的 β 值,整理后得 即梯形水力最佳断面的水力半径等于水深的一半。 即梯形水力最佳断面的水力半径等于水深的一半。
hm Rm = 2 的梯形断面。 矩形断面可以看成为 m = 0 的梯形断面。以 m = 0
代入以上各式可求得矩形水力最佳断面的 β m 及 Rm .
bm βm = = 2 即 bm = 2hm hm
χ = b + 2 h 1 + m 2 = 34 m + 2 × ( 2 . 7 m ) 1 + 1 . 5 2 = 43 . 74 m
102 . 74 m 2 R= = = 2 . 35 m χ 43 . 74 m A
查表可知, 查表可知,对渠线弯曲并已滋生杂草的土 n =0.03
1 1/ 6 1 C= R = (2.35)1/ 6 = 38.4m1/ 2 / s n 0.03
水力学基础课件——第五章 明渠恒定均匀流

A
(b mh)h
R
x b 2h 1 m2
第五章 明渠恒定均匀流
二、明渠的底坡 底坡:明渠渠底倾斜的程度称为底坡。以符号i表
示,i等于渠底线与水平线夹角口的正弦即i=Sinθ。 明渠有三种底坡:顺坡、平坡和逆坡
第五章 明渠恒定均匀流
➢顺坡: i>0,明槽槽底沿程降低者称为正坡或顺坡。 ➢平坡: i=0,明槽槽底高程沿程不变者称为平坡。 ➢逆坡: i<0,明槽槽底沿程增高者称为反坡或逆坡。
第五章 明渠恒定均匀流
5.1 明渠的类型及其对水流运动的影响
明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 ), 是水流边界的几何条件。一定形式的边界几何条件,给 予水流运动一定的影响。所以为了了解水流运动的特征, 必须先对影响明渠水流运动的边界几何条件进行分析。
第五章 明渠恒定均匀流
一、明渠的横断面 人工明渠的横断面,通常作成对称的几何形状。例如
二、允许流速
允许流速是为了保持渠道安全稳定运行在流速上的限 制,包括不冲流速、不淤流速和其它运行管理要求的流 速限制。在实际明渠均匀流计算中必须结合工程要求进 行校核。
第五章 明渠恒定均匀流
➢在设计中,要求渠道流速v在不冲、不淤的允许
流速范围内,即:
式中:
——不冲允许流速(m/s),根据壁面材料定。
➢ 如果您有任何问题, 请毫不犹豫地提出 !
In case of you have any question, DO NOT hesitate to ask me !
第五章 明渠恒定均匀流
5.2 明渠均匀流特性及其产生条件
一、明渠均匀流的特性: 1、均匀流过水断面的形状、尺寸沿流程不变,特别
是水深h沿程不变,这个水深也称为正常水深。 2、过水断面上的流速分布和断面平均流速沿流程不
水力学第五章
第五章
有压管路的水力计算
O
2 0 v0
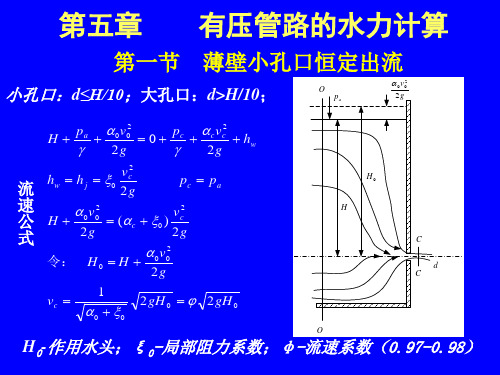
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
水力学-第5章 明渠恒定均匀流

R/m 1.625 1.866 2.090 2.310
C /( m
1/2
/ s)
Q AC
Ri /( m / s )
42.6 59.3 78.6 100.9
3
21.25 27.00 33.25 40.00
44.5 45.5 46.5 47.0
由上表绘出 h ~ Q 曲线。从曲线查得: 当 Q =70 m3/s 时,h = 3.3 m 。
5
nK
3 8 1 h 3 h m b b
根据上式就可绘出另一组曲线
h b
~
b
2 .6 7
(见附图II)
nK
现应用附图 II 解本例,
K Q i 70 m / s 1 800
3
1980 m / s
3
b
2 . 67
(6 m )
2 . 67 3
第五章
5.5
明渠恒定均匀流
明渠均匀流的水力计算
对于梯形渠道,各水力要素间存在着下列函数关系:
Q AC
Ri f ( m , b , h , i , n )
主要有下列几种类型:
一、已知渠道的断面尺寸b、m、h及底坡i、粗糙 系数n,求通过的流量(或流速)。 二、已知渠道的设计流量Q、底坡i、底宽b、边坡 系数m和粗糙系数n,求水深h。 三、已知渠道的设计流量Q、底坡i、水深h、边坡 系数m及粗糙系数n,求渠道底宽b。 四、已知渠道的设计流量Q,水深h、底宽b、粗糙 系数n及边坡系数m,求底坡i。 五、已知流量Q、流速v、底坡i、粗糙系数n和边 坡系数m,要求设计渠道断面尺寸。
i
(1)试算~图解法
可假设一系列 h 值,代入上式计算相应的 Q 值,并 绘成 h ~ Q曲线,然后根据已知流量,在曲线上即可查 出要求的 h 值。
计算水力学05

李光炽
计算水力学
内河道计算
令
消去Zi-1得
李光炽
计算水力学
内河道计L1+3,…,L2
李光炽
计算水力学
内河道计算
令: 由L2-1河段的差分方程有
消去QL2得
李光炽
计算水力学
内河道计算
与追赶方程 比较得
李光炽
计算水力学
内河道计算
把追赶关系 代入差分方程
李光炽
李光炽
计算水力学
最优编码解法
计算水力学
计算编程
(4)按计算追赶系数的逆顺序,回代出各 河道断面的水位和流量。 (a)由最后一条河道的边界条件,计算出 节点水位。 (b)ZL2=ZZ (末节点),由P、V、S、T 回代出断面的水位和流量。 (c)将ZL1赋到对应的首节点的水位ZZ (首节点)中。
李光炽
计算水力学
计算框图
李光炽
计算水力学
李光炽
计算水力学
河道1计算
边界条件 追赶方程
李光炽
计算水力学
河道2计算
边界条件 追赶方程
李光炽
计算水力学
节点3计算
节点③的相容方程
河道1、2末断面的追赶方程
李光炽
计算水力学
节点3计算
联立求解得
为河道3首断面的追赶方程
李光炽
计算水力学
河道3计算
利用递推公式可以计算河道3各断面的追 赶系数
李光炽
计算水力学
第二节 树状河网水流计算
树状河网结构的基本特征是任意河道都 不会组成环形回路。根据这种结构特征, 只要注意一定的计算次序,即可把河网 分解为一系列的单一河道,用上一章介 绍的追赶法求解。下面讨论树状河网的 计算方法。
水力学第五章

逐步充满整个断面。
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ,求水泵安装高度 H 。 计算内容:已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下,试分别比较孔口和管嘴出流的流速
流体力学
主 讲:赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程: 伯努利方程: 损失公式:
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
一、圆柱形外管嘴的恒定出流
1
v H 0 00 n 2g 2g 2g 1 v 2gH n 2gH n
n
1
v
2 0 0
v
2
2
l (3 ~ 4)d
H
0 d
c
2
0
பைடு நூலகம்
c
2
n
1
Q v n 2 gH 0
n n 0.82
§5.3 短管的水力计算
1.虹吸管的水力计算
例题2
§5.3 短管的水力计算
2.水泵吸水管的水力计算 hv ,求水泵安装高度 H 。 计算内容:已知 Q、d、l吸、、 进、 弯、
例题3
例题1
在 H 孔口 H n , d 孔口 d n 及流量。 1.流速比较 条件下,试分别比较孔口和管嘴出流的流速
流体力学
主 讲:赵 超
第五章 孔口、管嘴出流和有压管路
§5.1 液体经薄壁孔口的恒定出流 §5.2 液体经管嘴的恒定出流 §5.3 短管的水力计算
第五章 孔口、管嘴出流和有压管路
常用公式 连续性方程: 伯努利方程: 损失公式:
A1v1 A2 v2
2 p1 1v12 p2 2 v2 z1 z2 hw12 g 2g g 2g
2gH0 2gH0
1
c 0
速度系数 收缩系数 流量系数
Q Ac vc A 2 gH 0 A 2 gH 0
c /
三、薄壁小孔口的 淹没出流
2 2 vc vc H1 0 0 H2 0 0 0 se 2g 2g
l 3 ~ 4 d
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ux’ dAy ΔF uy’
b层
a层
m ρ u y ' dA y dt
到达b层时,立即具有一个x方向的脉动流速 ux’
dt 时间内 x方向的动量变化
( m )u x ' u x ' u y ' dAy dt
ux’ dAy ΔF uy’
dt 时间内x方向的动量变化 b层
( m )u x ' u x ' u y ' dAy dt
2
( k1 k 2 l1 l )
du x ( l ) dy
总切应力可以写成
d ux du x τ μ η d y dy
粘性切应力
紊流切应力
下图为管道中量
测到的总切应力
0.0 0.1 0.2 0.3 0.4
Ç Ð Ó ¦ Á ¦ Î É Á ÷Ç Ð Ó ¦ Á ¦
和紊流切应力的
ux'
ux
ux
5
t/ s
10
15
20
瞬时流速 时均流速
u x u x (t )
T
u x=
u (t ) d t
x 0
T
式中, T 为较长的时段
1000 900 800 700 600 500 400 300 200 100 0 0
-2
)
p( t) x
/ (k N.m u /cm/s
ux'
ux
Δ δ0
例如,在当冬季雪下得较厚时,在崎岖不平的 雪地上滑雪,感觉不到雪地的粗糙不平。
Δ δ0
3 水力粗糙面: δ0 << Δ(若干倍)
当Re 较大时,δ0 << Δ(若干倍) 时,粗糙度直 接深入到水流核心区,边壁的粗糙度对紊流已成为主 要的作用,而粘性底层的粘滞力只占据次要的地位, 与前者相比,几乎可以忽略不计。这种粗糙表面叫做 水力粗糙面。
du x du x u x ' u x-(u x l 1 ) l1 dy dy
假定
du x du x u x '= l 1 l1 dy dy du x u y ' k1 u x ' k1 l1 dy du x 2 du x 2 ux ' u y ' k 2 ux ' u y ' k1 k 2 l1 ( ) l( ) dy dy du x 2 du x 2=-u x ' u y '=l 2 ( ) dy dy
ux
5
t/ s
10
15
20
脉动流速
u x ' u x (t ) u x
式中,脉动流速可正、可负
1000 900 800 700 600 500 400 300 200 100 0 0
-2
)
p( t) x
/ (k N.m u /cm/s
ux'
ux
ux
5
t/ s
10
15
20
脉动流速
u x ' u x (t ) u x
5 液流形态与水头损失
5.1 水头损失及其分类 5.2 均匀流沿程水头损失与水流阻力关系
5.3 5.4 流动的两种形态与雷诺实验 层流运动
5.5 紊流运动 5.6 紊流的沿程水头损失 5.7 局部水头损失
5.5 紊流运动
5.5.1 紊流的产生 5.5.2 紊流的特征
5.5.2 紊流的特征
运动要素的脉动 紊流的基本特征是,流动中许多涡体在相互混掺的
粘性底层厚度计算公式
由于粘性底层较薄,假定在粘性底层范围内, 流速近似为直线分布,则
y
u
δ0
du x u 0 dy δ0 τ 0 μ u 0 du x u μ 0 dy 0 τ0 τ u 0 * μ μ ν
2
τ0
u δ0
摩阻流速
( u* τ0 ,[u* ] [V ] )
p p( t ) 1 p T ...
T
pdt
0
p' ( t ) p( t ) p
研究运动要素脉动时,经常用到几个表示脉动强
度的物理量,现介绍如下: 流速的脉动强度 x方向的流速脉动强度
u' 2
u x '2
y方向的流速脉动强度
紊动强度 x方向的紊动强度 y 方向的紊动强度
r/r0
试验曲线。可见, 实测曲线。可见,
两种切应力沿水
深方向的分布规
r r0
0.5 0.6 0.7 0.8 0.9 1.0 0.0 0.5
粘性切应力
du x du x dy τ t η dy
1.0 1.5
律。
总切应力可以写成
d ux du x τ μ η d y dy
τ
t
η
τ
t
du x ητ t η d u x dy dy
τ τ τ
1 1
τ
2
du x μ dy
脉动流速产生的附加切应力
用牛顿内摩擦定律和时均流速梯度计算粘性切应力 1 用普朗特动量传递理论推导紊流切应力 2
在液流中取一个垂直于y 轴上的微小截面dAy y y
ux’ dAy dAy u(y) Δ F uy’
b层
a层
ux’ dAy ΔF
b层
u y '2
Tu
v
v y Tu v
Tu
x
明渠中靠近水
面附近水流紊动强度
自由液面(管心)
1.0 0.9 0.8 0.7 0.6
渠底(管壁) 紊流 n
自由水面(管心)
最弱,靠近渠底附近
紊动最大。
y/ h
Tux Tuy
原因:靠近渠道
处流速梯度和切应力
0.5 0.4 0.3
比较大,壁面粗糙度
干扰的影响也较强,
0.2 0.1 0.0 0.00
因而靠近渠底的地方,
涡体最容易形成。
0.05
0.10
0.15
T ux ,T uy
明渠水流紊流强度实测曲线
自由液面(管心)
1.0 0.9
渠底(管壁) 紊流 n
自由水面(管心)
现代量测技 术表明,临近渠底
y/ h
0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.0 0.00
u x u y uz p = = = ... 0 t t t t t
非恒定流 运动要素的时均值随时间发生变化的流动
u
u’ u u t 非恒定流时均值随时间变化
1000 900 800 700 600 500 400 300 200 100 0 0
-2
ux’ dAy ΔF uy’
b层
a层
m ρ u y ' dA y dt
到达b层时,立即具有一个x方向的脉动流速 ux’
dt 时间内 x 方向的动量变化为
( m )u x ' u x ' u y ' dAy dt
ux’ dAy ΔF uy’
b层
a层
dt 时间内 x 方向动量变化为
( m )u x ' u x ' u y ' dA y dt
pdt
0
p' ( t ) p( t ) p
d ux du x τ μ η d y dy
5.5.4 紊流中存在粘性底层
紊动水流自边界起至最大流速处,可分
粘性底层 过渡区 紊流核心
5.5.5 水力光滑面和水力粗糙面
1 绝对粗糙度:
固体边壁表面粗糟不平,粗糙表面凸起高度叫绝对
粗糙度,用符号Δ表示。
uy’
a层
若a 层有一质点以横向脉动 流速uy’ 通过该截面进 入b层,则在dt 时间内该截 面的质量为
m ρ u y ' dA y dt
u x’
dAy
ΔF uy’
b层
l1
a层
假定液体质点在上下横向脉动距离l1 (称混合长 度)中瞬时流速保持不变,动量也保持不变,达到 新位置后,动量突然改变,与原位置上液体质点具 有的动量一致
a层
dt 时间内,截面dAy上产生的x方向冲量应等于动量变化
Fdt ρ u x ' u y ' dA y dt
紊流切应力为
F 2= u x ' u y ' dA 2 u x ' u y '
下面将紊流切应力用时均流速来表达 ux’ dAy
du x ux l1 dy
b层
δ0
Δ
4 过渡粗糙面
当粘性底层的厚度不足以完全掩盖边壁粗糙度 的影响,但是,粗糙度还没有起决定性的作用,这 种粗糙面叫做过渡粗糙面。
Δ δ0
注意 滑面、粗糙面、过渡粗糙面都是相对水流条件 而言。 原因:因为壁面粗糙度是一定的,但粘性底层厚度 是相对的。在水流条件一定时,边壁可能是光滑面;但 水流条件改变时,其就可能变为粗糙面了。 因此,这些
粘性底层厚度随Re 而变。因此,δ0 和Δ的关系有
2
Hale Waihona Puke 水力光滑面:δ0 >> Δ(若干倍)
当δ0 >> Δ(若干倍) 时,粗糙度对完全淹没 在水流粘性底层之中,粗糙度对水流的运动不产生 影响,边壁对水流的阻力主要是粘滞阻力。 从水力学的观点看,这种粗糙表面与光滑管的表 面是一样的,所以这种粗糙表面叫水力光滑面。
u 0 (N ) u*
0=
N
8
v
8 Nd 11.6 8d 32.8d vd Re Re
