水力学第5章资料
合集下载
流体力学 水力学 第五章
7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算（Q、d、H） 有压流：水沿管道满管流动的水力现象。 特点：水流充满管道过水断面，管道内不存在自 由水面，管壁上各点承受的压强一般不等于大 气压强。
短管：局部水头损失和 速度水头在总水头损失 中占有相当的比重，计 算时不能忽略的管道. （一般局部损失和速度 水头大于沿程损失 的5% ~ 10%）。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数： c 0 1 0
1 1 流速系数： c 0 1 0
实验得： 0.97 ~ 0.98 1 推求： 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3：如图所示圆形有压涵管，管长50m, 上下游水位差3m 沿程阻力系数为0.03，局部阻力系数：进口 1＝0.5。 第一个转弯 2＝0.71，第二个转弯 3＝0.65，出口
4＝1.0，要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g
v
v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g
v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g
水力学-第5章 明渠恒定均匀流1113
工程中采用最多的是梯形断面， 工程中采用最多的是梯形断面，其边坡系数 m 由 边坡稳定要求确定。 边坡稳定要求确定。在 m 已定的情况下，同样的过水 要求确定 已定的情况下， 面积 A ，湿周的大小因底宽与水深的比值 b / h 而异 。根据水力最佳断面的条件： 根据水力最佳断面的条件： 即
χ = 最小值 A = 常数
解：将已知条件代入基本公式，并用曼宁公 将已知条件代入基本公式， 式计算谢才系数， 式计算谢才系数，整理后可得
nQ( β + 2 1 + m 2 ) 2 / 3 h= 5 / 3 1/ 2 ( β + m) i
3/8
当为水力最佳断面时: 当为水力最佳断面时
β = 2( 1 + m 2 − m) = 2( 1 + 1.252 − 1.25) = 0.702
2
15
用 β m 代替上式中的 β 值，整理后得 即梯形水力最佳断面的水力半径等于水深的一半。 即梯形水力最佳断面的水力半径等于水深的一半。
hm Rm = 2 的梯形断面。 矩形断面可以看成为 m = 0 的梯形断面。以 m = 0
代入以上各式可求得矩形水力最佳断面的 β m 及 Rm .
bm βm = = 2 即 bm = 2hm hm
χ = b + 2 h 1 + m 2 = 34 m + 2 × ( 2 . 7 m ) 1 + 1 . 5 2 = 43 . 74 m
102 . 74 m 2 R= = = 2 . 35 m χ 43 . 74 m A
查表可知， 查表可知，对渠线弯曲并已滋生杂草的土 n =0.03
1 1/ 6 1 C= R = (2.35)1/ 6 = 38.4m1/ 2 / s n 0.03
第五章_给水管网水力分析
管段的水力特性方程： 管段的水力特性方程：hi=siqin 可将管段流量与水头相互转换， 个方程。 可将管段流量与水头相互转换，即N 个未知量对应 N 个方程。 管段流量 相互转换
（3）必须至少有一个定压节点 ）
• 管网中无定压节点（R=0）时，恒定流方程组无 管网中无定压节点（ ） 解。 • 因为若 j*为方程组解， Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解， 仍为方程组的 解，即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单， 比较简单，管段流量可以由节点流量连续性方程 组直接求出，不要求解非线性的能量方程组。 组直接求出，不要求解非线性的能量方程组。 水力分析计算分两步（P89例题 ）： 例题5.1）： 水力分析计算分两步（ 例题 • 1、用流量连续性条件计算管段流量，并计算出管 、用流量连续性条件计算管段流量， 段压降； 段压降； • 2、根据管段能量方程和管段压降，从定压节点出 、根据管段能量方程和管段压降， 发推求各节点水头。 发推求各节点水头。
可以看出：树状网中，各管段流量 可以看出：树状网中，各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程（根据能量守恒定律） 根据能量守恒定律）
管段两端节点水头之差等于该管段的压降： 管段两端节点水头之差等于该管段的压降： HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头； 管段i的上端点水头 管段 的上端点水头； HTi——管段 的下端点水头； 管段i的下端点水头； 管段 的下端点水头 hi——管段 的压降； 管段i的压降 管段 的压降； M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
（3）必须至少有一个定压节点 ）
• 管网中无定压节点（R=0）时，恒定流方程组无 管网中无定压节点（ ） 解。 • 因为若 j*为方程组解， Hj* +∆H仍为方程组的 因为若H 为方程组解 为方程组解， 仍为方程组的 解，即方程组无解。 即方程组无解。
(H + ∆H ) − (H + ∆H ) = H − H = h
* Fi * Ti * Fi * Ti
* i
5.3 单定压节点树状管网水力分析
比较简单， 比较简单，管段流量可以由节点流量连续性方程 组直接求出，不要求解非线性的能量方程组。 组直接求出，不要求解非线性的能量方程组。 水力分析计算分两步（P89例题 ）： 例题5.1）： 水力分析计算分两步（ 例题 • 1、用流量连续性条件计算管段流量，并计算出管 、用流量连续性条件计算管段流量， 段压降； 段压降； • 2、根据管段能量方程和管段压降，从定压节点出 、根据管段能量方程和管段压降， 发推求各节点水头。 发推求各节点水头。
可以看出：树状网中，各管段流量 可以看出：树状网中，各管段流量qi可以用节点流 表示出来。 量Qj表示出来。
5.1.2 管段能量方程（根据能量守恒定律） 根据能量守恒定律）
管段两端节点水头之差等于该管段的压降： 管段两端节点水头之差等于该管段的压降： HFi –HTi= hi i-1,2,…,M
HFi——管段 的上端点水头； 管段i的上端点水头 管段 的上端点水头； HTi——管段 的下端点水头； 管段i的下端点水头； 管段 的下端点水头 hi——管段 的压降； 管段i的压降 管段 的压降； M——管段模型中的管段总数。 管段模型中的管段总数。 管段模型中的管段总数
水力学基础课件——第五章 明渠恒定均匀流
A
(b mh)h
R
x b 2h 1 m2
第五章 明渠恒定均匀流
二、明渠的底坡 底坡：明渠渠底倾斜的程度称为底坡。以符号i表
示，i等于渠底线与水平线夹角口的正弦即i＝Sinθ。 明渠有三种底坡：顺坡、平坡和逆坡
第五章 明渠恒定均匀流
➢顺坡： i>0，明槽槽底沿程降低者称为正坡或顺坡。 ➢平坡： i=0，明槽槽底高程沿程不变者称为平坡。 ➢逆坡： i<0，明槽槽底沿程增高者称为反坡或逆坡。
第五章 明渠恒定均匀流
5.1 明渠的类型及其对水流运动的影响
明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 )， 是水流边界的几何条件。一定形式的边界几何条件，给 予水流运动一定的影响。所以为了了解水流运动的特征， 必须先对影响明渠水流运动的边界几何条件进行分析。
第五章 明渠恒定均匀流
一、明渠的横断面 人工明渠的横断面，通常作成对称的几何形状。例如
二、允许流速
允许流速是为了保持渠道安全稳定运行在流速上的限 制，包括不冲流速、不淤流速和其它运行管理要求的流 速限制。在实际明渠均匀流计算中必须结合工程要求进 行校核。
第五章 明渠恒定均匀流
➢在设计中，要求渠道流速v在不冲、不淤的允许
流速范围内，即：
式中：
——不冲允许流速（m/s），根据壁面材料定。
➢ 如果您有任何问题， 请毫不犹豫地提出 !
In case of you have any question, DO NOT hesitate to ask me !
第五章 明渠恒定均匀流
5.2 明渠均匀流特性及其产生条件
一、明渠均匀流的特性： 1、均匀流过水断面的形状、尺寸沿流程不变，特别
是水深h沿程不变，这个水深也称为正常水深。 2、过水断面上的流速分布和断面平均流速沿流程不
水力学第五章
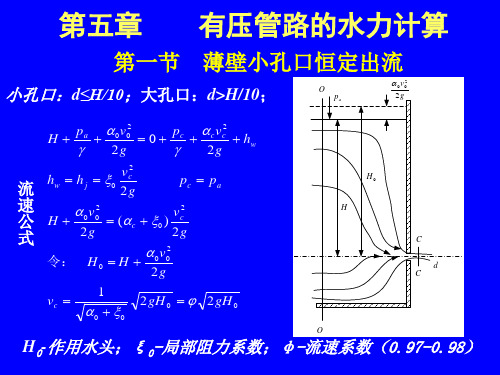
第五章
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口：d≤H/10；大孔口：d>H/10；
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令： H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头；ξ 0-局部阻力系数；φ -流速系数（0.97-0.98）
流量公式：
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为：串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路：总水头损失等于各分段水头损失之和；无奇点（流进、 流出）情况下，总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口：d≤H/10；大孔口：d>H/10；
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令： H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头；ξ 0-局部阻力系数；φ -流速系数（0.97-0.98）
流量公式：
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为：串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路：总水头损失等于各分段水头损失之和；无奇点（流进、 流出）情况下，总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
水力学-第5章 明渠恒定均匀流
R/m 1.625 1.866 2.090 2.310
C /( m
1/2
/ s)
Q AC
Ri /( m / s )
42.6 59.3 78.6 100.9
3
21.25 27.00 33.25 40.00
44.5 45.5 46.5 47.0
由上表绘出 h ~ Q 曲线。从曲线查得： 当 Q =70 m3/s 时，h = 3.3 m 。
5
nK
3 8 1 h 3 h m b b
根据上式就可绘出另一组曲线
h b
～
b
2 .6 7
（见附图II）
nK
现应用附图 II 解本例，
K Q i 70 m / s 1 800
3
1980 m / s
3
b
2 . 67
(6 m )
2 . 67 3
第五章
5.5
明渠恒定均匀流
明渠均匀流的水力计算
对于梯形渠道，各水力要素间存在着下列函数关系:
Q AC
Ri f ( m , b , h , i , n )
主要有下列几种类型：
一、已知渠道的断面尺寸b、m、h及底坡i、粗糙 系数n，求通过的流量（或流速）。 二、已知渠道的设计流量Q、底坡i、底宽b、边坡 系数m和粗糙系数n，求水深h。 三、已知渠道的设计流量Q、底坡i、水深h、边坡 系数m及粗糙系数n，求渠道底宽b。 四、已知渠道的设计流量Q，水深h、底宽b、粗糙 系数n及边坡系数m，求底坡i。 五、已知流量Q、流速v、底坡i、粗糙系数n和边 坡系数m，要求设计渠道断面尺寸。
i
（1）试算～图解法
可假设一系列 h 值，代入上式计算相应的 Q 值，并 绘成 h ~ Q曲线，然后根据已知流量，在曲线上即可查 出要求的 h 值。
《水力学》——水头损失
2.局部水头损失 2.局部水头损失 定义：由于液流局部边界的急剧改变所引起的阻力，从而引起流速的急剧变化， 流速的急剧变化 定义：由于液流局部边界的急剧改变所引起的阻力，从而引起流速的急剧变化，
加剧液流之间相互摩擦和碰撞而导致的附加阻力，称为局部阻力。 加剧液流之间相互摩擦和碰撞而导致的附加阻力，称为局部阻力。 局部阻力 单位质量液体克服局部阻力所损失的水头称为局部水头损失。 表示。 单位质量液体克服局部阻力所损失的水头称为局部水头损失。用hj表示。 局部水头损失
产生的物理原因：尽管局部阻力产生的原因各异， 产生的物理原因：尽管局部阻力产生的原因各异，但是其物理原因都是由于液体
存在粘滞性 任何断面形状的改变，都将引起流速的重新分布，改变了流体的流速。 粘滞性， 存在粘滞性，任何断面形状的改变，都将引起流速的重新分布，改变了流体的流速。
产生的条件：急变流区域。例如通过管道进口、突然扩大、突然收缩、 产生的条件：急变流区域。例如通过管道进口、突然扩大、突然收缩、
Rec＝2320
因此一般以下临界雷诺数作为判别流态的标准。如管径为d 管中流速为v 因此一般以下临界雷诺数作为判别流态的标准。如管径为d，管中流速为v，液体的 以下临界雷诺数作为判别流态的标准 运动粘滞系数为ν 则相应的雷诺数 雷诺数为 运动粘滞系数为ν，则相应的雷诺数为
由于临界流速有两个，故临界雷诺数也有两个， 由于临界流速有两个，故临界雷诺数也有两个，即 上临界雷诺数 下临界雷诺数 试验发现上临界雷诺数易受外界干扰，数值不稳定。 =12000， 试验发现上临界雷诺数易受外界干扰，数值不稳定。有的得到 =12000，有的 上临界雷诺数易受外界干扰 =20000。如在试验前将水静止几天后再做试验， 值可达到40000 50000。 40000～ 得到 =20000。如在试验前将水静止几天后再做试验， 值可达到40000～50000。 而下临界雷诺数却是个比较稳定的数值，试验得到管流的下临界雷诺 下临界雷诺数为 而下临界雷诺数却是个比较稳定的数值，试验得到管流的下临界雷诺数为
第五章 液体三元流动基本原理w
第 五 章 液 体 三 元 流 动 基 本 原 理
u dr 0
水力学
第 五 章 液 体 三 元 流 动 基 本 原 理
（2）流线方程：
由
u dr u x u y u z 0 dx dy dz
i
j
k
得出流线微分方程：
dx dy dz u x ( x, y , z , t ) u y ( x, y , z , t ) u z ( x, y , z , t )
1、液体微团运动形式： 平移、旋转和变形
u u0 dr ε dr
水力学
2、液体质点的基本运动形式分析
设微团平行于xoy平面的投影面为ABCD，在t瞬时，各 角点沿x,y方向的速度分量
第 五 章 液 体 三 元 流 动 基 本 原 理
水力学
液体质点的基本运动形式
d 1 u y ux ( ) z dt 2 x y
旋转角速度
水力学
角变形率
第 五 章 液 体 三 元 流 动 基 本 原 理
旋转角速度
1 uz u y ( ) x 2 y z
1 u y ux ( ) xy 2 x y 1 uz u y ( ) yz 2 y z
第 五 章 液 体 三 元 流 动 基 本 原 理
平移是指液体微团在运动
过程中任一线段的长度和
方位均不变。
平移速度为ux,uy
水力学
线变形是指液体微团在运动过程中仅存在各线段 的伸长或缩短。
第 五 章 液 体 三 元 流 动 基 本 原 理
ux (u x dx)dt u x dt x u x dxdt x
u y u x u z 线变形率分量： xx , yy , zz x y z
水力学第5章 量纲分析与相似模型
雷诺准则也是流动稳定性的重要判据。 适用范围：主要受水流阻力即粘滞力作用的流体流 动，凡是有压流动，重力不影响流速分布，主要受 粘滞力的作用，这类液流相似要求雷诺数相似。另 外，处于水下较深的运动潜体，在不至于使水面产 生波浪的情况下，也是以雷诺数相等保证液流动力 相似。如层流状态下的管道、隧洞中的有压流动和 潜体绕流问题等。 无粘性流是Re → ∞的极限情况。
几何相似
...... l 长度比尺： lm1 lm 2 lm p1 m1 p 2 m 2 l p1 l p2 lp
面积比尺： A AP 2 2 l Am lm
体积比尺： V
l3 VP p 3 3 l Vm lm
Qm
Qp
12 2 l l
模型比尺表
按雷诺准则和弗劳德准则导出的各物理 比 尺 量比尺 比 尺
雷诺准则 ＝ 1 ≠1 弗劳德 准则 名称 雷诺准则 ＝ 1 力的比尺F ≠1
2
名称
弗劳德 准则
长度比尺l
l
l
l
2 1 l
流速比尺
加速度比尺a 流量比尺Q 时间比尺t
lp lm lp lm
这样只有 l p lm ，即 l 1 时才可能
1）模型律的选择
当原型和模型为不同种流体时， p m ， 则有：
p lm lp ml p lm
p m
lp vm l m vp
32
p m 3 2 l
第五章 量纲分析与相似模型
一、量纲及其概念 二、量纲分析 三、相似理论与相似模型
一、量纲及其概念
水力学课件第五章
紊流
管中为石油时
vd 100 2 333.3 2300 Re 0.6 ν
层流
作业
1、2
均匀流沿程水头损失与切应力的关系
沿程水头损失与切应力的关系 在管道恒定均匀流中，取总流流段1-1到2-2，各 作用力处于平衡状态：F=0。
P1
1
0 0
2
P2 2 z2
z1 z2 sin l
p1 p2 hf g g
m 13600 ( 1)hp ( 1) 0.3 4.23m 900
设流动为层流
4Q v 2.73m / s 2 d
l v 2 64 l v 2 64 l v 2 hf d 2 g Re d 2 g vd d 2 g
Re
d 1.175 0.075 979 < 2300 4 0.9 10
层流
1 2 1 Q 1.175 d 3600 1.175 3.14 0.075 2 3600 18.68m 3 / h 4 4
2、求沿程水头损失
64 64 0.0654 Re 979
T
T
u x u x u x
T
1 1 1 ' ux (ux ux )dt ux dt ux dt ux ux 0 T0 T0 T0
其它运动要素也同样处理：
1 p T 1 p T
T
pdt
0 T 0
p p p
pdt 0
脉动值说明：
—局部损失系数(无量纲)
一般由实验测定
实际液体流动的两种形态
雷诺试验
实验条件：
【精品】第五章-明渠恒定均匀流---水力学课程主页
第五章-明渠恒定均匀流---水力学课程主页第五章 明渠恒定均匀流第一节 概 述一．明渠水流1、明渠定义：人工渠道、天然河道、未充满水流的管道统称为明渠。
2、明渠水流是指在明渠中流动，具有显露在大气中的自由表面，水面上各点的压强都等于大气压强。
故明渠水流又称为无压流。
明渠水流的运动是在重力作用下形成的。
在流动过程中，自由水面不受固体边界的约束（这一点与管流不同），因此，在明渠中如有干扰出现，例如底坡的改变、断面尺寸的改变、粗糙系数的变化等，都会引起自由水面的位置随之升降，即水面随时空变化，这就导致了运动要素发生变化，使得明渠水流呈现出比较多的变化。
在一定流量下，由于上下游控制条件的不同，同一明渠中的水流可以形成各种不同形式的水面线。
正因为明渠水流的上边界不固定，故解决明渠水流的流动问题远比解决有压流复杂得多。
明渠水流可以是恒定流或非恒定流，也可以是均匀流或非均匀流，非均匀流也有急变流和渐变流之分。
本章首先学习恒定均匀流。
明渠恒定均匀流是一种典型的水流，其有关的理论知识是分析和研究明渠水流各种现象的基础，也是渠道断面设计的重要依据。
对明渠水流而言，当然也有层流和紊流之分，但绝大多数水流（渗流除外）为紊流，并且接近或属于紊流阻力平方区。
因此，本章及以后各章的讨论将只限于此种情况。
二、渠槽的断面形式（一）按横断面的形状分类渠道的横断面形状有很多种。
人工修建的明渠，为便于施工和管理，一般为规则断面，常见的有梯形断面、矩形断面、U 型断面等，具体的断面形式还与当地地形及筑渠材料有关。
天然河道 一般为无规则，不对称，分为主槽与滩地。
在今后的分析计算中，常用的是渠道的过水断面的几何要素，主要包括：过水断面面积A 、湿周χ、水力半径R 、水面宽度B 。
对梯形断面而言，其过水断面几何要素计算公式如下：2)()h m h mh b A +=+=β（h m m h b )12(1222++=++=βχχA R = h m mh b B )2(2+=+=β式中，b 为底宽；m 为边坡系数；h 为水深；β为宽深比，定义为h b =β（二）按横断面形状尺寸沿流程是否变化分类棱柱体明渠是指断面形状尺寸沿流程不变的长直明渠。
水力学 第五章_有压管道的恒定流
式中 hw ——为管嘴的水头损失,等于进口损失与收缩断面后的 进口损失与收缩断面后的 扩大损失之和(管嘴沿程水头损失忽略),也就是相 扩大损失之和 当于管道锐缘进口的损失情况. ζn——管嘴阻力系数,即管道锐缘进口局部阻力系数, 一股取ζn =0.5; n ——管嘴流速系数 n = 1 / α + ζ n ≈ 1 / 1 + 0.5 = 0.82 μn——管嘴流量系数,因出口无收缩,故 n = n = 0.82
各种流速下的k值计算,其结果见表5—2. 为了计算方便,编制出各种管材,各种管径的比阻A的计算表 .钢管的 见表 钢管的A见表 见表5-4. 钢管的 见表5—3,铸铁管的 见表 ,铸铁管的A见表 .
2.串联管路 . 由直径不同的几段管路依次连接而成的管路,称为串联 由直径不同的几段管路依次连接而成的管路 管路.串联管路各管段通过的流量可能相同,也可能不同. 根据能量方程得(各管段的流量Q,直径d,流速v不同,整个 整个 串联管路的水头损失应等于各管段水头损失之和): 串联管路的水头损失应等于各管段水头损失之和
= ε = 0.54 × 0.97 = 0.62
2.大孔口的自由出流 大孔口的自由出流
适用上式, Ho为大孔口中心的水头, = ε
中ε较大.
在水利工程中,闸孔出流可按大孔口出流计算,其流量系数列 于表51中.
§5—2 液体经管嘴的恒定出流
1.圆柱形外管嘴的恒定出流 . 圆柱形外管嘴: 圆柱形外管嘴: 在孔口断面处接一直径与孔口直径完全相同 的圆柱形短管,其长度L=(3～4)d. 收缩断面C-C处水流与管壁分离,形成漩涡区;在管嘴出口断 面上,水流已完全充满整个断面. 列 管嘴为自由出流时的 伯努利方程 以通过管嘴断面形心的水平面为 基准面; 基准面; 对 断面 断面0-0 和 管嘴出口断面 b-b列方程.
各种流速下的k值计算,其结果见表5—2. 为了计算方便,编制出各种管材,各种管径的比阻A的计算表 .钢管的 见表 钢管的A见表 见表5-4. 钢管的 见表5—3,铸铁管的 见表 ,铸铁管的A见表 .
2.串联管路 . 由直径不同的几段管路依次连接而成的管路,称为串联 由直径不同的几段管路依次连接而成的管路 管路.串联管路各管段通过的流量可能相同,也可能不同. 根据能量方程得(各管段的流量Q,直径d,流速v不同,整个 整个 串联管路的水头损失应等于各管段水头损失之和): 串联管路的水头损失应等于各管段水头损失之和
= ε = 0.54 × 0.97 = 0.62
2.大孔口的自由出流 大孔口的自由出流
适用上式, Ho为大孔口中心的水头, = ε
中ε较大.
在水利工程中,闸孔出流可按大孔口出流计算,其流量系数列 于表51中.
§5—2 液体经管嘴的恒定出流
1.圆柱形外管嘴的恒定出流 . 圆柱形外管嘴: 圆柱形外管嘴: 在孔口断面处接一直径与孔口直径完全相同 的圆柱形短管,其长度L=(3～4)d. 收缩断面C-C处水流与管壁分离,形成漩涡区;在管嘴出口断 面上,水流已完全充满整个断面. 列 管嘴为自由出流时的 伯努利方程 以通过管嘴断面形心的水平面为 基准面; 基准面; 对 断面 断面0-0 和 管嘴出口断面 b-b列方程.
水力学资料第五章
解：（1）写出自由涡的流速分布r C r /,0==θμμ将m r r 3.00==处流速值u(0r )=2m/s 带入上式，得常数C=0.9，有 r /6.0=θμ在弯道内侧，;/3,2.011s m m r r ===θμ在弯道外侧，s m m r r /5.1,4.022===θμ。
依据同心圆弯道的压强微分式，有dr rdp 2θμρ=由1r r =和2r r =积分该式，得 ⎪⎪⎭⎫⎝⎛-==⎰⎰22212321122121r r dr rdp r r r r θθρμμρ故弯管内、外壁之压差为pa pa p p 33754.012.01210006.022212=⎪⎭⎫ ⎝⎛-⨯⨯=- （2）压强水头差m m g p p 344.010008.9337512=⨯=-ρ 流速水头差m m g 344.08.9235.12222122=⨯-=-θθμμ 可见，压强水头差等于流速水头差，故总机械能在弯道内、外壁处相等。
第五章 层流、紊流及其能量损失5-1（1）某水管的直径d=100mm,通过流量Q=4L/s,水温T=20C 0;(2)条件与以上相同，但水管中流过的是重燃油，其运动粘度s m /1015026-⨯=ν。
试判断以上两种情况下的流态。
解：（1）2000504251001.11.0004.0444Re 62>=⨯⨯⨯⨯====-πνππνd Q v d Qd Vd 流动为紊流流态。
（2）20005.339101501.0004.044Re 6<=⨯⨯⨯⨯===-πνπνd Q Vd 流动为层流流态。
5-2（2）温度为0C 0的空气，以4m/s 的速度在直径为100mm 的圆管中流动，试确定其流态（空气的运动粘度为s m /1037.125-⨯）。
若管中的流体换成运动粘度为s m /10792.126-⨯的水，问水在观众管中呈何流态？解 流体为空气时，有2000291971037.11.04Re 5>=⨯⨯==-νVd 紊流流态流体为水时，有200022321410792.11.04Re 6>=⨯⨯==-νVd 紊流流态 5-3（1）一梯形断面排水沟，底宽0.5m ，边坡系数5.1cot =θ(θ为坡角)，水温为C 020，水深0.4m ，流速为0.1m/s ，试判别流态；（2）如果水温保持不变，流速减小到多大时变为层流？ 解（1）梯形断面面积 2244.0)5.14.05.0(4.0)(m m hm b h A =⨯+⨯=+= 湿周 ()m m m h b 942.15.114.025.01222=+⨯⨯+=++=χ 水力半径 m m A R 2266.0942.144.0===χ雷诺数 5001024.21001.12266.01.0Re 46>⨯=⨯⨯==-νVR紊流流态 （2）层流的上界雷诺数500Re ==νVR。
水力学系统讲义课件第五章(1)-流动形态及水头损失
1
v1≈0 进口
0 1
转弯 突扩
突缩 阀门
H
2 V0 Q
2
h w12 hf hj
过水断面的形状和尺寸对沿程水头损失的影响
A
A
A
A1
A2
Χ1
Χ2
Χ3
Χ4
Χ5
圆形
正方形
长方形
(a)
(b)
湿周：过水断面上被液体湿润的固体周界长度，
记为χ。
1 2 3
hf1 hf 2 hf 3
产生原因：液体的粘滞性和液体质点间的动量 交换而引起的。
1
v1≈0 进口
0 1
转弯 突扩
突缩 阀门
H
2 V0 Q
2
局部水头损失：在水流方向、断面形状和尺寸 改变以及障碍处产生，记为hj。
产生原因：局部地区产生漩涡。漩涡的产生及 维持，漩涡水体与主流之间的动量交换，漩涡 间的碰撞与摩擦均需消耗能量而引起水头损失。
形过水断面渠道的水 力半径为
b
矩形过水断面渠道的水力 半径，令m=0，则
R bh mh2 b 2h 1 m2
R bh b 2h
对于h/b<1/10的宽矩形过水断面渠道的水力半径
R h h 1 2 h b
§5-2 均匀流中沿程水头损失的计算 公式
圆管总流中取出长度为s的一段作为控制体，研 究其平衡。假设流动是恒定的均匀流，且液体 是不可压缩的。
实验结论
1.同一种液体在同一个管道中流动，当流速不 同时液体有两种不同的运动型态：
（1）层流：是指在流速较小时，液体质点作有 条不紊的直线运动，水流各层上的质点互不掺 混。 （2）紊流（湍流）：是指在流速较大时，流层 逐渐不稳定，质点相互掺混，液体质点运动轨 迹极不规则的流动。
水力学 第五章 有压管路(道)
液体经薄壁孔口的恒定出流 液体经管嘴的恒定出流 短管的水力计算 长管的水力计算 离心水泵的水力计算
教学重点：
１.孔口出流及管嘴出流的计算。 ２.短管水力计算方法。
教学难点：
１.孔口出流及管嘴出流的流动现象。 ２.管嘴的长短为什么会影响管嘴的流动。 3.短管的计算要点。
§5-1 液体经薄壁孔口的恒定出流 （自由出流）
①对水来说，为防止汽化的容许真空度hv=7mH2O，因此， 其水头H就不能高于7/0.75=9.5m
②为达到增加外管嘴流量的目的，不应使管嘴太长或太短， 因此一般管嘴长度l=3-4d为宜。
3、常用管嘴的出流
1）流线型管嘴： 0.97
适用于要求流量大，水头损失小的情况。
2）收缩管嘴：出流量与收缩角度θ有关。
第五章 有压管路的 恒定流动
本章主要研究液体经孔口、管嘴、管路流动时 的特性，确定流速，流量及有关的影响因素。
有压管路：
液体在压差作用下流动时，液体整个周围都和固体 壁面相接触，没有自由表面。
在这样的流动中，固体壁面处处受到液体压强的作 用，并且压强的大小一般不等于大气压强。
§5-1 §5-2 §5-3 §5-4 §5-5
面处称为缩脉，用ωc来表示，ωc与小孔面积ω的比值
称为收缩系数ε 。
0v02
c
1 pa
2g
HH
0
c
如图列1-c截面间伯氏方程
0
d
c
H
p1
1v12
2g
0
pc
c vc2
2g
hm
1
此时只考虑局部水头损失，忽略沿程水头损失
∵ pc p1 pa
∴
H
1v12
水力学 第五章
故
H0
2v 2
2g
hf hj
上式表明，管道的总水头将全部消耗于管道的水头损 失和保持出口的动能。
l v2 因为沿程损失 h f d 2g
局部水头损失
v2 h j 2 g
有
l v2 H 0 ( 2 ) d 2g
3
取 2 1 管中流速 通过管道流量
K Q H l
由表4-1即可查出所
若为短管
d
4Q
c 2 gH
17
流量系数 c 与管径有关，需用试算法确定。
三、管线布置已定，当要求输送一定流量时， 确定所需的断面尺寸（圆形管道即确定管道直 径）。这时可能出现下述两种情况：
2．管道的输水量 Q，管长l 已知，要求选定所需的管径 及相应的水头。从技术和经济条件综合考虑。 (1) 管道使用要求： 管中流速大产生水击，流速小泥沙 淤积。 (2) 管道经济效益：管径小，造价低，但流速大，水头 损失也大，抽水耗费也增加。反之管径大，流速小，水头 损失减少，运转费用少，但管道造价高。 当根据技术要求确定流速后管 4Q d 道直径即可由右式计算： v 18
水利工程的有压输水管道水流一般属于紊流的水力粗糙
区，其水头损失可直接按谢齐公式计算，用 8 g 2
H 8g l v 8gl Q2 Q l 2 2 2 2 2 C d 2 g C 4R 2 gA AC R
2 2
C
则
令 K AC R ，即得
Q2 H hf 2 l K
或
QK
23
4-3 简单管道水力计算特例—— 虹吸管及水泵装置的水力计算
一、虹吸管的水力计算
虹吸管是一种压 力输水管道，其顶 部高程高于上游供 水水面。 特点：顶部真空理 论上不能大于10m H2g，一般其真空 值小于(7~8m )；虹 吸管长度一般不大，应按短管计算。
水力学教程 第5章
第五章孔口、管嘴出流和有压管流从本章开始，将在前面各章的理论基础上，具体研究各类典型流动。
孔口、管嘴出流和有压管流就是水力学基本理论的应用。
容器壁上开孔，水经孔口流出的水力现象称为孔口出流(Orifice Flow)；在孔口上连接长为3～4倍孔径的短管，水经过短管并在出口断面满管流出的水力现象称为管嘴出流(Spout Flow)；水沿管道满管流动的水力现象称为有压管流(Flow in Pressure Conduits)。
给排水工程中各类取水、泄水闸孔，以及某些量测流量设备均属孔口；水流经过路基下的有压涵管、水坝中泄水管等水力现象与管嘴出流类似，此外，还有消防水枪和水力机械化施工用水枪都是管嘴的应用；有压管道则是一切生产、生活输水系统的重要组成部分。
孔口、管嘴出流和有压管流的水力计算，是连续性方程、能量方程以及流动阻力和水头损失规律的具体应用。
§5-1 液体经薄壁孔口的恒定出流在容器壁上开一孔口，若孔壁的厚度对水流现象没有影响，孔壁与水流仅在一条周线上接触，这种孔口称为薄壁孔口，如图5-1-1所示。
图5-1-1一般说，孔口上下缘在水面下深度不同，经过孔口上部和下部的出流情况也不相同。
但是，当孔口直径d(或开度e)与孔口形心以上的水头高H相比较很小时，就认为孔口断面上各点水头相等，而忽略其差异。
因此，根据d/H的比值大小将孔口分为大孔口与小孔口两类：若d ≤H /10，这种孔口称为小孔口，可认为孔口断面上各点的水头都相等。
若d ≥H /10，称为大孔口。
当孔口出流时，水箱中水量如能得到源源不断的补充，从而使孔口的水头H 不变，这种情况称为恒定出流。
本节将着重讨论薄壁小孔口恒定出流。
1．小孔口的自由出流从孔口流出的水流进入大气，称自由出流(Free Efflux)，如图5-1-1所示，箱中水流的流线从各个方向趋近孔口，由于水流运动的惯性，流线不能成折角地改变方向，只能光滑、连续地弯曲，因此在孔口断面上各流线并不平行，使水流在出孔后继续收缩，直至距孔口约为d /2处收缩完毕，形成断面最小的收缩断面，流线在此趋于平行，然后扩散，如图5-1-1所示的c -c 断面称为孔口出流的收缩断面。
水力学第五章第五节资料
流速的脉动强度 x方向的流速脉动强度 y方向的流速脉动强度
紊动强度 x方向的紊动强度
y 方向的紊动强度
u'2
u '2 x
u '2 y
T uv
T x uv
T y
u
v
明渠中靠近水 面附近水流紊动强度 最弱，靠近渠底附近 紊动最大。
原因：靠近渠道 处流速梯度和切应力 比较大，壁面粗糙度 干扰的影响也较强， 因而靠近渠底的地方， 涡体最容易形成。
r 0.5 r0 0.6
0.7 0.8 0.9 1.0
0.0
切应力 紊流切应力
粘性切应力
τt
η dux dτyt
η dux
dy
0.5
1.0
1.5
τt
ητddt uyx η
dux dy
5.5.2 紊流的特征与处理方法 p p( t )
运动要素的脉动 运动要素的时均化处理
p 1 T pdt T0 p' ( t ) p( t ) p
显然：
ux'
ux
ux
5
10
15
20
t/ s
u x
'
u x
(t)
ux
u' x
u (t) x
ux＝ux (t)
u x＝ux
u x＝0
恒定流：任何运动要素均与时间无关的流动 ux ＝ u y ＝ uz ＝ p ... 0
t t t t t
引入层流和紊流概念 恒定流可更全面地定义为：
运动要素时均值与时间无关的流动
5.5 紊流运动
5.5.1 紊流的产生
5.5.2 紊流的特征与处理方法
运动要素的脉动 运动要素的时均化处理
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
整个管道单位重量流体能量损失
hw hf hj hw的量纲为长度 亦称水头损失
9
第5章 管流损失和水力计算5.2 粘性Fra bibliotek体的两种流动状态
10
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行实验，提 出了流体运动存在两种型态：层流和紊流。
R层e 流2000 R紊e 流2000
21
第5章 管流损失和水力计算
【例5-1】水在内径d=100mm的管中流动，流速v=0.5m/s，水的运动粘
度ν=1×10-6m2/s。试问水在管中呈何种流动状态？倘若管中的流体是 油，流速不变，但运动粘度ν’=31×10-6m2/s。试问油在管中又呈何种
当 Re R时e，cr 流动为紊流。 当 Recr Re时 ，Re可cr 能是层流或紊流，处于极不稳定状态。
20
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
上临界雷诺数在工程上没有实用意义 把下临界雷诺数Recr作为判别层流和紊流的准则 对于工业管道，一般取圆管的临界雷诺数 Recr 2000
6
第5章 管流损失和水力计算
5.1.1 沿程能量损失
单位重量流体的沿程损失
hf
L d
v2 2g
达西－魏斯巴赫公式
λ——沿程损失系数，与流体的粘度、流速、管道内径以及管壁粗糙 度等有关；
L ——管道长度； v2/2g ——单位重量流体的动压头（速度水头）。
7
第5章 管流损失和水力计算
5.1.2 局部能量损失
本章重点
沿程阻力（水头）损失计算 局部阻力（水头）损失计算
4
第5章 管流损失和水力计算
5.1 粘性流体管内流动的能量损失
5
第5章 管流损失和水力计算 5.1.1 沿程能量损失
简称沿程损失
是发生在缓变流整个流程中的能量损失 是由流体的粘滞力造成的损失 这种损失的大小与流体的流动状态有着密切的关系
过渡流
13
第5章 管流损失和水力计算 雷诺实验
水的流速增大到一定数值
振荡的流束突然破裂，在进口段的一定距离内完全消失，与周 围的流体混合。
流体质点作复杂的无规则运动。
紊流（湍流）
14
第5章 管流损失和水力计算 雷诺实验
由层流过渡到紊流的速度极限值称为上临界速度 vc。r
继续增大流速，进一步增加流动的紊乱程度。 管内流速自高于上临界速度逐渐降低，当速度降低到比上临界速
雷诺数是判别流体流动状态的准则数 Re vd vd
Recr
vcr d
vcr d
19
第5章 管流损失和水力计算
5.2 粘性流体的两种流动状态
不论流体的性质和管径如何变化，下临界雷诺数 Recr ,2上32临0 界
雷诺数
Re，cr 甚1至38更00高。
当 Re R时e，cr 流动为层流。
实验条件：液面高度恒定 水温恒定
11
第5章 管流损失和水力计算 雷诺实验
当水流速较低时
明晰的细小着色流束
不与周围的水混合 管内的整个流场呈一簇互相平行的流线
层流
12
第5章 管流损失和水力计算 雷诺实验
水的流速逐渐增大
开始时着色流束仍呈清晰的细线。 流速增大到一定数值，着色流束开始振荡，处于不稳定状态。
2
第5章 管流损失和水力计算
在同样的通道中流动的理想流体和粘性流体，它们沿截面的速度分布 是不同的。
对于流速分布不均匀的粘性流体，在流动的垂直方向上出现速度梯度， 在相对运动着的流层之间必定存在切向应力，形成阻力。
要克服阻力，维持粘性流体的流动，就要消耗机械能，并不可逆地转 化为热能。
3
第5章 管流损失和水力计算
起始状态和有无扰动等因素有关。
16
第5章 管流损失和水力计算 雷诺实验
雷诺在观察现象的同时，测量hf和v。 并绘制hf - v（或hf - lgv）的关系曲线。
17
雷诺实验
第5章 管流损失和水力计算
沿程损失与流动状态有关
流速由低到高升高时 OABCD 流速由高到低降低时 DCAO
lg hf lg k n lg v hf kvn
度更低的下临界速度 vcr (vcr 时v，cr )原先处于紊流状态的流动便会稳
定地转变为层流状态。
15
第5章 管流损失和水力计算 雷诺实验
粘性流体存在两种流动状态——层流和紊流
当流速超过上临界速度 vc时r ，层流转变为紊流。 当流速低于下临界速度 vc时r ，紊流转变为层流。 当流速介于 vc、r v之cr 间时，流动可能是层流或紊流，与实验的
k、n由实验确定
v vcr n 1 v vcr n 1.75 ~ 2
18
第5章 管流损失和水力计算
5.2 粘性流体的两种流动状态
靠临界流速来判别流体的流动状态和整理实验资料很不方便。
因为随着流体的粘度、密度以及流道线性尺寸的不同，临界流速也不 同。
要保证在粘滞力作用下的流动相似，两流动的雷诺数必须相等。
第5章 管流损失和水力计算
第5 章 管流损失和水力计算
1
第5章 管流损失和水力计算
实际流体都是有粘性的。 粘性流体流经固体壁面时，紧贴固体壁面的流体质点将粘附在固体壁
面上，它们之间的相对速度等于零，这一点与理想流体不同。 既然质点要粘附在固体壁面上，在固体壁面和流体的主流之间必定有
一个由固体壁面的速度过渡到主流速度的流速变化区域；倘若固体壁 面是静止不动的，则要有一个由零到主流速度的流速变化区域。
简称局部损失
是发生在流动状态急剧变化的急变流中的能量损失。 是在管件附近的局部范围内主要由流体速度分布急剧变化、流体微团
的碰撞、流体中产生的漩涡等造成的损失。
管道流动单位重量流体的局部能量损失
hj
v2 2g
ζ——局部损失系数，是一个零量纲系数，由实验确定。
8
第5章 管流损失和水力计算 5.1 粘性流体管内流动的能量损失
本章内容
5.1 粘性流体管内流动的能量损失 5.2 粘性流体的两种流动状态 5.3 管道进口段中粘性流体的流动 5.4 圆管中粘性流体的层流流动 5.5 粘性流体的紊流流动 5.6 沿程损失的实验研究 5.7 非圆形管道沿程损失的计算 5.8 局部损失 5.9 管道流动的水力计算 5.10 几种常用的技术装置 5.11 液体出流
hw hf hj hw的量纲为长度 亦称水头损失
9
第5章 管流损失和水力计算5.2 粘性Fra bibliotek体的两种流动状态
10
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行实验，提 出了流体运动存在两种型态：层流和紊流。
R层e 流2000 R紊e 流2000
21
第5章 管流损失和水力计算
【例5-1】水在内径d=100mm的管中流动，流速v=0.5m/s，水的运动粘
度ν=1×10-6m2/s。试问水在管中呈何种流动状态？倘若管中的流体是 油，流速不变，但运动粘度ν’=31×10-6m2/s。试问油在管中又呈何种
当 Re R时e，cr 流动为紊流。 当 Recr Re时 ，Re可cr 能是层流或紊流，处于极不稳定状态。
20
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
上临界雷诺数在工程上没有实用意义 把下临界雷诺数Recr作为判别层流和紊流的准则 对于工业管道，一般取圆管的临界雷诺数 Recr 2000
6
第5章 管流损失和水力计算
5.1.1 沿程能量损失
单位重量流体的沿程损失
hf
L d
v2 2g
达西－魏斯巴赫公式
λ——沿程损失系数，与流体的粘度、流速、管道内径以及管壁粗糙 度等有关；
L ——管道长度； v2/2g ——单位重量流体的动压头（速度水头）。
7
第5章 管流损失和水力计算
5.1.2 局部能量损失
本章重点
沿程阻力（水头）损失计算 局部阻力（水头）损失计算
4
第5章 管流损失和水力计算
5.1 粘性流体管内流动的能量损失
5
第5章 管流损失和水力计算 5.1.1 沿程能量损失
简称沿程损失
是发生在缓变流整个流程中的能量损失 是由流体的粘滞力造成的损失 这种损失的大小与流体的流动状态有着密切的关系
过渡流
13
第5章 管流损失和水力计算 雷诺实验
水的流速增大到一定数值
振荡的流束突然破裂，在进口段的一定距离内完全消失，与周 围的流体混合。
流体质点作复杂的无规则运动。
紊流（湍流）
14
第5章 管流损失和水力计算 雷诺实验
由层流过渡到紊流的速度极限值称为上临界速度 vc。r
继续增大流速，进一步增加流动的紊乱程度。 管内流速自高于上临界速度逐渐降低，当速度降低到比上临界速
雷诺数是判别流体流动状态的准则数 Re vd vd
Recr
vcr d
vcr d
19
第5章 管流损失和水力计算
5.2 粘性流体的两种流动状态
不论流体的性质和管径如何变化，下临界雷诺数 Recr ,2上32临0 界
雷诺数
Re，cr 甚1至38更00高。
当 Re R时e，cr 流动为层流。
实验条件：液面高度恒定 水温恒定
11
第5章 管流损失和水力计算 雷诺实验
当水流速较低时
明晰的细小着色流束
不与周围的水混合 管内的整个流场呈一簇互相平行的流线
层流
12
第5章 管流损失和水力计算 雷诺实验
水的流速逐渐增大
开始时着色流束仍呈清晰的细线。 流速增大到一定数值，着色流束开始振荡，处于不稳定状态。
2
第5章 管流损失和水力计算
在同样的通道中流动的理想流体和粘性流体，它们沿截面的速度分布 是不同的。
对于流速分布不均匀的粘性流体，在流动的垂直方向上出现速度梯度， 在相对运动着的流层之间必定存在切向应力，形成阻力。
要克服阻力，维持粘性流体的流动，就要消耗机械能，并不可逆地转 化为热能。
3
第5章 管流损失和水力计算
起始状态和有无扰动等因素有关。
16
第5章 管流损失和水力计算 雷诺实验
雷诺在观察现象的同时，测量hf和v。 并绘制hf - v（或hf - lgv）的关系曲线。
17
雷诺实验
第5章 管流损失和水力计算
沿程损失与流动状态有关
流速由低到高升高时 OABCD 流速由高到低降低时 DCAO
lg hf lg k n lg v hf kvn
度更低的下临界速度 vcr (vcr 时v，cr )原先处于紊流状态的流动便会稳
定地转变为层流状态。
15
第5章 管流损失和水力计算 雷诺实验
粘性流体存在两种流动状态——层流和紊流
当流速超过上临界速度 vc时r ，层流转变为紊流。 当流速低于下临界速度 vc时r ，紊流转变为层流。 当流速介于 vc、r v之cr 间时，流动可能是层流或紊流，与实验的
k、n由实验确定
v vcr n 1 v vcr n 1.75 ~ 2
18
第5章 管流损失和水力计算
5.2 粘性流体的两种流动状态
靠临界流速来判别流体的流动状态和整理实验资料很不方便。
因为随着流体的粘度、密度以及流道线性尺寸的不同，临界流速也不 同。
要保证在粘滞力作用下的流动相似，两流动的雷诺数必须相等。
第5章 管流损失和水力计算
第5 章 管流损失和水力计算
1
第5章 管流损失和水力计算
实际流体都是有粘性的。 粘性流体流经固体壁面时，紧贴固体壁面的流体质点将粘附在固体壁
面上，它们之间的相对速度等于零，这一点与理想流体不同。 既然质点要粘附在固体壁面上，在固体壁面和流体的主流之间必定有
一个由固体壁面的速度过渡到主流速度的流速变化区域；倘若固体壁 面是静止不动的，则要有一个由零到主流速度的流速变化区域。
简称局部损失
是发生在流动状态急剧变化的急变流中的能量损失。 是在管件附近的局部范围内主要由流体速度分布急剧变化、流体微团
的碰撞、流体中产生的漩涡等造成的损失。
管道流动单位重量流体的局部能量损失
hj
v2 2g
ζ——局部损失系数，是一个零量纲系数，由实验确定。
8
第5章 管流损失和水力计算 5.1 粘性流体管内流动的能量损失
本章内容
5.1 粘性流体管内流动的能量损失 5.2 粘性流体的两种流动状态 5.3 管道进口段中粘性流体的流动 5.4 圆管中粘性流体的层流流动 5.5 粘性流体的紊流流动 5.6 沿程损失的实验研究 5.7 非圆形管道沿程损失的计算 5.8 局部损失 5.9 管道流动的水力计算 5.10 几种常用的技术装置 5.11 液体出流