水力学第五章第五节资料
合集下载
水力学课件第五章

水头损失的叠加原理
总水头损失:hw=hf+ hm
工程上为了便于计算,假定沿程水头损失和局部水头损失时 单独发生作用的,互不影响,两者可以叠加。 注意: (1)局部水头损失实际上是在一定长度内发生的,为了 处理方便工程上把局部水头损失发生的地点认为是集中发生 在边界突变的断面上。 (2)把实际发生局部水头损失的流程中的沿程水头损失, 看作是未受局部水头损失而单独发生的。 (3)若两局部水头损失距离很近,用叠加法计算出的局部 水头损失会偏大,应作为整体进行试验确定hj。 (4)通常以流速水头的某一倍数表示水头损失。
2 pA umax pB 0 解: 1、求流量: 2g 2g 2 umax pB p A 汞 油 hp 2g 油
u max 19.6 2.35m / s
133.28 8.83 0.02 8.83
1 2
假设重油的流动为层流: u max 1.175 m / s
z1
O
1
G
O
P1
1
0 0
2
P2
2
z1 O
1
G
z2 x O
作用于该总流流段上的外力有: ①动水压力: P1=p1A P2=p2A ②重力:G=V= AL,在流动方向上的投影 Gx=ALsin ③摩擦阻力:T=0A'= 0 L
P
1
1
写出管轴方向的平衡方程: z 1
0 0
液体形态的判别:
雷诺从一系列试验中发现: 1)不同种类液体在相同直径的管中进行实验,所测得的临界 速度是各不相同的; 2)同种液体在不同直径的管中实验,所得的临界速度也不同。 故判定临界速度是液体的物理性质( , )和管径( d )的函 数。
水力学第5章资料

整个管道单位重量流体能量损失
hw hf hj hw的量纲为长度 亦称水头损失
9
第5章 管流损失和水力计算5.2 粘性Fra bibliotek体的两种流动状态
10
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行实验,提 出了流体运动存在两种型态:层流和紊流。
R层e 流2000 R紊e 流2000
21
第5章 管流损失和水力计算
【例5-1】水在内径d=100mm的管中流动,流速v=0.5m/s,水的运动粘
度ν=1×10-6m2/s。试问水在管中呈何种流动状态?倘若管中的流体是 油,流速不变,但运动粘度ν’=31×10-6m2/s。试问油在管中又呈何种
当 Re R时e,cr 流动为紊流。 当 Recr Re时 ,Re可cr 能是层流或紊流,处于极不稳定状态。
20
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
上临界雷诺数在工程上没有实用意义 把下临界雷诺数Recr作为判别层流和紊流的准则 对于工业管道,一般取圆管的临界雷诺数 Recr 2000
6
第5章 管流损失和水力计算
5.1.1 沿程能量损失
单位重量流体的沿程损失
hf
L d
v2 2g
达西-魏斯巴赫公式
λ——沿程损失系数,与流体的粘度、流速、管道内径以及管壁粗糙 度等有关;
L ——管道长度; v2/2g ——单位重量流体的动压头(速度水头)。
7
第5章 管流损失和水力计算
5.1.2 局部能量损失
本章重点
沿程阻力(水头)损失计算 局部阻力(水头)损失计算
4
第5章 管流损失和水力计算
hw hf hj hw的量纲为长度 亦称水头损失
9
第5章 管流损失和水力计算5.2 粘性Fra bibliotek体的两种流动状态
10
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
雷诺实验
1883年英国物理学家雷诺按图示试验装置对粘性流体进行实验,提 出了流体运动存在两种型态:层流和紊流。
R层e 流2000 R紊e 流2000
21
第5章 管流损失和水力计算
【例5-1】水在内径d=100mm的管中流动,流速v=0.5m/s,水的运动粘
度ν=1×10-6m2/s。试问水在管中呈何种流动状态?倘若管中的流体是 油,流速不变,但运动粘度ν’=31×10-6m2/s。试问油在管中又呈何种
当 Re R时e,cr 流动为紊流。 当 Recr Re时 ,Re可cr 能是层流或紊流,处于极不稳定状态。
20
第5章 管流损失和水力计算 5.2 粘性流体的两种流动状态
上临界雷诺数在工程上没有实用意义 把下临界雷诺数Recr作为判别层流和紊流的准则 对于工业管道,一般取圆管的临界雷诺数 Recr 2000
6
第5章 管流损失和水力计算
5.1.1 沿程能量损失
单位重量流体的沿程损失
hf
L d
v2 2g
达西-魏斯巴赫公式
λ——沿程损失系数,与流体的粘度、流速、管道内径以及管壁粗糙 度等有关;
L ——管道长度; v2/2g ——单位重量流体的动压头(速度水头)。
7
第5章 管流损失和水力计算
5.1.2 局部能量损失
本章重点
沿程阻力(水头)损失计算 局部阻力(水头)损失计算
4
第5章 管流损失和水力计算
流体力学 水力学 第五章

7 H [H0 ] 9m 0.75
§5.3 有压管道恒定流 5.3.1 短管水力计算(Q、d、H) 有压流:水沿管道满管流动的水力现象。 特点:水流充满管道过水断面,管道内不存在自 由水面,管壁上各点承受的压强一般不等于大 气压强。
短管:局部水头损失和 速度水头在总水头损失 中占有相当的比重,计 算时不能忽略的管道. (一般局部损失和速度 水头大于沿程损失 的5% ~ 10%)。一般L/d 1000
1 vc c 0
v
2 0 0
2 gH 0 2 gH 0
v hw h j 2g p c pa
2 c
1 1 流速系数: c 0 1 0
1 1 流速系数: c 0 1 0
实验得: 0.97 ~ 0.98 1 推求: 0 2 1 1 0.06 2 0.97 1
2
d2
5.126m 2g
例5 3:如图所示圆形有压涵管,管长50m, 上下游水位差3m 沿程阻力系数为0.03,局部阻力系数:进口 1=0.5。 第一个转弯 2=0.71,第二个转弯 3=0.65,出口
4=1.0,要求涵管通过流量大约3m 3 / s, 试设计管径d。
2 1 1
2g
v
v
2 2 2
2 2 2
2g
hw
2g
hw
H0 H
v
2 1 1
2g
v
2 2 2
2g
hw
hw h f h j (
l v
v d 2g 2g
2
2
l
v ) d 2g
第五章水力学详解

μc =
1
α
+
∑
λ
l d
+
∑
ζ
两公式的比较。
μc =
1
∑
λ
l d
+
∑ζ
§5-4 短管出流的水力计算
1
1
自由出流
O 1
2 H 淹没出流
O 2
1
Z
O
2 O
2
μc =
1
α
+
∑
λ
l d
+
∑ζ
两公式的比较。
μc =
1
∑
λ
l d
+
∑ζ
自由出流的作用水头一部分消耗于水流的沿程水头损失和 局部损失,另一部分转化为管道出口的流速水头。
+ hw
得
H0
=
H1
−
H2
=
H
=
hw
=ξ′
vc2 2g
因为 ζ ′ = ζ 0 + ζ se = ζ 0 +1
vc =
1
1+ζc
2gH = ϕ 2gH
Q = ϕε A 2gH = μ A 2gH
与自由出流的公式进行比较:
流量公式虽然与薄壁孔口出流相同, 但意义不一样。 孔口淹没出流的流量和流速与孔口 离液面的距离无关。
管嘴出流的局部损失由两部分组成,即孔口的局部水头损失 及收缩断面后扩展产生的局部损失,水头损失大于孔口出流。但 是管嘴出流为满流,收缩系数为1,因此流量系数仍比孔口大。
§5-2 液体经管嘴的恒定出流
v=
1
α +ζc
2gH0 = ϕn A 2gH
PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界

水力学讲义
诚础伪经攒戎撒荒肛窝廉雹缆拥硅皂戎酝贯摹金术苞玄充诅溅哮漏乔划赢PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 5.5 明渠均匀流的水力计算 一、验算渠道的输水能力 对已成渠道进行校核性的水力计算,特别是验算渠道的输水能力。即已知:n,i,b,h 确定Q ; 直接用公式:
第五章 明渠恒定均匀流 5.1 明渠的类型及其对水流运动的影响 明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 ),是水流边界的几何条件。一定形式的边界几何条件,给予水流运动一定的影响。所以为了了解水流运动的特征,必须先对影响明渠水流运动的边界几何条件进行分析。
水力学讲义
粉天删鲸般匪疹腥翘渐由助舞闷咋钥叔夏藩嗣跨伸揉汞辣准椰妈书斌邀蝶PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 一、明渠的横断面 人工明渠的横断面,通常作成对称的几何形状。例如常见的梯形、矩形或圆形等。至于河道的横断面,则常呈不规则的形状。 而根据渠道的断面形状、尺寸,就可以计算渠道过水断面的水利要素。
水力学讲义
旭系笔肝淆十习僵睦骤藏掠海躺察湃青卒遥袋招膨驴治聋拘酌哟抗症碗笼PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 工程中应用最广的是梯形渠道,其过水断面的诸水利要素关系如下: 水面宽度: B=b+2mh 过水断面面积: A=(b+mh)h 湿周: 水力半径:
水力学讲义
路努吨赶羹兄操缠捕砖粒链想口勃函苍蓝巷简悟积瓶店罚窒欣湃侠侥焚连PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
诚础伪经攒戎撒荒肛窝廉雹缆拥硅皂戎酝贯摹金术苞玄充诅溅哮漏乔划赢PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 5.5 明渠均匀流的水力计算 一、验算渠道的输水能力 对已成渠道进行校核性的水力计算,特别是验算渠道的输水能力。即已知:n,i,b,h 确定Q ; 直接用公式:
第五章 明渠恒定均匀流 5.1 明渠的类型及其对水流运动的影响 明渠的渠身及其沿流动方向的倾斜程度( 称作底坡 ),是水流边界的几何条件。一定形式的边界几何条件,给予水流运动一定的影响。所以为了了解水流运动的特征,必须先对影响明渠水流运动的边界几何条件进行分析。
水力学讲义
粉天删鲸般匪疹腥翘渐由助舞闷咋钥叔夏藩嗣跨伸揉汞辣准椰妈书斌邀蝶PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 一、明渠的横断面 人工明渠的横断面,通常作成对称的几何形状。例如常见的梯形、矩形或圆形等。至于河道的横断面,则常呈不规则的形状。 而根据渠道的断面形状、尺寸,就可以计算渠道过水断面的水利要素。
水力学讲义
旭系笔肝淆十习僵睦骤藏掠海躺察湃青卒遥袋招膨驴治聋拘酌哟抗症碗笼PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
第五章 明渠恒定均匀流 工程中应用最广的是梯形渠道,其过水断面的诸水利要素关系如下: 水面宽度: B=b+2mh 过水断面面积: A=(b+mh)h 湿周: 水力半径:
水力学讲义
路努吨赶羹兄操缠捕砖粒链想口勃函苍蓝巷简悟积瓶店罚窒欣湃侠侥焚连PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界PPT-第五章明渠恒定均匀流明渠水流在水利工程中或是在自然界
长管--《水力学》第五章

1. 简单管225282)24(2122alQ lQ d g d Q g d l gv d l f h H =====πλπλλ a ——比阻,528d g a πλ=,多查表取用。
流速较大时(阻力平方区),管道一定,a 为常数,即a 和管径、管材对应。
利用谢才公式和曼宁公式可进行比阻a 和糙率n 的互化。
流速较小时(水力光滑区或水力过渡区),还需考虑流速对它的影响。
2. 串联管1++=i Q i q i Q 22i Q i S i Q i l i a fih ==S i ——阻抗。
22i Q i l i a i Q i S fih H ∑∑∑===3. 并联管54321244423332222432Q B q Q Q Q A q Q Q l a Q l a Q l a f h f h f h +=+++=====4. 沿程均匀泄流管泄流总流量Q t ,取x 处dx 长管段,认为其流量Q x 不变,即t Q l xz Q x Q )1(-+=dx t Q l x z Q a dx x aQ f dh 2])1([2-+==整个管段视为由无数微小管段串联,总水头损失 ⎰⎰-+==l dx t Q lx z Q a l f dh f h 02])1([0 若管径和粗糙一定,流动处于阻力平方区,则)2312(tQ t Q z Q z Q al f h ++= 5.管网树状网、环状网计算类型:1. 设计计算已知管路布置、节点用水量和最小自由水头要求,求管径和作用水头。
∑==w h H v Qd π4满足流速要求(经济流速),以此确定管径。
结果不一定唯一。
2.复核计算已知管路布置、用水量、管径和作用水头,复核节点水压是否满足要求。
详见例题。
水力学第五章
第五章
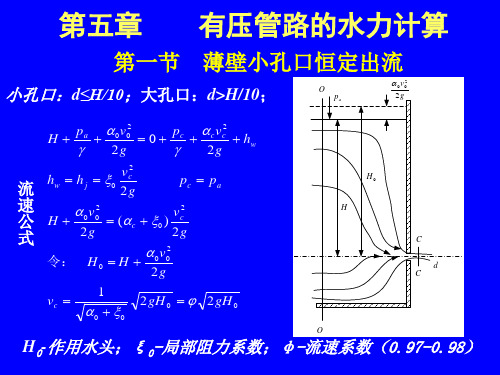
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
有压管路的水力计算
O
2 0 v0
第一节 薄壁小孔口恒定出流
小孔口:d≤H/10;大孔口:d>H/10;
H pa
pa
2g
2 0 v0
2g
0
pc
2 c vc
2g
hw
H0
流 2 2 速 0 v0 vc ( c 0 ) 公 H 2g 2g 式 2
令: H 0 H vc 1 0 0
2 vc hw h j 0 2g
pc pa
H
0 v0
2g
C d
C
2 gH 0 2 gH 0
O
H0-作用水头;ξ 0-局部阻力系数;φ -流速系数(0.97-0.98)
流量公式:
Q v c Ac A
2 gH 0 A 2 gH 0
0.62
0.64
复杂管路都可以分解为:串联管路和并联管路两种。
hf1 hf 2 hf 3
H
q1
q2
l1 d1 Q1
l 2 d 2 Q2
l3 d 3 Q3
串联管路:总水头损失等于各分段水头损失之和;无奇点(流进、 流出)情况下,总流量等于各分流量。
H
h fi
i 1
n
i
n
Ai li Qi2
Q Qi
C
b
hc bw cb pa pc
O
1 2 2 ( 1) 2 n H0 将 1, 0.64, n 0.82 pa pc
pcv
0.756 H 0
水力学第五讲
2
1 t +T 2 ∫t −T 2 u′yu′x dt = ρ u′xu′y T
du 2 y ) ,圆管 l = βy 1 − 为混合长度, β 为卡门常数。 为混合长度, 为卡门常数。 dy r0
紊流切应力为 τ = τ 1 + τ 2 =
µ
du du + ρl 2 ( ) 2 , 略去平均符号) (略去平均符号 。 (略去平均符号) dy dy
一、层流区 二、临界过渡区 三、紊流光滑区 四、紊流过渡区 五、紊流粗糙区(阻力平方区) 紊流粗糙区(阻力平方区)
λ = f1 (Re) λ = f 2 (Re)
λ = f 3 (Re)
λ = f 4 (Re, ∆ d )
λ = f 5 (∆ d )
§5-5 紊流沿程阻力系数 • 2紊流沿程阻力系数的计算公式 紊流沿程阻力系数的计算公式 • 阻力系数半理论公式
第五章
• • • •
流动阻力和能量损失
本章要解决能量方程中的能量损失问题 流动形态的区分 流动阻力的成因 能量损失的分类
§5-1两种流态和判别标准 两种流态和判别标准 • 1雷诺实验和两种流态 雷诺实验和两种流态 • 雷诺实验装置(区分层流与紊流,上、下临界流速) 雷诺实验装置(区分层流与紊流, 下临界流速) • 层流与紊流的分界是下临界流速
注意到剪切应力与圆管半径的关系 应力分布) 注意到剪切应力与圆管半径的关系 τ τ 0 = r r0 (应力分布) 剪切应力与 将达西公式的能量损失代入剪切应力式 τ 0 = ρv 2 达西公式的能量损失代 剪切应力式 公式 8 1 1 1 v2 λ 2 τ 0 = ρgr0 J = ρgr0 λ = ρv 2 2 d 2g 8
Q = 平均流速: 平均流速: v = A
1 t +T 2 ∫t −T 2 u′yu′x dt = ρ u′xu′y T
du 2 y ) ,圆管 l = βy 1 − 为混合长度, β 为卡门常数。 为混合长度, 为卡门常数。 dy r0
紊流切应力为 τ = τ 1 + τ 2 =
µ
du du + ρl 2 ( ) 2 , 略去平均符号) (略去平均符号 。 (略去平均符号) dy dy
一、层流区 二、临界过渡区 三、紊流光滑区 四、紊流过渡区 五、紊流粗糙区(阻力平方区) 紊流粗糙区(阻力平方区)
λ = f1 (Re) λ = f 2 (Re)
λ = f 3 (Re)
λ = f 4 (Re, ∆ d )
λ = f 5 (∆ d )
§5-5 紊流沿程阻力系数 • 2紊流沿程阻力系数的计算公式 紊流沿程阻力系数的计算公式 • 阻力系数半理论公式
第五章
• • • •
流动阻力和能量损失
本章要解决能量方程中的能量损失问题 流动形态的区分 流动阻力的成因 能量损失的分类
§5-1两种流态和判别标准 两种流态和判别标准 • 1雷诺实验和两种流态 雷诺实验和两种流态 • 雷诺实验装置(区分层流与紊流,上、下临界流速) 雷诺实验装置(区分层流与紊流, 下临界流速) • 层流与紊流的分界是下临界流速
注意到剪切应力与圆管半径的关系 应力分布) 注意到剪切应力与圆管半径的关系 τ τ 0 = r r0 (应力分布) 剪切应力与 将达西公式的能量损失代入剪切应力式 τ 0 = ρv 2 达西公式的能量损失代 剪切应力式 公式 8 1 1 1 v2 λ 2 τ 0 = ρgr0 J = ρgr0 λ = ρv 2 2 d 2g 8
Q = 平均流速: 平均流速: v = A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.0
自由水面(管心) 0.9
0.8
Tux
0.7
Tuy
0.6
0.5
0.4
0.3
0.2
0.1
0.0 0.00
0.05
0.10
0.15
T ux ,T uy
明渠水流紊流强度的试验曲线
5.5.3 紊流产生附加切应力
紊流切应力 层流中的切应力可按照牛顿内摩擦定律计算,但紊 流则不可。紊流中各流层间除了有相对运动外,还有上 下层、质点横向交换。因此,紊流中流层间的切应力 应由两部分组成,即
紊流的基本特征是,流动中许多涡体在相互混掺的 运动。涡体位置、大小、流速等都在时刻变化。
因此,当一系列参差不齐的涡体连续通过空间某一 给位置时,反映出这一定点的运动要素(如流速、压强 等)发生随机脉动。
运动要素随时间发生随机脉动的现象叫做运动要素 的脉动。
5
4
3
2
p
1 0
-1
-2
-3 -4
NO.3 P1
流速的脉动强度 x方向的流速脉动强度 y方向的流速脉动强度
紊动强度 x方向的紊动强度
y 方向的紊动强度
u'2
u '2 x
u '2 y
T uv
T x uv
T y
u
v
明渠中靠近水 面附近水流紊动强度 最弱,靠近渠底附近 紊动最大。
原因:靠近渠道 处流速梯度和切应力 比较大,壁面粗糙度 干扰的影响也较强, 因而靠近渠底的地方, 涡体最容易形成。
时均流速产生的粘滞切应力
τ τ 1 τ 2 τ 1 μ dux
dy
脉动流速产生的附加切应力
用牛顿内摩擦定律和时均流速梯度计算粘性切应力 1
用普朗特动量传递理论推导紊流切应力 2
在液流中取一个垂直于y 轴上的微小截面dAy
y
y
ux’
b层
dAy
dAy
u(y) ΔF
uy’
a层
ux’
b层
dAy
ΔF
u x
=
u y
=
u z
=
p
...
0
t t t t t
非恒定流 运动要素的时均值随时间发生变化的流动
u
u’ uu
t 非恒定流时均值随时间变化
p (utx)/c/(mk/Ns. m - 2 )
1000
900
800
700 600
ux'
500
400
300
200
ux
ux
100
Hale Waihona Puke 00510
15
20
t/ s
恒定流时均值随时间变化
uy’ a层
若a 层有一质点以横向脉动
流速uy’ 通过该截面进 入b层,则在dt 时间内该截
面的质量为
m ρ uy' dAydt
ux’
dAy
ΔF
l1
uy’
b层 a层
假定液体质点在上下横向脉动距离l1 (称混合长 度)中瞬时流速保持不变,动量也保持不变,达到 新位置后,动量突然改变,与原位置上液体质点具 有的动量一致
1000
900
800
700 600
ux'
500
400
300
200
ux
ux
100
0
0
5
10
15
20
t/ s
脉动流速
u x
'
u x
(t)
ux
式中,脉动流速可正、可负
p (utx)/c/(mk/Ns. m - 2 )
1000 900 800 700 600 500 400 300 200 100
0 0
脉动流速
5 液流形态与水头损失
5.1 水头损失及其分类 5.2 均匀流沿程水头损失与水流阻力关系 5.3 流动的两种形态与雷诺实验 5.4 层流运动 5.5 紊流运动 5.6 紊流的沿程水头损失 5.7 局部水头损失
5.5 紊流运动
5.5.1 紊流的产生 5.5.2 紊流的特征
5.5.2 紊流的特征
运动要素的脉动
-5
0 25 50 75 100 125 150 175 200 225 250 275 300
5
4 3
t /s
NO.3 P2
2
1
0 -1
河床底部水流动水压强随时间的变化曲线
-2
-3
-4
-5
0 25 50 75 100 125 150 175 200 225 250 275 300
5
4
NO.3 P3
Fdt ρ ux' uy' dAydt
紊流切应力为
= F u ' u '
2 dA
x
y
u ' u '
2
x
y
下面将紊流切应力用时均流速来表达
5.5.2 紊流的特征与处理方法
运动要素的脉动
运动要素随时间发生随机脉动的现象
运动要素的时均化处理
5.5.2 紊流的特征与处理方法
运动要素的脉动 运动要素的时均化处理
运动要素可表示为
p p( t )
p 1 T pdt T0 p' ( t ) p( t ) p ...
研究运动要素脉动时,经常用到几个表示脉动强 度的物理量,现介绍如下:
ux’
dAy ΔF
uy’
b层 a层
m ρ uy' dAydt
到达b层时,立即具有一个x方向的脉动流速 ux’ dt 时间内 x方向的动量变化
(m)u ' u 'u 'dA dt
x
x
y
y
ux’
dAy ΔF
uy’
dt 时间内x方向的动量变化
b层
(m)u ' u 'u 'dA dt
x
x
y
y
a层
dt 时间内,截面dAy上产生的x方向冲量应等于动量变化
显然:
ux'
ux
ux
5
10
15
20
t/ s
u x
'
u x
(t)
ux
u' x
u (t) x
ux=ux (t)
u x=ux
u x=0
恒定流:任何运动要素均与时间无关的流动 ux = u y = uz = p ... 0
t t t t t
引入层流和紊流概念 恒定流可更全面地定义为:
运动要素时均值与时间无关的流动
3
p (utx)/c/(mk/Ns. m - 2 )
1000 900 800 700 600 500 400 300 200 100
0 0
瞬时流速
时均流速
ux'
ux
ux
5
10
15
20
t/ s
u u (t)
x
x
T
u x
(
t
)
d
t
u =0
x
T
式中, T 为较长的时段
p (utx)/c/(mk/Ns. m - 2 )
ux’
b层
dAy
ΔF
uy’ a层
m ρ uy' dAydt
到达b层时,立即具有一个x方向的脉动流速 ux’ dt 时间内 x 方向的动量变化为
(m)u ' u 'u 'dA dt
x
x
y
y
ux’
b层
dAy
ΔF
uy’ a层
dt 时间内 x 方向动量变化为
( m )ux' ux' u y' dAydt
y/h
自由液面(管心) 渠底(管 紊流壁)n
1.0
自由水面(管心) 0.9
0.8
Tux
0.7
Tuy
0.6
0.5
0.4
0.3
0.2
0.1
0.0 0.00
0.05
0.10
0.15
T ux ,T uy
明渠水流紊流强度实测曲线
现代量测技 术表明,临近渠底 的区域是涡体发源 地
y/h
自由液面(管心) 渠底(管 紊流壁)n
自由水面(管心) 0.9
0.8
Tux
0.7
Tuy
0.6
0.5
0.4
0.3
0.2
0.1
0.0 0.00
0.05
0.10
0.15
T ux ,T uy
明渠水流紊流强度的试验曲线
5.5.3 紊流产生附加切应力
紊流切应力 层流中的切应力可按照牛顿内摩擦定律计算,但紊 流则不可。紊流中各流层间除了有相对运动外,还有上 下层、质点横向交换。因此,紊流中流层间的切应力 应由两部分组成,即
紊流的基本特征是,流动中许多涡体在相互混掺的 运动。涡体位置、大小、流速等都在时刻变化。
因此,当一系列参差不齐的涡体连续通过空间某一 给位置时,反映出这一定点的运动要素(如流速、压强 等)发生随机脉动。
运动要素随时间发生随机脉动的现象叫做运动要素 的脉动。
5
4
3
2
p
1 0
-1
-2
-3 -4
NO.3 P1
流速的脉动强度 x方向的流速脉动强度 y方向的流速脉动强度
紊动强度 x方向的紊动强度
y 方向的紊动强度
u'2
u '2 x
u '2 y
T uv
T x uv
T y
u
v
明渠中靠近水 面附近水流紊动强度 最弱,靠近渠底附近 紊动最大。
原因:靠近渠道 处流速梯度和切应力 比较大,壁面粗糙度 干扰的影响也较强, 因而靠近渠底的地方, 涡体最容易形成。
时均流速产生的粘滞切应力
τ τ 1 τ 2 τ 1 μ dux
dy
脉动流速产生的附加切应力
用牛顿内摩擦定律和时均流速梯度计算粘性切应力 1
用普朗特动量传递理论推导紊流切应力 2
在液流中取一个垂直于y 轴上的微小截面dAy
y
y
ux’
b层
dAy
dAy
u(y) ΔF
uy’
a层
ux’
b层
dAy
ΔF
u x
=
u y
=
u z
=
p
...
0
t t t t t
非恒定流 运动要素的时均值随时间发生变化的流动
u
u’ uu
t 非恒定流时均值随时间变化
p (utx)/c/(mk/Ns. m - 2 )
1000
900
800
700 600
ux'
500
400
300
200
ux
ux
100
Hale Waihona Puke 00510
15
20
t/ s
恒定流时均值随时间变化
uy’ a层
若a 层有一质点以横向脉动
流速uy’ 通过该截面进 入b层,则在dt 时间内该截
面的质量为
m ρ uy' dAydt
ux’
dAy
ΔF
l1
uy’
b层 a层
假定液体质点在上下横向脉动距离l1 (称混合长 度)中瞬时流速保持不变,动量也保持不变,达到 新位置后,动量突然改变,与原位置上液体质点具 有的动量一致
1000
900
800
700 600
ux'
500
400
300
200
ux
ux
100
0
0
5
10
15
20
t/ s
脉动流速
u x
'
u x
(t)
ux
式中,脉动流速可正、可负
p (utx)/c/(mk/Ns. m - 2 )
1000 900 800 700 600 500 400 300 200 100
0 0
脉动流速
5 液流形态与水头损失
5.1 水头损失及其分类 5.2 均匀流沿程水头损失与水流阻力关系 5.3 流动的两种形态与雷诺实验 5.4 层流运动 5.5 紊流运动 5.6 紊流的沿程水头损失 5.7 局部水头损失
5.5 紊流运动
5.5.1 紊流的产生 5.5.2 紊流的特征
5.5.2 紊流的特征
运动要素的脉动
-5
0 25 50 75 100 125 150 175 200 225 250 275 300
5
4 3
t /s
NO.3 P2
2
1
0 -1
河床底部水流动水压强随时间的变化曲线
-2
-3
-4
-5
0 25 50 75 100 125 150 175 200 225 250 275 300
5
4
NO.3 P3
Fdt ρ ux' uy' dAydt
紊流切应力为
= F u ' u '
2 dA
x
y
u ' u '
2
x
y
下面将紊流切应力用时均流速来表达
5.5.2 紊流的特征与处理方法
运动要素的脉动
运动要素随时间发生随机脉动的现象
运动要素的时均化处理
5.5.2 紊流的特征与处理方法
运动要素的脉动 运动要素的时均化处理
运动要素可表示为
p p( t )
p 1 T pdt T0 p' ( t ) p( t ) p ...
研究运动要素脉动时,经常用到几个表示脉动强 度的物理量,现介绍如下:
ux’
dAy ΔF
uy’
b层 a层
m ρ uy' dAydt
到达b层时,立即具有一个x方向的脉动流速 ux’ dt 时间内 x方向的动量变化
(m)u ' u 'u 'dA dt
x
x
y
y
ux’
dAy ΔF
uy’
dt 时间内x方向的动量变化
b层
(m)u ' u 'u 'dA dt
x
x
y
y
a层
dt 时间内,截面dAy上产生的x方向冲量应等于动量变化
显然:
ux'
ux
ux
5
10
15
20
t/ s
u x
'
u x
(t)
ux
u' x
u (t) x
ux=ux (t)
u x=ux
u x=0
恒定流:任何运动要素均与时间无关的流动 ux = u y = uz = p ... 0
t t t t t
引入层流和紊流概念 恒定流可更全面地定义为:
运动要素时均值与时间无关的流动
3
p (utx)/c/(mk/Ns. m - 2 )
1000 900 800 700 600 500 400 300 200 100
0 0
瞬时流速
时均流速
ux'
ux
ux
5
10
15
20
t/ s
u u (t)
x
x
T
u x
(
t
)
d
t
u =0
x
T
式中, T 为较长的时段
p (utx)/c/(mk/Ns. m - 2 )
ux’
b层
dAy
ΔF
uy’ a层
m ρ uy' dAydt
到达b层时,立即具有一个x方向的脉动流速 ux’ dt 时间内 x 方向的动量变化为
(m)u ' u 'u 'dA dt
x
x
y
y
ux’
b层
dAy
ΔF
uy’ a层
dt 时间内 x 方向动量变化为
( m )ux' ux' u y' dAydt
y/h
自由液面(管心) 渠底(管 紊流壁)n
1.0
自由水面(管心) 0.9
0.8
Tux
0.7
Tuy
0.6
0.5
0.4
0.3
0.2
0.1
0.0 0.00
0.05
0.10
0.15
T ux ,T uy
明渠水流紊流强度实测曲线
现代量测技 术表明,临近渠底 的区域是涡体发源 地
y/h
自由液面(管心) 渠底(管 紊流壁)n
