在直角坐标系中xoy中,直线l交y轴于点M
中考数学专题《一次函数与几何综合》高分必刷原卷

(培优特训)专项19.3 一一次函数与几何综合高分必刷1.(2023春•普兰店区期中)已知△ABC中,∠C=90°,AC=3,CD=4,BD =AD.点F从点A出发,沿AC﹣CD运动,速度为1cm/s,同时点E从点B 出发,沿BD﹣DA运动,运动速度为1cm/s,一个点到达终点,另一点也停止运动.(1)求BD的长;(2)设△AEF的面积为S,点P、Q运动时间为t,求S与的函数关系式,并写出的取值范围.2.(2023春•鼓楼区期中)如图1,已知直线l1:y=ax﹣6a交x轴于点A,交轴y于点B,直线l2:y=bx﹣18a交x轴于点C,交y轴于点D,交直线l1于点E.(1)求点A的坐标;(2)若点B为线段AE的中点,求证:EC=EA;(3)如图2,已知P(0,m),将线段P A绕点P逆时针方向旋转90°至PF,连接OF,求证:点F在某条直线上运动,并求OF的最小值.3.(2023春•苍南县期中)如图,在平面直角坐标系中,▱OABC的顶点A落在x轴上,点B的坐标为(7,4),AB=2,点D是OC的中点,点E是线段AD上一动点,EF⊥BC于点F,连结DF.(1)求点A、C的坐标.(2)求直线AD的函数表达式.(3)若△DEF是等腰三角形,求CF的长.4.(2023•佳木斯一模)如图,将矩形纸片OABC放在平面直角坐标系中,O为坐标原点.点A在y轴上,点C在x轴上,OA,OB的长是x2﹣16x+60=0的两个根,P是边AB上的一点,将△OAP沿OP折叠,使点A落在OB上的点Q处.(1)求点B的坐标;(2)求直线PQ的解析式;(3)点M在直线OP上,点N在直线PQ上,是否存在点M,N,使以A,C.M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.5.(2023春•顺德区校级月考)如图,请根据图象所提供的信息解答下列问题:(1)当x时,kx+b≥mx﹣n;(2)不等式kx+b<0的解集是;(3)求两个一次函数表达式;(4)若直线l1分别交x轴、y轴于点M、A,直线l2分别交x轴、y轴于点B、N,求点M的坐标和四边形OMPN的面积.6.(2023春•北碚区校级期中)如图,在平面直角坐标系中,直线y=2x﹣2与x 轴、y轴分别交于点A、点B,与直线CD:y=kx+b(k≠0)交于点P,OC =OD=4OA.(1)求直线CD的解析式;(2)连接OP、BC,若直线AB上存在一点Q,使得S△PQC =S四边形OBCP,求点Q的坐标;(3)将直线CD向下平移1个单位长度得到直线,直线l与x轴交于点E,点N为直线l上的一点,在平面直角坐标系中,是否存在点M,使以点O,E,N,M为顶点的四边形是矩形?若存在,请直接写出点M的坐标;若不存在,请说明理由.7.(2023春•宜兴市期中)如图,在平面直角坐标系中,已知A(0,4),点B、C都在x轴上,BC=12,AD∥BC,CD所在直线的函数表达式为y=﹣x+9,E是BC的中点,点P是BC边上一个动点.(1)当PB=时,以点P、A、D、E为顶点的四边形为平行四边形;(2)点P在BC边上运动过程中,以点P、A、D、E为顶点的四边形能否构成菱形?试说明理由.8.(2023春•工业园区校级期中)如图,在平面直角坐标系中,点A、点B分别在x轴与y轴上,直线AB的解析式为,以线段AB、BC为边作平行四边形ABCD.(1)如图1,若点C的坐标为(3,7),判断四边形ABCD的形状,并说明理由;(2)如图2,在(1)的条件下,P为CD边上的动点,点C关于直线BP的对称点是Q,连接PQ,BQ.①当∠CBP=°时,点Q位于线段AD的垂直平分线上;②连接AQ,DQ,设CP=x,设PQ的延长线交AD边于点E,当∠AQD=90°时,求证:QE=DE,并求出此时x的值.9.(2023•沈阳一模)如图,在平面直角坐标系中,直线y=kx+b与x轴交于点B(﹣5,0),与y轴交于点A,直线过点A,与x轴交于点C,点P 是x轴上方一个动点.(1)求直线AB的函数表达式;(2)若点P在线段AB上,且S△APC =S△AOB,求点P的坐标;(3)当S△PBC =S△AOB时,动点M从点B出发,先运动到点P,再从点P运动到点C后停止运动.点M的运动速度始终为每秒1个单位长度,运动的总时间为t(秒),请直接写出t的最小值.10.(2023春•鼓楼区期中)如图1,已知函数与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.(1)求直线BC的函数解析式;(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q.①若△PQB的面积为,求点M的坐标;②连接BM,如图2,若∠BMP=∠BAC,求点P的坐标.11.(2023春•顺德区校级期中)一次函数y=kx+b的图象经过点A(﹣2,0)、B(﹣1,1),且和一次函数y=﹣2x+a的图象交于点C,如图所示.(1)填空:不等式kx+b<0的解集是;(2)若不等式kx+b>﹣2x+a的解集是x>1,求点C的坐标;(3)在(2)的条件下,点P是直线y=﹣2x+a上一动点.且在点C上方,当∠P AC=15°时,求点P的坐标.12.(2023春•重庆期中)如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0,﹣1),与x轴以及y=x+1的图象分别交于点C,D,且点D的坐标为(1,n).(1)则k=,b=,n=;(2)求四边形AOCD的面积;(3)在x轴上是否存在点P,使得以点P,C,D为顶点的三角形是直角三角形,请求出点P的坐标.13.(2023春•崇川区校级月考)模型建立:如图1,等腰直角三角形ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过A作AD⊥ED于D,过B作BE⊥ED于E.(1)求证:△BEC≌△CDA;(2)模型应用:已知直线l1:y=﹣x﹣4与y轴交于A点.将直线l1绕着A 点逆时针旋转45°至l2,如图2,求l2的函数解析式.14.(2023春•崇川区校级月考)如图,在平面直角坐标系中,直线l1:y=﹣x+4分别与x轴,y轴交于点B,C.直线l2:y=x.(1)直接写出点B,C的坐标:B,C.(2)若D是直线l2上的点,且△COD的面积为6,求直线CD的函数表达式;(3)在(2)的条件下,且当点D在第一象限时,设P是射线CD上的点,在平面内存在点Q.使以O,C,P,Q为顶点的四边形是菱形,请直接求点Q的坐标.15.(2023•城固县模拟)如图,A、B两个长方体水箱放置在同一水平桌面上,开始时水箱A中没有水,水箱B盛满水,现以6dm3/min的流量从水箱B中抽水注入水箱A中,直至水箱A注满水为止.设注水时间为t(min),水箱A 的水位高度为y A(dm),水箱B中的水位高度为y B(dm).(抽水水管的体积忽略不计)(1)分别求出y A,y B与t之间的函数表达式;(2)当水箱A与水箱B中的水的体积相等时,求出此时两水箱中水位的高度差.16.(2022秋•常州期末)在平面直角坐标系中,一次函数的图象l1与x轴交于点A,一次函数y=x+6的图象l2与x轴交于点B,与l1交于点P.直线l3过点A且与x轴垂直,C是l3上的一个动点.(1)分别求出点A、P的坐标;(2)设直线PC对应的函数表达式为y=kx+b,且满足函数值y随x的增大而增大.若△PCA的面积为15,分别求出k、b的值;(3)是否存在点C,使得2∠PCA+∠P AB=90°?若存在,直接写出点C的坐标;若不存在,请说明理由.17.(2023春•靖江市期中)如图,平面直角坐标系中,已知点A(0,a)在y 轴正半轴上,点B(0,b)(a>b),点C(c,0)在x轴正半轴上,且a2﹣2ab+b2(1)如图1,求证:AB=OC;(2)如图2,当a=3,b=1时,过点B的直线与AC成45°夹角,试求该直线与AC交点的横坐标;(3)如图3,当b<0时,点D在OC的延长线上,且CD=OB,连接AD,射线BC交AD于点E.当点B在y轴负半轴上运动时,∠AEB的度数是否为定值?如果是,请求出∠AEB的度数;如果不是,请说明理由.18.(2023春•沙坪坝区校级期中)如图,在平面直角坐标系xOy中,直线AB:与直线CD:y=kx﹣2相交于点M(4,a),分别交坐标轴于点A,(1)求直线CD的解析表达式;(2)如图,点P是直线CD上的一个动点,当△PBM的面积为20时,求点P的坐标;(3)直线AB上有一点F,在平面直角坐标系内找一点N,使得以BF为一边,以点B,D,F,N为顶点的四边形是菱形,请直接写出符合条件的点N的坐标.19.(2023春•揭西县校级月考)在平面直角坐标系中,直线y1=kx+b经过点P (2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.(1)求出直线y1=kx+b的解析式;(2)当m<0时,直接写出y1<y2时自变量x的取值范围;(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△P AB是等腰三角形时,请直接写出符合条件的所有点B的坐标.20.(2023春•溧阳市校级月考)如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是由△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是2和4;(1)求直线BD的表达式;(2)求△OFH的面积;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.21.(2023春•江都区月考)如图,在平面直角坐标系中,直线y=﹣x+3与x 轴、y轴相交于A、B两点,动点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)求点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.22.(2023春•新城区校级月考)如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.(1)若直线l2上存在点P(不与B重合),满足S△COP=S△COB,求出点P的坐标;(2)在y轴右侧有一动直线平行于y轴,分别与l1,l2交于点M、N,且点M 在点N的下方,y轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.23.(2022秋•宿豫区期末)如图,直线l分别与x轴、y轴交于点A(4,0)、B (0,5),把直线l沿y轴向下平移3个单位长度,得到直线m,且直线m分别与x轴、y轴交于点C、D.(1)求直线l对应的函数表达式;(2)求四边形ABDC的面积.24.(2022秋•临淄区期末)如图,在直角坐标系中,四边形ABCD的顶点坐标分别为A(﹣1,0),B(0,2),C(2,3),D(4,0).(1)求直线BC的表达式;(2)线段AB与BC相等吗?请说明理由;(3)求四边形ABCD的面积;(4)已知点M在x轴上,且△MBC是等腰三角形,求点M的坐标.25.(2022秋•金牛区期末)如图1,在平面直角坐标系xOy中,直线AB:y=2x+b 与x轴交于点A(﹣2,0),与y轴交于点B.(1)求直线AB的解析式;(2)若直线CD:y=﹣x+与x轴、y轴、直线AB分别交于点C、D、E,求△BDE面积;(3)如图2,在(2)的条件下,点F为线段AC上一动点,将△EFC沿直线EF翻折得到△EFN,EN交x轴于点M.当△MNF为直角三角形时,求点N 的坐标.26.(2022秋•婺城区期末)如图,直线y=x+4与x轴、y轴分别交于点A、点B,点P是射线BO上的动点,过点B作直线AP的垂线交x轴于点Q,垂足为点C,连结OC.(1)当点P在线段BO上时,①求证:△AOP≌△BOQ;②若点P为BO的中点,求△OCQ的面积.(2)在点P的运动过程中,是否存在某一位置,使得△OCQ成为等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.27.(2022秋•郫都区期末)在直角坐标系xOy中,直线l1:y=﹣x+4与x轴、y 轴分别交于点A,点B.直线l2:y=mx+m(m>0)与x轴,y轴分别交于点C,点D,直线l1与l2交于点E.(1)若点E坐标为(,n).ⅰ)求m的值;ⅱ)点P在直线l2上,若S△AEP=3S△BDE,求点P的坐标;(2)点F是线段CE的中点,点G为y轴上一动点,是否存在点F使△CFG 为以FC为直角边的等腰直角三角形.若存在,求出m的值,若不存在,请说明理由.28.(2022秋•市中区期末)如图,直线y=kx+b经过点,点B(0,25),与直线交于点C,点D为直线AB上一动点,过D点作x轴的垂线交直线OC于点E.(1)求直线AB的表达式和点C的坐标;(2)当时,求△CDE的面积;(3)连接OD,当△OAD沿着OD折叠,使得点A的对应点A'落在直线OC 上,直接写出此时点D的坐标.29.(2022秋•新都区期末)如图1,在平面直角坐标系中,点A的坐标为(4,4),点B的坐标为(﹣4,0).(1)求直线AB的表达式;(2)点M是坐标轴上的一点,若以AB为直角边构造Rt△ABM,请求出满足条件的所有点M的坐标;(3)如图2,以A为直角顶点作∠CAD=90°,射线AC交x轴的正半轴于点C,射线AD交y轴的负半轴于点D,当∠CAD绕点A旋转时,求OC﹣OD 的值.30.(2022秋•皇姑区期末)如图,在平面直角坐标系中,直线AD:y=﹣x+4交y轴于点A,交x轴于点D.直线AB交x轴于点B(﹣3,0),点P为直线AB上的动点.(1)求直线AB的关系式;(2)连接PD,当线段PD⊥AB时,直线AD上有一点动M,x轴上有一动点N,直接写出△PMN周长的最小值;(3)若∠POA=∠BAO,直接写出点P的纵坐标.31.(2022秋•新都区期末)如图所示,直线l1:y=x﹣1与y轴交于点A,直线l2:y=﹣2x﹣4与x轴交于点B,直线l1与l2交于点C.(1)求点A,C的坐标;(2)点P在直线l1上运动,求出满足条件S△PBC=S△ABC且异于点A的点P的坐标;(3)点D(2,0)为x轴上一定点,当点Q在直线l1上运动时,请直接写出|DQ﹣BQ|的最大值.32.(2022秋•鸡西期末)如图,直角三角形ABC在平面直角坐标系中,直角边BC在y轴上,AB,BC的长分别是一元二次方程x2﹣14x+48=0的两个根,AB<BC,且BC=2OB,P为BC上一点,且∠BAP=∠C.(1)求点A的坐标;(2)求直线AP的解析式;(3)M为x轴上一点,在平面内是否存在点N,使以A,C,M,N为顶点的四边形为矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.33.(2022秋•锦江区校级期末)如图,直线y=kx+b与x轴、y轴分别交于点A 和点B,点C在线段AO上,将△ABC沿BC所在直线折叠后,点A恰好落在y轴上点D处,若OA=4,OD=2.(1)求直线AB的解析式.(2)求S△ABC :S△OCD的值.(3)直线CD上是否存在点P使得∠PBC=45°,若存在,请直接写出P的坐标.34.(2022秋•福田区校级期末)已知:如图,一次函数的图象分别与x 轴、y轴相交于点A、B,且与经过点C(2,0)的一次函数y=kx+b的图象相交于点D.点D的横坐标为4,直线CD与y轴相交于点E.(1)直线CD的函数表达式为:;(2)点Q为线段DE上的一个动点,连接BQ.①若直线BQ将△BDE的面积分为1:2两部分,求点Q的坐标;②点Q是否存在某个位置,将△BQD沿着直线BQ翻折,使得点D恰好落在直线AB下方的坐标轴上?若存在,请直接写出点Q的坐标;若不存在,请说明理由.35.(2022秋•抚州期末)如图,在平面直角坐标系xOy中,直线AP交x轴于点P(p,0),与y轴交于点A(0,a),且a,p满足=0.(1)求直线AP的解析式;(2)如图1,直线x=﹣2与x轴交于点N,点M在x轴上方且在直线x=﹣2上,若△MAP的面积等于6,请求出点M的坐标;(3)如图2,已知点C(﹣2,4),若点B为射线AP上一动点,连接BC,在坐标轴上是否存在点Q,使△BCQ是以BC为底边,点Q为直角顶点的等腰直角三角形,若存在,请直接写出点Q坐标;若不存在,请说明理由.36.(2022秋•天桥区期末)如图1,在平面直角坐标系xOy中,点O是坐标原点,直线AB:y=kx+与直线AC:y=﹣2x+b交于点A,两直线与x轴分别交于点B(﹣3,0)和C(2,0).(1)求直线AB和AC的表达式.(2)点P是y轴上一点,当P A+PC最小时,求点P的坐标.(3)如图2,点D为线段BC上一动点,将△ABD沿直线AD翻折得到△ADE,线段AE交x轴于点F,若△DEF为直角三角形,求点D坐标.37.(2023•桐乡市校级开学)如图,一次函数y=x+6的图象与x轴交于点A,与y轴交于点B,OC⊥AB于点C,点P在直线AB上运动,点Q在y轴的正半轴上运动.(1)求点A,B的坐标;(2)求OC的长;(3)若以O,P,Q为顶点的三角形与△OCP全等,求点Q的坐标.38.(2022秋•秦都区期末)如图,平面直角坐标系中,直线AB与x轴交于点A (﹣3,0)与y轴交于点B(0,6),点C是直线AB上的一点,它的坐标为(m,4),经过点C作直线CD∥x轴交y轴于点D.(1)求点C的坐标;(2)已知点P是直线CD上的动点,①若△POC的面积为4,求点P的坐标;②若△POC为直角三角形,请求出所有满足条件的点P的坐标.39.(2022秋•南海区期末)如图,在平面直角坐标系中,直线y=x+1分别交x 轴,y轴于点A、B.另一条直线CD与直线AB交于点C(a,6),与x轴交于点D(3,0),点P是直线CD上一点(不与点C重合).(1)求a的值.(2)当△APC的面积为18时,求点P的坐标.(3)若直线MN在平面直角坐标系内运动,且MN始终与AB平行,直线MN 交直线CD于点M,交y轴于点N,当∠BMN=90°时,求△BMN的面积.40.(2023•丰顺县校级开学)问题提出:如图,等腰Rt△ABC中,∠ACB=90°,CB=CA,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,求证:△BEC≌△CDA;问题探究:如图2,在平面直角坐标系中,一次函数与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°,求点C的坐标;问题解决:古城西安已经全面迎来地铁时代!继西安地铁2号线于2011年9月16日通车试运行以来,共有八条线路开通运营,极大促进了西安市的交通运输,目前还有多条线路正在修建中.如图,地铁某线路原计划按OA﹣AB的方向施工,由于在AB方向发现一处地下古建筑,地铁修建须绕开此区域.经实地勘测,若将AB段绕点A顺时针或逆时针方向旋转45°至AC或AD方向,则可以绕开此区域.已知OA长为1千米,以点O为原点,OA所在直线为x轴,1千米为单位长度,建立平面直角坐标系,且射线AB与直线y=﹣2x平行,请帮助施工队计算出AC和AD所在直线的解析式.41.(2022秋•碑林区校级期末)(1)模型建立:如图1,在等腰直角三角形ABC中,∠ACB=90°,CA=CB,直线ED经过点C,过点A作AD⊥ED于点D,过点B作BE⊥ED于点E,请直接写出图中相等的线段(除CA=CB);模型应用:(2)如图2,在平面直角坐标系xOy中,直线与x,y轴分别交于A、B两点,C为第一象限内的点,若△ABC是以AB为直角边的等腰直角三角形,请求出点C的坐标和直线BC的表达式;探究提升:(3)如图3,在平面直角坐标系xOy中,A(3,0),点B在y轴上运动,将AB绕点A顺时针旋转90°至AC,连接OC,求CA+OC的最小值,及此时点B坐标.42.(2023•南岸区校级开学)如图,已知直线l1:y=﹣x+b与直线l2:y=kx+3相交于y轴的B点,且分别交x轴于点A、C,已知OC=OA.(1)如图,求点C的坐标及k的值;(2)如图,若E为直线l1上一点,且E点的横坐标为,点P为y轴上一个动点,求当|PC﹣PE|最大时,点P的坐标;(3)若M为x轴上一点,当△ABM是等腰三角形时,直接写出点M的坐标.43.(2022秋•驿城区校级期末)(1)操作思考:如图1,在平面直角坐标系中,等腰直角△ACB的直角顶点C在原点,将其绕着点O旋转,若顶点A恰好落在点(1,2)处.则:①OA的长为;②点B的坐标为.(直接写结果)(2)感悟应用:如图2,在平面直角坐标系中,将等腰直角△ACB如图放置,直角顶点C(﹣1,0),点A(0,4),试求直线AB的函数表达式.(3)拓展研究:如图3,在直角坐标系中,点B(4,3),过点B作BA⊥y 轴,垂足为点A,作BC⊥x轴,垂足为点C,P是线段BC上的一个动点,点Q是直线y=2x﹣8上一动点,存在以点P为直角顶点的等腰直角△APQ,请直接写出点P的坐标.。
2020年江苏省常州市中考数学试卷(含解析版)

2020年江苏省常州市中考数学试卷一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,只有一项是正确的)1.(2分)2的相反数是()A.﹣2B.﹣C.D.22.(2分)计算m6÷m2的结果是()A.m3B.m4C.m8D.m123.(2分)如图是某几何体的三视图,该几何体是()A.圆柱B.三棱柱C.四棱柱D.四棱锥4.(2分)8的立方根为()A.B.C.2D.±25.(2分)如果x<y,那么下列不等式正确的是()A.2x<2y B.﹣2x<﹣2y C.x﹣1>y﹣1D.x+1>y+16.(2分)如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是()A.30°B.40°C.50°D.60°7.(2分)如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是()A.3B.4C.5D.68.(2分)如图,点D是▱OABC内一点,CD与x轴平行,BD与y轴平行,BD=,∠ADB=135°,S△ABD=2.若反比例函数y=(x>0)的图象经过A、D两点,则k的值是()A.2B.4C.3D.6二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把笞案直接填写在答题卡相应位置上)9.(2分)计算:|﹣2|+(π﹣1)0=.10.(2分)若代数式有意义,则实数x的取值范围是.11.(2分)地球的半径大约为6400km.数据6400用科学记数法表示为.12.(2分)分解因式:x3﹣x=.13.(2分)若一次函数y=kx+2的函数值y随自变量x增大而增大,则实数k的取值范围是.14.(2分)若关于x的方程x2+ax﹣2=0有一个根是1,则a=.15.(2分)如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC是等边三角形,则∠B=°.16.(2分)数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形ABCD中,AB=2,∠DAB=120°.如图,建立平面直角坐标系xOy,使得边AB在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是.17.(2分)如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=.18.(2分)如图,在△ABC中,∠B=45°,AB=6,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=3DG,且直线BF与直线DG互相垂直,则BG的长为.三、解答题(本大题共10小题,共84分.请在答题卡指定区域内作答,如无特殊说明,解答应写出文字说明、演算步骤或推理过程)19.(6分)先化简,再求值:(x+1)2﹣x(x+1),其中x=2.20.(8分)解方程和不等式组:(1)+=2;(2).21.(8分)为了解某校学生对球类运动的喜爱情况,调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查,并根据调查结果绘制成如图统计图.(1)本次抽样调查的样本容量是;(2)补全条形统计图;(3)该校共有2000名学生,请你估计该校最喜爱“打篮球”的学生人数.22.(8分)在3张相同的小纸条上分别标上1、2、3这3个号码,做成3支签,放在一个不透明的盒子中.(1)搅匀后从中随机抽出1支签,抽到1号签的概率是;(2)搅匀后先从中随机抽出1支签(不放回),再从余下的2支签中随机抽出1支签,求抽到的2支签上签号的和为奇数的概率.23.(8分)已知:如图,点A、B、C、D在一条直线上,EA∥FB,EA=FB,AB=CD.(1)求证:∠E=∠F;(2)若∠A=40°,∠D=80°,求∠E的度数.24.(8分)某水果店销售苹果和梨,购买1千克苹果和3千克梨共需26元,购买2千克苹果和1千克梨共需22元.(1)求每千克苹果和每千克梨的售价;(2)如果购买苹果和梨共15千克,且总价不超过100元,那么最多购买多少千克苹果?25.(8分)如图,正比例函数y=kx的图象与反比例函数y=(x>0)的图象交于点A(a,4).点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.(1)求a的值及正比例函数y=kx的表达式;(2)若BD=10,求△ACD的面积.26.(10分)如图1,点B在线段CE上,Rt△ABC≌Rt△CEF,∠ABC=∠CEF=90°,∠BAC=30°,BC=1.(1)点F到直线CA的距离是;(2)固定△ABC,将△CEF绕点C按顺时针方向旋转30°,使得CF与CA重合,并停止旋转.①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法).该图形的面积为;②如图2,在旋转过程中,线段CF与AB交于点O,当OE=OB时,求OF的长.27.(10分)如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点“,把PQ•PH 的值称为⊙I关于直线a的“特征数”.(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4).半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点(填“A”.“B”、“C”或“D”),⊙O关于直线m的“特征数”为;②若直线n的函数表达式为y=x+4.求⊙O关于直线n的“特征数”;(2)在平面直角坐标系xOy中,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线1相离,点N(﹣1,0)是⊙F关于直线1的“远点”.且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.28.(10分)如图,二次函数y=x2+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1,0),且顶点为D,连接AC、BC、BD、CD.(1)填空:b=;(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD =∠ACB,求点P的坐标;(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.2020年江苏省常州市中考数学试卷参考答案与试题解析一、选择题(本大题共8小题,每小题2分,共16分.在每小题所给出的四个选项中,只有一项是正确的)1.(2分)2的相反数是()A.﹣2B.﹣C.D.2【分析】利用相反数的概念:只有符号不同的两个数叫做互为相反数,进而得出答案.【解答】解:2的相反数是﹣2.故选:A.【点评】此题主要考查了相反数的概念,正确把握定义是解题关键.2.(2分)计算m6÷m2的结果是()A.m3B.m4C.m8D.m12【分析】利用同底数幂的除法运算法则计算得出答案.【解答】解:m6÷m2=m6﹣2=m4.故选:B.【点评】此题主要考查了同底数幂的除法运算,正确掌握运算法则是解题关键.3.(2分)如图是某几何体的三视图,该几何体是()A.圆柱B.三棱柱C.四棱柱D.四棱锥【分析】该几何体的主视图与左视图均为矩形,俯视图为正方形,易得出该几何体的形状.【解答】解:该几何体的主视图为矩形,左视图为矩形,俯视图是一个正方形,则可得出该几何体是四棱柱.故选:C.【点评】主要考查的是三视图的相关知识,解得此题时要有丰富的空间想象力.4.(2分)8的立方根为()A.B.C.2D.±2【分析】根据立方根的定义求出的值,即可得出答案.【解答】解:8的立方根是==2,故选:C.【点评】本题考查了对立方根的定义的理解和运用,注意:a的立方根是.5.(2分)如果x<y,那么下列不等式正确的是()A.2x<2y B.﹣2x<﹣2y C.x﹣1>y﹣1D.x+1>y+1【分析】根据不等式的性质逐个判断即可.【解答】解:A、∵x<y,∴2x<2y,故本选项符合题意;B、∵x<y,∴﹣2x>﹣2y,故本选项不符合题意;C、∵x<y,∴x﹣1<y﹣1,故本选项不符合题意;D、∵x<y,∴x+1<y+1,故本选项不符合题意;故选:A.【点评】本题考查了不等式的性质,能熟记不等式的性质的内容是解此题的关键.6.(2分)如图,直线a、b被直线c所截,a∥b,∠1=140°,则∠2的度数是()A.30°B.40°C.50°D.60°【分析】先根据邻补角互补求得∠3,然后再根据两直线平行、内错角相等即可解答.【解答】解:∵∠1+∠3=180°,∠1=40°,∴∠3=180°﹣∠1=180°﹣140°=40°∵a∥b,∴∠2=∠3=40°.故选:B.【点评】本题考查了平行线的性质,掌握“两直线平行、内错角相等”是解答本题的关键.7.(2分)如图,AB是⊙O的弦,点C是优弧AB上的动点(C不与A、B重合),CH⊥AB,垂足为H,点M是BC的中点.若⊙O的半径是3,则MH长的最大值是()A.3B.4C.5D.6【分析】根据直角三角形斜边中线的性质以及直径是圆中最大的弦,即可求得MH的最大值是3.【解答】解:∵CH⊥AB,垂足为H,∴∠CHB=90°,∵点M是BC的中点.∴MH=BC,∵BC的最大值是直径的长,⊙O的半径是3,∴MH的最大值为3,故选:A.【点评】本题考查了直角三角形斜边中线的性质,明确BC的最大值为⊙O的直径的长是解题的关键.8.(2分)如图,点D是▱OABC内一点,CD与x轴平行,BD与y轴平行,BD=,∠ADB=135°,S△ABD=2.若反比例函数y=(x>0)的图象经过A、D两点,则k的值是()A.2B.4C.3D.6【分析】根据三角形面积公式求得AE=2,易证得△AOM≌△CBD(AAS),得出OM =BD=,根据题意得出△ADE是等腰直角三角形,得出DE=AE=2,设A(m,),则D(m﹣2,3),根据反比例函数系数k的几何意义得出关于m的方程,解方程求得m=3,进一步求得k=6.【解答】解:作AM⊥y轴于M,延长BD,交AM于E,设BC与y轴的交点为N,∵四边形OABC是平行四边形,∴OA∥BC,OA=BC,∴∠AOM=∠CNM,∵BD∥y轴,∴∠CBD=∠CNM,∴∠AOM=∠CBD,∵CD与x轴平行,BD与y轴平行,∴∠CDB=90°,BE⊥AM,∴∠CDB=∠AMO,∴△AOM≌△CBD(AAS),∴OM=BD=,∵S△ABD==2,BD=,∴AE=2,∵∠ADB=135°,∴∠ADE=45°,∴△ADE是等腰直角三角形,∴DE=AE=2,∴D的纵坐标为3,设A(m,),则D(m﹣2,3),∵反比例函数y=(x>0)的图象经过A、D两点,∴k=m=(m﹣2)×3,解得m=3,∴k=m=6.故选:D.【点评】本题考查了反比例函数系数k的几何意义,反比例函数图象上点的坐标特征,平行四边形的性质,等腰直角三角形的判定和性质,三角形的面积等,表示出A、D的坐标是解题的关键.二、填空题(本大题共10小题,每小题2分,共20分.不需写出解答过程,请把笞案直接填写在答题卡相应位置上)9.(2分)计算:|﹣2|+(π﹣1)0=3.【分析】首先计算乘方和绝对值,然后计算加法,求出算式的值是多少即可.【解答】解:|﹣2|+(π﹣1)0=2+1=3,故答案为:3.【点评】此题主要考查了实数的运算,要熟练掌握,解答此题的关键是要明确:在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号里面的,同级运算要按照从左到右的顺序进行.另外,有理数的运算律在实数范围内仍然适用.10.(2分)若代数式有意义,则实数x的取值范围是x≠1.【分析】分式有意义时,分母x﹣1≠0,据此求得x的取值范围.【解答】解:依题意得:x﹣1≠0,解得x≠1,故答案为:x≠1.【点评】本题考查了分式有意义的条件.(1)分式有意义的条件是分母不等于零.(2)分式无意义的条件是分母等于零.11.(2分)地球的半径大约为6400km.数据6400用科学记数法表示为 6.4×103.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将6400用科学记数法表示为6.4×103.故答案为:6.4×103.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.(2分)分解因式:x3﹣x=x(x+1)(x﹣1).【分析】本题可先提公因式x,分解成x(x2﹣1),而x2﹣1可利用平方差公式分解.【解答】解:x3﹣x,=x(x2﹣1),=x(x+1)(x﹣1).故答案为:x(x+1)(x﹣1).【点评】本题考查了提公因式法,公式法分解因式,先提取公因式后再利用平方差公式继续进行因式分解,分解因式一定要彻底.13.(2分)若一次函数y=kx+2的函数值y随自变量x增大而增大,则实数k的取值范围是k>0.【分析】根据一次函数的性质,如果y随x的增大而增大,则一次项的系数大于0,据此求出k的取值范围.【解答】解:∵一次函数y=kx+2,函数值y随x的值增大而增大,∴k>0.故答案为:k>0.【点评】本题考查的是一次函数的性质,解答本题要注意:在一次函数y=kx+b(k≠0)中,当k>0时y随x的增大而增大.14.(2分)若关于x的方程x2+ax﹣2=0有一个根是1,则a=1.【分析】把x=1代入方程得出1+a﹣2=0,求出方程的解即可.【解答】解:∵关于x的方程x2+ax﹣2=0有一个根是1,∴把x=1代入方程得:1+a﹣2=0,解得:a=1,故答案为:1.【点评】本题考查了一元二次方程的解和解一元一次方程,能得出关于a的一元一次方程是解此题的关键.15.(2分)如图,在△ABC中,BC的垂直平分线分别交BC、AB于点E、F.若△AFC是等边三角形,则∠B=30°.【分析】根据垂直平分线的性质得到∠B=∠BCF,再利用等边三角形的性质得到∠AFC =60°,从而可得∠B的度数.【解答】解:∵EF垂直平分BC,∴BF=CF,∴∠B=∠BCF,∵△ACF为等边三角形,∴∠AFC=60°,∴∠B=∠BCF=30°.故答案为:30.【点评】本题考查了垂直平分线的性质,等边三角形的性质,三角形外角的性质,解题的关键是利用垂直平分线的性质得到∠B=∠BCF.16.(2分)数学家笛卡尔在《几何》一书中阐述了坐标几何的思想,主张取代数和几何中最好的东西,互相以长补短.在菱形ABCD中,AB=2,∠DAB=120°.如图,建立平面直角坐标系xOy,使得边AB在x轴正半轴上,点D在y轴正半轴上,则点C的坐标是(2,).【分析】根据直角三角形的性质可得OA和OD的长,根据菱形的性质和坐标与图形的性质可得答案.【解答】解:∵四边形ABCD是菱形,且AB=2,∴CD=AD=AB=2,∵∠DAB=120°,∴∠OAD=60°,Rt△AOD中,∠ADO=30°,∴OA=AD==1,OD==,∴C(2,),故答案为:(2,).【点评】此题主要考查了含30度角的直角三角形的性质,菱形的性质,坐标与图形的性质等知识,解题的关键是确定OD的长.17.(2分)如图,点C在线段AB上,且AC=2BC,分别以AC、BC为边在线段AB的同侧作正方形ACDE、BCFG,连接EC、EG,则tan∠CEG=.【分析】根据正方形的性质以及锐角三角函数的定义即可求出答案.【解答】解:连接CG,在正方形ACDE、BCFG中,∠ECA=∠GCB=45°,∴∠ECG=90°,设AC=2,BC=1,∴CE=2,CG=,∴tan∠GEC==,故答案为:.【点评】本题考查正方形,解题的关键是熟练运用正方形的性质以及锐角三角函数的定义,本题属于基础题型.18.(2分)如图,在△ABC中,∠B=45°,AB=6,D、E分别是AB、AC的中点,连接DE,在直线DE和直线BC上分别取点F、G,连接BF、DG.若BF=3DG,且直线BF与直线DG互相垂直,则BG的长为4或2.【分析】如图,过点B作BT⊥BF交ED的延长线于T,过点B作BH⊥DT于H,证明四边形DGBT是平行四边形,求出DH,TH即可解决问题.【解答】解:如图,过点B作BT⊥BF交ED的延长线于T,过点B作BH⊥DT于H.∵DG⊥BF,BT⊥BF,∴DG∥BT,∵AD=DB,AE=EC,∴DE∥BC,∴四边形DGBT是平行四边形,∴BG=DT,DG=BT,∠BDH=∠ABC=45°,∵AD=DB=3,∴BH=DH=3,∵∠TBF=∠BHF=90°,∴∠TBH+∠FBH=90°,∠FBH+∠F=90°,∴∠TBH=∠F,∴tan∠F=tan∠TBH===,∴=,∴TH=1,∴DT=TH+DH=1+3=4,∴BG=4.当点F在ED的延长线上时,同法可得DT=BG=3﹣1=2.故答案为4或2.【点评】本题考查相似三角形的性质,平行四边形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题.三、解答题(本大题共10小题,共84分.请在答题卡指定区域内作答,如无特殊说明,解答应写出文字说明、演算步骤或推理过程)19.(6分)先化简,再求值:(x+1)2﹣x(x+1),其中x=2.【分析】先根据完全平方公式和单项式乘以多项式法则算乘法,再合并同类项,最后代入求出即可.【解答】解:(x+1)2﹣x(x+1)=x2+2x+1﹣x2﹣x=x+1,当x=2时,原式=2+1=3.【点评】本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.20.(8分)解方程和不等式组:(1)+=2;(2).【分析】(1)方程两边都乘以x﹣1得出方程x﹣2=2(x﹣1),求出方程的解,再进行检验即可;(2)先求出每个不等式的解集,再求出不等式组的解集即可.【解答】解:(1)方程两边都乘以x﹣1得:x﹣2=2(x﹣1),解得:x=0,检验:把x=0代入x﹣1得:x﹣1≠0,所以x=0是原方程的解,即原方程的解是:x=0;(2),∵解不等式①得:x<3,解不等式②得:x≥﹣2,∴不等式组的解集是:﹣2≤x<3.【点评】本题考查了解分式方程和解一元一次不等式组,能把分式方程转化成整式方程是解(1)的关键,能根据不等式的解集找出不等式组的解集是解(2)的关键.21.(8分)为了解某校学生对球类运动的喜爱情况,调查小组就打排球、打乒乓球、打篮球、踢足球四项球类运动对该校学生进行了“你最喜爱的球类运动”的抽样调查,并根据调查结果绘制成如图统计图.(1)本次抽样调查的样本容量是100;(2)补全条形统计图;(3)该校共有2000名学生,请你估计该校最喜爱“打篮球”的学生人数.【分析】(1)根据打排球的人数和所占的百分比即可求出样本容量;(2)用总人数乘以打乒乓球的人数所占的百分比求出打乒乓球的人数,再用总人数减去其他项目的人数求出踢足球的人数,从而补全统计图;(3)用该校的总人数乘以“打篮球”的人数所占的百分比即可.【解答】解:(1)本次抽样调查的总人数是:25÷25%=100(人),则样本容量是100;故答案为:100;(2)打乒乓球的人数有:100×35%=35(人),踢足球的人数有:100﹣25﹣35﹣15=25(人),补全统计图如下:(3)根据题意得:2000×=300(人),答:估计该校最喜爱“打篮球”的学生人数有300人.【点评】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.22.(8分)在3张相同的小纸条上分别标上1、2、3这3个号码,做成3支签,放在一个不透明的盒子中.(1)搅匀后从中随机抽出1支签,抽到1号签的概率是;(2)搅匀后先从中随机抽出1支签(不放回),再从余下的2支签中随机抽出1支签,求抽到的2支签上签号的和为奇数的概率.【分析】(1)共有3种可能出现的结果,其中“抽到1号”的有1种,可求出概率;(2)用列表法表示所有可能出现的结果,找出“和为奇数”的情况,进而求出相应的概率.【解答】解:(1)共有3种可能出现的结果,其中“抽到1号”的有1种,因此“抽到1号”的概率为,故答案为:;(2)用列表法表示所有可能出现的结果情况如下:共有6种可能出现的结果,其中“和为奇数”的有4种,∴P(和为奇数)==.【点评】本题考查列表法和树状图求随机事件发生的概率,列举出所有可能出现的结果情况,是正确解答的关键.23.(8分)已知:如图,点A、B、C、D在一条直线上,EA∥FB,EA=FB,AB=CD.(1)求证:∠E=∠F;(2)若∠A=40°,∠D=80°,求∠E的度数.【分析】(1)首先利用平行线的性质得出,∠A=∠FBD,根据AB=CD即可得出AC=BD,进而得出△EAC≌△FBD解答即可;(2)根据全等三角形的性质和三角形内角和解答即可.【解答】证明:(1)∵EA∥FB,∴∠A=∠FBD,∵AB=CD,∴AB+BC=CD+BC,即AC=BD,在△EAC与△FBD中,,∴△EAC≌△FBD(SAS),∴∠E=∠F;(2)∵△EAC≌△FBD,∴∠ECA=∠D=80°,∵∠A=40°,∴∠E=180°﹣40°﹣80°=60°,答:∠E的度数为60°.【点评】此题主要考查了全等三角形的判定与性质等知识,解题时注意:两边及其夹角分别对应相等的两个三角形全等.根据已知得出△EAC≌△FBD是解题关键.24.(8分)某水果店销售苹果和梨,购买1千克苹果和3千克梨共需26元,购买2千克苹果和1千克梨共需22元.(1)求每千克苹果和每千克梨的售价;(2)如果购买苹果和梨共15千克,且总价不超过100元,那么最多购买多少千克苹果?【分析】(1)设每千克苹果的售价为x元,每千克梨的售价为y元,根据“购买1千克苹果和3千克梨共需26元,购买2千克苹果和1千克梨共需22元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设购买m千克苹果,则购买(15﹣m)千克梨,根据总价=单价×数量结合总价不超过100元,即可得出关于m的一元一次不等式,解之取其最大值即可得出结论.【解答】解:(1)设每千克苹果的售价为x元,每千克梨的售价为y元,依题意,得:,解得:.答:每千克苹果的售价为8元,每千克梨的售价为6元.(2)设购买m千克苹果,则购买(15﹣m)千克梨,依题意,得:8m+6(15﹣m)≤100,解得:m≤5.答:最多购买5千克苹果.【点评】本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.25.(8分)如图,正比例函数y=kx的图象与反比例函数y=(x>0)的图象交于点A(a,4).点B为x轴正半轴上一点,过B作x轴的垂线交反比例函数的图象于点C,交正比例函数的图象于点D.(1)求a的值及正比例函数y=kx的表达式;(2)若BD=10,求△ACD的面积.【分析】(1)把把点A(a,4)代入反比例函数关系式可求出a的值,确定点A的坐标,进而求出正比例函数的关系式;(2)根据BD=10,求出点B的横坐标,求出OB,代入求出BC,根据三角形的面积公式进行计算即可.【解答】解:(1)把点A(a,4)代入反比例函数y=(x>0)得,a==2,∴点A(2,4),代入y=kx得,k=2,∴正比例函数的关系式为y=2x,答:a=2,正比例函数的关系式为y=2x;(2)当BD=10=y时,代入y=2x得,x=5,∴OB=5,当x=5代入y=得,y=,即BC=,∴CD=BD﹣BC=10﹣=,∴S△ACD=××(5﹣2)=12.6,【点评】本题考查反比例函数、一次函数图象上点的坐标特征,把点的坐标代入是常用方法.26.(10分)如图1,点B在线段CE上,Rt△ABC≌Rt△CEF,∠ABC=∠CEF=90°,∠BAC=30°,BC=1.(1)点F到直线CA的距离是1;(2)固定△ABC,将△CEF绕点C按顺时针方向旋转30°,使得CF与CA重合,并停止旋转.①请你在图1中用直尺和圆规画出线段EF经旋转运动所形成的平面图形(用阴影表示,保留画图痕迹,不要求写画法).该图形的面积为;②如图2,在旋转过程中,线段CF与AB交于点O,当OE=OB时,求OF的长.【分析】(1)如图1中,作FD⊥AC于D.证明△ABC≌△CDF(AAS)可得结论.(2)线段EF经旋转运动所形成的平面图形如图所示,此时点E落在CF上的点H处.根据S阴=S△EFC+S扇形ACF﹣S扇形CEH﹣S△AHC=S扇形ACF计算即可.(3)如图2中,过点E作EH⊥CF于H.设OB=OE=x.在Rt△EOH中,利用勾股定理构建方程求解即可.【解答】解:(1)如图1中,作FD⊥AC于D,∵Rt△ABC≌Rt△CEF,∠ABC=∠CEF=90°,∠BAC=30°,BC=1.∴∠ACB=60°,∠FCE=∠BAC=30°,AC=CF,∴∠ACF=30°,∴∠BAC=∠FCD,在△ABC和△CDF中,,∴△ABC≌△CDF(AAS),∴FD=BC=1,故答案为1;(2)线段EF经旋转运动所形成的平面图形如图所示,此时点E落在CF上的点H处.S阴=S△EFC+S扇形ACF﹣S扇形CEH﹣S△AHC=S扇形ACF﹣S扇形ECH=﹣=.故答案为.(3)如图2中,过点E作EH⊥CF于H.设OB=OE=x.在Rt△ECF中,∵EF=1,∠ECF=30°,EH⊥CF,∴EC=EF=,EH=,CH=EH=,在Rt△BOC中,OC==,∴OH=CH﹣OC=﹣,在Rt△EOH中,则有x2=()2+(﹣)2,解得x=或﹣(不合题意舍弃),∴OC==,∵CF=2EF=2,∴OF=CF﹣OC=2﹣=.【点评】本题考查作图﹣旋转变换,解直角三角形,全等三角形的性质,扇形的面积等知识,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.27.(10分)如图1,⊙I与直线a相离,过圆心I作直线a的垂线,垂足为H,且交⊙I于P、Q两点(Q在P、H之间).我们把点P称为⊙I关于直线a的“远点“,把PQ•PH 的值称为⊙I关于直线a的“特征数”.(1)如图2,在平面直角坐标系xOy中,点E的坐标为(0,4).半径为1的⊙O与两坐标轴交于点A、B、C、D.①过点E画垂直于y轴的直线m,则⊙O关于直线m的“远点”是点D(填“A”.“B”、“C”或“D”),⊙O关于直线m的“特征数”为6;②若直线n的函数表达式为y=x+4.求⊙O关于直线n的“特征数”;(2)在平面直角坐标系xOy中,直线l经过点M(1,4),点F是坐标平面内一点,以F为圆心,为半径作⊙F.若⊙F与直线1相离,点N(﹣1,0)是⊙F关于直线1的“远点”.且⊙F关于直线l的“特征数”是4,求直线l的函数表达式.【分析】(1)①根据远点,特征数的定义判断即可.②如图1﹣1中,过点O作OH⊥直线n于H,交⊙O于Q,P.解直角三角形求出PH,PQ的长即可解决问题.(2)如图2﹣1中,设直线l的解析式为y=kx+b.分两种情形k>0或k<0,分别求解即可解决问题.【解答】解:(1)①由题意,点D是⊙O关于直线m的“远点”,⊙O关于直线m的特征数=DB•DE=2×5=20,故答案为D,20.②如图1﹣1中,过点O作OH⊥直线n于H,交⊙O于Q,P.设直线y=x+4交x轴于F(﹣,0),交y轴于E(0,4),∴OE=4,OF=∴tan∠FEO==,∴∠FEO=30°,∴OH=OE=2,∴PH=OH+OP=3,∴⊙O关于直线n的“特征数”=PQ•PH=2×3=6.(2)如图2﹣1中,设直线l的解析式为y=kx+b.当k>0时,过点F作FH⊥直线l于H,交⊙F于E,N.由题意,EN=2,EN•NH=4,∴NH=,∵N(﹣1,0),M(1,4),∴MN==2,∴HM===,∴△MNH是等腰直角三角形,∵MN的中点K(0,2),∴KN=HK=KM=,∴H(﹣2,3),把H(﹣2,3),M(1,4)代入y=kx+b,则有,解得,∴直线l的解析式为y=x+,当k<0时,同法可知直线i经过H′(2,1),可得直线l的解析式为y=﹣3x+7.综上所述,满足条件的直线l的解析式为y=x+或y=﹣3x+7.【点评】本题属于圆综合题,考查了一次函数的性质,解直角三角形,远点,特征数的定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.28.(10分)如图,二次函数y=x2+bx+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,抛物线过点C(1,0),且顶点为D,连接AC、BC、BD、CD.(1)填空:b=﹣4;(2)点P是抛物线上一点,点P的横坐标大于1,直线PC交直线BD于点Q.若∠CQD =∠ACB,求点P的坐标;(3)点E在直线AC上,点E关于直线BD对称的点为F,点F关于直线BC对称的点为G,连接AG.当点F在x轴上时,直接写出AG的长.【分析】(1)将点C坐标代入解析式可求解;(2)分两种情况讨论,当点Q在点D上方时,过点C作CE⊥AB于E,设BD与x轴交于点F,可得点E(1,3),CE=BE=3,AE=1,可得∠EBC=∠ECB=45°,tan∠ACE =,∠BCF=45°,由勾股定理逆定理可得∠BCD=90°,可求∠ACE=∠DBC,可得∠ACB=∠CFD,可得点F与点Q重合,即可求点P坐标;当点Q在点D下方上,过点C作CH⊥DB于H,在线段BH的延长线上截取HF=QH,连接CQ交抛物线于点P,先求直线BD解析式,点F坐标,由中点坐标公式可求点Q 坐标,求出CQ解析式,联立方程组,可求点P坐标;(3)设直线AC与BD的交点为N,作CH⊥BD于H,过点N作MN⊥x轴,过点E作EM⊥MN,连接CG,GF,先求出∠CNH=45°,由轴对称的性质可得EN=NF,∠ENB =∠FNB=45°,由“AAS”可证△EMN≌△NKF,可得EM=NK=,MN=KF,可求CF=6,由轴对称的性质可得点G坐标,即可求解.【解答】解:(1)∵抛物线y=x2+bx+3的图象过点C(1,0),∴0=1+b+3,∴b=﹣4,故答案为:﹣4;(2)∵b=4,∴抛物线解析式为y=x2﹣4x+3∵抛物线y=x2﹣4x+3的图象与y轴交于点A,过点A作x轴的平行线交抛物线于另一点B,∴点A(0,3),3=x2﹣4x,∴x1=0(舍去),x2=4,∴点B(4,3),∵y=x2﹣4x+3=(x﹣2)2﹣1,∴顶点D坐标(2,﹣1),如图1,当点Q在点D上方时,过点C作CE⊥AB于E,设BD与x轴交于点F,∵点A(0,3),点B(4,3),点C(1,0),CE⊥AB,∴点E(1,3),CE=BE=3,AE=1,∴∠EBC=∠ECB=45°,tan∠ACE=,∴∠BCF=45°,∵点B(4,3),点C(1,0),点D(2,﹣1),∴BC==3,CD==,BD==2,∵BC2+CD2=20=BD2,∴∠BCD=90°,∴tan∠DBC====tan∠ACE,∴∠ACE=∠DBC,∴∠ACE+∠ECB=∠DBC+∠BCF,∴∠ACB=∠CFD,又∵∠CQD=∠ACB,∴点F与点Q重合,∴点P是直线CF与抛物线的交点,∴0=x2﹣4x+3,∴x1=1,x2=3,∴点P(3,0);当点Q在点D下方上,过点C作CH⊥DB于H,在线段BH的延长线上截取HF=QH,连接CQ交抛物线于点P,∵CH⊥DB,HF=QH,∴CF=CQ,∴∠CFD=∠CQD,∴∠CQD=∠ACB,∵CH⊥BD,∵点B(4,3),点D(2,﹣1),∴直线BD解析式为:y=2x﹣5,∴点F(,0),∴直线CH解析式为:y=﹣x+,∴,解得,∴点H坐标为(,﹣),∵FH=QH,∴点Q(,﹣),∴直线CQ解析式为:y=﹣x+,联立方程组,解得:或,∴点P(,﹣);综上所述:点P的坐标为(3,0)或(,﹣);(3)如图,设直线AC与BD的交点为N,作CH⊥BD于H,过点N作MN⊥x轴,过点E作EM⊥MN,连接CG,GF,。
北京市上学期初中八年级期末考试数学试卷(含答案解析)

北京市上学期初中八年级期末考试数学试卷试卷满分:100分,考试时间:100分钟一、选择题(本题共30分,每小题3分)下面各题均有四个选项,其中只有一个..是符合题意的. 1. 2017年6月北京国际设计周面向社会公开征集“二十四节气”标识系统设计,以期通过现代设计的手段,尝试推动我国非物质文化遗产创新传承与发展.下面四幅作品分别代表“立春”、“芒种”、“白露”、“大雪”,其中是轴对称图形的是( ).2.科学家可以使用冷冻显微术以高分辨率测定溶液中的生物分子结构,使用此技术测定细菌蛋白结构的分辨率达到0.22纳米,也就是0.000 000 000 22米.将0.000 000 000 22用科学记数法表示为( ).A. 0.22×10-9B. 2.2×10-10C. 22×10-11D. 0.22×10-83.下列各式中,能用完全平方公式进行因式分解的是( ). A.x 2-2x-2 B.x 2+1 C.x 2-4x+4 D.x 2+4x+1 4.化简分式277()a ba b ++的结果是( ). A.7a b + B. 7a b + C. 7a b - D. 7a b- 5.在平面直角坐标系xOy 中,点M ,N ,P ,Q 的位置如图所示.若直线y=kx 经过第一、三象限,则直线y=kx-2可能经过的点是( ).A.点M B.点N C.点P D.点Q6.已知12xy=,则3x yy+的值为( ).A.7 B. 17C.52D.257.如图,在△ABC中,BC的垂直平分线分别交AC,BC于点D,E.若△ABC的周长为22,BE=4,则△ABD的周长为( ).A.14 B.18C.20 D.268.如图,在3×3的正方形网格中有四个格点A,B,C,D,以其中一个点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点可能是( ).A.点A B.点BC.点C D.点D9.某中学为了创建“最美校园图书屋”,新购买了一批图书,其中科普类图书平均每本书的价格是文学类图书平均每本书价格的1.2倍.已知学校用12000元购买文学类图书的本数比用这些钱购买科普类图书的本数多100本,那么学校购买文学类图书平均每本书的价格是多少元?设学校购买文学类图书平均每本书的价格是x元,则下面所列方程中正确的是( ).A .1200012000100 1.2x x =+ B .12000120001001.2x x =+ C .1200012000100 1.2x x =- D .12000120001001.2x x=- 10.如图,已知正比例函数y 1=ax 与一次函数212y x b =+的图象交于点P .下面有四个结论:①a<0;②b<0;③当x>0时,y 1>0;④当x<-2时,y 1>y 2.其中正确的是( ).A .①②B .②③C .①③D .①④二、填空题(本题共25分,第13题4分,其余每小题3分) 11.要使分式21x -有意义,则x 的取值范围是_________________. 12.点P(3,4)关于y 轴的对称点P'的坐标是______________.13.计算:(1) 223b a ⎛⎫⎪⎝⎭=_________________.(2)21054ab ac c÷=___________________. 14.如图,点B ,E ,C ,F 在同一条直线上,AB=DE ,∠B=∠DEF.要使△ABC ≌△DEF ,则需要再添加的一个条件是________________.(写出一个即可)15.如图,△ABC是等边三角形,AB =6,AD是BC边上的中线.点E在AC边上,且∠EDA=30°,则直线ED与AB的位置关系是_________________,ED的长为_______________.16.写出一个一次函数,使得它同时满足下列两个条件:①y随x的增大而减小;②图象经过点(1,-4).答:____________________.17.如图,在Rt△ABC中,∠B=90°.(1)作出∠BAC的平分线AM;(要求:尺规作图,保留作图痕迹,不写作法)(2)若∠BAC的平分线AM与BC交于点D,且BD=3,AC=10,则△DAC的面积为_____________________.18.小芸家与学校之间是一条笔直的公路,小芸从家步行前往学校的途中发现忘记带阅读分享要用的U盘,便停下给妈妈打电话,妈妈接到电话后,带上U盘马上赶往学校,同时小芸沿原路返回,两人相遇后,小芸立即赶往学校,妈妈沿原路返回家,并且小芸到达学校比妈妈到家多用了5分钟.若小芸步行的速度始终是每分钟100米,小芸和妈妈之间的距离y与小芸打完..后.步行..电话的时间x之间的函数关系如图所示,则妈妈从家出发__________分钟后与小芸相遇,相遇后妈妈回家的平均速度是每分钟________________米,小芸家离学校的距离为_________________米.三、解答题(本题共27分,第19、23题每小题6分,其余每小题5分) 19.分解因式:(1) 5a 2+10ab; (2)mx 2-12mx+36m. 解: 解:20.老师所留的作业中有这样一个分式的计算题:22511x x x +++-,甲、乙两位同学完成的过程分别如下:老师发现这两位同学的解答都有错误.请你从甲、乙两位同学中,选择一位同学的解答过程,帮助他分析错因,并加以改正. (1)我选择________同学的解答过程进行分析.(填“甲”或“乙”)该同学的解答从第____________步开始出现错误,错误的原因是____________________ _________________________________________________________________________; (2)请重新写出完成此题的正确解答过程.22511x x x +++- 解:21.如图,在△ABC 中,点D 在AC 边上,AE ∥BC ,连接ED 并延长交BC 于点F .若AD=CD ,求证:ED=FD.证明: 22.解分式方程:2521393x x x +=+--. 解:23.已知一次函数y=kx+b ,当x=2时y 的值为1,当x=-1时y 的值为-5. (1)在所给坐标系中画出一次函数y=kx+b 的图象; (2)求k ,b 的值;(3)将一次函数y=kx+b 的图象向上平移4个单位长度,求所得到新的函数图象与x 轴,y 轴的交点坐标.解:(2)(3)四、解答题(本题共18分,第24题5分,第25题6分,第26题7分)24.阅读材料:课堂上,老师设计了一个活动:将一个4 4的正方形网格沿着网格线划分成两部分(分别用阴影和空白表示),使得这两部分图形是全等的,请同学们尝试给出划分的方法.约定:如果两位同学的划分结果经过旋转、翻折后能够重合,那么就认为他们的划分方法相同.小方、小易和小红分别对网格进行了划分,结果如图1、图2、图3所示.小方说:“我们三个人的划分方法都是正确的.但是将小红的整个图形(图3)逆时针旋转90°后得到的划分方法与我的划分方法(图1)是一样的,应该认为是同一种方法,而小易的划分方法与我的不同.”老师说:“小方说得对.”完成下列问题:(1)图4的划分方法是否正确?答:____________________________.(2)判断图5的划分方法与图2小易的划分方法是否相同,并说明你的理由;答:____________________________________________________________________.(3)请你再想出一种与已有方法不同的划分方法,使之满足上述条件,并在图6中画出来.25.如图,在平面直角坐标系xOy中,直线l1:y=3x+l与y轴交于点A.直线l2:y=kx+b 与直线y=-x平行,且与直线l1交于点B(1,m),与y轴交于点C.(1)求m的值,以及直线l2的表达式;(2)点P在直线l2:y=kx+b上,且PA=PC,求点P的坐标;(3)点D在直线l1上,且点D的横坐标为a,点E在直线l2上,且DE∥y轴.若DE =6,求a的值.解:(1)(2)(3)26.在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F.(1)如图1,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;小东通过观察、实验,提出猜想:BE+CD=BC.他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.①下面是小东证明该猜想的部分思路,请补充完整:i)在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与_________________全等,判定它们全等的依据是______________;ii)由∠A= 60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=__________°;……②请直接利用....i),ii)已得到的结论,完成证明猜想BE+CD=BC的过程.证明:(2)如图2,若∠ABC=40°,求证:BF=CA.证明:附加题试卷满分:20分一、解答题(本题共12分,每小题6分)1.基础代谢是维持机体生命活动最基本的能量消耗,在身高、年龄、性别相同的前提下(不考虑其他因素的影响),可以利用某基础代谢估算公式,根据体重x(单位:kg)计算得到人体每日所需基础代谢的能量消耗y(单位:Kcal),且y是x的函数.已知六名身高约为170cm的15岁男同学的体重,以及计算得到的他们每日所需基础代谢的能量消耗,如下表所示:学生编号 A B C D E F体重x(kg)54 56 60 63 67 70每日所需基础代谢的能量消耗y( Kcal) 1596 1631 1701 1753.5 1823.5 1876请根据上表中的数据回答下列问题:(1)随着体重的增加,人体每日所需基础代谢的能量消耗______________;(填“增大”、“减小”或“不变”)(2)若一个身高约为170cm 的15岁男同学,通过计算得到他每日所需基础代谢的能量消耗为1792Kcal ,则估计他的体重最接近于( );A. 59kgB.62kgC.65kgD.68kg(3)当54≤x ≤70时,下列四个y 与x 的函数中,符合表中数据的函数是( ). A.y=x 2B.y=-10.5x+1071C.y=10x+1101D.y=17.5x+6512.我们把正n 边形(n ≥3)的各边三等分,分别以居中的那条线段为一边向外作正n 边形,并去掉居中的那条线段,得到一个新的图形叫做正n 边形的“扩展图形”,并将它的边数记为a n .如图1,将正三角形进行上述操作后得到其“扩展图形”,且a 3=12.图3、图4分别是正五边形、正六边形的“扩展图形”.(1)如图2,在5×5的正方形网格中用较粗的虚线画有一个正方形,请在图2中用实线画出此正方形的“扩展图形”;(2)已知a 3=12,a 4=20,a 5=30,则图4中a 6=_______________,根据以上规律,正n 边形的“扩展图形”中a n =___________________;(用含n 的式子表示)(3)已知345111111111,,,344556a a a =-=-=-……且345111197300n a a a a ++++=,则n=___________.二、解答题(本题8分)3.在平面直角坐标系xOy 中,直线l 1:12y x b =+与x 轴交于点A ,与y 轴交于点B ,且点C 的坐标为(4,-4).(1)点A 的坐标为___________,点B 的坐标为______________;(用含b 的式子表示) (2)当b=4时,如图1所示,连接AC ,BC ,判断△ABC 的形状,并证明你的结论; (3)过点C 作平行于y 轴的直线l 2,点P 在直线l 2上,当-5<b<4时,在直线l 1平移的过程中,若存在点P 使得△ABP 是以AB 为直角边的等腰直角三角形,请直接写出所有满足条件的点P的纵坐标.解:(2)△ABC的形状是____________________.证明:(3)点P的纵坐标为:__________________.参考答案一、选择题(本题共30分,每小题3分)题号 1 2 3 4 5 6 7 8 9 10 答案 D B C B A C A D B D二、填空题(本题共25分,第13题4分,其余每小题3分)11. x≠1 12. ( - 3,4) 13. (1)429ba;(2)8bc(各2分)14.答案不唯一.如:∠A=∠D. 15.平行,3.(第一个空1分,第二个空2分)16.答案不唯一.如:y=-4x.17.(1)如图所示;(2分)(2)15(1分)18. 8,60,2100(各1分)三、解答题(本题共27分,第19、23题每小题6分,其余每小题5分)19.解:(1) 5a2+ 10ab= 5a(a+2b);……………3分(2)mx2-12mx+36m= m(x2-12x+36) …………………………………………4分=m(x-6)2………………………………………………6分20.解:(1)选甲:一,理由合理即可,如:第—个分式的变形不符合分式的基本性质,分子漏乘x-1;………………………………………2分选乙:二,理由合理即可,如:与等式性质混淆,丢掉了分母;………………………………………2分 (2)22511x x x +++- 2(1)5(1)(1)(1)(1)x x x x x x -+=++-+-……………………3分225(1)(1)x x x x -++=+-33(1)(1)x x x +=+-……………………………………4分31x -………………………………5分 21.证明:如图, ∵AE ∥BC , ∴∠1=∠C ,∠E=∠2.…………………………………………2分在△AED 和△CFD 中, ∠1 =∠C, ∠E =∠2, AD=CD,∴△AED ≌△CFD.………………………………………………4分 ∴ED=FD.………………………………5分22.解:方程两边同乘(x+3)(x-3),得5(x-3)+2=x+3.…………………………2分 整理,得5x-15+2=x+3.……………………………………………3分 解得x=4.……………………………………………………4分经检验x=4是原分式方程的解.……………………………………………………5分 所以,原分式方程的解为x=4.23.解:(1)图象如图所示;……………………………………1分(2)∵当x=2时y的值为1,当x=-1时y的值为-5,∴ 2k +b=1,.…………………………3分解得k=2,……………………4分b=-3.(3)∵一次函数y=2x-3的图象向上平移4个单位长度后得到的新函数为y=2x+1,∴令y=0,12x=-;令x=0,y=1.∴新函数的图象与x轴,y轴的交点坐标分别为1(,0),(0,1)2-.……………………………6分四、解答题(本题共18分,第24题5分,第25题6分,第26题7分)24.解:(1)不正确;…………………………………………1分(2)相同,……………………………………………………2分理由合理即可,如:因为将图5沿直线翻折后得到的划分方法与图2的划分方法相同;……………………………………………………………………3分(3)答案不唯一,如:…………………………………………………………………………5分25.解:(1)∵点B(1,m,)在直线l1上,∴m=3×1+1=4.………………………………………………………………1分∵直线l2:y=kx+b与直线y=-x平行,∴k=-1.∵点B(1,4)在直线l2上,∴-1+b=4,解得b=5.∴直线l2的表达式为y=-x+5.………………………………2分(2)∵直线l1:y=3x+1与y轴交于点A,∴点A的坐标为(0,1).∵直线l2与y轴交于点C,∴点C的坐标为(0,5).∵PA=PC.∴点P在线段AC的垂直平分线上,∴点P的纵坐标为1+512=3.……………………………3分∵点P在直线l2上,∴-x+5=3,解得x=2.∴点P的坐标为(2,3).…………………………4分(3)∵点D在直线l1:y=3x+1上,且点D的横坐标为a,∴点D的坐标为(a,3a+1).∵点E在直线l2:y=kx+b上,且DE∥y轴,∴点E的坐标为(a,-a+5).∵DE=6.∴|3a+1-(-a+5)|=6.∴52a=或12-.………6分26.解:(1)①△BMF,边角边,60;……………………………………3分②证明:如图1.∵由i)知△BEF≌△BMF,∴∠2=∠1.∵由ii)知∠1=60°,︒=∠=∠︒=∠∴6013,602∴∠4=180°- ∠1 -∠2=60°.∴∠3=∠4.……………………4分∵CE是△ABC的角平分线,∴∠5=∠6.在△CDF和△CMF中,∠3 =∠4CF=CF,∠5=∠6.∴△CDF≌△CMF.∴CD=CM.∴BE+CD=BM+CM=BC.……………………5分(2)证明:作∠ACE的角平分线CN交AB于点N,如图2.∵∠A=60°,∠ABC=40°,∴∠ACB=180°-∠A -∠ABC=80°. ∵BD,CE分别是△ABC的角平分线,∴∠1=∠2=12∠ABC=20°,∠3 =∠ACE =12∠ACB = 40°.∵CN平分∠ACE,∴∠4=12∠ACE=20°.∴∠1=∠4.∵∠5 =∠2 +∠3 = 60°,∴∠5=∠A.∵∠6 = ∠1 +∠5,∠7 = ∠4 +∠A, ∴∠6=∠7.∴CE=CN.∵∠EBC=∠3 =40°,∴BE=CE.∴BE=CN.在△BEF和△CNA中 ,∠5=∠A∠1=∠4,BE=CN,∴△BEF≌△CNA.∴BF=CA.………………………………7分附加题一、解答题(本题共12分,每小题6分)1.解:(1)增大;……………………………………2分(2)C;……………………………………4分(3)D.…………………………6分2.解:(1)如图所示;……………………………………2分(2)42,n(n+1);…………………………………………4分(3)99.………………………………………………6分二、解答题(本题8分)3.解:(1)(-2b,0),(0,b);………………………………………………2分(2)等腰直角三角形;……………………………………………………3分证明:过点C作CD⊥y轴于点D,如图,则∠BDC=∠AOB=90°.∵点C的坐标为(4,-4),∴点D的坐标为(0,-4),CD=4.∵当b=4时,点A,B的坐标分别为(-8,0),(0,4),∴AO=8,BO=4,BD=8.∴AO=BD.BO=CD.在△AOB和△BDC中,AO=BD,∠AOB=∠BDC,BO=CD,∴△AOB≌△BDC. …………………………………4分∴∠1=∠2,AB=BC.∵∠1+∠3=90°,∴∠2+∠3=90°,即∠ABC=90°.∴△ABC是等腰直角三角形.…………………………5分(3) -12,83,8………………………………8分。
2023年中考数学总复习专题18二次函数与旋转变换综合问题(学生版)

专题18二次函数与旋转变换综合问题【例1】(2022•凉山州)在平面直角坐标系xOy中,已知抛物线y=﹣x2+bx+c经过点A (﹣1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.(1)求抛物线的解析式;(2)求点P的坐标;(3)将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.【例2】.(2022•梧州)如图,在平面直角坐标系中,直线y=﹣x﹣4分别与x,y轴交于点A,B,抛物线y=x2+bx+c恰好经过这两点.(1)求此抛物线的解析式;(2)若点C的坐标是(0,6),将△ACO绕着点C逆时针旋转90°得到△ECF,点A 的对应点是点E.①写出点E的坐标,并判断点E是否在此抛物线上;②若点P是y轴上的任一点,求BP+EP取最小值时,点P的坐标.【例3】.(2022•辽宁)如图,抛物线y=ax2﹣3x+c与x轴交于A(﹣4,0),B两点,与y 轴交于点C(0,4),点D为x轴上方抛物线上的动点,射线OD交直线AC于点E,将射线OD绕点O逆时针旋转45°得到射线OP,OP交直线AC于点F,连接DF.(1)求抛物线的解析式;(2)当点D在第二象限且=时,求点D的坐标;(3)当△ODF为直角三角形时,请直接写出点D的坐标.【例4】.(2022•河池)在平面直角坐标系中,抛物线L1:y=ax2+2x+b与x轴交于两点A,B(3,0),与y轴交于点C(0,3).(1)求抛物线L1的函数解析式,并直接写出顶点D的坐标;(2)如图,连接BD,若点E在线段BD上运动(不与B,D重合),过点E作EF⊥x轴于点F,设EF=m,问:当m为何值时,△BFE与△DEC的面积之和最小;(3)若将抛物线L1绕点B旋转180°得抛物线L2,其中C,D两点的对称点分别记作M,N.问:在抛物线L2的对称轴上是否存在点P,使得以B,M,P为顶点的三角形为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.一.解答题(共20小题)1.(2022•碑林区校级三模)如图,在平面直角坐标系中,抛物线W1与x轴交于A,B两点,与y轴交于点C(0,﹣6),顶点为D(﹣2,2).(1)求抛物线W1的表达式;(2)将抛物线W1绕原点O旋转180°得到抛物线W2,抛物线W2的顶点为D′,在抛物线W2上是否存在点M,使S△D′AD=S△D′DM?若存在,请求出点M的坐标;若不存在,请说明理由.2.(2022•双流区模拟)如图,抛物线C:y=ax2+6ax+9a﹣8与x轴相交于A,B两点(点A 在点B的左侧),已知点B的横坐标是2,抛物线C的顶点为D.(1)求a的值及顶点D的坐标;(2)点P是x轴正半轴上一点,将抛物线C绕点P旋转180°后得到抛物线C1,记抛物线C1的顶点为E,抛物线C1与x轴的交点为F,G(点F在点G的右侧).当点P与点B重合时(如图1),求抛物线C1的表达式;(3)如图2,在(2)的条件下,从A,B,D中任取一点,E,F,G中任取两点,若以取出的三点为顶点能构成直角三角形,我们就称抛物线C1为抛物线C的“勾股伴随同类函数”.当抛物线C1是抛物线C的勾股伴随同类函数时,求点P的坐标.3.(2022•灞桥区校级模拟)已知:如图,在平面直角坐标系xOy中,直线y=x+6与x 轴、y轴的交点分别为A、B,其中点C是x轴上一点,OC=3.(1)求过A、B、C三点的抛物线L的解析式;(2)将抛物线L绕着点O旋转180°得到抛物线L1,抛物线L1与x轴交于F点、E点(点F在点E的左侧),与y轴交于点M,则抛物线L1的对称轴上是否存在一点Q,使|QF﹣QM|的值最大?若存在,求出点Q的坐标及其最大值,若不存在,请说明理由.4.(2022•莲湖区二模)已知抛物线W1:y=ax2﹣bx﹣3与x轴交于A(﹣1,0)、B(3,0)两点与y轴交于点C,顶点为D.(1)求抛物线W1的表达式;(2)将抛物线W1绕原点O旋转180°后得到抛物线W2,W2的顶点为D',点M为W2上的一点,当△D'DM的面积等于△ABC的面积时,求点M的坐标.5.(2022•深圳三模)已知抛物线y=ax2+c过点A(﹣2,0)和D(﹣1,3)两点,交x轴于另一点B.(1)求抛物线解析式;(2)如图1,点P是BD上方抛物线上一点,连接AD,BD,PD,当BD平分∠ADP时,求P点坐标;(3)将抛物线图象绕原点O顺时针旋转90°形成如图2的“心形”图案,其中点M,N 分别是旋转前后抛物线的顶点,点E、F是旋转前后抛物线的交点.①直线EF的解析式是;②点G、H是“心形”图案上两点且关于EF对称,则线段GH的最大值是.6.(2022•无锡二模)二次函数y=ax2+bx+4的图象与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0).(1)求此二次函数的表达式;(2)①如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标;②如图2,点M在抛物线上,且点M的横坐标是1,将射线MA绕点M逆时针旋转45°,交抛物线于点P,求点P的坐标;(3)已知Q在y轴上,T为二次函数对称轴上一点,且△QOT为等腰三角形,若符合条件的Q恰好有2个,直接写出T的坐标.7.(2022•沙湾区模拟)如图,抛物线f(x):y=a(x+1)(x﹣5)与x轴交于点A、B(点A 位于点B左边),与y轴交于点C(0,.(1)求抛物线f(x)的解析式;(2)作点C关于x轴的对称点C',连接线段AC,作∠CAB的平分线AE交抛物线于点E,将抛物线f(x)沿对称轴向下平移经过点C'得到抛物线f'(x).在射线AE上取点F,连接FC,将射线FC绕点F逆时针旋转120°交抛物线f'(x)于点P.当△ACF为等腰三角形时,求点P的横坐标.8.(2022•灌南县二模)如图,抛物线y=ax2+bx+3经过点A(1,0),B(3,0)两点,与y轴交于点C,其顶点为M,连接MA,MC,AC,过点C作y轴的垂线l.(1)求该抛物线的表达式;(2)直线l上是否存在点N,使得S△MBN=2S△MAC?若存在,求出点N的坐标;若不存在,请说明理由.(3)如图2,若将原抛物线绕点C逆时针旋转45°,求新抛物线与y轴交点P坐标.9.(2022•红花岗区三模)如图(1),△ABC中,AC=BC=6,∠C=90°,点P在线段AC 上,从C点向A点运动,∠PBE=90°,BP=BE,PE交BC于点D,完成下列问题:(1)①点E到BC边的距离为;②若CD=x,△BDE的面积为S,则S与x的函数关系式为;(不写自变量取值范围)(2)当△BDE的面积为15时,若PC<AC,以C为原点,AC、BC所在直线分别为x、y轴建立坐标系如图(2),抛物线C1过点A、D、B;①点Q在抛物线C1上,且位于线段PB的下方,过点Q作QN⊥PB,垂足为点N,是否存在点Q,使得QN最长,若存在,请求出QN的长度和Q点坐标;若不存在,请说明理由;②将抛物线C1绕原点C旋转180°,得到抛物线C2,当﹣2a≤x≤﹣a时(a>0),抛物线C2有最大值2a,求a值.10.(2022•乳源县三模)如图,对称轴为直线x=﹣1的抛物线y=a(x﹣h)2+k(a≠0)图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,其中点B的坐标为(2,0),点C的坐标为(0,4).(1)求该抛物线的解析式;(2)如图1,若点P为抛物线上第二象限内的一个动点,点M为线段CO上一动点,当△APC的面积最大时,求△APM周长的最小值;(3)如图2,将原抛物线绕点A旋转180°,得新抛物线y',在新抛物线y'的对称轴上是否存在点Q使得△ACQ为等腰三角形?若存在,请直接写出点Q的坐标;若不存在,说明理由.11.(2021秋•亭湖区期末)如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(0,﹣3),与x轴的交点为B、C,直线l:y=2x+2与抛物线相交于点C,与y轴相交于点D,P是直线l下方抛物线上一动点.(1)求抛物线的函数表达式;(2)过点P作线段PM∥x轴,与直线l相交于点M,当PM最大时,求点P的坐标及PM的最大值;(3)把抛物线绕点O旋转180°,再向上平移使得新抛物线过(2)中的P点,E是新抛物线与y轴的交点,F为原抛物线对称轴上一点,G为平面直角坐标系中一点,直接写出所有使得以B、E、F、G为顶点、BF为边的四边形是菱形的点G的坐标,并把求其中一个点G的坐标的过程写出来.12.(2021秋•北京期中)定义:如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,则称抛物线C1与C2关联.例如,如图,抛物线y=x2的顶点(0,0)在抛物线y=﹣x2+2x上,抛物线y=﹣x2+2x的顶点(1,1)也在抛物线y=x2上,所以抛物线y=x2与y=﹣x2+2x关联.(1)已知抛物线C1:y=(x+1)2﹣2,分别判断抛物线C2:y=﹣x2+2x+1和抛物线C3:y=2x2+2x+1与抛物线C1是否关联;(2)抛物线M1:的顶点为A,动点P的坐标为(t,2),将抛物线M1绕点P(t,2)旋转180°得到抛物线M2,若抛物线M1与M2关联,求抛物线M2的解析式;(3)抛物线M1:的顶点为A,点B是与M1关联的抛物线的顶点,将线段AB绕点A按顺时针方向旋转90°得到线段AB1,若点B1恰好在y轴上,请直接写出点B1的纵坐标.13.(2021•锡山区一模)如图,抛物线y=x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(﹣3,0)和B,将抛物线y=x2+bx+c绕点B逆时针方向旋转90°,点M1、A1为点M、A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.(1)写出点B的坐标及求原抛物线的解析式;(2)求证A,M,A1三点在同一直线上;(3)设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD 的面积最大?如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.14.(2022秋•道里区校级期中)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+3交x轴于点A,y轴于点D,抛物线y=x2+bx﹣3与x轴交于A,B两点,交y轴于点C.(1)求抛物线的解析式;(2)P在第三象限抛物线上,P点横坐标为t,连接AP、DP,△APD的面积为s,求s 关于t的函数关系式;(不要求写自变量t的取值范围)(3)在(2)的条件下,PD绕点P逆时针旋转,与线段AD相交于点E,且∠EPD=2∠PDC,过点E作EF⊥PD交PD于G,y轴于点F,连接PF,若,求线段PF的长.15.(2022秋•大兴区期中)在平面直角坐标系xOy中,已知四边形OABC是平行四边形,点A(4,0),∠AOC=60°,点C的纵坐标为,点D是边BC上一点,连接OD,将线段OD绕点O逆时针旋转60°得到线段OE.给出如下定义:如果抛物线y=ax2+bx(a≠0)同时经过点A,E,则称抛物线y=ax2+bx(a≠0)为关于点A,E的“伴随抛物线”.(1)如图1,当点D与点C重合时,点E的坐标为,此时关于点A,E的“伴随抛物线”的解析式为;(2)如图2,当点D在边BC上运动时,连接CE.①当CE取最小值时,求关于点A,E的“伴随抛物线”的解析式;②若关于点A,E的“伴随抛物线”y=ax2+bx(a≠0)存在,直接写出a的取值范围.16.(2020秋•天心区期末)如图1,在平面直角坐标系xOy中,抛物线C:y=﹣x2+bx+c 与x轴相交于A,B两点,顶点为D,其中A(﹣4,0),B(4,0),设点F(m,0)是x轴的正半轴上一点,将抛物线C绕点F旋转180°,得到新的抛物线C'.(1)求抛物线C的函数解析式;(2)若抛物线C'与抛物线C在y轴的右侧有两个不同的公共点,求m的取值范围;(3)如图2,P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C'上的对应点P',设M是C上的动点,N是C'上的动点,试探究四边形PMP'N能否成为正方形?若能,求出m的值;若不能,请说明理由.17.(2022•大庆模拟)如图1,在平面直角坐标系xOy中,直线l:与x轴、y轴分别交于点A和点B(0,﹣1),抛物线经过点B,且与直线l的另一个交点为C(4,n).(1)求n的值和抛物线的解析式;(2)点D在抛物线上,且点D的横坐标为t(0<t<4).DE∥y轴交直线l于点E,点F 在直线l上,且四边形DFEG为矩形(如图2).若矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;(3)M是平面内一点,将△AOB绕点M沿逆时针方向旋转90°后,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的横坐标.18.(2022•苏州一模)如图,二次函数y=x2+bx+4的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣8,0),P是抛物线上一点(点P与点A、B、C不重合).(1)b=,点B的坐标是;(2)连接AC、BC,证明:∠CBA=2∠CAB;(3)点D为AC的中点,点E是抛物线在第二象限图象上一动点,作DE,把点A沿直线DE翻折,点A的对称点为点G,点E运动时,当点G恰好落在直线BC上时,求E 点的坐标.19.(2022•大连模拟)已知抛物线G:y=(m+1)x2+2(n﹣1)x+n+1(m≠﹣1,m为常数)的对称轴与直线y=kx+k(k>0,k为常数)相交于x轴上一点P.(1)求m与n的数量关系;(2)若直线y=kx+k与y轴交于点Q,且OQ=OP,①把直线y=kx+k绕点Q顺时针旋转45°得到的直线与抛物线G相交于A、B两点,若AB=4,求m的值;②将直线y=kx+k向上平移2k个单位,得到的直线与抛物线G的两个交点的横坐标x1,x2满足﹣2<x1<x2<2,求m的取值范围.20.(2021•兰州)如图1,二次函数y=a(x+3)(x﹣4)图象交坐标轴于点A,B(0,﹣2),点P为x轴上一动点.(1)求二次函数y=a(x+3)(x﹣4)的表达式;(2)过点P作PQ⊥x轴分别交线段AB,抛物线于点Q,C,连接AC.当OP=1时,求△ACQ的面积;(3)如图2,将线段PB绕点P逆时针旋转90°得到线段PD.当点D在抛物线上时,求点D的坐标.。
(完整)中考数学压轴题精选及答案
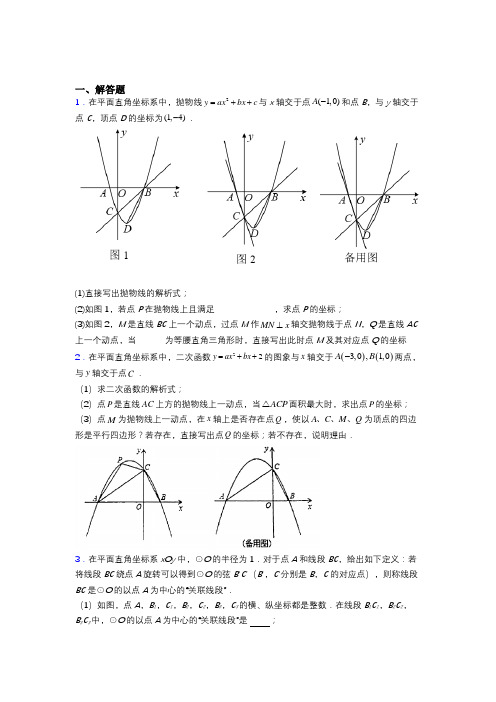
一、解答题1.在平面直角坐标系中,抛物线2y ax bx c =++与x 轴交于点(1,0)A -和点B ,与y 轴交于点C ,顶点D 的坐标为(1,4)-.(1)直接写出抛物线的解析式;(2)如图1,若点P 在抛物线上且满足,求点P 的坐标; (3)如图2,M 是直线BC 上一个动点,过点M 作MN x ⊥轴交抛物线于点N ,Q 是直线AC 上一个动点,当为等腰直角三角形时,直接写出此时点M 及其对应点Q 的坐标2.在平面直角坐标系中,二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,与y 轴交于点C .(1)求二次函数的解析式;(2)点P 是直线AC 上方的抛物线上一动点,当ACP △面积最大时,求出点P 的坐标;(3)点M 为抛物线上一动点,在x 轴上是否存在点Q ,使以A C M Q 、、、为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标;若不存在,说明理由.3.在平面直角坐标系xOy 中,⊙O 的半径为1.对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到⊙O 的弦B ′C ′(B ′,C ′分别是B ,C 的对应点),则称线段BC 是⊙O 的以点A 为中心的“关联线段”.(1)如图,点A ,B 1,C 1,B 2,C 2,B 3,C 3的横、纵坐标都是整数.在线段B 1C 1,B 2C 2,B 3C 3中,⊙O 的以点A 为中心的“关联线段”是 ;(2)△ABC 是边长为1的等边三角形,点A (0,t ),其中t ≠0.若BC 是⊙O 的以点A 为中心的“关联线段”,求t 的值;(3)在△ABC 中,AB =1,AC =2.若BC 是⊙O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长.4.综合与探究如图,在平面直角坐标系中,点()0,10A ,点B 是x 轴的正半轴上的一个动点,连接AB ,取AB 的中点M ,将线段MB 绕着点B 按顺时针方向旋转90°,得到线段BC .过点B 作x 轴的垂线交直线AC 于点D .设点B 坐标是(),0t(1)当6t =时,点M 的坐标是 ;(2)用含t 的代数式表示点C 的坐标;(3)是否存在点B ,使四边形AOBD 为矩形?若存在,请求出点B 的坐标;若不存在,请说明理由;(4)在点B 的运动过程中,平面内是否存在一点N ,使得以A 、B 、N 、D 为顶点的四边形是菱形?若存在,请直接写出点N 的纵坐标(不必要写横坐标);若不存在,请说明理由.5.如图(1),在菱形ABCD 中,∠ABC =60°,点E 在边CD 上(不与点C ,D 重合),连结AE ,交BD 于点F .(1)如图(2),若点M 在BC 边上,且DE =CM ,连结AM ,EM .求证:三角形AEM 为等边三角形;(2)设DF x BF=,求tan ∠AFB 的值(用x 的代数式表示); (3)如图(3),若点G 在线段BF 上,且FG =2BG ,连结AG 、CG ,DF x BF =,四边形AGCE 的面积为S 1,ABG 的面积为S 2,求12S S 的最大值.6.如图,在平面直角坐标系中,ABC 的边AB 在x 轴上,且OB OA >,以AB 为直径的圆过点C .若点C 的坐标为()0,4,10AB =,(1)求抛物线的解析式;(2)点P 为该函数在第一象限内的图象上一点(不与BC 重合),过点P 作PQ BC ⊥,垂足为点Q ,连接PC .若以点P 、C 、Q 为顶点的三角形与COA 相似,求点P 的坐标;(3)若ACB ∠平分线所在的直线l 交x 轴与点E ,过点E 任作一直线l '分别交射线CA ,CB (点C 除外)于点M ,N .则11CM CN+的是否为定值?若是,求出该定值;若不是,请说明理由.7.如图1,⊙I 与直线a 相离,过圆心I 作直线a 的垂线,垂足为H ,且交⊙I 于P 、Q 两点(Q 在P 、H 之间).我们把点Q 称为⊙I 关于直线a 的“近点”,点P 称为⊙I 关于直线a 的“远点”把PQ ·QH 的值称为⊙I 关于直线a 的“特征数”.(1)如图2,在平面直角坐标系xOy 中,点E 的坐标为(0,3).半径为1的⊙O 与两坐标轴交于点A 、B 、C 、D .①过点E 画垂直于y 轴的直线m ,则⊙O 关于直线m 的“近点”“远点”分别是点_____和_____(填“A ”、“B ”、“C ”或“D ”),⊙O 关于直线m 的“特征数”为_____;②若直线n 的函数表达式为33y x =-+.求⊙O 关于直线n 的“特征数”;(2)在平面直角坐标系xOy 中,直线l 经过点M (1,2),点F 是坐标平面内一点,以F 5为半径作⊙F .若⊙F 与直线l 相离,点N (1-,0)是⊙F 关于直线l 的“近点”.且⊙F 关于直线l 的“特征数”是6,求直线l 的函数表达式.8.如图,抛物线y=-x2+bx+c与x轴交于A,B两点,其中A(3,0),B(-1,0),与y轴交于点C,抛物线的对称轴交x轴于点D,直线y=kx+b1经过点A、C,连接CD.(1)分别求抛物线和直线AC的解析式;(2)在直线AC下方的抛物线上,是否存在一点P,使得△ACP的面积是△ACD面积的2倍,若存在,请求出点P的坐标;若不存在,请说明理由;(3)在抛物线的对称轴上是否存在一点Q,使线段AQ绕Q点顺时针旋转90°得到线段QA1,且点A1恰好落在该抛物线上?若存在,求出点Q的坐标;若不存在,请说明理由.9.已知:如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,以OA,OC为边作矩形ABCO,矩形ABCO的面积是36.(1)求直线AC的解析式.(2)点P为线段AB上一点,点Q为第一象限内一点,连接PO,PQ,∠OPQ=90°,且OP=PQ,设AP的长为t,点Q的横坐标为d,求d与t的函数关系式.(不要求写出自变量t的取值范围)(3)在(2)的条件下,过点Q作QE∥PO交AB的延长线于点E,作∠POC的平分线OF 交PE于点F,交PQ于点K,若KQ=2EF,求点Q的坐标.10.如图,平面直角坐标系中,点O为原点,抛物线交x轴于()2,05,0B两点,交y轴于点C.A-、()(1)求抛物线解析式;(2)点P在第一象限内的抛物线上,过点P作x轴的垂线,垂足为点H,连AP交y轴于点E,设P点横坐标为t,线段EC长为d,求d与t的函数解析式;(3)在(2)条件下,点M在CE上,点Q在第三象限内抛物线上,连接PC、PQ、PM,PQ与y轴交于W,若,,,求点Q的坐标.11.已知:如图1,点A(a,b),AB x⊥轴于点B2++-+=.a b a b24(8)0(1)试判断△AOB的形状,并说明理由;(2)如图2,若点C为线段AB的中点,连OC并作OD OC⊥,且OD OC=,连AD交x轴于点E,试求点E的坐标;(3)如图3,若点M为点B的左边x轴负半轴上一动点,以AM为一边作45∠=︒交MANy轴负半轴于点N,连MN,在点M运动过程中,试猜想式子OM MN ON+-的值是否发生变化?若不变,求这个不变的值;若发生变化,试求它变化的范围.12.直角三角板ABC的斜边AB的两个端点在⊙O上,已知∠BAC=30°,直角边AC与⊙O 相交于点D,且点D是劣弧AB的中点.(1)如图1,判断直角边BC所在直线与⊙O的位置关系,并说明理由;(2)如图2,点P是斜边AB上的一个动点(与A、B不重合),DP的延长线交⊙O于点Q,连接QA、QB.①AD=6,PD=4,则AB= ;PQ= ;②当点P在斜边AB上运动时,求证:QA+QB=3QD.13.如图,已知四边形ABCD内接于⊙O,直径DF交BC于点G.(1)如图1,求证:∠BAD-∠BCF=90°;(2)如图2,连接AC,当∠BAC=∠CFD+∠ACD时,求证:CA=CB;(3)如图3,在(2)的条件下,AC交DF于点H,∠BAC=∠DGB,45CGBG,AC=9,求△CDH的面积.14.同学们学过正方形与等腰三角形发现它们都是轴对称图形,它们之间有很多相似,在正边形ABCD中,E是对角线AC上一点(不与点A、C重合),以AD、AE为邻边作平行四边形AEGD,GE交CD于点M,连接CG.(1)如图1,当12AE AC<时,过点E作EF BE⊥交CD于点F,连接GF并延长交AC于点H.求证:EB EF=;(2)在ABC中,AB AC=,90BAC∠=︒.过点A作直线AP,点C关于直线AP的对称点为点D,连接BD,CD直线BD交直线AP于点E.如图2,①依题意补全图形;②请用等式表示线段EB,ED,BC之间的数量关系,并予以证明.15.如图,在平面直角坐标系中,抛物线y=x2+bx+c与x轴交于点A和点B(1,0),与y轴交于点C(0,﹣3).(1)求抛物线的函数表达式.(2)若点P为第三象限内抛物线上一动点,作PD⊥x轴于点D,交AC于点E,过点E作AC 的垂线与抛物线的对称轴和y轴分别交于点F、G,设点P的横坐标为m.①求PE2的最大值;②连接DF、DG,若∠FDG=45°,求m的值.16.【问题提出】如图①,在△ABC中,若AB=8,AC=4,求BC边上的中线AD的取值范围.【问题解决】解决此问题可以用如下方法:延长AD 到点E ,使DE =AD ,再连结BE (或将△ACD 绕着点D 逆时针旋转180°得到△EBD ),把AB 、AC ,2AD 集中在△ABE 中,利用三角形三边的关系即可判断.由此得出中线AD 的取值范围是__________【应用】如图②,如图,在△ABC 中,D 为边BC 的中点、已知AB =10,AC =6,AD =4,求BC 的长.【拓展】如图③,在△ABC 中,∠A =90°,点D 是边BC 的中点,点E 在边AB 上,过点D 作D F⊥DE 交边AC 于点F ,连结EF .已知BE =5,CF =6,则EF 的长为__________.17.已知二次函数()20y x bx c a =++≠的图象与x 轴的交于A 、B (1,0)两点,与y 轴交于点()03C -,.(1)求二次函数的表达式及A 点坐标;(2)D 是二次函数图象上位于第三象限内的点,若点D 的横坐标为m ,ACD △的面积为S ,求S 与m 之间的函数关系式,并写出ACD △的面积取得最大值时点D 的坐标;(3)M 是二次函数图象对称轴上的点,在二次函数图象上是否存在点N .使以M 、N 、B 、O 为顶点的四边形是平行四边形?若有,请写出点N 的坐标(不写求解过程).18.如图,在平面直角坐标系中,已知二次函数图像222(1)2y x a x a a =-+++的顶点为P ,点B 39(2,)16- 是一次函数5119216y x =+上一点.(1)当a =0时,求顶点P 坐标;(2)若a >0,且一次函数2y x b =-+的图象与此抛物线没有交点,请你写出一个符合条件的一次函数关系式(只需写一个,不必写出过程);(3)作直线OC :12y x =与一次函数5119216y x =+交于点C .连结OB ,当抛物线与△OBC 的边有两个交点时,求a 的取值范围.19.已知O 为ABC ∆的外接圆,AC BC =,点D 是劣弧AB 上一点(不与点A ,B 重合),连接DA ,DB ,DC .(1)如图1,若AB 是直径,将ACD ∆绕点C 逆时针旋转得到BCE ∆.若4CD =,求四边形ADBC 的面积;(2)如图2,若AB AC =,半径为2,设线段DC 的长为x .四边形ADBC 的面积为S . ①求S 与x 的函数关系式;②若点M ,N 分别在线段CA ,CB 上运动(不含端点),经过探究发现,点D 运动到每一个确定的位置.DMN ∆的周长有最小值t ,随着点D 的运动,t 的值会发生变化.求所有t 值中的最大值,并求此时四边形ADBC 的面积S .20.如图,在ABCD 中,90ABD ∠=︒,5cm AD =,8cm BD =.点P 从点A 出发,沿折线AB BC -向终点C 运动,点P 在AB 边、BC 边上的运动速度分别为1cm/s 、5cm /s .在点P 的运动过程中,过点P 作AB 所在直线的垂线,交边AD 或边CD 于点Q ,以PQ 为一边作矩形PQMN ,且2QM PQ =,MN 与BD 在PQ 的同侧.设点P 的运动时间为t (秒),矩形PQMN 与ABCD 重叠部分的面积为()2cm S .(1)求边AB 的长.(2)当04t <<时,PQ = ,当48t <<时,PQ = .(用含t 的代数式表示)(3)当点M 落在BD 上时,求t 的值.(4)当矩形PQMN 与ABCD 重叠部分图形为四边形时,求S 与t 的函数关系式.【参考答案】参考答案**科目模拟测试一、解答题1.(1)223y x x =--;(2),; (3),;,;,;,; ,;,. 【解析】【分析】(1)根据顶点的坐标,设抛物线的解析式为y =a (x ﹣1)2﹣4,将点A (﹣1,0)代入,求出a 即可得出答案;(2)利用待定系数法求出直线BD 解析式为y =2x ﹣6,过点C 作CP 1∥BD ,交抛物线于点P 1,再运用待定系数法求出直线CP 1的解析式为y =2x ﹣3,联立方程组即可求出P 1(4,5),过点B 作y 轴平行线,过点C 作x 轴平行线交于点G ,证明△OCE ≌△GCF(ASA),运用待定系数法求出直线CF解析式为y=12x﹣3,即可求出P2(52,﹣74);(3)利用待定系数法求出直线AC解析式为y=﹣3x﹣3,直线BC解析式为y=x﹣3,再分以下三种情况:①当△QMN是以NQ为斜边的等腰直角三角形时,②当△QMN是以MQ为斜边的等腰直角三角形时,③当△QMN是以MN为斜边的等腰直角三角形时,分别画出图形结合图形进行计算即可.(1)解:∵顶点D的坐标为(1,﹣4),∴设抛物线的解析式为y=a(x﹣1)2﹣4,将点A(﹣1,0)代入,得0=a(﹣1﹣1)2﹣4,解得:a=1,∴y=(x﹣1)2﹣4=x2﹣2x﹣3,∴该抛物线的解析式为y=x2﹣2x﹣3;(2)解:∵抛物线对称轴为直线x=1,A(﹣1,0),∴B(3,0),设直线BD解析式为y=kx+e,∵B(3,0),D(1,﹣4),∴,解得:,∴直线BD解析式为y=2x﹣6,过点C作CP1∥BD,交抛物线于点P1,设直线CP1的解析式为y=2x+d,将C(0,﹣3)代入,得﹣3=2×0+d,解得:d=﹣3,∴直线CP1的解析式为y=2x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=2x﹣3,解得:x1=0(舍),x2=4,故P1(4,5),过点B作y轴平行线,过点C作x轴平行线交于点G,∵OB=OC,∠BOC=∠OBG=∠OCG=90°,∴四边形OBGC是正方形,设CP1与x轴交于点E,则2x﹣3=0,解得:x=32,∴E(32,0),在x轴下方作∠BCF=∠BCE交BG于点F,∵四边形OBGC是正方形,∴OC=CG=BG=3,∠COE=∠G=90°,∠OCB=∠GCB=45°,∴∠OCB﹣∠BCE=∠GCB﹣∠BCF,即∠OCE=∠GCF,∴△OCE≌△GCF(ASA),∴FG=OE=32,∴BF=BG﹣FG=3﹣32=32,∴F(3,﹣32),设直线CF解析式为y=k1x+e1,∵C(0,﹣3),F(3,﹣32),∴,解得:,∴直线CF解析式为y=12x﹣3,结合抛物线y=x2﹣2x﹣3,可得x2﹣2x﹣3=12x﹣3,解得:x1=0(舍),x2=52,∴P2(52,﹣74),综上所述,符合条件的P点坐标为:(4,5)或(52,﹣74);(3)解:(3)设直线AC解析式为y=m1x+n1,直线BC解析式为y=m2x+n2,∵A(﹣1,0),C(0,﹣3),∴,解得:,∴直线AC解析式为y=﹣3x﹣3,∵B(3,0),C(0,﹣3),∴,解得:,∴直线BC解析式为y=x﹣3,设M(t,t﹣3),则N(t,t2﹣2t﹣3),∴MN=|t2﹣2t﹣3﹣(t﹣3)|=|t2﹣3t|,①当△QMN是以NQ为斜边的等腰直角三角形时,此时∠NMQ=90°,MN=MQ,如图2,∵MQ∥x轴,∴Q(﹣13t,t﹣3),∴|t2﹣3t|=|t﹣(﹣13t)|,∴t2﹣3t=±43t,解得:t=0(舍)或t=53或t=133,∴,;,;②当△QMN是以MQ为斜边的等腰直角三角形时,此时∠MNQ=90°,MN=NQ,如图3,∵NQ∥x轴,∴Q(,t2﹣2t﹣3),∴NQ=|t﹣|=13|t2+t|,∴|t2﹣3t|=13|t2+t|,解得:t=0(舍)或t=5或t=2,∴M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);③当△QMN是以MN为斜边的等腰直角三角形时,此时∠MQN=90°,MQ=NQ,如图4,过点Q作QH⊥MN于H,则MH=HN,∴H(t,),∴Q(,),∴QH=|t﹣|=16|t2+5t|,∵MQ=NQ,∴MN=2QH,∴|t2﹣3t|=2×16|t2+5t|,解得:t=7或1,∴M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3);综上所述,点M及其对应点Q的坐标为:,;,;M3(5,2),Q3(﹣5,12);M4(2,﹣1),Q4(0,﹣3);M5(7,4),Q5(﹣7,18);M6(1,﹣2),Q6(0,﹣3).【点睛】本题是二次函数综合题,主要考查了待定系数法求一次函数和二次函数解析式,求一次函数与二次函数图象交点坐标,全等三角形判定和性质,正方形判定和性质,等腰直角三角形性质等,本题属于中考压轴题,综合性强,难度较大,熟练掌握待定系数法、等腰直角三角形性质等相关知识,运用数形结合思想、分类讨论思想是解题关键.2.(1)224233y x x =--+;(2)35(,)22P -(3)存在,12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【解析】【分析】(1)根据待定系数法求抛物线解析式;(2)设224(,)33P t t --根据(1)的结论求得C 的坐标,进而求得AC 的解析式,过P 作PD ⊥x 轴交AC 于点D ,进而求得PD 的长,根据12APC C A S PD x x =⋅⋅-△求得APC S 的表达式,进而根据二次函数的性质求得取得最大值时,t 的值,进而求得P 点的坐标;(3)分情况讨论,①//CM AQ ,②//AC MQ ,根据抛物线的性质以及平行四边形的性质先求得M 的坐标进而求得Q 点的坐标.【详解】(1)二次函数22y ax bx =++的图象与x 轴交于()()3,0,1,0A B -两点,则093202a b a b =-+⎧⎨=++⎩解得2343a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴抛物线解析式为224233y x x =--+ (2)抛物线224233y x x =--+与y 轴交于点C ,令0x =,则2y = (0,2)C ∴设直线AC 的解析式为y kx b =+,由(3,0)A -,(0,2)C ,则302k b b -+=⎧⎨=⎩解得232k b ⎧=⎪⎨⎪=⎩ ∴直线AC 的解析式为223y x =+, 如图,过P 作PD ⊥x 轴交AC 于点D ,设224(,)33P t t --,则2(,2)3D t t +, 2224222223333PD t t t t t ⎛⎫∴=--+-+=-- ⎪⎝⎭∴12APC C A S PD x x =⋅⋅-△212(2)323t t =⨯--⨯2239324t t t ⎛⎫=--=-++ ⎪⎝⎭ ∴当32t =-时,APC S 取得最大值,此时222423435223332322t t ⎛⎫⎛⎫--+=-⨯--⨯-+= ⎪ ⎪⎝⎭⎝⎭ ∴35(,)22P - (3)存在,理由如下抛物线解析式为224233y x x =--+()228133x =-++ ∴抛物线的对称轴为直线1x =①如图,当//CM AQ 时,Q 点在x 轴上,//CM x 轴∴,M C 关于抛物线的对称轴直线1x =对称,(0,2)C(2,2)M ∴-2CM ∴=122AQ AQ ∴==(3,0)A -12(1,0),(5,0)Q Q ∴--②当//AC MQ 时,如图,设M 的纵坐标为n ,四边形ACQM 是平行四边形,点A ,Q 在x 轴上,则,AQ MC 的交点也在x 轴上, 202n +∴= 解得2n =-设(,2)M m -,2242233x x ∴-=--+ 解得17x =-(17,2)M ∴--A 点到C 点是横坐标加3,纵坐标加2∴M 点到Q 点也是横坐标加3,纵坐标加2 即(173,0)Q -±34(27,0),(27,0)Q Q ∴综上所述,存在点Q ,使得以A C M Q 、、、为顶点的四边形是平行四边形,Q 点的坐标为12(1,0),(5,0)Q Q --,34(27,0),(27,0)Q Q .【点睛】本题考查了二次函数综合,待定系数法,二次函数最值,二次函数的图象与性质,平行四边形的性质,综合运用以上知识是解题的关键.3.(1)B 2C 2;(233-3)OA 最小值为1,相应的3BC =OA 最大值为2,相应的6BC =【解析】【分析】(1)结合题意,根据旋转和圆的性质分析,即可得到答案;(2)根据题意,分B C ''在x 轴上方和x 轴上方两种情况;根据等边三角形、勾股定理、全等三角形的性质,得32AD OD ==,从而完成求解; (3)结合题意,得当AC '为⊙O 的直径时,OA 取最小值;当A 、B '、O 三点共线时,OA 取最大值;根据勾股定理、等腰三角形的性质计算,即可得到答案.【详解】(1)线段B 1C 1绕点A 旋转得到的11B C '',均不能成为⊙O 的弦∴线段B 1C 1不是⊙O 的以点A 为中心的“关联线段”;线段B 2C 2绕点A 旋转得到的22B C '',如下图:∴线段B 2C 2是⊙O 的以点A 为中心的“关联线段”;线段B 3C 3绕点A 旋转得到的33B C '',均不能成为⊙O 的弦∴线段B 3C 3不是⊙O 的以点A 为中心的“关联线段”;故答案为:B 2C 2;(2)∵△ABC 是边长为1的等边三角形,点A (0,t ),⊙O 的半径为1 ∴//B C x ''轴分B C ''在x 轴上方和x 轴上方两种情况:当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:∵1OB OC ''==∴1122B D B C '''== ∴2232OD OB B D ''=-=∵△ABC 是边长为1的等边三角形,即△AB C ''是边长为1的等边三角形, ∴AC D OC D ''∠=∠,AD B C ''⊥ ∴AC D OC D ''△≌△∴32AD OD == ∴3AO AD OD =+=∴3t =;当B C ''在x 轴上方时,B C ''与y 轴相交于点D ,见下图:同理,3AO AD OD =+=∴()0,3A -;∴t 3=-;∴3t =或3-;(3)当AC '为⊙O 的直径时,OA 取最小值,如下图:∴OA 最小值为1,90AB C ''∠=︒ ∴223BC B C AC AB ''''==-=;当A 、B '、O 三点共线时,OA 取最大值,2OA AC '== ,如下图:作AE OC '⊥交OC '于点E ,作C F AO '⊥交AO 于点F ,如下图∵2OA AC '==∴1122OE OC '==∴2215AE AO OE - ∵11222AE OC OB C F '''⨯=⨯⨯ ∴1152C F AE '==∴2214OF OC C F ''=-=∴34B F OB OF ''=-=∴262BC B C C F B F ''''==+=∴OA 最小值为1,相应的3BC =;OA 最大值为2,相应的62BC =. 【点睛】本题考查了旋转、圆、等边三角形、勾股定理、全等三角形、等腰三角形的知识;解题的关键是熟练掌握旋转、圆周角、等腰三角形三线合一、勾股定理的性质,从而完成求解.4.(1)(3,5)M ,(2)1(5,)2C t t +;(3)(20,0)B ;(4)154或10. 【解析】 【分析】(1)利用中点坐标公式计算即可.(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .证明()MEB BFC AAS ∆≅∆,利用全等三角形的性质即可解决问题.(3)如图2中,存在.由题意当CF OA =时,可证四边形AOBD 是矩形,构建方程即可解决问题.(4)分三种情形:①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为6.③因为BD AB ≠,所以不存在以AD 为对角线的菱形. 【详解】解:(1)如图1中,(0,10)A ,(6,0)B ,AM BM =, (3,5)M ∴,(2)如图1中,作ME OB ⊥于E ,CF x ⊥轴于F .//ME OA ,AM BM =, 12OE EB t ∴==,152ME OA ==,90MEB CFB CBM ∠=∠=∠=︒,90MBE CBF ∴∠+∠=︒,90MBE BME ∠+∠=︒, BME CBF ∴∠=∠,()MEB BFC AAS ∴∆≅∆,5BF ME ∴==,12CF BE t ==,5OF OB BF t ∴=+=+, 1(5,)2C t t ∴+.(3)存在.如图2中,作ME OB ⊥于E ,CF x ⊥轴于F .理由:由题意当=10CF OA =时,//OA CF , ∴四边形AOFC 是平行四边形,90AOF ∠=︒,∴四边形AOFC 是矩形,90DAO AOB DBO ∴∠=∠=∠=︒,∴四边形AOBD 是矩形,又∵由(2)得12CF BE t ==, 即:1102t =,解得:20t =.(20,0)B ∴.(4)①如图3中,当AD BD =时,以AB 为对角线可得菱形ADBN ,此时点N 在y 轴上.AD BD =, BAD ABD ∴∠=∠,OAB ABD ∴∠=∠,OAB BAD ∴∠=∠. tan tan OAB BAD ∴∠=∠, ∴12OB BC OA BA ==,即1102t =,5t ∴=,5OB ∴=,设AN NB m ==,在Rt OBN △中,则有2225(10)m m =+-, 解得254m =, 25151044ON OA AN ∴=-=-=, ∴点N 的纵坐标为154. ②如图4中,当AD AB =时,以BD 为对角线可得菱形ABND .此时点N 的纵坐标为10.③BD AB ≠,∴不存在以AD 为对角线的菱形. 综上所述,满足条件的点N 的纵坐标为154或10. 【点睛】本题属于四边形综合题,考查了矩形的判定和性质,菱形的判定和性质,翻折变换,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.5.(1)证明见解析;(23333xx;(3)194【解析】 【分析】(1)如图,连接,AC 证明,ACB ACD 都为等边三角形,可得,AC AD = 再证明,ACM ADE ≌从而可得答案;(2)如图,记,AC BD 交于点,O 设,,DFa OFb 四边形ABCD 为菱形,60,ABC ∠=︒表示33,33OA OB a b 利用,2DF ax BF a b则2,1a xb x再利用三角函数的定义可得答案;(3)如图,设,DFESn 证明,DFE BFA ∽ 2,BFAnSx 再表示2222,,33ABGAGFn nSS S x x 结合菱形的轴对称的性质可得:2=,3CBG nS x 表示,AFDn S x可得2=,BCD ABDn n S Sxx 可得2212243334,3nn n S x x x x n S x 再利用二次函数的性质可得答案.【详解】证明:(1)如图,连接,AC 菱形ABCD 中,∠ABC =60°,,60,120,60,AB BC CDAD ABC ADC BAD BCD BAC CAD ACB,ACB ACD 都为等边三角形,,AC AD ∴=,60,DE CM ACM ADE,ACM ADE ≌ ,,AMAE MAC EAD 60,MACCAECAEEADAME ∴是等边三角形(2)如图,记,AC BD 交于点,O设,,DF a OF b 四边形ABCD 为菱形,60,ABC ∠=︒,,30,ACBD OB OD a b ABO33,33OAOB a b ,2DF a x BFa b1221,a b bx a a 11,22b ax 则2,1ax bx333tan 13a b OAa AFBOFbb32331,3133xxxx(3)如图,设,DFESn四边形ABCD 是平行四边形,,DFE BFA ∽22=,BFAn DF x S BF2,BFAn SxFG =2BG , 2222,,33ABGAGFn n SS S xx根据菱形的轴对称的性质可得:2=,3CBG n S x ,AFD ABFS DF x SBF2,AFDn n S x x x 2=,BCDABD n n SSxx1222224=333n n n n n nS nn x x x x x x, 2212243334,3n n n S x x x x n S x 30,a所以12S S 有最大值, 当31232x时,最大值为:1119334.424【点睛】本题考查的是菱形的性质,全等三角形的判定与性质,等边三角形的判定与性质,相似三角形的判定与性质,列二次函数关系式,二次函数的性质,锐角三角函数的应用,灵活运用以上知识解题是解本题的关键.6.(1)213442y xx =-++;(2)点P 的坐标为:(6,41,2);(3)11NC MC +=【解析】 【分析】(1)根据题意,先证明AOC ∆∽COB ∆,得到AO OCCO OB=,求出点A 、B 的坐标,然后利用待定系数法,即可求出抛物线解析式;(2)根据题意,可分为两种情况:AOC ∆∽PQC ∆或AOC ∆∽CQP ∆,结合解一元二次方程,相似三角形的判定和性质,分别求出点P 的坐标,即可得到答案;(3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,然后由角平分线的性质定理,得到EI =EJ ,再证明△MEI ∽△MNC ,△NEJ ∽△NMC ,得到111NC MC EI+=,然后求出EI 一个定值,即可进行判断. 【详解】解:(1)∵以AB 为直径的圆过点C , ∴∠ACB =90°, ∵点C 的坐标为()0,4, ∴CO ⊥AB ,∴∠AOC =∠COB =90°,∴∠ACO +∠OCB =∠ACO +∠OAC =90°, ∴∠OCB =∠OAC , ∴AOC ∆∽COB ∆,∴AO OCCO OB=, ∵4CO =,10AO BO AB +==, ∴10AO OB =-, ∴1044OB OB-=, 解得:2OB =或8OB =, 经检验,满足题意, ∵OB OA >, ∴8OB =,∴点A 为(2-,0),点B 为(8,0).设抛物线的解析式为2y ax bx c =++,把点A 、B 、C 三点的坐标代入,有44206480c a b c a b c =⎧⎪-+=⎨⎪++=⎩,解得:14324a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式为213442y x x =-++;(2)根据题意,如图:当AOC ∆∽PQC ∆时, ∴ACO PCQ ∠=∠, ∵90ACO OCB ∠+∠=︒, ∴90PCQ OCB ∠+∠=︒, ∴PC ⊥OC , ∴点P 的纵坐标为4,当4y =时,有2134442x x -++=,解得:16x =或20x =(舍去); ∴点P 的坐标为(6,4);当AOC ∆∽CQP ∆时,则此时BC 垂直平分OP ,作PG ⊥y 轴,垂足为G ,如上图, ∴90CQP AOC ∠=∠=︒,∴AC ∥OP , ∴∠ACO =∠POG , ∵90PGO AOC ∠=∠=︒, ∴AOC ∆∽PGO ∆, ∴AO OCPG GO=, 设点P 为(x ,213442x x -++), ∴PG x =,213442GO x x =-++,∴22413442x x x =-++, 解得:171x =±-, ∵点P 在第一象限, ∴171x =-,∴2134217242x x -++=-,∴点P 的坐标为(171-,2172-);综合上述,点P 的坐标为:(6,4)或(171-,2172-); (3)过点E 作EI ⊥AC 于I ,EJ ⊥CN 于J ,如图:∵CE 是∠ACB 的角平分线, ∴EI =EJ ,∵EI ∥CN ,EJ ∥CM ,∴△MEI ∽△MNC ,△NEJ ∽△NMC , ∴EI ME NC MN =,EJ NE MC MN =, ∴1EI EJ ME NENC MC MN MN +=+=, ∴1EI EI NC MC +=, ∴111NC MC EI+=, ∵△ACO ∽△AEI ,∴12AI AO EI CO ==,∵AC = ∵AC AI IC AI EI =+=+,12=,解得:EI =∴111NC MC EI +==∴11NC MC+是一个定值. 【点睛】本题考查了二次函数的综合应用,求二次函数的解析式,二次函数的性质,相似三角形的判定和性质,解一元二次方程,角平分线的性质定理等知识,解题的关键是熟练掌握题意,正确的作出辅助线,运用数形结合的思想进行解题.7.(1)①B ;D ;4;②1;(2)1522y x =-+或24y x =-+【解析】 【分析】(1)①根据“近点”、“远点”以及“ 特征数”的定义判断即可;②过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P .先分别求得点E 、F 的坐标,进而可求得EF 的长,再利用等积法求得OH 的长,进而即可解决问题;(2)如图,先求得“近点”N 到直线l 的距离NH AOB AHN △∽△即可求得答案. 【详解】解:(1)①由题意,点B 是O 关于直线m 的“近点”, 点D 是O 关于直线m 的“远点”, ∵点E 的坐标为(0,3).⊙O 的半径为1, ∴OE =3,OB =OD =1,∴BE =OE -OB =2,DB =OB +OD =2,O 关于直线m 的特征数224DB BE =⋅=⨯=, 故答案为:B ;D ;4;②如图,过点O 作OH ⊥直线n 于点H ,交O 于点Q ,P ,设直线33y x =-+交x 轴于点F ,交y 轴于点E , 令y =0,则x =3;令x =0,则y =3, ∴(3F ,0),(0,3)E ,3OE ∴=,3OF =,22223(3)23EF OE OF ∴=+=+=,∵1122EOF S OE OF EF OH =⋅=⋅△, ∴11332322OH ⨯⨯=⨯⋅, 解得:32OH =, 12QH OH OQ ∴=-=, 又∵2PQ OQ OP =+=,O ∴关于直线n 的“特征数” 1212PQ QH =⋅=⨯=;(2)如图,设直线l 交x 轴于点A ,交y 轴于点B ,过点F 作FH ⊥直线l ,垂足为点H ,交⊙F 于N ,G ,∵⊙F 5,∴FN =FG 5,∴GN =FN +FG 5∵⊙F 关于直线l 的“特征数”是6, ∴GN·NH =6,NH =6, 解得:NH设直线l 的解析式是y kx b =+, ∵直线l 经过点M (1,2),∴将(1,2)代入y kx b =+,得:2k b +=, 2b k ∴=-,(2)y kx k ∴=+-,∴当0x =时,2y k =-,∴点B 坐标为(0,2-k ),|2|OB k ∴=-,当0y =时,(2)0kx k +-=, 解得:2k x k-=, ∴点A 坐标为(2k k-,0), 2||k OA k -∴=,22|(1)||1|k k AN k k--=--=+,AB ∴2||k k-= BAO NAH ∠=∠,90AOB AHN ∠=∠=︒, AOB AHN ∴△∽△,∴NH ANOB AB=,∴|2|522|1|||k k k k k-=--+, 整理,得:22520k k ++=,解得:12k =-或2k =-,∴直线l 的解析式为1522y x =-+或24y x =-+.【点睛】本题属于圆综合题,考查了一次函数的性质,相似三角形的判定和性质运用以及勾股定理的运用,远点,近点,特征数等新定义等知识,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考压轴题.8.(1)y =-x 2+2x +3,y =-x +3;(2)存在,(-1,0)或(4,-5);(3)存在,(1,2)或(1,-3) 【解析】 【分析】(1)将点A ,B 坐标代入抛物线解析式中,求出b ,c 得出抛物线的解析式,进而求出点C 的坐标,再将点A ,C 坐标代入直线AC 的解析式中,即可得出结论;(2)利用抛物线的对称性得出BD AD =,进而判断出ABC 的面积和ACP △的面积相等,即可得出结论;(3)分点Q 在x 轴上方和在x 轴下方,构造全等三角形即可得出结论. 【详解】(1)把(30)A ,、(10)B -,代入2y x bx c =-++, 解得2b =、3c =∴抛物线的解析式为2y x 2x 3=-++则C 点为(0,3),又(30)A ,,代入1y kx b =+, 得1k =-,13b =, ∴直线AC 的解析式为3y x =-+, (2)如图,连接BC ,∵点D 是抛物线的对称轴与x 轴的交点, ∴AD BD =, ∴2ABCACDSS=,∵2ACP ACD S S =△△,∴ACP ABC S S =△△,此时,点P 与点B 重合, 即:(10)P -,, 过B 点作PB AC ∥交抛物线于点P ,则直线BP 的解析式为1y x =--①, ∵抛物线的解析式为2y x 2x 3=-++②,联立①②解得,10x y =-⎧⎨=⎩或45x y =⎧⎨=-⎩,∴P (4,﹣5),∴即点P 的坐标为(﹣1,0)或(4,﹣5); (3)由(1)可知,抛物线解析式为()214y x =--+ 把1x =代入直线AC 解析式3y x =-+得AC 与抛物线对称轴的交点(1,2)M ,如下图所示:22222BM AM ==+,4AB =即222BM AM AB +=则MAB △是等腰直角三角形,符合题意,M 点即为所求Q 点的一种情况,当Q 点在x 轴下方时,设Q 为(1,)m ,0m <, 因为线段AQ 绕Q 点顺时针旋转90°得到线段1QA 过A1作直线DQ 的垂线于E 点,则1ADQ QEA ≌ ∴2AD QE ==,1DQ EA m ==- ∴12(1)A m m --,∵点A1恰好落在抛物线2y x 2x 3=-++上, 代入,解得m=-3或2m = (舍去) ∴Q (1,-3)综上,Q 点坐标为(1,2)或(1,-3), 【点睛】本题考查的是二次函数的综合题,涉及解析式的求解,与三角形面积有关的问题,全等三角形的判定与性质,解题的关键是利用数形结合的思想,设点坐标并结合几何图形的性质列式求解.9.(1)直线AC 的解析式为y =﹣x +6;(2)d =4-t ;(3)Q (212,1). 【解析】 【分析】(1)先由解析式求出得A 、C 点的坐标,得OA =OC ,得四边形ABCO 为正方形,再根据正方形的面积求得边长,便可得b 的值;(2)过点Q 作QG ⊥AB 交AB 延长沿于点G ,证明Rt △AOP ≌Rt △GPQ (AAS ),得到AP =GQ ,进而求得结论便可;(3)过点P 作PH ⊥OF 于点H ,延长PH 交EQ 的延长线于点R ,EQ 的延长线与x 轴交于点N ,过Q 作QM ⊥x 轴于点M .证明Rt △AOP ≌Rt △GPQ (CCS ),得PK =QR ,∠R=∠OKP,再证明∠R=∠FPR,得EP=ER,再证FE=NR,设FE=NR=k,NQ=m,在Rt△PQE中,由勾股定理列出方程,得到k与m的关系,解Rt△PQE得tan∠PEQ,进而把这个函数值运用到△OAP中,求得t的值,再运用(2)中结论得Q的纵坐标d的值,再运用到△QNM中求得NM,NQ的值,进而求得ON,便可得Q的横坐标的值.【详解】解:(1)∵直线y=﹣x+b(b>0)交x轴于点A,交y轴于点C,A b C b,∴(,0),(0,)∴OA=OC=b,∴矩形ABCO为正方形,∵矩形ABCO的面积是36.∴b=6,即直线AC的解析式为y=﹣x+6;(2)如图,过点Q作QG⊥AB交AB延长沿于点G,∵∠OPQ=90°,∴∠APO+∠GPQ=90°,∵∠APO+∠AOP=90°,∴∠AOP=∠GPQ,∵在矩形ABCO,∠OAP=90°,QG⊥AB,∴∠QGP=∠OAP=90°,∵PQ=OP,∴Rt△AOP≌Rt△GPQ(AAS),∴AP=GQ,∵AP=t,∴GQ=t,∴d=4-t;(2)过点P作PH⊥OF于点H,延长PH交EQ的延长线于点R,EQ的延长线与y轴交于点N,过Q作QM⊥y轴于点M.则AP=t,QM=d,且d=6-t.∵OF 平分∠POC , ∴∠POF =∠COF =∠PFO , ∴PF =PO ,∵PH ⊥OF ,∠OPQ =90°, ∴∠OPH =∠FPH ,∠KPH =∠POH , 在△OPK 和△PQR 中, 90OPK PQR PO QP POK QPR ∠∠︒⎧⎪⎨⎪∠∠⎩====, ∴△OPK ≌△PQR (ASA ), ∴PK =QR ,∠R =∠OKP ,∵∠OKP +∠POK =∠POK +∠OPH =90°, ∴∠OKP =∠OPH , ∴∠R =∠OPH , ∵PO =PF ,PH ⊥OF , ∴∠OPH =∠FPH , ∴∠R =∠FPR , ∴EP =ER ,∵PE ∥ON ,OP ∥EN , ∴四边形OPEN 是平行四边形, ∴EN =PO =PF , ∴PE -PF =ER -EN , ∴FE =NR ,设FE =NR =k ,则KQ =2FE =2k , 又设NQ =m ,∴PK=QR=m+k,∴PQ=m+3k,∴PO=EN=PF=m+3k,∴QE=EN-QR=m+3k-m=3k,PE=PF+FE=4k+m,在Rt△PQE中,∵PE2=PQ2+QE2,∴(4k+m)2=(3k+m)2+(3k)2,∴k1=0(舍去),k2=m,∴PQ=4m,QE=3m,∴tan∠PEN=43 PQQE=,∵OP∥EN,∴∠OPA=∠PEN,∴tan∠APO=43,∵AO=6,∴AP=4.5,∴t=4.5,∴QM=d=6-t=1.5,∵PE∥OC,∴∠QNM=∠PEN,∴tan∠QNM=tan∠PEN=43,∴NM=9 tan8QMQNM=∠,∴m=NQ158 =,∴PE=ON=4k+m=5m=758,∴OM=ON+NM=212,∴Q(212,1).【点睛】本题是一次函数与四边形的综合题,主要考查了一次函数的图象与性质,全等三角形的性质与判定,正方形的性质,旋转的性质,解直角三角形的应用,等腰三角形的性质与判定,平行四边形的性质与判定,是一道综合性极强的题目,解决这类问题常用到数形结合、方程和转化等数学思想方法.构造全等三角形是解题的关键,也是问题的突破口.10.(1);(2);(3)【解析】 【分析】(1)由抛物线的二次项系数 再根据交点式可得抛物线为从而可得答案;(2)先画好图形,证明利用相似三角形的性质求解从而可得答案;(3)如图,过P 作轴于,K 过M 作于,N 证明即再求解则,再解方程可得 4,t = 再求解的解析式,再联立解析式解方程可得答案. 【详解】 解:(1) 抛物线交x 轴于()2,0A -、()5,0B 两点,所以可得抛物线为:(2)如图,过P 作于,H 连AP 交OC 于则,x 则令0,(3)如图,过P作轴于,K过M作于,N 由(2)得:,,轴,则轴,,即结合(1)可得:四边形为矩形,。
2023年辽宁省沈阳市第一二六中学中考数学压轴题专项训练

辽宁省沈阳市第一二六中学中考数学压轴题专项训练(学生版)中考数学压轴题(1)一次函数、反比例函数与几何综合1.如图,在平面直角坐标系中,一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,9),与直线OC交于点C(8,3).(1)求直线AB的函数表达式;(2)过点C作CD⊥x轴于点D,将△ACD沿射线CB平移得到的三角形记为△A′C′D′,点A,C,D的对应点分别为A′,C′,D′,若△A′C′D′与△BOC重叠部分的面积为S,平移的距离CC′=m,当点A′与点B重合时停止运动.①若直线C′D′交直线OC于点E,则线段C′E的长为(用含有m的代数式表示);②当0<m<时,S与m的关系式为;③当S=时,m的值为.2.如图,平面直角坐标系中,O是坐标原点,直线y=kx+15(k≠0)经过点C(3,6),与x 轴交于点A,与y轴交于点B.线段CD平行于x轴,交直线y=x于点D,连接OC,AD.(1)填空:k=,点A的坐标是(,);(2)求证:四边形OADC是平行四边形;(3)动点P从点O出发,沿对角线OD以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线DO以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.①当t=1时,△CPQ的面积是.②当点P,Q运动至四边形CP AQ为矩形时,请直接写出此时t的值.3.在平面直角坐标系中,直线y=kx+4(k≠0)交x轴于点A(8,0),交y轴于点B.(1)k的值是;(2)点C是直线AB上的一个动点,点D和点E分别在x轴和y轴上.①如图,点E为线段OB的中点,且四边形OCED是平行四边形时,求▱OCED的周长;②当CE平行于x轴,CD平行于y轴时,连接DE,若△CDE的面积为,请直接写出点C的坐标.4.如图,直线y=x+6分别与x轴、y轴交于点A、B,点C为线段AB上一动点(不与A、B重合),以C为顶点作∠OCD=∠OAB,射线CD交线段OB于点D,将射线OC绕点O顺时针旋转90°交射线CD 于点E,连结BE.(1)证明:=;(用图1)(2)当△BDE为直角三角形时,求DE的长度;(用图2)(3)点A关于射线OC的对称点为F,求BF的最小值.(用图3)5.如图,△AOB是等边三角形,过点A作y轴的垂线,垂足为C,点C的坐标为(0,).P是直线AB上在第一象限内的一动点,过点P作y轴的垂线,垂足为D,交AO于点E,连接AD,作DM⊥AD交x轴于点M,交AO于点F,连接BE,BF.(1)填空:若△AOD是等腰三角形,则点D的坐标为;(2)当点P在线段AB上运动时(点P不与点A,B重合),设点M的横坐标为m.①求m值最大时点D的坐标;②是否存在这样的m值,使BE=BF?若存在,求出此时的m值;若不存在,请说明理由.6.如图,在平面直角坐标系中,四边形ABCD,A在y轴的正半轴上,B,C在x轴上,AD∥BC,BD平分∠ABC,交AO于点E,交AC于点F,∠CAO=∠DBC.若OB,OC的长分别是一元二次方程x2﹣5x+6=0的两个根,且OB>OC.请解答下列问题:(1)求点B,C的坐标;(2)若反比例函数y=(k≠0)图象的一支经过点D,求这个反比例函数的解析式;(3)平面内是否存在点M,N(M在N的上方),使以B,D,M,N为顶点的四边形是边长比为2:3的矩形?若存在,请直接写出在第四象限内点N的坐标;若不存在,请说明理由.7.如图,直线MN与x轴,y轴分别相交于A,C两点,分别过A,C两点作x轴,y轴的垂线相交于B点,且OA,OC(OA>OC)的长分别是一元二次方程x2﹣14x+48=0的两个实数根.(1)求C点坐标;(2)求直线MN的解析式;(3)在直线MN上存在点P,使以点P,B,C三点为顶点的三角形是等腰三角形,请直接写出P点的坐标.8.如图,在平面直角坐标系中,点A坐标为(6,0),点B坐标为(2,﹣2),直线AB与y轴交于点C.(1)求直线AB的函数表达式及线段AC的长;(2)点B关于y轴的对称点为点D.①请直接写出点D的坐标为;②在直线BD上找点E,使△ACE是直角三角形,请直接写出点E的横坐标为.9.在平面直角坐标系中,y关于x的一次函数y=x+5﹣c(c为常数),其图象与y轴交于点A,与x轴交于点B.(1)当c=4时,求线段OA的长;(2)若△OAB的面积为18.①求出满足条件的一次函数表达式;②若点A在y轴正半轴,点B在x轴负半轴上,且点C在直线AB上,当S△OAC=5S△OBC时,请直接写出点C的坐标.10.如图,在平面直角坐标系中,一次函数y=x+12的图象分别交x,y轴于点A和B,与经过点C(,0),D(0,﹣3)的直线交于点E.(1)求直线CD的函数解析式及点E的坐标;(2)点P是线段DE上的动点,连接BP.①当BP分△BDE面积为1:2时,请直接写出点P的坐标;②将△BPE沿着直线BP折叠,点E对应点E',当点E'落在坐标轴上时,直接写出点P的坐标.11.如图,在平面直角坐标系中,直线AB与y轴交于点A,与x轴交于点B,OB=2OA,点N在线段OB 上,过点N作NM⊥AB于M,当动点D从点A匀速运动到点M时,动点E恰好从点B匀速运动点O;当点D运动到线段AM中点时,动点E恰好运动到点N,设AD=x,OE=y,且.(1)求线段OA的长;(2)求线段BM的长;(3)连接DE,当△DEB的面积最大时,直接写出x的值.12.如图,在平面直角坐标系中,矩形OABC的边OA在x轴的正半轴上,OC在y轴的正半轴上,OA=3,OC=.动点P从C点出发沿折线CB﹣BA向终点A运动、在边CB上以每秒1个单位长度的速度匀速运动,在边BA上以每秒个单位长度的速度匀速运动.过点P作线段PD与射线OA相交于点D,且∠PDO=60°,连接PO,BO,PD与BO相交于点E.设点P的运动时间为t,△OPD与△OAB重合部分的面积为S.(1)直接写出点B的坐标(,);(2)当点P与点C重合时,求OD的长;(3)当点P在边BA上运动时,求BP的长(用含t的代数式表示);(4)直接写出S关于t的函数关系式及自变量t的取值范围.13.如图,在平面直角坐标系中,菱形OABC的边OA在x轴的正半轴上,点B,C在第一象限,∠C=120°,边OA=8.点P从原点O出发,沿x轴正半轴以每秒1个单位长度的速度做匀速运动:点Q从点A出发,沿边AB→BC→CO以每秒2个单位长度的速度做匀速运动.过点P作直线EP垂直于x轴并交折线OCB于E,交对角线OB于F,点P和点Q同时出发,分别沿各自路线运动,点Q运动到原点O时,P 和Q两点同时停止运动.(1)请直接填写点A的坐标(,),B的坐标(,),C的坐标(,);(2)当t=1时,求线段EF的长;(3)求t为何值时,点E与点Q重合;(4)设△AEQ的面积为S,当4≤t≤8,请直接写出s与t的函数关系式.14.如图,在平面直角坐标系xOy中,直线AB的表达式为y=kx+2,且经过点(1,4),与x轴、y轴分别交于点A、B,将直线AB向下平移4个单位得到直线l.(1)求直线l的表达式;(2)将△AOB绕点O逆时针旋转90°后得到△A′OB′(点A的对应点是点A′,点B的对应点是点B′),求直线A′B′与直线AB的交点坐标;(3)设直线l与x轴交于点C,点D为该平面直角坐标系内的点,如果以点A、B、C、D为顶点的四边形是平行四边形,求点D的坐标.15.如图,在平面直角坐标系中,直线y=﹣3x+3与x轴交于点A,与y轴交于点B,将线段AB绕点A顺时针旋转90°,得到线段AC,过点B,C作直线,交x轴于点D.(1)点C的坐标为;求直线BC的表达式;(2)若点E为线段BC上一点,且△ABE的面积为,求点E的坐标;(3)在(2)的条件下,在平面内是否存在点P,使以点A,B,E,P为顶点的四边形为平行四边形,直接写出点P的坐标16.已知,在平面直角坐标系中,点O为坐标原点,直线y=kx+3与x轴交于点B,与y轴交于点A,OA =OB.(1)如图1,求直线AB的解析式;(2)如图2,点C是第一象限内一点,BC⊥OB,AD⊥AC交x轴负半轴于点D,若点D的横坐标为t,线段BC的长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);(3)如图3,在(2)的条件下,当d=﹣2t时,点E是线段AB上,点F在线段OA上,OF=BE,连接CE,作FG∥x轴,连接CG交线段AB于点H,连接DF、AG,若∠ECG=45°,DF=AG,求点H的坐标.17.如图,直线y=kx+b与x轴交于点A(4,0),与y轴交于点B(0,2),P是x轴上的动点.(1)求k的值.(2)连结PB,当∠PBA=90°时,求OP的长.(3)过点P作AB的平行线,交y轴于点M,点Q在直线x=2上.是否存在点Q,使得△PMQ是等腰直角三角形?若存在,请直接写出所有符合条件的点Q的坐标,若不存在,请说明理由.18.如图,在平面直角坐标系中,直线l1:y=kx+1交y轴于点A,交x轴于点B(4,0),过点E(2,0)的直线l2平行于y轴,交直线l1于点D,点P是直线l2上一动点(异于点D),连接P A、PB.(1)求直线l1的解析式;(2)设P(2,m),求△ABP的面积S的表达式(用含m的代数式表示);(3)当△ABP的面积为3时,则以点B为直角顶点作等腰直角△BPC,请直接写出点C的坐标.19.如图1,在平面直角坐标系中,已知直线l:y=kx+b与x轴交于点A,与y轴交于点B,直线CD相交于点D,其中AC=14,C(﹣6,0),D(2,8).(1)求直线l函数表达式;(2)如图2,点P为线段CD延长线上的一点,连接PB,当△PBD的面积为7时,将线段BP沿着y 轴方向平移,使得点P落在直线AB上的点P'处,求点P'到直线CD的距离;(3)若点E为直线CD上的一点,在平面直角坐标系中是否存在点F,使以点A、D、E、F为顶点的四边形为菱形,若存在请直接写出点F的坐标;若不存在,请说明理由.20.如图,在平面直角坐标系中,直线l1的解析式为y=﹣x,直线l2与l1交于点A(a,﹣a),与y轴交于点B(0,b),其中a,b满足﹣a=3.(1)求直线l2的解析式.(2)在平面直角坐标系中第二象限有一点P(m,5),使得S△AOP=S△AOB,请求出点P的坐标.(3)已知平行于y轴左侧有一动直线,分别与l1,l2交于点M、N,且点M在点N的下方,点Q为y 轴上一动点,且△MNQ为等腰直角三角形,请求出满足条件的点Q的坐标.21.如图1,已知直线y=2x+2与y轴,x轴分别交于A,B两点,以B为直角顶点在第二象限作等腰Rt△ABC(1)求点C的坐标,并求出直线AC的关系式;(2)如图2,直线CB交y轴于E,在直线CB上取一点D,连接AD,若AD=AC,求证:BE=DE.(3)如图3,在(1)的条件下,直线AC交x轴于点M,P(﹣,k)是线段BC上一点,在x轴上是否存在一点N,使△BPN面积等于△BCM面积的一半?若存在,请求出点N的坐标;若不存在,请说明理由.22.把正方形纸片放在直角坐标系中,如图所示,正方形纸片ABCD的边长为3,点E、F分别在BC、CD 上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,已知3BE=BC.(1)请直接写出D、E两点的坐标,并求出直线EF的解析式;(2)在直线EF上是否存在点M,使得△AFM的面积是△AEF的面积的一半,若存在,请求出点M的坐标,若不存在,请说明理由.(3)若点P、Q分别是线段AG、AF上的动点,则EP+PQ的最小值是多少?并求出此时点Q的坐标.23.在平面直角坐标系中,点A的坐标为(﹣,0),点B在直线l:上,过点B作AB的垂线,过原点O作直线l的垂线,两垂线相交于点C.(1)如图,点B,C分别在第三、二象限内,BC与AO相交于点D.①若BA=BO,求证:CD=CO.②若∠CBO=45°,求四边形ABOC的面积.(2)是否存在点B,使得以A,B,C为顶点的三角形与△BCO相似?若存在,求OB的长;若不存在,请说明理由.24.如图,平面直角坐标系中,直线AC解析式为y=mx+b与y轴交于点A,与x轴交于点C,直线BE解析式为y=nx+b﹣10交y轴于点E,与x轴交于点B.(1)求线段AE长;(2)连接AB,K为线段AB上一点,F为线段AC上一点,连接FK交y轴于点G,若直线FK解析式为y=﹣x+k,求tan∠AGK的值;(3)在(2)的条件下,若∠ABE=45°,∠ACB=2∠EBO,AC=15,取AG中点H,连接KH,若KH =3,求F点坐标.25.如图在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b分别交x轴,y轴于点A、B,OA=4,∠OBA的外角平分线交x轴于点D.(1)求点D的坐标;(2)点P是线段BD上一点(不与B、D重合),过点P作PC⊥BD交x轴于点C,设点P的横坐标为t,△BCD的面积为S,求S与t之间的函数解析式(不要求写出自变量t的取值范围);(3)在(2)的条件下,PC的延长线交y轴于点E,当PC=PB时,将射线EP绕点E旋转45°交直线AB于点F,求F点坐标.26.如图1,在平面直角坐标系中,直线l1:y=﹣x+2与x轴交于点A,与y轴交于点B,与直线l2交于点C(m,3),直线l2与x轴交于点D(﹣2,0).(1)求直线l2的解析式;(2)如图2,点P在线段CD上,连接AP,3S△APD=2S△ACD,过点P的直线交x轴负半轴于点M,交y轴正半轴于点N,请问:+是否为定值?若是,求出定值;若不是,请说明理由.(3)当点E在直线l1上运动时,平面内是否存在一点F,使得以点C、D、E、F为顶点的四边形是菱形?若存在,求出点E的坐标;若不存在,请说明理由.27.在正方形ABCD中,点E是直线BC上一点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)如图1,若点E是BC的中点.求证:AE=EF;(2)如图2,若点E是BC边上任意一点(不含B,C),结论“AE=EF”还成立吗?若成立,请证明;若不成立,请说明理由;(3)如图3,若点E是BC延长线上任意一点,结论“AE=EF”还成立吗?若成立,请证明若不成立,请说明理由;(4)如图4,在平面直角坐标系xOy中,点O与点B重合,正方形的边长为4,若点F恰好落在直线y =x+7上,请直接写出此时点E的坐标.28.如图,在平面直角坐标系xOy中,点A在y轴的正半轴上,点B在x轴的正半轴上,OA=OB=10.(1)求直线AB的解析式;(2)若点P是直线AB上的动点,当S△OBP=S△OAP时,求点P的坐标;(3)将直线AB向下平移10个单位长度得到直线l,点M,N是直线l上的动点(M,N的横坐标分别是x M,x N,且x M<x N),MN=4,求四边形ABNM的周长的最小值,并说明理由.29.如图1,在平面直角坐标系中,O为坐标原点,直线y=ax+10a分别交x轴、y轴于点A、B,△AOB 的面积为25.(1)求a的值;(2)如图2,点D为AB上一点(D不与A、B重合),C为x轴正半轴一点,连接CD交y轴于点E,C、D关于点E对称,设点D的横坐标为t,∠DCA的正切值为s,求s关于t的函数关系式;(3)如图3,在(2)的条件下,F为DE上一点,K为CF的中点,连接BK,2∠ACD=90°﹣∠BKF,P为第一象限一点,CP⊥OC,连接FP、FB,将FP沿FB翻折交BD于点Q,FQ=FP,当s=时,求直线PQ的解析式.30.直线y=kx+10k交x轴、y轴于A、B两点.(1)如图1,求点A坐标;(2)如图2,点D为第三象限内一点,连接DB交x轴于点C,若BA=BD,∠DAC=∠ABD,设点D 的横坐标为t,求AC长(用t的代数式来表示);(3)如图3,在(2)的条件下,作射线DO,当DO∥AB时,在射线DO上是否存在一点E,使得∠AEB =45°,若存在,请求出直线BE的解析式;若不存在,请说明理由.31.如图1,在平面直角坐标系xOy中,已知直线AB:y=﹣x+3与直线CD:y=kx﹣2相交于点M(4,a),分别交坐标轴于点A、B、C、D,点P是线段CD延长线上的一个点,△PBM的面积为15.(1)求直线CD解析式和点P的坐标;(2)如图2,当点P为线段CD上的一个动点时,将BP绕点B逆时针旋转90°得到BQ,连接PQ与OQ.点Q随着点P的运动而运动,请求出点Q运动所形成的线段所在直线的解析式,以及OQ的最小值.(3)在(1)的条件下,直线AB上有任意一点F,平面直角坐标系内是否存在点N,使得以点B、D、F、N为顶点的四边形是菱形,如果存在,请直接求出点N的坐标;如果不存在,请说明理由.32.如图,直线y=k(x﹣6)交x轴正半轴于点A,交y轴正半轴于点B,且△AOB的面积等于27.(1)求直线AB的解析式;(2)P为线段AB上一点,过点B作BD∥x轴,交OP延长线于点D,设点P的横坐标为m,线段BD 的长为d,求d与m的函数关系式;(3)在(2)的条件下,过点P作PE⊥x轴,垂足为E,连接AE交OP于点F,Q为PE延长线上一点,若DE+EF=AF,∠AQD=45°,求PQ的长.33.如图,在平面直角坐标系xOy中,直线l1:y=x+m与y轴交于点A(0,3),直线l2:y=x﹣与x轴交于点B,点M,N分别是直线l1,l2在第一象限内的动点,且∠MON=60°,连接MN.(1)直接写出m的值,点B的坐标,∠OAM及∠OBN的度数;(2)求AM•BN的值;(3)当△MON是直角三角形时,直接写出点M的坐标.34.如图,在平面直角坐标系中,矩形OABC的边OC、OA分别在x轴、y轴上,点B的坐标为(8,4),连接AC.动点P从点A出发,以每秒个单位长度的速度沿对角线AC向终点C匀速运动,动点Q从点C出发,以每秒4个单位长度的速度沿C→O→A路线,向终点A匀速运动,两点同时出发,一点到达终点,另一点即停,连接PQ.设运动时间为t秒(t>0).(1)用含t的代数式表示:CQ=;CP=;(2)当点Q在边OC上,且△PQC为直角三角形时,直接写出t的值:t=;(3)过点P作PE⊥AB交AB于点E,连接EQ交对角线AC于点F,①t=时,S△EFP:S△EF A=2:3;②当0<t<2时,t=,EQ取得最小值;当2<t<3时,QE的最小值为.35.如图,在平面直角坐标系中,直线y=3x+6与x轴交于点B,与y轴交于点A,点C(3,0),连接AC 作点O关于直线AB的对称点E,线段OE交直线AB于点F,过点E作EH⊥x轴于点H,连接EB.(1)求证:△EHO∽△BOA;(2)①设HE=a,用含a的代数式表示HO=;②求a的值,并直接写出直线BE的表达式;(3)点M在直线BE上,连接AM,以线段AM为边作正方形AMPN(点A、M、P、N以逆时针方向排序),点Q在平面内,当四边形BCNQ为菱形时,连接PQ,请直接写出PQ的长度.36.如图,在平面直角坐标系中,矩形ABCO的顶点B的坐标是(6,4),动点P从点A出发,以每秒1个单位的速度沿线段AB运动,动点Q从点C出发,以每秒2个单位的速度沿线段OC运动,连接OB,连接PQ与线段PQ相交于点D,两点同时出发,当点Q到达点O时,P、Q同时停止运动,设运动时间为t(t>0).(1)AP=,OQ=;(请用含t的代数式表示)(2)当时,求t的值;(3)在P、Q运动的过程中,将矩形AOCB沿PQ折叠,点A,点O的对应点分别是点E,点F,①当点F恰好落在线段OB上时,直接写出此时的t值;②连接PF,连接OF,当∠PFO=45°时,直接写出此时点F的坐标.37.如图1,在坐标系中的△ABC,点A、B在x轴,点C在y轴,且∠ACB=90°,∠B=30°,AC=4,D是AB的中点.(1)求直线BC的表达式.(2)如图2,若E、F分别是边AC,CD的中点,矩形EFGH的顶点都在△ACD的边上.①请直接写出下列线段的长度:EF=,FG=.②将矩形EFGH沿射线AB向右平移,设矩形移动的距离为m,矩形EFGH与△CBD重叠部分的面积为S,当S=时,请直接写出平移距离m的值.(3)如图3,在(2)的条件下,在矩形EFGH平移过程中,当点F在边BC上时停止平移,再将矩形EFGH绕点G按顺时针方向旋转,当点H落在直线CD上时,此时矩形记作E1F1GH1,由H1向x轴作垂线,垂足为Q,则=.38.如图,点A、B在x轴上,点C在y轴上,且OA=2,OB=4,OC=8,直线MN过AB的中点且与y 轴平行,与直线BC交于点M,与x轴交于点N.(1)求点M的坐标.(2)若点P是直线MN上的一个动点,直接写出点P的坐标,使以P、C、M为顶点的三角形与△MNB 相似.(3)D为CO的中点,一个动点G从D点出发,先到达x轴上的点E,再走到直线MN上的点F,最后返回到点C.要使动点G走过的路程最短,请直接写出点E、F的坐标,并直接写出最短路程.(4)点Q是y轴上的一点,点R在x轴上,直接写出使△MQR为等腰直角三角形的Q的坐标.39.如图,在平面直角坐标系中,直线l1:y=x+与过点A(3,0)的直线l2交于点C(1,m),与x 轴交于点B.(1)点B坐标,直线l2的表达式;(2)点P是直线l2上的一个动点,过点P作EF⊥x轴于点E,交直线l1于点F,利用(1)中的结论,解答下列各问:①若PF=AB,求点P的横坐标;②过点P作PQ⊥l1于点Q,若PQ=2PE,请直接写出点P的坐标;③直线l1与y轴交于点D,过点B作y轴的平行线l3,在x轴上方的l3上有一点G,在线段BD上有一点H,若DH=BG,请直接写出OG+OH的最小值.40.在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象经过点A(6,0)和点B(0,9).与直线y=x相交于点C,过点C作CE⊥x轴于点E,将△OCE沿射线OC平移,移动后的三角形记为△O′C′E′(点O,C,E的对应点分别记为点O′,C′,E′),点O′与点C重合时运动停止.(1)求直线AB的表达式及点C的坐标;(2)①如图,当点E′落在线段AB上时,设点E′的横坐标为a,求a的值;②设△O′C′E′与△ACE重叠部分面积为S,△OCE沿射线OC平移的距离OO′为t,直接写出S=时,t的值.41.如图①,在矩形OABC中,OA=4,OC=3,分别以OC、OA所在的直线为x轴、y轴,建立如图所示的坐标系,连接OB,反比例函数y=(x>0)的图象经过线段OB的中点D,并与矩形的两边交于点E和点F,直线l:y=kx+b经过点E和点F.(1)求反比例函数的解析式;(2)在第一象限内,请直接写出关于x的不等式kx+b≤的解集:.(3)如图②,将线段OB绕点O顺时针旋转一定角度,使得点B的对应点H恰好落在x轴的正半轴上,连接BH,作OM⊥BH,点N、点G为线段OM.上的动点,且GN=.①的值为;②求四边形CGNH周长的最小值.42.已知,矩形OCBA在平面直角坐标系中的位置如图所示,点C在x轴的正半轴上,点A在y轴的正半轴上,已知点B的坐标为(4,2),反比例函数y=的图象经过AB的中点D,且与BC交于点E,设直线DE的解析式为y=mx+n,连接OD,OE.(1)求反比例函数y=的表达式和点E的坐标;(2)点M为y轴正半轴上一点,若△MBO的面积等于△ODE的面积,求点M的坐标;(3)点P为x轴上一点,点Q为反比例函数y=图象上一点,是否存在点P、Q使得以点P,Q,D,E为顶点的四边形为平行四边形?若存在,直接写出点Q的坐标;若不存在,请说明理由.43.如图1,矩形OABC的顶点A、C分别落在x轴、y轴的正半轴上,点B(4,3),反比例函数y=(x >0)的图象与AB、BC分别交于D、E两点,BD=1,点P是线段OA上一动点.(1)求反比例函数关系式和点E的坐标;(2)如图2,连接PE、PD,求PD+PE的最小值;(3)如图3,当∠PDO=45°时,求线段OP的长.44.如图,在平面直角坐标系中,一次函数y=﹣x+1与反比例函数y=的图象在第四象限相交于点A(2,﹣1),一次函数的图象与x轴相交于点B.(1)求反比例函数的表达式及点B的坐标;(2)当一次函数值小于反比例函数值时,请直接写出x的取值范围是;(3)点C是第二象限内直线AB上的一个动点,过点C作CD∥x轴,交反比例函数y=的图象于点D,若以O,B,C,D为顶点的四边形为平行四边形,请直接写出点C的坐标为.45.如图,一次函数y=kx+b(k>0)的图象与反比例函数y=(x>0)的图象交于点A,与x轴交于点B,与y轴交于点C,AD⊥x轴于点D,CB=CD,点C关于直线AD的对称点为点E.(1)点E是否在这个反比例函数的图象上?请说明理由;(2)连接AE、DE,若四边形ACDE为正方形.①求k、b的值;②若点P在y轴上,当|PE﹣PB|最大时,求点P的坐标.46.如图,一次函数y=x+1的图象与反比例函数y=(x>0)的图象交于点A(a,3),与y轴交于点B.(1)求a,k的值;(2)直线CD过点A,与反比例函数图象交于点C,与x轴交于点D,AC=AD,连接CB.①求△ABC的面积;②点P在反比例函数的图象上,点Q在x轴上,若以点A,B,P,Q为顶点的四边形是平行四边形,请求出所有符合条件的点P坐标.47.如图,在平面直角坐标系xOy中,一次函数y=﹣x+5的图象与反比例函数y=(k>0)的图象交于A、B两点(点A在点B左边),交x轴于点C,延长AO交反比例函数y=(k>0)的图象于点E,点F为第四象限内一点,∠AFE=90°,连接OF.(1)填空:FO AO(填“>”、“=”或“<”);(2)连接CF,若AF平分∠OAC.①若△AFC的面积为10,求k的值;②连接BF,四边形AOFB能否为菱形?若能,直接写出符合条件的k的值;若不能,说明理由.48.如图1,在平面直角坐标系中,直线l:y=﹣2x+2与x轴交于点A,将直线l绕着点A顺时针旋转45°后,与y轴交于点B,过点B作BC⊥AB,交直线l于点C.(1)求点A和点C的坐标;(2)如图2,将△ABC以每秒3个单位的速度沿y轴向上平移t秒,若存在某一时刻t,使A、C两点的对应点D、F恰好落在某反比例函数的图象上,此时点B对应点E,求出此时t的值;(3)在(2)的情况下,若点P是x轴上的动点,是否存在这样的点Q,使得以P、Q、E、F四个点为顶点的四边形是菱形?若存在,请直接写出符合题意的点Q的坐标;若不存在,请说明理由.49.如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点B在反比例函数y=的第一象限内的图象上,OA=6,OC=10,动点P在x轴的上方,且满足S△P AO=.(1)若点P在这个反比例函数的图象上,求点P的坐标;(2)连接PO、P A,求PO+P A的最小值;(3)若点Q是平面内一点,使得以A、B、P、Q为顶点的四边形是菱形,则请你直接写出满足条件的所有点Q的坐标.50.如图,在平面直角坐标系中,四边形ABCO为矩形,B(5,4),D(﹣3,0),点P从点A出发,以每秒1cm的速度沿AB方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿DC方向向终点C运动,已知动点P、Q同时出发,当点P、Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.(1)用含t的代数式表示:BP=cm,CQ=cm;(2)函数y=的图象在第一象限内的一支双曲线经过点P,且与线段BC交于点M,若出△POM的面积为7.5cm2,试求此时t的值;(3)点P、Q在运动过程的中,是否存在某一时刻t,使坐标平面上存在点E,以P、Q、C、E为顶点的四边形刚好是菱形?若存在,请求出所有满足条件的t的值,若不存在,请说明理由.51.在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点B,并与反比例函数y=(k≠0)的图象在第一象限相交于点C,且点B是AC的中点.(1)如图1,求反比例函数y=(k≠0)的解析式;(2)如图2,若矩形FEHG的顶点E在直线AB上,顶点F在点C右侧的反比例函数y=(k≠0)图象上,顶点H,G在x轴上,且EF=4.①求点F的坐标;②若点M是反比例函数的图象第一象限上的动点,且在点F的左侧,连结MG,并在MG左侧作正方形GMNP.当顶点N或顶点P恰好落在直线AB上,直接写出对应的点M的横坐标.52.如图(一),平面直角坐标系中,已知A(2,0)、B(0,4),以AB为直角边作等腰直角△ABC,其中∠BAC=90°,AC=AB,点C在第一象限内.双曲线y=经过点C.(1)求双曲线y=的表达式;(2)过点B的直线BE交x轴于点E,交线段AC于点D,若∠DBC=∠OBA.求直线BE的解析式;(3)在(2)的条件下,直线BE沿y轴正方向平移,恰好经过点C时,与双曲线k的另一个交点为F (m,n),如图(二).①连接FB、FD,则四边形ABFD的面积是;②连接OF,求OF的长度.53.如图,在平面直角坐标系中,一次函数y1=x﹣2的图象与反比例函数(k≠0)的图象交于A(﹣2,a)、B(m,2)两点,与y轴交于点C,与x轴交于点D,连接OA、OB.(1)求反比例函数(k≠0)的表达式;(2)求△AOB的面积;(3)点N为坐标轴上一点,点M为y2的图象上一点,当以点C、D、M、N为顶点的四边形是平行四边形时,请直接写出所有满足条件的N点的坐标.54.如图,一次函数y1=k1x+4与反比例函数y2=的图象交于点A(2,m)和B(﹣6,﹣2),与y轴交于点C.(1)求一次函数与反比例函数的表达式;(2)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点,设直线OP与线段AD交于点E,当S四边形ODAC:S△ODE=5:1时,求点P的坐标;(3)在(2)的条件下,点M是直线OP上的一个动点,当△MBC是以BC为斜边的直角三角形时,求点M的坐标.55.如图,等边△OAB和等边△AEF的一边都在x轴上,双曲线y=(k>0)经过OB的中点C和AE的中点D.已知等边△OAB的边长为4.(1)求k的值;(2)求等边△AEF的边长;(3)将等边△AEF绕点A任意旋转,得到等边△AE'F',P是E'F'的中点(如图2所示),连结BP,直接写出BP的最大值.56.如图,在平面直角坐标系中,直线y=3x+b经过点A(﹣1,0),与y轴正半轴交于B点,与反比例函数y=(x>0)交于点C,且AC=3AB,BD∥x轴交反比例函数y=(x>0)于点D.(1)求b、k的值;(2)如图1,若点E为线段BC上一点,设E的横坐标为m,过点E作EF∥BD,交反比例函数y=(x >0)于点F.若EF=BD,求m的值.(3)如图2,在(2)的条件下,连接FD并延长,交x轴于点G,连接OD,在直线OD上方是否存在。
成都市中考核心考点-第九讲 函数与图形综合(24题)(B卷)

2.(17成都)在平面直角坐标系 中,对于不在坐标轴上的任意一点 ,我们把点 称为点 的“倒影点”.直线 上有两点 ,它们的倒影点 均在反比例函数 的图像上.若 ,则 ____________.
3、(15成都)如果关于 的一元二次方程 有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,以下关于倍根方程的说法,正确的是.(写出所有正确说法的序号)
10成都图
7.(11成都)在平面直角坐标系 中,已知反比例函数 满足:当 时,y随x的增大而减小。若该反比例函数的图象与直线 都经过点P,且 ,则实数k=_________.
8.(10成都)如图,在 中, , , ,动点 从点 开始沿边 向 以 的速度移动(不与点 重合),动点 从点 开始沿边 向 以 的速度移动(不与点 重合).如果 、 分别从 、 同时出发,那么经过_____________秒,四边形 的面积最小.
5.(13成都)在平面直角坐标系 中,直线 ( 为常数)与抛物线 交于 , 两点,且 点在 轴左侧, 点的坐标为 ,连接 .有以下说法: ; 当 时, 的值随 的增大而增大; 当 时, ; 面积的最小值为 .其中正确的是_______.(写出所有正确说法的序号)
6.(12成都)如图,在平面直角坐标系xOy中,直线AB与x轴、y轴分别交于点A,B,与反比例函数 ( 为常数,且 )在第一象限的图象交于点E,F.过点E作EM⊥y轴于M,过点F作FN⊥x轴于N,直线F的面积为 ,则 =________.(用含 的代数式表示)
9.(18成华区一诊)如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴的负半轴,y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形OA´B´C´,BC与OA´相交于点M.若经过点M的反比例函数y= (x<0)的图象交AB于点N矩形OABC的面积为S,tan∠A′OB′= ,则BN的长为。
【八年级上册数学培优竞赛-素养提升】专题09 一次函数中k、b的意义

专题09 一次函数中k 、b 的意义[专题解读]一次函数y=kx+b 中的系数k 、b 的正负性,决定图像的大致位置、y 随x 的变化情况、与坐标轴的交点坐标以及直线的倾斜程度,是研究函数图像及性质的重要依据.熟悉并掌握k 、b 的意义,可以帮助我们更深刻地理解一次函数.思维索引例1.已知关于 x 的一次函数y =(6+3m )x +(n -4). (1)当m 、n 满足什么条件时,函数图象经过原点;(2)当m 、n 满足什么条件时,函数图象与y 轴的交点在x 轴下方;(3)当m 、n 满足什么条件时,y 随着x 的增大而减小,且不经过第三象限; (4)当m 、n 满足什么条件时,函数的图象平行于直线y =3x -3;(5)若n =2m ,则不论m 取何实数这个函数的图象都过定点,试求这个定点的坐标.答案:(1) m≠-2, n=4; (2) m≠-2, n<4; (3) m<-2,n≥4; (4) m=-1, n≠1; (5)( 32,-8)例2.如图,直线y =(m +1)x +2(m -1) (m 为常数)与x 轴交于点A ,与y 轴交于点B,△ABC 是等边三角形(其中A ,B ,C 为逆时针标注的三个点). (1)当x =-2时,求y 的值;(2)△ABC 中的AB 边不可能在第几象限?并说明理由.答案:(1) y=-4; (2) AB 不可能在第一象限素养提升1.两条直线y=ax+b 与y= bx+a 在同一直角坐标系中的图象位置可能是()A B C D2.在平面直角坐标系xOy 中,A (1, 1),B (2,2),一次函数y = -2x +b 与线段AB 有公共点,则b 的取值范围是( )A.3≤b ≤6B. 3≤b ≤4C. 1≤b ≤2D. -2≤b ≤-1答案:A3.已知一次函数y=ax-x-a +1 (a 为常数),则其函数图象一定过象限( ) A.一、二 B.二、三 C.三、四 D.一、四 答案:D4.已知直线y =(m -3)x -3m +1不经过第一象限,则m 的取值范围是( ) A. m ≥31B. m ≤31 C. 31<m <3 D. 31≤m ≤3 答案:D5.一次函数y=kx +4的图象与x 轴正半轴、y 轴分别相交于点A ,B ,将△AOB 沿直线AB 翻折,得△ACB ,若BC 所在直线解析式y 随x 的增大而减小,则k 的取值范围是( ) A. k <0 B. k <-1 C. -1<k <0 D. -1≤k <0 答案:B6.一次函数y =(m 2-3)x +(1-m )和y =(m +2)x +(m 2+m -5)的图象分别与y 轴交于点P 和Q ,这两点关于x 轴对称,则m 的值 是 答案:27.已知关于x 的一次函数y=mx +2m -7 (m≠0)在-1≤x ≤5上的函数值总是为正数,则m 的取值范围是 答案: m>78.已知一次函数y=kx+b ,当-3≤x ≤1 时,对应y 的值为1≤y ≤9,则k+b 的值为 答案: 9或19.已知一次函数y 1=kx +2 (k ≠0)和y 2=x -3. 当x <1时,y 1>y 2, 则常数k 的取值范围为 答案: -4≤k <0或0<k≤110. A (0, 1),M (3,2),动点P 从点A 出发,沿y 轴以每秒1个单位长度的速度向上移动,且过点P 的直线l : y=-x+b 也随之移动,设移动时间为t 秒,当t =______时,点M 关于l 的对称点落在坐标轴上.答案: t=1或211.已知一次函数y=(4m+1)x-(m+1).(1)m为何值时,y随x的增大而增大?(2)m为何值时,图象经过第二、三、四象限?(3)m为何值时,与直线y=-3x+2平行?答案:(1)m>-14;(2)-1<m<-14;(3)m=-1.12.若两个一次函数y=k1x+b1(k1≠0),y=k2x+b2(k2≠0),则称函数y=(k1+k2)x+b1b2为这两个函数的组合函数.(1)一次函数y=3x+2与y=-4x+3的组合函数为 .(2)若一次函数y=ax-2,y=-x+b的组合函数为y=3x+2,求a,b的值;(3)若一次函数y=-x+b与y=kx-3的组合函数的图象不经过第三象限,求k、b的取值范围.答案:(1)y=-x+6;(2)a=4,b=-1;(3)k<1,b≤0.13.已知关于x的一次函数为y=(m-2)x+6.(1)若函数y随x增大而增大,求m的取值范围;(2)当一2≤x≤4时,y≤10,求m的取值范围.答案:(1)m>2;(2)2<m≤3或0≤m<2.14.已知关于x的一次函数y=mx+4m-2.(1)不论m取何实数这个函数的图象都过定点,试求这个定点的坐标;(2)求原点到一次函数图象的最大值.答案:(1)(-4,-2);(2).15.在平面直角坐标系xOy中,点A(0,4),B(3,0),以AB为边在第一象限内作正方形ABCD(A,B,C,D按照逆时针顺序排列),直线l:y=kx+3.(1)当直线l经过D点时,求k的值;(2)当直线l与正方形有两个交点时,直接写出k的取值范围.答案:(1)k=1;(2)k>-1;16.如图,已知一次函数y=kx+3(k<0)的图象与x轴、y轴分别相交于点A、B,且0B=20A,点P(a,b)是在该函数的图象上的一点.(1)求k的值;(2)若点P到x轴、y轴的距离之和等于2,求点P的坐标;(3)设a=1-m,如果在两个实数a与b之间(不包括a和b)有且只有一个整数,求实数m的取值范围.答案:(1)k=-2;(2)P(1,1)或(53,-13):(3)-12≤m≤12,且m≠0.。
