2009年高考数学试题分类汇编——函数
2009年全国各地高考数学试题及解答分类汇编大全(03函数的性质及其应用)

2009年全国各地高考数学试题及解答分类汇编大全(03函数的性质及其应用)、选择题1 . (2009北京文、理)为了得到函数y的图像,只需把函数 10A .向左平移3个单位长度,再向上平移B .向右平移3个单位长度,再向上平移C .向左平移3个单位长度,再向下平移 1个单位长度D .向右平移3个单位长度,再向下平移 1个单位长度 1.【解析】本题主要考查函数图象的平移变换 .属于基础知识、基本运算的考查A y =lg x 3 1 =lg10 x 3 ,B . y =lg x 「3iT=lg10 x -3C .x +3 y -lg x 3 -1 一 lg 10D.x —3y =lg x -3 -1 =lg故应选C.12. (2009福建文)下列函数中,与函数 y有相同定义域的是J x1XA .f(x)=lnxB. f (x)C. f(x)=|x|D. f (x)二 ex112.解析 解析 由y可得定义域是x • 0. f (x) =ln x 的定义域x 0 ; f (x) 的定义域是xV x x丰0; f (x) =| x |的定义域是 x R ;f(x)=e x 定义域是R 。
故选A.3. (2009福建文)定义在R 上的偶函数f x 的部分图像如右图所示,则在-2,0上,下列函数中与f x 的单调性不同的是2A . y =x 1 B. y =| x | 12x 1,x — 0e x ,x _oC. y =3D . y x[x 3+1,x v 0[e ,xv03.解析解析根据偶函数在关于原点对称的区间上单调性相反, 故可知求在-2,0上单调递减,注意到要与f x 的单调性不同, 故所求的函数在 -2,0上应单调递增。
而函数 y =x 2,1在(-°°,1】上递减;函数y = x +1在(—°°,0】时单调递减;函数 y =递减,理由如下y'=3x 2>0(x<0),故函数单调递增,显然符合题意;而函数y =lg x 的图像上所有的点1个单位长度一1个单位长度 N+1,xA 0,有在―,0]上单调y'=-e"x<0(x<0),故其在(-°°,0]上单调递减,不符合题意,综上选C。
2009年新课标地区高考数学试题汇编 三角(理科)部分

2009年普通高等学校招生全国统一考试理科数学试题汇编三角部分.1.(山东3)将函数y=sin 2x 的图像向左平移4π个单位,再向上平移1个单位,所得图像的函数解析式是(A )y=cos2x (B )y=22cos x (C )y=1+sin 24x π⎛⎫+⎪⎝⎭(D )y=22sin x 【解析】:将函数sin 2y x =的图象向左平移4π个单位,得到函数sin 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选B.答案:B【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.2.(山东17)设函数()2cos(2)sin 3f x x x π=++。
(Ⅰ)求函数()f x 的最大值和最小正周期;(Ⅱ)设A ,B ,C 为ABC ∆的三个内角,若11cos ,()324c B f ==-,且C为锐角,求解: (1)f(x)=cos(2x+)+sin x.= EMBED Equation.DSMT4 所以函数f(x),最小正周期π. (2)()2c f=12C =-41,所以sin C = 因为C 为锐角, 所以3C π=ABC 中, cosB= , 所以 EMBED Equation.DSMT4 , 所以INCLUDEPICTURE "http://192.168.15.6/UpFile/UpAttachment/2009-1/2009189344.jpg" \* MERGEFORMAT INCLUDEPICTURE"http://192.168.15.6/UpFile/UpAttachment/2009-1/2009189344.jpg" \* MERGEFORMAT11sin sin()sin cos cos sin2326A B C B C B C=+=+=+⨯= .【命题立意】:本题主要考查三角函数中两角和差的弦函数公式、二倍角公式、三角函数的性质以及三角形中的三角关系.3.(福建1)函数sin2x最小值是A.??????????????????????B??sin2x??????????????????????????C??sin2x???????????????? ????????????????D????.(广东????)已知向量(sin,2)(1,cos)a bθθ=-=与.(??(2)\* MERGEFORMAT ,求 EMBED的值.解:(??)∵sin2x与sin2x互相垂直,即代又 ,∴ EMBED Equation.3 55cos,552sin==θθ.(2)∵,2πθ<<,∴10103)(sin1)cos(2=--=-ϕθϕθ,∴cosϕ3Ĭ5.汏苅4뼉函数 为常 L0,0)A ω>>在闽医해[,0]π- 上的图象如噾所焺=则EMBA EqqAt) n.DCMT4EMBEDĠÅqu ɡtion.D ]T4 032T π=,12 所䛥??13EMBE 聄??EqqationDSIT??????”ā,[解析] 考查三角函数的周期矅쯂EMBEDĠÅqu ɡtion.D ]T4 032T π=,12 所䛥??13EMBE 聄??EqqationDSIT??????”ā,14.(江苏????)设向量sin 2x ‘(??)若sin 2x 与“??ŅMBED??Eq ɵa ⁴i n D MT?????? 垂直,求sin 2x 璄值;(??!求||+b c 的朠大值; (3)若tan tan 16αβ=(求諁:∥b .[裣析]!挬小题主要考查向量的基本概念,后时考揥同角三角函数的基木关系式、京倍觚的正弦、两角岌的正弦与佑弦凬式,考查诐算和证明得基本能犛。
2009年高考数学试题分类汇编——三角函数

2009年高考数学试题分类汇编——三角函数一、选择题1.(2009年广东卷文)已知ABC ∆中,C B A ∠∠∠,,的对边分别为,,a b c 若62a c ==+且75A ∠=,则b =B .4+23C .4—23D .62- 【答案】A【解析】026sin sin 75sin(3045)sin 30cos 45sin 45cos304A +==+=+= 由62a c ==+可知,075C ∠=,所以030B ∠=,1sin 2B =由正弦定理得261sin 2sin 2264ab B A+=⋅=⨯=+,故选A2.(2009年广东卷文)函数1)4(cos 22--=πx y 是A .最小正周期为π的奇函数 B. 最小正周期为π的偶函数 C. 最小正周期为2π的奇函数 D. 最小正周期为2π的偶函数【答案】A【解析】因为22cos ()1cos 2sin 242y x x x ππ⎛⎫=--=-= ⎪⎝⎭为奇函数,22T ππ==,所以选A. 3.(2009全国卷Ⅰ理)如果函数()cos 2y x φ=3+的图像关于点43π⎛⎫⎪⎝⎭,0中心对称,那么||ϕ的最小值为(C )(A )6π (B )4π (C )3π (D) 2π解: 函数()cos 2y x φ=3+的图像关于点43π⎛⎫⎪⎝⎭,0中心对称 423k πφπ∴⋅+=42()3k k Z πφπ∴=-⋅∈由此易得min ||3πφ=.故选C 4.(2009全国卷Ⅰ理)若42x ππ<<,则函数3tan 2tan y x x =的最大值为 。
解:令tan ,x t =142x t ππ<<∴>,5.(2009浙江理)已知a 是实数,则函数()1sin f x a ax =+的图象不可能...是 ( ) 答案:D【解析】对于振幅大于1时,三角函数的周期为2,1,2T a T aππ=>∴<,而D 不符合要求,它的振幅大于1,但周期反而大于了2π.6.(2009浙江文)已知a 是实数,则函数()1sin f x a ax =+的图象不可能...是( ) D 【命题意图】此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度. 【解析】对于振幅大于1时,三角函数的周期为2,1,2T a T aππ=>∴<,而D 不符合要求,它的振幅大于1,但周期反而大于了2π. 7.(2009北京文)“6πα=”是“1cos 22α=”的 A . 充分而不必要条件 B .必要而不充分条件 C . 充分必要条件 D .既不充分也不必要条件 【答案】A【解析】本题主要考查本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查. 当6πα=时,1cos 2cos32πα==, 反之,当1cos 22α=时,有()2236k k k Z ππαπαπ=+⇒=+∈, 或()2236k k k Z ππαπαπ=-⇒=-∈,故应选A.8.(2009北京理)“2()6k k Z παπ=+∈”是“1cos 22α=”的 ( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件 【答案】A【解析】本题主要考查三角函数的基本概念、简易逻辑中充要条件的判断. 属于基础知识、基本运算的考查. 当2()6k k Z παπ=+∈时,1cos 2cos 4cos 332k ππαπ⎛⎫=+== ⎪⎝⎭,反之,当1cos 22α=时,有()2236k k k Z ππαπαπ=+⇒=+∈, 或()2236k k k Z ππαπαπ=-⇒=-∈,故应选A.9.(2009山东卷理)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A.cos 2y x =B.22cos y x = C.)42sin(1π++=x y D.22sin y x =【解析】:将函数sin 2y x =的图象向左平移4π个单位,得到函数sin 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选B.答案:B【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.10.(2009山东卷文)将函数sin 2y x =的图象向左平移4π个单位, 再向上平移1个单位,所得图象的函数解析式是( ).A. 22cos y x = B. 22sin y x = C.)42sin(1π++=x y D. cos 2y x =【解析】:将函数sin 2y x =的图象向左平移4π个单位,得到函数sin 2()4y x π=+即sin(2)cos 22y x x π=+=的图象,再向上平移1个单位,所得图象的函数解析式为21cos 22cos y x x =+=,故选A.答案:A【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.11.(2009全国卷Ⅱ文)已知△ABC 中,12cot 5A =-,则cos A = (A) 1213 (B) 513 (C) 513- (D) 1213-答案:D解析:本题考查同角三角函数关系应用能力,先由cotA=125-知A 为钝角,cosA<0排除A 和B ,再由1312cos 1cos sin ,512sin cos cot 22-==+-==A A A A A A 求得和选D 12.(2009全国卷Ⅱ文)若将函数)0)(4tan(>+=ωπωx y 的图像向右平移6π个单位长度后,与函数)6tan(πω+=x y 的图像重合,则ω的最小值为 (A)61 (B)41 (C)31(D)21答案:D解析:本题考查正切函数图像及图像平移,由平移及周期性得出ωmin =21 13.(2009安徽卷理)已知函数()3sin cos (0)f x x x ωωω=+>,()y f x =的图像与直线2y =的两个相邻交点的距离等于π,则()f x 的单调递增区间是(A )5[,],1212k k k Z ππππ-+∈ (B )511[,],1212k k k Zππππ++∈(C )[,],36k k k Z ππππ-+∈ (D )2[,],63k k k Zππππ++∈[解析]:()2sin()6f x x πω=+,由题设()f x 的周期为T π=,∴2ω=,由222262k x k πππππ-≤+≤+得,,36k x k k z ππππ-≤≤+∈,故选C14.(2009安徽卷文)设函数,其中,则导数的取值范围是A.B.C.D.【解析】21(1)sin 3x f x xθθ='=⋅⋅sin 32sin()3πθθθ=+=+520,sin()(1)2,21232f πθπθ⎤⎡⎤⎡⎤'∈∴+∈∴∈⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦,选D 。
2002009年高考数学试题汇编及2009年高考模拟试题汇编---函数与基本初等函数Ⅰ60页

第二章函数与基本初等函数I2009年高考题答案A解析函数有意义,需使e x-e」=0,其定义域为:x|x = 0?,排除C,D,又因为【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质•本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.2.(2009山东卷理)定义在R上的函数f(x)满足f(x)=丿则f( 2009)的值为解析由已知得f(_1) =|og22 =1, f(0) =0, f (1)= f(0) - f (-1)=-1,f (2) = f(1)- f(0) = -1, f (3)二f(2) - f(1)= -1 -(-1) = 0,f (4) = f(3) - f (2) =0 -(-1) =1, f(5) = f ⑷- f(3) =1, f(6) = f (5) - f (4) =0,所以函数f(x)的值以6为周期重复性出现•,所以f (2009)= f( 5)=1,故选C.【命题立意】:本题考查归纳推理以及函数的周期性和对数的运算e x+ e^3.(2009山东卷文)函数y x x的图像大致为().1. (2009山东卷理)函数y二的图像大致为( ).x -xe e2xex -xe -e2xe=1 • J2,所以当x - 0时函数为减函数e -1 ,故选A.Iog2(1 -X),x 一0f(x_1) - f (x_2),x 0A.-1B. 0答案CC.1D. 2x . x e -ee -e答案 A.解析 函数有意义,需使e x -e 」=O ,其定义域为〈x|x = O?,排除C,D,又因为_x 2x e e 1 2x1 • p ,所以当x 0时函数为减函数,故选A.e -1 e -1【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质•本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质 4.(2009全国卷I 理)函数f(X )的定义域为R ,若f (x 1与f(X-1)都是奇函数,则( )A. f (x)是偶函数 C. f(x)二 f (X 2) D. f(x 3)是奇函数答案 D解析 V f (x 1)与f(x-1)都是奇函数,.f(-x 1) - -f (x 1),f (-X -1) - -f(x-1),-函数f (x)关于点(1,0),及点(-1,0)对称,函数f (x)是周期T =2[1-(-1)]=4的周 期函数..f ( -X -14) - - f (x -1 4) , f ( -X 3) - - f (x 3),即 f (x 3)是奇函数。
2009高考试题分析(一)-函数与导数部分
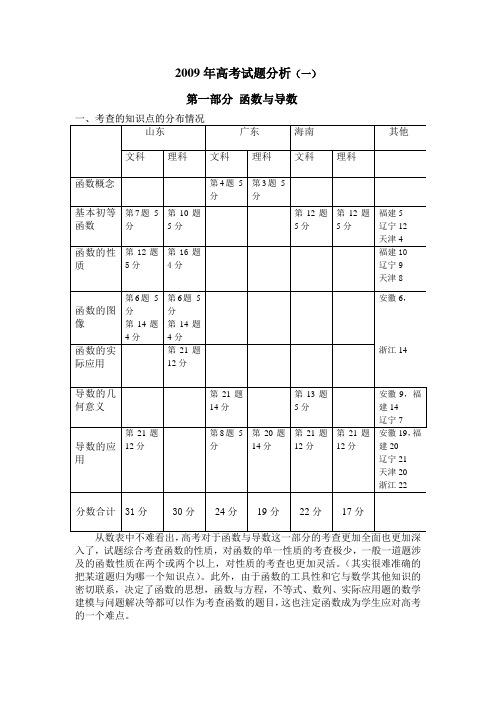
2009年高考试题分析(一)第一部分函数与导数入了,试题综合考查函数的性质,对函数的单一性质的考查极少,一般一道题涉及的函数性质在两个或两个以上,对性质的考查也更加灵活。
(其实很难准确的把某道题归为哪一个知识点)。
此外,由于函数的工具性和它与数学其他知识的密切联系,决定了函数的思想,函数与方程,不等式、数列、实际应用题的数学建模与问题解决等都可以作为考查函数的题目,这也注定函数成为学生应对高考的一个难点。
(二)考点分析考点一:函数图像----山东理科的第6题例题:(2009山东卷理)函数x xx x e e y e e--+=-的图像大致为( ).【解析】:函数有意义,需使0xxe e--≠,其定义域为{}0|≠x x ,排除C,D,又因为22212111x x x x x x x e e e y e e e e --++===+---,所以当0x >时函数为减函数,故选A.分析:【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.数学解题过程是个体的思维能力作用于数学活动的心理过程,是思维活动. 考生解题的切入点不同,运用的思想方法不同,体现出不同的思维水平. 本题的设置体现了试题很好地注意研究题目信息的配置,考虑从不同角度运用不同的思想方法,创设多条解题路径,使不同思维层次的考生都有表现的机会,从而有效地区分出考生不同的数学能力.考点二:函数性质---山东理科第10题例题:(2009山东卷理)定义在R 上的函数f(x )满足f(x)= ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ,则f (2009)的值为( )A.-1B. 0C.1D. 2【解析】:由已知得2(1)log 21f -==,(0)0f =,(1)(0)(1)1f f f =--=-,(2)(1)(0)1f f f =-=-,(3)(2)(1)1(1)0f f f =-=---=,(4)(3)(2)0(1)1f f f =-=--=,(5)(4)(3)1f f f =-=,(6)(5)(4)0f f f =-=,所以函数f(x)的值以6为周期重复性出现.,所以f (2009)= f (5)=1,故选C. 答案:C.分析:【命题立意】:本题考查归纳推理以及函数的周期性和对数的运算.本题貌似一道简单的函数求值题,实质上考查的相当有深度。
专题02 函数-十年高考(2009-)之高三数学(理)分项与解读(北京专版)

专题02 函数【考情概览】【应试策略】1.利用基本初等函数的单调性与图像:只需作出函数的图象便可判断函数在相应区间上的单调性;性质法:(1)增函数+增函数=增函数,减函数+减函数=减函数,增函数-减函数=增函数,减函数-增函数=减函数;(2)函数()f x -与函数()f x 的单调性相反; (3)0k >时,函数()f x 与()k f x 的单调性相反(()0f x ≠);0k <时,函数()f x 与()k f x 的单调性相同(()0f x ≠).2.导数法:()0f x '≥在区间D 上恒成立,则函数()f x 在区间D 上单调递增;()0f x '≤在区间D 上恒成立,则函数()f x 在区间D 上单调递减.4.定义法:作差法与作商法(常用来函数单调性的证明,一般使用作差法).【注】分段函数的单调性要求每段函数都满足原函数的整体单调性,还需注意断点处两边函数值的大小比较.2. 判断函数的奇偶性,其中包括两个必备条件:(1)定义域关于原点对称,这是函数具有奇偶性的必要不充分条件,所以首先考虑定义域; (2)判断()f x 与()f x -是否具有相等关系或者相反关系.在判断奇偶性的运算中,可以转化为判断奇偶性的等价关系式()0()f x f x +-= (奇函数)或()0()f x f x --= (偶函数)是否成立.3. 有关图象辨识问题的常见类型及解题思路(1)由实际情景探究函数图像:关键是将生活问题转化为我们熟悉的数学问题求解,但要注意实际问题中的定义域。
(2)由解析式确定函数的图象。
此类问题往往从以下几方面判断:①从函数的定义域,判断图象左右的位置,从函数的值域,判断图象的上下位置; ②从函数的单调性,判断图象的变化趋势; ③从函数的奇偶性,判断图象的对称性; ④从函数的周期性,判断图象的循环往复。
利用上述方法,排除、筛选错误或正确的选项。
4. 已知函数有零点(方程有根)求参数取值范围常用的方法(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围. (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.【真题展示】1. 【2009高考北京理第3题】为了得到函数3lg 10x y +=的图像,只需把函数lg y x =的图像上所有的点 ( )A .向左平移3个单位长度,再向上平移1个单位长度B .向右平移3个单位长度,再向上平移1个单位长度C .向左平移3个单位长度,再向下平移1个单位长度D .向右平移3个单位长度,再向下平移1个单位长度 【答案】C考点:函数图象的平移变换.2. 【2011高考北京理第6题】根据统计,一名工人组装第x 件某产品所用的时间(单位:分钟)为()x A xf x x A A<⎪⎪=⎨⎪≥⎪⎩(A ,c 为常数)。
2009年高考数学试题

2009年高考数学试题2009年高考数学试题是中国高考中的一套数学试题,该试题对考生的数学知识和解题能力进行了全面考察。
下面将对2009年高考数学试题进行逐题分析和解答,以帮助考生更好地理解和应对类似的数学考试题目。
一、选择题1. 设函数f(x) = 3x^2 + 2x - 1,若f(ax^2 - bx + 1) = 0恰好有一个实数根,则实数a和b的乘积为多少?解答:首先代入f(ax^2 - bx + 1) = 0,得到3(ax^2 - bx + 1)^2 +2(ax^2 - bx + 1) - 1 = 0。
展开并整理得到3a^2x^4 - (6ab - 2a)x^3 + (2a^2 - 2)b^2x^2 + (2a^2 - 2b - 2)x + (3a^2 + 2a - 1) = 0。
由于方程有一个实数根,根据实根系数定理可知系数a^2大于等于0,故3a^2 + 2a - 1 = 0。
解此方程得到a = 1/3或a = -1。
考虑a = 1/3的情况,将3ax^2 - bx + 1带入f(x) = 0得到3(1/3x^2 -bx + 1)^2+ 2(1/3x^2 - bx + 1) - 1 = 0,化简后得到x^2 - 9bx + 25 = 0。
由于方程有一个实数根,根据判别式可知b^2 - 4ac = (-9b)^2 - 4(1)(25) =81b^2 - 100 ≥ 0。
解此不等式得到 -10/9 ≤ b ≤ 10/9。
因此,当a = 1/3时,b的取值范围为[-10/9, 10/9]。
考虑a = -1的情况,将-3x^2 - bx + 1带入f(x) = 0得到3(-x^2 - bx + 1)^2 + 2(-x^2 - bx + 1) - 1 = 0,化简后得到x^2 + 5bx + 6 = 0。
由于方程有一个实数根,根据判别式可知b^2 - 4ac = (5b)^2 - 4(1)(6) = 25b^2 - 24≥ 0。
2009年全国各地高考数学试题及解答分类汇编大全(04导数及其应用)

x 22009年全国各地高考数学试题及解答分类汇编大全(04导数及其应用)、选择题:1. (2009安徽文、理)设a v b,函数y = (x -a)2(x -b)的图像可能是/ /2a +b1.[解析]:y = (x -a)(3x -2a -b),由 y = 0得x=a,x ,•••当 x = a 时,y 取极大值0,3当x = ------ 时y 取极小值且极小值为负。
故选C 。
3或当x ::: b 时y ::: 0,当x b 时,y . 0选C2. (2009安徽理)已知函数f(x)在R 上满足f (x) =2f (2-x)-x 2 • 8x -8,则曲线y=f(x)在点(1,f(1))处的切线方程是- (A ) y=2x-1( B ) y=x (C ) y=3x-2 ( D ) y - -2x 3 高…2.[解析]:由 f(x) =2f(2_x) _x 2 8x_8得 f(2_x) =2f(x)_(2_x)2 8(2_x)_8 , 即 2 f (x) - f (2-x) = x 2 4x-4 ,• f(x)=x 2 •f /(x)=2x ,•切线方程为y -1 =2(x -1),即 2x -y -1 =0 选 A3.(2009安徽文)设函数 f(xH Si ^x^3CO^x 2 tan :,其中[0,—],则导数「(1)的3 2 12取值范围是A. [-2,2]B.卜、2,、、3]C.[ .、. 3,2]D. [、、2,2]3.【解析】f"(1) = sin 日 x 2+75cos 日 x 乂二=sin 日+ 75cos^=2sin (日+三)3V 日乏」0,空兀I sin (日+上)壬|返,1 I f "(1)乏I V2, 2 I ,选D 。
1 12」3 2 - -兀4. (2009 福建理).^ (1 cosx)dx 等于2x 2D. ■: +2JI JI n n=(— sin—) -[ sin( )] - 二2.故选D2 2 2 2C. - -2 X[解析]■/原式=x +sin x 25. (2009广东文)函数f (x) =(x -3)e x的单调递增区间是A. -::,2B. (0, 3)C. (1,4) D. 2,::5.解:f (x) =e x (x -3)e x二(x -2)e x,令f (x) . 0 ,解得x>2,故答D。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2009年高考数学试题分类汇编——函数
一、选择题
1.(2009年广东卷文)若函数()y f x =是函数1x
y a a a =>≠(0,且)的反函数,且
(2)1f =,则()f x =
A .x 2log
B .x 21
C .x 2
1log D .22
-x 【答案】A
【解析】函数1x
y a a a =>≠(0,且)的反函数是()log a f x x =,又(2)1f =,即log 21a =,
所以,2a =,故2()log f x x =,选A.
2.(2009年广东卷文)函数x
e x x
f )3()(-=的单调递增区间是 A. )2,(-∞ B.(0,3) C.(1,4) D. ),2(+∞ 【答案】D
【解析】()()(3)(3)(2)x x
x
f x x e x e
x e
'''=-+-=-,令()0f x '>,解得2x >,故选D
6.(2009浙江文)若函数2
()()a
f x x a x
=+
∈R ,则下列结论正确的是( ) A .a ∀∈R ,()f x 在(0,)+∞上是增函数 B .a ∀∈R ,()f x 在(0,)+∞上是减函数 C .a ∃∈R ,()f x 是偶函数 D .a ∃∈R ,()f x 是奇函数
C 【命题意图】此题主要考查了全称量词与存在量词的概念和基础知识,通过对量词的考查结合函数的性质进行了交汇设问.
【解析】对于0a =时有()2
f x x =是一个偶函数
7.(2009北京文)为了得到函数3
lg
10
x y +=的图像,只需把函数lg y x =的图像上所有的点 ( )
A .向左平移3个单位长度,再向上平移1个单位长度
B .向右平移3个单位长度,再向上平移1个单位长度
C .向左平移3个单位长度,再向下平移1个单位长度
D .向右平移3个单位长度,再向下平移1个单位长度
【答案】C
【解析】本题主要考查函数图象的平移变换. 属于基础知识、基本运算的考查. A .()()lg 31lg103y x x =++=+,
B .()()lg 31lg103y x x =-+=-,
C .()3
lg 31lg 10x y x +=+-=, D .()3
lg 31lg 10
x y x -=--=.
故应选C.
11.(2009山东卷文)函数x x
x x
e e y e e
--+=-的图像大致为( ).
【解析】:函数有意义,需使0x
x
e e
--≠,其定义域为{}0|≠x x ,排除C,D,又因为
22212111
x x x x x x x e e e y e e e e --++===+---,所以当0x >时函数为减函数,故选A.
答案:A.
12. (2009山东卷文)定义在R 上的函数f(x )满足f(x)= ⎩
⎨⎧>---≤-0),2()1(0),4(log 2x x f x f x x ,则
f (3)的值为( )
A.-1
B. -2
C.1
D. 2
【解析】:由已知得2(1)log 5f -=,2(0)log 42f ==,2(1)(0)(1)2log 5f f f =--=-,
2(2)(1)(0)log 5f f f =-=-,22(3)(2)(1)log 5(2log 5)2f f f =-=---=-,故选B.
答案:B.
【命题立意】:本题考查对数函数的运算以及推理过程.
13.(2009山东卷文)已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]
D
上是增函数,则( ).
A.(25)(11)(80)f f f -<<
B. (80)(11)(25)f f f <<-
C. (11)(80)(25)f f f <<-
D. (25)(80)(11)f f f -<<
【命题立意】:本题综合考查了函数的奇偶性、单调性、周期性等性质,运用化归的数学思想和数形结合的思想解答问题.
14.(2009全国卷Ⅱ文)函数(x ≤0)的反函数是
(A )2
y x =(x ≥0) (B )2
y x =-(x ≥0) (B )2
y x =(x ≤0) (D )2
y x =-(x ≤0)
答案:B
15.(2009全国卷Ⅱ文)函数y=2
2log 2x
y x
-=+的图像 (A ) 关于原点对称 (B )关于主线y x =-对称 (C ) 关于y 轴对称 (D )关于直线y x =对称
答案:A
解析:本题考查对数函数及对称知识,由于定义域为(-2,2)关于原点对称,又f(-x)=-f(x),故函数为奇函数,图像关于原点对称,选A 。
16.(2009全国卷Ⅱ文)设2
lg ,(lg ),a e b e c ===
(A )a b c >> (B )a c b >> (C )c a b >> (D )c b a >> 答案:B
解析:本题考查对数函数的增减性,由1>lge>0,知a>b,又c=2
1
lge, 作商比较知c>b,选B 。
22.(2009江西卷文)函数y x
=的定义域为
A .[4,1]-
B .[4,0)-
C .(0,1]
D .[4,0)(0,1]-
答案:D
23.(2009江西卷文)已知函数()f x 是(,)-∞+∞上的偶函数,若对于0x ≥,都有
(2()f x f x +=),且当[0,2)x ∈时,2()log (1f x x =+),则(2008)(2009)f f -+的值
为
A .2-
B .1-
C .1
D .2
答案:C
【解析】12
22(2008)(2009)(0)(1)log log 1f f f f -+=+=+=,故选C.
25.(2009江西卷文)若存在过点(1,0)的直线与曲线3
y x =和215
94
y ax x =+-都相切,则a 等于 A .1-或25-64 B .1-或214 C .74-或25-64 D .74
-或7 答案:A
【解析】设过(1,0)的直线与3
y x =相切于点300(,)x x ,所以切线方程为
320003()y x x x x -=-
即23
0032y x x x =-,又(1,0)在切线上,则00x =或032
x =-
, 当00x =时,由0y =与2
1594
y ax x =+-相切可得2564a =-,
当032x =-时,由272744y x =-与215
94
y ax x =+-相切可得1a =-,所以选A .
30.(2009天津卷文)设函数⎩⎨⎧<+≥+-=0
,60
,64)(2x x x x x x f 则不等式)1()(f x f >的解集是( )
A ),3()1,3(+∞⋃-
B ),2()1,3(+∞⋃-
C ),3()1,1(+∞⋃-
D )3,1()3,(⋃--∞
【答案】A
【考点定位】本试题考查分段函数的单调性问题的运用。
以及一元二次不等式的求解。
31.(2009天津卷文)设函数f(x)在R 上的导函数为f ’(x),且2f(x)+xf ’(x)>x 2
,x 下面的不等式在R 内恒成立的是
A 0)(>x f
B 0)(<x f
C x x f >)(
D x x f <)(
【答案】A
【解析】由已知,首先令0=x ,排除B ,D 。
然后结合已知条件排除C,得到A
【考点定位】本试题考察了导数来解决函数单调性的运用。
通过分析解析式的特点,考查了分析问题和解决问题的能力。
33.(2009四川卷文)函数)(2
1
R x y x ∈=+的反函数是
A. )0(log 12>+=x x y
B. )1)(1(log 2>-=x x y
C. )0(log 12>+-=x x y
D. )1)(1(log 2->+=x x y 【答案】C
【解析】由y x y x y x 221
log 1log 12
+-=⇒=+⇒=+,又因原函数的值域是0>y ,
∴其反函数是)0(log 12>+-=x x y
34.(2009四川卷文)已知函数)(x f 是定义在实数集R 上的不恒为零的偶函数,且对任意实数x 都有
)()1()1(x f x x xf +=+,则)2
5(f 的值是 A. 0 B. 21 C. 1 D. 2
5 【答案】A
【解析】若x ≠0,则有)(1)1(x f x
x x f +=
+,取21
-=x ,则有:
)21()21()21(2
121
1)121()21(f f f f f -=--=---
=
+-=(∵)(x f 是偶函数,则)2
1
()21(f f =- )
由此得0)2
1
(=f
于
是
,
0)21(5)21(]2
121
1[35)121(35)23(35)23(23231)12
3
()25(==+
=+==+
=+=f f f f f f f。
