复化Simpson公式
数值分析复化梯形公式,复化Simpson公式MATLAB程序

分别用复化梯形公式、复化Simpson 公式计算定积分dx e x ⎰+201,取n=2,4,8,16分别验证结果(精确值I=4.006994)。
复化梯形公式求定积分:
function I=tquad(x,y)
%复化梯形求积公式,其中,
%x 为向量,被积函数自变量的等距结点; %y 为向量,被积函数在结点处的函数值; n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同 h=(x(n)-x(1))/(n-1);
a=[1 2*ones(1,n-2) 1];
I=h/2*sum(a.*y);
复化Simpson 公式求定积分:
function I=squad(x,y)
%复化Simpson 求积公式,其中,
%x 为向量,被积函数自变量的等距结点; %y 为向量,被积函数在结点处的函数值; n=length(x);
m=length(y);
%积分自变量的结点数应与它的函数值的个数相同 if rem(n-1,2)~=0
I=tquad(x,y);
return;
end
N=(n-1)/2;
h=(x(n)-x(1))/N;
a=zeros(1,n);
for k=1:N
a(2*k-1)=a(2*k-1)+1;
a(2*k)=a(2*k)+4;
a(2*k+1)=a(2*k+1)+1;
end
I=h/6*sum(a.*y);。
复化梯形公式和复化辛普森公式的精度比较(共7页)
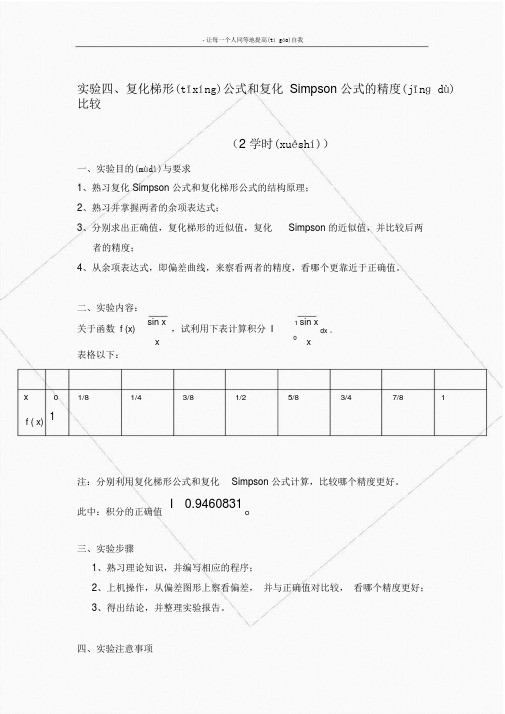
- 让每一个人同等地提高(tí gāo)自我实验四、复化梯形(tīxíng)公式和复化Simpson 公式的精度(jīnɡ dù)比较(2 学时(xuéshí))一、实验目的(mùdì)与要求1、熟习复化 Simpson 公式和复化梯形公式的结构原理;2、熟习并掌握两者的余项表达式;3、分别求出正确值,复化梯形的近似值,复化Simpson 的近似值,并比较后两者的精度;4、从余项表达式,即偏差曲线,来察看两者的精度,看哪个更靠近于正确值。
二、实验内容:关于函数 f (x) sin x,试利用下表计算积分 I 1sin xdx 。
x x表格以下:x 0 1/8 1/4 3/8 1/2 5/8 3/4 7/8 1 f ( x)1注:分别利用复化梯形公式和复化Simpson 公式计算,比较哪个精度更好。
此中:积分的正确值I0.9460831。
三、实验步骤1、熟习理论知识,并编写相应的程序;2、上机操作,从偏差图形上察看偏差,并与正确值对比较,看哪个精度更好;3、得出结论,并整理实验报告。
四、实验注意事项11- 让每一个人同等地提高(tí gāo)自我1、复化梯形公式,程序主体(zhǔtǐ)部分:for n=2:10T(n)=*T(n-1)for i=1:2^(n-2);endend2、复化 Simpson 公式(gōngshì),程序主体部分:for i=1:10n=2.^ix=0:1/n:1f=sin(x)./xf(1)=1s=0for j=1:n/2s=s+f(2*j)endt=0for j=1:(n/2-1)t=t+f(2*j-1)endS(i)=1/3/n*(f(1)+4*s+2*t+f(n+1))end五.实验(shíyàn)内容复化梯形(tīxíng)公式和复化辛普森公式的引入22- 让每一个(yī ɡè)人同等地提高自我复化梯形(tīxíng)公式:T n n 1 h [ f (x k f ( x k 1 )] ;k 0 2复化辛普森公式:S n n 1 h4 f ( x 1 ) f (x k 1 )] ;[ f (x kk 0 6k2依据题意(tí yì)和复化梯形公式、复化辛普森公式的原理编写程序求解代码以下:Matlab 代码(dài mǎ)clcs=quad( 'sin(x)./x',0,1)p1=zeros(10,1);p2=zeros(10,1);for k=6:15s1=0;s2=0;x=linspace(0,1,k);y=sin(x)./x;z=(1/(2*(k-1))):(1/(k-1)):1;sz=sin(z)./z;y(1)=1;for i=1:(k-1)s1=s1+*(x(i+1)-x(i))*(y(i)+y(i+1));endfor j=1:(k-1)s2=s2+(1/6)*(x(j+1)-x(j))*(y(j)+y(j+1)+4*sz(j));endp1(k-5)=s1-s;p2(k-5)=s2-s;endp1;33- 让每一个人同等地提高(tí gāo)自我p2;s1=s+p1(4)s2=s+p2(4)format longfor k=1:length(p1)p1(k)=abs(p1(k));p2(k)=abs(p2(k));endp1p2plot(6:1:15,p1,'-r' )hold onplot(6:1:15,10000*(p2),'-c' )hold off部分(bù fen)程序结果输出:s=s1 =s2 =结果剖析1 sin( x);依据结果输出可知:积分 I dx 的正确值为: I=x44- 让每一个人同等(tóngděng)地提高自我经过复化梯形公式(gōngshì)和复化辛普森公式获得的积分值为:s1 =:s2 =;相对偏差为:S 1 I 100 4.15 10 4 ; 1I 100S 2 I 100 1.62 10 8 ; 2 I 100明显,从相对偏差可知经过辛普森公式获得(huòdé)的结果偏差小精度高。
利用复化梯形公式、复化simpson 公式计算积分

1、运用复化梯形公式、复化simpson公式计算积分
2、比较计算误差与实际误差
实验原理(算法流程图或者含注释旳源代码)
取n=2,3,…,10分别运用复化梯形公式、复化simpson公式计算积分 ,并与真值进行比较,并画出计算误差与实际误差之间旳曲线。
运用复化梯形公式旳程序代码如下:
function f=fx(x)
functionf=fx1(x)
f=x.^4;
a=0;%积分下线
b=1;%积分上线
T=[];%用来装不同n值所计算出旳成果
forn=2:10
h=(b-a)/(2*n);%步长
x=zeros(1,2*n+1);%给节点定初值
for i=1:2*n+1
x(i)=a+(i-1)*h;%给节点赋值
end
y=x.^4;%给相应节点处旳函数值赋值
实
验
结
果
分
析
及
心
得
体
会
上图是运用复化梯形公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。-0.0017是计算误差。0.0417、0.0185、0.0104、0.00670.0046、0.0034、0.0026、0.0021、0.0017是n值分别为2到10旳实际误差。
上图是运用复化simpson公式所画出旳误差。其中:红线是计算误差,‘*’号是实际误差。
t=0;
for i=1:n
t=t+h/3*(y(2*i-1)+4*y(2*i)+y(2*i+1));%运用复化simpson公式求值
end
T=[T,t];%把不同n值所计算出旳成果装入T中
end
4.3 复化求积公式

点,将新增加的分点处的函数值从求和记号中分离出来,就有:
b a
n1
n1
T2n
4n
f
(a)
2
k 1
f
(xk )
2
k 0
f
( xk 1
2
)
f
(b)
1 2
h 2
f
(a)
n1
2
k 1
f
(xk )
f
(b)
h 2
n k 0
0
1/4
例4.14 对于函数 f (x) sin x x
试用数据表应用复化梯形法计算积分
1 sin x
I ( f ) 0 x dx
2/4
x 0 1/8
解 将区间[0,1]划分为n=8等分,h=1/8, 应 2/8
用复化梯形法求得
3/8
T8
h 2
f
7
(a) 2
k 1
f
(xk )
x
k
1
)
2
f
( xk 1)]
xk
x k1
x k 1
2
b
n1
f (x)dx
xk1 f (x)dx
a
x k 0 k
4 4
xk 1 xk 6
m1 f
k0
xk
4f
(
x
k
1
)
2
f
( xk 1 )
4
4
4
称Sn为复化 Simpson公式
复化辛普森公式应用

在公路中线坐标计算中,我们通常采用切线支距公式来计算曲线上各点的坐标。
但当在不同的曲线上计算时就需用不同的计算公式,这为计算也带来不便。
在设有缓和曲线的圆曲线半径较小或是卵形曲线上的坐标计算时,如公式选用不当就会出现较大计算误差,即便是能对切线支距公式进行多项展开,也会增加计算的难度。
而用复化辛卜生公式不仅能解决不同曲线线型或直线上的坐标计算问题,而且用复化辛卜生公式计算完全是可逆的(即:可顺前进方向也可逆向计算),尤其在计算第二缓和曲线和卵形曲线时显得尤为方便。
用辛卜生公式计算坐标的精度可由人为或程序自行判断,其计算结果完全能保证坐标计算的精度要求。
因此,可以说复化辛卜生公式是一个计算公路中线坐标的万能公式。
下面本人就该公式在公路中线坐标计算中的具体应用进行实例解析。
一、复化辛卜生公式式中:H=(Z i-Z A)/n(公式2)(公式3)Zi —待求点桩号Z A—曲线元起点桩号Z B—曲线元终点桩号ρA—曲线元起点曲率ρB—曲线元终点曲率a i曲线上任意一点处切线方位角的计算方法有以下三种方法:1.利用公式(3)求得曲率代入公式(2)计算2.利用曲线元上已知起点和终点曲率用内插法求得曲率代入公式(2)计算3.利用切线角公式计算二、算例例:已知雅(安)攀(枝花)高速公路西昌西宁立交A匝道一卵形曲线(卵形曲线相关参数见图一,其计算略。
),相关设计数据见下表。
现用辛卜生公式来计算卵形曲线中桩坐标。
图一已知相关设计数据见下表:(一)由+271.881推算Zi=+223.715的坐标,n取2等分用公式(3)、公式(2)计算+247.798处曲线及方位角:ρ+247.798=1÷75+(1÷50-1÷75)(247.798-271.881) ÷(223.715-271.881)=0.01666666666666667a+247.798=71°24’18.5” +(0.016666667+1÷75)(247.798-271.881)×180÷π÷2=50°42’26.37”其它各点依次代入公式计算,结果见下表:切线方位角图示1将计算出的数据代入公式(1)求得+223.715中桩坐标如下:X=9880.438+(271.881-223.715)÷2÷6×(cos71°24’18.5”+4(cos61°37’52.22”+cos38°38’0.96”)+2cos50°42’26.37”+ cos25°24’35.99”)=9910.5975 (设计值:9910.603)Y=10100.904+(223.715-271.881)÷2÷6×(sin71°24’18.5”+4(sin61°37’52.22”+sin38°38’0.96”) +2sin50°42’26.37”+ sin25°24’35.99”)=10136.7945 (设计值:10136.791)(二)由+223.715推算Zi=+271.881的坐标,n取2等分用公式(3)计算+247.798处曲线及方位角:ρ+247.798=1÷50+(1÷75-1÷50)(247.798-223.715)÷(271.881-223.715)=.01666666666666667a+247.798=205°24’33.6”+ (0.016666667+1÷50)(247.798-223.715)×180÷π÷2=230°42’23.98”其它各点依次代入公式计算,结果见下表:切线方位角图示2X=9910.603+(271.881-223.715)÷2÷6×(cos205°24’33.6”+4(cos218°37’58.87”+cos241°37’49.83”)+2cos230°42’23.98”+ cos251°24’16.11”)=9880.4431 (设计值:9880.438)Y=10136.791+(271.881-223.715)÷2÷6×(sin205°24’33.6”+4(sin218°37’58.87”+sin241°37’49.83”)+2sin230°42’23.98”+ sin251°24’16.11”)=10100.9008 (设计值:10100.904)由上可知,利用复化辛卜生公式计算路线坐标时可顺向或逆向计算。
matlab实现复化梯形公式,复化simpson公式以及romberg积分

(一) 实验目的熟悉并掌握数值积分的方法,重要训练复化梯形公式,复化simpson 公式以及romberg 积分。
(二) 问题描述问题三数值积分椭圆周长的计算。
考虑椭圆22221x y a b+=,为计算其周长,只要计算其第一象限的长度即可.用参数方程可以表示为cos (0/2)sin x a t t y b t π=⎧≤≤⎨=⎩,计算公式为/0π⎰为计算方便,我们可以令1a =,即计算下面的积分/0π⎰/0π=⎰(/0π⎰/0a π=⎰可以归结为上面的形式)采用复化梯形公式,复化Simpson 公式以及Romberg 积分的方法计算积分/0()I b π=⎰给出通用程序,该通用程序可以计算任何一个函数在任意一个区间在给定的精度下的数值积分。
程序输出为计算出的数值积分值以及计算函数值的次数。
(三) 算法介绍首先利用给出的各迭代公式,设计程序。
在matlab 对话框中输入要计算的函数,给出区间和精度。
复化梯形的迭代公式为:;复化simpson迭代公式为:;Romberg迭代公式为:。
(四)程序对于复化梯形公式和复化simpson公式,我们放在中。
(%标记后的程序可用来把b看为变量时的算法实现)%复化梯形公式function y=jifenn(f,n,a,b) (说明:f表示任一函数,n精度,a,b为区间)fi=f(a)+f(b);h=(b-a)/n;d=1;%function f=jifen(n,a,b,c)%syms t%y=sqrt(1+(c^2-1)*cos(t)^2);%ya=subs(y,t,a);%yb=subs(y,t,b);%fi=ya+yb;for i=1:n-1x=a+i*h;fi=fi+2*f(x);d=d+1;%yx=subs(y,t,x);%fi=fi+2*yx;endf4=h/2*fi,d%复化simposon公式f1=0;f2=0;dd=1;for i=1:n-1dd=dd+1;if rem(i,2)~=0;x1=a+i*h;f1=f1+f(x1);else rem(i,2)==0;x2=a+i*h;f2=f2+f(x2) ;endendf3=(h/3)*(f(a)+4*f1+2*f2+f(b)),dd对于romberg积分,建立文件。
c.2数值积分中复化simpson公式和变步长梯形法内容

c.2数值积分中复化simpson公式和变步长梯形法内容1. 引言1.1 概述数值积分是数学领域中重要的计算方法之一,广泛应用于工程、物理、经济学等多个学科。
它通过近似求解定积分来解决无法进行解析求解的复杂函数问题。
在数值积分方法中,复化Simpson公式和变步长梯形法都是常见且有效的技术手段。
1.2 文章结构本文将围绕复化Simpson公式和变步长梯形法展开讨论,并对它们进行比较与选择。
文章主要分为引言、复化Simpson公式、变步长梯形法、两者比较与选择以及结论部分。
1.3 目的本文旨在介绍复化Simpson公式和变步长梯形法这两种数值积分方法,探讨它们的基本原理、方法步骤以及在实际应用中的优势和适用场景。
通过对比与选择这两种方法,可以为读者提供更好地理解和运用数值积分技术的指导,并为未来研究方向和改进空间提供一定参考。
2. 复化Simpson公式:2.1 基本原理:复化Simpson公式是一种数值积分方法,用于近似计算定积分的值。
它基于简单的Simpson公式,并将区间等分为若干子区间,在每个子区间上应用Simpson公式来进行积分计算。
2.2 方法步骤:下面是复化Simpson公式的具体步骤:1. 将要积分的区间[a, b]等分为n个子区间,每个子区间宽度为h。
2. 根据Simpson公式,计算每个子区间的积分值。
3. 将所有子区间的积分值相加,得到整个区间[a, b]上的近似积分值。
具体而言,对于每个子区间[x(i-1), x(i)], i从1到n,使用Simpson公式进行积分近似。
即将该子区间均匀地划分为两部分,并以梯形面积和抛物线面积来逼近曲线下面积。
然后将所有n个子区间的近似积分值相加,得到最终的数值积分结果。
2.3 应用和优势:复化Simpson公式在数学和工程领域中广泛应用于需要进行定积分计算的问题。
它的优势包括:1. 相比于简单的Simpson公式,复化Simpson公式可以更准确地近似计算定积分的值。
复化梯形公式和复化Simpson公式

数值计算方法上机题目3一、计算定积分的近似值:221x e xe dx =⎰ 要求:(1)若用复化梯形公式和复化Simpson 公式计算,要求误差限71021-⨯=ε,分别利用他们的余项估计对每种算法做出步长的事前估计;(2)分别利用复化梯形公式和复化Simpson 公式计算定积分;(3)将计算结果与精确解比较,并比较两种算法的计算量。
1.复化梯形公式程序:程序1(求f (x )的n 阶导数:syms xf=x*exp(x) %定义函数f (x )n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n 阶导数结果1输入n=2f2 =2*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(2*exp(x) + x*exp(x))','x') %定义f(x)的二阶导数,输入程序1里求出的f2即可。
f3='-(2*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,以便求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的二阶导数的最小值点,也就是求二阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/12*((b-a)/n)^2*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hTn1=0for k=1:n-1 %求连加和xk=a+k*hTn1=Tn1+f(xk)endTn=h/2*((f(a)+2*Tn1+f(b)))z=exp(2)R=Tn-z %求已知值与计算值的差fprintf('用复化梯形算法计算的结果 Tn=')disp(Tn)fprintf('等分数 n=')disp(n) %输出等分数fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用复化梯形算法计算的结果 Tn= 7.3891等分数 n=7019已知值与计算值的误差 R= 2.8300e-0082. Simpson公式程序:程序1:(求f(x)的n阶导数):syms xf=x*exp(x) %定义函数f(x)n=input('输入所求导数阶数:')f2=diff(f,x,n) %求f(x)的n阶导数结果1输入n=4f2 =4*exp(x) + x*exp(x)程序2:clcclearsyms x%定义自变量xf=inline('x*exp(x)','x') %定义函数f(x)=x*exp(x),换函数时只需换该函数表达式即可f2=inline('(4*exp(x) + x*exp(x))','x') %定义f(x)的四阶导数,输入程序1里求出的f2即可f3='-(4*exp(x) + x*exp(x))'%因fminbnd()函数求的是表达式的最小值,且要求表达式带引号,故取负号,一边求最大值e=5*10^(-8) %精度要求值a=1 %积分下限b=2 %积分上限x1=fminbnd(f3,1,2) %求负的四阶导数的最小值点,也就是求四阶导数的最大值点对应的x值for n=2:1000000 %求等分数nRn=-(b-a)/180*((b-a)/(2*n))^4*f2(x1) %计算余项if abs(Rn)<e %用余项进行判断break% 符合要求时结束endendh=(b-a)/n %求hSn1=0Sn2=0for k=0:n-1 %求两组连加和xk=a+k*hxk1=xk+h/2Sn1=Sn1+f(xk1)Sn2=Sn2+f(xk)endSn=h/6*(f(a)+4*Sn1+2*(Sn2-f(a))+f(b)) %因Sn2多加了k=0时的值,故减去f(a)z=exp(2)R=Sn-z %求已知值与计算值的差fprintf('用Simpson公式计算的结果 Sn=')disp(Sn)fprintf('等分数 n=')disp(n)fprintf('已知值与计算值的误差 R=')disp(R)输出结果显示:用Simpson公式计算的结果 Sn= 7.3891等分数 n=24已知值与计算值的误差 R= 2.7284e-008用复化梯形公式计算的结果为:7.3891,与精确解的误差为:2.8300e-008。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012-2013(1)专业课程实践论文
复化Simpson公式
肖云龙,0818180214,R数学08-2班
Simpson 公式是一个数值积分公式,在计算一些多项式函数(三次或三次一下)的定积分时会得出精确值。
但容易验证它对于)(x f =4x 通常是不准确的,因此,Simpson 公式实际上具有三次代数精度。
提高阶的途径并不总能取得满意的效果。
为了改善求积的精度,通常采用复化求积法。
Simpson 公式
)]()2
(4)([6b f b
a f a f a
b S +++-= 将定积分⎰=b
a dx x f I )(的积分区间],[
b a 分隔为n 等分,各节点为
n j jh a x j ,,1,0, =+= n
a
b h -=
复化梯形公式的形式
])()(2)([21
1
∑-=++=n j j n b f x f a f h
T
记子区间[1,+j j x x ] 的中点为2
1+
j x
则复化Simpson 公式:
n S ])(4)(2)()((61
02
111∑∑-=+-=+++=n j j n j j x f x f b f a f h
#include<iostream.h>
#include<math.h>
double function(double x)
{ double s;
s=x/(4+x*x);
return s;
}
double ReiterationOfSimpson(double a,double b,double n,double f(double x)) { double h,fa,fb,xk,xj;
h=(b-a)/n;
fa=f(a);
fb=f(b);
double s1=0.0;
double s2=0.0;
for(int k=1;k<n;k++)
{ xk=a+k*h;
s1=s1+f(xk);}
for(int j=0;j<n;j++)
{ xj=a+(j+0.5)*h;
s2=s2+f(xj);}
double sn;
sn=h/6*(fa+fb+2*s1+4*s2);
return sn;
}
main()
{
double a,b,Result,n;
cout<<"请输入积分下限:"<<endl;
cin>>a;
cout<<"请输入积分上限:"<<endl;
cin>>b;
cout<<"请输入分割区间数n:"<<endl;
cin>>n;
cout<<"复化Simpson公式计算结果:";
Result=ReiterationOfSimpson(a,b,n,function);
cout<<Result<<endl;
return 0;}
例1.用Simpson 公式求积分⎰
+1
02
4x x
解:运行程序
(1) 请输入积分下限:输入a 的值为0,回车。
(2) 请输入积分上限:输入b 的值为1,回车。
(3) 请输入分割区间数n :输入n 的值为10,回车。
(4) 显示结果:复化Simpson 公式计算结果:0.111572
例2.用Simpson 公式求积分⎰1
02x
解:运行程序
(1) 请输入积分下限:输入a 的值为0,回车。
(2) 请输入积分上限:输入b 的值为1,回车。
(3) 请输入分割区间数n :输入n 的值为10,回车。
(4) 显示结果:复化Simpson 公式计算结果:0.333333。
