三角函数复习PPT优秀课件
合集下载
2024年度高中数学必修四三角函数PPT课件

建筑设计
在建筑设计中,利用三角函数计算建筑物的角度、高度和距离等 参数,确保设计的准确性和美观性。
机械设计
在机械设计中,三角函数用于计算齿轮、轴承等机械元件的尺寸和 角度,保证机械传动的精确性和稳定性。
航空航天工程
在航空航天工程中,利用三角函数分析飞行器的姿态、航向和速度 等参数,确保飞行安全。
21
2024/3/24
32
THANKS
感谢观看
2024/3/24
33
周期性、奇偶性、单调性等
解三角形
正弦定理、余弦定理及应用
29
常见题型解析及技巧点拨
01
三角函数求值问题:利 用同角关系式、诱导公 式等求解
2024/3/24
02
三角函数的图像与性质 应用:判断单调性、周 期性等
03
04
三角恒等变换的应用: 证明等式、化简表达式 等
30
解三角形问题:利用正 弦定理、余弦定理求解 边或角
易错知识点剖析及防范措施
混淆三角函数定义域和值域
注意定义域和值域的区别,避免混淆
忽视三角函数的周期性
在解题时要考虑周期性,避免漏解或 多解
2024/3/24
错误使用三角恒等变换公式
注意公式的适用条件和变形方式,避 免误用
忽视解三角形的限制条件
在解三角形时要注意边和角的限制条 件,避免得出不符合题意的解
第三象限
正弦、余弦均为负、正切为正 。
第四象限
正弦为负、余弦为正、正切为 负。
2024/3/24
7
02 三角函数诱导公 式与变换
2024/3/24
8
诱导公式及其应用
2024/3/24
诱导公式的基本形式
高三一轮复习三角函数的图像与性质精品PPT课件

三角函数的单调性与周期性
例 2 写出下列函数的单调区间及周期: (1)y=sin-2x+π3;(2)y=|tan x|.
(2)观察图象可知,y=|tan x|的增区间是kπ,kπ+π2,k∈Z,减 区间是kπ-π2,kπ,k∈Z.最小正周期:T=π.
探究提高
(1)求形如 y=Asin(ωx+φ)或 y=Acos(ωx+φ) (其中 A≠0,ω>0) 的函数的单调区间,可以通过解不等式的方法去解答.列不等 式的原则是:①把“ωx+φ (ω>0)”视为一个“整体”;②A>0 (A<0)时,所列不等式的方向与 y=sin x(x∈R),y=cos x(x∈R) 的单调区间对应的不等式方向相同(反).
三角函数的图像和性质
考纲下载 理解正弦函数,余弦函数、正切函数的图像;会用 “五点法”画正弦函数、余弦函数和函数y=Asin(ωx+ φ)的简图,理解A、ω、φ的物理意义. 了解周期函数与最小正周期的意义,会求一些简单 三角函数的周期,了解三角函数的奇偶性、单调性、对 称性,并会运用这些性质解决问题
三角函数的对称性与奇偶性
例 3 (1)已知 f(x)=sin x+ 3cos x(x∈R),函数 y=f(x+φ) |φ|≤π2的图象关于直线 x=0 对称,则 φ 的值为________. (2)如果函数 y=3cos(2x+φ)的图象关于点43π,0中心对称, 那么|φ|的最小值为________.
Learning Is Not Over. I Hope You Will Continue To Work Hard
演讲人:XXXXXX 时 间:XX年XX月XX日
1. “五点法”作图原理
在确定正弦函数y=sinx在[0, 2π]上的图象形状时,
三角函数复习 ppt PT课件

高考要求:
3 掌握两角和与两角差的正弦、余弦、 正切公式;掌握二倍角的正弦、余弦、 正切公式;通过公式的推导,了解他们 的内在联系,从而培养逻辑推理能力。 能正确运用上述公式进行简单三角函 数式的化简、求值和恒等式证明。
高考要求:
4 了解如何利用正弦线、正切线画出正弦函 数、正切函数的图像,了解利用诱导公式由正 弦函数的图像画出余弦函数的图像;并通过这 些图像了解正弦、余弦、正切函数的性质;会 用“五点法”画出正弦函数、余弦函数和 y=Asin(bx+c)的简图。
3
T 2
2
例2(04—京15)
在 ABC 中,sin A cos A 2 , AC 2, 2
AB 3, 求 tan A 的值和 ABC 的面积 . 分析:sin A cos A 2 cos( A 45 ) 2
2 cos( A 45 ) 1 , 0 A 180
在三角函数式恒等变型中,化简最常 见,其主要途径是:
(1)降低式子的次数(常用半角公式); (2)减少角的种类; (3)减少三角函数的种类。 指导思想:注重大思路,淡化小技巧。 基本方向是通过等价变形,努力造成合并、约
分和特殊角。 在运算能力上注意精算与估算结合、以图助算、
列表分析等方法。
三角函数
知识网络
角的推广
角的度量(弧度制) 三角函数线 三角函数图象
三
任意角的三角 函数的定义
诱导公式(九组)
角 函 数
的
同角三角函数基本关系式
性
两角和与差
质
(和、差、倍、半公式)
的三角函数
高考要求(考什么):
1 理解任意角的概念、弧度的意义;能正确地 进行弧度与角度的换算。
(中职)三角函数复习PPT课件

y
O
x
2k kZ
-
4
四、任意角的三角函数定义
r x2 y2
siny,cos x,tany
r
r
x
y P(x,y) 的终边 ● r
o
x
五、同角三角函数的基本关系式
平方关系:
si2 nco 2s 1商数Biblioteka 系:tan sin cos
-
5
例1.已知sinα= 4,求tanα.
5
方法指导:此类例题的结果可分为以下二种情况. (1)已知一个角的某三角函数值,又知角所在象限,有 一解. (2)已知一个角的某三角函数值,但不知角所在象限, 有两解.
(2) cos2tansin360o
-
12
第五章 三角函数复习
主 要
三角函数的相关概念
内 三角变换与求值
容
-
1
一、角的有关概念
y
1、角的概念的推广
( , )
o
的终边
的终边
正角 零角
负角 x
2、角度与弧度的互化
180
1弧度(180)57.305718, π
1 π 180
-
2
二、弧长公式
弧长公式:
l= r
R
L
α
-
3
三、终边相同的角
终边相同的角与相等角的区别 终边相同的角不一定相等,相等的角终边一定相同。
tan( ) tan
诱导公式三 sin( ) sin cos( ) cos
tan( ) tan
诱导公式四 sin( ) sin , cos( ) cos ,
tan( ) - tan .
公式记忆 (把α看成锐角)
三角函数公开课(高三复习) PPT课件 图文

(2)由S=12bcsin A=12bc·23= 43bc=5 3,得bc=20.又b= 5,知c=4.由余弦定理得a2=b2+c2-2bccos A=25+16-20= 21,故a= 21.
又由正弦定理得sin Bsin C=basin A·acsin A=bac2sin2A=2201 ×34=57.
(1)求ω的值; (2)求 f(x)在区间 π,32π 上的最大值和最小值.
[自主解答]
(1)f(x)= 3- 3sin2ωx-sin ωxcos ωx 2
= 3- 2
3·1-cos 2
2ωx-12sin
2ωx
=
3cos 2
2ωx-1sin 2
2ωx=-sin
2ωx-π 3
.
因为图像的一个对称中心到最近的对称轴的距离为π, 4
入手); (3)将已知条件代入所求式子,化简求值. 2.三角恒等变换的“五遇六想” (1)遇正切,想化弦;(2)遇多元,想消元;(3)遇差异,想联
系;(4)遇高次,想降次;(5)遇特角,想求值;(6)想消元,引辅 角.
——————————————————————
练习 1.(2013·北京高考)已知函数 f(x)=(2cos2x-1)sin 2x+ 1cos 4x. 2
(1)求三角函数的周期、单调区间、最值及判断三角函数 的奇偶性,往往是在定义域内,先化简三角函数式,尽量化 为y=Asin(ωx+φ)的形式,然后再求解.
(2)对于形如y=asin ωx+bcos ωx型的三角函数,要通过
引入辅助角化为y= a2+b2 sin(ωx+φ) cos φ= a2a+b2,
b
=cos C,求函数 f(A)的取值范围. cos B
三角函数复习绝佳PPT课件

2、已知 0, ,且sin ,cos
是方程5x2 -x- 12 =0的两个根,求 5
sin 3 + cos 3 、tan +cot
以及tan -cot的值
例3、若sin
=
m-3 m+5
,cos
=
4-2m m+5
,
2
,
,则m的取值范围?
45
44
45
cos( ) 5 ,且 (0, ),sin( ) 12
4 13
4
4 13
上式 ( 4 5 3 12) 56 5 13 5 13 65
应用:找出已知角与未知角之间的关系
例4:已知
tan 2 2
2,2
(
2
,
),求
45
4 13
44
4
求sin( )
解:
sin(
)
cos[
2
[cos(
()cos)(]co) s[s(in(4))(sin(4)]
)]
4
4
4
4
sin( ) 3 ,且 ( , 3 )cos( ) 4
关键:弦
切
练习:
1、已知tan =2,求值:
1 sin cos 2sin cos
sin cos
(3) sin 2 2cos 2 1
注:公式的正用、反用、变形、“1”的变通。
例2、已知sin
+cos
=
1, 5
0, ,求cot的值
y=tanx, x ( , ) 的反函数y=arctanx, x R
锐角三角函数练习课件.ppt
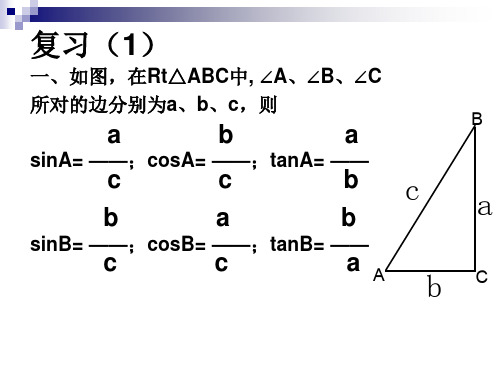
30°
1 2 3 2
3 3
3
45°
2 2
2 2
1
1
60°
3 2
1 2
3
3 3
sin A和tan A均随角度的增大而增大
cos A和cot A均随角度的增大而减小
同角三角函数的关系
⑴平方关系 sin2 A cos2 A 1
⑵商数关系 sinA
cos A
tan A cot A
cos A
s inA
⑶倒数关系 tanA cotA 1
互余两角的三角函数之间的关系
已知A为锐角, 则
sinA cos90 A
cos A sin90 A
tan A cot90 A
cot A tan90 A
1、 已知在ABC中, C 90, 设sin B n,当
B是这三角形最小的内角时,n 的取值范围是A
A.0<n< 2 B .0<n< 1
2
2
C.0<n< 3D.0<n< 3
3
2
3、 下列说法正确的是C
A.在RtABC中, 若 tan A 3 ,则a 4, b 3
4
B.在RtABC中, 若a 3, b 4,则 tan A 3
4
C.在RtABC中, C 90, 则sin 2 A sin 2 B 1
(2)2sin 60 1 1
0
3 1
(3)
1
2
4cos60sin 45 tan 60 22
2 3
(4) cos30 cot45 sin 45 cos45 sin 90 tan 60 tan 30 cot60
(5) tan2 cot2 2(0 90)
复习(1)
高三数学第二轮复习三角函数的图像与性质课件ppt.ppt

则同时具有以下两个性质的函数是( A ) ①最小正周期是π ②图象关于点(π/6,0)对称.
2.已知f(x)=sin(x+π/2),g(x)=cos(x-π/2),则下列结论
中正确的是( D) (A)函数y=f(x)·g(x)的周期为2π (B)函数y=f(x)·g(x)的最大值为1 (C)将f(x)的图象向左平移π/2单位后得g(x)的图象 (D)将f(x)的图象向右平移π/2单位后得g(x)的图象
直于 x 轴的直线, 对称中心为图象与 x 轴的交点).
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
[2k5.单+ 2调, 性2k:+y=3s2in]x(k在[Z2)k上-单2调, 2递k减+2;
](kZ)上单调递增, 在
6
是 (k ,k ],k z 使 g(x) 0 且递减的区间是
12
6
(k ,k 5 ],k z ,
6
12
∴当 0 a 1时,函数 f (x) 的递增的区间是
(k ,k 5 ],k z ,
6
12
当 a 1时,函数 f (x) 的递增的区间是 (k ,k ],k z .
且f (0) 3 , f ( ) 1 .
2 42
(1)求 f (x) 的最小正周期; (2)求 f (x) 的单调递减区间; (3)函数 f (x) 的图象经过怎样的平移才能 使所得图象对应的函数成为奇函数?
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
病原体侵入机体,消弱机体防御机能 ,破坏 机体内 环境的 相对稳 定性, 且在一 定部位 生长繁 殖,引 起不同 程度的 病理生 理过程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例9.(07江西文2)函数y= 5tan(2x+1)的最小正周期为____ . 2 解:根据函数y=Asin(x+)的最
2 小正周期为T=| | 得,函数y= 5tan(2x+1)的最小正周期T= . 2
例10.(07浙江理2)若函数f(x)= 2sin(x+),x∈R(其中>0, ||< 2 )的最小正周期是, 3 f(0)= 3 ,则=____ . 2 ,=____ 解:根据公式T= 得,=2.又 3 f(0)= 3 ,所以sin= 2 , 又||< 2 ,故= 3 .
2.同角三角函数的基本关系式(B) sin2x+cos2x=1
sin x tan x cos x
例2.(07全国Ⅰ卷(理)1) 是第四象限角,tan=-
5 1 2
,
则sin = _____________.
解:因为tan=- ,所以cos
1 2 1 2 =- 5
2 2 sin,又sin +cos =1,
2 | |
例11.(07山东理5)函数 y=sin(2x+ )+cos(2x+ )
5
2 5 所以代入得sin2= 169
.
又因为是第四象限角, 5 所以sin<0.所以sin=- 1 3 .
例2.(07全国Ⅰ卷(理)1) 是第四象限角,tan=- , 1 2 5 则sin = _________ . 13
5
3.正弦、余弦的诱导公式(B) k360+,180+,180-,- ,360-这些角的三角函数等于 角的同名函数,前面加上一个把 看成锐角时原函数值的符号. 90± .
例7.(07江苏5)函数 f(x)=sinx- 3 cosx,x∈[-,0] 的单调递增区间是________.
解法一:因为f(x)=2sin(x- 3 ), 由x∈[-,0]得 4 x- 3 ∈[- ,- ] , 3 3 所以当- 2 ≤x- 3 ≤- , 3 即- 6 ≤x≤0时,函数单调递增.所 以所求函数的单调递增区间是 [- 6 ,0].
高三《三角函数》复习
一.三角函数的主要内容 1.三角函数的图象与性质 函数y=sinx,y=cosx,y=tanx, y=Asin(x+) 的图象、对称性、定 义域、值域、单调性、奇偶性、周 期性、 最值.
2.三角恒等变形 (1) 主要公式 同角三角函数基本关系式 、 诱导公式、 两角和与差的三角函数公式 、 二倍角的三角函数公式。
解法二:f(x)=2sin(x- 由2k- 2 ≤x-
3
),
2
3
≤2k +
得2k-6 ≤x≤2k+ 与x∈[-,0]求交集得 - 6 ≤x≤0,从而所求的函数的单调 递增区间是[- , 0] . 6
5 . k ∈ Z . 6
例7.(07江苏5)函数 f(x)=sinx- 3 cosx,x∈[-,0] 的单调递增区间是 [- ,0] 6 ________.
例3.(07全国Ⅱ文1)cos330 3 = 2 _______ . 解:cos330=cos(360-30) =cos30=
3 2
例4.(07浙江文2)已知 cos( +)=
2
3 2
,且||< ,则
2
tan=_________.
解:因为cos( +)=
2
3 2
,
所以sin=- 因为||< ,
则f(x)的定义域是
{x|x∈R且x≠k+ , (k∈Z)}. 2 _________________________
例6.(06浙江文12) 函数y=2sinxcosx-1,x∈R [-2,0] 的值域是_____________ . 解: y = 2sinxcosx - 1 = sin2x - 1 , 因为sin2x∈[-1,1], 所以y=sin2x-1∈[-2,0]. 即函数y=2sinxcosx-1的 值域是[-2,0].
例5.(06北京文15(1))
1 s in 2 x 已知函数f(x)= . cos x
则f(x)的定义域是____________.
解:由cosx≠0得 x≠k+
2
, (k∈Z),
故f(x)的定义域为 {x|x∈R且x≠k+
2
, (k∈Z)}.
例5.(06北京文15(1))
1 s in 2 x 已知函数f(x)= . cos x
③任意角的三角函数 任意角的正弦、余弦、正切的 定义.单位圆,正弦、余弦、 正切的三角函数线.三角函数 的符号.
例1.(04辽宁卷1)若cos>0 ,且sin2<0,则角的终边在 四 象限. 第______ 解:由sin2<0, 得2sincos<0. 又cos>0, 所以sin<0. 因此角的终边在第四象限
(2) 变形思路
发现差异(观察角、函数、运算、 结构的差异).
寻找联系(找出差异的内在联系、
联想相关的公式). 合理转化(选择恰当的公式、 促使差异的转化).
二.考点分析与应用举例 1.三角函数的有关概念(B) ①任意角 正角,负角,零角.象限角. 终边相同的角的集合.
②弧度制 角度制.1弧度角,弧度制.弧 度与角度的换算,弧长公式, 扇形面积公式.
例8.(06江苏1)已知a∈R,函数 f(x)=sinx-|a|,x∈R为奇函数,则a 0 . =_____
解法一:因为f(x)是R上的奇函数,故f(0) =0.即0=0-|a|,故|a|=0,a=0. 解法二:因为f(x)是R上的奇函数,故对 x∈R,f(-x)=-f(x),即sin(-x)-|a|= -sinx+|a|,所以|a|=0,a=0.
2
3 2
.
1 所以cos= . 2
所以tan=- 3 .
例4.(07浙江文2)已知 cos( +)=
2
3 2
,且||< ,则
2
3 tan=______ 的图象和性质 (B) 周期函数,周期,最小正周期.图 象,五点法.定义域,值域,最值 ,单调性,奇偶性,周期性.
