边坡及挡土墙变形局部化分析
某学校边坡挡土墙破坏分析及加固

物探方法的应用[J].城市地质,2017,12(2):96101. [3] 姜志海,岳建华,刘志新.矿井瞬变电磁法在老窑水超前探
测中的应用[J].工程地球物理学报,2007,4(4):291293.
Theintegratedgeophysicalexplorationadvanced detectiontechnologyanditsapplicationundergroundcoalmine
收稿日期:20181216 作者简介:张 颖(1987),女,助理工程师; 张 磊(1985),男,助理工程师
·62·
第 45卷 第 2019年
26期月 山
第20451卷9年第 26期月
山 西 建 筑
SHANXI ARCHITECTURE
FVeobl..4 52N0o1.96
·61·
文章编号:10096825(2019)06006102
某学校边坡挡土墙破坏分析及加固
张 颖1 张 磊2
(1.邯郸市成祥房地产开发有限公司,河北 邯郸 056000; 2.中勘冶金勘察设计研究院有限责任公司,河北 保定 071069)
2 挡土墙破坏情况
挡土墙后填土区域(宽度 6.00m)上覆钢筋混凝土面层出现 大量平行于 挡 土 墙 方 向 的 裂 缝,几 近 贯 通,裂 缝 宽 度 5mm ~ 20mm,裂缝出现在离挡土墙面板 1m~2m的范围内,破除钢筋 混凝土面层后的探槽(0.5×1.0×6.5)显示,挡墙后的第 2排桩 桩顶已向外(教学楼方向)倾斜,桩顶与后缘填土间裂缝宽度已达 2cm~4cm。
Hale Waihona Puke +,-."'/
关于挡土墙施工质量问题报告最终版
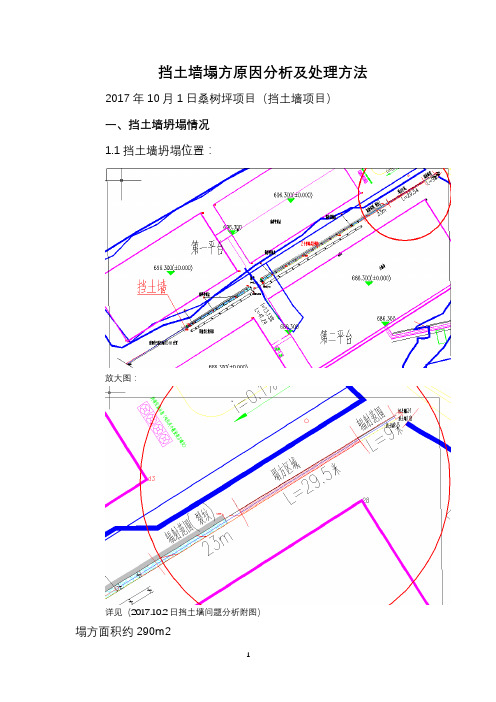
挡土墙塌方原因分析及处理方法2017年10月1日桑树坪项目(挡土墙项目)一、挡土墙坍塌情况1.1挡土墙坍塌位置:放大图:详见(2017.10.2日挡土墙问题分析附图)塌方面积约290m2塌方图片:29.5m图片一9m图片二破坏性裂纹图片三1.4、根据施工现场查看,施工挡土墙身尺寸不符合图纸要求1.5、施工现场实际倾斜度未按照图纸施工要求施工挡土墙塌方原因二、对于挡土墙出现塌方的原因分析1、根据一般规定,砂的含泥量不得大于5%,但现场施工用砂中含杂质(树皮、树根、杂草)较多,未得到认可,未清理彻底,私自使用,导致砂浆强度下降。
2、塌方部位,5m处被土覆盖,未求清理到位,多次要求清理,但未清理彻底。
造成挡土墙出现薄弱层。
影响整体性3、挡土墙虚填区,填料不密实,存在较多大碎石,间隙多,造成存水现象(如下图)该图显示的区域为挡土墙外侧,未做处理。
4、近期,雨水较多,塌方部位,地势较低,大量雨水流入该部位,塌方部位,排水管道间距(技术要求每隔2-3m设置泄水孔)未按图纸要求预留,不能满足排水要求,造成雨水渗透墙体5、挡土墙内砂浆必须包裹石头,实际施工过程中,监管不到位处,出现石头摞石头,砂浆不饱满,存在间隙。
影响挡土墙整体性6、挡土墙宽度,现场石料,均为破碎石料,当碰到大石料压到挡墙时,直接将大石块砌筑至挡土墙内,造成挡土墙内存在冲击缺口。
如:这种缺口7、挡土墙施工时未按照原设计图纸施工,(为保证第一平台宽度)原设计图坡度比为1:0.46,实际施工挡土墙坡度比1:0.1。
宽度底部2m宽,收口至1m8、该部位在8月21日发现存在的问题,未处理彻底,留下隐患(详见8月21日工程质量整改通知书)三、塌方段范围发生的事项3.1、2017.8.21在进入现场,该部位已砌筑至5m的位置,并挡土墙发现未按图纸施工,挡土墙存在较多瞎缝,孔洞,要求施工单位返工处理,将不合格工程拆除后方可进入下一道施工工序。
3.2、2017.8.22日,在桑树坪项目部将挡土墙出现的质量问题进行汇总,并组织会议(详见会议记录),施工单位对出现的问题做阐述,并表态;关于挡土墙未按图纸施工,若按图纸施工,将不能保证第一平台宽度,所有按1比0.1的坡度进行施工。
挡土墙的变形分析

挡土墙的变形分析引言:挡土墙是一种用于抵御土方压力的结构工程,广泛应用于水利、交通、建筑等领域。
然而,在挡土墙的使用过程中,由于外界环境因素和工程质量等原因,挡土墙可能会出现不同程度的变形。
本文将对挡土墙的变形进行分析,并讨论其影响因素以及相关解决方法。
一、挡土墙变形的类型及表现挡土墙的变形主要可以分为垂直变形和水平变形两种类型。
1. 垂直变形:垂直变形是指挡土墙沿垂直方向(高度方向)发生的变形。
常见的垂直变形形式包括上部挤压、下部下沉、整体沉降以及局部沉降等。
上部挤压:挡土墙顶部由于土方压力或外力作用,造成顶部向前方突出。
下部下沉:挡土墙底部由于土方压力或外力作用,造成底部向后方下沉。
整体沉降:整个挡土墙的高度下沉。
局部沉降:挡土墙某一部分出现下沉现象,常见于基础不均匀或土方压力不均匀的情况。
2. 水平变形:水平变形是指挡土墙沿水平方向(长度方向)发生的变形。
常见的水平变形形式包括整体倾斜、裂缝以及局部变形等。
整体倾斜:挡土墙整体向一侧倾斜,常见于承台坍塌或地基不均匀的情况。
裂缝:挡土墙出现裂缝,常见于土方压力过大或结构设计不合理造成的情况。
局部变形:挡土墙某一部分出现形状失真或局部倾斜等情况。
二、挡土墙变形的影响因素挡土墙的变形受到多种因素的综合影响,主要包括以下几个方面:1. 土层特性:土壤的力学性质、水含量、可塑性等因素会直接影响挡土墙的变形。
不同类型的土壤对挡土墙的变形程度有不同的影响。
2. 土压力:土方压力是导致挡土墙变形的主要原因之一。
土方压力的大小与土方的高度、重度、干湿度等因素有关。
3. 外力作用:外力作用包括交通振动、地震力、风力等因素,这些因素会给挡土墙带来额外的力学反应,增加了其变形的可能性。
4. 基础条件:挡土墙的基础条件,包括地基土的承载力、稳定性等因素,对挡土墙的变形有重要影响。
5. 结构设计:挡土墙的结构设计合理与否也是影响其变形的重要因素。
结构设计时需考虑合理的截面形状、布置钢筋等细节,以增强挡土墙的稳定性。
高边坡多级填方挡土墙的变形及受力情况分析

高边坡多级填方挡土墙的变形及受力情况分析摘要:根据对某工程现场对高边坡多级填方挡土墙的变形及受力情况进行了现场监测,通过对挡土墙的水平位移、高程位移数据、土压力和深部倾斜四种参数的初步分析,结合实际施工情况和时间、环境等其它因素的影响, 揭示了高边坡多级填方挡土墙的外部变形和内部监测数据两者之间的关联性,建设性提出了高边坡多级填方挡土墙变形及其稳定性的变化规律。
关键词: 高边坡、多级填方挡土墙、变形监测、稳定性本项目的高边坡多级填方挡土墙全长1800米,分别位于项目区南侧和东侧。
其中南侧最高处约42.1m,东侧最高处约35.75m。
挡土墙采用网箱挡土墙支护体系。
在本项目中主要监测挡土墙的水平位移、高程位移、土压力和深部倾斜四种参数。
监测点共41个,水平坐标和高程值是使用电台式遥控TCA2003分别采用极坐标法和三角高程法测得。
采用埋设于不同断面、不同深度的土压力盒的方法来获得土压力,共选择3个断面,11个位置。
深部倾斜情况主要是通过安置在不同位置的深部测斜管来获取数据来分析。
共安置7处。
1、监测内容对于高边坡多级填方挡土墙监测,主要是从应变和应力出发进行监测。
对于应变而言,主要是通过表面监测平面位移、垂直位移以及深部位移的方法来实现的。
对于应变而言,主要是通过监测埋设于挡土墙内土压力盒和深部测斜管方法来实现。
2、精度要求控制点及观测站水平位移观测精度≤±3.0mm,垂直位移观测精度≤±0.50mm。
深部测斜观测精度0.25%F.S。
表1 变形监测精度要求3、监测技术方法平面位置:变形点的坐标采用双测站极坐标法高程位置:挡土墙变形点的高程采用光电测距三角高程测量法。
土压力:选择三个断面、不同深度,共11个土压力盒,所埋位置如图1所示。
深部测斜:在边坡的分级平台处按测量深度钻孔,将在地面上连接好的测斜管下放至孔底,孔内间隙采用水泥沙浆填充。
测斜管连接时对接良好,无缝隙,接头处牢固固定、密封。
公路高边坡工程变形破坏机理分析及处治措施

公路高边坡工程变形破坏机理分析及处治措施摘要:随着我国社会经济水平的不断提升,我国交通事业发展的脚步逐渐加快,然而在进行公路施工过程中,若未能有效加固处理路基边坡,则极易出现路基边坡滑塌现象,不但威胁人们的生命安全,而且会影响公路的交通安全,对公路工程的整体施工质量造成极大的影响。
关键词:公路工程;边坡防护;措施引言在我国现代化交通运输行业发展过程中,多项大型公路工程的建设,使得交通运输效率得以快速提升,同时保障了交通运输安全性。
在公路工程建设中,边坡防护是一项关键要点,是保障车辆行驶以及公路安全的重要结构,所以需要采用科学的边坡防护技术,其中边坡绿化技术具有良好的应用效果,不仅能够提升边坡防护体系强度,还能够发挥出一定的环境保护作用。
1公路路基边坡防护设计对公路挖方路基边坡而言,裸露边坡体容易遭受自然环境影响,如雨水冲刷、水流侵蚀等,从而导致边坡表面土体失稳;同时,边坡表面会因膨胀收缩效应而产生变形,从而导致边坡体抗剪强度下降,降低边坡体稳定性。
除此之外,挖方边坡的地表水流速度较大,容易出现边坡表层土体剥落等工程病害,若采取防护措施不当,会使得防护效果适得其反。
考虑到挖方路段边坡失稳具有突发性和渐进性,若无法采取合理有效的防护措施,会导致公路路基存在安全隐患,进而影响公路正常运行。
综上,为提高公路路基设计中边坡防护方案的合理性,基于安全经济、合理有效的设计原则,设计人员应合理规划边坡设计,综合考虑多种影响因素,采用针对性防护措施,提升边坡防护技术的应用效果,降低工程成本。
同时,由于挖方路基边坡长期暴露,在风化作用下岩土结构会发生改变,严重情况下会形成滑塌等情形,因此,设计人员应做好路基边坡排水设计。
考虑到路基两侧的防护区域较大,应合理设计景观绿化方案,从而提高路基生态环境效果。
2公路路基边坡滑塌的产生原因2.1外部因素在公路路基边坡的外部,如果随意堆载,则路基边坡外部在堆载作用下将会受到很大的影响,如果路基边坡坡面的整体摩擦力、荷载力小于外力,极易导致堆载物品落下或者滑动,进而出现滑塌事故。
某工程挡墙变形原因分析及处理方法

某工程挡墙变形原因分析及处理方法付烨;肖保怀;唐家富【摘要】该文通过对出现变形外倾的某滨河浸水挡墙的水文资料、设计资料和监测资料调查以及挡墙实体检测、墙背填料勘查等,经综合分析确定了该挡墙变形外倾的主要原因.一方面,挡墙泄水孔堵塞在挡墙内外形成水位差,进而在挡墙墙背形成静水压力;另一方面,河水倒灌导致挡墙墙背填料饱和,造成抗剪强度降低、主动土压力增大.针对挡墙外倾原因提出增大泄水孔孔径、增加双反滤和对墙背填料局部注浆加固等处理措施,其经验教训可供有关工程技术人员参考.【期刊名称】《重庆建筑》【年(卷),期】2017(016)010【总页数】2页(P28-29)【关键词】浸水挡墙;挡土墙变形;反滤;泄水孔【作者】付烨;肖保怀;唐家富【作者单位】重庆市建筑科学研究院,重庆 400016;重庆市建筑科学研究院,重庆400016;重庆市建筑科学研究院,重庆 400016【正文语种】中文【中图分类】TU476+4某滨河路总长度为1619m,其中K0+223.8-K1+619段毗邻大河,位于河漫滩上。
工程所在地为山区,水文地质资料显示,河水水位受降水影响较大,水位涨降迅速。
滨河路路基宽度14m,地形标高为342.37~353.93m,设计路面高程354.7~361.1m,路基平均填高约12m,平时水位标高约为345m。
其中,K0+223.8~K1+580段左侧衡重式路肩墙设计采用C15片石混凝土,墙身平均高度15m,挡墙基础设计采用扩大基础。
中密实土卵石层段不设扩大基础,其余地段均设C20混凝土扩大基础,设计高度1.5~2.0m。
墙背填料计算内摩擦角φ=35°;墙背圬工与填料间摩擦角Φ/2(块石);墙背填料计算内摩擦角Φ=35°;填料容重21kN/m3;挡土墙稳定系数[1]:抗滑动稳定系数KC≥1.3,抗倾覆稳定系数Ko≥1.5;基底合力偏心距:土质地基不应大于B/6,岩石地基不应大于B/4。
山区软土边坡变形原因分析及治理
@
2 1 S i eh E gg 0 1 c T c. nr. .
交 通 运 输
山 区软 土 边 坡 变 形 原 因分 析 及 治 理
雷相 国 郭 一鹏 钟 艳 红 赖 正发 ’
( 云南 省 上 基 房地 产 开 发 有 限公 司 , 明 6 05 ; 明理 工 大学 建 筑 工 程学 院。 昆 明 6 0 0 昆 50 1 昆 , 5 50 中国 有 色金 属 工 业 昆 明勘 察 设 计 研究 院 , 明 60 5 ) 昆 50 1
1 工 程 概 况
昆明某 高校运 动场 区边 坡 位 于运 动 场南 侧 , 地 处昆 明断陷湖 盆地北 部 与 盆地 边缘 丘 陵 交 汇地 带 , 形成 近东西 走 向 , 总体 向北 西 倾 斜 的边 坡 , 长 约 总 2 0米 。坡 顶为昆 明某研究 所 。在运 动 场 区平 整场 8
中图 法 分 类 号
变形原 因
弱膨胀性
文 献 标 志码
治理
B
U 1 .4; 461
昆 明地 处 高 原 , 泊 , 区众 多 , 炭 、 湖 坝 泥 泥炭 质 土分布较 为广 泛 。泥炭 土 往往 与 淤 泥质 土 、 粉质
脚处 筑 以边坡 挡墙 进 行 防护 ,0 0年 6月 ~1 20 2月 ,
ma l g o i e g 9 7@ 1 3 e I 。 i:u yp n 1 8 6 . OT l
3 0期
雷相国 , : 等 山区软土边坡变形原 因分析及治理
7 6 43
图 1 边 坡 平 面
西 段 ( _,— ) 约 7 77 88 长 7m。坡 顶 标高 19 2 1 2 . ~
对高差 1 m左右 。坡顶建有 4 5 层大楼 , 墙面上出现
山区拓宽公路路基挡土墙的受力变形特征分析
山区拓宽公路路基挡土墙的受力变形特征分析摘要:信息和经济的飞速发展让我国各个地区越来越成为了一个有机的整体,这就更加要求着交通的便利和发达。
尤其是山区公路的维护和扩建更是重中之重。
山区路段的公路建设有着自己的特征和应注意的问题,同时由于严峻的自然环境使山区路面更加容易受到影响和破坏。
本文针对山区扩宽公路挡土墙路基的手力和变形进行了系统的分析和研究,在充分调研的基础上提出了在山区公路扩宽时有效保护老路基,使挡墙不至变形的方法和规律。
关键词:山区公路路基挡土墙变形特征分析前言:山区路段的研究和治理是一个新的课题,在九十年代初期我国对于公路的问题还始终偏向于建设方面,而还没有提出系统的公路改造和治理计划。
在近年才提出了对于旧公路进行维护方案。
在课题的研究过程当中我们要看到,城市的道路与山区道路的改造和扩宽所面对的难点和情况是不一样的,山区公路在扩宽时受到的阻力要更加的巨大。
1.对山区拓宽公路挡土墙路基受力变形的简单分析1.1挡土墙受力变形的基本特征我们在以往的案例当中可以了解到,公路在施工结束之后比较容易沉降的部位大多发生在两个地方:新老路基的结合处与挡墙和路基的结合处。
这和山区公路的自然环境是分不开的,由于山区自然环境当中土质相对松软,在过往汽车运输当中的碾压和施压作用下挡墙十分容易发生下沉和变形。
而在挡墙变形的现象发生当中,新建成的公路和改造的公路之间又有着很大的不同。
新建的公路最大的沉降点集中在公路地基的中部,而拓宽改建的公路下沉则显示出明显的‘勺子形态’(如图-1),会根据山体的原有走势发生变化。
也就是在以上所述的新老路基结合处和挡墙路基的结合处,所以在治理当中这两个部位成了重中之重。
图-11.2在公路改造过程当中老路基所造成的影响在山区公路的改造过程当中老路基对于工程的影响是不可忽视的。
旧公路的路堤坡度一般都是随着地形而发生变化,这就要求在拓宽公路的施工当中注意分析各个路段挡墙在不同坡度中所受的压力,计算其变形的程度。
某边坡挡土墙垮塌原因分析
3 32 主 动 土 压 力 ..
墙
根 据现场实际情况 , 土墙 高 1 墙 后土体 重度 = 挡 0 m, 1 N m , 8k / 内摩擦角 3 。 挡土墙厚 50 m 仰斜 角度为 5 , 5, 0 m, 。 上部坡度 6 。则计算 如下 。 5,
破裂角度为 :
挡 土墙 自建成 以后 , 身处 于力学平 衡状 态 , 本 当环 境情 况发生变化 时就破坏 了原有 的平衡 状态 , 一旦超过 极限状态 就会发 生破 坏。通过现场察看 , 在原有 的挡土墙 上部和 旁边 堆有 大量 的建筑 材 料 , 这使 得 挡土 墙 的受 力状 况 发生 了变
化 , 压力增大 , 土 加速 了挡 土 墙 的 破 坏 。此 外 , 土 墙 底 部 正 挡
和状态甚至积水 。当挡土墙后 的土体 达到饱 和状 态后 , 墙体
所 受 的 主 动 土 压 力 会 增 加 很 多 , 土 体 的抗 剪 强 度 会 有 大 幅 而
度 的降低 , 墙后土体有 滑坡趋 势 , 这使 得挡 土墙所 受到 的压
力更大 , 土墙达到承载力极限而破坏 。 挡
32 . 环境 分析
发生破坏。根据《 混凝土结 构设计 规范》 G 0 1 2 0 ) ( B 50 0— 02 第 7 5 3条要求 , .. 单位 长度上混凝 土的斜截面抗剪能力为 :
≤07 c h .卢ob 0 7×10 ×1 1×1 0 , 0= . . . 0×50N = 0 0
3 5 0 = 38 N 8 00 N 5k
2 计 算 模型及 材 料特 性
根据现场实 际情 况 , 以建立 如 图 1所示 的力 学模 型 。 可 其 中, 山坡 土体为砂土带 有黏 土 , 黏土 内摩 擦角 为 3 。 内 其 5,
挡土墙的变形与沉降分析
挡土墙的变形与沉降分析挡土墙是一种常用的土木工程结构,用于支撑和稳定土体。
然而,在使用过程中,经常会出现挡土墙的变形与沉降现象。
本文将就挡土墙的变形原因、沉降机制以及相应的分析方法进行深入探讨。
一、挡土墙的变形原因挡土墙的变形主要受以下几个因素的影响:1.土壤力:挡土墙作为土体的支撑结构,受到土壤力的作用。
土壤力分为主动土压力和被动土压力,两者在挡土墙的上、下部分产生了不同的压力,导致挡土墙的变形。
2.地下水位:挡土墙常常会遭遇地下水的渗透。
当地下水位升高时,会增加背后土体的湿度,从而改变土壤的力学性质,导致挡土墙产生变形。
3.挡土墙的结构:挡土墙的材料、施工方式及设计参数等因素都会影响挡土墙的变形。
如挡土墙的材料强度、抗滑抗倾参数的选取是否合理,施工中是否存在工艺不当等都会导致挡土墙的变形。
二、挡土墙的沉降机制挡土墙的沉降主要与以下几个因素相关:1.土壤压缩:土壤在受到荷载作用时会发生压缩行为,从而导致挡土墙的沉降。
土壤的压缩性受到土壤类型、含水量、固结性等因素的影响。
2.地下水位变化:地下水位的升降会直接影响土体的湿度,进而改变土壤的压缩性和承载能力。
当地下水位升高时,挡土墙常常会相应地发生沉降。
3.土体的活动性:挡土墙中的土体可能存在活动性,即土壤颗粒内部存在变形、重排和相对移动的现象。
这种土体的活动性将导致挡土墙沉降。
三、挡土墙变形与沉降的分析方法为了准确分析挡土墙的变形和沉降情况,可以采用以下方法进行:1.现场观测:通过在挡土墙周围设置测点,使用变形仪器进行监测,可以实时记录挡土墙的变形和沉降情况。
2.数值模拟:采用有限元分析等数值模拟方法,根据挡土墙的材料属性、结构参数以及施工情况,建立相应的模型,通过模拟计算得出挡土墙的变形和沉降情况。
3.实验室试验:通过室内试验,模拟挡土墙的受力情况,观察土壤的变形行为,并通过试验数据得出挡土墙的变形和沉降规律。
四、挡土墙变形与沉降的控制与预防为了有效控制挡土墙的变形和沉降,需要采取以下措施:1.合理设计:在挡土墙的设计中,需要根据具体情况合理选取墙体的参数,确保其承载能力和变形性能满足工程要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(8)
& = 0 ,由此可导出塑性乘子率表达式 f
& f T De ε f T De f + kH
&= λ
(9)
另外,考虑变形局部化时材料的大应变和有限转动效应时,当前位形下应力对空间变形率求Lie导数
2
水
2004 年 12 月
利
学
报
第 12 期
∇
SHUILI
XUEBAO
可得客观应力率,文献[6]对不同形式的客观应力率有精辟论述,Jaumann应力率 σ 通过Lie导数求得为
& + ωσ − σω T 1 2 (Lvσ 3 + Lvσ 2 ) = σ = σ
式中: σ 2 = σ j e ⊗ ei ;
i j
∇
(10a)
& −u & T )为旋率张 & 为Chauchy应力率; ω = 1 2 (u σ 3 = σ ij ei ⊗ e j ; e为坐标基矢; σ
&F −1 ,F为变形梯度。 &=F 量, u
&f (σ ) &p = λ ε
相应的加卸载条件为
(4)
&f (σ , k ) = 0 & ≥ 0 , f (σ , k ) ≤ 0 , λ λ
(5)
& 为塑性乘子率;f≡ ∂ f/ ∂ σ为屈服函数的 其中:ε为总应变;εp为塑性应变;De为材料的弹性刚度, λ
梯度,由此定义塑性流动方向。 软化损伤量κ反应塑性流动诱致材料微观结构的变化,其变化率一般与塑性应变率相关,可由以下形 式表示
由于莫尔-库仑和Druker-Prager模型比较简单,土料弹模、摩擦角、剪胀角和孔隙比在计算时被视为 常数。而事实上这些量与加荷条件、应力路径和孔隙水压力等是密切相关的,所以可应用次塑性 (Hypoplasticity)模型。该模型的基本特点在于不需人为定义屈服函数和塑性势,将弹性和塑性变形综合 在一起不区分开,它能很好体现土颗粒密度和土料结构张量随变形历史、应力状态而改变的基本性态,次 塑性的详细论述参见文献[7]。该模型相应的率表达形式为
1 非局部连续模型的基本形式及其边界条件
一般而言,非局部场变量可引入任意材料的本构模型中。在具有各向同性软化损伤内变量的标准塑性 [5] 流动理论中 ,屈服函数为以下形式 f(σ,κ)=F(σ)-σY(κ) 式中:σ为应力;κ为软化损伤量;F(σ)为等效应力;σY为当前屈服应力。 (1)
收稿日期:2003-10-14 作者简介:冯吉利(1963-),男,博士,副教授,主要研究方向为应用力学、结构材料及岩土工程。 1
k * (x ) =
Vr (x ) ∫V
1
w( x )k ( x + x )dx
(11)
式中:x为所考察点的整体坐标;为局部坐标;w为一非局部权函数;Vr称为材料特征尺度体积,
Vr ( x ) = ∫ wx dx 。
V
权函数一般用钟型函数表达:
2 2 w(x ) = 1 − x / R 0
由于式(11)为卷积形式,具体计算将以数值离散形式实现。则某点i对非局部量κ 的贡献由下式给出:
**k源自w( x − x )k (x )V (x ) = ∑ ∑ w( x − x )V
nipt i j j i nipt i j j
j
(14)
式中:nipt为积分点数;Vj为积分点特征体积;xj为积分点j处的坐标。 上面看起来似乎很简单的数值积分加权运算,在具体实现 时还得有一些比较复杂的具体问题需要解决。其中最重要的一 点是边界条件的非局部处理,在物体边界发生软化损伤后,移 动卷积核运动到此位置时,将会遇到计算上的困难,这是因为 此时在变形体当前位形下找不到与卷积核中的加权系数相对 应的全部软化损伤项。换言之,某点的特征体积不完全被包括 在变形体内,卷积核悬挂在变形体边界上,只要变形体边界出 现非线性软化损伤,这种现象就必然存在。上述问题的解决方 案有多种,本文设计了一种新的简单有效的方法,即在变形体 边界上的积分点一旦有软化损伤出现,则在该点影响域内将有 部分量是从变形体内映射复制而来,复制的量位于该积分点在 变形体内的影响域内,以便使边界上的积分点影响域是完整
图1 变形体边界上积分点的 非局部内变量影响域
的。需要强调指出,只要积分点的材料特征尺度超出变形体边界,都可用这一方式进行处理,该方法的基 本思路参见图1所示。
2 边坡和挡土墙变形破坏分析
对于将有限元法用于边坡或堤坝的稳定分析问题,已有Griffiths [10] 等 和Loukidis等 分别进行了充分论述。 对于由复杂材料和几何边界 条件组成的土工结构物,传统极限平衡法和图表法很难适用,这时有 限元法可以非常容易的针对上述结构物计算得到相应问题的安全系数 和极限载荷,而且已经证明用有限元法计算所得安全系数在相应问题 [10] 的塑性极限平衡上、下限解的范围内 。另外,有限元法可以考虑水 的孔隙压力和土的应力变形特性,而传统极限平衡法和图表法则是以 刚体作为基本前提的。
4
水
2004 年 12 月
利
学
报
第 12 期
SHUILI
XUEBAO
能直接由实验测定,但通过对实验结果逆分析可间接推得。可靠的材料参数只有通过精心设计以反映材料 非局部效应的实验进行验证。材料特征尺度测定方面的相关实验目前仍不充分,特别是有关土料特征尺度 参数测定方法和结果的报道更为缺少。从物理直观的意义出发,局部剪切过程带至少应当包括两个材料参 2 2 数即宽度和长度, 而且宽度和长度应是独立的。 断裂力学中典型的Irwin参数rp=K c/(πσ 0)便是反映弹塑 性断裂裂尖周围塑性区大小的特征尺度(其中Kc为断裂韧度,σ0为屈服应力)。行之有效的一种方法是拟合 试样名义强度的尺寸效应以确定材料的非局部特征尺度,换言之,将几何相似但具有不同尺寸的试样通过 [1] 实验来测定相应试样尺度的峰值荷载 (本文算例均按此方法反演确定土料特征尺度)。 为了检验本文所用非局部连续模型对网格 的敏感度,采用两种不同网格(单元数分别为400 和1600,采用4结点等参单元)进行计算。首先逐 步分段加载形成边坡的初始重力场,然后将所得 各点位移重新置零,接着开始模拟坡顶建筑物作 用下边坡的变形应力过程。随着外载的不断增 加,边坡沿某一部位逐渐产生软化损伤,最后形 成剪切局部化变形带,致使边坡失稳破坏,见图 3。从图3(a、c)可以发现,在非局部等效应变较 大部位可形成一条贯穿性剪切带;图3(b、d)给 出了边坡局部化破坏的可能形式和在局部、非局 部软化线性耦合条件下,非局部软化损伤的演化 方向。对非局部和局部连续模型的计算结果进行 比较后不难发现,非局部模型的结果对网格的划
图3 非局部等效塑性应变和变形演化矢量
分不敏感,因而结果显示出客观性;相反,局部连续模型应变软化随网格的精化,能量耗散趋于零,这在 物理上是不现实的(参见图4)。
图4 边坡顶部建筑物底竖向应力与竖向位移
图5 挡土墙尺寸及边界约束(单位:m)
下面检验局部与非局部连续模型计算分析挡土墙三维被动破坏问题的能力,事实上该问题可用平面问 题进行计算,这里主要是检验非局部连续模型能否在计算三维稳定破坏问题中发挥作用。挡土墙的形状尺 寸和边界约束条件如图5所示,左侧上半部水平向强制发生变形以模拟挡土墙后的土体产生被动土压力, 同样的几何尺寸用不同密度网格以检验结果对网格的敏感度。计算采用空间8结点等参单元,分别用两种 网格(1536和6566个单元)对局部连续和非局部连续模型进行计算。土本构关系采用次塑性模型,以说明非 局部连续模型对材料不同本构模型具有广泛适用性。土临界磨擦角φc=31°(如果忽略土的黏结力,可近
&= ε &p k
或软化/硬化假设
(6)
& = σ Tε & p / F (σ ) k
将流动表达式(4)代入式(6)或式(7),可得到
(7)
& = kλ & k
其中:k=‖f(σ)‖时,为应变软化;k=σ f(σ)/F(σ)时,为功软化。 在塑性屈服过程中,屈服函数必须满足等于零的条件,因此基本变量的变化率必须满足一致条件
水
2004 年 12 月
利
学
报
第 12 期
SHUILI
XUEBAO
屈服应力的演化由下列软化损伤定律表示 σY(κ)=σ0+h(κ) 式中:σ0为屈服应力;h为软化损伤函数。导数H=dh/dκ称为软化塑性模量(一般为负)。 相关联弹塑性基本方程包括弹性应力应变关系: σ=De(ε-εp) 流动法则为 (3) (2)
水
2004 年 12 月 文章编号: 0559-9350(2004)12-0021-06
利
学
报
第 12 期
SHUILI
XUEBAO
边坡及挡土墙变形局部化分析
冯吉利1,孙东亚2,丁留谦2,隋允康1
(1.北京工业大学,北京 100022;2.中国水利水电科学研究院 防洪减灾研究所,北京 100044) 摘要:本文将局部和非局部软化损伤线性结合在一起表示非局部软化损伤内变量,给出变形体边界上积分点非局 部内变量的复合映射方式。用非局部连续莫尔-库仑模型和次塑性模型(Hypoplasticity),分别对边坡和挡土墙的 变形局部化破坏过程进行了模拟分析。二维、三维有限元计算结果表明,本文采用的软化损伤内变量非局部方式 和非局部边界的处理是行之有效的,反映材料微观性态的特征尺度以统计平均的方式表达,在材料本构关系中加 以体现,所得计算结果对有限元网格的划分具有不敏感性,因而用非局部连续模型模拟土工建筑物的变形破坏过 程具有可行性。 关键词:变形局部化;软化损伤;边坡稳定;次塑性模型;有限元 中图分类号:O347 文献标识码:A
(
)
2
0≤ x ≤R R≤x
(12)
